The Engine Combustion Phasing Prediction Based on the Support Vector Regression Method
Abstract
:1. Introduction
2. Data Collection and ML Modeling
2.1. SI Engine Setup
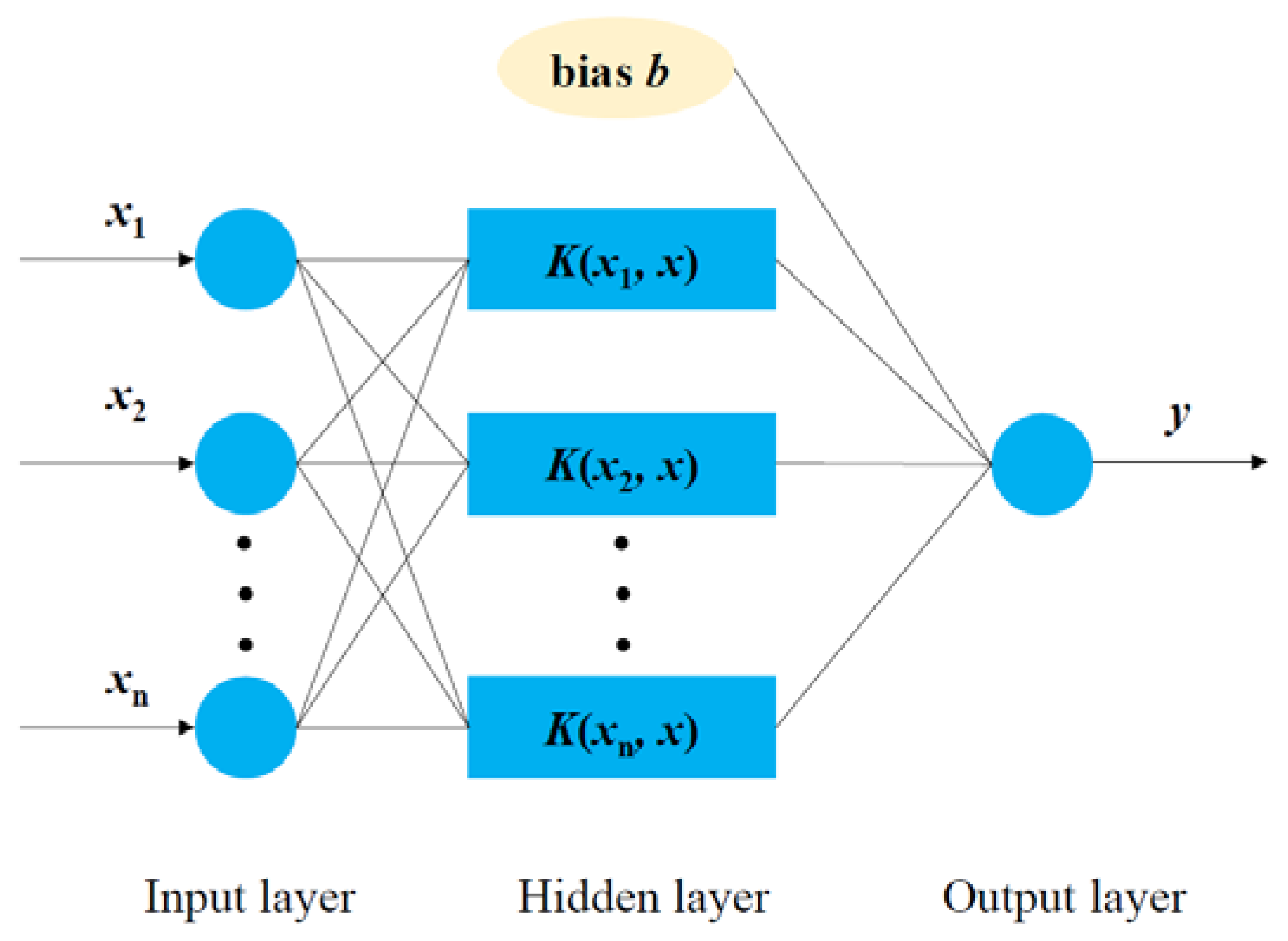
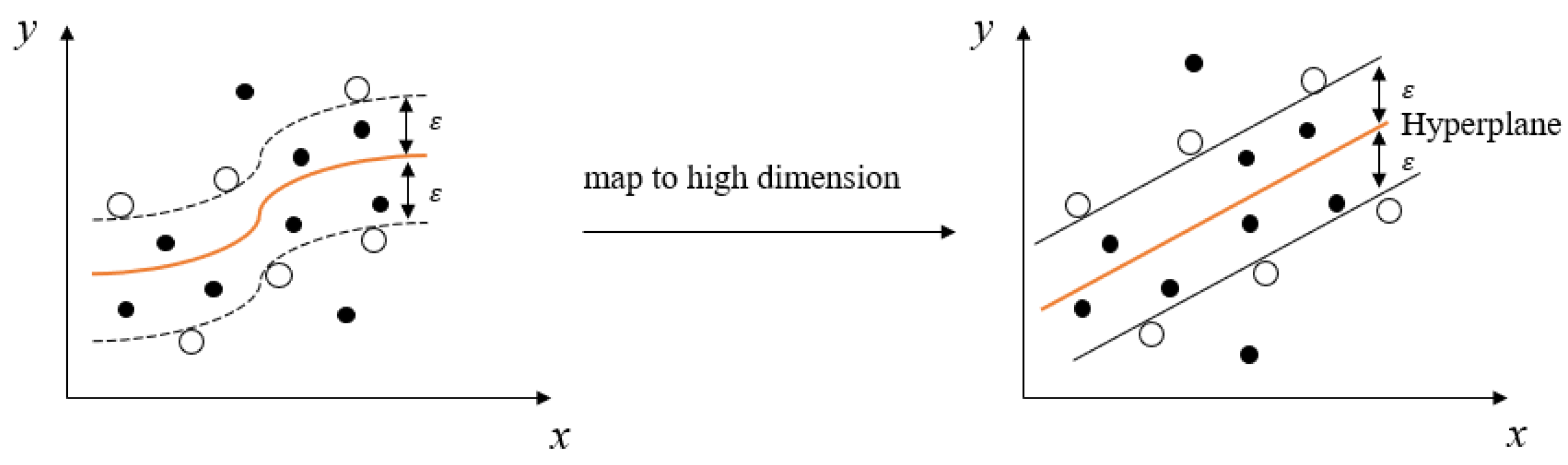
2.2. SVR Method
2.3. Gray Wolf Optimization Method
2.4. Data Processing
3. Results and Discussion
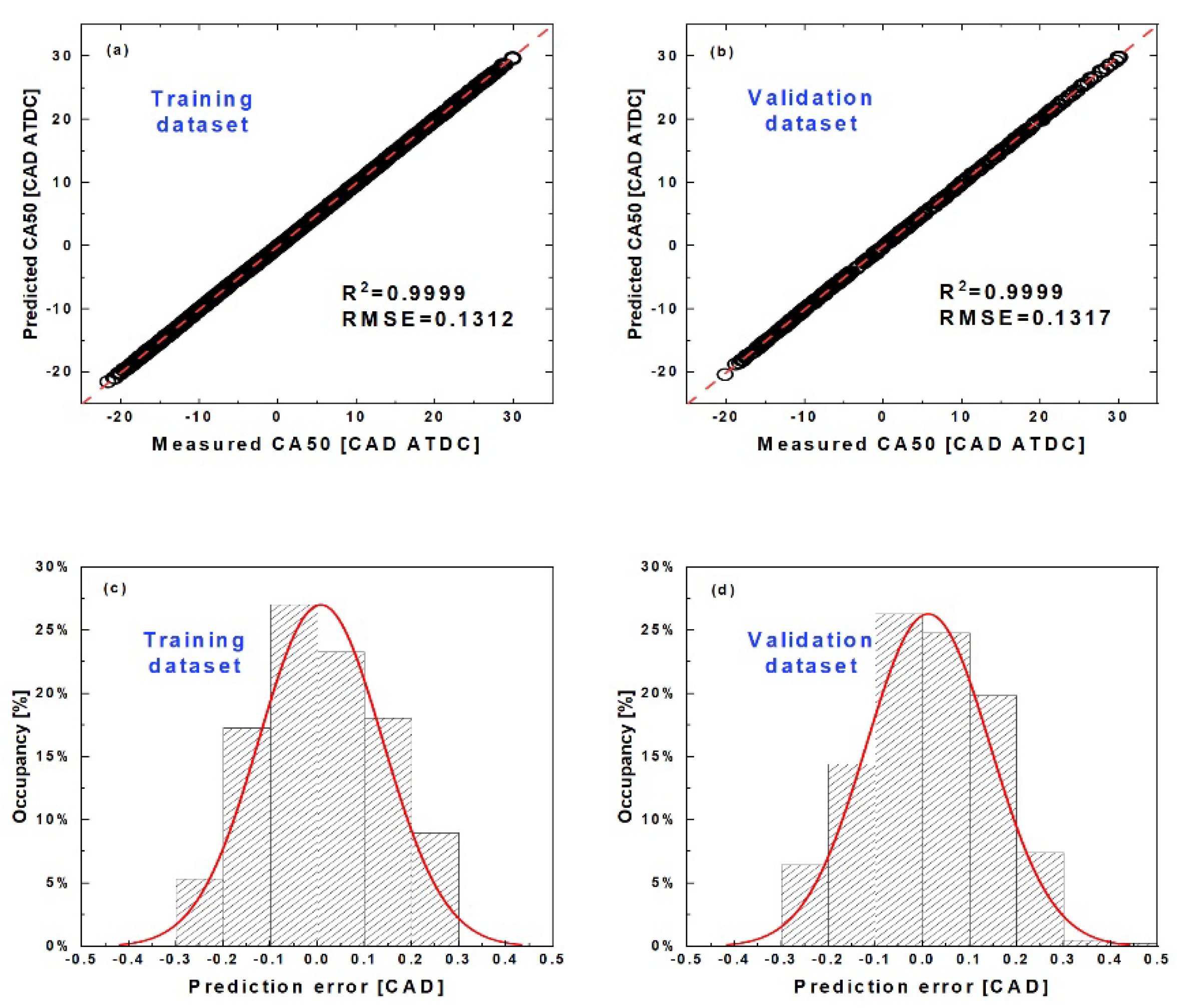
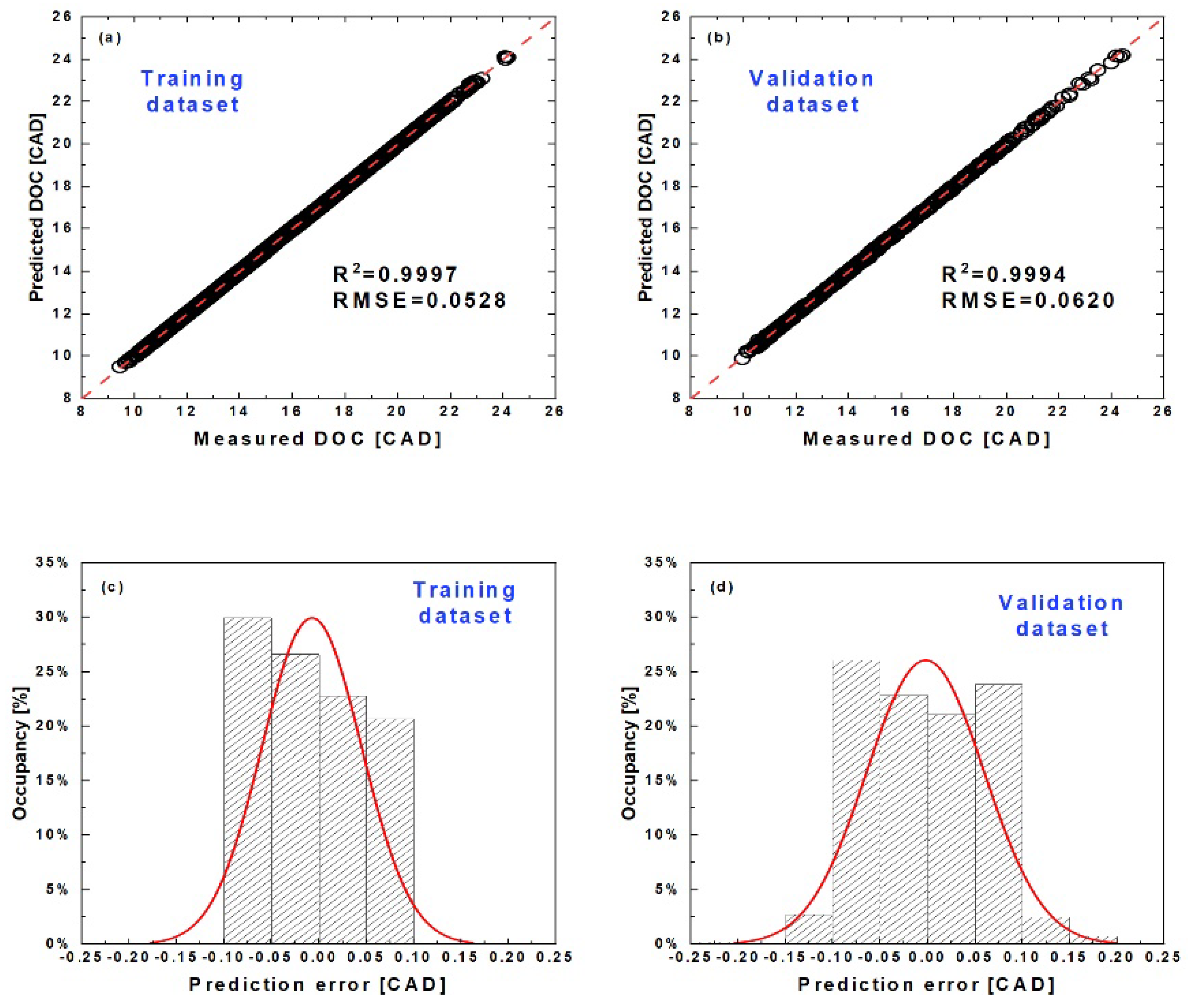
3.1. Combustion Phasing Prediction
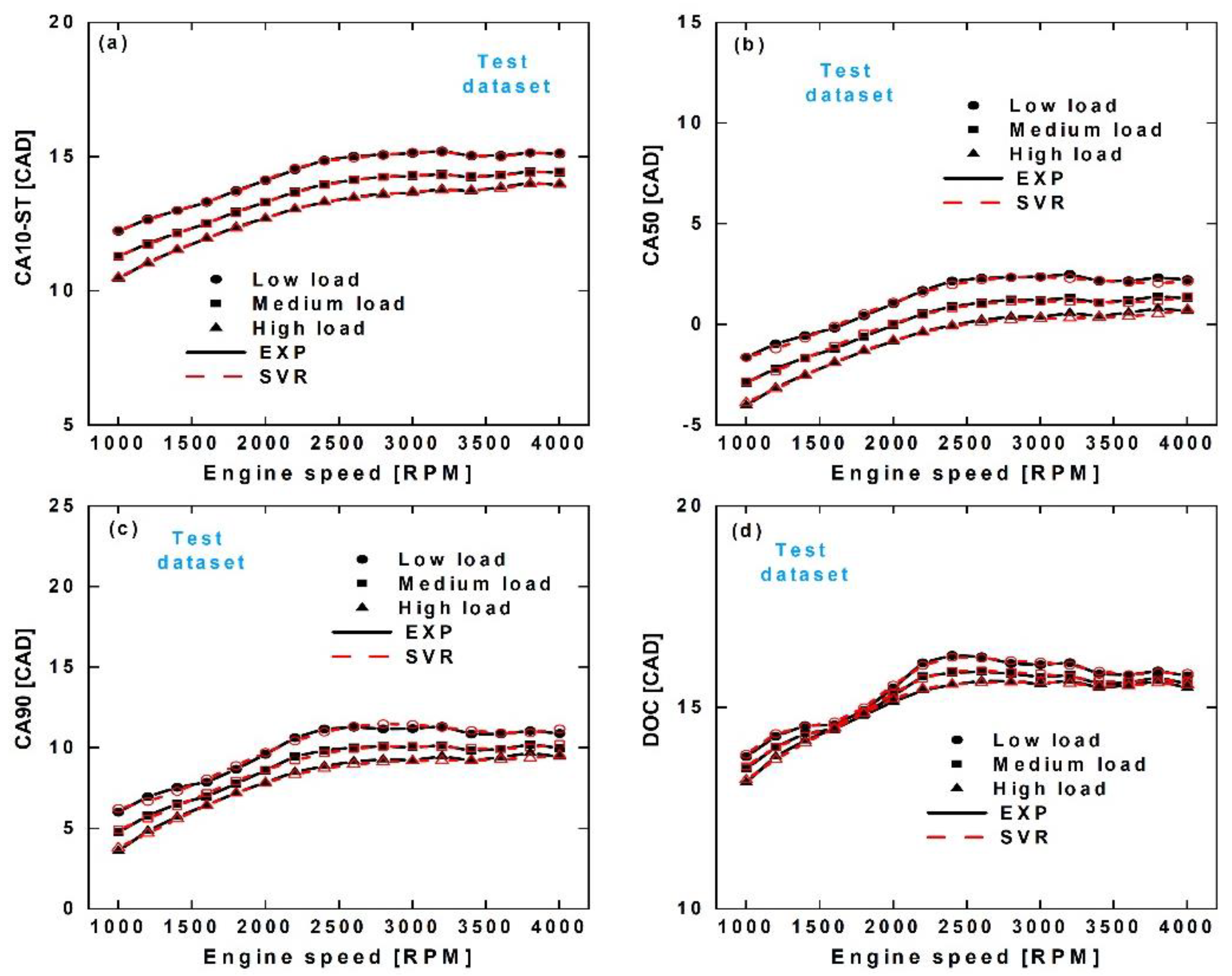
3.2. Steady-State Prediction
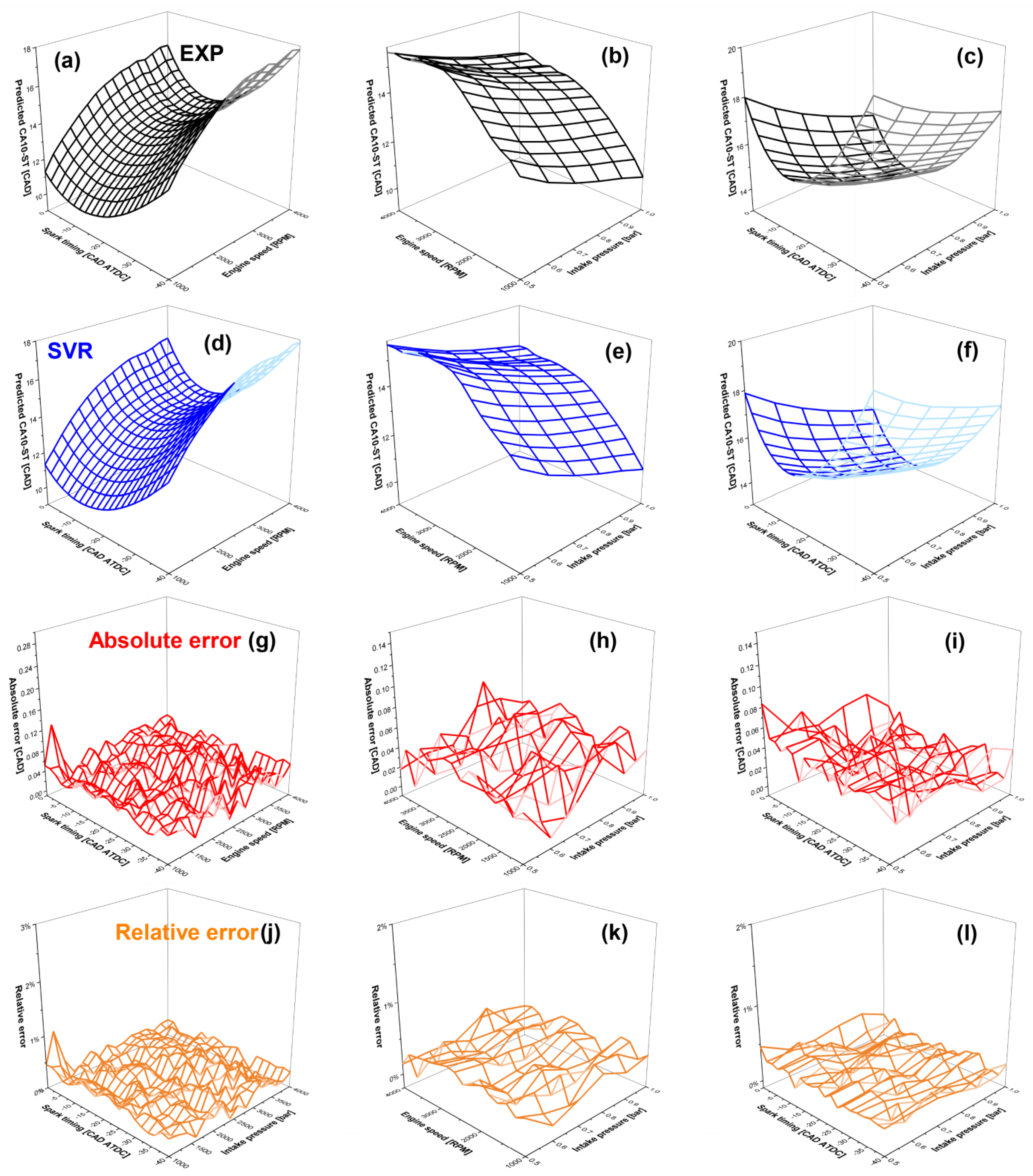
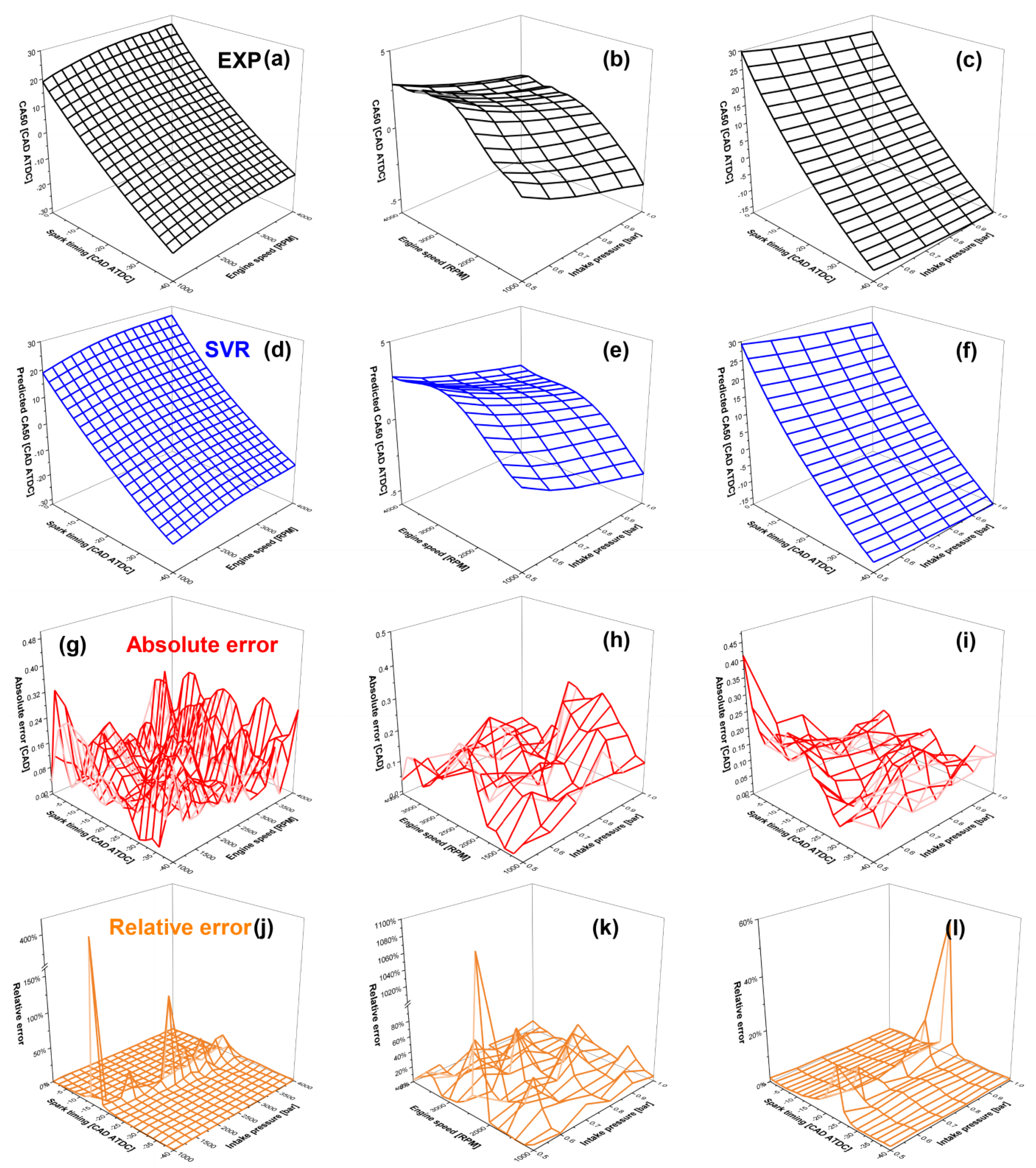
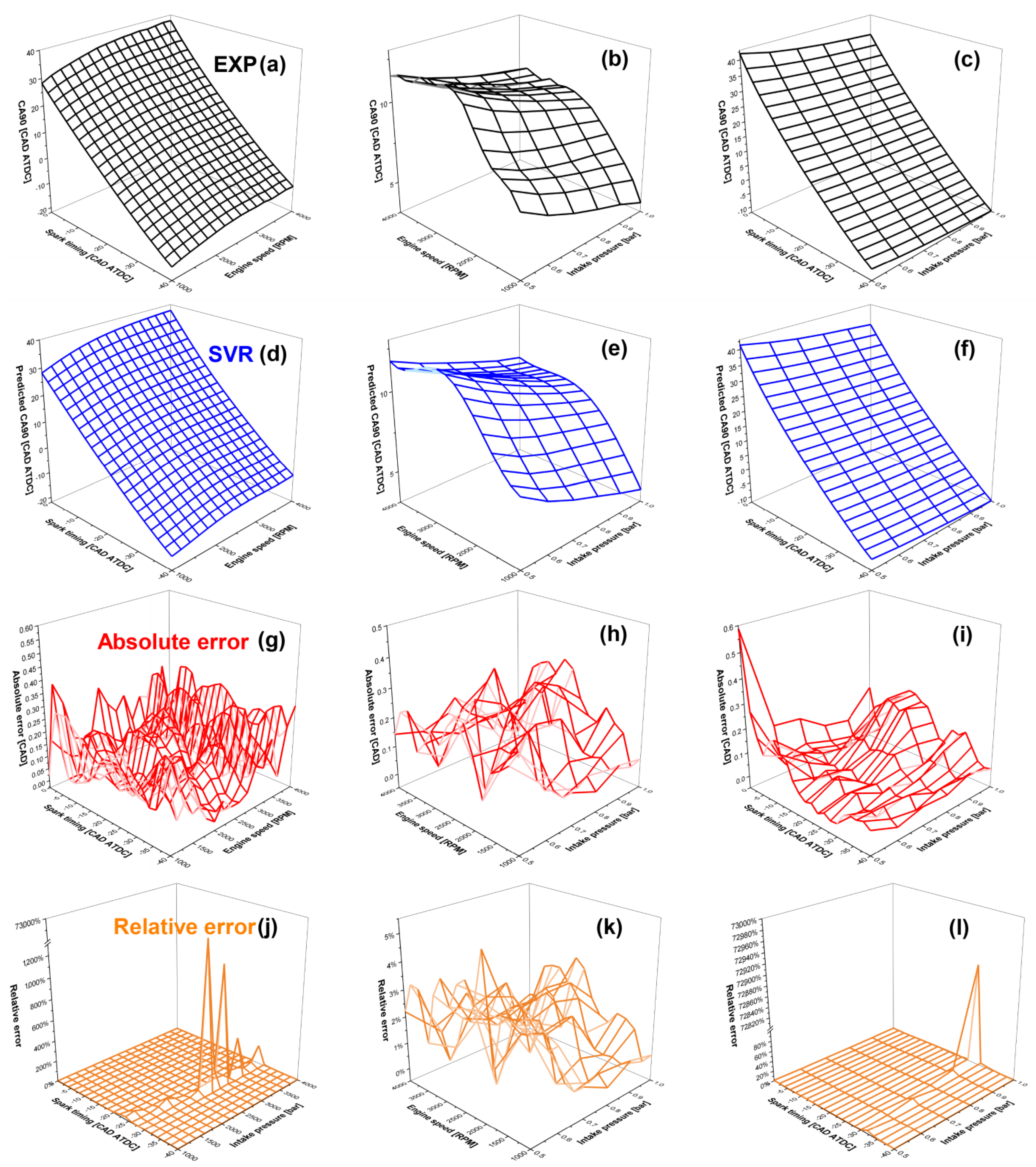
3.3. Engine Map Prediction
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABDC | After bottom dead center |
| ATDC | After top dead center |
| BBDC | Before bottom dead center |
| BMEP | Brake mean effective pressure |
| BTDC | Before top dead center |
| CA | Crank angle |
| CA10 | The crank angle where 10% of fuel has burnt |
| CA10−ST | The duration between spark timing to CA10 |
| CA50 | The crank angle where 50% of fuel has burnt |
| CA90 | The crank angle where 90% of fuel has burnt |
| CAD | Crank angle degree |
| CNN | Convolutional Neural Networks |
| DOC | The duration between CA10 to CA90 |
| ELM | Extreme learning machine |
| GWO | Gray Wolf Optimization |
| HDMR | High-dimensional input–output relationship |
| KNN | K-nearest Neighbors |
| MBT | Maximum brake torque |
| ML | Machine Learning |
| RF | Random Forest |
| SI | Spark ignition |
| SVR | Support Vector Regression |
| 0D | Zero-dimensional |
| 1D | One-dimensional |
| 3D | Three-dimensional |
References
- Bommisetty, H.; Liu, J.; Kooragayala, R.; Dumitrescu, C. Fuel Composition Effects in a CI Engine Converted to SI Natural Gas Operation; SAE Technical Paper: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Z.; Wen, M.; Cui, Y.; Ming, Z.; Wang, T.; Zhang, C.; Ampah, J.D.; Jin, C.; Huang, H.; Liu, H. Effects of Methanol Application on Carbon Emissions and Pollutant Emissions Using a Passenger Vehicle. Processes 2022, 10, 525. [Google Scholar] [CrossRef]
- Gasbarro, L.; Liu, J.; Dumitrescu, C.; Ulishney, C.; Battistoni, M.; Ambrogi, L. Heavy-Duty Compression-Ignition Engines Retro-fitted to Spark-Ignition Operation Fueled with Natural Gas; SAE Technical Paper: Warrendale, PA, USA, 2019. [Google Scholar]
- Gainey, B.; Hariharan, D.; Yan, Z.; Zilg, S.; Boldaji, M.R.; Lawler, B. A split injection of wet ethanol to enable thermally stratified compression ignition. Int. J. Engine Res. 2018, 21, 1441–1453. [Google Scholar] [CrossRef]
- Dumitrescu, C.E.; Padmanaban, V.; Liu, J. An Experimental Investigation of Early Flame Development in an Optical Spark Ignition Engine Fueled With Natural Gas. J. Eng. Gas Turbines Power 2018, 140, 082802. [Google Scholar] [CrossRef]
- Yan, Z.; Gainey, B.; Gohn, J.; Hariharan, D.; Saputo, J.; Schmidt, C.; Caliari, F.; Sampath, S.; Lawler, B. A comprehensive experimental investigation of low-temperature combustion with thick thermal barrier coatings. Energy 2021, 222, 119954. [Google Scholar] [CrossRef]
- Yan, Z.; Gainey, B.; Hariharan, D.; Lawler, B. Improving the controllability of partial fuel stratification at low boost levels by applying a double late injection strategy. Int. J. Engine Res. 2021, 22, 1101–1115. [Google Scholar] [CrossRef]
- Stocchi, I.; Liu, J.; Dumitrescu, C.E.; Battistoni, M.; Grimaldi, C.N. Effect of Piston Crevices on the Numerical Simulation of a Heavy-Duty Diesel Engine Retrofitted to Natural-Gas Spark-Ignition Operation. J. Energy Resour. Technol. 2019, 141, 1112204. [Google Scholar] [CrossRef]
- Yan, Z.; Gainey, B.; Lawler, B. A parametric modeling study of thermal barrier coatings in low-temperature combustion engines. Appl. Therm. Eng. 2021, 200, 117687. [Google Scholar] [CrossRef]
- Hairuddin, A.A.; Yusaf, T.; Wandel, A.P. A review of hydrogen and natural gas addition in diesel HCCI engines. Renew. Sustain. Energy Rev. 2014, 32, 739–761. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Yan, Y.; Yang, R.; Wang, Q.; Zhang, B.; Gan, Q.; Liu, Z.; Fu, J. Study of In-Cylinder Heat Transfer Boundary Conditions for Diesel Engines Under Variable Altitudes Based on the CHT Model. Front. Energy Res. 2022, 10, 828215. [Google Scholar] [CrossRef]
- Ambrogi, L.; Liu, J.; Battistoni, M.; Dumitrescu, C.; Gasbarro, L. CFD Investigation of the Effects of Gas’ Methane Number on the Performance of a Heavy-Duty Natural-Gas Spark-Ignition Engine; SAE Technical Paper: Warrendale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Senčić, T.; Mrzljak, V.; Medica-Viola, V.; Wolf, I. CFD Analysis of a Large Marine Engine Scavenging Process. Processes 2022, 10, 141. [Google Scholar] [CrossRef]
- Zhao, W.; Wei, H.; Jia, M.; Lu, Z.; Luo, K.H.; Chen, R.; Zhou, L. Flame–spray interaction and combustion features in split-injection spray flames under diesel engine-like conditions. Combust. Flame 2019, 210, 204–221. [Google Scholar] [CrossRef]
- Liu, J.; Ulishney, C.; Dumitrescu, C.E. Prediction of Efficient Operating Conditions Inside a Heavy-Duty Natural Gas Spark Ignition Engine Using Artificial Neural Networks. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2020; IMECE2020-23987. [Google Scholar]
- Tong, J.; Li, Y.; Liu, J.; Cheng, R.; Guan, J.; Wang, S.; Liu, S.; Hu, S.; Guo, T. Experiment analysis and computational optimization of the Atkinson cycle gasoline engine through NSGA Ⅱ algorithm using machine learning. Energy Convers. Manag. 2021, 238, 113871. [Google Scholar] [CrossRef]
- Liu, J.; Dumitrescu, C.E. Single and double Wiebe function combustion model for a heavy-duty diesel engine retrofitted to natural-gas spark-ignition. Appl. Energy 2019, 248, 95–103. [Google Scholar] [CrossRef]
- Huang, H.; Lv, D.; Zhu, J.; Zhu, Z.; Chen, Y.; Pan, Y.; Pan, M. Development of a new reduced diesel/natural gas mechanism for dual-fuel engine combustion and emission prediction. Fuel 2019, 236, 30–42. [Google Scholar] [CrossRef]
- Pan, T.; Cai, Y.; Chen, S. Development of an Engine Calibration Model Using Gaussian Process Regression. Int. J. Automot. Technol. 2021, 22, 327–334. [Google Scholar] [CrossRef]
- Millo, F.; Arya, P.; Mallamo, F.; Krope, J.; Olabi, A.G.; Goričanec, D.; Božičnik, S. Optimization of automotive diesel engine calibration using genetic algorithm techniques. Energy 2017, 158, 807–819. [Google Scholar] [CrossRef]
- Liu, J.; Ulishney, C.; Dumitrescu, C.E. Random Forest Machine Learning Model for Predicting Combustion Feedback Information of a Natural Gas Spark Ignition Engine. J. Energy Resour. Technol. 2020, 143, 012301. [Google Scholar] [CrossRef]
- Huang, Q.; Liu, J.; Ulishney, C.E.; Dumitrescu, C. On the use of artificial neural networks to model the performance and emissions of a heavy-duty natural gas spark ignition engine. Int. J. Engine Res. 2021, 14680874211034409. [Google Scholar] [CrossRef]
- Liu, J.; Huang, Q.; Ulishney, C.; Dumitrescu, C. A Support-Vector Machine Model to Predict the Dynamic Performance of a Heavy-Duty Natural Gas Spark Ignition Engine; SAE Technical Paper: Warrendale, PA, USA, 2021. [Google Scholar] [CrossRef]
- Yang, R.; Yan, Y.; Sun, X.; Wang, Q.; Zhang, Y.; Fu, J.; Liu, Z. An Artificial Neural Network Model to Predict Efficiency and Emissions of a Gasoline Engine. Processes 2022, 10, 204. [Google Scholar] [CrossRef]
- Liu, J.; Ulishney, C.; Dumitrescu, C.E. Improving machine learning model performance in predicting the indicated mean ef-fective pressure of a natural gas engine. In Internal Combustion Engine Division Fall Technical Conference; American Society of Mechanical Engineers: New York, NY, USA, 2020. [Google Scholar]
- Liu, J.; Huang, Q.; Ulishney, C.; Dumitrescu, C.E. Comparison of Random Forest and Neural Network in Modeling the Performance and Emissions of a Natural Gas Spark Ignition Engine. J. Energy Resour. Technol. 2022, 144, 032310. [Google Scholar] [CrossRef]
- Liu, J.; Huang, Q.; Ulishney, C.; Dumitrescu, C.E. Prediction of exhaust gas temperature of a natural gas spark ignition engine using machine learning methods. Int. Conf. Appl. Energy 2020, 300, 117413. [Google Scholar] [CrossRef]
- Liu, J.; Huang, Q.; Ulishney, C.; Dumitrescu, C.E. Machine learning assisted prediction of exhaust gas temperature of a heavy-duty natural gas spark ignition engine. Appl. Energy 2021, 300, 117413. [Google Scholar] [CrossRef]
- Gao, J.; Wu, Y.; Shen, T. On-line statistical combustion phase optimization and control of SI gasoline engines. Appl. Therm. Eng. 2017, 112, 1396–1407. [Google Scholar] [CrossRef]
- Caton, J.A. Combustion phasing for maximum efficiency for conventional and high efficiency engines. Energy Convers. Manag. 2014, 77, 564–576. [Google Scholar] [CrossRef]
- Yousefzadeh, A.; Jahanian, O. Using detailed chemical kinetics 3D-CFD model to investigate combustion phase of a CNG-HCCI engine according to control strategy requirements. Energy Convers. Manag. 2017, 133, 524–534. [Google Scholar] [CrossRef]
- Liu, H.; Wang, X.; Zheng, Z.; Gu, J.; Wang, H.; Yao, M. Experimental and simulation investigation of the combustion characteristics and emissions using n -butanol/biodiesel dual-fuel injection on a diesel engine. Energy 2014, 74, 741–752. [Google Scholar] [CrossRef]
- Khoa, N.X.; Lim, O. The effects of combustion duration on residual gas, effective release energy, engine power and engine emissions characteristics of the motorcycle engine. Appl. Energy 2019, 248, 54–63. [Google Scholar] [CrossRef]
- Mahdisoozani, H.; Mohsenizadeh, M.; Bahiraei, M.; Kasaeian, A.; Daneshvar, A.; Goodarzi, M.; Safaei, M.R. Performance En-hancement of Internal Combustion Engines through Vibration Control: State of the Art and Challenges. Appl. Sci. 2019, 9, 406. [Google Scholar] [CrossRef] [Green Version]
- Oh, J.; Noh, K.; Lee, C. A Theoretical Study on the Thermodynamic Cycle of Concept Engine with Miller Cycle. Processes 2021, 9, 1051. [Google Scholar] [CrossRef]
- Ranganatha Swamy, L.; Banapurmath, N.R.; Chandrashekar, T.K.; Soudagar, M.E.; Gul, M.; Nik-Ghazali, N.N.; Mujtaba, M.A.; Sha-hapurkar, K.; Ağbulut, Ü.; Alshehri, H.M.; et al. Effect of injection timing and duration on the performance of diesel engine fueled with port injection of oxygenated fuels. Chem. Eng. Commun. 2021, 1–13. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, H.; Yang, C.; Wang, Y. Development and validation of a marine sequential turbocharging diesel engine com-bustion model based on double Wiebe function and partial least squares method. Energy Convers. Manag. 2017, 151, 481–495. [Google Scholar] [CrossRef]
- Liu, J.; Ulishney, C.; Dumitrescu, C.E. Machine Learning Assisted Analysis of Heat Transfer Characteristics of a Heavy-Duty Natural Gas Engine; SAE Technical Paper: Warrendale, PA, USA, 2022. [Google Scholar]
- Liu, J.; Ulishney, C.; Dumitrescu, C.E. Comparative performance of machine learning algorithms in predicting nitrogen oxides emissions of a heavy duty natural gas spark ignition engine. Int. Conf. Appl. Energy 2021, 29, 71. [Google Scholar]
- Liu, J.; Wang, H. Machine learning assisted modeling of mixing timescale for LES/PDF of high-Karlovitz turbulent premixed combustion. Combust. Flame 2021, 238, 111895. [Google Scholar] [CrossRef]
- Wang, H.; Ji, C.; Su, T.; Shi, C.; Ge, Y.; Yang, J.; Wang, S. Comparison and implementation of machine learning models for predicting the combustion phases of hydrogen-enriched Wankel rotary engines. Fuel 2021, 310, 122371. [Google Scholar] [CrossRef]
- Yoon, M.; Lee, K.; Sunwoo, M. A method for combustion phasing control using cylinder pressure measurement in a CRDI diesel engine. Mechatronics 2007, 17, 469–479. [Google Scholar] [CrossRef]
- Robertson, D.; Prucka, R. Evaluation of control-oriented flame propagation models for production control of a spark-assisted compression ignition engine. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2021, 236, 334–342. [Google Scholar] [CrossRef]
- Blurock, E.S.; Tuner, M.; Mauss, F. Phase optimized skeletal mechanisms for engine simulations. Combust. Theory Model. 2010, 14, 295–313. [Google Scholar] [CrossRef]
- Di, H.; Zhang, Y.; Shen, T. Chaos theory-based time series analysis of in-cylinder pressure and its application in combustion control of SI engines. J. Therm. Sci. Technol. 2020, 15, JTST0001. [Google Scholar] [CrossRef] [Green Version]
- Han, W.; Sun, Z.; Scholtissek, A.; Hasse, C. Machine Learning of ignition delay times under dual-fuel engine conditions. Fuel 2020, 288, 119650. [Google Scholar] [CrossRef]
- Liu, J.; Ulishney, C.; Dumitrescu, C.E. Application of Random Forest Machine Learning Models to Forecast Combustion Profile Parameters of a Natural Gas Spark Ignition Engine. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2020; IMECE2020-23973. [Google Scholar]
- Liu, J.; Ulishney, C.; Dumitrescu, C.E. Predicting the Combustion Phasing of a Natural Gas Spark Ignition Engine Using the K-Nearest Neighbors Algorithm. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2020; IMECE2020-23982. [Google Scholar]
- Schölkopf, B.; Smola, A.J.; Williamson, R.C.; Bartlett, P.L. New Support Vector Algorithms. Neural Comput. 2000, 12, 1207–1245. [Google Scholar] [CrossRef]
- Karimipour, A.; Bagherzadeh, S.A.; Taghipour, A.; Abdollahi, A.; Safaei, M.R. A novel nonlinear regression model of SVR as a substitute for ANN to predict conductivity of MWCNT-CuO/water hybrid nanofluid based on empirical data. Phys. A Stat. Mech. Its Appl. 2019, 521, 89–97. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, Q.; Chen, X.; Yan, Y.; Yang, R.; Liu, Z.; Fu, J. The Prediction of Spark-Ignition Engine Performance and Emissions Based on the SVR Algorithm. Processes 2022, 10, 312. [Google Scholar] [CrossRef]
- Najafi, G.; Ghobadian, B.; Moosavian, A.; Yusaf, T.; Mamat, R.; Kettner, M.; Azmi, W.H. SVM and ANFIS for prediction of perfor-mance and exhaust emissions of a SI engine with gasoline–ethanol blended fuels. Appl. Therm. Eng. 2016, 95, 186–203. [Google Scholar] [CrossRef] [Green Version]
- Niu, X.; Yang, C.; Wang, H.; Wang, Y. Investigation of ANN and SVM based on limited samples for performance and emissions prediction of a CRDI-assisted marine diesel engine. Appl. Therm. Eng. 2017, 111, 1353–1364. [Google Scholar] [CrossRef]
- Shahpouri, S.; Norouzi, A.; Hayduk, C.; Rezaei, R.; Shahbakhti, M.; Koch, C.R. Hybrid Machine Learning Approaches and a Sys-tematic Model Selection Process for Predicting Soot Emissions in Compression Ignition Engines. Energies 2021, 14, 7865. [Google Scholar] [CrossRef]
- Wang, H.; Ji, C.; Shi, C.; Ge, Y.; Wang, S.; Yang, J. Development of cyclic variation prediction model of the gasoline and n-butanol rotary engines with hydrogen enrichment. Fuel 2021, 299, 120891. [Google Scholar] [CrossRef]
- Aliramezani, M.; Norouzi, A.; Koch, C.R. Support vector machine for a diesel engine performance and NOx emission control-oriented model. IFAC-PapersOnLine 2020, 53, 13976–13981. [Google Scholar] [CrossRef]
- Ji, C.; Wang, H.; Shi, C.; Wang, S.; Yang, J. Multi-objective optimization of operating parameters for a gasoline Wankel rotary engine by hydrogen enrichment. Energy Convers. Manag. 2021, 229, 113732. [Google Scholar] [CrossRef]
- Niu, X.; Wang, H.; Hu, S.; Yang, C.; Wang, Y. Multi-objective online optimization of a marine diesel engine using NSGA-II coupled with enhancing trained support vector machine. Appl. Therm. Eng. 2018, 137, 218–227. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef] [Green Version]
- Gamma Technologies. GT-SUITE Engine Performance Application Manual; Gamma Technologies: Belgrad, Serbia, 2019. [Google Scholar]
- Wei, S.; Zhang, Z.; Li, X.; Wu, C.; Yang, F. Simulation Analysis of Fuel Economy of the GDI Engine with a Miller Cycle and EGR Based on GT-Power. Processes 2022, 10, 319. [Google Scholar] [CrossRef]
- Yang, R.; Sun, X.; Liu, Z.; Zhang, Y.; Fu, J. A Numerical Study Into the Importance of Equivalence Ratio Measurement Accuracy for Spark Ignition Engines. In ASME International Mechanical Engineering Congress and Exposition; American Society of Mechanical Engineers: New York, NY, USA, 2021; IMECE2021-70992. [Google Scholar]
- Miklánek, Ľ.; Vitek, O.; Gotfryd, O.; Klir, V. Study of Unconventional Cycles (Atkinson and Miller) with Mixture Heating as a Means for the Fuel Economy Improvement of a Throttled SI Engine at Part Load. SAE Int. J. Engines 2012, 5, 1624–1636. [Google Scholar] [CrossRef]
- Gürgen, S.; Ünver, B.; Altın, I. Prediction of cyclic variability in a diesel engine fueled with n-butanol and diesel fuel blends using artificial neural network. Renew. Energy 2018, 117, 538–544. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Duan, H.; Huang, Y.; Mehra, R.K.; Song, P.; Ma, F. Study on influencing factors of prediction accuracy of support vector machine (SVM) model for NOx emission of a hydrogen enriched compressed natural gas engine. Fuel 2018, 234, 954–964. [Google Scholar] [CrossRef]
- Gordon, D.; Norouzi, A.; Blomeyer, G.; Bedei, J.; Aliramezani, M.; Andert, J.; Koch, C.R. Support vector machine based emissions modeling using particle swarm optimization for homogeneous charge compression ignition engine. Int. J. Engine Res. 2021, 14680874211055546. [Google Scholar] [CrossRef]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. (TIST) 2011, 2, 1–27. [Google Scholar] [CrossRef]
- Hao, D.; Mehra, R.K.; Luo, S.; Nie, Z.; Ren, X.; Fanhua, M. Experimental study of hydrogen enriched compressed natural gas (HCNG) engine and application of support vector machine (SVM) on prediction of engine performance at specific condition. Int. J. Hydrog. Energy 2020, 45, 5309–5325. [Google Scholar] [CrossRef]
- Liu, J.; Zhu, G.; Fu, J.; Xu, Z.; Yao, J.; Zhan, Z. Quantitative study on in-cylinder combustion and heat release characteristic pa-rameters of gasoline engine based on single variable sweeping tests. Appl. Therm. Eng. 2017, 117, 487–500. [Google Scholar] [CrossRef]
- Yan, Y.; Yang, R.; Sun, X.; Li, R.; Liu, Z. Numerical investigations of injection timing effects on a gasoline direct injection engine performance: Part A, in-cylinder combustion process. Front. Energy Res. 2022, 10, 828167. [Google Scholar] [CrossRef]
- Zhang, Y.; Yang, R.; Yan, Y.; Li, R.; Fu, J.; Liu, Z. Numerical investigations of injection timing effects on a GDI engine performance: Part B, in-cylinder emission formation and oxidation process. Front. Energy Res. 2022, 10, 823386. [Google Scholar] [CrossRef]









| Study | Engine Type | Input | Output | Performance (R2) |
|---|---|---|---|---|
| [53] | Diesel engine | Rail pressure, Injection timing, Charge pressure, Charge temperature, Max pressure | Max pressure | 0.99 |
| [54] | Diesel engine | Speed, brake mean effective pressure (BMEP) | Soot emissions | 0.97 |
| [55] | Hydrogen enriched engine | Excess air ratio, speed, injection timing, Fuel, hydrogen volume percentage | Cyclic variation of speed | 0.99 |
| [56] | Diesel engine | Engine speed, amount of injected fuel, rail pressure, BMEP | BMEP | 0.99 |
| [57] | Hydrogen enriched engine | Excess air ratio, hydrogen volume percentage, injection timing | CO emissions | 0.99 |
| [58] | Diesel engine | Injection pressure, injection timing | Max pressure | 0.99 |
| Engine Type | Single-Cylinder 4-Stroke SI Gasoline Engine |
|---|---|
| Stroke × Bore | 86.07 mm × 86 mm |
| Intake valve open | 9 CAD BTDC |
| Intake valve close | 84 CAD ABDC |
| Exhaust valve open | 55 CAD BBDC |
| Exhaust valve close | 38 CAD ATDC |
| Compression ratio | 9.5 |
| Connecting rod length | 175 mm |
| Title | Range | Step |
|---|---|---|
| Engine speed | 1000~4000 RPM | 200 RPM |
| Intake pressure | 0.5~1 bar | 0.1 bar |
| Spark timing | −40~0 CAD ATDC | 2 CAD |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Yang, R.; Sun, X.; Liu, Z.; Zhang, Y.; Fu, J.; Li, R. The Engine Combustion Phasing Prediction Based on the Support Vector Regression Method. Processes 2022, 10, 717. https://doi.org/10.3390/pr10040717
Wang Q, Yang R, Sun X, Liu Z, Zhang Y, Fu J, Li R. The Engine Combustion Phasing Prediction Based on the Support Vector Regression Method. Processes. 2022; 10(4):717. https://doi.org/10.3390/pr10040717
Chicago/Turabian StyleWang, Qifan, Ruomiao Yang, Xiaoxia Sun, Zhentao Liu, Yu Zhang, Jiahong Fu, and Ruijie Li. 2022. "The Engine Combustion Phasing Prediction Based on the Support Vector Regression Method" Processes 10, no. 4: 717. https://doi.org/10.3390/pr10040717
APA StyleWang, Q., Yang, R., Sun, X., Liu, Z., Zhang, Y., Fu, J., & Li, R. (2022). The Engine Combustion Phasing Prediction Based on the Support Vector Regression Method. Processes, 10(4), 717. https://doi.org/10.3390/pr10040717







