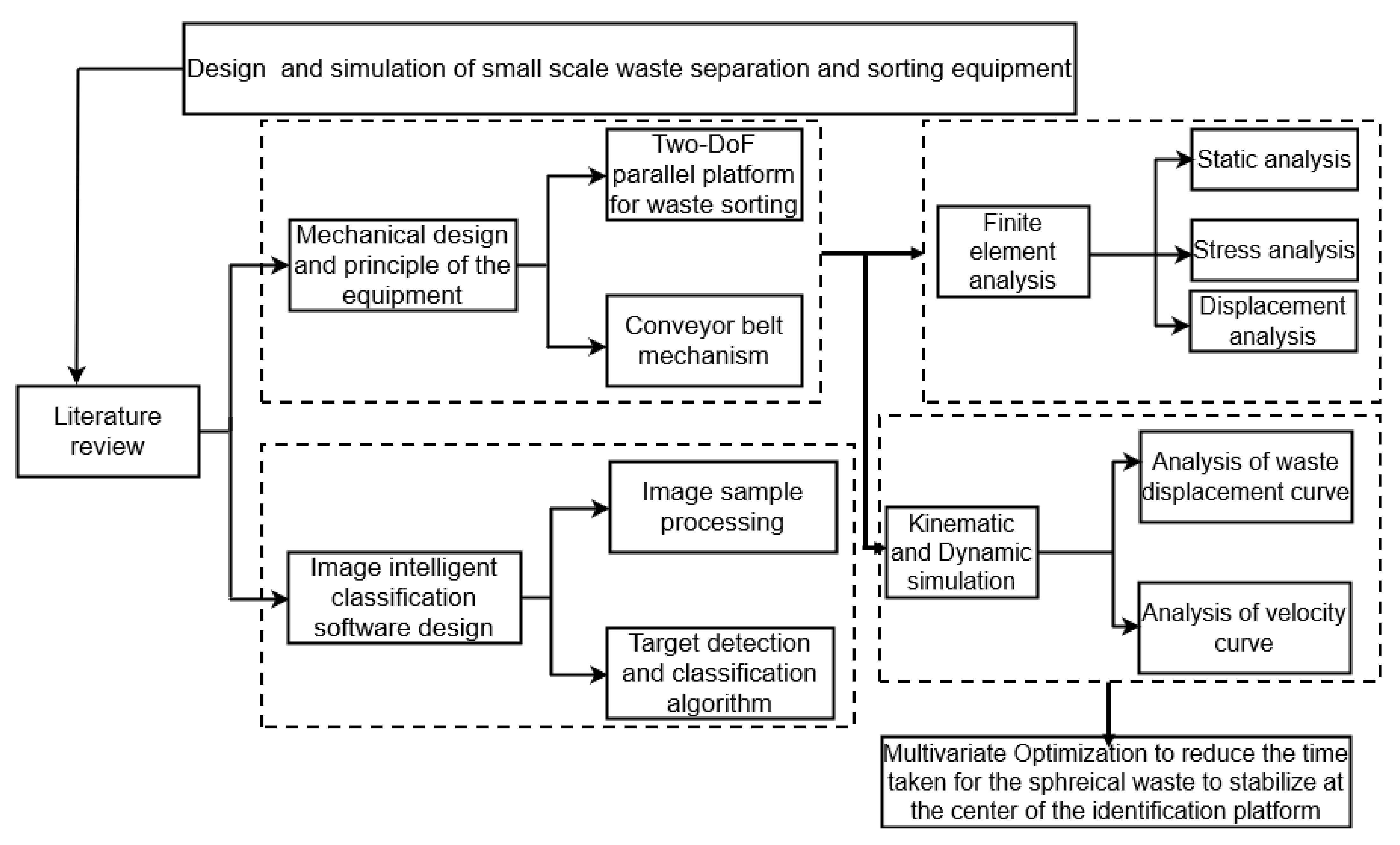
Figure 1.
Schematic illustration of the study design. The schematic diagram shows the mechanical design, working principle, and software system design of waste management equipment. Finite element simulation and dynamic simulation of the waste separation process were carried out. Finally, the structural parameters were optimized to improve the efficiency of waste management equipment.
Figure 1.
Schematic illustration of the study design. The schematic diagram shows the mechanical design, working principle, and software system design of waste management equipment. Finite element simulation and dynamic simulation of the waste separation process were carried out. Finally, the structural parameters were optimized to improve the efficiency of waste management equipment.
Figure 2.
3D model of the waste separation mechanism and the sorting mechanism.
Figure 2.
3D model of the waste separation mechanism and the sorting mechanism.
Figure 3.
Two-degree-of-freedom parallel platform. 1. Base, 2. Lower steering gear, 3. Upper steering gear, 4. Waste identification platform.
Figure 3.
Two-degree-of-freedom parallel platform. 1. Base, 2. Lower steering gear, 3. Upper steering gear, 4. Waste identification platform.
Figure 4.
Processing effects before and after color space separation and filtering. The sample is an image of a rolling potato taken with a 2-megapixel camera: (a) Pre-processing effect of color space separation and filtering. (b) Post-processing effect of color space separation and filtering; in the black background, the material entity is the main part, with some noise occurring in the background. The noise appears in the form of tiny white patches in the picture.
Figure 4.
Processing effects before and after color space separation and filtering. The sample is an image of a rolling potato taken with a 2-megapixel camera: (a) Pre-processing effect of color space separation and filtering. (b) Post-processing effect of color space separation and filtering; in the black background, the material entity is the main part, with some noise occurring in the background. The noise appears in the form of tiny white patches in the picture.
Figure 5.
Processing effect before and after noise processing: (a) Effect before noise processing; noise is detected, which is presented as the white patches occurring at the middle and edge of the figure. (b) Effect after noise processing; unnecessary or redundant interfering information in the image data is completely eliminated.
Figure 5.
Processing effect before and after noise processing: (a) Effect before noise processing; noise is detected, which is presented as the white patches occurring at the middle and edge of the figure. (b) Effect after noise processing; unnecessary or redundant interfering information in the image data is completely eliminated.
Figure 6.
Processing effect before and after the pattern centering conversion: (a) Effect before centering transformation; (b) Effect after centering transformation.
Figure 6.
Processing effect before and after the pattern centering conversion: (a) Effect before centering transformation; (b) Effect after centering transformation.
Figure 7.
Loss function curves for training and test sets of the YOLOv5 network. The x-axis and the y-axis represent the epochs experienced and the loss function value, respectively. The loss function value converges rapidly as the epoch grows.
Figure 7.
Loss function curves for training and test sets of the YOLOv5 network. The x-axis and the y-axis represent the epochs experienced and the loss function value, respectively. The loss function value converges rapidly as the epoch grows.
Figure 8.
Confusion matrix image of test set results. The prediction results of all test sets for the eight categories are consistent with the actual values.
Figure 8.
Confusion matrix image of test set results. The prediction results of all test sets for the eight categories are consistent with the actual values.
Figure 9.
Meshing quality. The overall quality of the mesh ranges between 0.85 and 1.
Figure 9.
Meshing quality. The overall quality of the mesh ranges between 0.85 and 1.
Figure 10.
Stress analysis.
Figure 10.
Stress analysis.
Figure 11.
Displacement map of the platform.
Figure 11.
Displacement map of the platform.
Figure 12.
Servo drive function curve. The motor is driven by angular velocity. The x-axis and y-axis represent time and angular velocity, respectively. The angular velocity of the steering gear increases from 0 °/s to 50 °/s within 5 s.
Figure 12.
Servo drive function curve. The motor is driven by angular velocity. The x-axis and y-axis represent time and angular velocity, respectively. The angular velocity of the steering gear increases from 0 °/s to 50 °/s within 5 s.
Figure 13.
Coordinate system of the model.
Figure 13.
Coordinate system of the model.
Figure 14.
Displacement curve of the waste during the sorting process. The x-axis represents time, and the y-axis indicates the position coordinates of the material center of mass on each axis of the ground coordinate system: (a) X-axis direction; (b) Y-axis direction; (c) Z-axis direction.
Figure 14.
Displacement curve of the waste during the sorting process. The x-axis represents time, and the y-axis indicates the position coordinates of the material center of mass on each axis of the ground coordinate system: (a) X-axis direction; (b) Y-axis direction; (c) Z-axis direction.
Figure 15.
Waste velocity curve. The x-axis represents time, and the y-axis denotes the size of the garbage combined velocity.
Figure 15.
Waste velocity curve. The x-axis represents time, and the y-axis denotes the size of the garbage combined velocity.
Figure 16.
Comparison of the sub-velocity curves of the garbage along with the x, y, and z directions. The sub-velocity of the garbage along the y-axis is stable before the sorting device performs the dumping action, and there is a small deviation around vy = 0. The sub-velocity curve of the garbage along with the x-axis and z-axis assumes a wave shape.
Figure 16.
Comparison of the sub-velocity curves of the garbage along with the x, y, and z directions. The sub-velocity of the garbage along the y-axis is stable before the sorting device performs the dumping action, and there is a small deviation around vy = 0. The sub-velocity curve of the garbage along with the x-axis and z-axis assumes a wave shape.
Figure 17.
Flipping speed of the sorting mechanism.
Figure 17.
Flipping speed of the sorting mechanism.
Figure 18.
A representation of the experimental sorting mechanism. It comprises the slideway, the two-DoF parallel platform, and the surveillance camera.
Figure 18.
A representation of the experimental sorting mechanism. It comprises the slideway, the two-DoF parallel platform, and the surveillance camera.
Figure 19.
The velocity curve of the sphere. The x-axis represents time, and the y-axis denotes the size of the garbage combined velocity. It takes 18.68 s for the sphere to stabilize.
Figure 19.
The velocity curve of the sphere. The x-axis represents time, and the y-axis denotes the size of the garbage combined velocity. It takes 18.68 s for the sphere to stabilize.
Figure 20.
A velocity curve of the sphere in the x-axis direction.
Figure 20.
A velocity curve of the sphere in the x-axis direction.
Figure 21.
Line graph comparing the time point obtained from numerical simulation and prototype test when Vx = 0. The x-axis represents serial number of the time point, and the y-axis denotes the time when the velocity of sphere becomes zero in the x-axis direction. The maximum absolute error of the 14 points is 1.02 s, with a relative error of 13%. The absolute error of other time points is below 0.67 s, which satisfies the requirements of the prototype.
Figure 21.
Line graph comparing the time point obtained from numerical simulation and prototype test when Vx = 0. The x-axis represents serial number of the time point, and the y-axis denotes the time when the velocity of sphere becomes zero in the x-axis direction. The maximum absolute error of the 14 points is 1.02 s, with a relative error of 13%. The absolute error of other time points is below 0.67 s, which satisfies the requirements of the prototype.
Figure 22.
Variation curve of the optimization target in the iterative process. The x-axis represents the number of iterations, and the y-axis indicates the time taken by the spherical material to fall from the top of the slideway to stably rest at the center of the identification table, which represents, the objective function value.
Figure 22.
Variation curve of the optimization target in the iterative process. The x-axis represents the number of iterations, and the y-axis indicates the time taken by the spherical material to fall from the top of the slideway to stably rest at the center of the identification table, which represents, the objective function value.
Figure 23.
Comparison of the velocity of the spherical waste before and after optimization. The time taken by the spherical material to roll down from the top of the slideway to the stable and stationary position at the center of the identification table was shorter after optimization, and the speed convergence effect significantly improved.
Figure 23.
Comparison of the velocity of the spherical waste before and after optimization. The time taken by the spherical material to roll down from the top of the slideway to the stable and stationary position at the center of the identification table was shorter after optimization, and the speed convergence effect significantly improved.
Table 1.
Material properties of each component for the mechanisms.
Table 1.
Material properties of each component for the mechanisms.
| Component | Material | Density (g/cm³) | Elastic Modulus (GPa) | Poisson’s Ratio | Tensile Strength (MPa) | Yield Strength (MPa) |
|---|
| Base | Q345 | 7.86 | 209 | 0.29 | 620 | 345 |
| Steering arm | Q235 | 7.85 | 205 | 0.29 | 460 | 235 |
| Waste identification platform | Q235 | 7.85 | 205 | 0.29 | 460 | 235 |
Table 2.
Calculated values of the objects under the condition of different mesh quantities.
Table 2.
Calculated values of the objects under the condition of different mesh quantities.
| Mesh Quantity | Maximum Static Stress
(MPa) | Maximum Displacement
(mm) |
|---|
| 29,636 | 49.285 | 0.0439 |
| 31,778 | 37.456 | 0.0465 |
| 43,797 | 25.244 | 0.0393 |
| 87,963 | 20.001 | 0.0287 |
| 119,415 | 18.521 | 0.0311 |
| 165,115 | 18.524 | 0.0307 |
Table 3.
Number and types of the restraint pairs of the waste sorting mechanism.
Table 3.
Number and types of the restraint pairs of the waste sorting mechanism.
| Type | Number | DoF Constraint |
|---|
| Rotary hinge pair | 2 | 5 |
| Fixed hinge pair | 5 | 6 |
Table 4.
Parameter values of the impact function.
Table 4.
Parameter values of the impact function.
| Contact Entities | Stiffness Coefficient | Exponent of Force | Maximum Damping Coefficient | Depth (mm) |
|---|
| Spherical waste and slideway | 5000.0 | 1.5 | 50 | 0.1 |
| Spherical waste and platform | 5000.0 | 1.5 | 100 | 0.1 |
Table 5.
Friction coefficients of the spherical waste and the sorting system.
Table 5.
Friction coefficients of the spherical waste and the sorting system.
| Static Coefficient | Dynamic Coefficient | Static Slip Velocity (mm/s) | Dynamic Slip Velocity (mm/s) |
|---|
| 0.8 | 0.85 | 0.1 | 1.0 |
Table 6.
Time taken for the spherical waste to stabilize at the identification platform.
Table 6.
Time taken for the spherical waste to stabilize at the identification platform.
| SERIAL NUMBER | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | Average |
|---|
| Measurement (s) | 19.80 | 20.51 | 18.45 | 19.02 | 20.78 | 20.88 | 19.53 | 19.64 | 18.81 | 19.56 | 19.698 |
Table 7.
Variation range and initial value of four parameters.
Table 7.
Variation range and initial value of four parameters.
| Parameters | Variation Range | Initial Value | Fixed Step Size |
|---|
| Slideway obliquity | 15°/90° | 15° | 10% |
| First-stage inclination angle | 10°/30° | 10° | 10% |
| Second-stage inclination angle | 30°/55° | 40° | 5% |
| Third-stage inclination angle | 55°/75° | 55° | 5% |
Table 8.
Calculated values of sensitivity factors and evaluation of sensitivity level.
Table 8.
Calculated values of sensitivity factors and evaluation of sensitivity level.
| Parameters | Sensitivity Factor | Sensitivity Level |
|---|
| Slideway obliquity | −0.3175 | Sensitive |
| First-stage inclination angle | −0.53125 | Sensitive |
| Second-stage inclination angle | 0.35375 | Sensitive |
| Third-stage inclination angle | −0.681 | Sensitive |
Table 9.
Values of the optimization variables.
Table 9.
Values of the optimization variables.
| Input Variables | Initial Value | Variation Range |
|---|
| Slideway obliquity | 15° | 15°/90° |
| First-stage inclination angle | 21° | 10°/30° |
| Second-stage inclination angle | 55° | 30°/55° |
| Third-stage inclination angle | 75° | 55°/75° |
Table 10.
Waste sorting time and variables before and after optimization.
Table 10.
Waste sorting time and variables before and after optimization.
| | Before Optimization | After Optimization |
|---|
| OBJECTIVE-Time | 6.0999 s | 3.94 s |
| Slideway obliquity | 15° | 15.0011° |
| First-stage inclination angle | 30° | 30° |
| Second-stage inclination angle | 55° | 54.9995° |
| Third-stage inclination angle | 66° | 66.1187° |