Effect of Liquid Properties on Frictional Pressure Drop in a Gas-Liquid Two-Phase Microchannel
Abstract
:1. Introduction
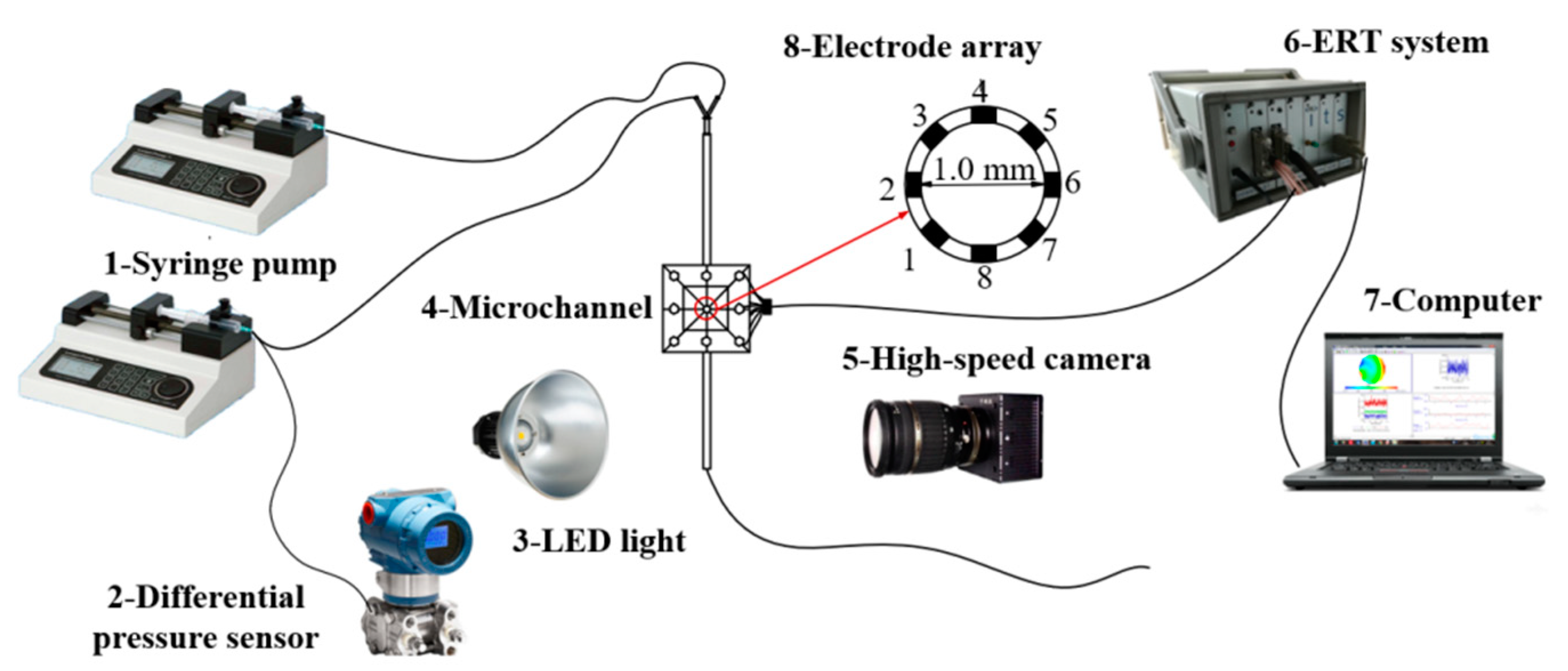
2. Experimental
2.1. Experimental Equipment
2.2. Physical Properties of Fluids
2.3. Frictional Pressure Drop
2.3.1. The Homogeneous Flow Model
2.3.2. The Separated Flow Model
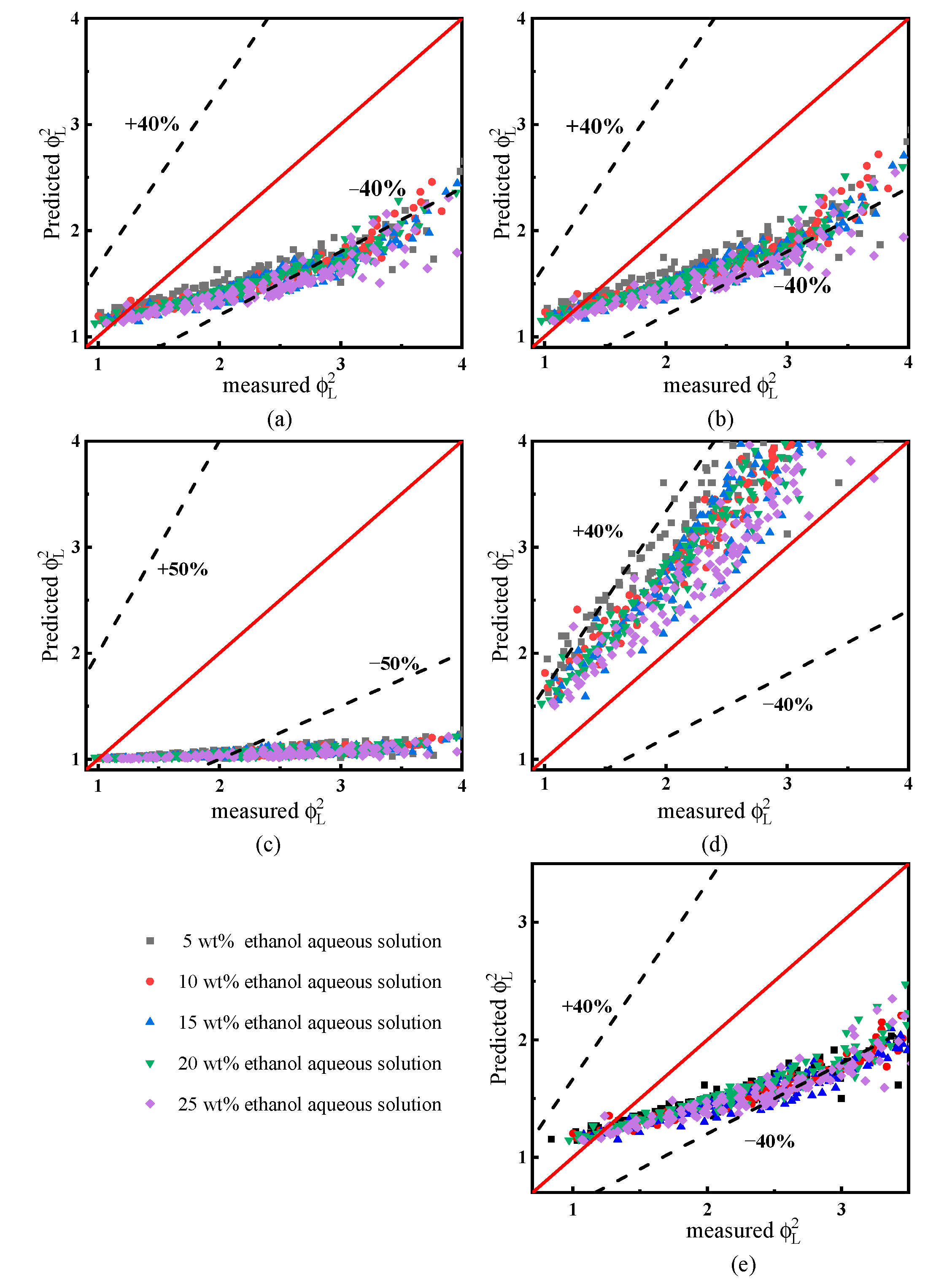
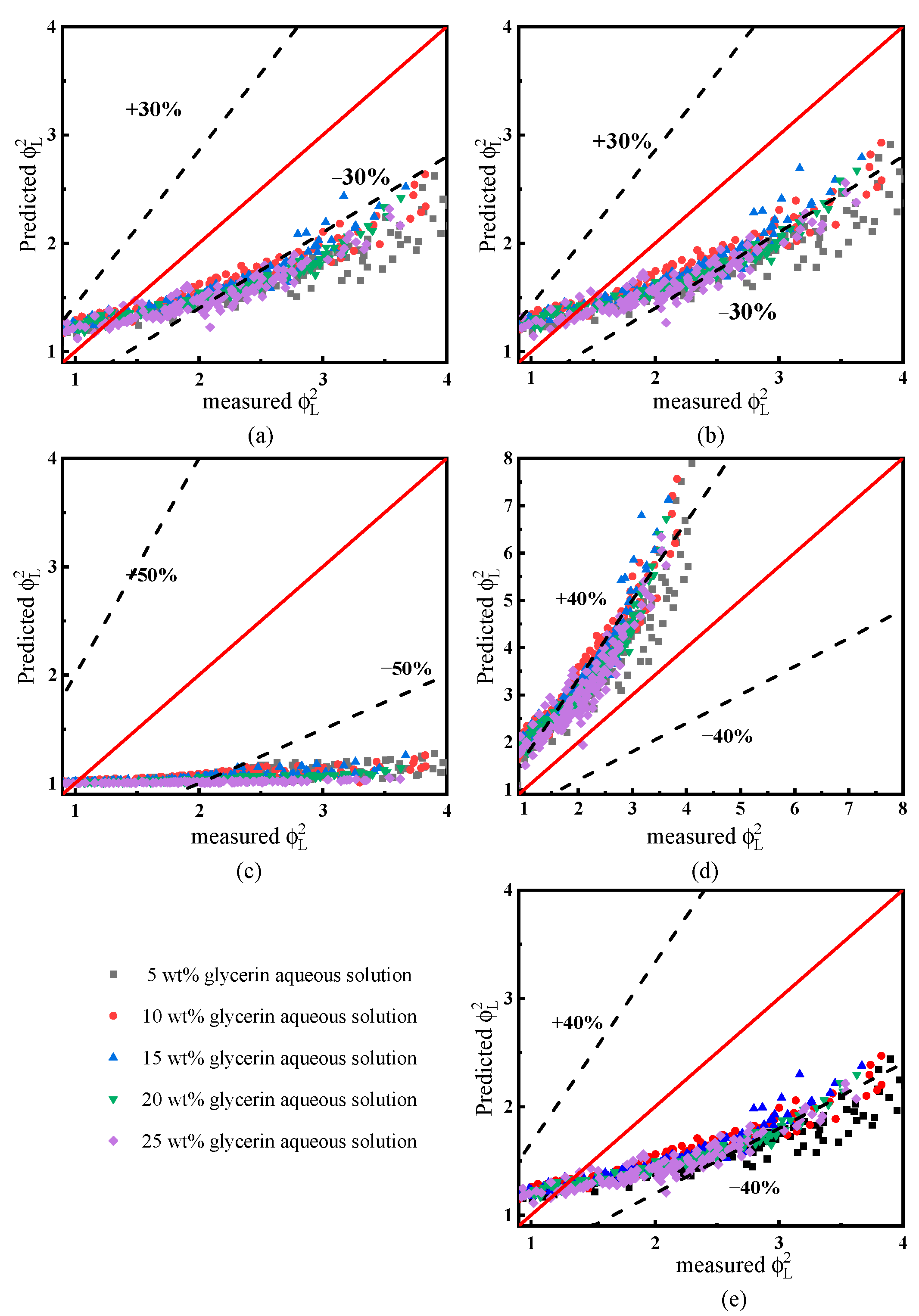
3. Experimental Results and Discussion
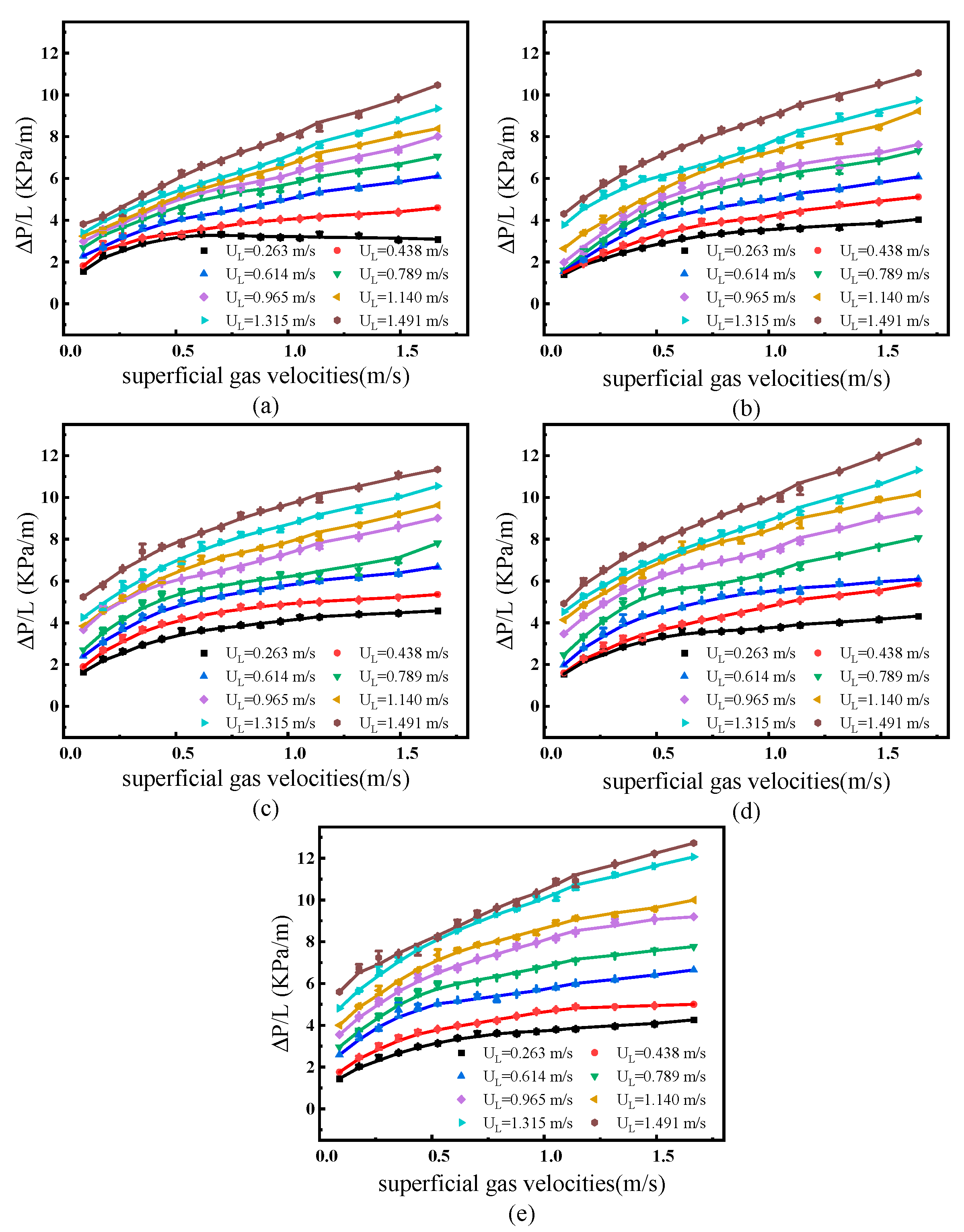
3.1. Experimental Results and Analysis of Frictional Pressure Drop
3.2. Influence of Liquid Surface Tension
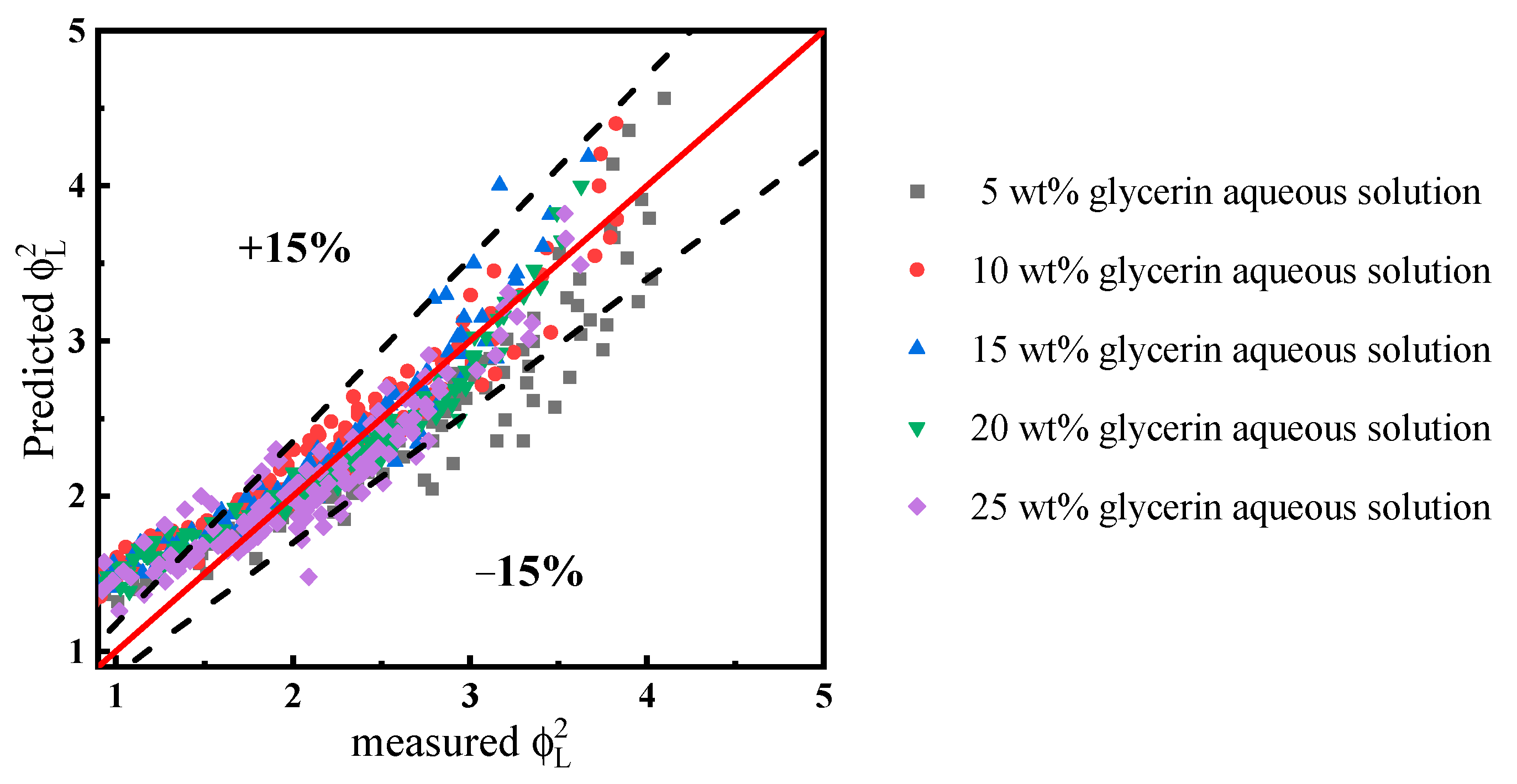
3.3. Influence of Liquid Viscosity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kawahara, A.; Chung, M.Y.; Kawaji, M. Investigation of two-phase flow pattern, void fraction and pressure drop in a microchannel. Int. J. Multiph. Flow 2002, 28, 1411–1435. [Google Scholar] [CrossRef]
- Lalegani, F.; Saffarian, M.R.; Moradi, A.; Tavousi, E. Effects of different roughness elements on friction and pressure drop of laminar flow in microchannels. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 1664–1683. [Google Scholar] [CrossRef]
- Kawahara, A.; Yonemoto, Y.; Arakaki, Y. Pressure Drop for Gas and Polymer Aqueous Solution Two-Phase Flows in Horizontal Circular Microchannel. Appl. Sci. Res. 2020, 105, 1325–1344. [Google Scholar] [CrossRef]
- Ronshin, F.V.; Dementyev, Y.A. Influence of Liquid Properties on Gas-Liquid Flow Regimes and Pressure Drop in a Flat Microchannel. J. Eng. Thermophys. 2021, 30, 661–671. [Google Scholar] [CrossRef]
- Moradikazerouni, A.; Shoele, K.; Alireza Moradikazerouni Team; Kourosh Shoele Team. Computational study of Rayleigh-Bernard convection in a cylindrical pressurized cryogenic tank. APS Div. Fluid Dyn. Meet. Abstracts 2021, F06.001. Available online: https://ui.adsabs.harvard.edu/abs/2021APS..DFDF06001M (accessed on 27 March 2022).
- Estebe, C.; Liu, Y.; Vahab, M.; Sussman, M.; Moradikazerouni, A.; Shoele, K.; Guo, W. A Low Mach Number, Adaptive Mesh Method for Simulating Multi-phase Flows in Cryogenic Fuel Tanks. In Proceedings of the SIAM Conference on Computational Science and Engineering, Philadelphia, PA, USA, 25 August 2021. [Google Scholar]
- Triplett, K.A.; Ghiaasiaan, S.M.; Abdelkhalik, S.I.; Sadowski, D.L. Gas-liquid two-phase flow in microchannels Part I: Two-phase flow patterns. Int. J. Multiph. Flow 1999, 25, 377–394. [Google Scholar] [CrossRef]
- Fujioka, H.; Grotberg, J. Steady propagation of a liquid plug in a two-dimensional channel. J. Biomech. Eng. 2004, 126, 567–577. [Google Scholar] [CrossRef]
- Jing, S. Characteristics of gas-liquid two-phase flow in microchannels. J. Qingdao Univ. Sci. Technol. 2006, 27, 299–303. [Google Scholar]
- Chisholm, D. A theoretical basis for the Lockhart-Martinelli correlation for two-phase flow. Int. J. Heat Mass Transf. 1967, 10, 1767–1778. [Google Scholar] [CrossRef]
- Lee, H.J.; Lee, S.Y. Pressure drop correlations for two-phase flow within horizontal rectangular channels with small heights. Int. J. Multiph. Flow 2001, 27, 783–796. [Google Scholar] [CrossRef]
- Dukler, A.E.; Wicks, M.; Cleveland, R.G. Frictional pressure drop in two-phase flow: A. A comparison of existing correlations for pressure loss and holdup. AIChE J. 1964, 10, 38–43. [Google Scholar] [CrossRef]
- Mcadams, W.H.; Woods, W.K.; Bryan, R.L. Vaporization inside horizontal tubes-II-benzene-oil mixtures. Trans. ASME 1942, 64, 193. [Google Scholar]
- Chicchitti, A.; Lombardi, C.; Silvestri, M.; Soldaini, G.; Zavattarelli, R. Two-phase cooling experiments-pressure drop, heat transfer and burnout measurements. Energia Nucl. 1960, 7, 407–425. [Google Scholar]
- Beattie, D.R.H.; Whalley, P.B. A simple two-phase frictional pressure drop calculation method. Int. J. Multiph. Flow 1982, 8, 83–87. [Google Scholar] [CrossRef]
- Lin, S.; Kwok, C.C.K.; Li, R.-Y.; Chen, Z.-H.; Chen, Z.-Y. Local frictional pressure drop during vaporization of R-12 through capillary tubes. Int. J. Multiph. Flow 1991, 17, 95–102. [Google Scholar] [CrossRef]
- Awad, M.M.; Muzychka, Y.S. Effective property models for homogeneous two-phase flows. Exp. Therm. Fluid Sci. 2008, 33, 106–113. [Google Scholar] [CrossRef]
- Tao, F.; Jin, H.; He, G.; Guo, X.; Ma, L.; Zhang, R. Two-phase flow characteristics of gas-liquids in microchannels using electrical resistance tomography. Int. J. Heat Mass Transf. 2021, 58, 99–114. [Google Scholar] [CrossRef]
- Lockhart, R.W.; Martinelli, R.C. Proposed correlation of data for isothermal two-phase, two-component flow in pipes. Chem. Eng. Sci. 1949, 45, 39–48. [Google Scholar]
- Zhang, T.; Cao, B.; Fan, Y. Gas-liquid flow in circular microchannel. Part I: Influence of liquid physical properties and channel diameter on flow patterns. Chem. Eng. Sci. 2011, 66, 5791–5803. [Google Scholar] [CrossRef]
- Mishima, K.; Hibiki, T.; Zhang, W. Correlations of two-phase frictional pressure drop and void fraction in mini-channel. Heat Mass Transf. 2010, 53, 453–465. [Google Scholar]
- Li, W.; Wu, Z. A general correlation for adiabatic two-phase pressure drop in micro/mini-channels. Int. J. Heat Mass Transf. 2010, 53, 2732–2739. [Google Scholar] [CrossRef]





| Fluid | Density ρ (Kg/m3) | Viscosity η (mPa·s) | η fluid/η water | Surface Tension σ (mN/m) | σ fluid/σ water | Range of |
|---|---|---|---|---|---|---|
| Air | 1.18 | 0.018 | - | - | - | |
| Water | 997.05 | 0.885 | 1 | 72 | 1 | 296–1680 |
| 5 wt% Ethanol aqueous solution | 989.91 | 1.170 | 1.32 | 57.7 | 0.80 | 233–1321 |
| 10 wt% Ethanol aqueous solution | 981.60 | 1.330 | 1.50 | 50.1 | 0.70 | 194–1100 |
| 15 wt% Ethanol aqueous solution | 975.54 | 1.510 | 1.71 | 48 | 0.67 | 170–963 |
| 20 wt% Ethanol aqueous solution | 967.32 | 1.700 | 1.92 | 40 | 0.56 | 150–848 |
| 25 wt% Ethanol aqueous solution | 961.80 | 1.820 | 2.06 | 38.7 | 0.54 | 139–788 |
| 5 wt% Glycerin aqueous solution | 1010.59 | 1.100 | 1.24 | 72 | 1 | 242–1370 |
| 10 wt% Glycerin aqueous solution | 1025.98 | 1.228 | 1.39 | 71.4 | 0.99 | 220–1246 |
| 15 wt% Glycerin aqueous solution | 1041.65 | 1.431 | 1.61 | 71.1 | 0.99 | 191–1085 |
| 20 wt% Glycerin aqueous solution | 1052.51 | 1.653 | 1.87 | 70.5 | 0.98 | 168–949 |
| 25 wt% Glycerin aqueous solution | 1061.21 | 1.912 | 2.16 | 70.0 | 0.97 | 146–828 |
| margin of error | 0.1–8% | 0–9% | 0–10% | 1–7% | 0.01–0.1% | - |
| Researchers | Correlation | Ranges |
|---|---|---|
| Lockhart and Martinelli | = 5 | Laminar flow of gas and liquid |
| Mishima and Hibiki | = 1–4 mm, circular section | |
| Lee and Lee | Laminar flow of gas and liquid | |
| Zhang et al. | Modified Mishima and Hibiki’s correlation to extend to microscale | |
| Li and Wu | = 0.148–3.25 mm |
| References | Ethanol Aqueous Solution, MAE (%) | |||||
|---|---|---|---|---|---|---|
| 5 wt% | 10 wt% | 15 wt% | 20 wt% | 25 wt% | Mean | |
| McAdams et al. | 22.72 | 23.02 | 18.84 | 21.07 | 25.35 | 22.2 |
| Cicchitti et al. | 23.59 | 26.36 | 21.74 | 32.40 | 38.47 | 28.512 |
| Dukler et al. | 49.99 | 49.91 | 47.20 | 44.51 | 45.36 | 47.394 |
| Beattie and Whalley | 20.93 | 29.23 | 23.74 | 37.52 | 41.36 | 30.556 |
| Lin et al. | 23.18 | 25.67 | 20.93 | 30.86 | 36.70 | 27.468 |
| Awad and Myuztchka | 22.85 | 24.63 | 19.79 | 26.96 | 32.48 | 25.342 |
| References | Ethanol Aqueous Solution, MAE (%) | |||||
|---|---|---|---|---|---|---|
| 5 wt% | 10 wt% | 15 wt% | 20 wt% | 25 wt% | Mean | |
| Lockhart and Martinelli | 29.28 | 32.57 | 32.99 | 30.90 | 37.59 | 32.67 |
| Mishima and Hibiki | 25.37 | 28.67 | 29.17 | 27.17 | 34.05 | 28.89 |
| Lee and Lee | 48.75 | 61.85 | 51.60 | 48.74 | 52.66 | 52.72 |
| Zhang et al. | 51.77 | 40.15 | 35.72 | 37.93 | 26.02 | 38.32 |
| Li and Wu | 29.81 | 31.70 | 31.74 | 27.79 | 32.63 | 30.73 |
| References | Glycerin Aqueous Solution MAE (%) | |||||
|---|---|---|---|---|---|---|
| 5 wt% | 10 wt% | 15 wt% | 20 wt% | 25 wt% | Mean | |
| McAdams et al. | 27.07 | 27.12 | 25.74 | 26.14 | 24.51 | 26.13 |
| Cicchitti et al. | 26.59 | 26.35 | 28.86 | 28.51 | 33.34 | 28.73 |
| Dukler et al. | 54.72 | 53.95 | 51.08 | 50.88 | 49.27 | 51.98 |
| Beattie and Whalley | 25.10 | 24.57 | 28.72 | 31.79 | 39.58 | 29.95 |
| Lin et al. | 26.36 | 26.09 | 28.13 | 27.69 | 31.97 | 28.05 |
| Awad and Myuztchka | 26.33 | 26.20 | 27.03 | 26.66 | 28.80 | 27.00 |
| References | Glycerin Aqueous Solution, MAE (%) | |||||
|---|---|---|---|---|---|---|
| 5 wt% | 10 wt% | 15 wt% | 20 wt% | 25 wt% | Mean | |
| Lockhart and Martinelli | 31.71 | 26.31 | 25.84 | 27.29 | 27.27 | 27.68 |
| Mishima and Hibiki | 27.76 | 22.94 | 22.55 | 24.28 | 24.09 | 24.32 |
| Lee and Lee | 47.93 | 44.47 | 44.06 | 44.29 | 45.60 | 45.27 |
| Zhang et al. | 34.24 | 69.25 | 66.53 | 58.82 | 54.04 | 56.58 |
| Li and Wu | 51.72 | 28.25 | 27.65 | 28.73 | 28.72 | 33.01 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Tao, F.; Jin, H.; Guo, X.; He, G.; Ma, L.; Zhang, R.; Gu, Q.; Yang, S. Effect of Liquid Properties on Frictional Pressure Drop in a Gas-Liquid Two-Phase Microchannel. Processes 2022, 10, 799. https://doi.org/10.3390/pr10050799
Zhang R, Tao F, Jin H, Guo X, He G, Ma L, Zhang R, Gu Q, Yang S. Effect of Liquid Properties on Frictional Pressure Drop in a Gas-Liquid Two-Phase Microchannel. Processes. 2022; 10(5):799. https://doi.org/10.3390/pr10050799
Chicago/Turabian StyleZhang, Ruijie, Fangfang Tao, Haibo Jin, Xiaoyan Guo, Guangxiang He, Lei Ma, Rongyue Zhang, Qingyang Gu, and Suohe Yang. 2022. "Effect of Liquid Properties on Frictional Pressure Drop in a Gas-Liquid Two-Phase Microchannel" Processes 10, no. 5: 799. https://doi.org/10.3390/pr10050799
APA StyleZhang, R., Tao, F., Jin, H., Guo, X., He, G., Ma, L., Zhang, R., Gu, Q., & Yang, S. (2022). Effect of Liquid Properties on Frictional Pressure Drop in a Gas-Liquid Two-Phase Microchannel. Processes, 10(5), 799. https://doi.org/10.3390/pr10050799







