The Role of Diffusivity in Oil and Gas Industries: Fundamentals, Measurement, and Correlative Techniques
Abstract
:1. Introduction
2. Fundamental Aspects
2.1. Phenomenological Approach: Driving Force and Non-Equilibrium Thermodynamics
Nonequilibrium Thermodynamics and Multicomponent Diffusion
- (1)
- Quasi-equilibrium postulate: while real systems may lie very far from the equilibrium, especially when the gradients (in pressure, temperature, concentration, etc.) present in the system are very strong, these systems could be assumed to be in quasi-equilibrium locally, where equilibrium thermodynamics could still be applicable. Since nonequilibrium thermodynamics is still a developing area, this assumption enables us to use the equilibrium thermodynamics equations for relating state variables (especially the first and the second law of thermodynamics) as expressed by:where , and are total internal energy, entropy and volume of the system, respectively; P and T are pressure and temperature, respectively; is the chemical potential of its component, is the number of moles of ith component; and is the number of components present in the system. While, in reality, the change in internal energy of the system (left-hand side of Equation (3)) is either less than or equal to the right-hand side term, locally, they are assumed to be the same.
- (2)
- Linearity postulate: all the fluxes in the system may be expressed as a linear combination of all the forces present in the system. This is a very important assumption that suggests that all the fluxes, such as heat flux, mass flux, momentum flux, etc., can be written as a linear function of all the driving forces, including temperature gradient (), concentration or activity gradients ( or ) of each component, pressure gradient (), velocity gradient () and external forces such as gravity. This is a very important postulate that also indicates that the driving force for diffusion of species could also include the concentration/activity gradient of other species.
- (3)
- Curie postulate [101]: when the flux and driving forces have tensorial orders that differ by an odd number, then they are not coupled with each other. Note that the heat and mass transfer fluxes are vectors (tensor of order unity) while the gradient in velocity () is a second order-tensor. Thus, the deference in their tensorial order is unity (an odd number) and, hence, according to the Curie postulate, the heat and mass transfer fluxes cannot depend on velocity gradient directly. In other words, heat and mass transfer fluxes depend directly only on concentration/activity gradients, pressure gradients, temperature gradients and external forces. Indirectly, these fluxes can depend on the velocity gradient only when it creates gradients in concertation, temperature and/or pressure.
- (4)
- Symmetry (Onsager’s reciprocal approximation [102,103]): the coefficient matrix relating the flux and driving force is symmetric. This leads to the diffusivity and conductivity matrices being symmetric. (Note: it was shown later by Truesdell [104] using second law of thermodynamics that the diffusivity and conductivity tensors must be positive definite.)
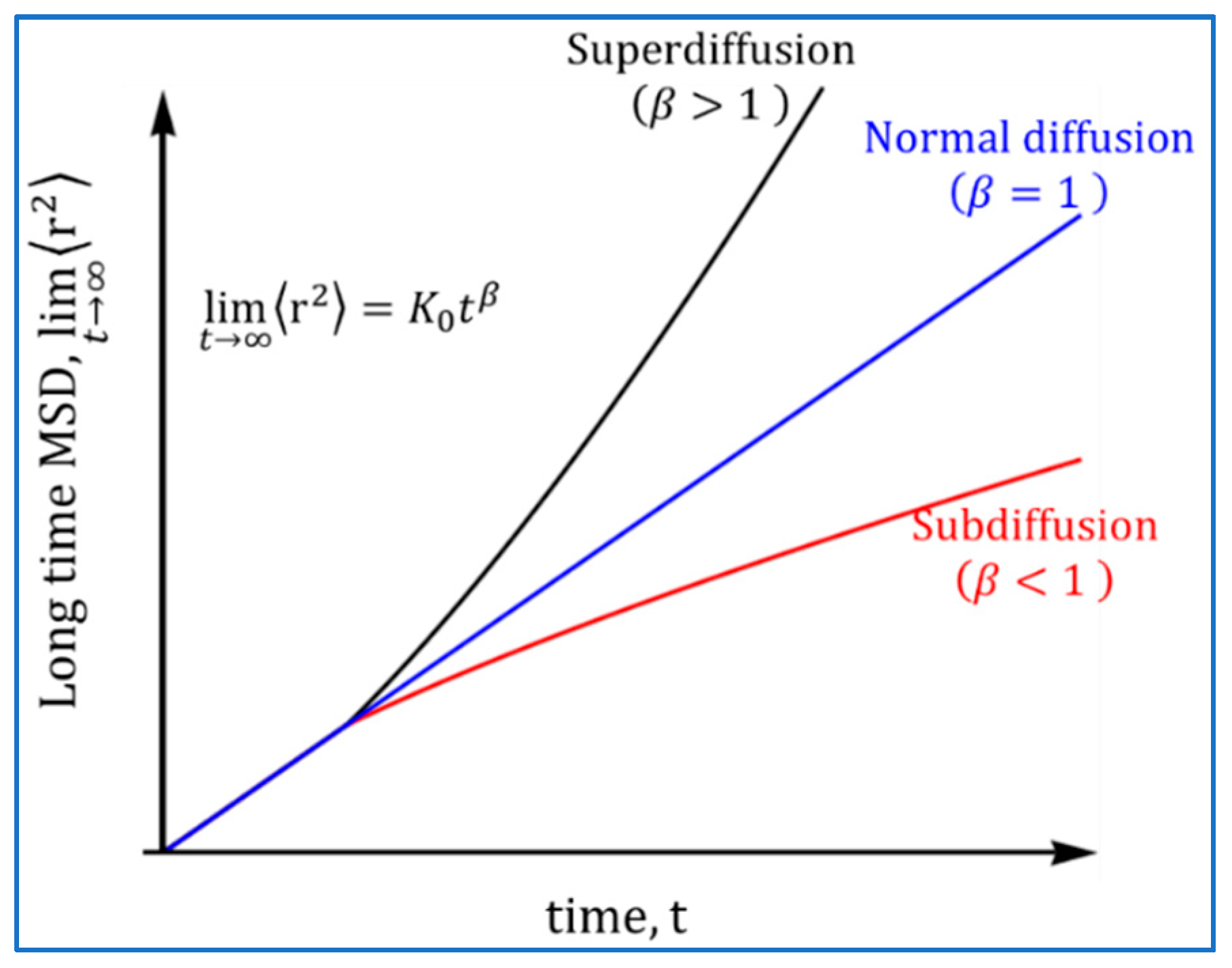
2.2. Atomistic Approach: Normal and Anomalous Diffusion
3. Physics-Based and Empirical Correlations for Diffusivity Estimation
3.1. Various Mechanism of Diffusion in a Capillary
3.2. Diffusion in Gas-Filled Pores
3.2.1. Knudsen Diffusion ( or )
3.2.2. Bulk Diffusion ( or )
3.3. Diffusion of Gases in Porous Media
3.4. Diffusion of Gases in Liquids
4. Measurement Techniques
4.1. Conventional Techniques
4.1.1. Graham’s Diffusion Tube Method
4.1.2. Diaphragm Cell Method
4.1.3. Taylor Dispersion Method
4.2. Unconventional Methods
4.2.1. Interferometry Method
4.2.2. PD Method
5. Summary and Final Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; John Wiley & Sons: Hoboken, NJ, USA, 2006; Volume 1. [Google Scholar]
- Jackson, R. Transport in Porous Catalysts; Elsevier Science & Technology: Amsterdam, The Netherlands, 1977; Volume 4. [Google Scholar]
- Froment, G.F.; Bischoff, K.B.; De Wilde, J. Chemical Reactor Analysis and Design; Wiley: New York, NY, USA, 1990; Volume 2. [Google Scholar]
- Ratnakar, R.R.; Balakotaiah, V. Coarse-graining of diffusion–reaction models with catalyst archipelagos. Chem. Eng. Sci. 2014, 110, 44–54. [Google Scholar] [CrossRef]
- Cussler, E.L.; Cussler, E.L. Diffusion: Mass Transfer in Fluid Systems; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Balakotaiah, V. Hyperbolic averaged models for describing dispersion effects in chromatographs and reactors. Korean J. Chem. Eng. 2004, 21, 318–328. [Google Scholar] [CrossRef]
- Katsanos, N.A.; Thede, R.; Roubani-Kalantzopoulou, F. Diffusion, adsorption and catalytic studies by gas chromatography. J. Chromatogr. A 1998, 795, 133–184. [Google Scholar] [CrossRef]
- Smith, I. Chromatography; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Nam, S.-E.; Lee, K.-H. Preparation and characterization of palladium alloy composite membranes with a diffusion barrier for hydrogen separation. Ind. Eng. Chem. Res. 2005, 44, 100–105. [Google Scholar] [CrossRef]
- Nauman, E.B.; He, D.Q. Nonlinear diffusion and phase separation. Chem. Eng. Sci. 2001, 56, 1999–2018. [Google Scholar] [CrossRef]
- Babarao, R.; Jiang, J. Diffusion and separation of CO2 and CH4 in silicalite, C168 schwarzite, and IRMOF-1: A comparative study from molecular dynamics simulation. Langmuir 2008, 24, 5474–5484. [Google Scholar] [CrossRef] [PubMed]
- Rayleigh, L.L. Theoretical considerations respecting the separation of gases by diffusion and similar processes. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1896, 42, 493–498. [Google Scholar] [CrossRef] [Green Version]
- Harstad, K.; Bellan, J. High-pressure binary mass diffusion coefficients for combustion applications. Ind. Eng. Chem. Res. 2004, 43, 645–654. [Google Scholar] [CrossRef]
- Mardani, A.; Tabejamaat, S.; Ghamari, M. Numerical study of influence of molecular diffusion in the Mild combustion regime. Combust. Theory Model. 2010, 14, 747–774. [Google Scholar] [CrossRef]
- Matta, L.; Neumeier, Y.; Lemon, B.; Zinn, B. Characteristics of microscale diffusion flames. Proc. Combust. Inst. 2002, 29, 933–939. [Google Scholar] [CrossRef]
- Peters, N. Turbulent Combustion; IOP Publishing: Tokyo, Japan, 2001. [Google Scholar]
- Heck, R.M.; Farrauto, R.J.; Gulati, S.T. Catalytic Air Pollution Control: Commercial Technology; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Ratnakar, R.R.; Bhattacharya, M.; Balakotaiah, V. Reduced order models for describing dispersion and reaction in monoliths. Chem. Eng. Sci. 2012, 83, 77–92. [Google Scholar] [CrossRef]
- Kumar, P.; Gu, T.; Grigoriadis, K.; Franchek, M.; Balakotaiah, V. Spatio-temporal dynamics of oxygen storage and release in a three-way catalytic converter. Chem. Eng. Sci. 2014, 111, 180–190. [Google Scholar] [CrossRef]
- Stalkup, F.I. Displacement of oil by solvent at high water saturation. Soc. Pet. Eng. J. 1970, 10, 337–348. [Google Scholar] [CrossRef]
- Huang, E.T.; Tracht, J.H. The displacement of residual oil by carbon dioxide. In Proceedings of the SPE Improved Oil Recovery Symposium, Tulsa, OK, USA, 22–24 April 1974. [Google Scholar]
- Shelton, J.; Schneider, F. The effects of water injection on miscible flooding methods using hydrocarbons and carbon dioxide. Soc. Pet. Eng. J. 1975, 15, 217–226. [Google Scholar] [CrossRef]
- Grogan, A.; Pinczewski, W. The role of molecular diffusion processes in tertiary CO2 flooding. J. Pet. Technol. 1987, 39, 591–602. [Google Scholar] [CrossRef]
- Yanze, Y.; Clemens, T. The Role of Diffusion for Non-Miscible Gas Injection into a Fractured Reservoir. In Proceedings of the SPE EUROPEC/EAGE Annual Conference and Exhibition, Vienna, Austria, 23–26 May 2011. [Google Scholar]
- Boustani, A.; Maini, B. The role of diffusion and convective dispersion in vapour extraction process. J. Can. Pet. Technol. 2001, 40. [Google Scholar] [CrossRef]
- Yang, C.; Gu, Y. Diffusion coefficients and oil swelling factors of carbon dioxide, methane, ethane, propane, and their mixtures in heavy oil. Fluid Phase Equilibria 2006, 243, 64–73. [Google Scholar] [CrossRef]
- Li, X.; Yortsos, Y. Theory of multiple bubble growth in porous media by solute diffusion. Chem. Eng. Sci. 1995, 50, 1247–1271. [Google Scholar] [CrossRef]
- Policarpo, N.; Ribeiro, P. Experimental measurement of gas-liquid diffusivity. Braz. J. Pet. Gas 2011, 5. [Google Scholar] [CrossRef]
- Ratnakar, R.; Kalia, N.; Balakotaiah, V. Carbonate matrix acidizing with gelled acids: An experiment-based modeling study. In Proceedings of the SPE International Production and Operations Conference & Exhibition, Doha, Qatar, 14–16 May 2012. [Google Scholar]
- Ratnakar, R.R.; Kalia, N.; Balakotaiah, V. Modeling, analysis and simulation of wormhole formation in carbonate rocks with in situ cross-linked acids. Chem. Eng. Sci. 2013, 90, 179–199. [Google Scholar] [CrossRef]
- Neogi, P. Transport phenomena in polymer membranes. Diffus. Polym. 1996, 32, 173–209. [Google Scholar]
- Barrie, J.A. Diffusion in polymers. In Proceedings of the Polymers in a Marine Environment Conference, London, UK, 31 October–2 November 1984. [Google Scholar]
- Vieth, W.R. Diffusion in and Through Polymers: Principles and Applications; Carl Hanser Verlag GmbH & Co.: Berlin, Germany, 1991; Volume 81. [Google Scholar]
- Hansen, C.M. Diffusion in polymers. Polym. Eng. Sci. 1980, 20, 252–258. [Google Scholar] [CrossRef]
- Duncan, B.; Urquhart, J.; Roberts, S. Review of Measurement and Modelling of Permeation and Diffusion in Polymers; National Physical Laboratory: Teddington, UK, 2005. [Google Scholar]
- Adelstein, S.J.; Manning, F.J. Isotopes for Medicine and the Life Sciences; National Academies Press: Washington, DC, USA, 1995. [Google Scholar]
- Maton, A.; Lahart, D.; Hopkins, J.; Warner, M.Q.; Johnson, S.; Wright, J.D. Cells: Building Blocks of Life; Pearson Prentice Hall: Hoboken, NJ, USA, 1997. [Google Scholar]
- Acar, B.; Sadikoglu, H.; Doymaz, I. Freeze-Drying Kinetics and Diffusion Modeling of Saffron (C rocus sativus L.). J. Food Process. Preserv. 2015, 39, 142–149. [Google Scholar] [CrossRef]
- Aguerre, R.; Gabitto, J.; Chirife, J. Utilization of Fick’s second law for the evaluation of diffusion coefficients in food processes controlled by internal diffusion. Int. J. Food Sci. Technol. 1985, 20, 623–629. [Google Scholar] [CrossRef]
- Karel, M.; Saguy, I. Effects of water on diffusion in food systems. Water Relatsh. Foods 1991, 302, 157–173. [Google Scholar]
- Nam, S.-E.; Lee, K.-H. Hydrogen separation by Pd alloy composite membranes: Introduction of diffusion barrier. J. Membr. Sci. 2001, 192, 177–185. [Google Scholar] [CrossRef]
- Street, R.; Tsai, C.; Kakalios, J.; Jackson, W. Hydrogen diffusion in amorphous silicon. Philos. Mag. B 1987, 56, 305–320. [Google Scholar] [CrossRef]
- Song, A.; Ma, J.; Xu, D.; Li, R. Adsorption and diffusion of xylene isomers on mesoporous beta zeolite. Catalysts 2015, 5, 2098–2114. [Google Scholar] [CrossRef] [Green Version]
- Ma, Y.; Zhang, F.; Yang, S.; Lively, R.P. Evidence for entropic diffusion selection of xylene isomers in carbon molecular sieve membranes. J. Membr. Sci. 2018, 564, 404–414. [Google Scholar] [CrossRef]
- Jones, A.L.; Milberger, E.C. Separation of organic liquid mixtures by thermal diffusion. Ind. Eng. Chem. 1953, 45, 2689–2696. [Google Scholar] [CrossRef]
- Ratnakar, R.R.; Dindoruk, B. Measurement of gas diffusivity in heavy oils and bitumens by use of pressure-decay test and establishment of minimum time criteria for experiments. SPE J. 2015, 20, 1167–1180. [Google Scholar] [CrossRef]
- Ratnakar, R.; Dindoruk, B. On the Exact Representation of Pressure Decay Tests: New Modeling and Experimental Data for Diffusivity Measurement in Gas-Oil/Bitumen Systems. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, United Arab Emirates, 26–28 September 2016. [Google Scholar]
- Ratnakar, R.R.; Dindoruk, B. Analysis and interpretation of pressure-decay tests for gas/bitumen and oil/bitumen systems: Methodology development and application of new linearized and robust parameter-estimation technique using laboratory data. SPE J. 2019, 24, 951–972. [Google Scholar] [CrossRef]
- Ratnakar, R.R.; Dindoruk, B.; Odikpo, G.; Lewis, E.J. Measurement and Quantification of Diffusion-Induced Compositional Variations in Absence of Convective Mixing at Reservoir Conditions. Transp. Porous Media 2019, 128, 29–43. [Google Scholar] [CrossRef]
- Ratnakar, R.R.; Dindoruk, B. Effect of GOR on gas diffusivity in reservoir-fluid systems. SPE J. 2020, 25, 185–196. [Google Scholar] [CrossRef]
- Campbell, B.T.; Orr, F.M. Flow visualization for CO2/crude-oil displacements. Soc. Pet. Eng. J. 1985, 25, 665–678. [Google Scholar] [CrossRef]
- Bosse, D.; Bart, H.-J. Prediction of diffusion coefficients in liquid systems. Ind. Eng. Chem. Res. 2006, 45, 1822–1828. [Google Scholar] [CrossRef]
- Dill, K.A.; Bromberg, S.; Stigter, D. Molecular Driving Forces: Statistical Thermodynamics in Biology, Chemistry, Physics, and Nanoscience; Garland Science: New York, NY, USA, 2010. [Google Scholar]
- Hayduk, W.; Buckley, W. Effect of molecular size and shape on diffusivity in dilute liquid solutions. Chem. Eng. Sci. 1972, 27, 1997–2003. [Google Scholar] [CrossRef]
- Hayduk, W.; Minhas, B. Correlations for prediction of molecular diffusivities in liquids. Can. J. Chem. Eng. 1982, 60, 295–299. [Google Scholar] [CrossRef]
- Jamialahmadi, M.; Emadi, M.; Müller-Steinhagen, H. Diffusion coefficients of methane in liquid hydrocarbons at high pressure and temperature. J. Pet. Sci. Eng. 2006, 53, 47–60. [Google Scholar] [CrossRef]
- Riazi, M.R.; Whitson, C.H. Estimating diffusion coefficients of dense fluids. Ind. Eng. Chem. Res. 1993, 32, 3081–3088. [Google Scholar] [CrossRef]
- Sigmund, P.M. Prediction of molecular diffusion at reservoir conditions. Part 1-Measurement and prediction of binary dense gas diffusion coefficients. J. Can. Pet. Technol. 1976, 15. [Google Scholar] [CrossRef]
- Einstein, A. Investigations on the Theory of the Brownian Movement; Courier Corporation: Chelmsford, MA, USA, 1956. [Google Scholar]
- Schmidt, T. Mass Transfer by Diffusion. AOSTRA Technical Handbook on Oil Sands, Bitumen and Heavy Oils; Alberta Oil Sands Technology and Research: Edmonton, AB, Canada, 1989. [Google Scholar]
- Nguyen, T.; Ali, S. Effect of nitrogen on the solubility and diffusivity of carbon dioxide into oil and oil recovery by the immiscible WAG process. J. Can. Pet. Technol. 1998, 37. [Google Scholar] [CrossRef]
- Riazi, M.R. A new method for experimental measurement of diffusion coefficients in reservoir fluids. J. Pet. Sci. Eng. 1996, 14, 235–250. [Google Scholar] [CrossRef]
- Sachs, W. The diffusional transport of methane in liquid water: Method and result of experimental investigation at elevated pressure. J. Pet. Sci. Eng. 1998, 21, 153–164. [Google Scholar] [CrossRef]
- Zhang, Y.; Hyndman, C.; Maini, B. Measurement of gas diffusivity in heavy oils. J. Pet. Sci. Eng. 2000, 25, 37–47. [Google Scholar] [CrossRef]
- Creux, P.; Meyer, V.; Cordelier, P.R.; Franco, F.; Montel, F. Diffusivity in heavy oils. In Proceedings of the SPE International Thermal Operations and Heavy Oil Symposium, Calgary, AB, Canada, 1–3 November 2005. [Google Scholar]
- Etminan, S.R.; Maini, B.B.; Hassanzadeh, H.; Chen, Z.J. Determination of concentration dependent diffusivity coefficient in solvent gas heavy oil systems. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 4–7 October 2009. [Google Scholar]
- Zamanian, E.; Hemmati, M.; Beiranvand, M.S. Determination of gas-diffusion and interface-mass-transfer coefficients in fracture-heavy oil saturated porous matrix system. Nafta 2012, 63, 351–358. [Google Scholar]
- Sheikha, H.; Pooladi-Darvish, M.; Mehrotra, A.K. Development of graphical methods for estimating the diffusivity coefficient of gases in bitumen from pressure-decay data. Energy Fuels 2005, 19, 2041–2049. [Google Scholar] [CrossRef]
- Renner, T. Measurement and correlation of diffusion coefficients for CO2 and rich-gas applications. SPE Reserv. Eng. 1988, 3, 517–523. [Google Scholar] [CrossRef]
- Wen, Y.; Kantzas, A. Monitoring bitumen−solvent interactions with low-field nuclear magnetic resonance and X-ray computer-assisted tomography. Energy Fuels 2005, 19, 1319–1326. [Google Scholar] [CrossRef]
- Afsahi, B.; Kantzas, A. Advances in diffusivity measurement of solvents in oil sands. J. Can. Pet. Technol. 2007, 46. [Google Scholar] [CrossRef]
- Song, L.; Kantzas, A.; Bryan, J. Investigation of CO2 diffusivity in heavy oil using X-ray computer-assisted tomography under reservoir conditions. In Proceedings of the SPE International Conference on CO2 Capture, Storage, and Utilization, New Orleans, LA, USA, 10–12 November 2010. [Google Scholar]
- Moganty, S.S.; Baltus, R.E. Diffusivity of carbon dioxide in room-temperature ionic liquids. Ind. Eng. Chem. Res. 2010, 49, 9370–9376. [Google Scholar] [CrossRef]
- Yang, C.; Gu, Y. New experimental method for measuring gas diffusivity in heavy oil by the dynamic pendant drop volume analysis (DPDVA). Ind. Eng. Chem. Res. 2005, 44, 4474–4483. [Google Scholar] [CrossRef]
- Ratnakar, R.R.; Lewis, E.J.; Dindoruk, B. Effect of Dilution on Acoustic and Transport Properties of Reservoir Fluid Systems and Their Interplay. SPE J. 2020, 25, 2867–2880. [Google Scholar] [CrossRef]
- Ratnakar, R.R.; Balakotaiah, V. Exact averaging of laminar dispersion. Phys. Fluids 2011, 23, 023601. [Google Scholar] [CrossRef]
- Ratnakar, R.R.; Balakotaiah, V. Reduced order multimode transient models for catalytic monoliths with micro-kinetics. Chem. Eng. J. 2015, 260, 557–572. [Google Scholar] [CrossRef]
- Aris, R. On the dispersion of a solute in a fluid flowing through a tube. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1956, 235, 67–77. [Google Scholar]
- Taylor, G. Dispersion of a solute in a solvent under laminar conditions. Proc. R. Soc. Lond. Ser. A 1953, 219, 186–203. [Google Scholar]
- Taylor, G.I. Conditions under which dispersion of a solute in a stream of solvent can be used to measure molecular diffusion. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1954, 225, 473–477. [Google Scholar]
- Dindoruk, B.; Ratnakar, R.R.; He, J. Review of recent advances in petroleum fluid properties and their representation. J. Nat. Gas Sci. Eng. 2020, 83, 103541. [Google Scholar] [CrossRef]
- He, J.; Dindoruk, B. Modeling pore proximity using a modified simplified local density approach. J. Nat. Gas Sci. Eng. 2020, 73, 103063. [Google Scholar] [CrossRef]
- Yang, X.; Dindoruk, B.; Lu, L. A comparative analysis of bubble point pressure prediction using advanced machine learning algorithms and classical correlations. J. Pet. Sci. Eng. 2020, 185, 106598. [Google Scholar] [CrossRef]
- Einstein, A. On the motion of small particles suspended in liquids at rest required by the molecular-kinetic theory of heat. Ann. Der Phys. 1905, 17, 208. [Google Scholar]
- Helfferich, F. Ion-exchange kinetics. 1 III. Experimental test of the theory of particle-diffusion controlled ion exchange. J. Phys. Chem. 1962, 66, 39–44. [Google Scholar] [CrossRef]
- Schlögl, R.; Helfferich, F. Comment on the significance of diffusion potentials in ion exchange kinetics. J. Chem. Phys. 1957, 26, 5–7. [Google Scholar] [CrossRef]
- Patlak, C.S. Derivation of an equation for the diffusion potential. Nature 1960, 188, 944–945. [Google Scholar] [CrossRef]
- Lai, W.M.; Mow, V.C.; Sun, D.D.; Ateshian, G.A. On the electric potentials inside a charged soft hydrated biological tissue: Streaming potential versus diffusion potential. J. Biomech. Eng. 2000, 122, 336–346. [Google Scholar] [CrossRef]
- Soret, C. Concentrations differentes d’une dissolution dont deux parties sont a’des temperatures differentes. Arch. Sci. Phys. Nat. 1879, 2, 48–61. [Google Scholar]
- Chapman, S.; Dootson, F. XXII. A note on thermal diffusion. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1917, 33, 248–253. [Google Scholar] [CrossRef]
- Eastman, E. Theory of the Soret effect. J. Am. Chem. Soc. 1928, 50, 283–291. [Google Scholar] [CrossRef]
- Rahman, M.; Saghir, M. Thermodiffusion or Soret effect: Historical review. Int. J. Heat Mass Transf. 2014, 73, 693–705. [Google Scholar] [CrossRef]
- Firoozabadi, A.; Dindoruk, B.; Chang, E. Areal and vertical composition variation in hydrocarbon reservoirs: Formulation and one-D binary results. Entropie 1996, 32, 109–118. [Google Scholar]
- Clusius, K.; Dickel, G. Das Trennrohr. Z. Für Phys. Chem. 1939, 44, 397–450. [Google Scholar] [CrossRef]
- Grodzka, P.G.; Facemire, B. Clusius-Dickel separation: A new look at an old technique. Sep. Sci. 1977, 12, 103–169. [Google Scholar] [CrossRef]
- Loyalka, S.; Chandola, V.; Thomas, L. Clusius-Dickel Effect in a Nuclear Fuel Rod. Nucl. Sci. Eng. 1979, 71, 55–57. [Google Scholar] [CrossRef]
- Müller, G.; Vasaru, G. The Clusius-Dickel Thermal Diffusion Column–50 Years after Its Invention; Taylor & Francis: Abingdon, UK, 1988. [Google Scholar]
- Maxwell, J.C. On the dynamical theory of gases. Proc. R. Soc. Lond. 1866, 15, 167–171. [Google Scholar]
- Stefan, J. Über das Gleichgewicht und die Bewegung, insbesondere die Diffusion von Gasgemengen. Sitzber. Akad. Wiss. Wien 1871, 63, 63–124. [Google Scholar]
- de Groot, S.R.; Mazur, P. Non-Equilibrium Thermodynamics; Courier Corporation: Chelmsford, MA, USA, 1984. [Google Scholar]
- Curie, P. Oeuvres de Pierre Curie: Publiées par les Soins de la Société Française de Physique; Hachette Livre Bnf: France, Paris, 1908. [Google Scholar]
- Onsager, L. Reciprocal relations in irreversible processes. I. Phys. Rev. 1931, 37, 405. [Google Scholar] [CrossRef]
- Onsager, L. Reciprocal relations in irreversible processes. II. Phys. Rev. 1931, 38, 2265. [Google Scholar] [CrossRef] [Green Version]
- Truesdell, C. Rational Thermodynamics: A Course of Lectures on Selected Topics; McGraw-Hill: New York, NY, USA, 1969. [Google Scholar]
- Toor, H. Solution of the linearized equations of multicomponent mass transfer: II. Matrix methods. AIChE J. 1964, 10, 460–465. [Google Scholar] [CrossRef]
- Toor, H. Solution of the linearized equations of multicomponent mass transfer: I. AIChE J. 1964, 10, 448–455. [Google Scholar] [CrossRef]
- Cussler, E.L. Multicomponent Diffusion; Elsevier: Amsterdam, The Netherlands, 2013; Volume 3. [Google Scholar]
- Standart, G.; Taylor, R.; Krishna, R. The Maxwell-Stefan formulation of irreversible thermodynamics for simultaneous heat and mass transfer. Chem. Eng. Commun. 1979, 3, 277–289. [Google Scholar] [CrossRef]
- Taylor, R.; Krishna, R. Multicomponent Mass Transfer; John Wiley & Sons: Hoboken, NJ, USA, 1993; Volume 2. [Google Scholar]
- Curtiss, C.F.; Hirschfelder, J.O. Transport properties of multicomponent gas mixtures. J. Chem. Phys. 1949, 17, 550–555. [Google Scholar] [CrossRef]
- Brown, R. A Brief Account of Microscopical Observations Made... on the Particles Contained in the Pollen of Plants, and on the General Existence of Active Molecules in Organic and Inorganic Bodies. Philos. Mag. 1828, 4, 161–173. [Google Scholar] [CrossRef] [Green Version]
- Brown, R. Mikroskopische Beobachtungen über die im Pollen der Pflanzen enthaltenen Partikeln, und über das allgemeine Vorkommen activer Molecüle in organischen und unorganischen Körpern. Ann. Der Phys. 1828, 90, 294–313. [Google Scholar] [CrossRef] [Green Version]
- Richardson, L.F. Atmospheric diffusion shown on a distance-neighbour graph. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1926, 110, 709–737. [Google Scholar]
- Buldyrev, S.V.; Goldberger, A.L.; Havlin, S.; Peng, C.-K.; Stanley, H.E. Fractals in biology and medicine: From DNA to the heartbeat. In Fractals in Science; Springer: Berlin/Heidelberg, Germany, 1994; pp. 49–88. [Google Scholar]
- Koscielny-Bunde, E.; Bunde, A.; Havlin, S.; Roman, H.E.; Goldreich, Y.; Schellnhuber, H.-J. Indication of a universal persistence law governing atmospheric variability. Phys. Rev. Lett. 1998, 81, 729. [Google Scholar] [CrossRef]
- Bronstein, I.; Israel, Y.; Kepten, E.; Mai, S.; Shav-Tal, Y.; Barkai, E.; Garini, Y. Transient anomalous diffusion of telomeres in the nucleus of mammalian cells. Phys. Rev. Lett. 2009, 103, 018102. [Google Scholar] [CrossRef] [Green Version]
- Weigel, A.V.; Simon, B.; Tamkun, M.M.; Krapf, D. Ergodic and nonergodic processes coexist in the plasma membrane as observed by single-molecule tracking. Proc. Natl. Acad. Sci. USA 2011, 108, 6438–6443. [Google Scholar] [CrossRef] [Green Version]
- Sagi, Y.; Brook, M.; Almog, I.; Davidson, N. Observation of anomalous diffusion and fractional self-similarity in one dimension. Phys. Rev. Lett. 2012, 108, 093002. [Google Scholar] [CrossRef]
- Regner, B.M.; Vučinić, D.; Domnisoru, C.; Bartol, T.M.; Hetzer, M.W.; Tartakovsky, D.M.; Sejnowski, T.J. Anomalous diffusion of single particles in cytoplasm. Biophys. J. 2013, 104, 1652–1660. [Google Scholar] [CrossRef] [Green Version]
- Jeon, J.-H.; Leijnse, N.; Oddershede, L.B.; Metzler, R. Anomalous diffusion and power-law relaxation of the time averaged mean squared displacement in worm-like micellar solutions. New J. Phys. 2013, 15, 045011. [Google Scholar] [CrossRef]
- Colbrook, M.J.; Ma, X.; Hopkins, P.F.; Squire, J. Scaling laws of passive-scalar diffusion in the interstellar medium. Mon. Not. R. Astron. Soc. 2017, 467, 2421–2429. [Google Scholar] [CrossRef] [Green Version]
- Katz, O.S.; Efrati, E. Self-driven fractional rotational diffusion of the harmonic three-mass system. Phys. Rev. Lett. 2019, 122, 024102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oliveira, F.A.; Ferreira, R.; Lapas, L.C.; Vainstein, M.H. Anomalous diffusion: A basic mechanism for the evolution of inhomogeneous systems. Front. Phys. 2019, 7, 18. [Google Scholar] [CrossRef] [Green Version]
- Sabri, A.; Xu, X.; Krapf, D.; Weiss, M. Elucidating the origin of heterogeneous anomalous diffusion in the cytoplasm of mammalian cells. Phys. Rev. Lett. 2020, 125, 058101. [Google Scholar] [CrossRef]
- Zhang, Z.; Angst, U. A dual-permeability approach to study anomalous moisture transport properties of cement-based materials. Transp. Porous Media 2020, 135, 59–78. [Google Scholar] [CrossRef]
- Weisz, P. Zeolites-new horizons in catalysis. Chemtech 1973, 498–505. [Google Scholar] [CrossRef]
- Weisz, P. Sorption-diffusion in heterogeneous systems. Part 1.—General sorption behaviour and criteria. Trans. Faraday Soc. 1967, 63, 1801–1806. [Google Scholar] [CrossRef]
- Hands, B. Cryopumping. Vacuum 1987, 37, 621–627. [Google Scholar] [CrossRef]
- Hobson, J. Cryopumping. J. Vac. Sci. Technol. 1973, 10, 73–79. [Google Scholar] [CrossRef]
- Ratnakar, R.R.; Gupta, N.; Zhang, K.; van Doorne, C.; Fesmire, J.; Dindoruk, B.; Balakotaiah, V. Hydrogen supply chain and challenges in large-scale LH2 storage and transportation. Int. J. Hydrogen Energy 2021, 46, 24149–24168. [Google Scholar] [CrossRef]
- Reid, R.C.; Prausnitz, J.M.; Poling, B.E. The Properties of Gases and Liquids; McGraw-Hill Professional Pub.: New York, NY, USA, 1987. [Google Scholar]
- Lennard-Jones, J.E. Cohesion. Proc. Phys. Soc. (1926–1948) 1931, 43, 461. [Google Scholar] [CrossRef]
- Jones, J.E. On the determination of molecular fields.—I. From the variation of the viscosity of a gas with temperature. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1924, 106, 441–462. [Google Scholar]
- Jones, J.E. On the determination of molecular fields.—II. From the equation of state of a gas. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1924, 106, 463–477. [Google Scholar]
- Neufeld, P.D.; Janzen, A.; Aziz, R.A. Empirical equations to calculate 16 of the transport collision integrals Ω (l, s)* for the Lennard-Jones (12–6) potential. J. Chem. Phys. 1972, 57, 1100–1102. [Google Scholar] [CrossRef]
- Fuller, E.N.; Schettler, P.D.; Giddings, J.C. New method for prediction of binary gas-phase diffusion coefficients. Ind. Eng. Chem. 1966, 58, 18–27. [Google Scholar] [CrossRef]
- Pollard, W.; Present, R.D. On gaseous self-diffusion in long capillary tubes. Phys. Rev. 1948, 73, 762. [Google Scholar] [CrossRef]
- Wohlfahrt, K. The design of catalyst pellets. Chem. Eng. Sci. 1982, 37, 283–290. [Google Scholar] [CrossRef]
- Wilke, C.; Chang, P. Correlation of diffusion coefficients in dilute solutions. AIChE J. 1955, 1, 264–270. [Google Scholar] [CrossRef]
- Rao, S.S.; Bennett, C. Steady state technique for measuring fluxes and diffusivities in binary liquid systems. AIChE J. 1971, 17, 75–81. [Google Scholar] [CrossRef]
- Graham, T. A short account of experimental researches on the diffusion of gases through each other, and their separation by mechanical means. Q. J. Sci. Lit. Art 1829, 27, 74–83. [Google Scholar]
- Stokes, R. The diffusion coefficients of eight uni-univalent electrolytes in aqueous solution at 25. J. Am. Chem. Soc. 1950, 72, 2243–2247. [Google Scholar] [CrossRef]
- Stokes, R. Integral diffusion coefficients of potassium chloride solutions for calibration of diaphragm cells. J. Am. Chem. Soc. 1951, 73, 3527–3528. [Google Scholar] [CrossRef]
- Balakotaiah, V.; Ratnakar, R.R. On the use of transfer and dispersion coefficient concepts in low-dimensional diffusion–convection-reaction models. Chem. Eng. Res. Des. 2010, 88, 342–361. [Google Scholar] [CrossRef]
- Wicke, E.; Kallenbach, R. Counter diffusion through porous pellet. Kolloid Z. 1941, 97, 135. [Google Scholar] [CrossRef]
- Duduković, M. An analytical solution for the transient response in a diffusion cell of the Wicke-Kallenbach type. Chem. Eng. Sci. 1982, 37, 153–158. [Google Scholar] [CrossRef]
- Soukup, K.; Schneider, P.; Šolcová, O. Wicke–Kallenbach and Graham’s diffusion cells: Limits of application for low surface area porous solids. Chem. Eng. Sci. 2008, 63, 4490–4493. [Google Scholar] [CrossRef]
- Howell, S.K. The Development and Use of the Rayleigh Interferometer to Study Molecular Diffusion in an Applied Magnetic Field; University of British Columbia: Vancouver, BC, Canada, 1983. [Google Scholar]
- Bollenbeck, P.H.; Ramirez, W.F. Use of a Rayleigh Interferometer for Membrane Transport Studies. Ind. Eng. Chem. Fundam. 1974, 13, 385–393. [Google Scholar] [CrossRef]
- Holmes, J.T.; Wilke, C.R.; Olander, D.R. Convective mass transfer in a diaphragm diffusion cell. J. Phys. Chem. 1963, 67, 1469–1472. [Google Scholar] [CrossRef]
- Boussinesq, J. Theorie de l’ecoulement tourbillant. Mem. Acad. Sci. 1877, 23, 46. [Google Scholar]
- Evans, E.; Kenney, C. Gaseous dispersion in laminar flow through a circular tube. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1965, 284, 540–550. [Google Scholar]
- Crank, J. The Mathematics of Diffusion; Clarendon Press: Oxford, UK, 1956; p. 347. [Google Scholar]
- Miller, D.G. The History of interferometry for measuring diffusion coefficients. J. Solut. Chem. 2014, 43, 6–25. [Google Scholar] [CrossRef]
- Rard, J.A.; Miller, D.G. Mutual diffusion coefficients of SrCl2–H2O and CsCl—H2O at 25 C from Rayleigh interferometry. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1982, 78, 887–896. [Google Scholar] [CrossRef]
- Civan, F.; Rasmussen, M.L. Accurate measurement of gas diffusivity in oil and brine under reservoir conditions. In Proceedings of the SPE Production and Operations Symposium, Oklahoma City, OK, USA, 24–27 March 2001. [Google Scholar]
- Civan, F.; Rasmussen, M.L. Improved measurement of gas diffusivity for miscible gas flooding under nonequilibrium vs. equilibrium conditions. In Proceedings of the SPE/DOE Improved Oil Recovery Symposium, Tulsa, OK, USA, 13–17 April 2002. [Google Scholar]








| Atomic and Structural Diffusion Volume Increment for Various Substances | |||||||
|---|---|---|---|---|---|---|---|
| C | 15.9 | H | 2.31 | O | 6.11 | N | 4.54 |
| F | 14.7 | Cl | 21.0 | Br | 21.9 | I | 29.8 |
| S | 22.9 | Atomic ring or Heterocyclic ring | −18.3 | ||||
| Diffusion volume for simple molecules | |||||||
| He | 2.67 | Ne | 5.98 | Ar | 16.2 | Kr | 24.5 |
| Xe | 32.7 | H2 | 6.12 | D2 | 6.84 | N2 | 18.5 |
| O2 | 16.3 | CO | 19.0 | CO2 | 26.9 | N2O | 35.9 |
| NH3 | 20.7 | H2O | 13.1 | SF6 | 71.3 | Cl2 | 38.4 |
| Br2 | 69.0 | SO2 | 41.8 | Air | 19.7 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ratnakar, R.R.; Dindoruk, B. The Role of Diffusivity in Oil and Gas Industries: Fundamentals, Measurement, and Correlative Techniques. Processes 2022, 10, 1194. https://doi.org/10.3390/pr10061194
Ratnakar RR, Dindoruk B. The Role of Diffusivity in Oil and Gas Industries: Fundamentals, Measurement, and Correlative Techniques. Processes. 2022; 10(6):1194. https://doi.org/10.3390/pr10061194
Chicago/Turabian StyleRatnakar, Ram R., and Birol Dindoruk. 2022. "The Role of Diffusivity in Oil and Gas Industries: Fundamentals, Measurement, and Correlative Techniques" Processes 10, no. 6: 1194. https://doi.org/10.3390/pr10061194
APA StyleRatnakar, R. R., & Dindoruk, B. (2022). The Role of Diffusivity in Oil and Gas Industries: Fundamentals, Measurement, and Correlative Techniques. Processes, 10(6), 1194. https://doi.org/10.3390/pr10061194







