Exergy Analysis of Reactive Distillation Coupled with High-Pressure Column for the Synthesis of Dimethyl Carbonate
Abstract
:1. Introduction
- The system was also solved using Aspen Plus for the comparison purpose of a steady-state simulation; however, ProSimPlus was used mainly in this work, because it is still uniquely capable of thermodynamic analysis, especially the exergy balance analysis.
- An exergy analysis was performed for the overall DMC system to determine the irreversibilities (or exergy destruction) and exergy efficiencies while keeping the DMC product as its desired specifications.
- A wide range of parametric study was conducted via figuring out the effect of the main operational variables of the DMC plant on the irreversibilities, exergy efficiency, and DMC purity.
2. Process System Modeling and Simulation
2.1. Chemical Reaction Rate
2.2. Phase Equilibria Models
2.3. Thermodynamic Analysis
2.4. Process System Simulation
3. Results and Discussion
3.1. RD Reflux Ratio
3.2. HP Reflux Ratio
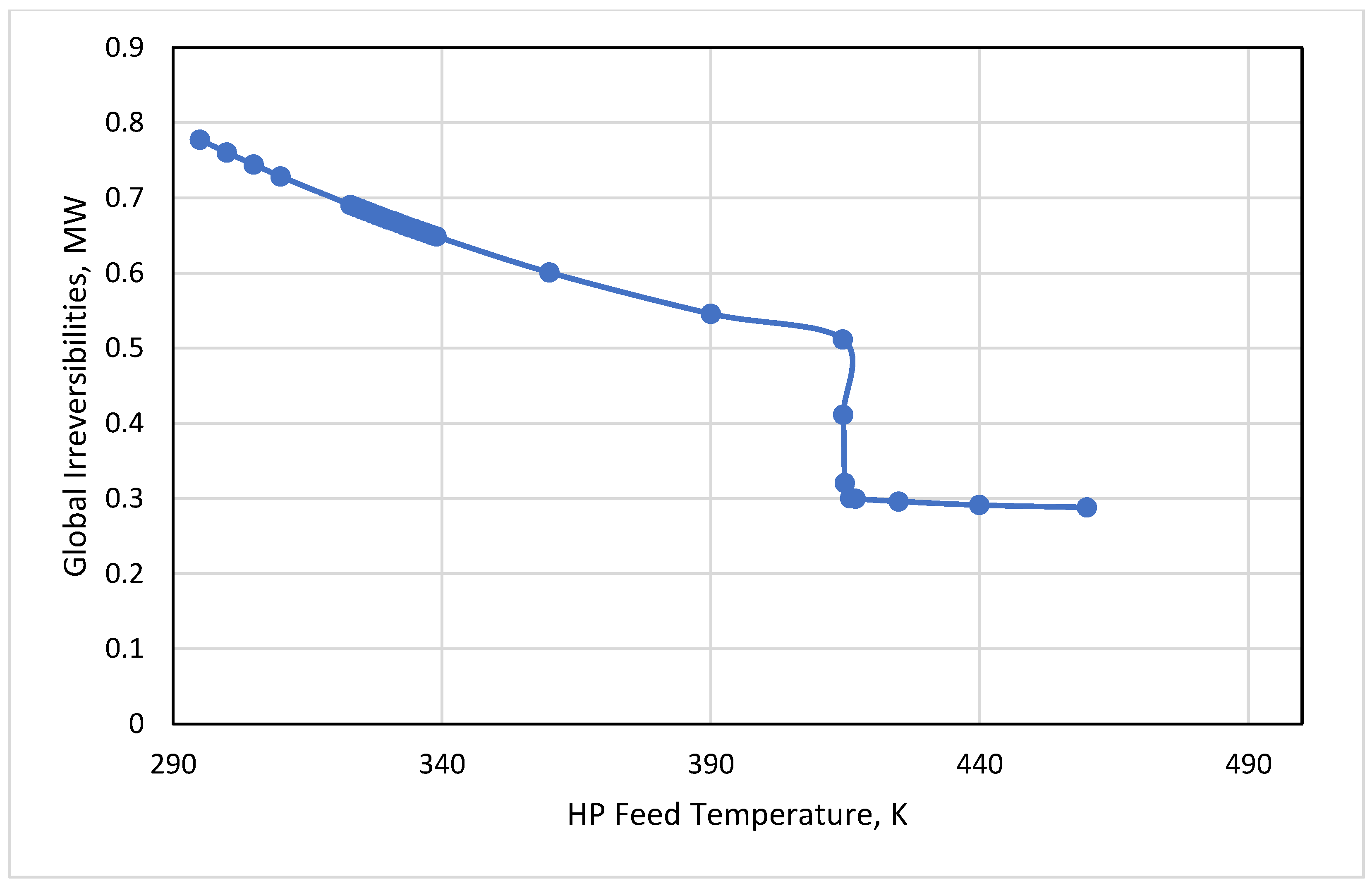
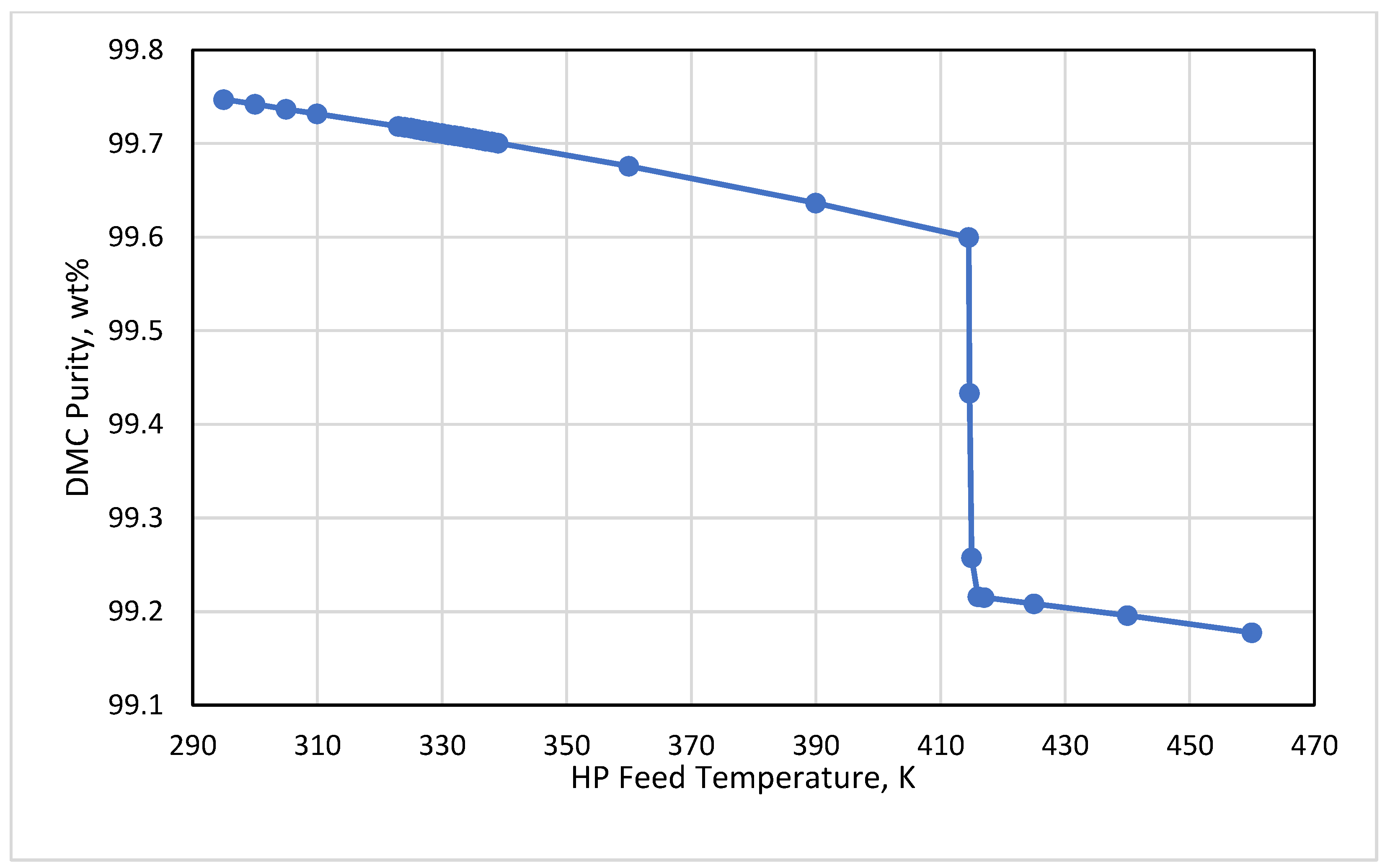
3.3. HP Feed Temperature
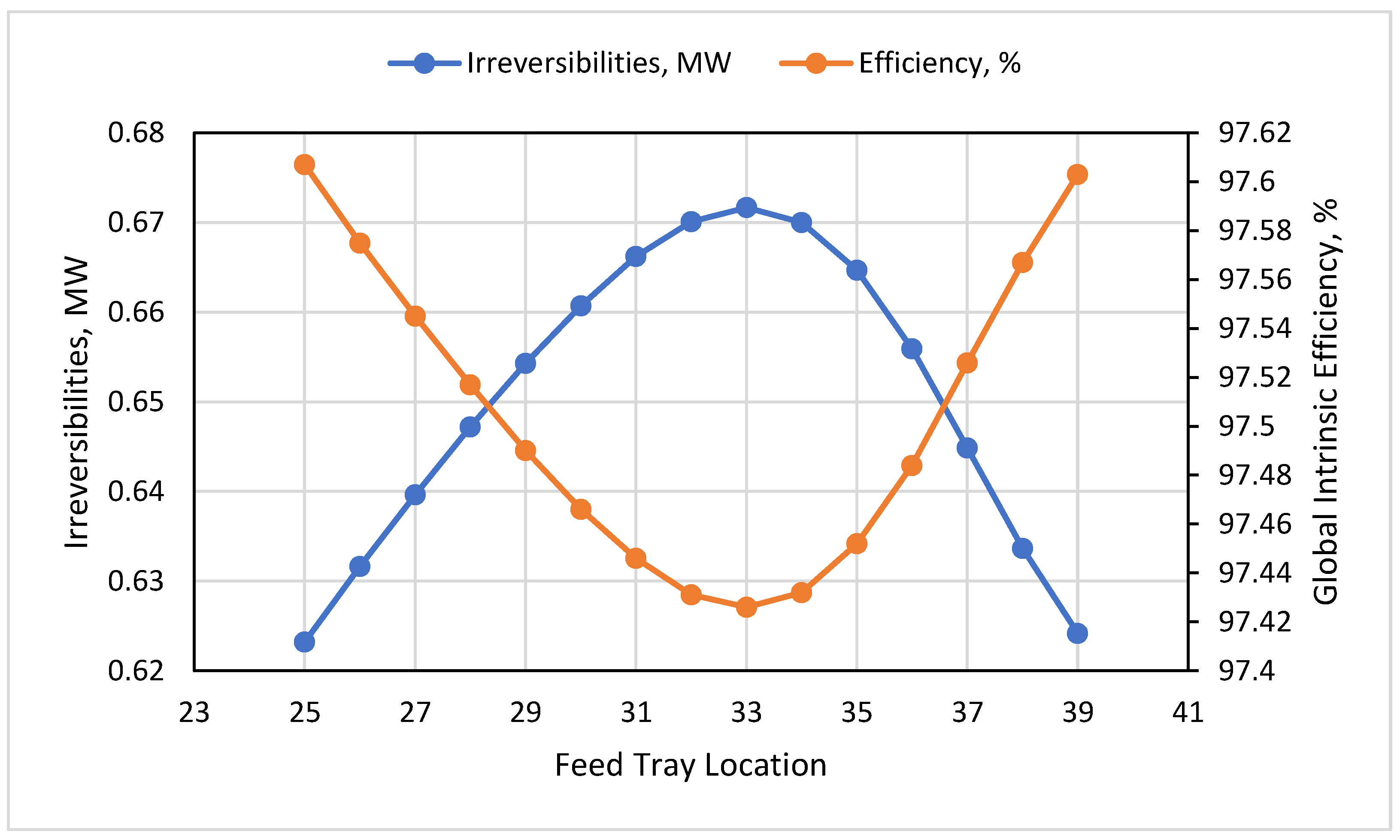
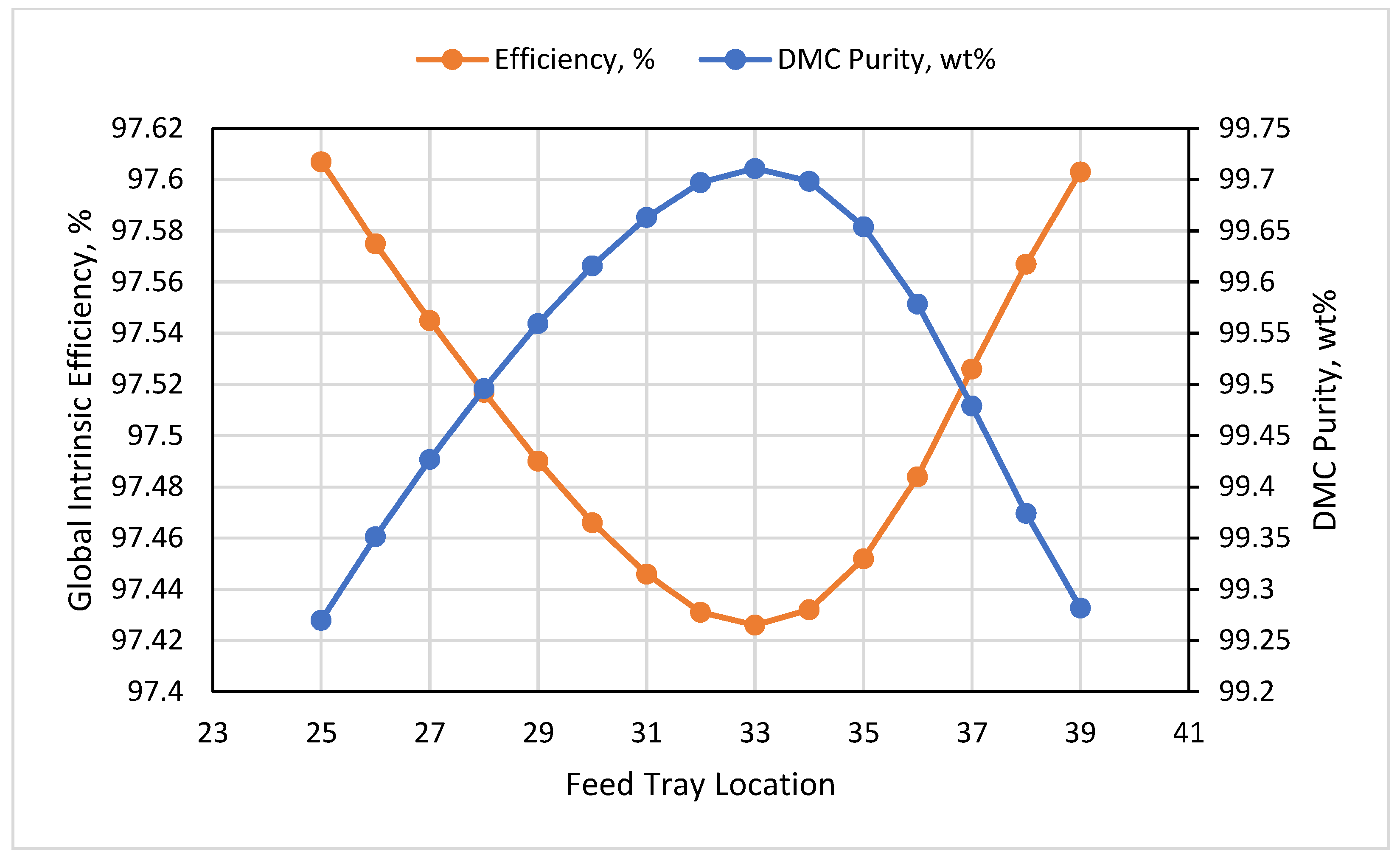
3.4. HP Feed Tray
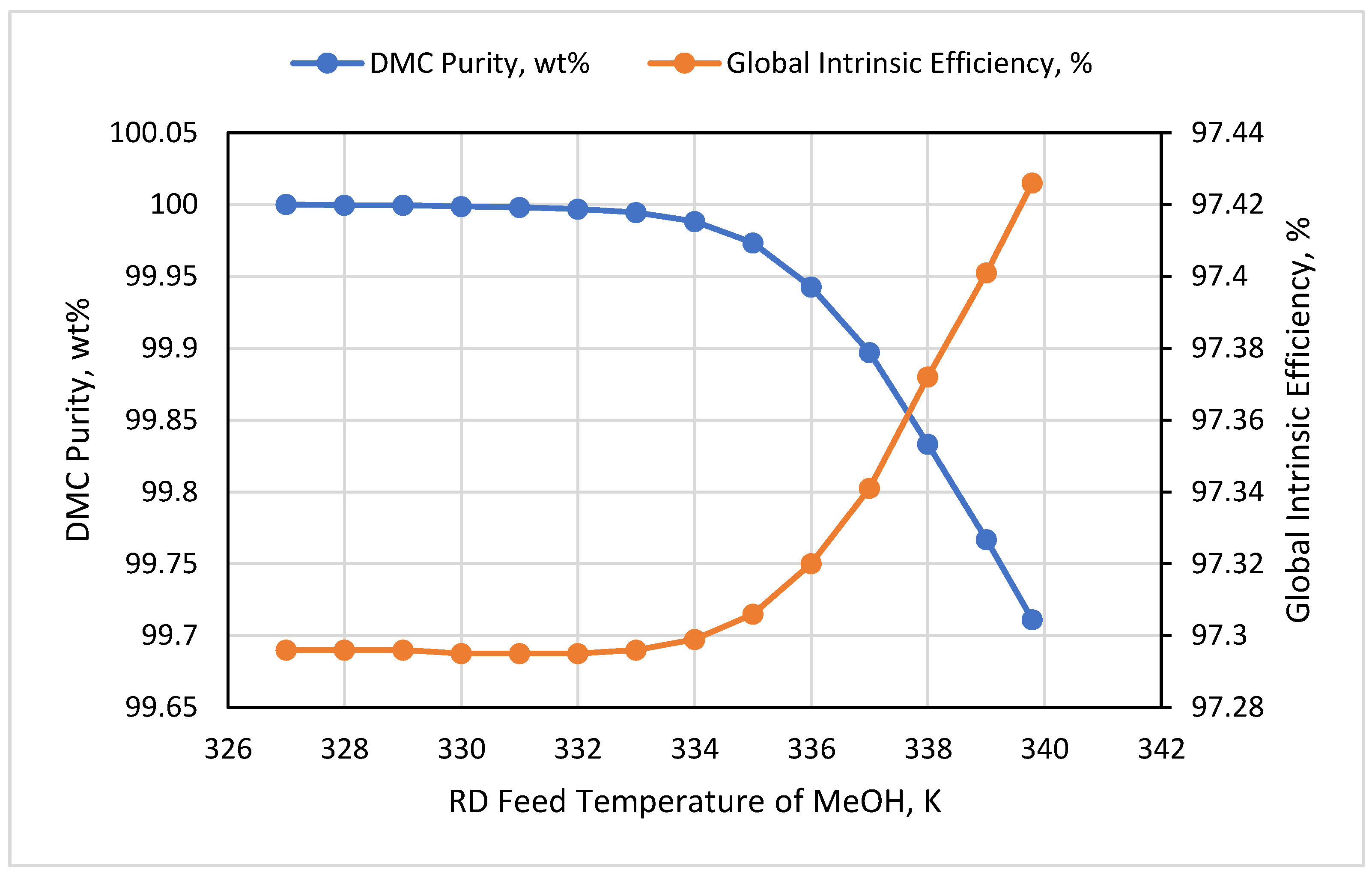
3.5. RD Feed Temperature
4. Conclusions
- The positive variation in the RD reflux ratio played a crucial role on raising both the global irreversibilities and DMC purity. The results showed the critical change in destruction and purity after reaching the optimal reflux ratio used in the simulation (0.87), while there was no effect on the reboiler and condenser duties.
- The effect of the HP reflux ratio was more feasible. The change in this ratio from 0.5 to 1.55 proportionally increased the irreversibilities and decreased both the exergy efficiency and the DMC purity. A major increase was observed in the HP reboiler and condenser duties. For the same reflux ratio range from 0.5 to 1.55, the reboiler duty was increased from 4.74 MW to 7.75 MW, respectively. The condenser duty was increased from 3.85 MW to 6.83 MW for the same range of the reflux ratio.
- Keeping the HP feed temperature at its bubble condition or below this point was of high importance to hold the product at the desired purity. A tradeoff between the purity and irreversibilities could be performed by the process engineer to minimize the energy based on the economic targets.
- The impact of the feed tray reflected that at tray 33, the exergy destruction was at maximum at 0.67 MW, and the global intrinsic efficiency was at a minimum at 97.43%, while the maximum DMC purity was determined to be 99.7 wt% at tray 33.
- The exergy destruction had low change under the effect of the RD feed temperatures. Effective energy management can be achieved when holding these temperatures at their bubble points.
Funding
Acknowledgments
Conflicts of Interest
References
- Pyo, S.-H.; Park, J.H.; Chang, T.-S.; Hatti-Kaul, R. Dimethyl carbonate as a green chemical. Curr. Opin. Green Sustain. Chem. 2017, 5, 61–66. [Google Scholar] [CrossRef]
- Tundo, P.; Selva, M. The Chemistry of Dimethyl Carbonate. Acc. Chem. Res. 2002, 35, 706–716. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Li, J.; Wang, L.; Jiang, H.; Qiu, T. Novel Procedure for the Synthesis of Dimethyl Carbonate by Reactive Distillation. Ind. Eng. Chem. Res. 2014, 53, 3321–3328. [Google Scholar] [CrossRef]
- Fukuoka, S.; Fukawa, I.; Tojo, M.; Oonishi, K.; Hachiya, H.; Aminaka, M.; Hasegawa, K.; Komiya, K. A Novel Non-Phosgene Process for Polycarbonate Production from CO2: Green and Sustainable Chemistry in Practice. Catal. Surv. Asia 2010, 14, 146–163. [Google Scholar] [CrossRef]
- Deng, W.; Shi, L.; Yao, J.; Zhang, Z. A review on transesterification of propylene carbonate and methanol for dimethyl carbonate synthesis. Carbon Resour. Convers. 2019, 2, 198–212. [Google Scholar] [CrossRef]
- Fang, Y.-J.; Xiao, W.-D. Experimental and modeling studies on a homogeneous reactive distillation system for dimethyl carbonate synthesis by transesterification. Sep. Purif. Technol. 2004, 34, 255–263. [Google Scholar] [CrossRef]
- Hsu, K.-Y.; Hsiao, Y.-C.; Chien, I.-L. Design and Control of Dimethyl Carbonate−Methanol Separation via Extractive Distillation in the Dimethyl Carbonate Reactive-Distillation Process. Ind. Eng. Chem. Res. 2009, 49, 735–749. [Google Scholar] [CrossRef]
- Huang, Z.; Lin, Y.; Wang, X.; Ye, C.; Li, L. Optimization and control of a reactive distillation process for the synthesis of dimethyl carbonate. Chin. J. Chem. Eng. 2017, 25, 1079–1090. [Google Scholar] [CrossRef]
- Kenney, W.F. Energy Conservation in the Process Industries; Academic Press: San Diego, CA, USA. [CrossRef]
- Dincer, I.; Zamfirescu, C. Advanced Power Generation Systems. Available online: http://elsevier.com/locate/permissions (accessed on 15 June 2022).
- Ghannadzadeh, A.; Thery-Hetreux, R.; Baudouin, O.; Baudet, P.; Floquet, P.; Joulia, X. General methodology for exergy balance in ProSimPlus® process simulator. Energy 2012, 44, 38–59. [Google Scholar] [CrossRef] [Green Version]
- Shi, Y.; Liu, H.; Wang, K.; Xiao, W.; Hu, Y. Measurements of isothermal vapor–liquid equilibrium of binary methanol/dimethyl carbonate system under pressure. Fluid Phase Equilibria 2005, 234, 1–10. [Google Scholar] [CrossRef]
- Kumar, P.; Srivastava, V.C.; Mishra, I.M. Dimethyl carbonate synthesis via transesterification of propylene carbonate with methanol by ceria-zinc catalysts: Role of catalyst support and reaction parameters. Korean J. Chem. Eng. 2015, 32, 1774–1783. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Wei, T.; Sun, Y.; Wei, W.; Zhong, B. Synthesis of Dimethyl Carbonate from Propylene Carbonate and Methanol over Mesoporous Solid Base Catalyst; Marcel Dekker, Inc.: New York, NY, USA, 2003; pp. 659–666. [Google Scholar]








| Component ID | Temperature/K |
|---|---|
| MeOH | 337.69 |
| DMC | 363.37 |
| PC | 514.97 |
| PG | 460.76 |
| Pressure/kPa | Predicted Value by ProSimPlusTM | Experimental Value [12] | ||
|---|---|---|---|---|
| Tb/K | Mass Fraction | Tb/K | Mass Fraction | |
| 101.3 | 336.80 | (0.6996, 0.3004) | 337.35 | (0.7000, 0.3000) |
| 405.2 | 377.15 | (0.7864, 0.2136) | 377.15 | (0.7929, 0.2071) |
| 607.8 | 391.06 | (0.8170, 0.1830) | 391.15 | (0.8249, 0.1751) |
| 1013.0 | 410.23 | (0.8591, 0.1409) | 411.15 | (0.8761, 0.1239) |
| 1519.5 | 426.90 | (0.8951, 0.1049) | 428.15 | (0.9300, 0.0700) |
| Pressure/kPa | Predicted Value by ProSimPlusTM | Predicted Value by Aspen PlusTM | ||
|---|---|---|---|---|
| Tb/K | Mass Fraction | Tb/K | Mass Fraction | |
| 101.3 | 336.80 | (0.6996, 0.3004) | 336.80 | (0.7007, 0.2993) |
| 405.2 | 377.15 | (0.7864, 0.2136) | 377.18 | (0.7910, 0.2090) |
| 607.8 | 391.06 | (0.8170, 0.1830) | 391.10 | (0.8240, 0.1760) |
| 1013.0 | 410.23 | (0.8591, 0.1409) | 410.28 | (0.8713, 0.1287) |
| 1519.5 | 426.90 | (0.8951, 0.1049) | 426.94 | (0.9677, 0.0323) |
| Original Design [3] | Optimized Design [8] | Simulated Design (Current Study) | ||||
|---|---|---|---|---|---|---|
| RD | HP | RD | HP | RD | HP | |
| Total Stage | 35 | 23 | 45 | 42 | 45 | 42 |
| Pressure/MPa | 0.1 | 1.1 | 0.1 | 1.1 | 0.1 | 1.1 |
| Feed Stage | NF1 = 10 | NF = 10 | NF1 = 5 | NF = 33 | NF1 = 5 | NF = 33 |
| NF2 = 30 | NF2 = 45 | NF2 = 45 | ||||
| NFR = 16 | NFR = 16 | NFR = 16 | ||||
| Reflux Ratio (Rr) | 2.34 | 2.5 | 0.87 | 1.37 | 0.87 | 1.37 |
| Condenser Duty/MW | 8.03 | 5.99 | 6.12 | 5.95 | 6.10 | 6.34 |
| Reboiler Duty/MW | 8.27 | 6.30 | 5.57 | 6.98 | 5.57 | 7.26 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alharthi, M.A. Exergy Analysis of Reactive Distillation Coupled with High-Pressure Column for the Synthesis of Dimethyl Carbonate. Processes 2022, 10, 1219. https://doi.org/10.3390/pr10061219
Alharthi MA. Exergy Analysis of Reactive Distillation Coupled with High-Pressure Column for the Synthesis of Dimethyl Carbonate. Processes. 2022; 10(6):1219. https://doi.org/10.3390/pr10061219
Chicago/Turabian StyleAlharthi, Mathkar A. 2022. "Exergy Analysis of Reactive Distillation Coupled with High-Pressure Column for the Synthesis of Dimethyl Carbonate" Processes 10, no. 6: 1219. https://doi.org/10.3390/pr10061219
APA StyleAlharthi, M. A. (2022). Exergy Analysis of Reactive Distillation Coupled with High-Pressure Column for the Synthesis of Dimethyl Carbonate. Processes, 10(6), 1219. https://doi.org/10.3390/pr10061219






