Influence of Step Casings on the Cavitation Characteristics of Inducers
Abstract
:1. Introduction
2. Materials and Methodology
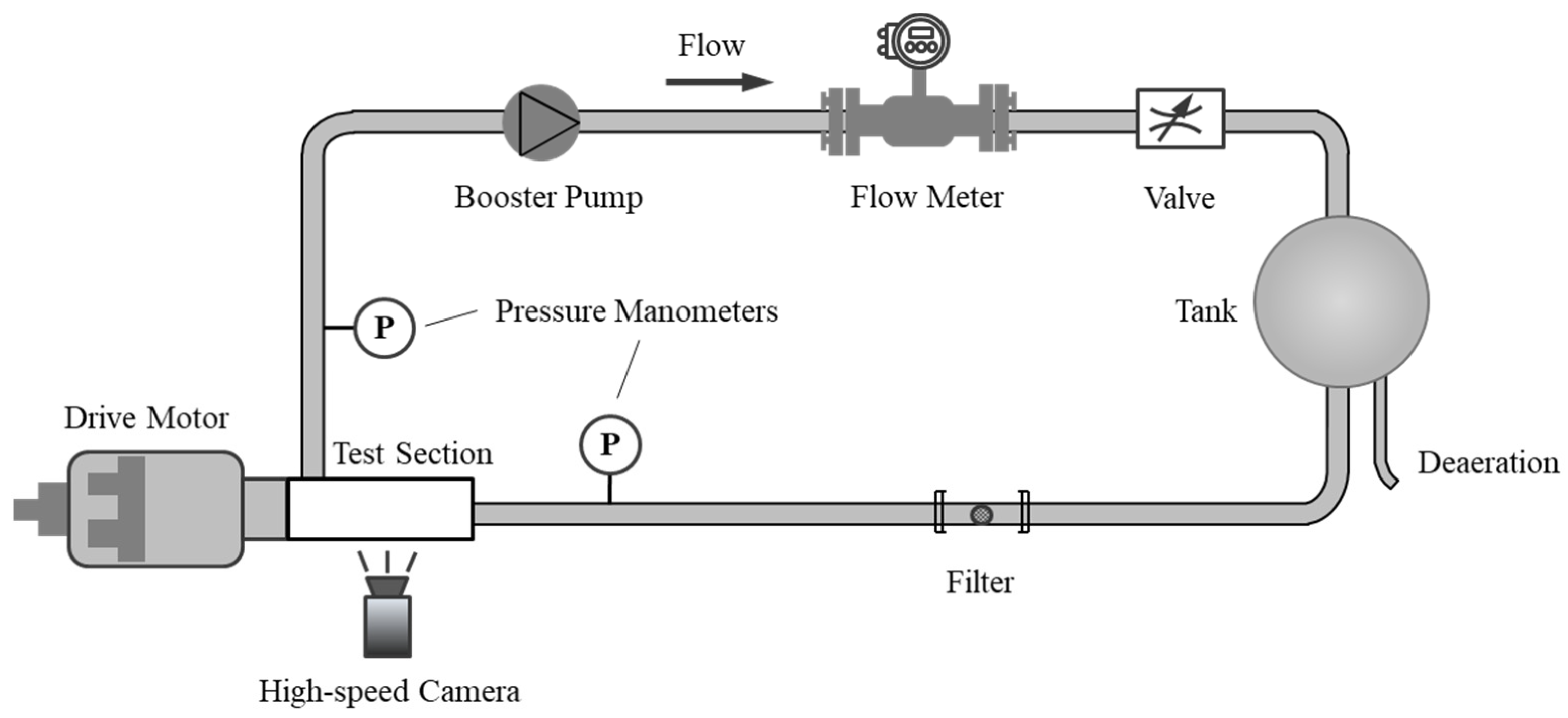
2.1. Experimental Set-Up
2.2. Geometry of the Test Inducer (Model O)
2.3. Original Casing and Step Casing Strategy
2.4. Numerical Methodology
3. Results and Discussion
3.1. Numerical Validation
3.2. Effects of Step Casing Models
3.2.1. Cavitation Performance
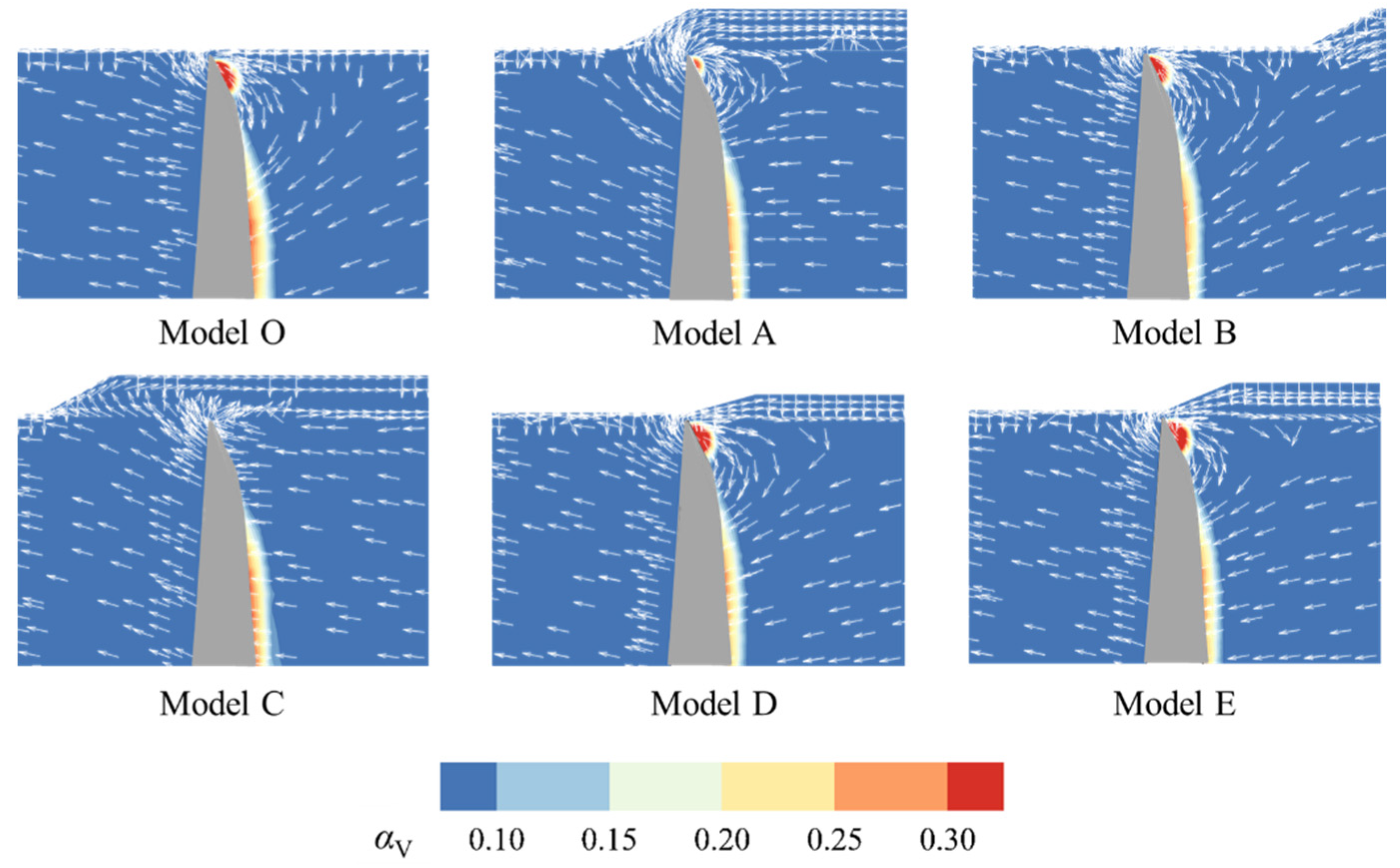
3.2.2. Cavity Structures
3.2.3. Blade Loading
3.2.4. Radial Forces
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tsujimoto, Y.; Yoshida, Y.; Watanabe, Y.; Hashimoto, T. Observations of Oscillating Cavitation of an Inducer. J. Fluids Eng. 1997, 119, 775–781. [Google Scholar] [CrossRef]
- Tsujimoto, Y. Cavitation Instabilities in Inducers. In Design and Analysis of High Speed Pumps; Educational Notes RTO-EN-AVT-143, 8-2–8-26; von Karman Institute: Sint-Genesius-Rode, Belgium, 2006; Available online: https://www.sto.nato.int/publications/STO%20Educational%20Notes/RTO-EN-AVT-143/EN-AVT-143-08.pdf (accessed on 21 January 2022).
- Xiang, L.; Tang, Y.; Chen, H.; Xu, K.F. Experimental investigation of cavitation instabilities in inducer with different tip clearances. Chin. J. Aeronaut. 2021, 34, 168–177. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, E.Z.; Tan, Y.H. Rotating cavitation of the high-speed rotational inducer of LRE. J. Propuls. Technol. 2009, 30, 390–395. (In Chinese) [Google Scholar]
- Wang, Y.; Manfredi, M.; Pasini, A.; Spakovszky, Z. Dynamic Model-Based Identification of Cavitation Compliance and Mass Flow Gain Factor in Rocket Engine Turbopump Inducers. J. Eng. Gas Turbines Power 2021, 143, 021011. [Google Scholar] [CrossRef]
- Zhang, H.; Zuo, Z.; Morch, K.A.; Liu, S. Thermodynamic effects on Venturi cavitation characteristics. Phys. Fluids 2019, 31, 097107. [Google Scholar]
- Lettieri, C.; Spakovszky, Z.S.; Jackson, D.; Schwille, J. Characterization of Cavitation Instabilities in a Four-Bladed Turbopump Inducer. J. Propul. Power 2018, 34, 510–520. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, H.C.; Chen, H.; Li, Y.P.; Zuo, Z.G.; Liu, S.H. Geometrical optimization of an inducer with respect to rotating cavitation generated radial forces by using an orthogonal experiment. J. Appl. Fluid Mech. 2018, 11, 1591–1598. [Google Scholar] [CrossRef]
- Fujii, A.; Uchiumi, M.; Kurokawa, J.; Tsujimoto, Y. Suppression of Rotating Cavitation in an Inducer by J-Groove. Trans. Jpn. Soc. Mech. Eng. Ser. B 2006, 72, 2496–2504. [Google Scholar] [CrossRef]
- Shimiya, N.; Fujii, A.; Horiguchi, H.; Uchiumi, M.; Kurokawa, J.; Tsujimoto, Y. Suppression of Cavitation Instabilities in an Inducer by J Groove. J. Fluids Eng. 2008, 130, 021302. [Google Scholar] [CrossRef]
- Choi, Y.D.; Kurokawa, J.; Imamura, H. Suppression of Cavitation in Inducers by J-Grooves. J. Fluids Eng. 2007, 129, 15. [Google Scholar] [CrossRef]
- Kang, D.; Arimoto, Y.; Yonezawa, K.; Hironori, H.; Kawata, Y.; Hah, C.I.; Tsujimo, Y. Suppression of Cavitation Instabilities in an Inducer by Circumferential Groove and Explanation of Higher Frequency Components. Int. J. Fluid Mach. Syst. 2010, 3, 137–149. [Google Scholar] [CrossRef]
- Li, X.; Hu, S.C.; Zhou, Y.J.; Xiao, L.M.; Liu, C.; Wang, J. Study on Cavitation Performance of a Inducer with Helical Grooves. J. Propuls. Technol. 2020, 41, 553–558. (In Chinese) [Google Scholar] [CrossRef]
- Timushev, S.; Klimenko, D.; Kazennov, I.; Li, J.W. Unsteady Flow and Pressure Pulsations in a Model Axial-Vortex Stage Inducer. J. Propuls. Technol. 2019, 40, 1458–1466. [Google Scholar] [CrossRef]
- Kamijo, K.; Yoshida, M.; Tsujimoto, Y. Hydraulic and Mechanical Performance of LE-7 LOX Pump Inducer. J. Propuls. Power 1993, 9, 819–826. [Google Scholar] [CrossRef]
- Fujii, A.; Azuma, S.; Yoshida, Y.; Tsujimoto, Y.; Uchiumi, M.; Warashina, S. Effects of Inlet Casing Geometries on Unsteady Cavitation in an Inducer. Trans. Jpn. Soc. Mech. Eng. B 2004, 16, 1450–1458. [Google Scholar] [CrossRef]
- Shimagaki, M.; Kimura, T.; Hashimoto, T.; Watanabe, M. Investigation of Backflow Structure in a Turbopump Inducer with the PIV Method. In Proceedings of the 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Cincinnati, OH, USA, 8–11 July 2007. [Google Scholar]
- Shimagaki, M.; Hashimoto, T.; Watanabe, M.; Hasegawa, S. PIV observation of Prewhirl Flow Upstream of a Turbopump Inducer. J. Flow Vis. Image Process. 2010, 17, 85–98. [Google Scholar] [CrossRef]
- Yu, L.; Zhang, H.; Chen, H.; Zuo, Z.; Liu, S. Numerical study on the influence of step casing on cavitating flows and instabilities in inducers with equal and varying pitches. Processes 2020, 8, 1103. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Zwart, P.J.; Gerber, A.G.; Belamri, T. A two-phase flow model for predicting cavitation dynamics. In Proceedings of the Fifth International Conference on Multiphase Flow (ICMF), Yokohama, Japan, 30 May–4 June 2004. [Google Scholar]















| Parameter | Value |
|---|---|
| Number of blades, N | 3 |
| Blade tip diameter, D0 (mm) | 100 |
| Hub inlet diameter, D1 (mm) | 15.5 |
| Hub outlet diameter, D2 (mm) | 35.5 |
| Blade root thickness, Tr (mm) | 5.25 |
| Blade tip thickness, Tt (mm) | 2 |
| Sweepback angle of leading edge, α (°) | 120 |
| Tip clearance, τ (mm) | 0.5 |
| Model | O | A | B | C | D | E |
|---|---|---|---|---|---|---|
| Ψ1 (at σ1 = 0.5) | 0.158 | 0.150 | 0.156 | 0.140 | 0.157 | 0.158 |
| Percentage | baseline | 94.9% | 98.7% | 88.6% | 99.4% | 100% |
| Ψ2 (at σ2 = 0.074) | 0.156 | 0.150 | 0.154 | 0.145 | 0.155 | 0.157 |
| Percentage | baseline | 96.2% | 98.7% | 92.9% | 99.4% | 100.6% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, H.; Geng, D.; Xiang, L.; Xu, K.; Ren, Z.; Liu, S.; Zuo, Z. Influence of Step Casings on the Cavitation Characteristics of Inducers. Processes 2022, 10, 1598. https://doi.org/10.3390/pr10081598
Han H, Geng D, Xiang L, Xu K, Ren Z, Liu S, Zuo Z. Influence of Step Casings on the Cavitation Characteristics of Inducers. Processes. 2022; 10(8):1598. https://doi.org/10.3390/pr10081598
Chicago/Turabian StyleHan, Huan, Da Geng, Le Xiang, Kaifu Xu, Zibo Ren, Shuhong Liu, and Zhigang Zuo. 2022. "Influence of Step Casings on the Cavitation Characteristics of Inducers" Processes 10, no. 8: 1598. https://doi.org/10.3390/pr10081598
APA StyleHan, H., Geng, D., Xiang, L., Xu, K., Ren, Z., Liu, S., & Zuo, Z. (2022). Influence of Step Casings on the Cavitation Characteristics of Inducers. Processes, 10(8), 1598. https://doi.org/10.3390/pr10081598






