Flow Characteristics and Optimization Design of the Stator–Rotor Cavity of the Full Tubular Pump
Abstract
:1. Introduction
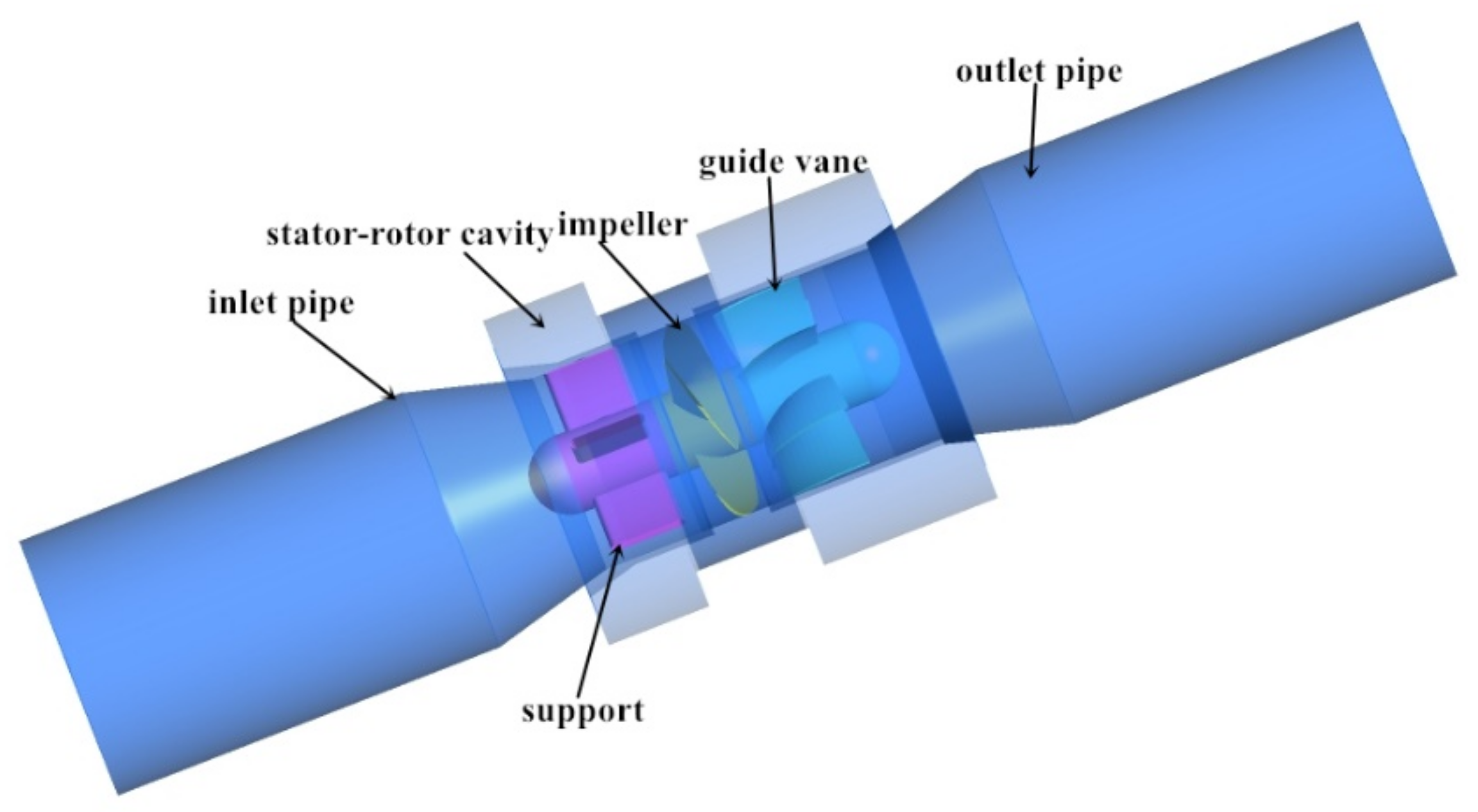
2. Numerical Method
2.1. Turbulence Model
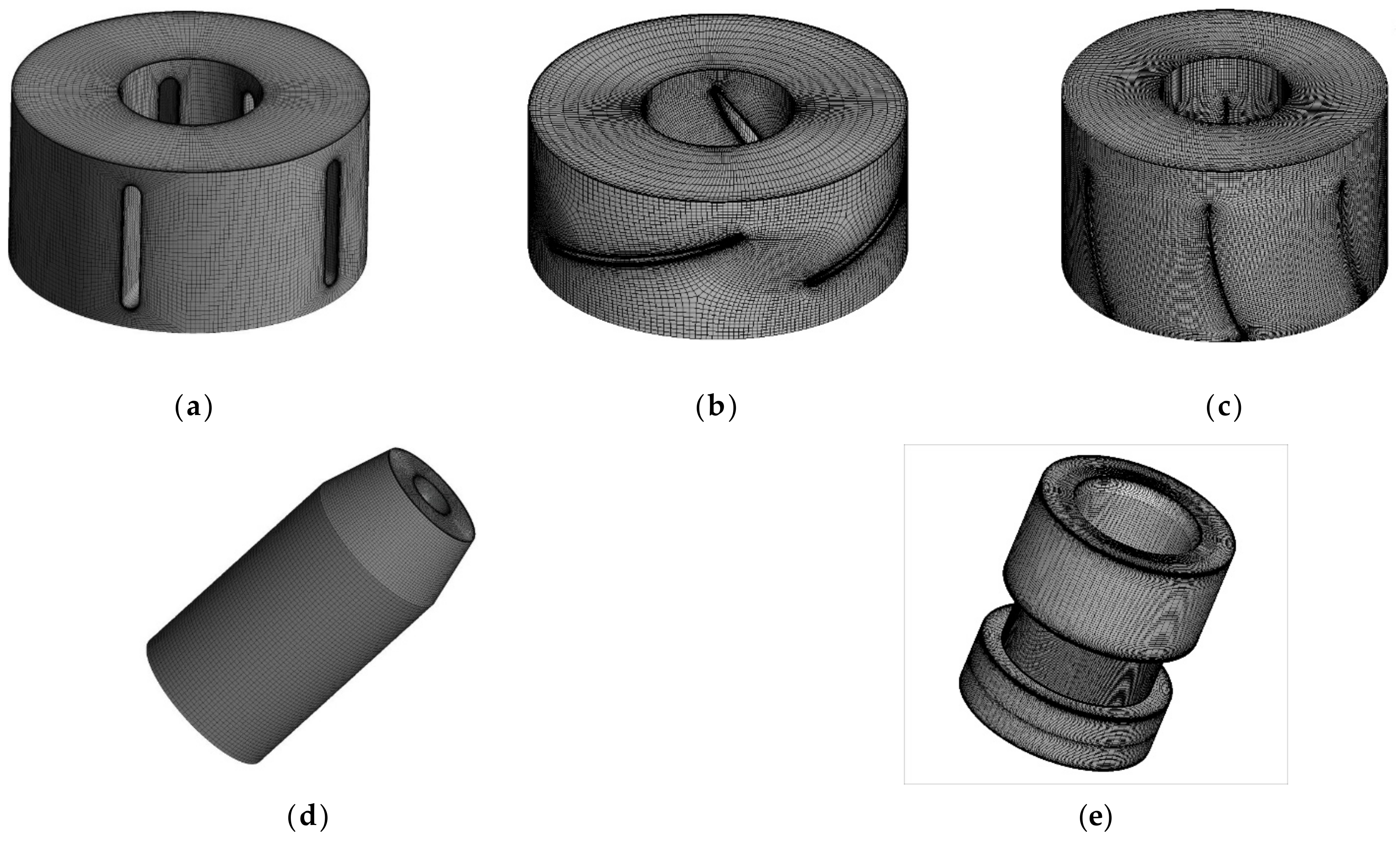
2.2. Grid
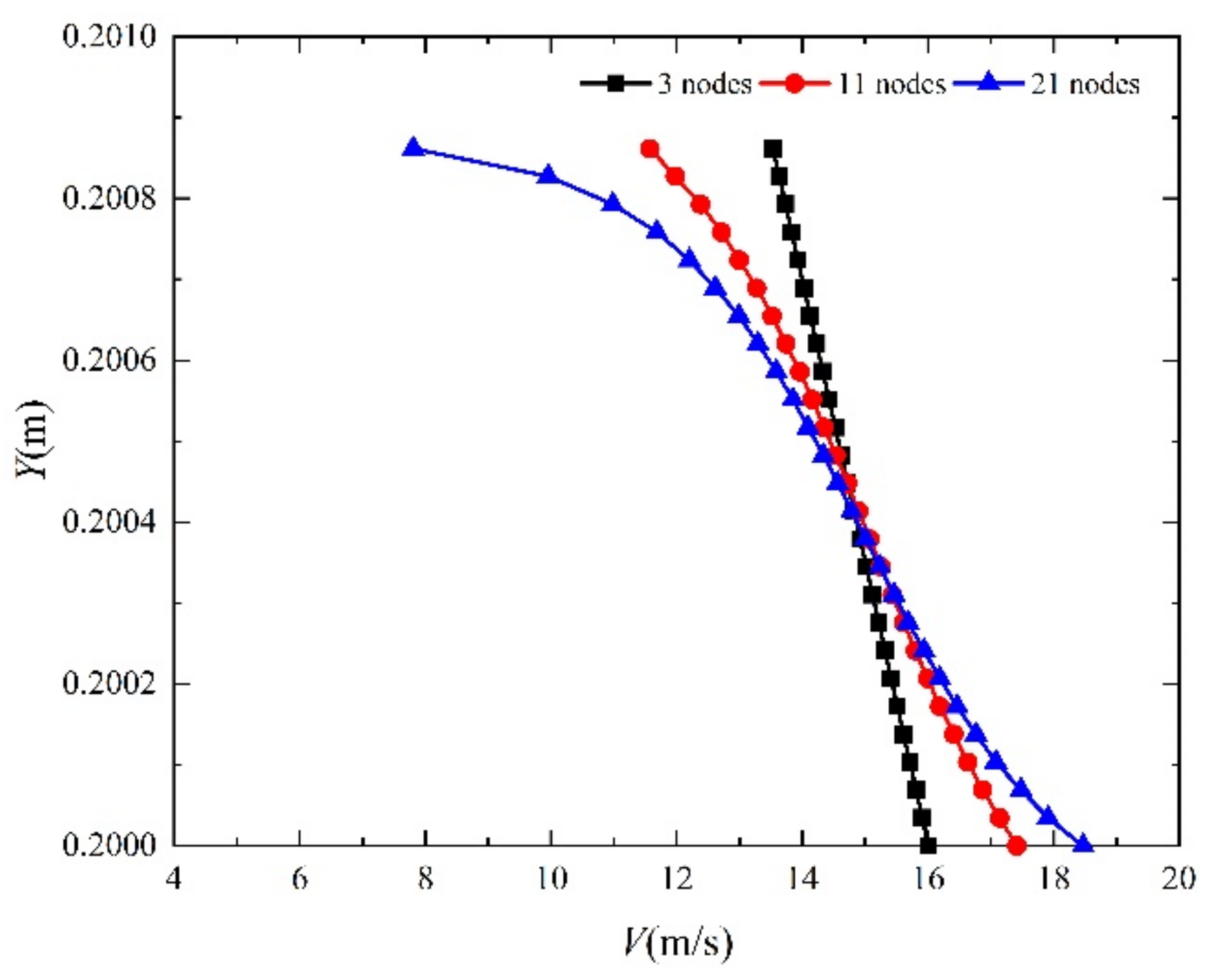
2.3. Grid-Independent Analysis
2.4. Boundary Conditions
3. Results
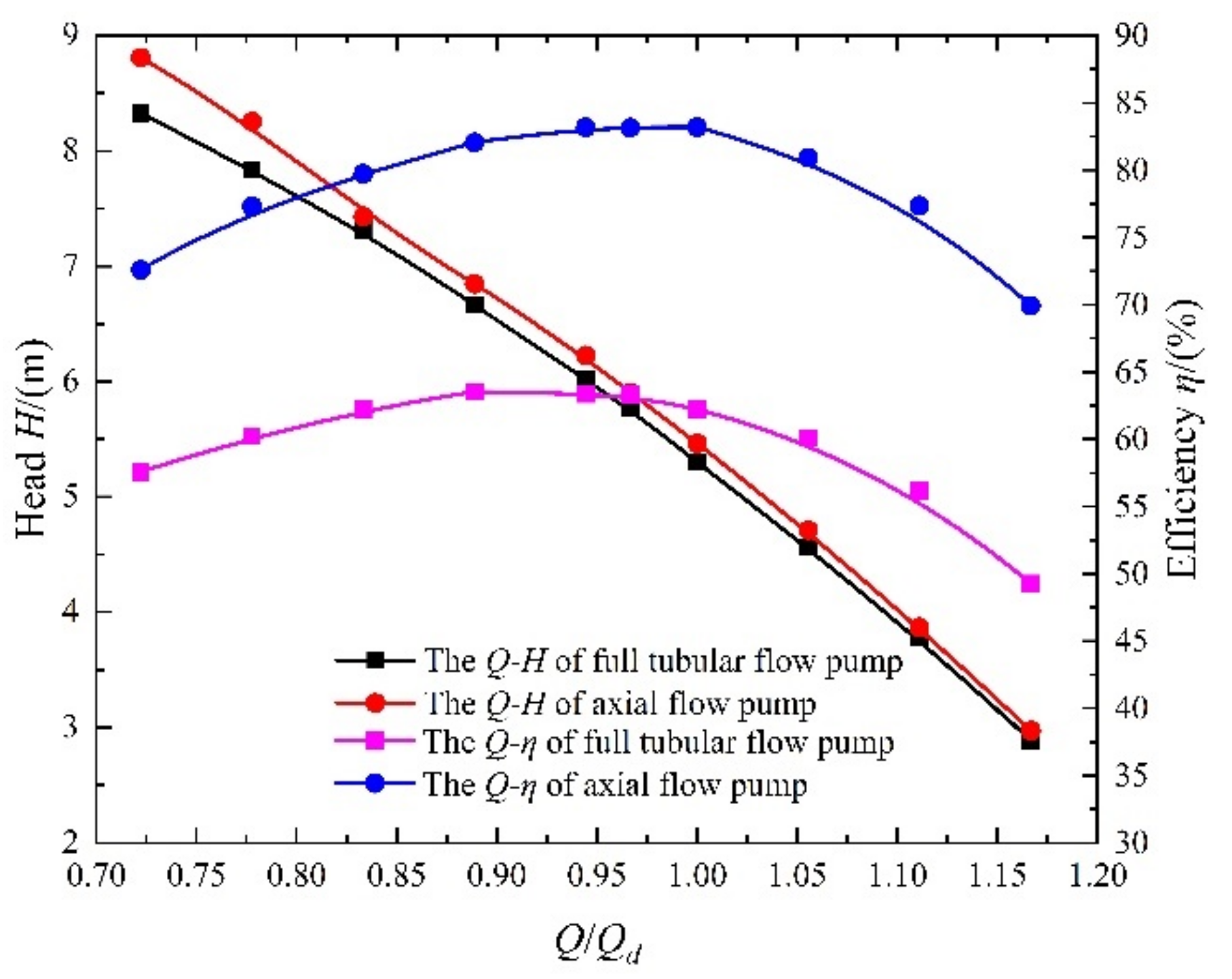
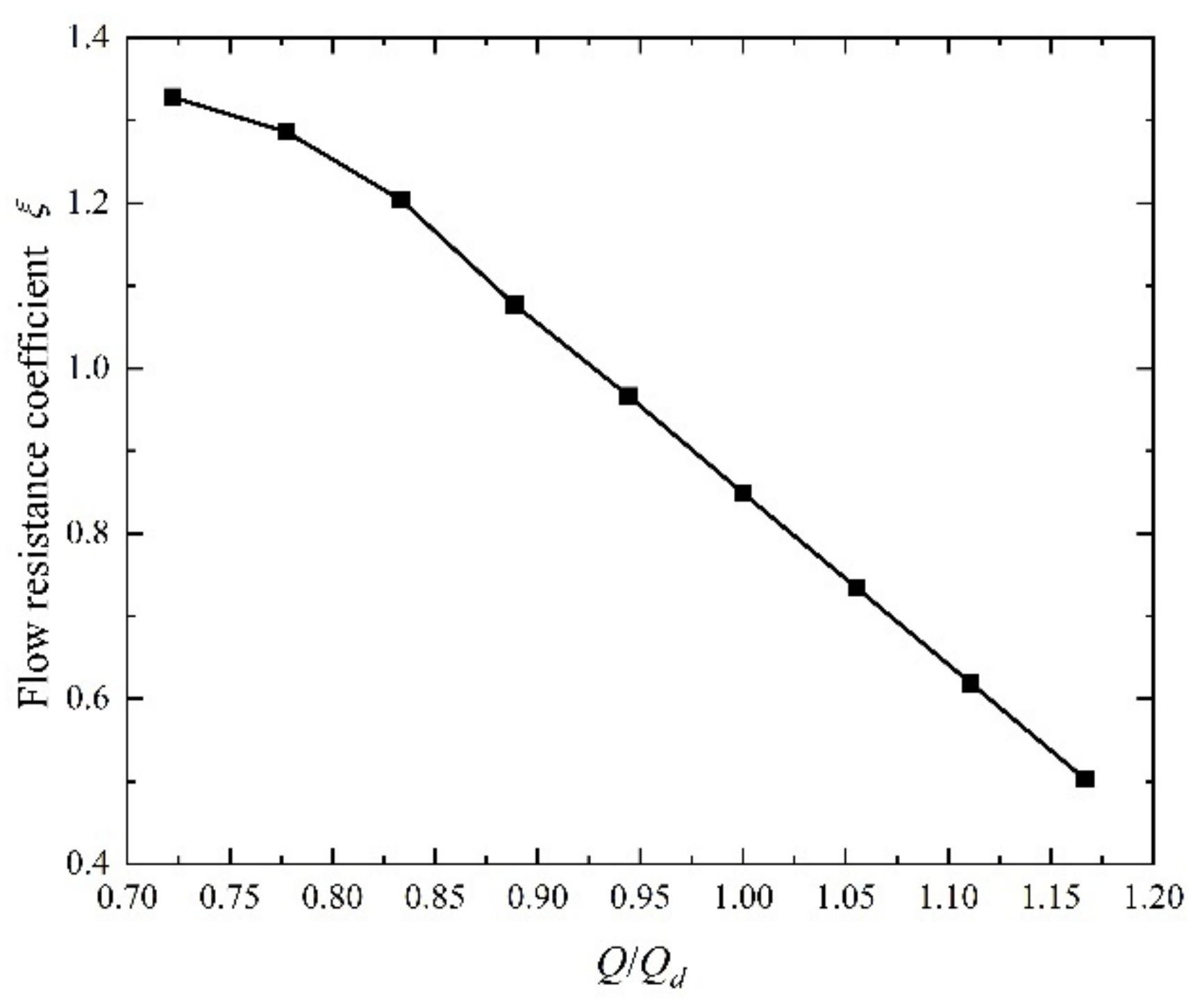
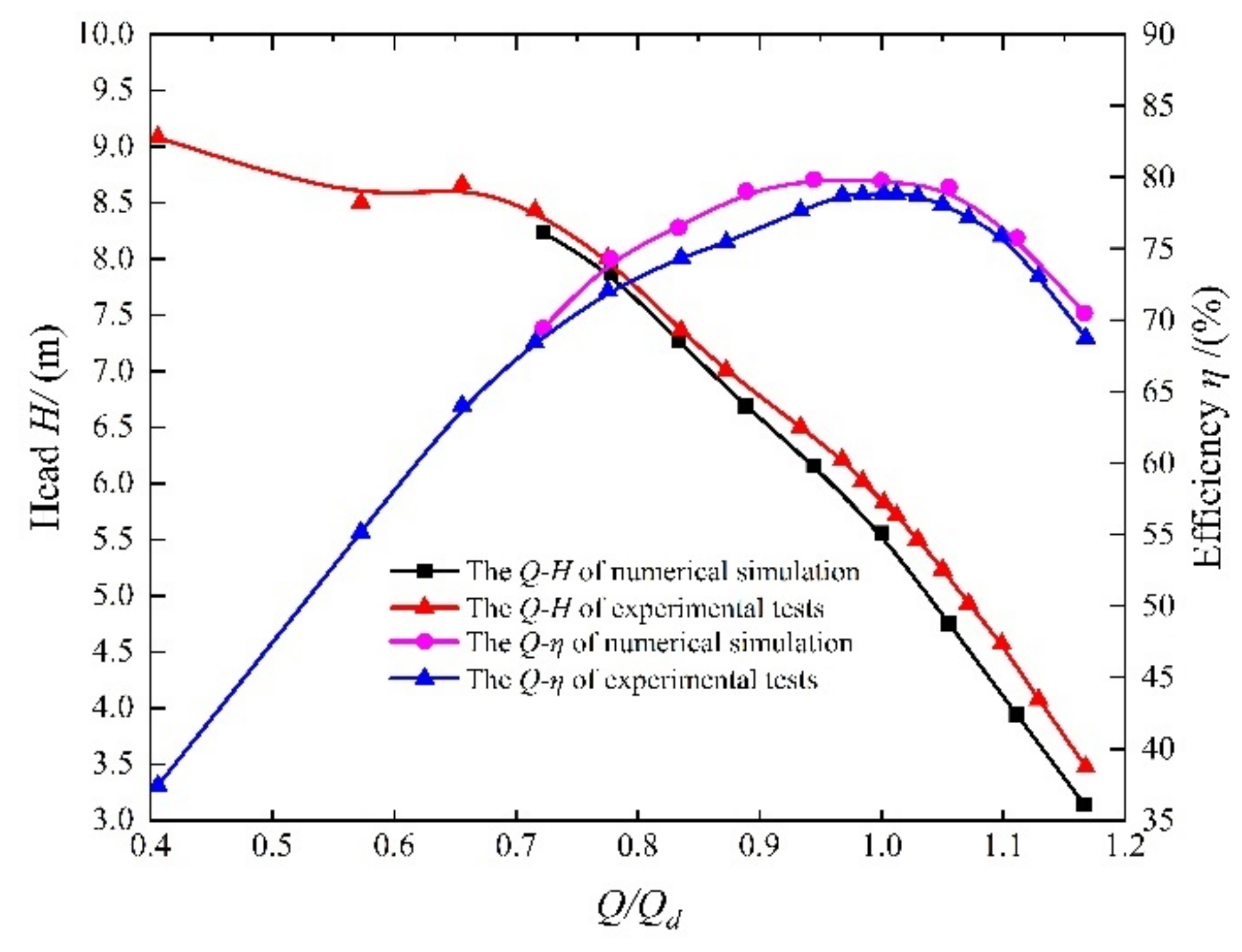
3.1. Energy Characteristics Analysis
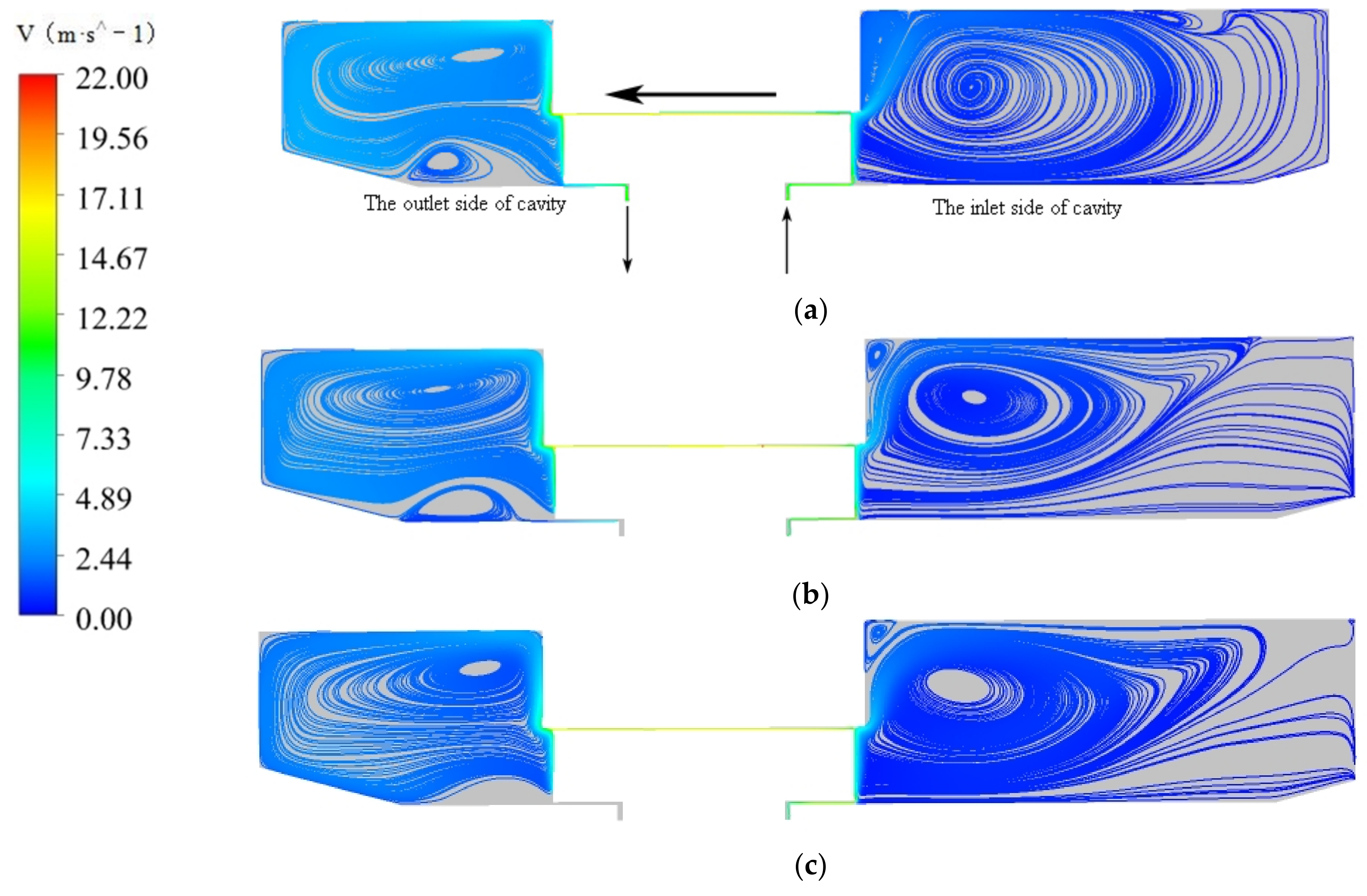
3.2. Flow Field Analysis
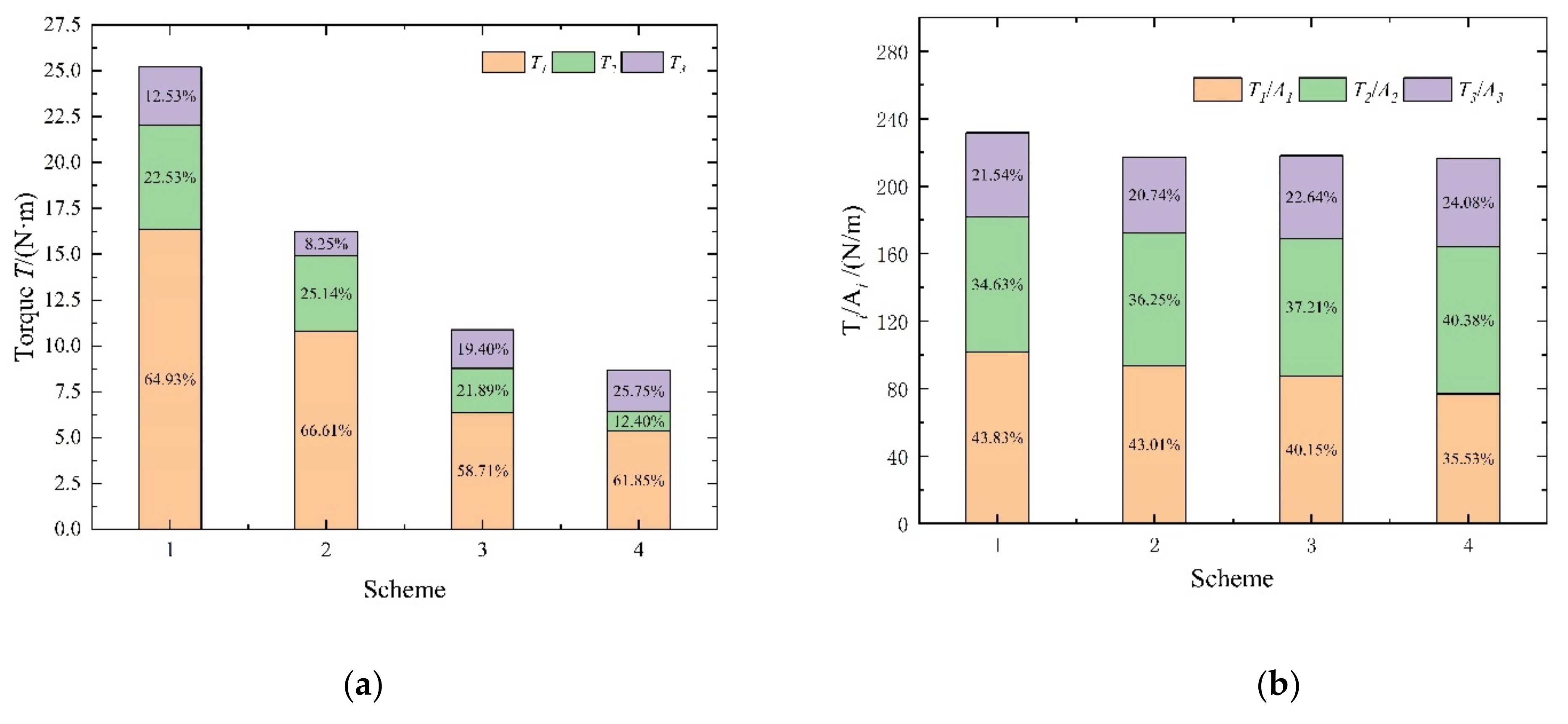
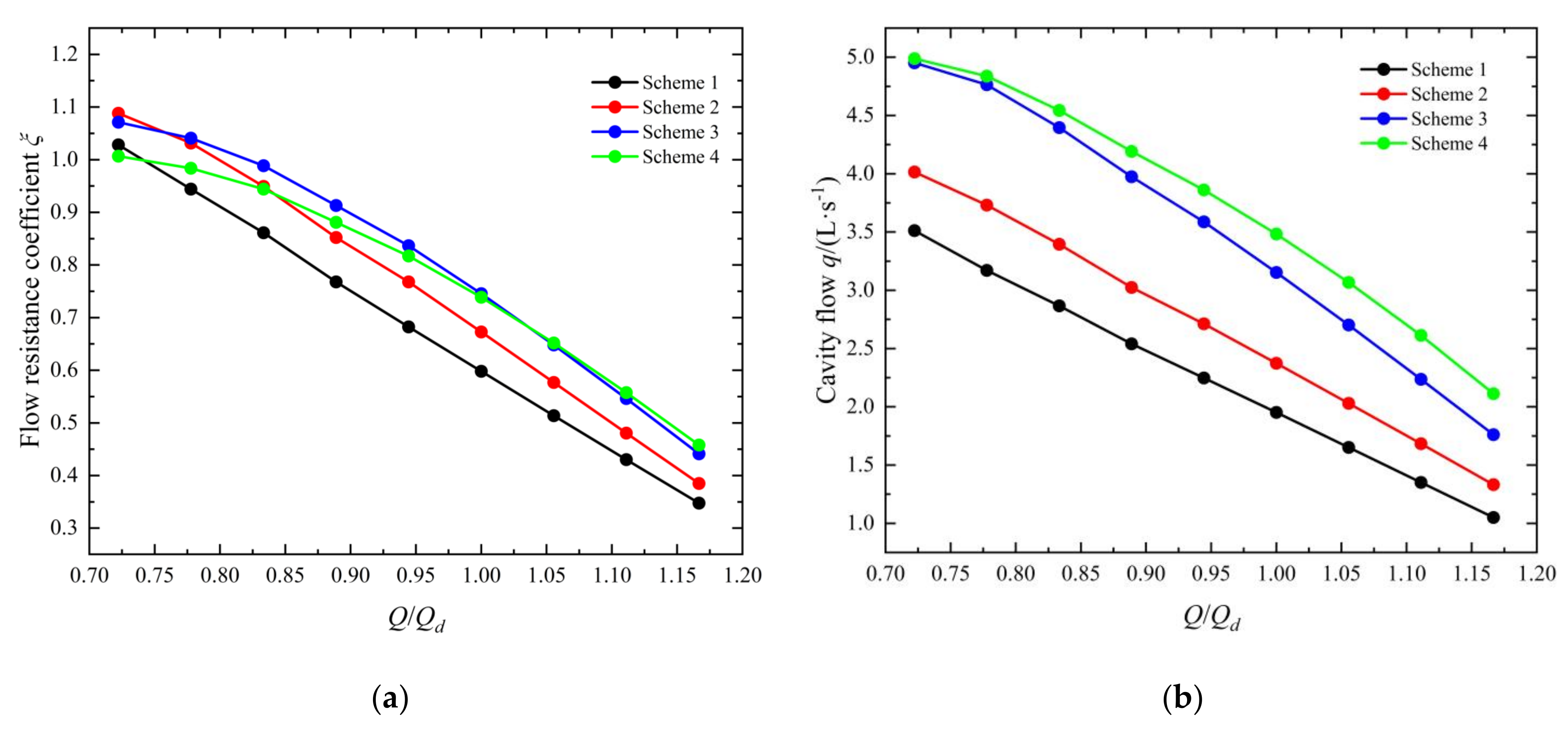
3.3. Structure Optimization of the Rotor
3.4. Model Test Validation
4. Conclusions
- 1.
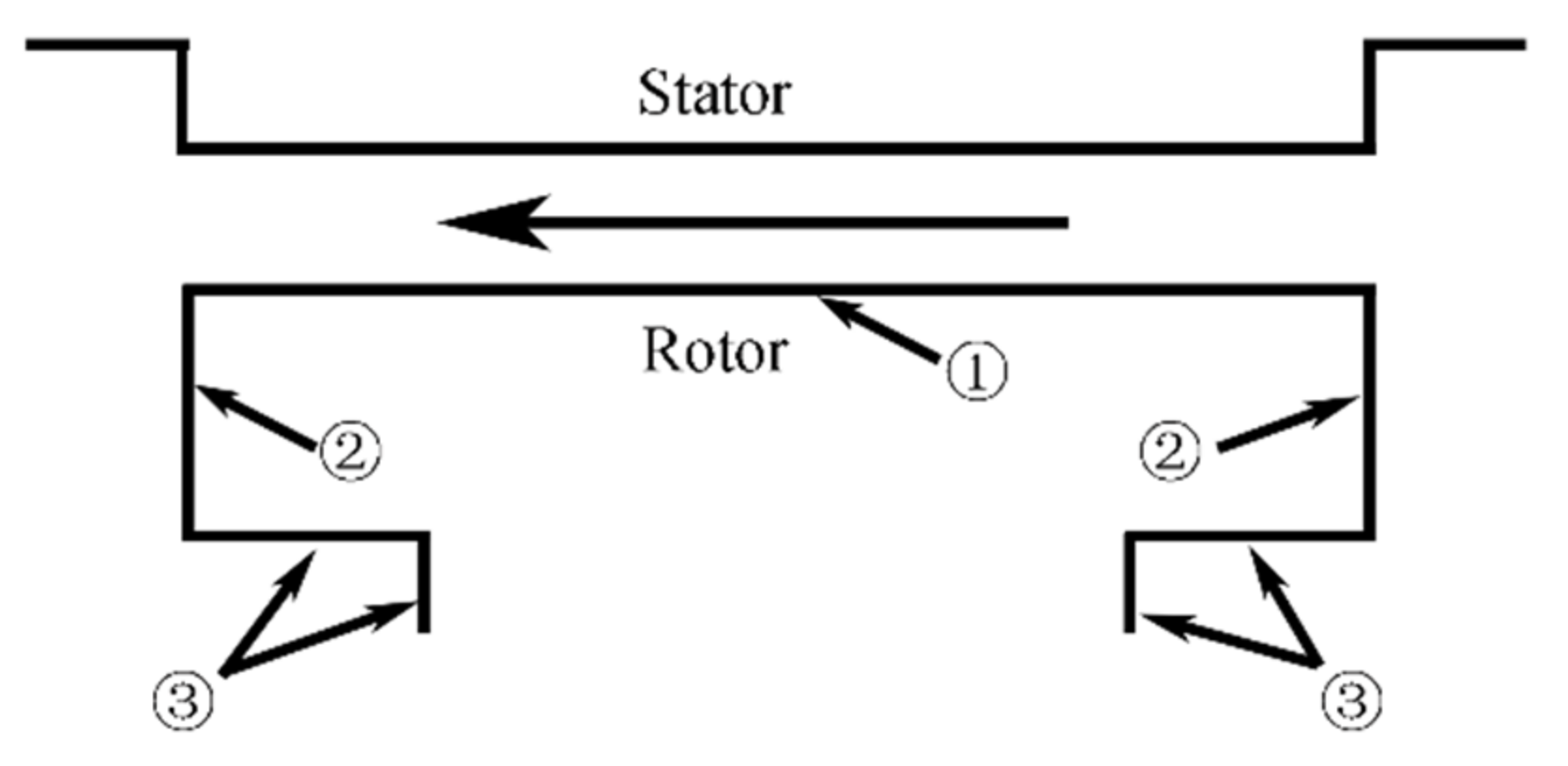
- There are large-area vortex structures on both sides of the cavity, and the backflow intensity is low. Due to the centrifugal effect caused by the rotor rotation, the flow velocity around the rotor in the cavity is higher. The vortex in the stator–rotor cavity is mainly concentrated on the inlet side, and the change in the vortex size in the cavity is mainly affected by the cavity flow.
- 2.
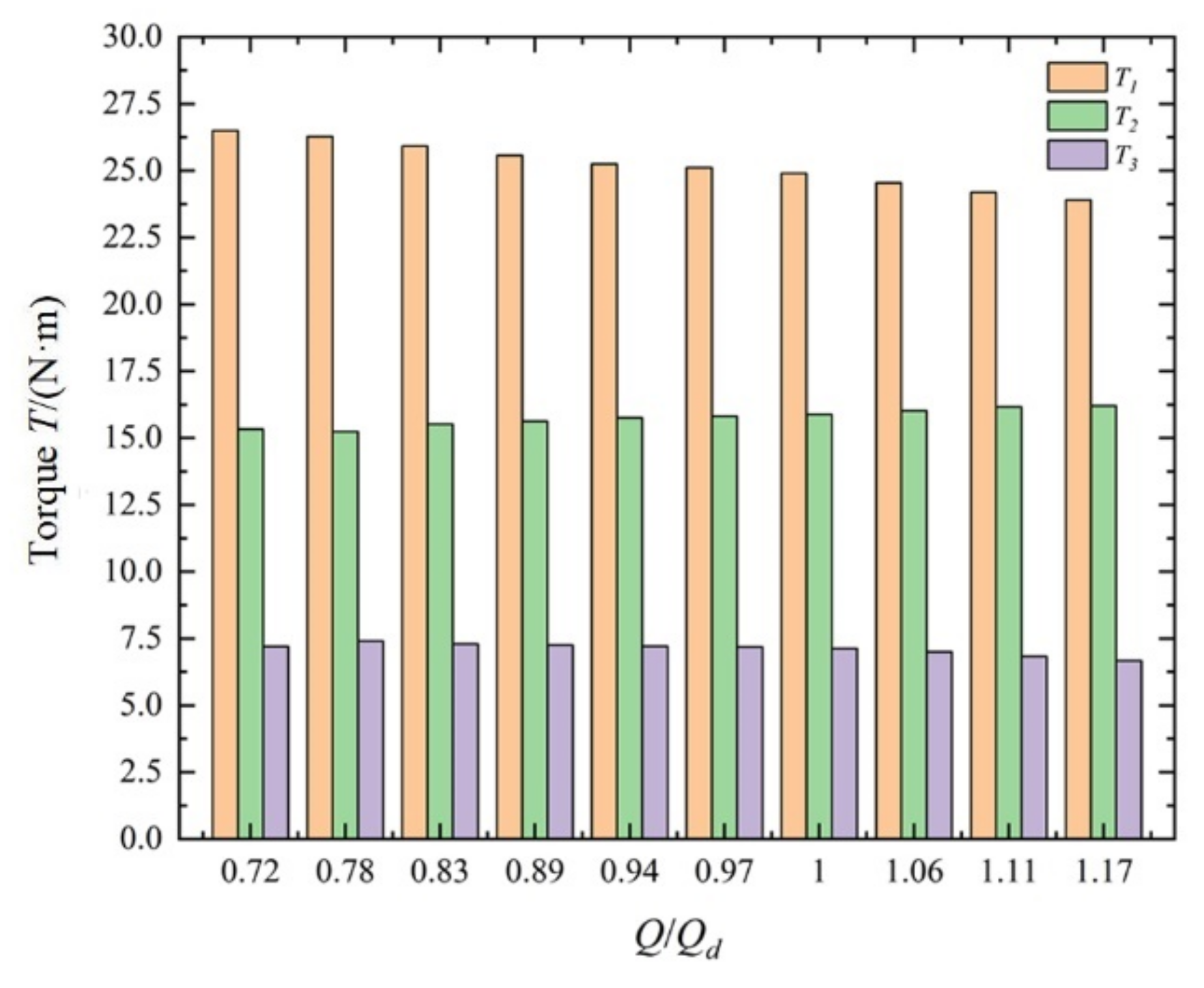
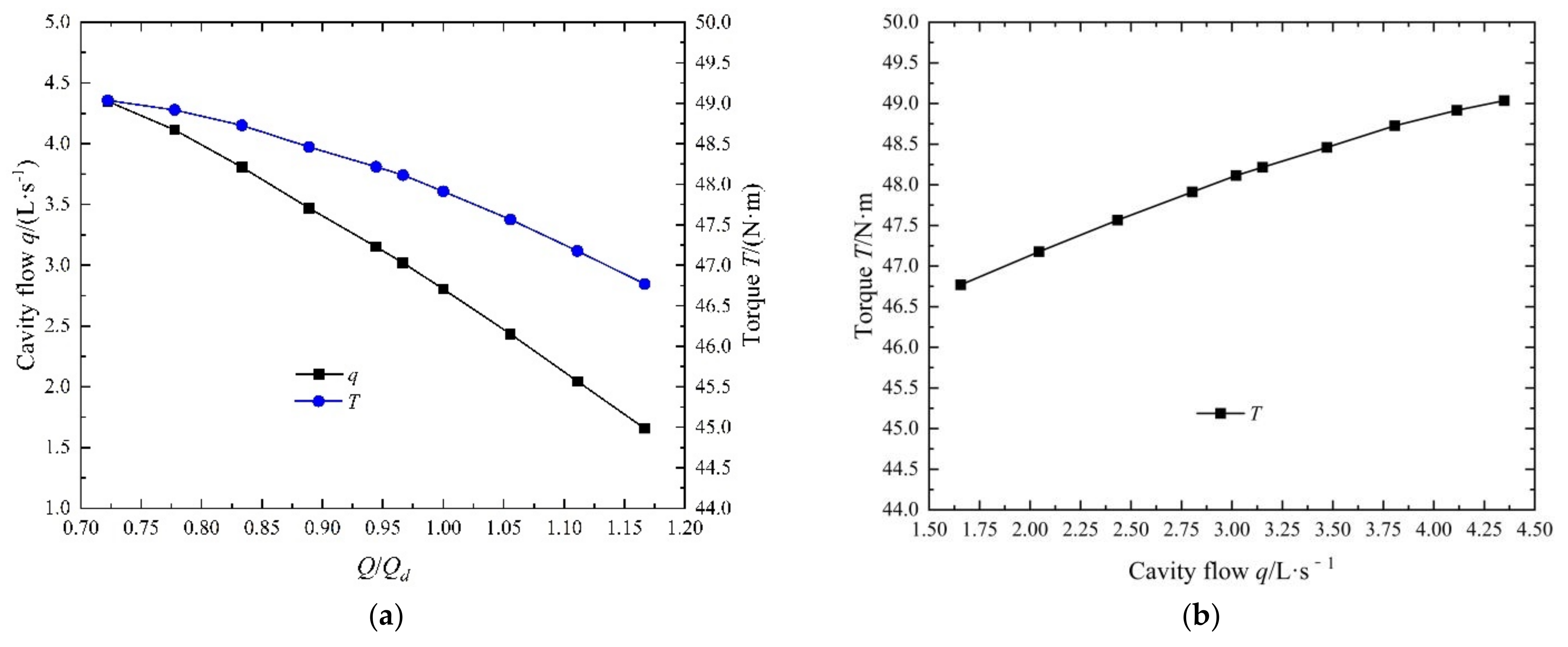
- Under the design condition, the torque on the rotor clearance is relatively large, reaching about 50% of the total rotor torque. By comparing the axial forces of the impeller and the rotor, it is found that the rotor accounts for 79.1%, 76.77%, and 63.35% of the impeller under various flow conditions. From its proportion, it can be seen that the load acting on the rotor increases due to the large force area of the rotor.
- 3.
- By optimizing the rotor structure, it is found that it has a great influence on the efficiency of the full tubular pump. Compared with the original model, the efficiency is increased by 14.04% and the torque is reduced by 39.25 N m. Under the design condition, the head decreases by 0.11 m at most and the leakage increases by 1.53 L/s. It shows that the operating efficiency of the pump device is closely related to the area of the rotor structure, and the area of the rotor structure needs to be controlled in the actual design process.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| D | impeller diameter, mm |
| Qd | design flow, L/s |
| ρ | density, kg/m3 |
| ξ | flow resistance coefficient |
| g | local acceleration of gravity, m/s2 |
| H | head, m |
| η | efficiency, % |
| n | rotation speed, r/min |
| bep | best efficiency point |
| α | velocity Eddy Strength |
| μ | Poisson ratio |
| y+ | distance to the nearest wall |
| ν | kinematic viscosity |
| k | turbulent energy, m2/s2 |
| i, j | stands for the x, y, z direction |
| uj | stands for the velocity in different coordinate directions, m/s |
| xj | stands for the coordinate component, m |
References
- Gu, Z.S. Development and application of a new type submersible tubular pump. Water Resour. Hydropower Eng. 2010, 41, 54–57. [Google Scholar]
- Liu, C. Researches and Developments of Axial-flow Pump System. Trans. Chin. Soc. Agric. Mach. 2015, 46, 49–59. [Google Scholar]
- Zhang, C.Y. Numerical Simulation and Optimization of a Motor-Pump System; Yangzhou University: Yangzhou, China, 2020. [Google Scholar]
- Zhang, C.; Liu, C.; Feng, X.; Chu, C.; Xie, L.; Lei, Z.; Hydraulic, S.O. Numerical simulation of flow characteristics and performance prediction of a motor pump. Southto-North Water Transf. Water Sci. Technol. 2019, 17, 185–192. [Google Scholar]
- Shi, L.J.; Jiao, H.F.; Gou, J.L.; Yuan, Y.; Tang, F.P.; Yang, F. Influence of Backflow Gap Size on Hydraulic Performance of Full-flow Pump. Trans. Chin. Soc. Agric. Mach. 2020, 51, 139–146. [Google Scholar]
- Shi, L.J.; Zhang, W.P.; Jiao, H.F.; Tang, F.; Wang, L.; Sun, D.; Shi, W. Numerical Simulation and Experimental Study on the Comparison of the Hydraulic Characteristics of an Axial-Flow Pump and a Full Tubular Pump. Renew. Energy 2020, 153, 1455–1464. [Google Scholar] [CrossRef]
- Cheng, S. Starting Performance and Electromagnetic Noise Analysis of Submersible Motor with Welded Rotor in Entirely Tubular Electric Pump; Hefei University of Technology: Hefei, China, 2020. [Google Scholar]
- Xu, X.F.; Ge, Q. Fault Diagnosis of Tubular Motor Pump Based on BP Neural Network. Intern. Combust. Engine Parts 2021, 2, 139–140. [Google Scholar]
- Cao, L.J.; Liu, C.Y.; Zhong, Y.F. Application of Full Tubular Submersible Pump and Stability Analysis of Self-Coupling Installation at Water Outlet; Hunan Hydro & Power: Changsha, China, 2015; pp. 87–91. [Google Scholar]
- Jiang, P.H. Comparison and Selection of Pump Types for the Reconstruction and Expansion Project of Youyi Electric Discharge Station; Heilongjiang Hydraulic Science and Technology: Harbin, China, 2020; Volume 48, pp. 102–103. [Google Scholar]
- Zhu, H.M. Research on the Application of Fully Tubular Submersible Gate Pump. Jianghuai Water Resour. Sci. Technol. 2015, 36, 18–19. [Google Scholar]
- Jiao, H.F. Study on the Hydraulic Performance and Radial Gap Size of the Full-flow Pump; Yangzhou University: Yangzhou, China, 2020. [Google Scholar]
- Li, Y.J.; Shen, J.F.; Yi, Y.P.; Liu, Z.Q. Numerical Investigation of Pressure Fluctuations on Axial-flow Pump Blades Affected by Tip-gap Size. Trans. Chin. Soc. Agric. Mach. 2014, 45, 59–64. [Google Scholar]
- Yang, C.M.; Chen, C.C.; Wang, J.N.; Song, W.W.; Xia, P.F. Numerical Study for Behavior of Tip Clearance Flow in Axial-Flow Pump. J. Mech. Eng. 2003, 39, 49–51. [Google Scholar] [CrossRef]
- Dai, C.C.; Guo, P.C.; Luo, X.Q. Numerical Analysis of Tip Clearance F Low Characteristic N Axial-Flow Pump. Fluid Mach. 2009, 37, 32–35. [Google Scholar]
- You, D.; Mittal, R.; Wang, M.; Moin, P. Computational Methodology for Large-Eddy Simulation of Tip-Clearance Flows. AIAA J. 2004, 42, 271–279. [Google Scholar] [CrossRef]
- Laborde, R.; Chantrel, P.; Mory, M. Tip Clearance and Tip Vortex Cavitation in an Axial Flow Pump. J. Electron. Packag. Trans. ASME 1997, 119, 680–685. [Google Scholar] [CrossRef]
- Meng, F.; Li, Y.J.; Yuan, S.Q. Effect of Hub Clearance on Hydraulic Performance in Bidirectional Axial-flow Pump. Trans. Chin. Soc. Agric. Mach. 2020, 51, 131–138. [Google Scholar]
- Li, Y.B.; Hu, P.L.; Li, R.N.; Li, P.H.; Bi, Z. Numerical analysis for effects of different blade tip clearance on performance in mixed-flow pump. Trans. Chin. Soc. Agric. Mach. 2014, 30, 86–93. [Google Scholar]
- Oweis, G.F.; Fry, D.; Chesnakas, C.J.; Jessup, S.D.; Ceccio, S.L. Development of a Tip-Leakage Flow-Part 1: The Flow Over a Range of Reynolds Numbers. J. Fluids Eng. 2006, 128, 751–764. [Google Scholar] [CrossRef]
- Wu, H.X.; Tan, D.; Miorini, R.L.; Katz, J. Three-Dimensional Flow Structures and Associated Turbulence in the Tip Region of a Waterjet Pump Rotor Blade. Exp. Fluids 2011, 51, 1721–1737. [Google Scholar] [CrossRef]
- Xi, S.; Desheng, Z.; Bin, X.; Yongxin, J.; Weidong, S.; Van Esch, B.P.M. Experimental Investigation of the Transient Patterns and Pressure Evolution of Tip Leakage Vortex and Induced-Vortices Cavitation in an Axial Flow Pump. J. Fluids Eng. 2020, 142, 101206. [Google Scholar] [CrossRef]
- Dreyer, M.; Decaix, J.; Münch-Alligné, C.; Farhat, M. Mind the Gap: A New Insight into the Tip Leakage Vortex Using Stereo-PIV. Exp. Fluids 2014, 55, 1849. [Google Scholar] [CrossRef]
- Zhang, X.; Tang, F.; Liu, C.; Shi, L.; Liu, H.; Sun, Z.; Hu, W. Numerical Simulation of Transient Characteristics of Start-Up Transition Process of Large Vertical Siphon Axial Flow Pump Station. Front. Energy Res. 2021, 9, 706975. [Google Scholar] [CrossRef]
- Wang, W.; Tai, G.; Pei, J.; Pavesi, G.; Yuan, S. Numerical investigation of the effect of the closure law of wicket gates on the transient characteristics of pump-turbine in pump mode. Renew. Energy 2022, 194, 719–733. [Google Scholar] [CrossRef]
- Zhang, X.W.; Tang, F.P. Investigation on hydrodynamic characteristics of coastal axial flow pump system model under full working condition of forward rotation based on experiment and CFD method. Ocean. Eng. 2022, 253, 111286. [Google Scholar] [CrossRef]
- Kan, K.; Zheng, Y.; Chen, H.; Zhou, D.; Dai, J.; Binama, M.; Yu, A. Numerical simulation of transient flow in a shaft extension tubular pump unit during runaway process caused by power failure. Renew. Energy 2020, 154, 1153–1164. [Google Scholar] [CrossRef]
- Kan, K.; Yang, Z.; Lyu, P.; Zheng, Y.; Shen, L. Numerical study of turbulent flow past a rotating axial-flow pump based on a level-set immersed boundary method. Renew. Energy 2021, 168, 960–971. [Google Scholar] [CrossRef]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Menter, F.R. Zonal Two Equation k-ω Turbulence Models for Aerodynamic Flows. In Proceeding of the 24rd Fluid Dynamics Conference, Orlando, FL, USA, 6 July 1993. [Google Scholar]
- Menter, F.R.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with the SST Turbulence Model. Turbul. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Zi, D.; Wang, F.; Tao, R.; Hou, K.Y. Research for impacts of boundary layer grid scaleon flow field simulation results in pumping station. J. Hydraul. Eng. 2016, 47, 139–149. [Google Scholar]
- Khanarmuei, M.; Rahimzadeh, H.; Sarkardeh, H. Effect of Dual Intake Direction on Critical Submergence and Vortex Strength. J. Hydraul. Res. 2019, 57, 272–279. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, F.; Yuan, S.; Chen, K.; Wei, X.; Appiah, D. Effect of Unrans and Hybrid Rans-Les Turbulence Models on Unsteady Turbulent Flows Inside a Side Channel Pump. J. Fluids Eng. 2020, 142, 061503. [Google Scholar] [CrossRef]
- Liu, C. Pumps and Pumping Stations; China Water & Power Press: Beijing, China, 2009. [Google Scholar]







| Part | Blade | Hub | Stator | Rotor |
|---|---|---|---|---|
| Average y+ | 31.68 | 19.40 | 10.95 | 14.27 |
| Flow | Axial Force (Fz)/N | Radial Force (F)/N | ||
|---|---|---|---|---|
| Impeller | Rotor | Impeller | Rotor | |
| 0.78 Qd | −4307.68 | −3407.76 | 16.04 | 10.4 |
| Qd | −3128.52 | −2401.68 | 29.10 | 9.75 |
| 1.17 Qd | −2079.46 | −1442.06 | 42.80 | 10.18 |
| Rotor Area (A) | Length (L) | Outer Diameter (Dz) | Head (H)/m | Efficiency (η)/% | Leakage Flow (q)/L s−1 | |
|---|---|---|---|---|---|---|
| Scheme 1 | 0.75 A | 0.8 L | 0.96 Dz | 5.35 | 70.73 | 1.95 |
| Scheme 2 | 0.5 A | 0.6 L | 0.92 Dz | 5.32 | 74.37 | 2.37 |
| Scheme 3 | 0.37 A | 0.4 L | 0.87 Dz | 5.26 | 76.46 | 3.15 |
| Scheme 4 | 0.32 A | 0.4 L | 0.83 Dz | 5.24 | 77.39 | 3.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, L.; Zhu, J.; Li, J.; Tang, F.; Chen, B.; Jiang, Y.; Xu, T.; Chai, Y. Flow Characteristics and Optimization Design of the Stator–Rotor Cavity of the Full Tubular Pump. Processes 2022, 10, 1688. https://doi.org/10.3390/pr10091688
Shi L, Zhu J, Li J, Tang F, Chen B, Jiang Y, Xu T, Chai Y. Flow Characteristics and Optimization Design of the Stator–Rotor Cavity of the Full Tubular Pump. Processes. 2022; 10(9):1688. https://doi.org/10.3390/pr10091688
Chicago/Turabian StyleShi, Lijian, Jun Zhu, Jindong Li, Fangping Tang, Beishuai Chen, Yuhang Jiang, Tian Xu, and Yao Chai. 2022. "Flow Characteristics and Optimization Design of the Stator–Rotor Cavity of the Full Tubular Pump" Processes 10, no. 9: 1688. https://doi.org/10.3390/pr10091688





