Geometric Calculation of the Influence of an Oscillating Sieve’s Actuation Mechanism Position on Its Motion

Abstract

This article offers a general approach to studying a four-bar mechanism from a geometric viewpoint. The four-bar mechanism form is used in a large number of existing pieces of machinery and equipment. This type of mechanism, used to drive a screen and generate its oscillating motion, is referred to in this article for its application in separation systems. In the literature, there are numerous approaches for analyzing such a mechanism. In addition to determining this mechanism’s geometry, an examination of the influence of the drive system’s position on the motion of the tie rods, or the support system of an oscillating site, is also conducted. In the investigation, the connecting rod angle was adjusted between −45 degrees and 60 degrees without respect to the horizontal. The following parameters, which correspond to the operation of the oscillating sieve motion, were obtained from the determined mathematical relations: the movement made by the free end of the tie rod; the tie rod’s angle in relation to the crank movement varies; and variation in the angle the tie rod achieves based on the drive system’s inclination angle. From the analysis, it was discovered that the drive system’s position in relation to the other components of the assembly had a direct influence. The calculation steps were designed to be performed using Mathcad 15.

1. Introduction

The process of separating the components of a heterogeneous mixture involves different types of equipment that perform the process using different working principles. One of the most widely used methods of separating a mixture of solid particles is by separating the size of the solid particles using sieves.

The working principle of a separation system based on sieves presupposes the existence of a surface with holes of different shapes and sizes through which the solid particles pass and a drive system for the respective surface. The simplest drive system for a sieve is the crank mechanism, a system that generates an oscillating motion [1,2,3].

From a constructive point of view, the assembly made by the crank mechanism and the support system of the sieve, the tie rod, is nothing more than a system of four bars [4,5,6,7]. Four-bar flat connections are widely used in various automatic devices and equipment such as automobiles, biometric prostheses, steam engine mechanisms, bicycle and solar panel rotating mechanisms, automatic garage door openers, machine steering mechanisms, medical equipment, robotics, etc., in which it is necessary to transform rotational movement into translational movement [8,9,10,11,12,13,14,15,16,17,18,19,20,21].

Though there are many research methods for determining the geometric parameters of the links that ensure continuous motion, in contrast, elements of the system, including the construction of the mechanism, meeting workspace restrictions, and the kinematic and dynamic conditions of the transmission motion, are incompletely specified, and most of them are analyzed graphically [4,5,6,7,9,10,11,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45].

The system elements described above are commonly analyzed from a theoretical point of view by applying a series of methods: the hybrid cuckoo and firefly algorithm [8]; the Euler–Lagrange method [16]; the four-bar linkage kinematic model by Suh and Radcliffe as an objective function [26]; the grasshopper algorithm [28]; the multiple ladder method and the multi-frequency nature of the inertial force [32]; an algorithm based on the particle swarm optimization method [34]; a numerical synthesis procedure for a four-bar link that combines motion and function generation [35] or a robust mathematical formulation [36]; a mathematical model using the Eksergian equation of motion [39]; and an objective function that has been defined based on the least-squares error between the generated and desired function [42]. In addition, many studies also analyzed these mechanism from a planar [10,30,33,34,41,43], Cartesian [37], or spatial [25] point of view, as well as through the application of different types of simulations [11,23,29].

The system elements are also analyzed in terms of existing models: mechanical models [12,15,17,22,31,44] and biological models [9,13,14,27]. New directions for the use of this mechanism have been generated, especially in robotics [18,19,20,21,24,38,45]. With an aim to achieve a proper design concept to develop routines, which can more easily account for uncertainties in geometric parameters developed for links, especially for the four-bar link, and can synthesize the complete set of design solutions [40]. All these studies mainly aimed at determining the movement of this type of mechanism, but in addition to this, the speed and acceleration of tracked components were also determined [9,23,38,39,44].

In the case of oscillating separators (where the working surface is horizontal), depending on the positioning of the components making up the 4-bar mechanism, they can perform different functions [46,47,48], such as:

(1)

Mechanical separators—which perform the separation of heterogeneous mixtures of solid particles;

(2)

Oscillating transport—transporting a mixture of solid particles by jumps.

The article presents a calculation method for the four-bar mechanism, from a geometric point of view, following the influence exerted by the position of the mechanism of actuation of the oscillating sieve on the behavior of the free end of the tie rod. This study was conducted because there are very few studies in the literature with this aim. In general, these studies are based on the impact of the sieve inclination on the behavior of the solid particles with very little focus on the mechanism that operates the sieve, i.e., the movement exerted by the free end of the tie rod [1,2,3,46,47,48].

The purpose of this theoretical study is to identify the motion of the oscillating sieve and, depending on this motion, determine if it is possible (considering what has been presented before) to identify the specific behavior of the solid particle on the oscillating surface [49].

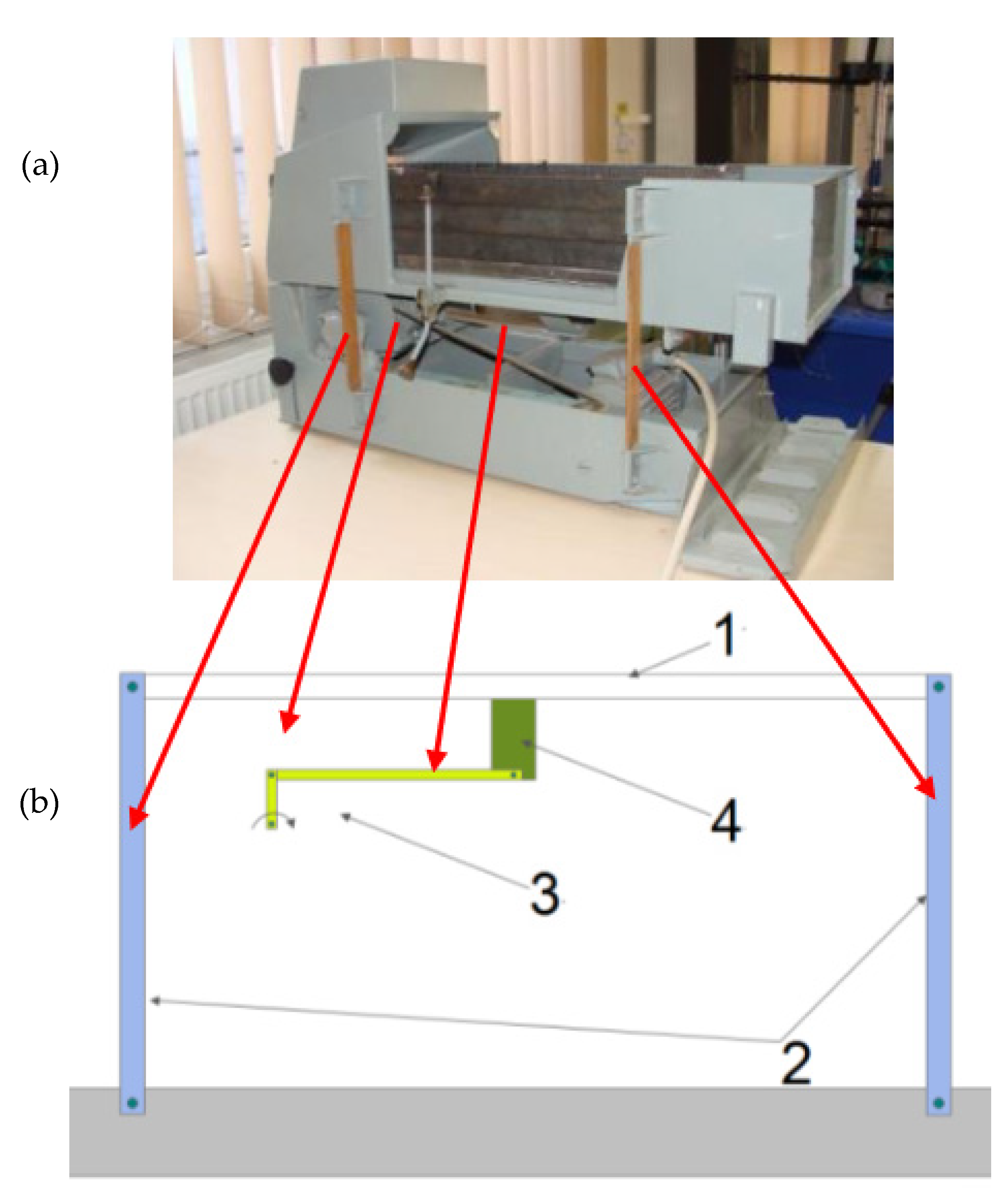
2. Equipment

For the analysis of the influence exerted by the position of the driving mechanism of the sieve on its movement, a sieve was chosen to present an oscillating movement (Figure 1). The classic sieves block drive system used consisted of:

①

A sieve;

②

The tyrants;

③

Sieve drive mechanism—crank mechanism;

④

A fastening element of the crank mechanism on the sieve.

Figure 1. Sieve block drive system [46,47]: (a) laboratory equipment; (b) schematic representation of the laboratory stand.

Figure 1. Sieve block drive system [46,47]: (a) laboratory equipment; (b) schematic representation of the laboratory stand.

After analysis of the action system, it was concluded that the assembly could be completed in a simplified way. Figure 2b shows the model that was used in the study [50,51].

The location of the crank mechanism [52], the one that drives the movement of the gripping joint, varied in a range of +60° and −45°, and the study was performed for a variation of the position from 15° to 15° (Figure 3).

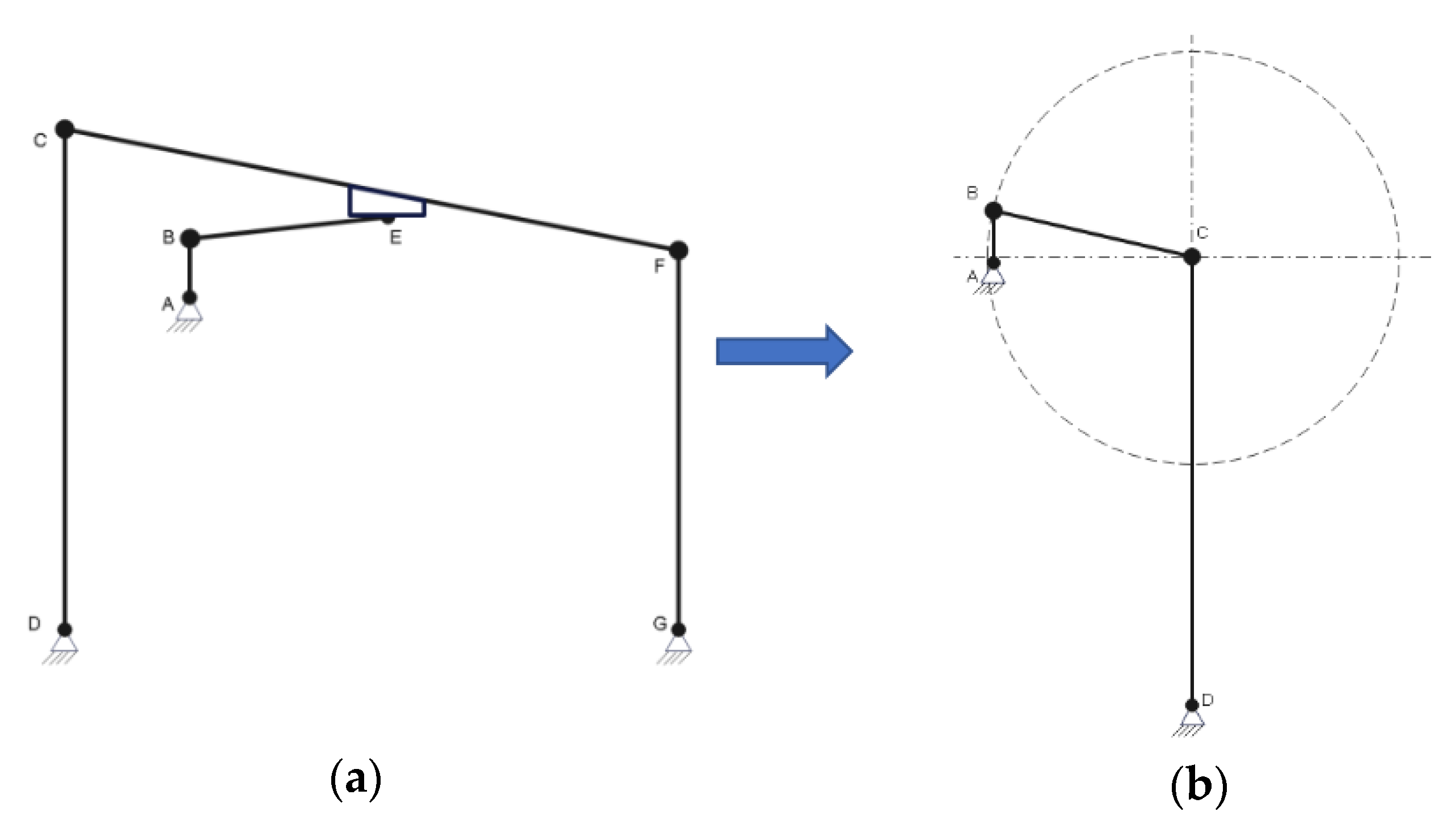
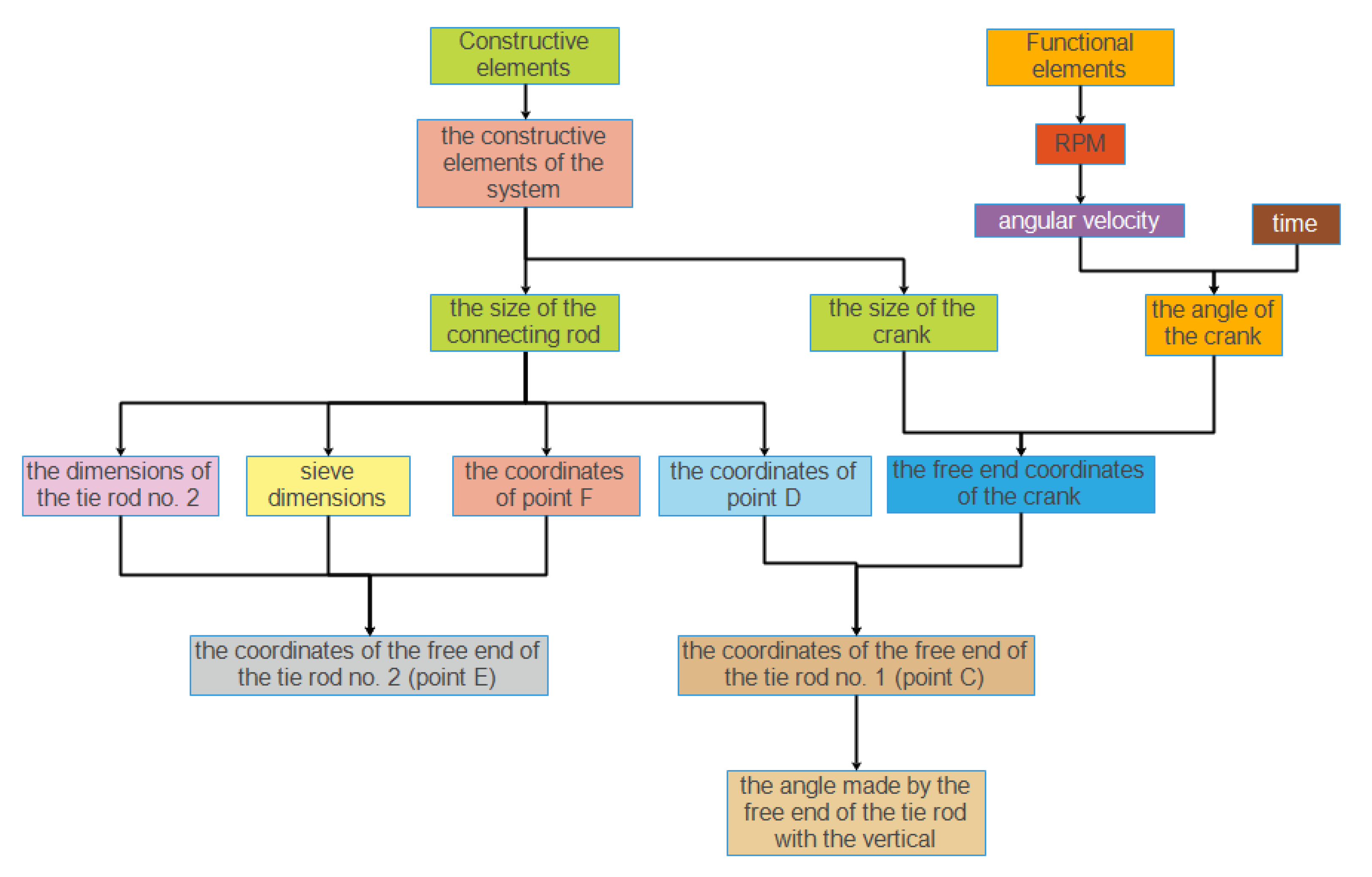
3. Geometric Construction of a Dynamic Mechanism

The mechanism makes a series of angular and linear movements, and depending on these, the movement is performed by other gear components. A series of work programs can be used to calculate the movement of such a mechanism, from the simplest and most common programs, such as Excel, to the most complex programs, such as Mathcad or Mathematica.

The article presents the working steps for calculating the motion of the mechanism under analysis using the Mathcad 15 program, starting from the fixed element and operating values of the mechanism.

The calculation of the motion of the mechanism under analysis was performed via the following calculation steps using the Mathcad software.

A point with coordinates x₀ and y₀ corresponding to values of (0, 0) was chosen as the reference point on which to start building the mechanism (noted as A in Figure 4).

The constructive elements of the mechanism were defined, respectively (Figure 4):

○

Lengths:

• The crank (AB) has the size a;
• Connecting rod (BC) has the size b;
• Tie rod no. 1 (CD) has the size c;
• Tie rod no. 2 (EF) has the size e;
• The sieve (CE) has the size d.

○

Angles:

• The angle of inclination of the crank about the horizontal α;
• The inclination angle of the connecting rod with the horizontal β;
• The inclination angle of the tie rod no. 1 with the horizontal φ;
• The inclination angle of the tie rod no. 2 with the horizontal θ₁;
• The angle of inclination of the sieve with the horizontal θ₀.

To perform dynamic analysis, the rpm of the crank, n_AB, was needed as the parameter was converted into angular velocity.

One end of the crank corresponded to the fixed point A with the coordinates x₀ and y₀, and the other to the coordinates of point B, which were determined using the calculation relation:

x_B = x₀ + a cos α

(1)

y_B = y₀ + a sin α

(2)

−

The correlation between the angular velocity and the angle described by the crank about the horizontal was identified. For this, the connection was made between the value of the angular velocity, the angle described by the crank, and the time necessary to achieve a complete rotation [3].

The first step of the calculation was the determination of the angular velocity, which was determined according to the literature [3]:

$$\omega =\frac{\pi n_{AB}}{30}$$

(3)

A function was created using the Mathcad 15 program, through which a time interval was generated about which the angular variation of the crank was defined [53]:

−

The reference time from which the analysis starts, i.e., t₁ = 0.000001 s;

−

The time required to make a complete rotation (360°):

$$nr=\frac{360}{{\omega }_g}$$

(4)

−

A time variation interval was created using the calculation relation:

$$t_{i+1}=t_i+\frac{nr}{n}$$

(5)

where n is the maximum number of possible values of the studied interval (the person performing the computation imposes this value), and i; i is the studied value range (0… n).

The correlation between time and the angle described by the crank was created:

$$\propto =\frac{{\omega }_g·t_i}{1+t_1}$$

(6)

The coordinates of the fixed point D were determined by:

x_D = x₀ + a cosα + b cosβ + c cosφ

(7)

y_D = y₀ − c sinφ +a sinα + b sinβ

(8)

The values of the angles α, β, and φ were taken as the initial positions, α = φ = 90° and β = 0°.

Using the calculation relations (9) and (10), it was possible to determine the movement performed by point C, the free end of the tie rod:

$$\begin{array}{ll}{x}_C=x_D+& \left\{\frac{\left[-b^2+c^2+w\right]·\left(x_D-x_0+x_B\right)}{2·w}\right\}\\ & -\left\{\frac{\sqrt{b+c+\sqrt{w}}·\sqrt{b+c-\sqrt{w}}·\sqrt{b-c+\sqrt{w}}·\sqrt{-b+c+\sqrt{w}}·\left(y_D-y_0-y_B\right)}{2·w}\right\}\end{array}$$

(9)

$$\begin{array}{ll}{y}_C=y_D-& \left\{\frac{\sqrt{b+c+\sqrt{w}}·\sqrt{b+c-\sqrt{w}}·\sqrt{b-c+\sqrt{w}}·\sqrt{-b+c+\sqrt{w}}·\left(x_0-x_D+x_B\right)}{2·w}\right\}\\ & +\left\{\frac{\left[-b^2+c^2+w\right]·\left(x_0-x_D+x_B\right)}{2·w}\right\}\end{array}$$

(10)

in which it was noted:

$$w=z_x+z_y$$

(11)

$$z_x={\left(x_D-x_0-x_B\right)}^2$$

(12)

$$z_y={\left(y_D-y_0-y_B\right)}^2$$

(13)

Using the coordinates of the points that made up the mechanism and the values of the constructive components, the value of the angle described by the tie rod with the vertical could be calculated. In our case, the value of the angle ψ (Figure 5) during the movement of the tie rod was described by the calculation relation (14).

$$\mathsf{\psi }=ArcTan\left[\frac{\left(\frac{\left(a·\cos \left[\alpha \right]+x_A-x_D\right)\left(-b^2+c^2+f1\right)}{2·f1}-\frac{\left(\left(-a·\sin \left[\alpha \right]-y_A+y_D\right)·f2\right)}{2\left(f1\right)}\right)}{\left(\frac{\left(a·\sin \left[\alpha \right]+y_A-y_D\right)\left(-b^2+c^2+f1\right)}{2·\mathrm{f}1}-\frac{\left(\left(a·\cos \left[\alpha \right]+x_A-x_D\right)·f2\right)}{2·\mathrm{f}1}\right)}\right]$$

(14)

where:

$$f1={\left(-a·cos\left[\alpha \right]-x_A+x_D\right)}^2+{\left(-a·sin\left[\alpha \right]-y_A+y_D\right)}^2$$

(15)

and

$$f2=\sqrt{b+c-\sqrt{f1}}·\sqrt{b-c+\sqrt{f1}}·\sqrt{-b+c+\sqrt{f1}}·\sqrt{b+c+\sqrt{f1}}$$

(16)

Then, knowing the coordinates for the initial position (respectively for the position of the angle β = 0) of all the components of the system, the variation of the angle ψ could be determined (for different angles of the drive mechanism, respectively for different values of the angle β) (Figure 3).

Knowing the coordinates of point C (Equations (9) and (10)), as well as the dimensions of the elements EF and CE (Figure 4), it was possible to determine the coordinates of point E using the calculation relations (17) and (18):

$$x_E=x_c+d·\cos \left({\theta }_0\right)$$

(17)

$$y_E=y_c+d·\sin \left({\theta }_0\right)$$

(18)

−

The coordinates for the fixed point F (respectively x_F and y_F—the element representing the fixed end of the tie rod) can be determined using equations:

$$x_F=x_C+d·cos\left({\theta }_0\right)+e·cos\left({\theta }_1\right)$$

(19)

$$y_F=y_C+d·sin\left({\theta }_0\right)+e·sin\left({\theta }_1\right)$$

(20)

where θ₀ represents the angle made by the sieve about the horizontal, relation (23):

$${\theta }_0=arcsin\left(\frac{\left|e-c\right|}{d}\right)$$

(21)

and θ₁ represents the angle made by tie rod no. 2 about the horizontal with an initial imposed value of 90°.

−

Since the aim was to obtain a general relationship, it must be taken into account that in some situations the correlations between terms may change (from + to −).

4. Methodology

This study aimed to identify the mode of movement of a tie rod used to support a sieve that performs an oscillating motion from a mathematical point of view.

Due to the calculation complexity, the calculation program Mathcad 15 was used. Using the calculation relations presented above and the calculation steps shown in Figure 6, the analysis of the movement achieved by the free end of the tie rod was performed.

To determine, from a value point of view, the influence exerted by the position of the drive device on the trajectory of the free end of the tie rod no. 1, a series of values were used (the notation of the elements was defined according to Figure 4):

−

Tie rod no. 1, c = 0.587 m;

−

Crank, a = 0.065 m;

−

Connecting rod, b = 0.27 m;

−

Sieve length, d = 1 m;

−

Rpm of the rod-crank mechanism, n_AB = 100 rot/min;

−

Coordinates of point A are x₀, y₀ = 0, 0;

−

Tie rod no. 2, e = 0.587 m.

To determine the influence exerted by the position of the sieve drive device on the movement made by the sieve, the angle that the connecting rod makes about the horizontal varied in the range of values −45–60° (see Figure 3).

5. Results

From the performed calculations, a series of results were obtained, which are presented below. All graphical representations in this section were constructed for the evaluation of the alpha angle starting from 0 degrees. In the first part of the mathematical determinations, it was possible to identify the movement executed by the free end of tie rod no. 1, a movement influenced by the position of the drive device. This motion is shown in three-dimensional form in Figure 7.

The values obtained (Figure 7) for the two axes OY (displacement on the OX axis (mm)) and OZ (displacement on the OY axis (mm)) depended on the position of the drive device, respectively the value of the angle β.

From the analysis of the graphical representations obtained by substituting the imposed values into the developed equations, it was found that the trajectory described by the free end of the tie rod (point C and point E when the two tie rods have equal dimensions) is in the form of a saddle. The depth is maximum for a value of the inclination angle of 60° of the connecting rod about the horizontal. This depth decreases, turning into a hump as the value of the connecting rod angle decreases about the horizontal, and for negative values of this angle, respectively, for the value of −45°.

The values of the displacement variation on the OY axis are closely related to the variation of the angle β. It must also be taken into account that the coordinates of the center of the system coincide with point A (0.0).

This change in the trajectory exerted by the free end of the tie rod affects how the screen moves. The movement of the sieve plays an important role in the behavior of the solid particles on its surface and the process of mechanical separation according to the size of the solid particles.

To determine the value of the angle ψ (Equation (14)), the first position of the tie rod drive mechanism was chosen, respectively, for the angle β = 0°. The values obtained are presented in Figure 8.

The analysis of the graphical representation (Figure 8) shows that the values of the angle ψ are grouped into positive and negative values. These values correspond to the position of the tie rod about the vertical, respectively (Figure 4), where:

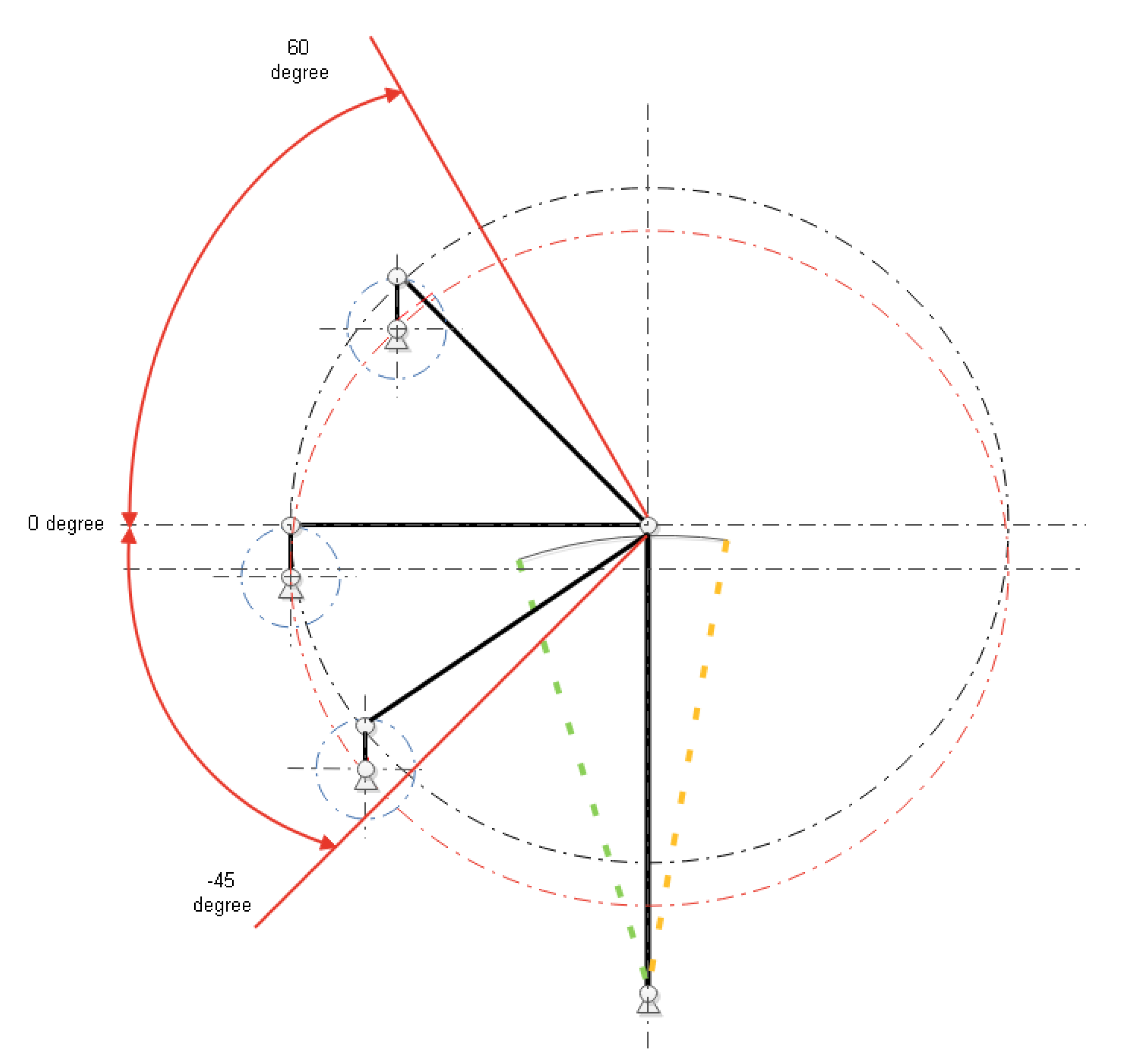
o

Positive values correspond to the position on the left side of the vertical;

o

Negative values correspond to the position on the right side of the vertical.

The graphical representation of the angle variation was generated according to the variation of the crank angle α, so the time variation of this angle, the value described by the free end of the tie rod, for a complete crank cycle is the sum of the two maximum angle values for the two positions.

For each position of the tie rod actuation mechanism, a certain displacement of the free end of the tie rod was obtained, corresponding to different values of the angle ψ, values which are shown in Figure 9.

By analyzing the variation of the angle ψ about the variation of the angle β, it was observed that angle ψ has minimum values for the range of angle β from 0–30°, with a minimum of 13°. Once the value of the angle β was different from this interval, it was found that the angle ψ increased in value, reaching a maximum of 32° for the angle β = −45°.

In addition, by knowing the trajectory of the free end of the tie rod over a period, it was possible to determine its speed of movement, as represented in Figure 10.

Following the analysis conducted on the variation of the displacement speed of the free end of the tie rod, the following conclusions could be drawn:

• The position of the driving device had a direct impact on the form of the variation in the speed of movement of the tie rod’s free end;
• The largest difference between the maximum and minimum value of the studied parameter was recorded for an angle of 45 degrees and corresponded to 3.082 m/s;
• The smallest difference between the maximum and minimum value of the studied parameter was recorded for an angle of −15 degrees and corresponded to 0.69 m/s;
• Regardless of the position of the driver, it was found that there are two points with a value of 0, corresponding to the change in the direction of travel of the free end of the tie rod;
• In order to identify the behavior of a solid particle on the surface of the screen subjected to an oscillatory motion, an analysis must be carried out, combining information about the motion of the free end of the tie rod and its velocity;
• In the case of positioning the drive device at an angle value of 45 degrees, as compared to other positions, there is a sudden increase in the value of the displacement speed of the free end of the tie rod after a period of an approximately constant value;
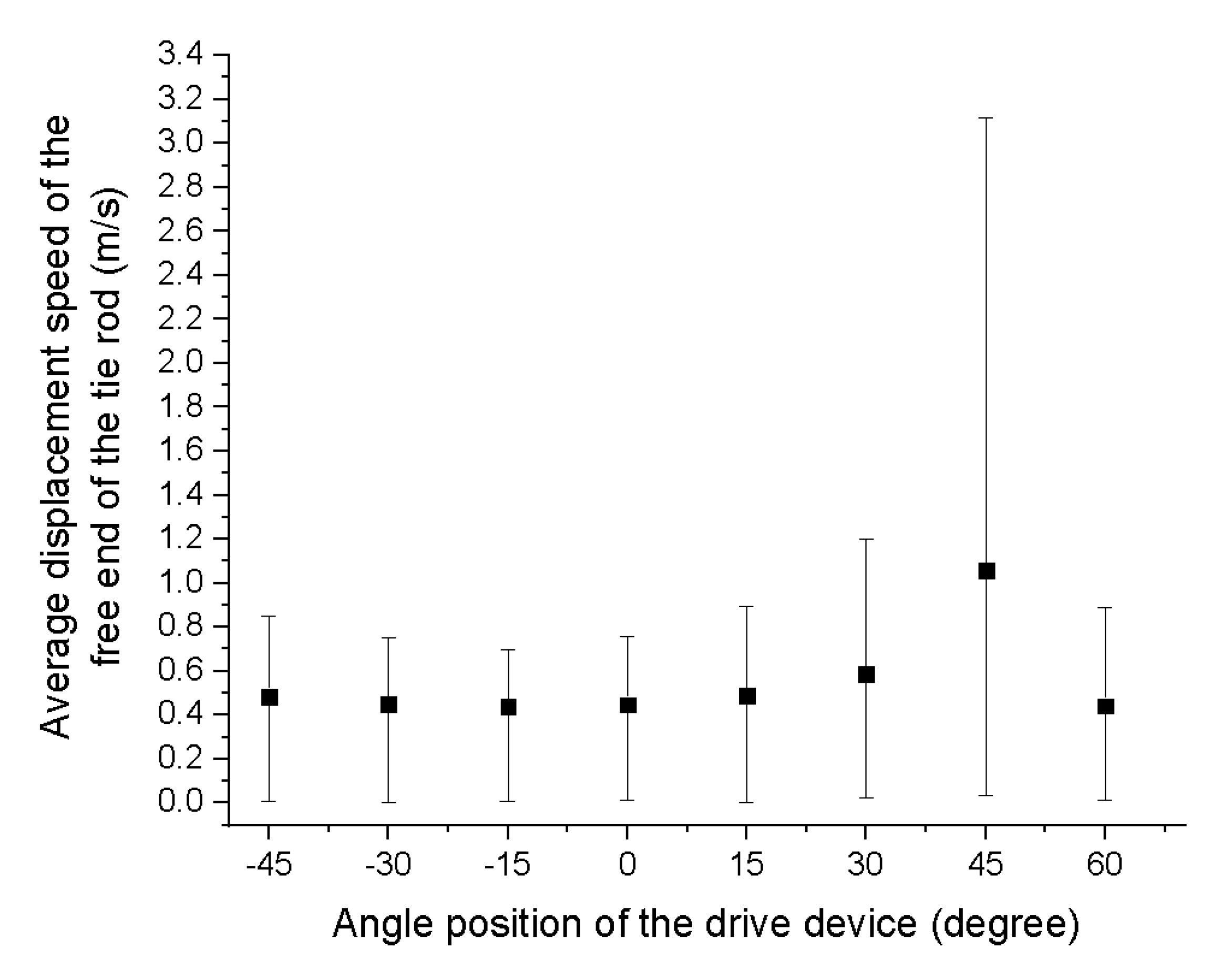
• Analyzing the average value of the free end displacement speed of the tie rod (Figure 11), it was identified that the highest value corresponded to the position of 45 degrees and the lowest to the position of −15 degrees.

Following the analysis conducted on the results displayed in Figure 11, the following conclusions could be drawn:

−

The highest value of the parameter presented was obtained for a β angle of 45 degrees and corresponded to 1.05 m/s;

−

The lowest value of the presented parameter was obtained for a β angle of −15 degrees and corresponded to 0.43 m/s;

−

By analyzing the corresponding error representations, the lowest value was 0.00136 m/s (for a β angle of 15 degrees) and the highest is 3.115 m/s (for a β angle of 45 degrees).

By analyzing the results obtained through the mathematical calculations presented above and the results identified in the literature, it can be stated that [6,22,34,39,42,54,55,56,57,58]:

−

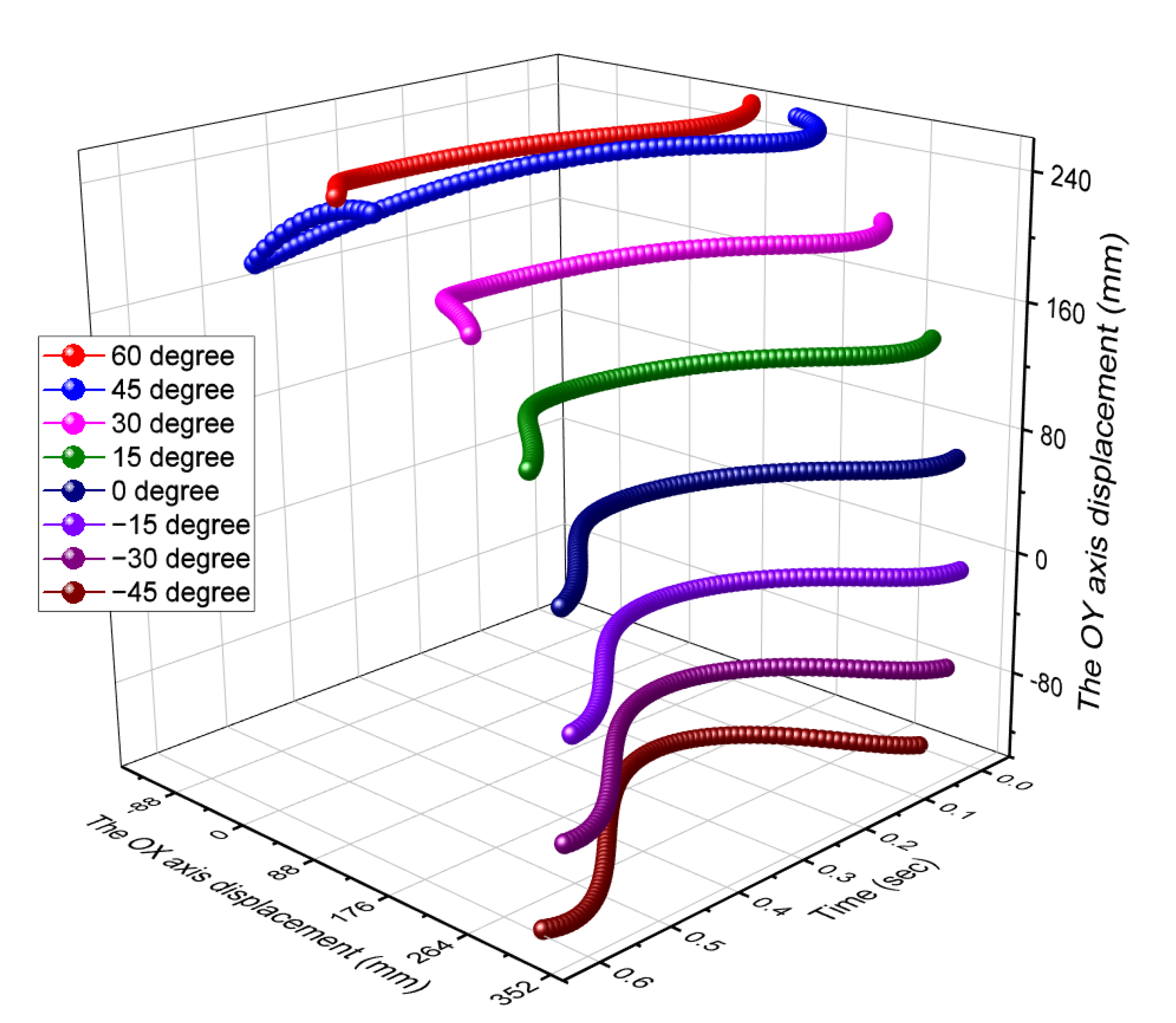
The trajectories obtained from the mathematical analysis (Figure 7) coincide with those found in the literature;

−

Compared to the literature, the article presents how to determine the position of the studied mechanism components. These mathematical relations have a general computational character, respecting the specific constructive requirements of this mechanism;

−

The calculation relations identified (relations (9), (10), and (14)) have not been found in the literature, therefore, the present article is distinguished from the existing ones by these;

−

No studies have been identified in the literature aimed at identifying the influence of the position of the drive device (connecting rod-crank) on the movement of an oscillating screen.

6. Conclusions

The mechanical separation process is widely used, and several types of equipment can be used for device construction. For the mechanical separation of a heterogeneous mixture of solid particles, a screen subjected to different types of movements is generally used.

The most used training system for mechanical separation uses a crank mechanism to achieve an oscillating movement.

Many studies have been performed to determine, from a constructive point of view, the mode of movement of the drive mechanism of the oscillating screen.

The studies presented in the literature aim to determine the geometric coordinates of the training system for its imposed positions. In this article, the influence of the position of the connecting rod-crank mechanism on the horizontal (initial position of the connecting rod) was analyzed.

From the analysis of the motion exerted by the free end of the tie rod, the element under analysis in this study, it was observed that its motion varies as follows:

−

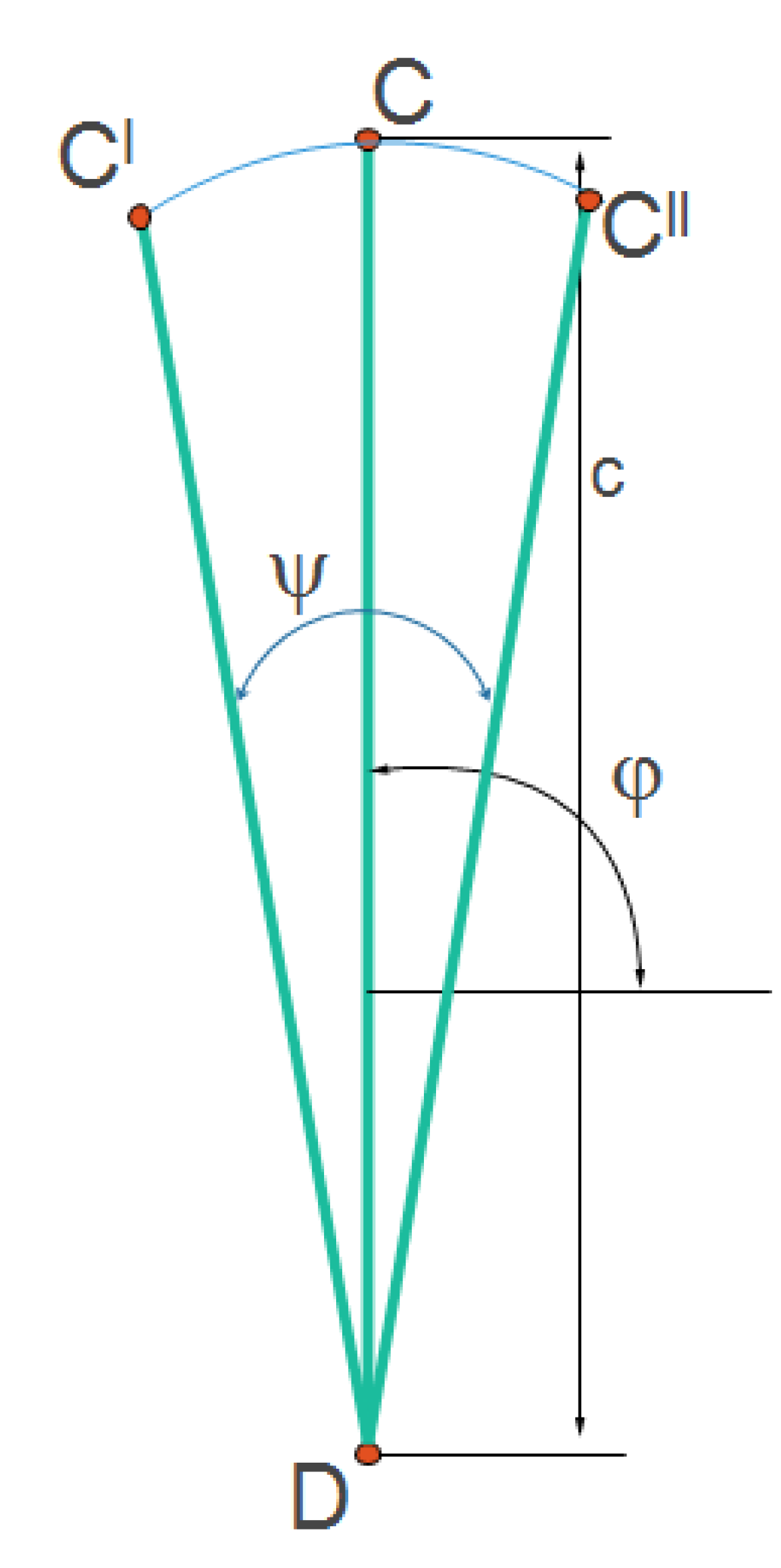
For a maximum value of β = 60°, the free end of the tie rod moved predominantly to the left side;

−

For a minimum value of β = −45°, the free end of the tie rod moved predominantly to the right side;

−

For the value of the angle β = 0°, the movement executed by the titan was symmetrical concerning the vertical.

Through conducting this study, it was found that the angle generated by the tie rod (the angle between the two extreme positions of the free end of the tie rod) was influenced by the variation of the position of the drive mechanism, respectively:

−

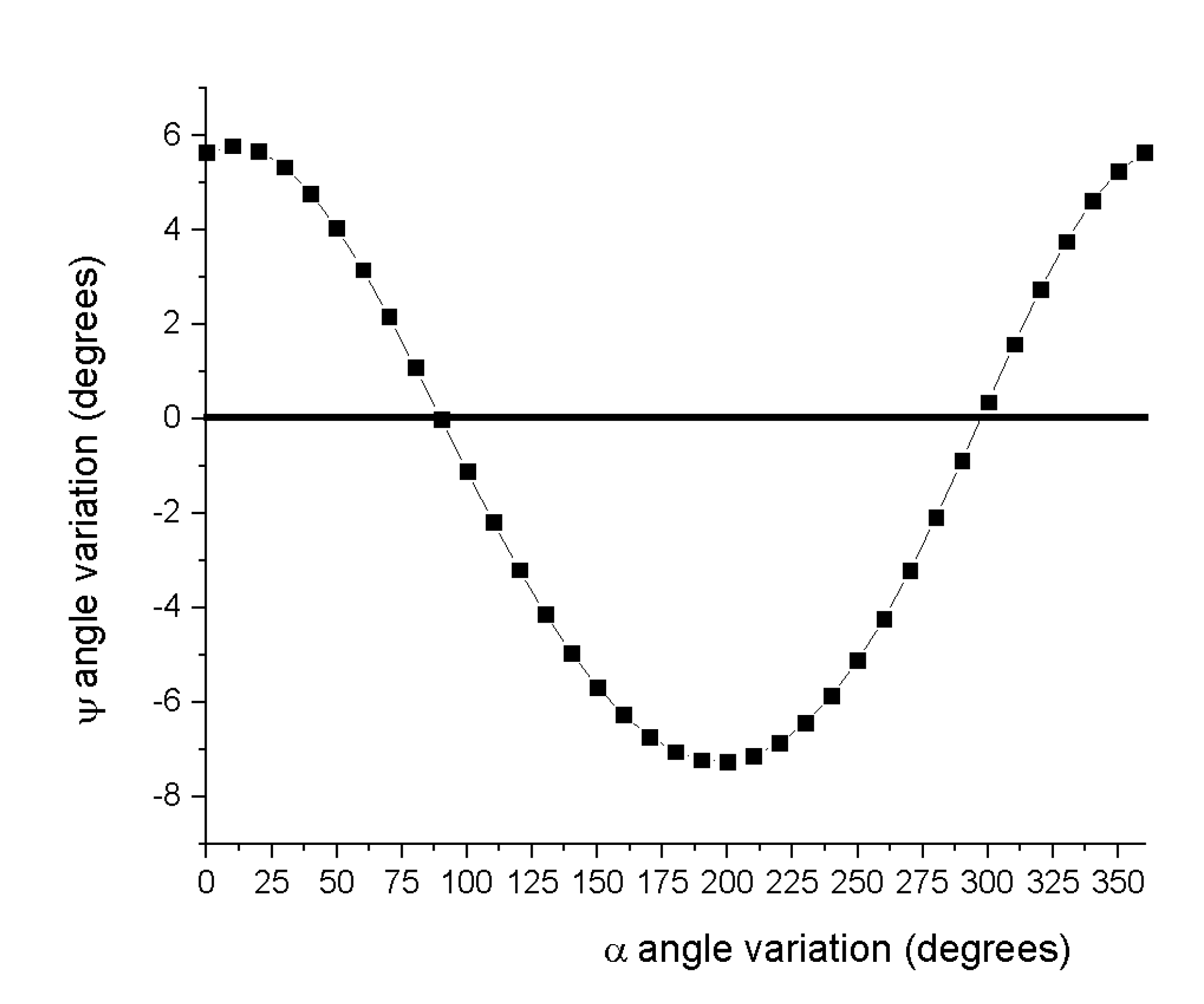
The smallest value of the angle ψ = 12.7° was obtained for a β angle of 30°.

−

The smallest value of the angle ψ = 31.45° was obtained for a β angle of −45°.

−

It is also found that the speed of movement of the free end of the tie rod was influenced by the position of the sieve drive mechanism, respectively. By analyzing the variation of the displacement speed of the free end of the tie rod, according to Figure 10, it can be stated that:

o

For β angle values between 0 and −45 degrees, an approximate sinusoidal graphical representation was obtained, and for the other values of the reference angle, an irregular speed variation was obtained;

o

The smallest value of the represented parameter, 0.00136 m/s, was obtained for the β angle of 15 degrees at a time of 0.036 s;

o

The highest value of the represented parameter, 3.115 m/s, was obtained for the β angle of 45 degrees at a time of 0.522 s.

−

Following the analysis of the graphical representation of the average displacement speed of the free end of the tie rod (Figure 11), it was concluded that:

o

The highest value of the average displacement velocity of the free end of the tie rod was obtained for a β angle of 45 degrees corresponding to 1.05 m/s. This value was obtained due to the large difference between the minimum and maximum values of the studied parameter;

o

The minimum value of the average displacement velocity of the free end of the tie rod was obtained for a β angle of −15 degrees corresponding to 0.438 m/s. This value was also closely related to the mode of speed variation, as shown in the graph in Figure 10.

This has an impact on how a solid particle moves on the surface of the oscillating sieve. This study can help in the construction and design of equipment used for the separation and transportation of heterogeneous solid particle mixtures.