A Sustainable Supply Chain Integrated with Autonomated Inspection, Flexible Eco-Production, and Smart Transportation
Abstract
:1. Introduction
- (i)
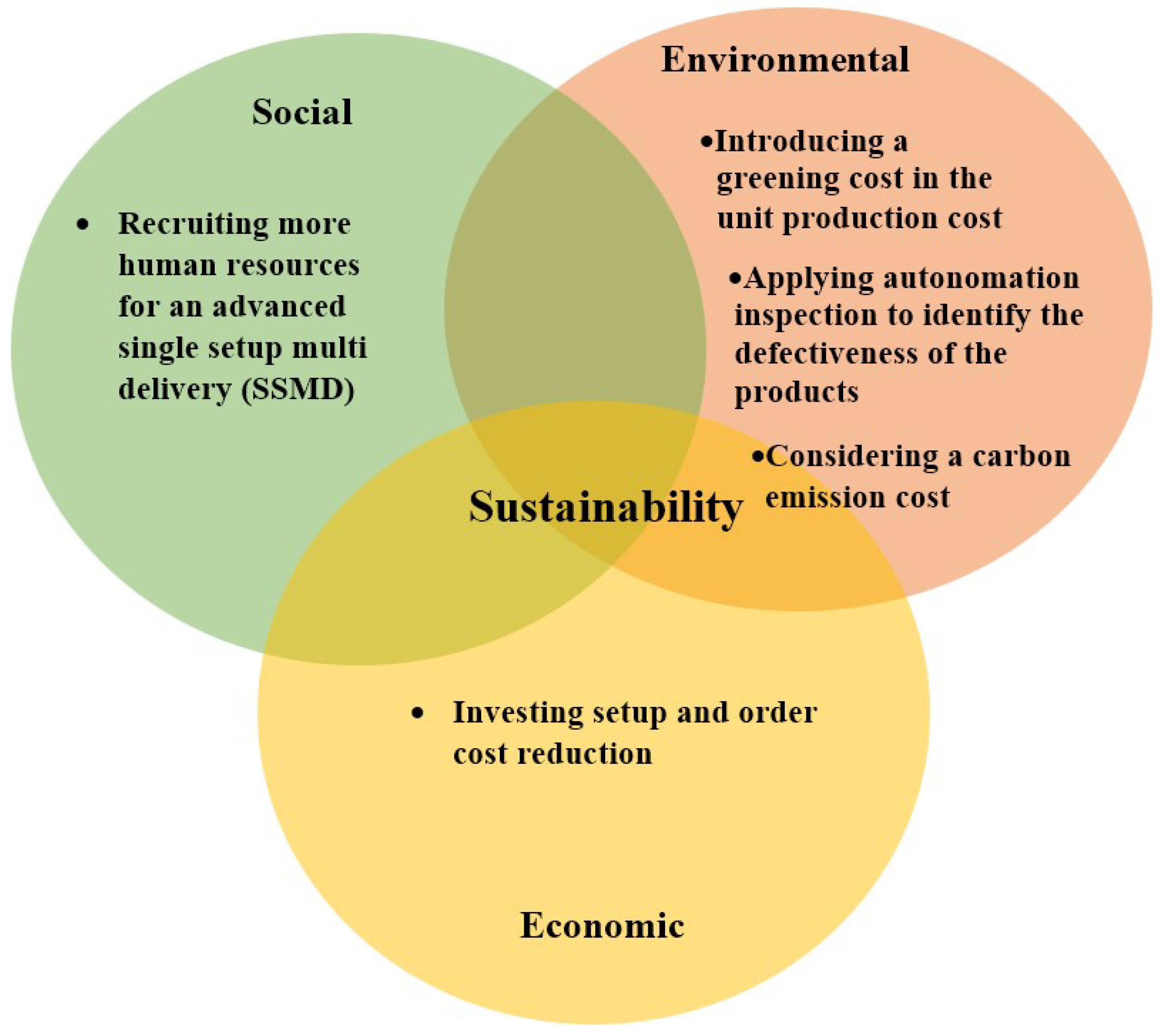
- Several supply chain models were designed based on the concept of sustainability [9,15,16]. However, a sustainable supply chain model, in which smart autonomated inspection is considered to enhance reliability, has not been reported so far. Thus, an effort is made in the present study to incorporate smart autonomation technology which enhances the system’s reliability and economic sustainability.
- (ii)
- Many supply chain models dealt with a fixed ordering cost, and fixed setup cost [17,18,19]. However, these approaches lack practicability. Thus, in this study, we consider these costs as model variables, especially when they can be reduced by some investment. This constitutes a new approach to enhance the economic sustainability of a supply chain.
- (iii)
- (iv)
- The SSMD strategy concept has been utilized in some previously reported supply chain models [18,22,23,24]. Nonetheless, the quantity, container, and distance-dependent advanced transportation strategy remained largely unexplored. Here, we employ such an advanced SSMD policy to make the system more socially sustainable.
- (v)
- For more practicality, selling price, product-quality-dependent demand, and a variable production rate are considered.
2. Background and Motivation
2.1. Autonomated Inspection
2.2. Order and Setup Cost Reduction
2.3. Eco-Production
2.4. Advanced Transportation Strategy
3. Model
3.1. Notation
| Decision | Variables |
| Retailer | |
| safety factor of the inventory | |
| l | lead time to receive a order from manufacturer after placing the order (weeks) |
| investment to reduce ordering cost ($/order) | |
| Manufacturer | |
| r | production rate of manufacturer (units/time) |
| probability for transferring the production process to out-of-control state from in-control state, (a probability) | |
| investment to reduce setup cost ($/setup) | |
| Both players | |
| p | selling price of each item ($/unit) |
| q | product’s quality level (percentage) |
| v | number of quantities in each shipment(unit) |
| z | number of shipments in a lot (unit) |
| Parameters | |
| initial setup cost to run manufacturing process ($/setup) | |
| setup cost with investments , where r is a parameter | |
| number of a load quantity with a fixed cost from manufacturer to retailer (unit) | |
| retailer’s unit purchase cost per unit ($/unit purchased) | |
| die-tool cost per unit ($/unit) | |
| manufacturing cost per unit ($/unit) | |
| order cancelation cost per item for retailer ($/item) ($/unit) | |
| variable carbon emission cost of manufacturer for transportation per container ($/container) | |
| fixed carbon emission cost of retailer ($/shipment) | |
| fixed carbon emission cost of manufacturer for transportation ($/shipment) | |
| h | inventory holding cost per unit per unit time of retailer ($/unit/time) |
| inventory holding cost per unit per unit time of manufacturer ($/unit/time) | |
| distance from retailer’s warehouse to manufacturer’s warehouse (kilometer) | |
| consumer’s total number during lead time l | |
| M | demand rate of the retailer (units) |
| i-th component of lead-time with as crashing cost per unit time ($/unit time), | |
| total amount purchased by time l | |
| unit wholesale price of the manufacturer ($/unit) | |
| initial OC for retailer ($/unit) | |
| lot size (units) | |
| initial reliability to the imperfect production rate(a probability) | |
| total crashing cost related to the lead time ($/week) | |
| S | replenishment cost for defective item ($/unit) |
| carbon emission cost of manufacturer for production ($/unit) | |
| T | cycle time, (time unit) |
| fixed transportation cost ($/shipment) | |
| fixed transportation cost for manufacturer ($/shipment) | |
| variable transportation cost per container | |
| i-th component of lead time with as minimum duration(days), | |
| i-th component of lead time with as normal duration(days), per unit distance for manufacturer ($/container.unit distance) | |
| variable cot for transportation per container ($/container/unit distance) | |
| variable cost for carbon emission of consume by container ($/container) | |
| a, b, r, | scaling parameter related to investment |
| annual fractional cost related to selling price (a scaling parameter) | |
| price elasticity parameter | |
| annual fractional cost related to quality (a scaling parameter) | |
| Parameters | |
| quality elasticity parameter | |
| scaling parameter related to retailer transportation cost | |
| unit shortage cost per unit ($/unit shortage) | |
| per unit environmental cost ($/unit) | |
| reorder point | |
| standard normal probability density function | |
| standard normal cumulative distribution function | |
| capacity of the container of retailer (ton) | |
| capacity of the container of manufacturer (ton) | |
| total cost for the retailer | |
| total profit for the retailer | |
| total cost for the manufacturer | |
| total profit for the manufacturer | |
| joint expected total cost for the entire SC | |
| joint total profit of the entire SC | |
3.2. Assumptions
- 1.
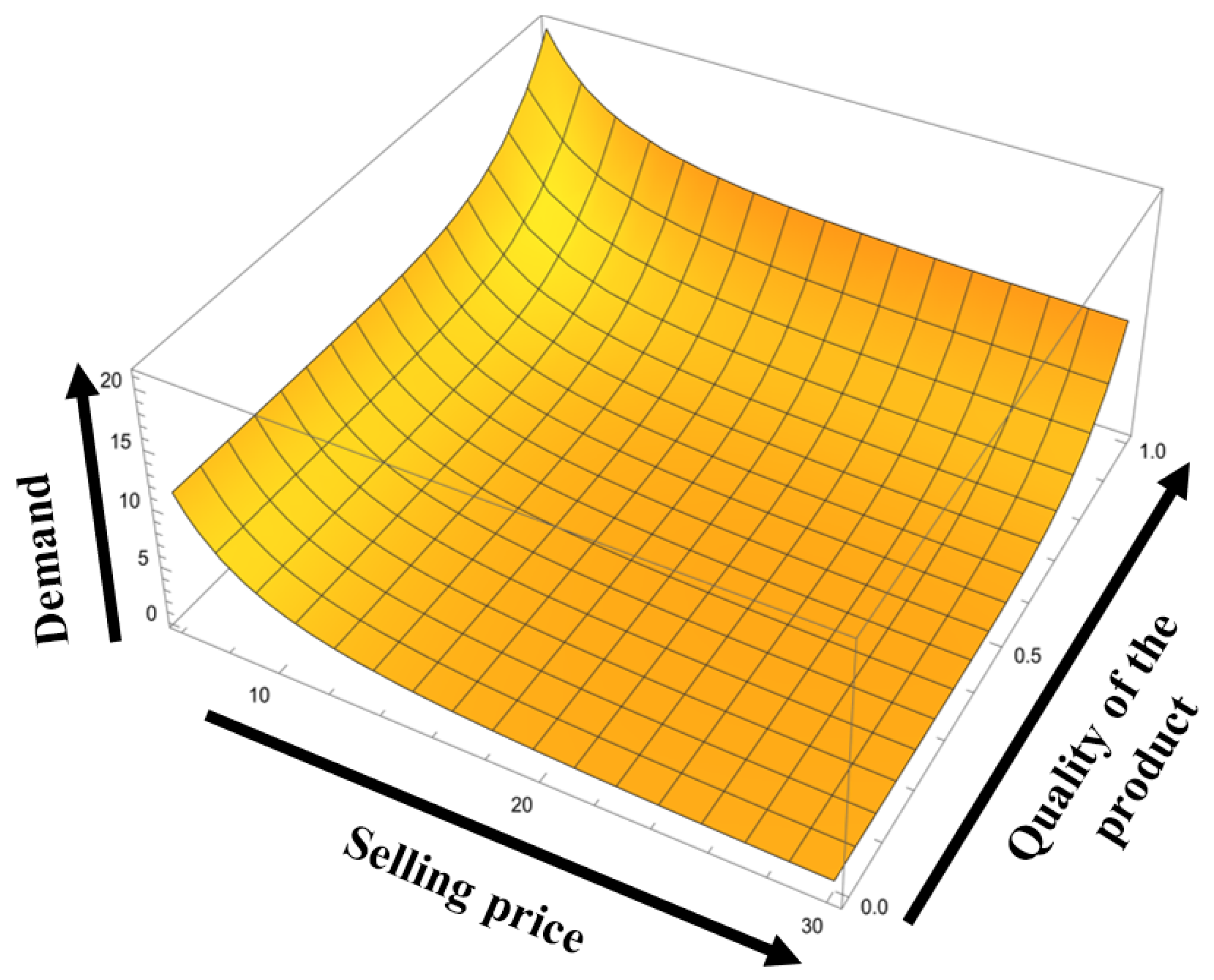
- A sustainable supply chain with a single retailer and manufacturer is considered, and a single type of environment friendly product is considered. In reality, customers prefer good quality products at less price. Hence, we assumed that the demand depends on the quality and selling price (Dey et al. [5]) i.e., (See Figure 2).
- 2.
- The demand during lead time is unpredictable. Thus, it is considered that the demand during the lead time follows a Poisson distribution with a mean . The are independent and identically normally distributed with mean and standard deviation and, then is a compound Poisson process ([7]). Due to high demand, shortages are fully backordered. To satisfy customers, safety stock is considered in this research, where the reorder point is calculated by summing up the expected lead time demand and the safety stock, i.e., reorder point .
- 3.
- Every consumer wants their desired product on their doorstep as early as possible. Thus, lead time reduction can improve service quality. This model introduces several crashing costs for mutually independent components to reduce lead time. It is taken that and are the normal and minimum duration, respectively, for the i-th component, such that the per unit crashing cost satisfies the relation . Let the lead time duration be which let the components crash to minimum duration, and let . Then and the crashing cost expression will be , for . [47].
- 4.
- 5.
- An environment friendly product is essential these days to keep our environment clean. Thus, the unit production cost of an item is dependent on variable production rate, material cost, and environment-related costs. The cost expression for unit product is (Dey et al. [20]).
- 6.
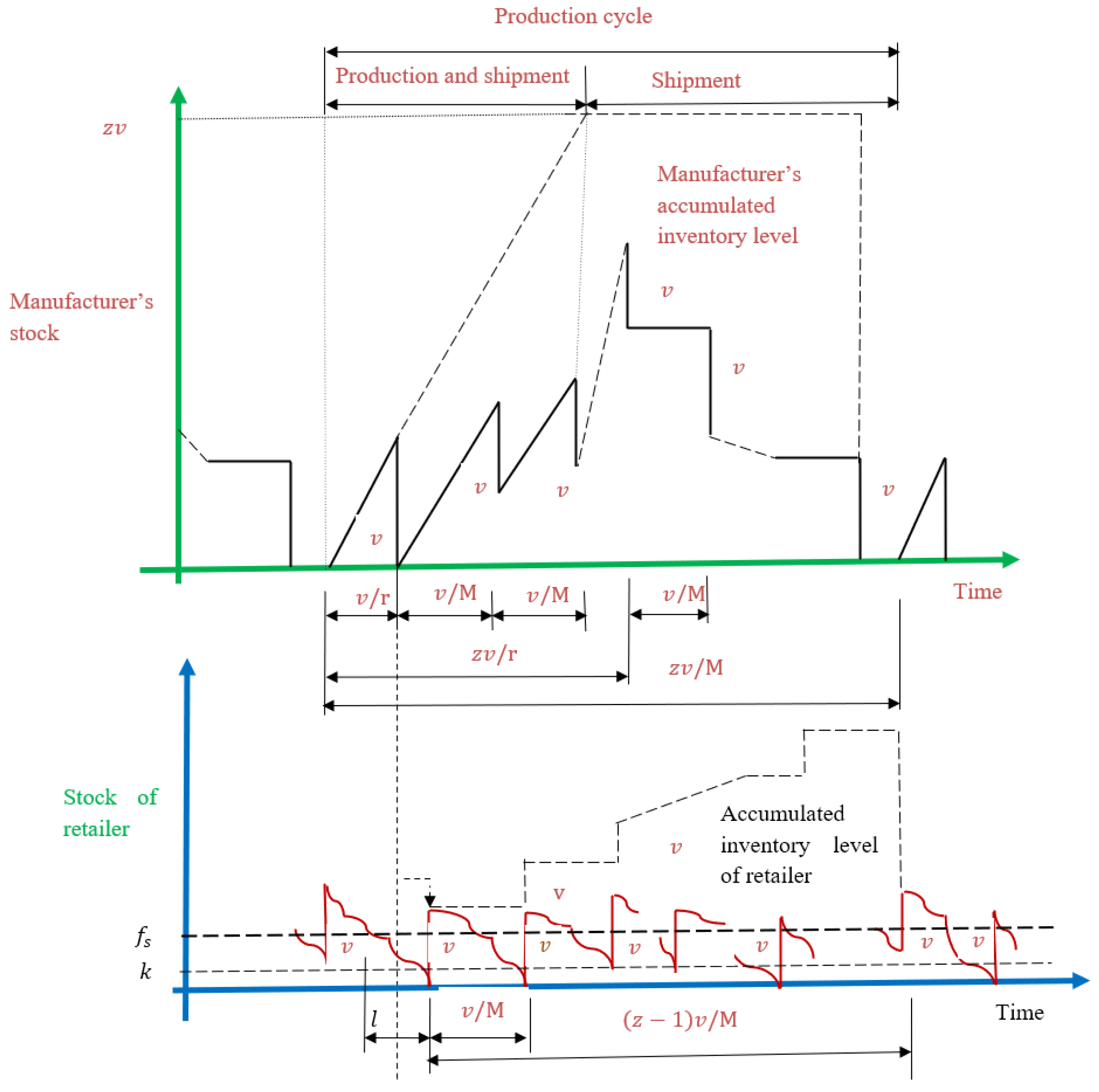
- The concept of SSMD policy ([18]) is adopted along with an advanced strategy. The transportation company charges a fixed cost for a certain number of fixed quantities. The rest of the quanity will be delivered by variable transportation costs. It is calculated through unit transportation cost, container capacity, and distance between retailer to manufacturer’s warehouses.
- 7.
- Carbon emission cost is calculated for retailer and manufacturer separately. For retailers, carbon emission is calculated only for transporting the defective product to the manufacturer, whereas for the manufacturer, carbon emission is calculated for transportation and production simultaneously.
3.3. Mathematical Model
3.3.1. Retailer’s Profit
Holding Cost for the Retailer
Ordering Cost
Investment to Enhance the Sustainability by Reducing Ordering Cost
Shortage Cost
Lead Time Crashing Cost
Smart Transportation Cost for Retailer
Carbon Emission Cost for Retailer
3.3.2. Manufacturer’s Profit
Setup Cost for Manufacturer
Investment for Reducing Setup Cost
Production and Environmental Cost
Investment for Improving the Reliability of the System through Autonomation
Holding Cost for the Manufacturer
Smart Transportation Cost under SSMD Policy
Carbon Emission Cost
4. Solution Methodology
Solution Algorithm
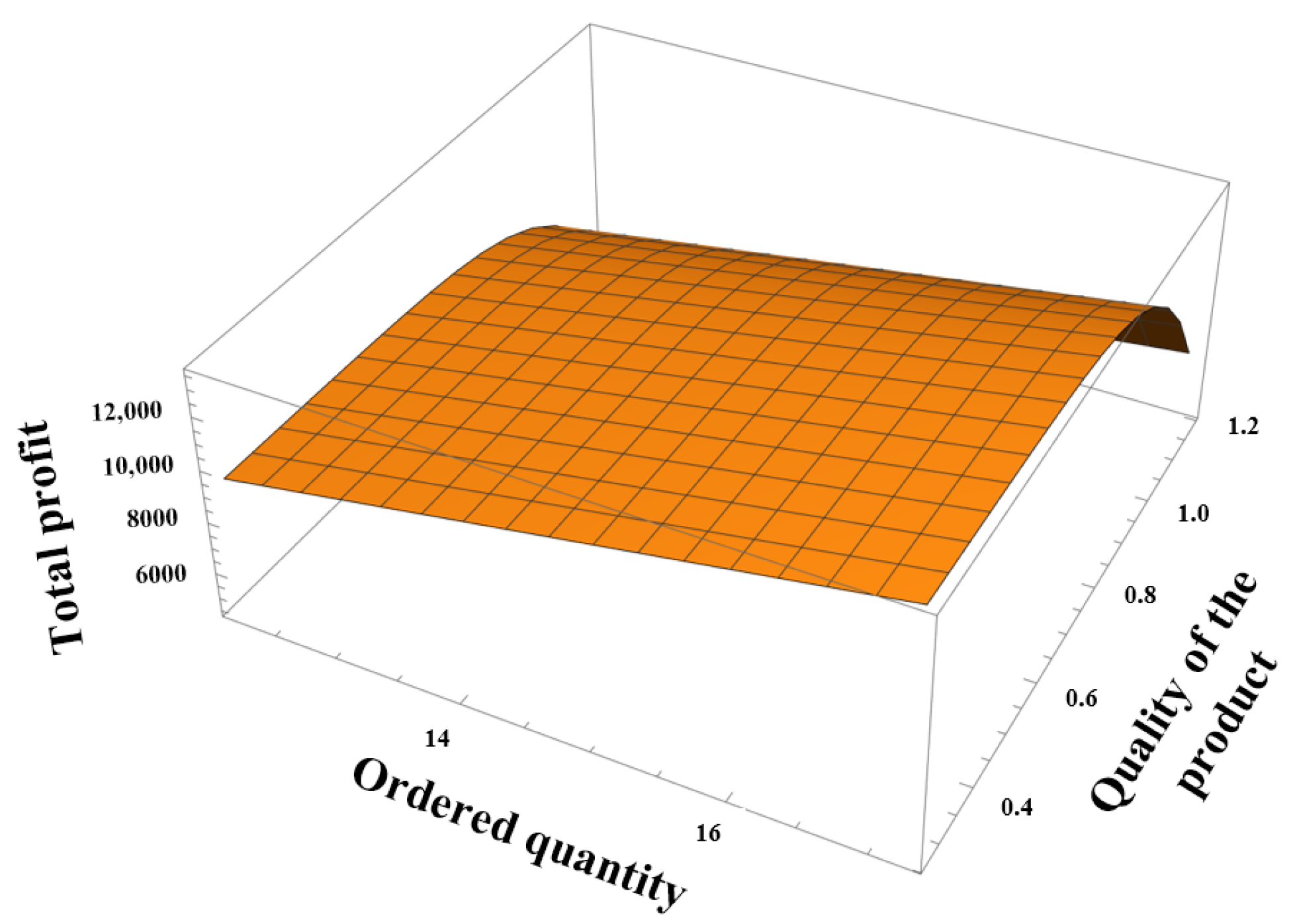
5. Numerical Examples and Analyses
5.1. Results
5.2. Special Case: When the Production Rate Is Fixed
5.3. Comparison with Previous Literature
6. Sensitivity Analysis
- (i)
- Holding cost significantly affects the total profit. An increase in holding cost always leads to increased total system cost, and system profit is reduced due to a high holding cost, which is more sensitive for the manufacturer compared to the retailer’s holding cost.
- (ii)
- Defective items in any imperfect production system always lead to less profit. This is the reason for incorporating autonomation to upgrade the reliability of the system.
- (iii)
- The fixed unit carbon emission cost for transportation and unit carbon emission costs for production are very sensitive in maximizing the profit. Reduction in those unit costs naturally increases the total system profit. Simultaneously, variable carbon emission cost per unit is slightly sensitive in the supply chain’s total profit. Similarly, carbon emission cost for the retailer due to transportation is also sensitive.
- (iv)
- More setup cost always leads to less profit. An investment is introduced to reduce the initial setup cost, which leads to a more significant profit gain.
- (v)
- Due to imperfect production processes, unit shortages occur, which are harmful to any production system, as clearly observed from the sensitivity analysis table. Small changes in shortage costs are very much effective for the total supply chain profit.
7. Managerial Insights
- (i)
- Product quality and selling price always enhance the demand for the product. Thus, managers of any industry can decide how much the selling price and quality of the products help optimize total system profit.
- (ii)
- The manager should maintain the investment to enhance the system’s reliability through autonomated inspection. Autonomated inspection for the production process can help perfectly detect the imperfection in the production process. Suppose the industry’s manager can control the movement of out-of-control from the in-control state of the production process. In that case, he can optimize the industry’s total profit by reducing the generation of the defective product. Simultaneously, managers can enhance the industry’s profit by managing the investment in setup and ordering costs.
- (iii)
- The industry managers may focus on their SCM performance by variable lead time. Because reduced lead time controls customer satisfaction as well as fulfills the market demand.
- (iv)
- Variable production rates are always beneficial for the industry to maintain its sustainability. Here, considerable unit production costs depend on development, tool/die, and environment-related costs. The investment for development cost helps the modification of product quality and helps to survive in competition. Eco-production helps to enhance environmental sustainability and improve total profit. Tool/die cost helps to reduce system failure and continues the production process. The industry manager can take this idea for their business strategy.
- (v)
- One other important finding is the variable safety factor. Variable safety factors largely control the holding cost based on fluctuating market demand. In the case of enormous demand, the holding cost is sometimes increased to stock the products, and in another point of low demand, the holding cost is reduced by limiting stock. Thus, making the right decision on safety stock is crucial. However, by the findings of this study, managers can make the right decision on safety stock.
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
References
- Garai, A.; Sarkar, B. Economically independent reverse logistics of customer-centric closed-loop supply chain for herbal medicines and biofuel. J. Clean Prod. 2022, 334, 129977. [Google Scholar] [CrossRef]
- Seok, H.; Nof, S.Y.; Filip, F.G. Sustainability decision support system based on collaborative control theory. Annu. Rev. Control 2012, 36, 85–100. [Google Scholar] [CrossRef]
- Sardar, S.K.; Sarkar, B.; Kim, B. Integrating Machine Learning, Radio Frequency Identification, and Consignment Policy for Reducing Unreliability in Smart Supply Chain Management. Processes 2021, 9, 247. [Google Scholar] [CrossRef]
- Dumitrascu, O.; Dumitrascu, M.; Dobrotǎ, D. Performance Evaluation for a Sustainable Supply Chain Management System in the Automotive Industry Using Artificial Intelligence. Processes 2020, 8, 1384. [Google Scholar] [CrossRef]
- Dey, B.K.; Pareek, S.; Tayyab, M.; Sarkar, B. Autonomation policy to control work-in-process inventory in a smart production system. Int. J. Prod. Res. 2021, 59, 1258–1280. [Google Scholar] [CrossRef]
- Sarkar, M.; Chung, B.D. Flexible work-in-process production system in supply chain management under quality improvement. Int. J. Prod. Res. 2020, 58, 3821–3838. [Google Scholar] [CrossRef]
- Dey, B.K.; Sarkar, B.; Sarkar, M.; Pareek, S. An integrated inventory model involving discrete setup cost reduction, variable safety factor, selling price dependent demand, and investment. Rairo-Oper. Res. 2019, 53, 39–57. [Google Scholar] [CrossRef]
- Sarkar, B.; Chaudhuri, K.; Moon, I. Manufacturing setup cost reduction and quality improvement for the distribution free continuous-review inventory model with a service level constraint. J. Manuf. Syst. 2015, 34, 74–82. [Google Scholar] [CrossRef]
- Sana, S. Price competition between green and non green products under corporate social responsible firm. J. Retail. Consum. Serv. 2020, 55, 102118. [Google Scholar] [CrossRef]
- Mishra, U.; Wu, J.Z.; Sarkar, B. A sustainable production-inventory model for a controllable carbon emissions rate under shortages. J. Clean Prod. 2020, 256, 120268. [Google Scholar] [CrossRef]
- Liu, K.; Li, W.; Jia, F.; Lan, Y. Optimal strategies of green product supply chains based on behaviour-based pricing. J. Clean Prod. 2022, 335, 130288. [Google Scholar] [CrossRef]
- Sepehri, A.; Mishra, U.; Sarkar, B. A sustainable production-inventory model with imperfect quality under preservation technology and quality improvement investment. J. Clean Prod. 2022, 310, 127332. [Google Scholar] [CrossRef]
- Sarkar, B.; Ullah, M.; Kim, N. Environmental and economic assessment of closed-loop supply chain with remanufacturing and returnable transport items. Comput. Ind. Eng. 2017, 111, 148–163. [Google Scholar] [CrossRef]
- Sarkar, B.; Sarkar, M.; Ganguly, B.; Cárdenas-Barrón, L.E. Combined effects of carbon emission and production quality improvement for fixed lifetime products in a sustainable supply chain management. Int. J. Prod. Econ. 2021, 231, 107867. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Ahmadzadeh, K.; Ghavamifar, A. Designing an optimal sustainable supply chain system considering pricing decisions and resilience factors. J. Clean Prod. 2022, 332, 129895. [Google Scholar] [CrossRef]
- Abdel-Basset, M.; Mohamed, R.; Sallam, K.; Elhoseny, M. A novel decision-making model for sustainable supply chain finance under uncertainty environment. J. Clean Prod. 2020, 269, 122324. [Google Scholar] [CrossRef]
- Pal, B.; Sana, S.S.; Chaudhuri, K. Two-echelon manufacturer–retailer supply chain strategies with price, quality, and promotional effort sensitive demand. Int. Trans. Oper. Res. 2015, 22, 1071–1095. [Google Scholar] [CrossRef]
- Sarkar, B.; Ahmed, W.; Kim, N. Joint effects of variable carbon emission cost and multi-delay-in-payments under single-setupmultiple-delivery policy in a global sustainable supply chain. J. Clean Prod. 2018, 185, 421–445. [Google Scholar] [CrossRef]
- Bhuniya, S.; Pareek, S.; Sarkar, B. A supply chain model with service level constraints and strategies under uncertainty. Alex. Eng. J. 2021, 60, 6035–6052. [Google Scholar] [CrossRef]
- Dey, B.K.; Bhuniya, S.; Sarkar, B. Involvement of controllable lead time and variable demand for a smart manufacturing system under a supply chain management. Expert Syst. Appl. 2021, 184, 115464. [Google Scholar] [CrossRef]
- Sarkar, M.; Seo, Y.W. Renewable energy supply chain management with flexibility and automation in a production system. J. Clean Prod. 2021, 324, 129149. [Google Scholar] [CrossRef]
- Kim, S.L.; Banerjee, A.; Burton, J. Production and delivery policies for enhanced supply chain partnerships. Int. J. Prod. Res. 2008, 46, 6207–6229. [Google Scholar] [CrossRef]
- Chauhan, R.; Kumar, V.; Jana, T.K.; Majumder, A. A Modified Customization Strategy in a Dual-Channel Supply Chain Model with Price-Sensitive Stochastic Demand and Distribution-Free Approach. Math. Probl. Eng. 2021, 2021, 5549882. [Google Scholar] [CrossRef]
- Nandra, R.; Majumder, A.; Mishra, M. A multi-retailer sustainable supply chain model with information sharing and quality deterioration. Rairo-Oper. Res. 2021, 55, S2773–S2794. [Google Scholar] [CrossRef]
- Hong, Z.; Guo, X. Green product supply chain contracts considering environmental responsibilities. Omega 2019, 83, 155–166. [Google Scholar] [CrossRef]
- Huang, C.K.; Cheng, T.; Kao, T.; Goyal, S. An integrated inventory model involving manufacturing setup cost reduction in compound Poisson process. Int. J. Prod. Res. 2011, 49, 1219–1228. [Google Scholar] [CrossRef]
- Khouja, M.; Mehrez, A. Economic production lot size model with variable production rate and imperfect quality. J. Oper. Res. Soc. 1994, 45, 1405–1417. [Google Scholar]
- Majumder, A.; Jaggi, C.K.; Sarkar, B. A multi-retailer supply chain model with backorder and variable production cost. Rairo-Oper. Res. 2018, 52, 943–954. [Google Scholar] [CrossRef]
- Yu, W.; Han, R. The impact of pollution taxation on competitive green product choice strategies. Comput. Ind. Eng. 2019, 137, 106012. [Google Scholar] [CrossRef]
- Sarkar, B.; Sana, S.S.; Chaudhuri, K. An imperfect production process for time varying demand with inflation and time value of money–an EMQ model. Expert Syst. Appl. 2011, 38, 13543–13548. [Google Scholar] [CrossRef]
- Li, Q.; Zheng, S. Joint inventory replenishment and pricing control for systems with uncertain yield and demand. Oper. Res. 2006, 54, 696–705. [Google Scholar] [CrossRef]
- Song, Y.; Wang, Y. Periodic review inventory systems with fixed order cost and uniform random yield. Eur. J. Oper. Res. 2017, 257, 106–117. [Google Scholar] [CrossRef]
- Porteus, E.L. Optimal lot sizing, process quality improvement and setup cost reduction. Oper. Res. 1986, 34, 137–144. [Google Scholar] [CrossRef]
- Dey, B.K.; Sarkar, B.; Pareek, S. A two-echelon supply chain management with setup time and cost reduction, quality improvement and variable production rate. Mathematics 2019, 7, 328. [Google Scholar] [CrossRef]
- Wee, H.M.; Lee, M.C.; Jonas, C.; Wang, C.E. Optimal replenishment policy for a deteriorating green product: Life cycle costing analysis. Int. J. Prod. Econ. 2011, 133, 603–611. [Google Scholar] [CrossRef]
- Su, J.C.; Wang, L.; Ho, J.C. The impacts of technology evolution on market structure for green products. Math. Comput. Model. 2012, 55, 1381–1400. [Google Scholar] [CrossRef]
- Halat, K.; Hafezalkotob, A. Modeling carbon regulation policies in inventory decisions of a multi-stage green supply chain: A game theory approach. Comput. Ind. Eng. 2019, 128, 807–830. [Google Scholar] [CrossRef]
- Darvish, M.; Archetti, C.; Coelho, L.C. Trade-offs between environmental and economic performance in production and inventoryrouting problems. Int. J. Prod. Econ. 2019, 217, 269–280. [Google Scholar] [CrossRef]
- Ahmadini, A.A.H.; Modibbo, U.M.; Shaikh, A.A.; Ali, I. Multi-objective optimization modelling of sustainable green supply chain in inventory and production management. Alex. Eng. J. 2021, 60, 5129–5146. [Google Scholar] [CrossRef]
- Becerra, P.; Mula, J.; Sanchis, R. Green supply chain quantitative models for sustainable inventory management: A review. J. Clean Prod. 2021, 328, 129544. [Google Scholar] [CrossRef]
- Tang, S.; Wang, W.; Zhou, G. Remanufacturing in a competitive market: A closed-loop supply chain in a Stackelberg game framework. Expert Syst. Appl. 2020, 161, 113655. [Google Scholar] [CrossRef]
- Sarkar, B.; Bhunia, S. A sustainable flexible manufacturing–remanufacturing model with improved service and green investment under variable demand. Expert Syst. Appl. 2022, 202, 117154. [Google Scholar] [CrossRef]
- Kim, S.L.; Ha, D. A JIT lot-splitting model for supply chain management: Enhancing buyer–supplier linkage. Int. J. Prod. Econ. 2003, 86, 1–10. [Google Scholar] [CrossRef]
- Wang, S.; Sarker, B.R. An assembly-type supply chain system controlled by kanbans under a just-in-time delivery policy. Eur. J. Oper. Res. 2005, 162, 153–172. [Google Scholar] [CrossRef]
- Bhuniya, S.; Pareek, S.; Sarkar, B.; Sett, B. A Smart Production Process for the Optimum Energy Consumption with Maintenance Policy under a Supply Chain Management. Processes 2021, 9, 19. [Google Scholar] [CrossRef]
- Ben-Said, A.; Moukrim, A.; Guibadj, R.N.; Verny, J. Using decomposition-based multi-objective algorithm to solve Selective Pickup and Delivery Problems with Time Windows. Comput. Oper. Res. 2022, 145, 105867. [Google Scholar] [CrossRef]
- Tiwari, S.; Kazemi, N.; Modak, N.M.; Cárdenas-Barrón, L.E.; Sarkar, S. The effect of human errors on an integrated stochastic supply chain model with setup cost reduction and backorder price discount. Int. J. Prod. Econ. 2020, 226, 107643. [Google Scholar] [CrossRef]
- Guo, X.; Liu, W.; Zhang, T. Pricing and ordering decisions for the supply chain integrating of online and offline channels. Environ. Dev. Sustain. 2022, 1–25, in press. [Google Scholar] [CrossRef]
- Cheng, R.; Duan, Y.; Zhang, J.; Ke, H. Impacts of store-brand introduction on a multiple-echelon supply chain. Eur. J. Oper. Res. 2022, 292, 652–662. [Google Scholar] [CrossRef]
- Hota, S.K.; Sarkar, B.; Ghosh, S.K. Effects of unequal lot size and variable transportation in unreliable supply chain management. Mathematics 2020, 8, 357. [Google Scholar] [CrossRef] [Green Version]

| Researchers | Process Reliability | Demand Depend on | Production Rate | Investment for Setup & Order Cost Reduction | Transportation Policy |
|---|---|---|---|---|---|
| Dey et al. [5] | NA | SPQ | Var. | NA | NA |
| Dey et al. [7] | Inc. | SP | Con. | SC | SSMD |
| Hong & Guo [25] | NA | Con. | Con. | NA | NA |
| Huang et al. [26] | NA | Con. | Con. | SC | NA |
| Khouja & Mehrez [27] | NA | Con. | Var. | NA | NA |
| Kim et al. [22] | NA | Con. | Var. | NA | SSMD |
| Majumder et al. [28] | Inc. | Con. | Var. | SC | SSMD |
| Pal et al. [17] | NA | SP | Con. | NA | NA |
| Sarkar et al. [8] | Inc. | Con. | Con. | SC | SSSD |
| Sarkar and Chung [6] | Inc. | Con. | Var. | SC | SSMD |
| Yu & Han [29] | NA | Con. | Con. | NA | NA |
| This study | AI | SPQ | Var. | SOC | Smart |
| SSMD |
| Lead Time | Normal Duration | Minimum Duration | Unit Crashing |
|---|---|---|---|
| Component i | (days) | (days) | Cost ($/day) |
| 1 | 20 | 6 | 0.4 |
| 2 | 20 | 6 | 1.2 |
| 3 | 16 | 9 | 5.0 |
| Lead-Time (Week) | Crashing Cost ($) |
|---|---|
| 8 | 0 |
| 6 | 5.6 |
| 4 | 22.4 |
| 3 | 57.4 |
| Investment | Ordering Cost | Setup Cost |
|---|---|---|
| 0 | 500 | 1000 |
| 50 | 109 | 606 |
| 100 | 61 | 368 |
| 200 | 33 | 135 |
| 300 | 22 | 50 |
| 400 | 17 | 18 |
| Decision | of Retailer | |||||
|---|---|---|---|---|---|---|
| Variables | ||||||
| l (weeks) | 4 | 4 | 4 | 4 | 4 | 4 |
| ($/order) | 0 | 100 | 100 | 200 | 300 * | 400 |
| 0.845 | 0.845 | 0.536 | 0.782 | * | 0.845 | |
| Decision | of manufacturer | |||||
| variables | ||||||
| ($/setup) | 0 | 0 | 100 | 200 | 300 * | 400 |
| 0.00048 | 0.00046 | 0.00045 | 0.00038 | * | 0.00042 | |
| r (units) | 200.65 | 266.66 | 281.21 | 323.01 | * | 271.27 |
| Decision | for both | |||||
| variables | players | |||||
| z | 3 | 4 | 4 | 5 | 5 * | 4 |
| p ($/units) | 22.76 | 22.93 | 20.04 | 22.37 | * | 24.03 |
| q | 0.71 | 0.62 | 0.59 | 0.55 | * | 0.63 |
| v (units) | 26.58 | 17.95 | 10.97 | 12.21 | * | 18.74 |
| Total profit ($/cycle) | 6110.13 | 8390.20 | 8590.82 | 9586.11 | 10,303.50 * | 8765.36 |
| I | z | P | q | Total Profit | |||||
|---|---|---|---|---|---|---|---|---|---|
| (Weeks) | ($/Order) | ($/Setup) | ($/Units) | (Units) | ($/Cycle) | ||||
| 4 * | 300 * | 300 * | 4 * | * | * | * | * | * | * |
| 4 | 0 | 0 | 3 | 0.00048 | 28.81 | 0.69 | 0.783 | 31.72 | 7311.85 |
| Pal et al. [17] | Dey et al. [34] | Dey et al. [5] | This Model | |
|---|---|---|---|---|
| Ordering | NA | (constant) | NA | (reduced) |
| cost reduction | - | $200 | - | $478 |
| Production | NA | (constant) | (variable) | (variable) |
| rate | - | 3200 unit | 5994.25 unit | 316.22 unit |
| Total Profit | 2864 ($/cycle) | 1802 ($/cycle) | 6860 ($/cycle) | 10,303 ($/cycle) |
| Parameters | Changes | Parameters | Changes | ||
|---|---|---|---|---|---|
| (In%) | (In%) | (In%) | (In%) | ||
| +25 | |||||
| h | |||||
| +25 | |||||
| S | |||||
| +25 | |||||
| +25 | |||||
| +25 | |||||
| +25 | |||||
| +25 | |||||
| +25 | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dey, B.K.; Yilmaz, I.; Seok, H. A Sustainable Supply Chain Integrated with Autonomated Inspection, Flexible Eco-Production, and Smart Transportation. Processes 2022, 10, 1775. https://doi.org/10.3390/pr10091775
Dey BK, Yilmaz I, Seok H. A Sustainable Supply Chain Integrated with Autonomated Inspection, Flexible Eco-Production, and Smart Transportation. Processes. 2022; 10(9):1775. https://doi.org/10.3390/pr10091775
Chicago/Turabian StyleDey, Bikash Koli, Ibrahim Yilmaz, and Hyesung Seok. 2022. "A Sustainable Supply Chain Integrated with Autonomated Inspection, Flexible Eco-Production, and Smart Transportation" Processes 10, no. 9: 1775. https://doi.org/10.3390/pr10091775
APA StyleDey, B. K., Yilmaz, I., & Seok, H. (2022). A Sustainable Supply Chain Integrated with Autonomated Inspection, Flexible Eco-Production, and Smart Transportation. Processes, 10(9), 1775. https://doi.org/10.3390/pr10091775







