Gas Flow and Ablation of 122 mm Supersonic Rocket Nozzle Investigated by Conjugate Heat Transfer Analysis
Abstract
:1. Introduction
2. Conjugate Heat Transfer Analysis (CHTA)
2.1. CFD
2.2. FEA
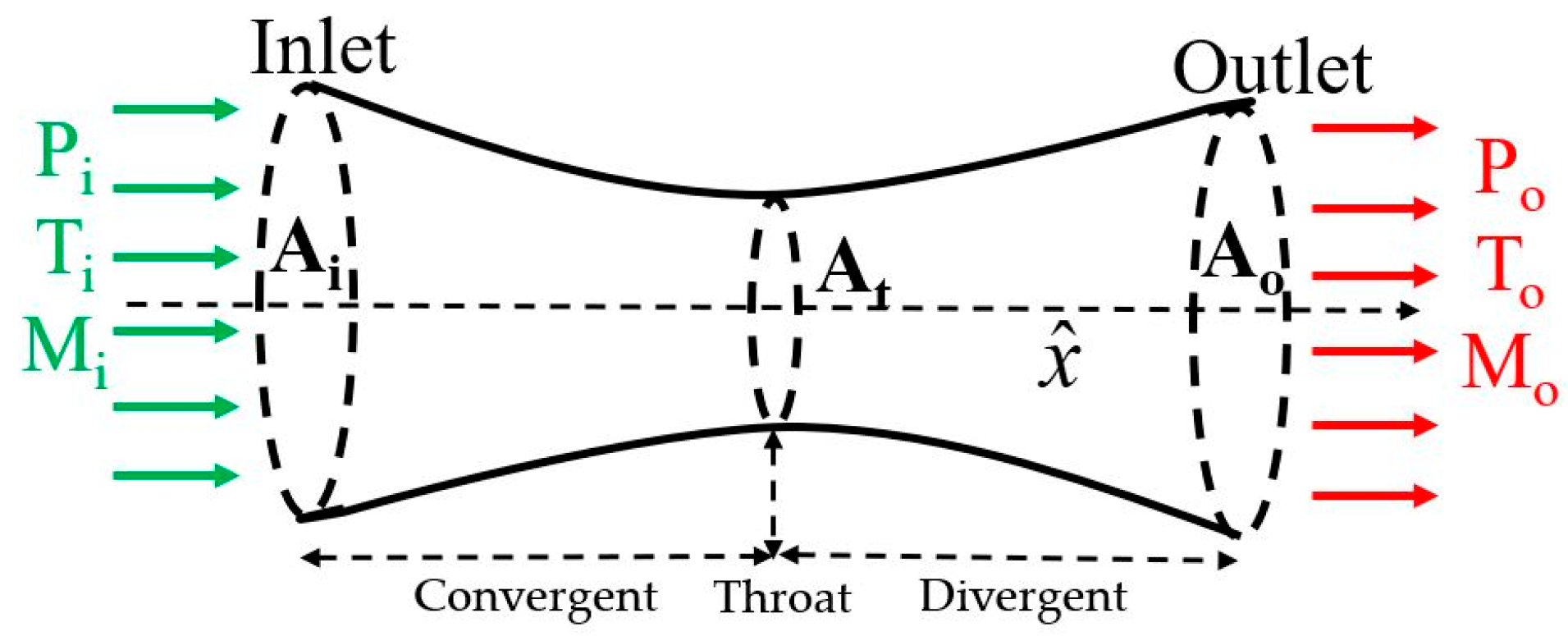
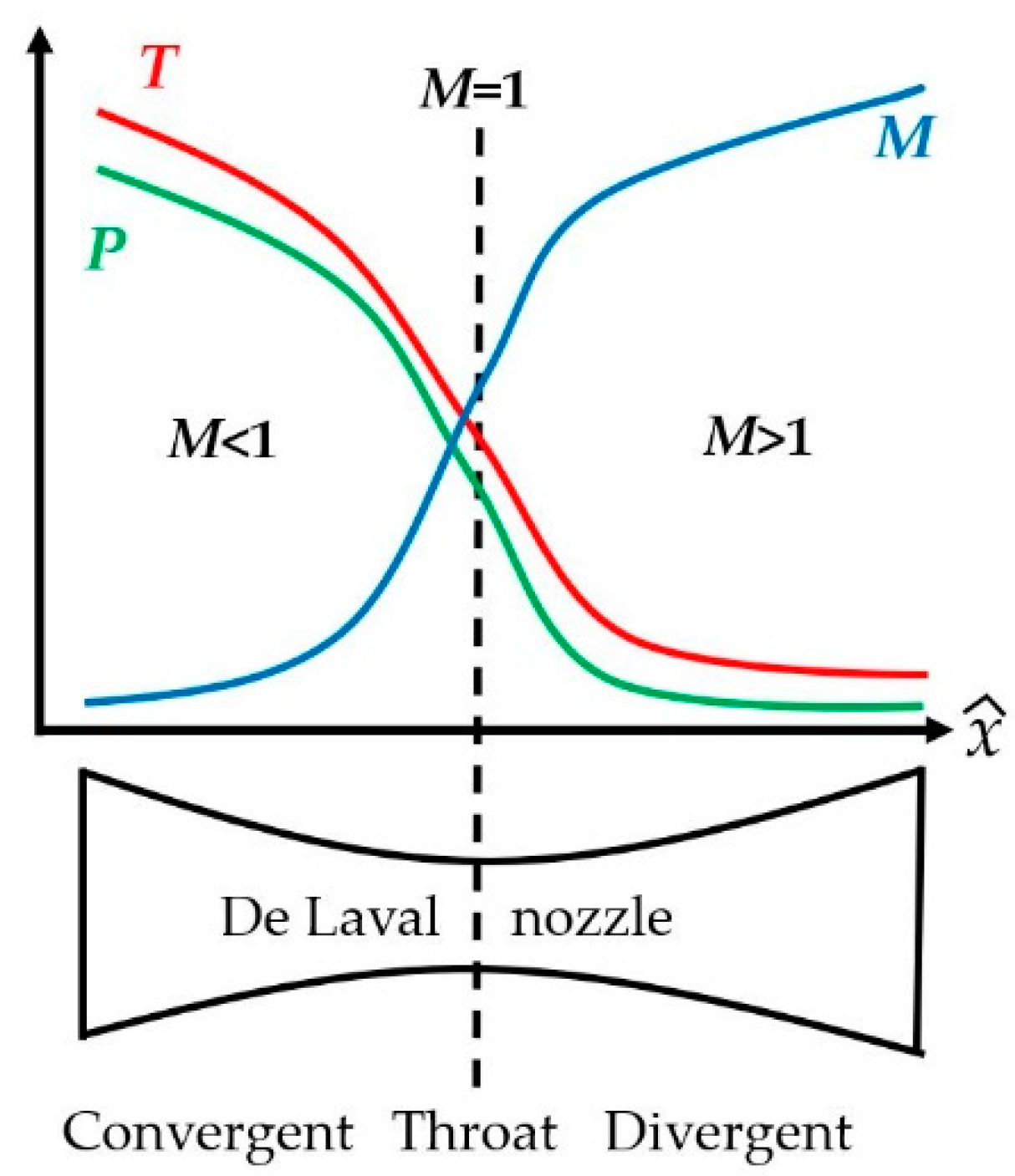
2.3. Rocket Thrust Equations in a De Laval Nozzle
2.4. Equivalent Von Mises Stress
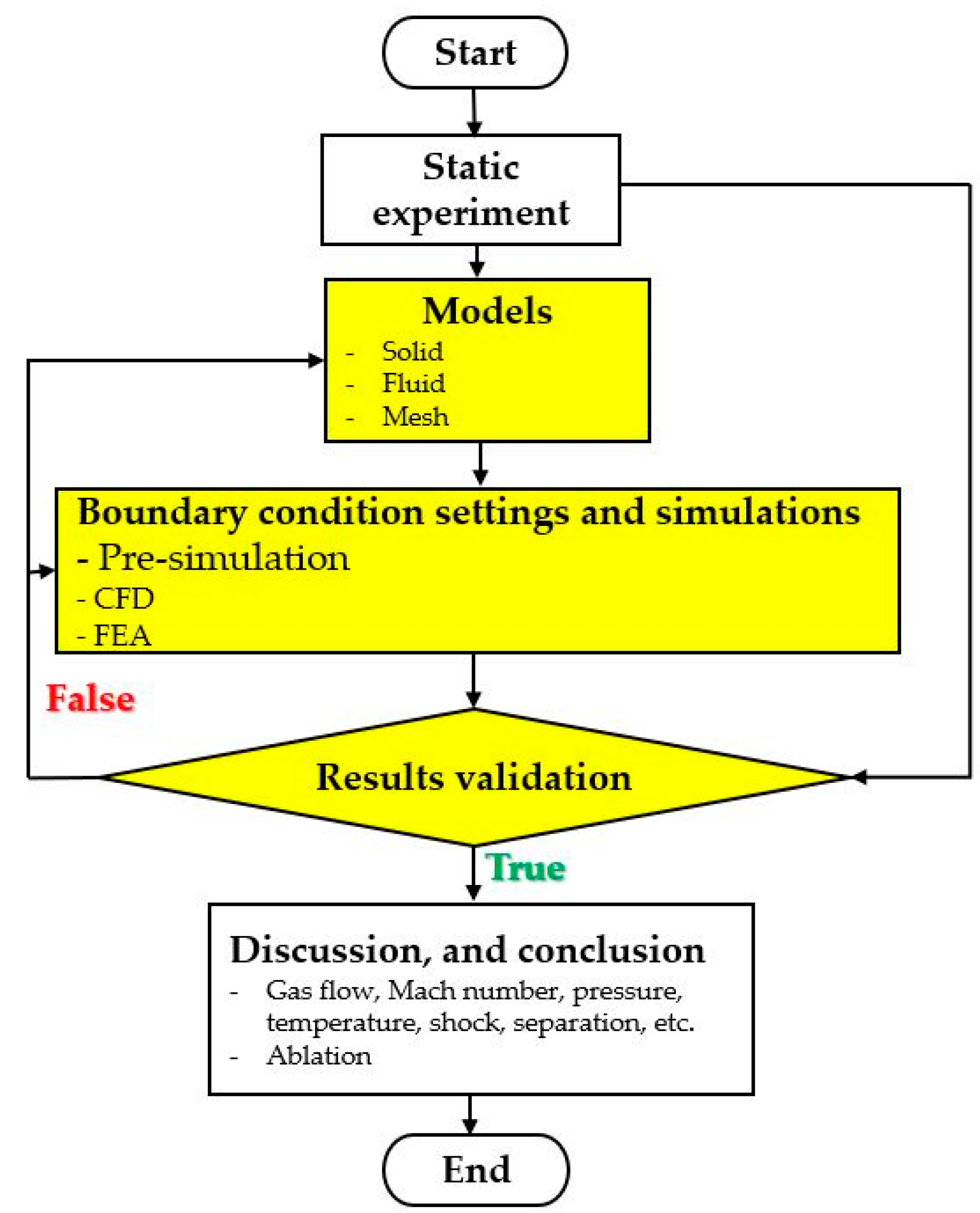
3. Methodology
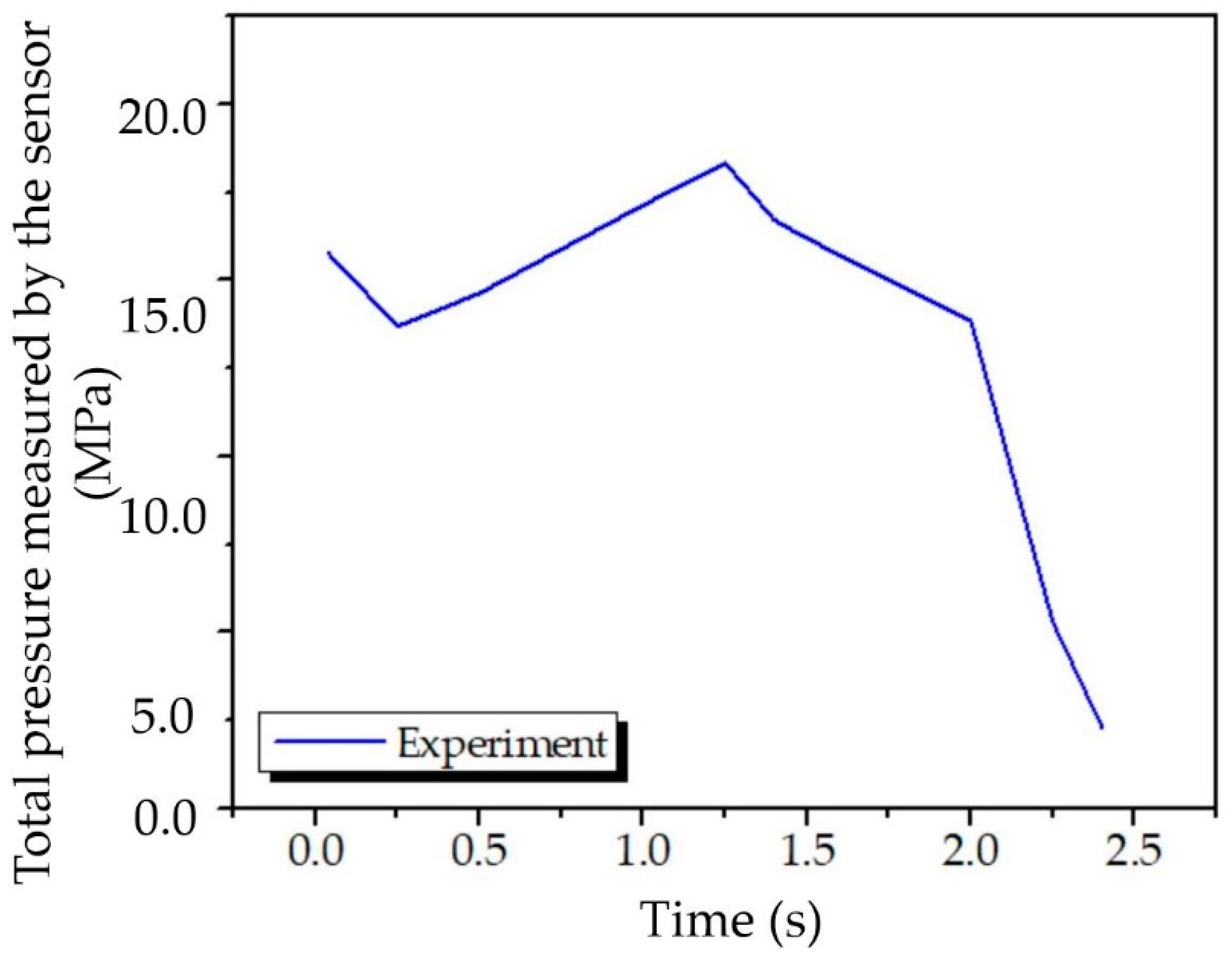
3.1. Static Experiment
3.2. Models
3.3. Boundary Conditions and Simulations
4. Results and Discussion
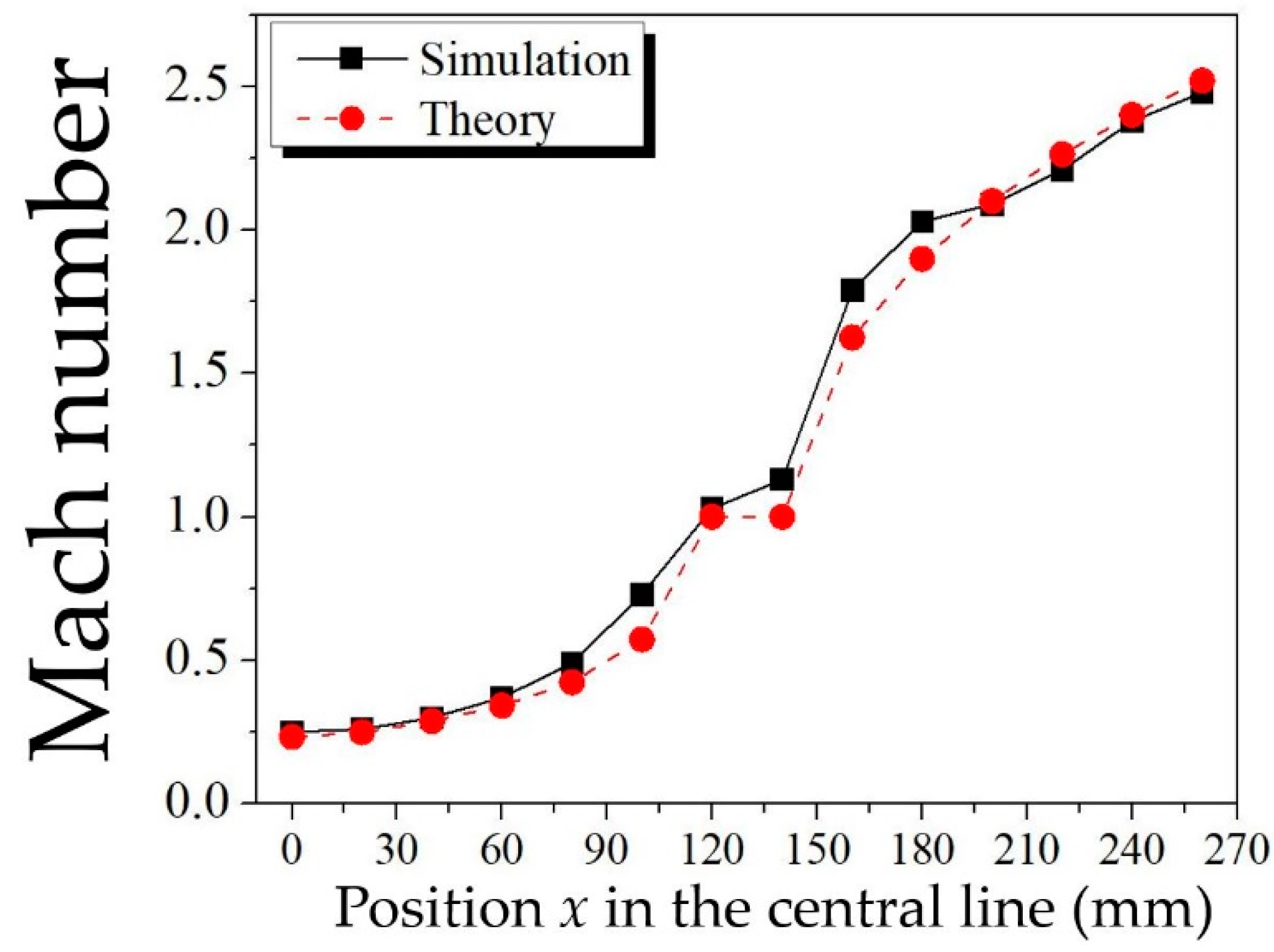
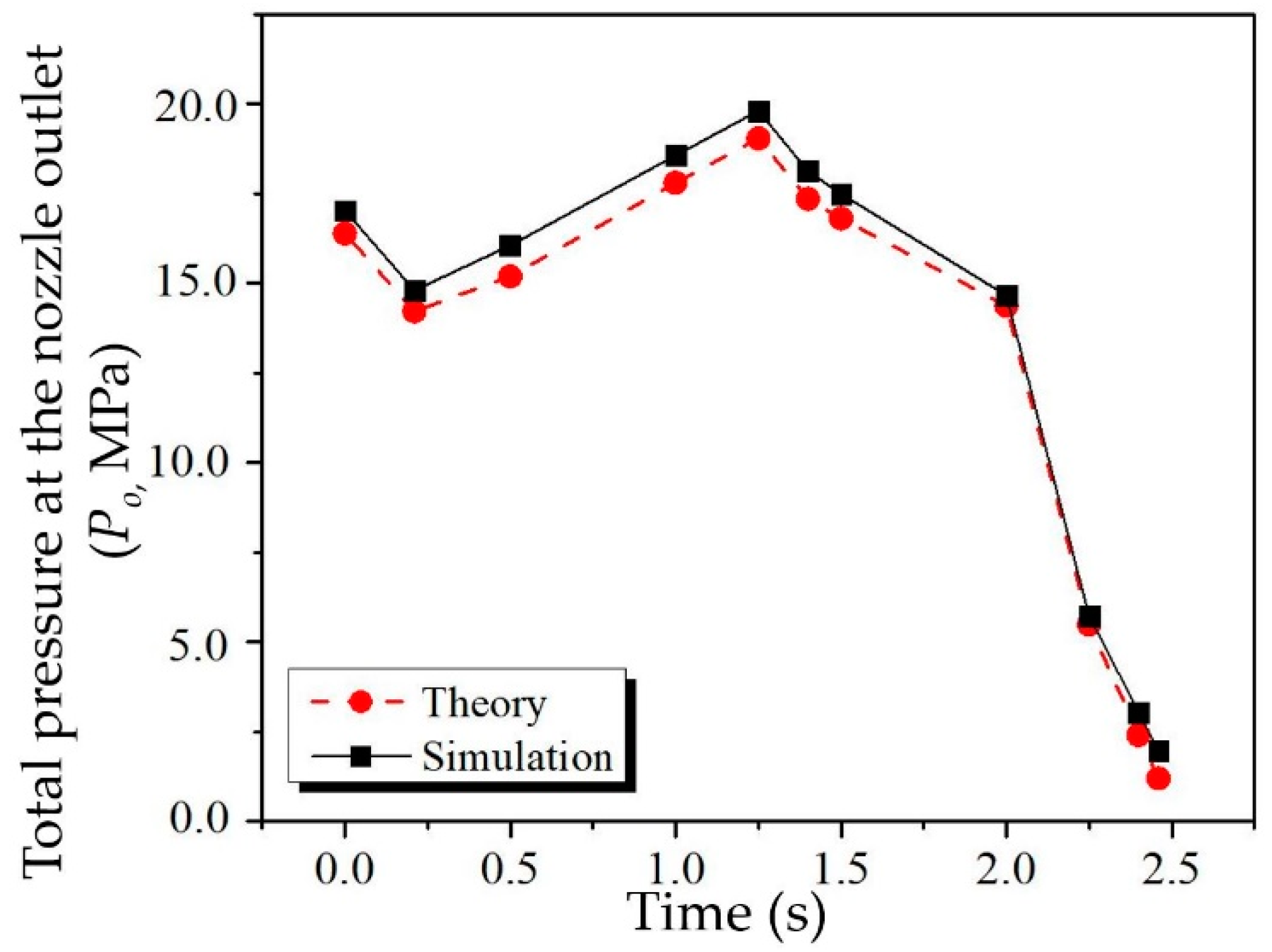
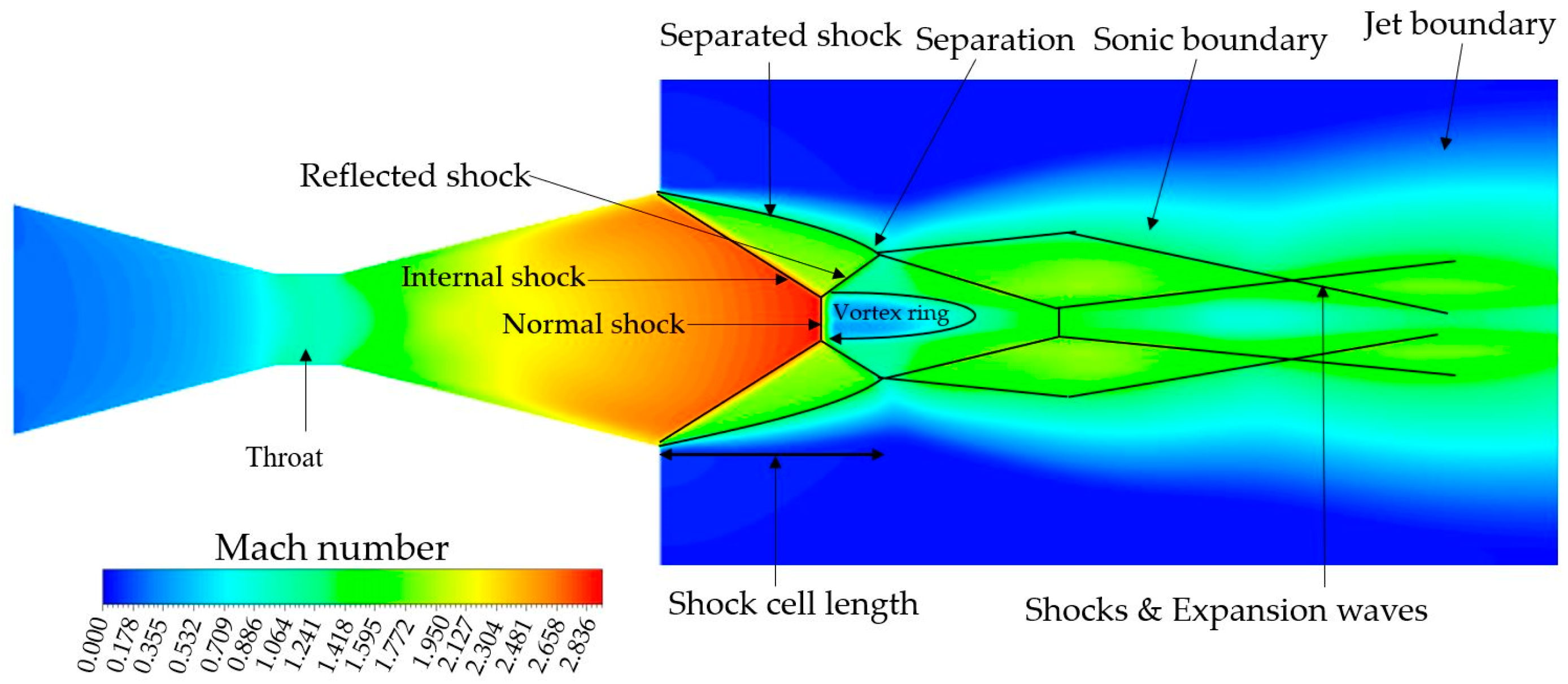
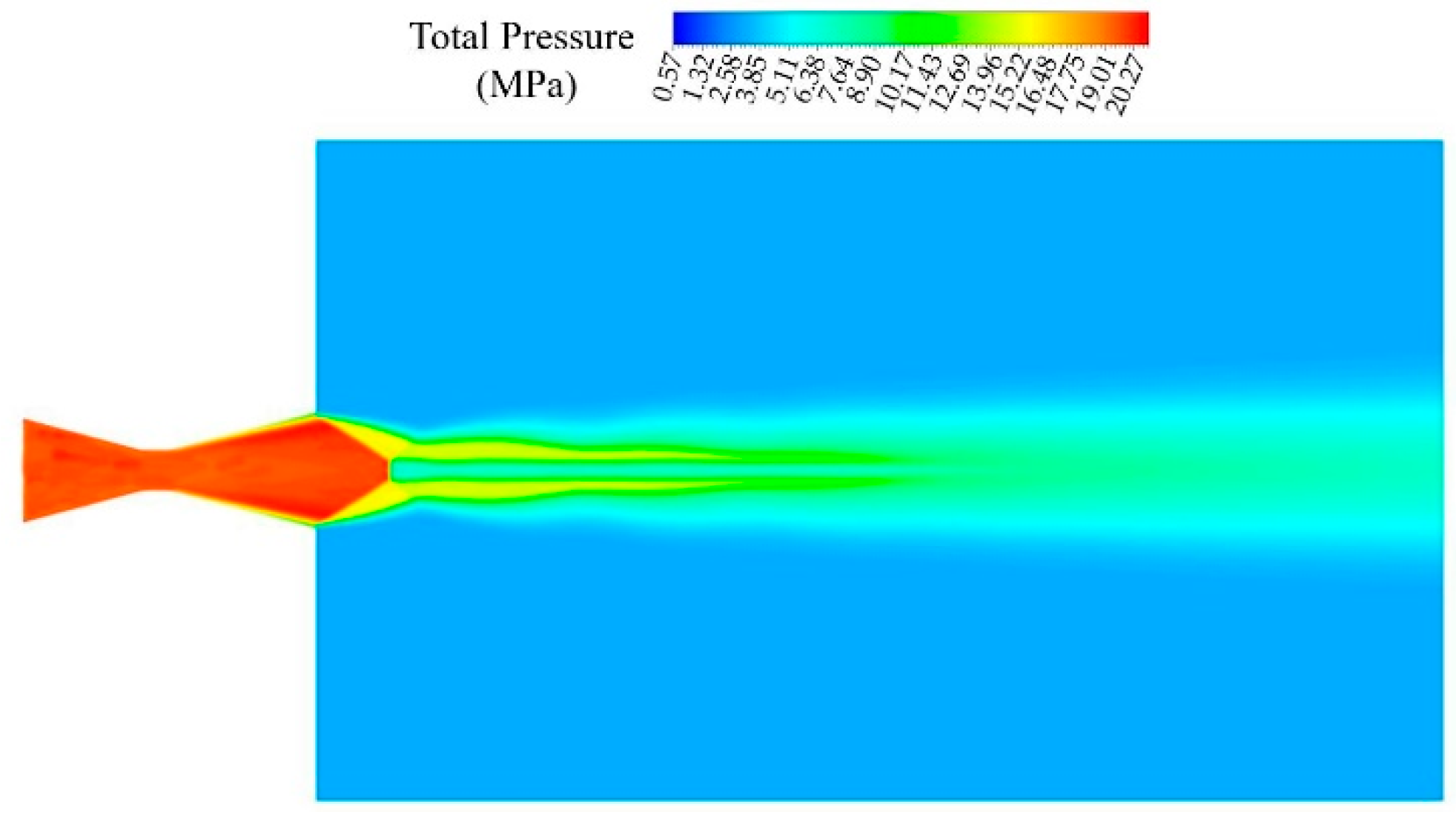
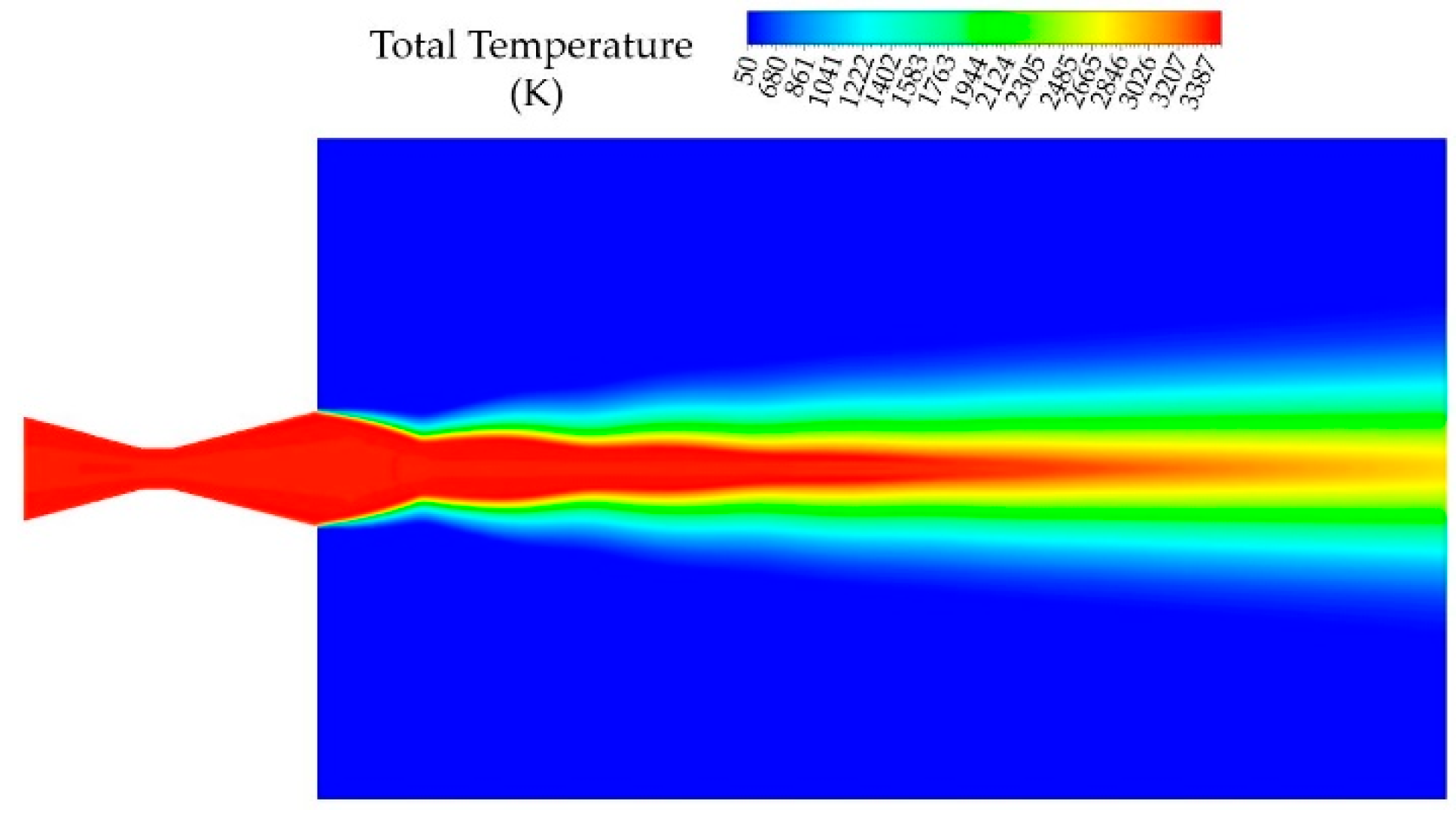
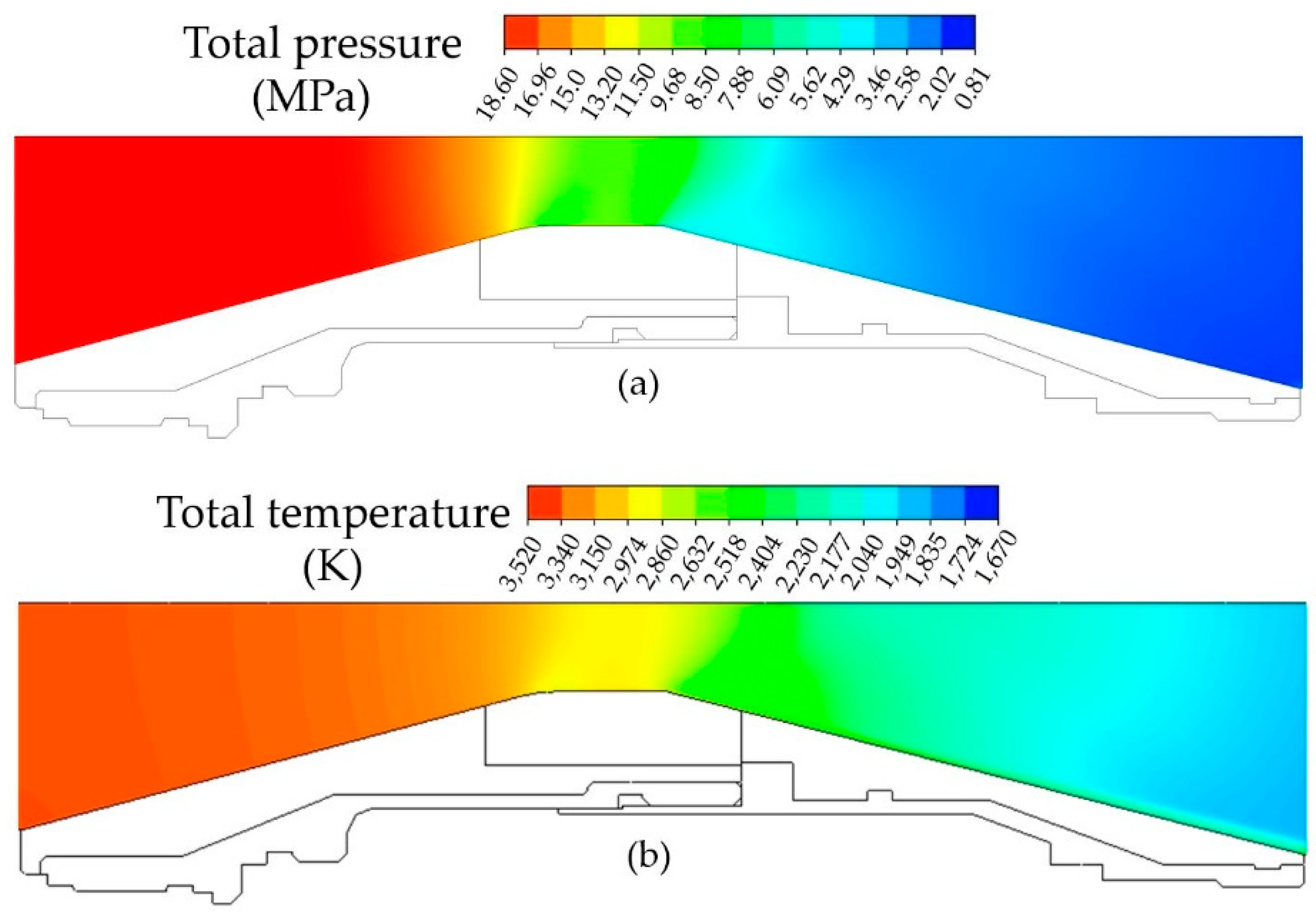
4.1. Gas Flow Behavior
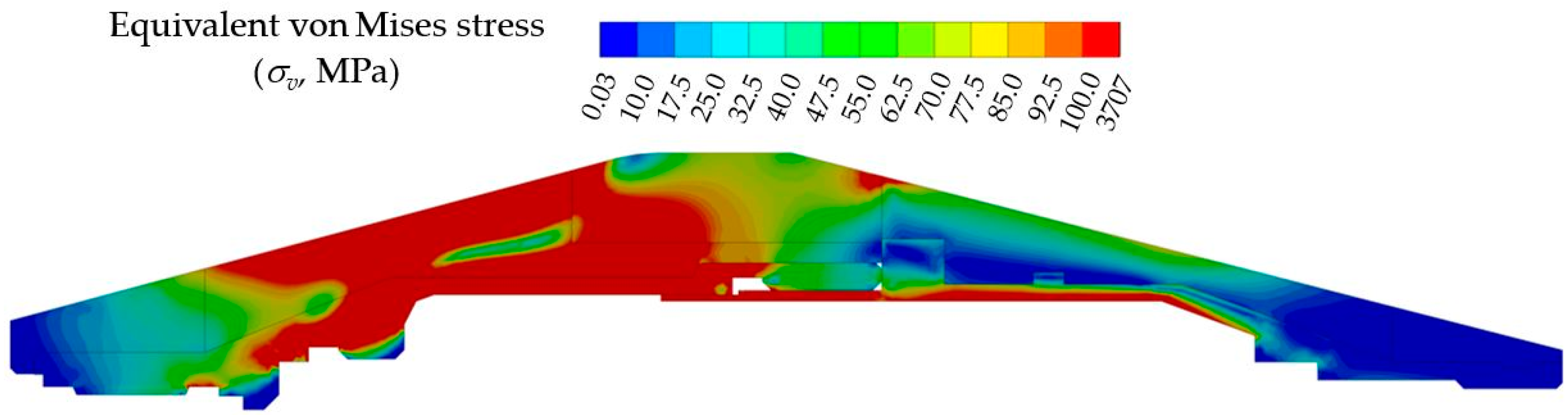
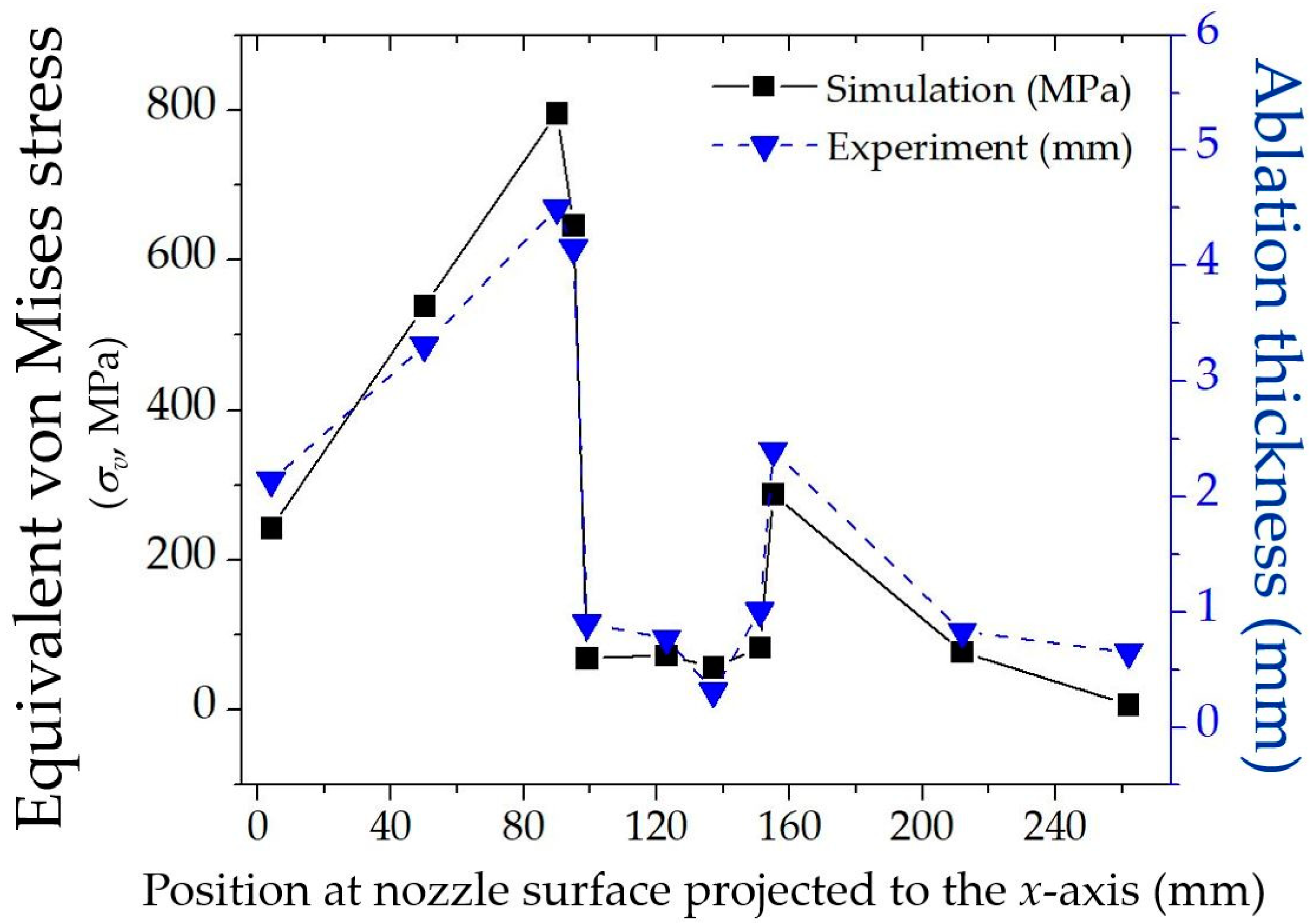
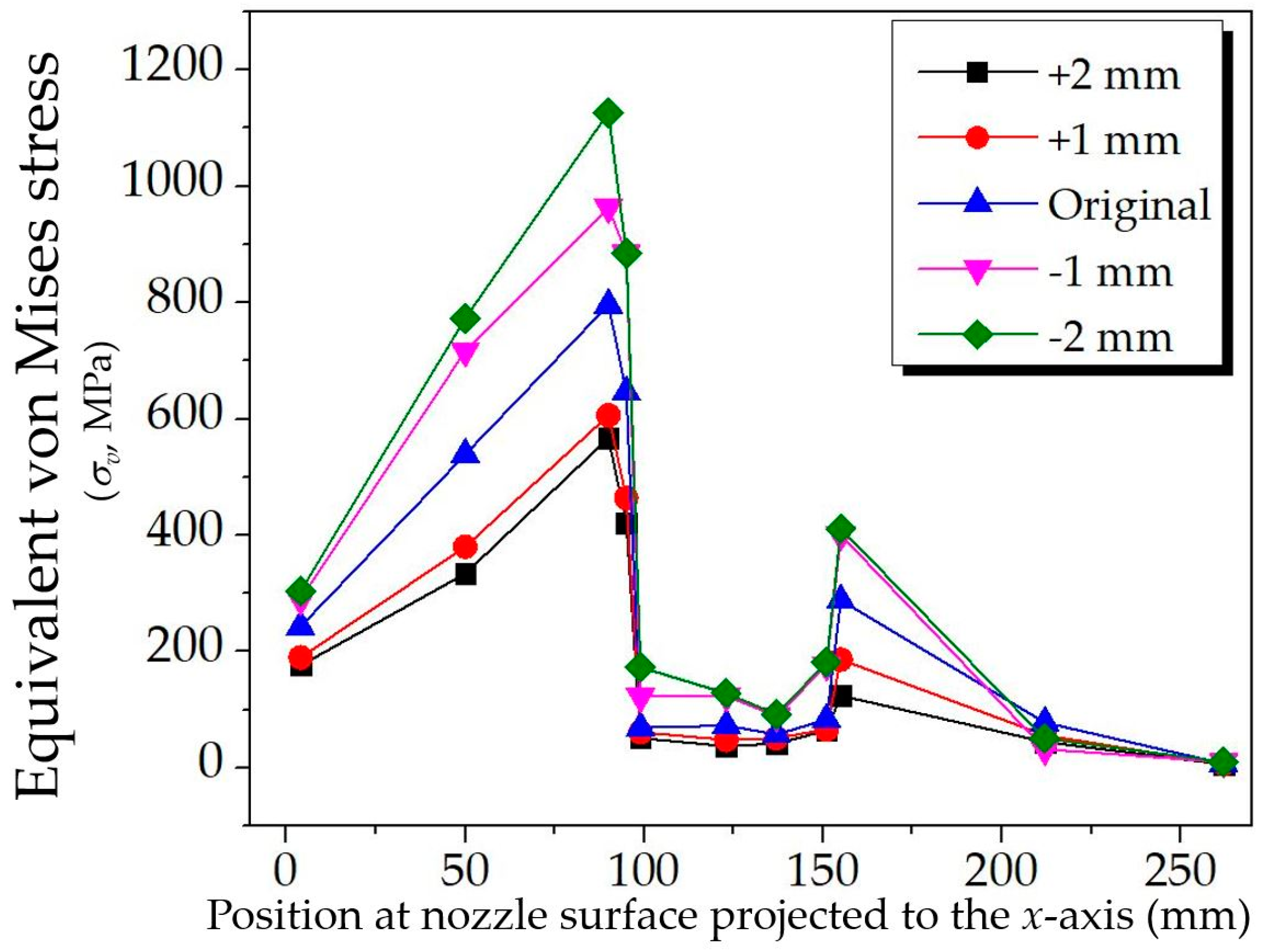
4.2. Ablation
5. Conclusions and Limitations
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclatures
| F1 | Blending function in the SST k-ω turbulence model |
| [C] | Capacitance matrix (F) |
| ui, uj, and uk | Cartesian velocities in each direction (m/s) |
| Change in nodal vector temperature (K/s) | |
| α3, β3, σk3, σω3 | Coefficients of the SST k-ω turbulence model |
| ρ | Density (kg/m3) |
| μt | Eddy viscosity (m2/s) |
| Keff | Effective conductivity (W/m-K) |
| E | Energy (J) |
| External force (F) | |
| Gravitational force (F) | |
| M | Mach number |
| {T} | Nodal vector temperature (K) |
| x | Position in x-axis (mm) |
| P | Pressure (Pa) |
| Pk | Shear production of turbulence (Pa) |
| ω | Specific dissipation rate (1/s) |
| γ | Specific heat ration |
| σI, σj and σk | Stress in each direction (Pa) |
| Stress tensor (Pa) | |
| {Q} | Thermal load vector (K) |
| [K] | Thermal stiffness matrix (W/K) |
| t | Time (s) |
| K | Turbulence kinetic energy (J/kg) |
| Velocity vector (m/s) |
References
- Darbandi, M.; Roohi, E. Study of subsonic-supersonic gas flow through micro/nanoscale nozzle using unstructured DSMC solver. Microfluid Nanofluid 2011, 10, 321–335. [Google Scholar] [CrossRef]
- Prathibha, M.; Gupta, M.S.; Naidu, S. CFD Analysis on a Different Advanced Rocket Nozzles. Int. J. Eng. Adv. Technol. 2015, 4, 14–22. [Google Scholar]
- Roy, P.; Mondal, A.; Barai, B. CFD Analysis Of Rocket Engine Nozzle. Int. J. Adv. Eng. Res. Sci. 2015, 4, 14–22. [Google Scholar]
- Nayeem, S.; Chaitanya, K.L.V.B.S.S.S.; Murali krishna, G.; Dileep, C.; Ramana, D.V. Optimization of Convergent—Divergent Taper Angle with Combustion Chamber of Rocket Engine through Numerical Analysis. Int. J. Innov. Technol. Explor. Eng. 2020, 9, 76–81. [Google Scholar] [CrossRef]
- Baidya, R.; Pesyridis, A.; Cooper, M. Ramjet Nozzle Analysis for Transport Aircraft Configuration for Sustained Hypersonic Flight. Appl. Sci. 2018, 8, 574. [Google Scholar] [CrossRef]
- Afzali, B.; Karimi, H. Numerical Investigation on Thermo-Acoustic Effects and Flow Characteristics in Semi-Conical Hartmann–Sprenger Resonance Tube. J. Aerosp. Eng. 2016, 231, 2706–2722. [Google Scholar] [CrossRef]
- Dipen, R.D.; Parth, B.T.; Atal, B.H. Flow Analysis of Roket Nozzle using Method of Characteristics. In Proceedings of the 6th International Conference on Recent Trends in Engineering, Science & Management, Shri Guru Teg Bahadur Khalsa College Anandpur Sahib, Punjab, India, 8 January 2017. [Google Scholar]
- Sae-ngow, C.; Palsarn, S.; Boonpan, A. Insulation Analysis for Rocket’s Nozzle to Reduce Deformation of Nozzle Shape. In Proceedings of the 35th Conference of Mechanical Engineering Network of Thailand (ME-NETT), Nakhon Pathom, 20–23 July 2021. (In Thai). [Google Scholar]
- Hui, W.H.; Bao, F.T.; Wei, X.G.; Liu, Y. Ablation Performance of a 4D-Braided C/C Composite in a Parameter-Variable Channel of a Laval Nozzle in a Solid Rocket Motor. New Carbon Mater. 2017, 32, 365–373. [Google Scholar] [CrossRef]
- Peter, G.C.; Boyd, I.D. Reduced Reaction Mechanism for Rocket Nozzle Ablation Simulations. J. Thermophys. Heat Transf. 2018, 32, 429–439. [Google Scholar]
- Peter, G.C.; Boyd, I.D. Conjugate Analysis of Rocket Nozzle Ablation. In Proceedings of the 47th AIAA Thermophysics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Xiaotian, Z.; Zhengkang, W.; Ruiqing, W.; Chengyang, L.; Ruipeng, Y.; Hui, T. Numerical Simulation of Chemical Ablation and Mechanical Erosion in Hybrid Rocket Nozzle. Acta Astronaut. 2022, 192, 82–96. [Google Scholar]
- Gudlavalleti, V.B.; Murthy, V.B. Prediction of Thermal Ablation in Rocket Nozzle Using CFD and FEA. Int. J. Comput. Mater. Sci. Eng. 2020, 9, 2050014. [Google Scholar]
- How Fluid-Structure Interaction Works and Why It’s Important. Available online: https://www.ansys.com/blog/fluid-structure-interaction-explained (accessed on 1 June 2022).
- Huc, N. Conjugate Heat Transfer. Available online: https://www.comsol.com/blogs/author/nicolas-huc/ (accessed on 1 June 2022).
- Thongsri, J.; Tangsopa, W.; Kaewbumrung, M.; Phanak, M.; Busayaporn, W. Derosion Lattice Performance and Optimization in Solving an End Effect Assessed by CFD: A Case Study in Thailand’s Beach. Water 2022, 14, 1358. [Google Scholar] [CrossRef]
- Khongsin, J.; Thongsri, J. Numerical Investigation on the Performance of Suction Head in a Cleaning Process of Hard Disk Drive Factory. ECTI Trans. Electr. Eng. Electron. Commun. 2020, 18, 28–33. [Google Scholar] [CrossRef]
- Puangburee, L.; Busayaporn, W.; Kaewbumrung, M.; Thongsri, J. Evaluation and Improvement of Ventilation System Inside Low-Cost Automation Line to Reduce Particle Contamination. ECTI Trans. Electr. Eng. Electron. Commun. 2020, 18, 35–44. [Google Scholar] [CrossRef]
- Thongsri, J.; Tangsopa, W.; Khongsin, J. A Suitable Shape of the Suction Head for a Cleaning Process in a Factory Developed by Computational Fluid Dynamics. Processes 2021, 9, 1902. [Google Scholar] [CrossRef]
- Jansaengsuk, T.; Kaewbumrung, M.; Busayaporn, W.; Thongsri, J. A Proper Shape of the Trailing Edge Modification to Solve a Housing Damage Problem in a Gas Turbine Power Plant. Processes 2021, 9, 705. [Google Scholar] [CrossRef]
- Ansys, Inc. Ansys Mechanical Heat Transfer. Nonlinear and Transient Thermal Electric; ANSYS, Inc.: Canonsburg, PA, USA, 2016. [Google Scholar]
- Narayana, K.P.S.S.; Reddy, K.S. Simulation of Convergent Divergent Rocket Nozzle using CFD Analysis Ansys Thermal. J. Mech. Civ. Eng. 2016, 4, 58–65. [Google Scholar]
- Nikhil, D.D.; Suyash, S.V.; Pratik, R.M.; Rutuja, S.J.; Jagtap, K.R. Theoretical & CFD Analysis of Delaval Nozzle. In Proceedings of the IRF International Conference, Pune, India, 16 March 2014. [Google Scholar]
- Malay, S.P.; Sulochan, D.M.; Raman, M. Concepts and CFD Analysis of De-Laval Nozzle. Int. J. Mech. Eng. Technol. 2016, 7, 221–240. [Google Scholar]
- Rocket Thrust Summary. Available online: https://www.grc.nasa.gov/www/k-12/rocket/rktthsum.html#:~:text=Thrust%20is%20produced%20according%20to,the%20design%20of%20the%20nozzle. (accessed on 1 June 2022).
- ANSYS, Inc. Solid Mechanics 1-Understanding the Physics. In Equivalent Stress; ANSYS, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Elean, I.; Jabra, R.; Arafeh, M.H. Preparation and Ablation Performance of Lightweight Phenolic Composite Material under Oxyacetylene Torch Environment. J. Aerosp. Technol. Manag. 2018, 10, e3118. [Google Scholar] [CrossRef]
- Ellis, R. Solid Rocket Nozzle-NASA Space Vehicle Design Criteria (Chemical Propulsion); NASA: Cleveland, OH, USA, 1975. [Google Scholar]


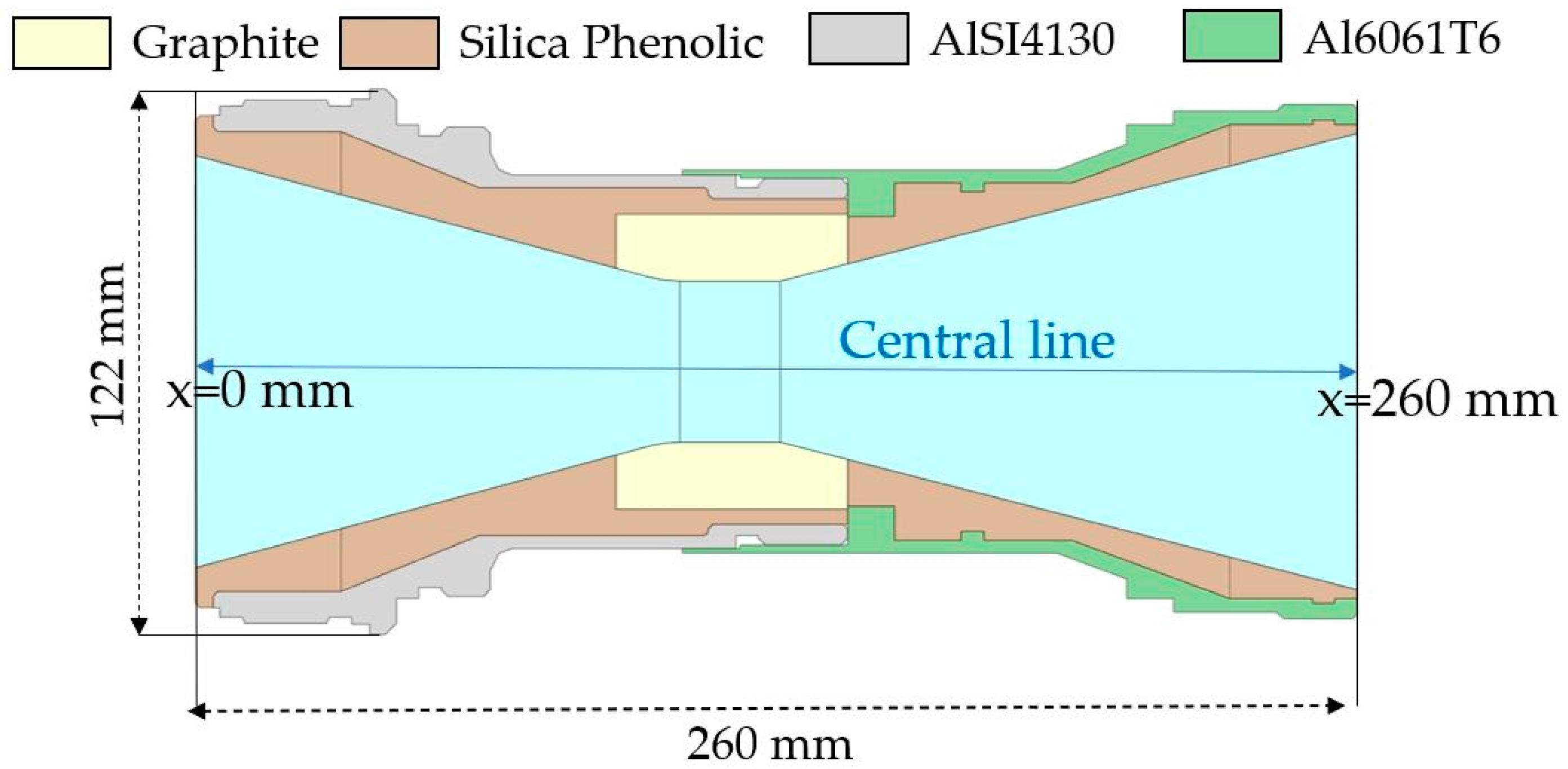
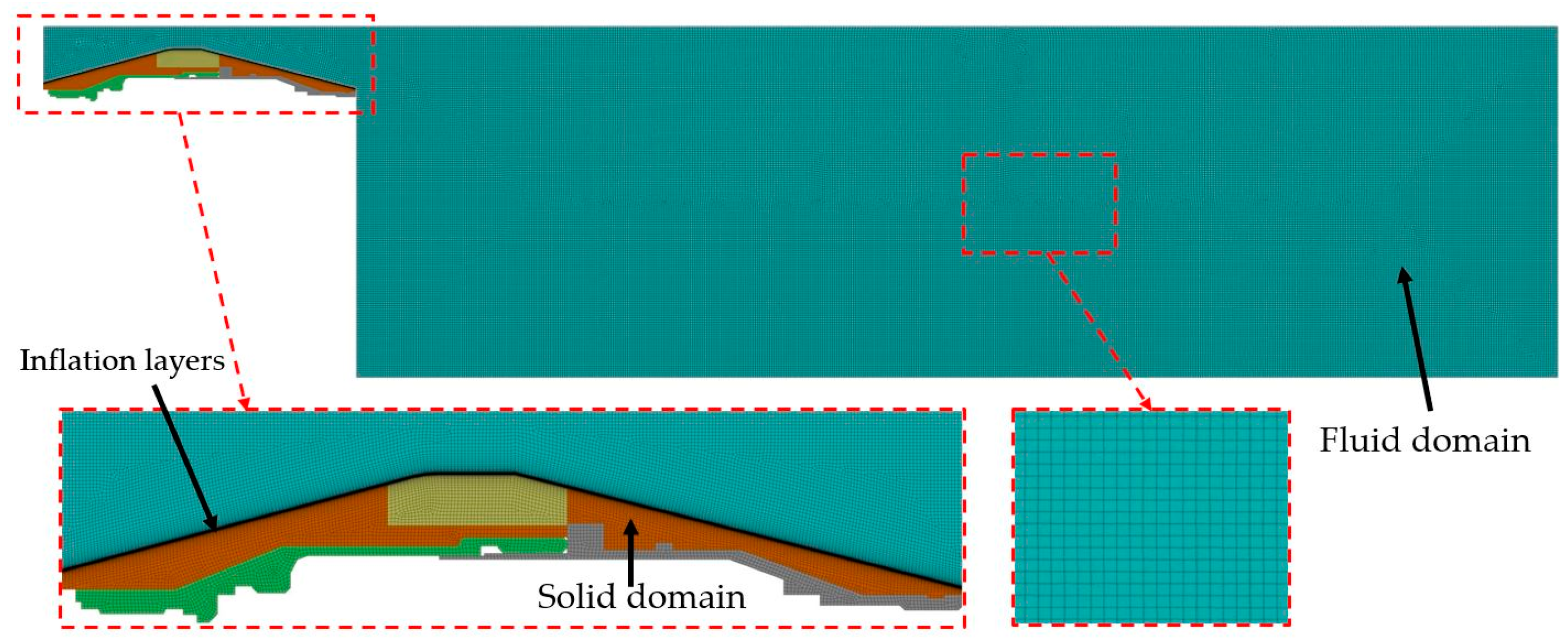
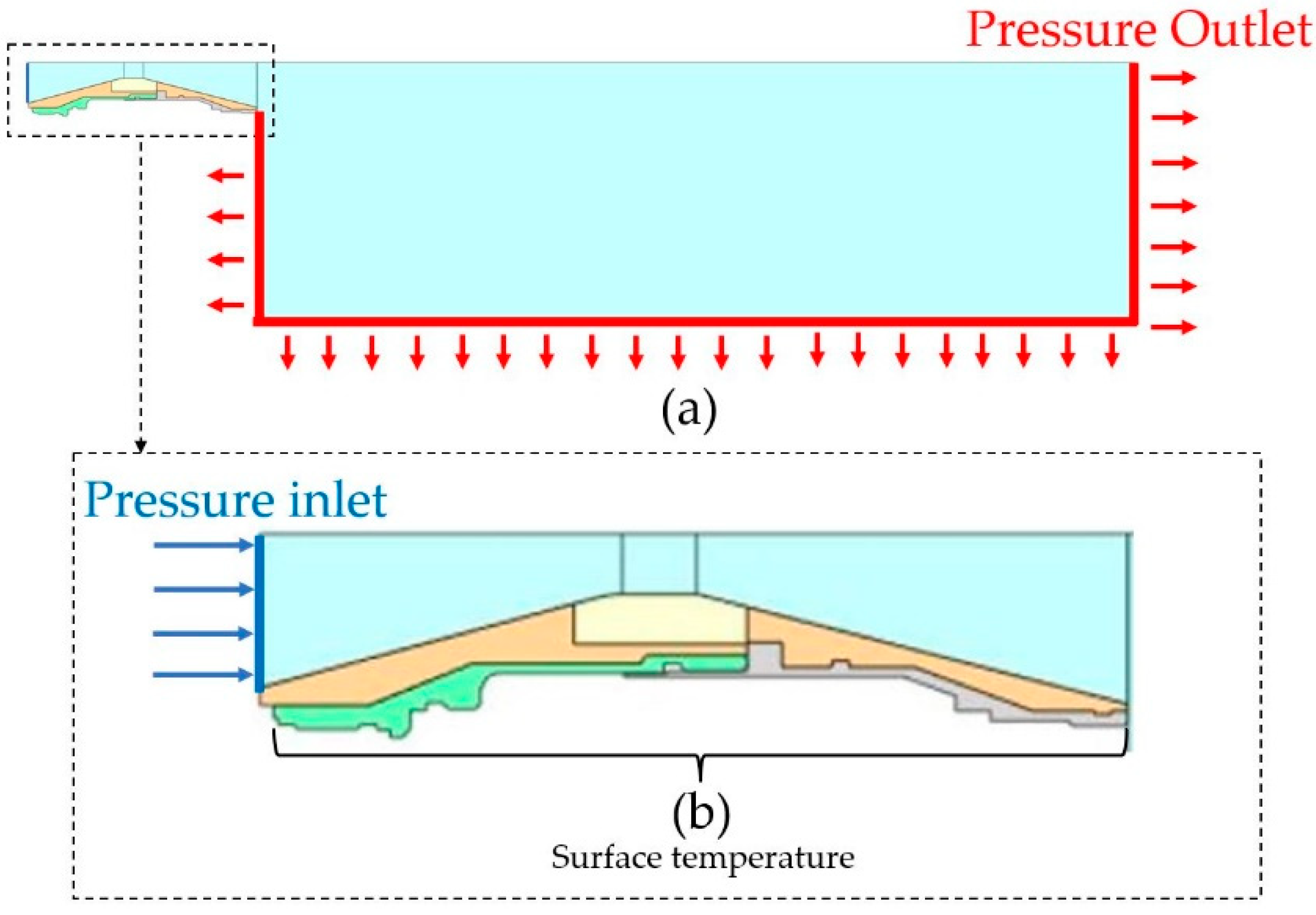


| Type | Setting |
|---|---|
| Pressure inlet: pressure far-field | Gauge pressure: UDF * |
| Mach number: 0.234 | |
| Temperature: 3364.40 K | |
| Pressure outlet | Gauge pressure: UDF * |
| Temperature: 540.15 K | |
| H2 | Density: ideal gas |
| Viscosity: Sutherland | |
| Specific heat ratio: 1.4 | |
| Transient setting | Time step size: 0.01 |
| Number of time steps: 2400 | |
| Iteration per time step: 20 |
| Properties | Materials * | |||
|---|---|---|---|---|
| Silica Phenolic | Graphite | AlSI4130 | Al6061T6 | |
| Density (kg/m3) | 1656 | 2490 | 7850 | 2700 |
| Thermal conductivity (W/m-K) | 250 | 114 | 42.7 | 167 |
| Young’s modulus (GPa) | 36.6 | 27.6 | 200 | 68.9 |
| Poisson’s ratio | 0.15 | 0.23 | 0.30 | 0.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thongsri, J.; Srathonghuam, K.; Boonpan, A. Gas Flow and Ablation of 122 mm Supersonic Rocket Nozzle Investigated by Conjugate Heat Transfer Analysis. Processes 2022, 10, 1823. https://doi.org/10.3390/pr10091823
Thongsri J, Srathonghuam K, Boonpan A. Gas Flow and Ablation of 122 mm Supersonic Rocket Nozzle Investigated by Conjugate Heat Transfer Analysis. Processes. 2022; 10(9):1823. https://doi.org/10.3390/pr10091823
Chicago/Turabian StyleThongsri, Jatuporn, Kamonwan Srathonghuam, and Adulyasak Boonpan. 2022. "Gas Flow and Ablation of 122 mm Supersonic Rocket Nozzle Investigated by Conjugate Heat Transfer Analysis" Processes 10, no. 9: 1823. https://doi.org/10.3390/pr10091823
APA StyleThongsri, J., Srathonghuam, K., & Boonpan, A. (2022). Gas Flow and Ablation of 122 mm Supersonic Rocket Nozzle Investigated by Conjugate Heat Transfer Analysis. Processes, 10(9), 1823. https://doi.org/10.3390/pr10091823








