New Relaxed Static Output Feedback Stabilization of T–S Fuzzy Systems with Time-Varying Delays
Abstract
:1. Introduction
2. Preliminaries
2.1. Fuzzy Time-Delay Models
2.2. Fuzzy SOF Controller under IPM
2.3. Useful Lemmas
- (1)
- There exists a symmetric and positive-definite matrix satisfying
- (2)
- There exists a symmetric and positive-definite matrix and matrix satisfying
3. Main Results
3.1. Membership-Function-Independent Stabilization Conditions
3.2. MFD Stabilization Conditions
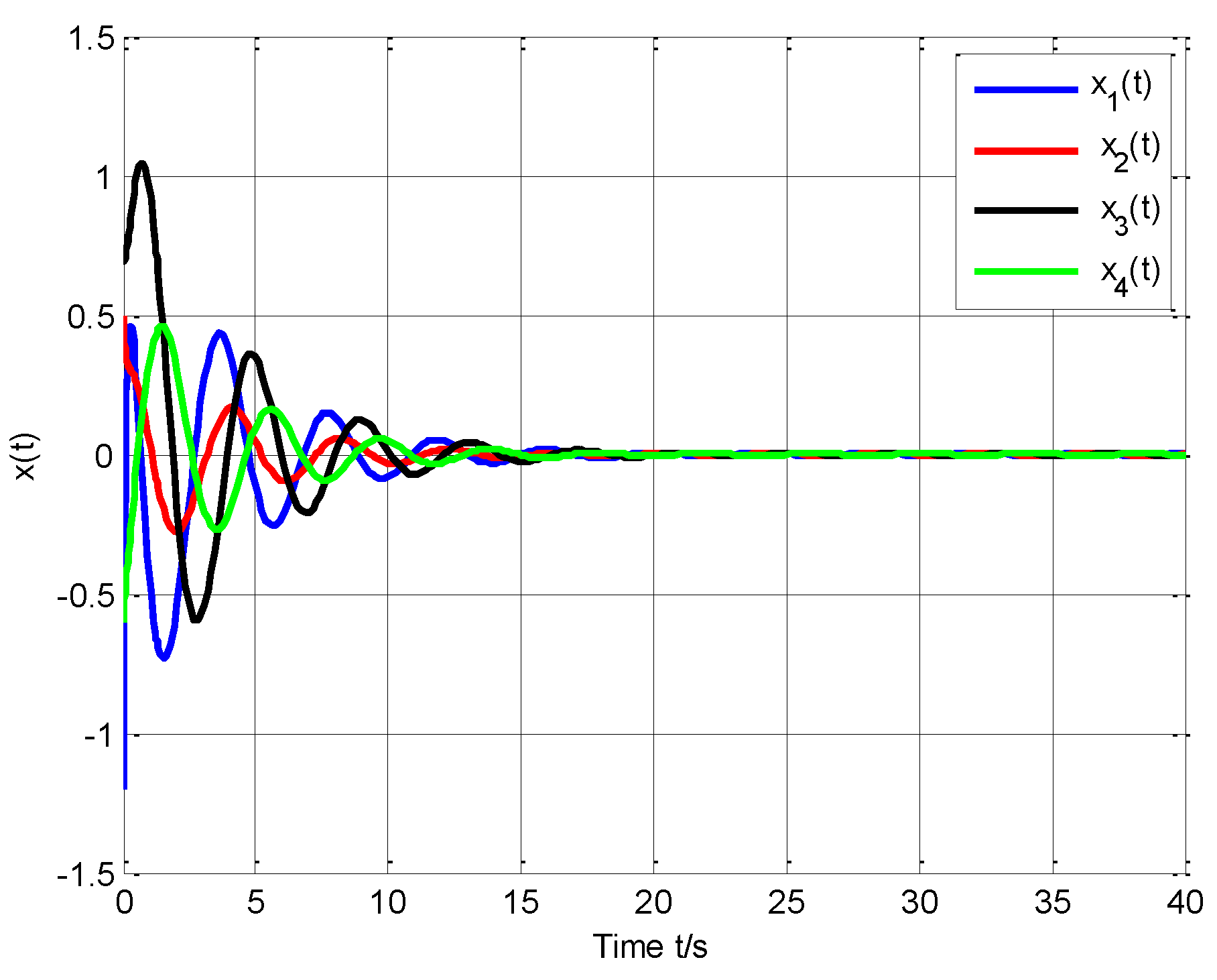
4. Simulation Examples
- Rule 1: IF is and is , THEN
- Rule 2: IF is and is , THEN
- Rule 3: IF is and is , THEN
- Rule 4: IF is and is , THEN
- Rule 1: IF is , THEN
- Rule 2: IF is , THEN
- Rule 1: IF is 0 rad, THEN
- Rule 2: IF is rad or rad, THEN
- Rule 1: IF is , THEN
- Rule 2: IF is , THEN
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tian, Y.F.; Wang, Z.S. Asynchronous extended dissipative filtering for T–S fuzzy Markov jump systems. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 3915–3925. [Google Scholar] [CrossRef]
- Sun, S.X.; Zhang, H.G.; Liu, C.; Liu, Y. Dissipativity-based intermittent fault detection and tolerant control for multiple delayed uncertain switched fuzzy stochastic systems with unmeasurable premise variables. IEEE Trans. Cybern. 2022, 52, 8766–8780. [Google Scholar] [CrossRef] [PubMed]
- Chang, W.J.; Lin, Y.W.; Lin, Y.H.; Pen, C.L.; Tsai, M.H. Actuator saturated fuzzy controller design for interval type-2 Takagi-Sugeno fuzzy models with multiplicative noises. Processes 2021, 9, 823. [Google Scholar] [CrossRef]
- Sheng, Y.; Huang, T.W.; Zeng, Z.G. Exponential Stabilization of Fuzzy Memristive Neural Networks With Multiple Time Delays Via Intermittent Control. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 3092–3101. [Google Scholar] [CrossRef]
- Zhou, K.; Wang, B.R.; Qi, S.N. New relaxed stability and stabilization conditions for T-S fuzzy systems with time-varying delays. IET Control Theory Appl. 2021, 15, 1849–1867. [Google Scholar] [CrossRef]
- Chadli, M.; Didier, M.; José, R. Static Output Feedback for Takagi-Sugeno Systems: An LMI approach. In Proceedings of the 10th Mediterranean Conference on Control and Automation, Lisbon, Portugal, 9–12 July 2002. [Google Scholar]
- Islam, S.I.; Lim, C.C.; Shi, P. Robust fault detection of TS fuzzy systems with time-delay using fuzzy functional observer. Fuzzy Sets Syst. 2020, 392, 1–23. [Google Scholar] [CrossRef]
- El Hajjaji, A.; Chadli, M.; Oudghiri, M.; Pagès, O. Observer-Based Robust Fuzzy Control for Vehicle Lateral Dynamics. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006. [Google Scholar]
- Wang, Y.Q.; Ren, W.J.; Liu, Z.Q.; Li, J.; Zhang, D. T-S Fuzzy Model-Based Fault Detection for Continuous Stirring Tank Reactor. Processes 2021, 9, 2127. [Google Scholar] [CrossRef]
- Li, X.D.; Li, P. Stability of time-delay systems with impulsive control involving stabilizing delays. Automatica 2021, 124, 109336. [Google Scholar] [CrossRef]
- Nguyen, M.C.; Tan, P.; Trinh, H. Sliding mode observer for estimating states and faults of linear time-delay systems with outputs subject to delays. Automatica 2021, 124, 109274. [Google Scholar] [CrossRef]
- Kong, M.R.; Liu, L. Exponential Stabilization for a Class of Strict-Feedback Nonlinear Time Delay Systems via State Feedback Control Scheme. Processes 2022, 10, 1259. [Google Scholar] [CrossRef]
- Li, G.L.; Peng, C.; Xie, X.P.; Xie, S.R. On Stability and Stabilization of T-S Fuzzy Systems With Time-Varying Delays via Quadratic Fuzzy Lyapunov Matrix. IEEE Trans. Fuzzy Syst. 2022, 30, 3762–3773. [Google Scholar] [CrossRef]
- Lian, Z.; He, Y.; Wu, M. Stability and stabilization for delayed fuzzy systems via reciprocally convex matrix inequality. Fuzzy Sets Syst. 2021, 402, 124–141. [Google Scholar] [CrossRef]
- Liu, C.; Guo, Y.R.; Rao, H.X.; Lin, M.; Xu, Y. Finite-time synchronization for periodic T-S fuzzy master-slave neural networks with distributed delays. J. Frankl. Inst. 2021, 358, 2367–2381. [Google Scholar] [CrossRef]
- Datta, R.; Saravanakumar, R.; Dey, R.; Bhattacharya, B.; Ahn, C.-K. Improved stabilization criteria for Takagi-Sugeno fuzzy systems with variable delays. Inf. Sci. 2021, 579, 591–606. [Google Scholar] [CrossRef]
- Pan, X.J.; Yang, B.; Cao, J.J.; Zhao, X.-D. Improved stability analysis of Takagi-Sugeno fuzzy systems with time-varying delays via an extended delay-dependent reciprocally convex inequality. Inf. Sci. 2021, 571, 24–37. [Google Scholar] [CrossRef]
- Sheng, Z.L.; Lin, C.; Chen, B.; Wang, Q.G. An asymmetric Lyapunov-Krasovskii functional method on stability and stabilization for T-S fuzzy systems with time delay. IEEE Trans. Fuzzy Syst. 2022, 30, 2135–2140. [Google Scholar] [CrossRef]
- Wang, X.; Park, J.H.; Yang, H.L.; Zhao, G.Z.; Zhong, S.-M. An improved fuzzy sampled-data control to stabilization of T-S fuzzy systems with state delays. IEEE Trans. Cybern. 2020, 50, 3125–3135. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.K.; Liu, J.J.; Lam, H.K. Further study on stabilization for continuous-time Takagi-Sugeno fuzzy systems with time delay. IEEE Trans. Cybern. 2021, 51, 5637–5643. [Google Scholar] [CrossRef]
- Li, X.M.; Mehran, K.; Bao, Z.Y. Stability Analysis of Discrete-Time Polynomial Fuzzy-Model-Based Control Systems With Time Delay and Positivity Constraints Through Piecewise Taylor Series Membership Functions. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 7517–7529. [Google Scholar] [CrossRef]
- Vadivel, R.; Saravanan, S.; Unyong, B.; Hammachukiattikul, P.; Hong, K.-S.; Lee, G.-M. Stabilization of Delayed Fuzzy Neutral-type Systems Under Intermittent Control. Int. J. Control Autom. Syst. 2021, 19, 1408–1425. [Google Scholar] [CrossRef]
- Lian, Z.; He, Y.; Zhang, C.K.; Wu, M. Stability and stabilization of T-S fuzzy systems with time-varying delays via delay-product-type functional method. IEEE Trans. Cybern. 2020, 50, 2580–2589. [Google Scholar] [CrossRef] [PubMed]
- Wang, G.; Jia, L.; Zhang, H.G. Stability and stabilization of T-S fuzzy time-delay system via relaxed integral inequality and dynamic delay partition. IEEE Trans. Fuzzy Syst. 2021, 29, 2829–2843. [Google Scholar] [CrossRef]
- Crusius, C.A.R.; Trofino, A. Sufficient LMI conditions for output feedback control problems. IEEE Trans. Autom. Control 1999, 44, 1053–1057. [Google Scholar] [CrossRef]
- Wu, H.N. An ILMI approach to robust H2 static output feedback fuzzy control for uncertain discrete-time nonlinear systems. Automatica 2008, 44, 2333–2339. [Google Scholar] [CrossRef]
- Huang, D.; Nguang, S.K. Robust H∞ Static Output Feedback Control of Fuzzy Systems: An ILMI Approach. IEEE Trans. Syst. Man Cybern. Cybern. 2006, 36, 216–222. [Google Scholar] [CrossRef]
- Huang, D.; Nguang, S.K. Static output feedback controller design for fuzzy systems: An ILMI approach. Inf. Sci. 2007, 177, 3005–3015. [Google Scholar] [CrossRef]
- Saifia, D.; Chadli, M.; Labiod, S.; Guerra, T.-M. Robust H∞ static output feedback stabilization of T-S fuzzy systems subject to actuator saturation. Int. J. Control Autom. Syst. 2012, 10, 613–622. [Google Scholar] [CrossRef]
- Jiang, S.; Fang, H.J. H∞ static output feedback control for nonlinear networked control systems with time delays and packet dropouts. ISA Trans. 2013, 2, 215–222. [Google Scholar] [CrossRef]
- Chen, J.; Lin, C.; Chen, B.; Wang, G.Q. Fuzzy-model-based admissibility analysis and output feedback control for nonlinear discrete-time systems with time-varying delay. Inf. Sci. 2017, 412, 116–131. [Google Scholar] [CrossRef]
- Ma, Y.C.; Yang, P.J.; Zhang, Q.L. Robust H∞ control for uncertain singular discrete T-S fuzzy time-delay systems with actuator saturation. J. Frankl. Inst. 2016, 13, 3290–3311. [Google Scholar] [CrossRef]
- Ma, Y.C.; Fu, L. Finite-time H∞ control for discrete-time switched singular time-delay systems subject to actuator saturation via static output feedback. Int. J. Syst. Sci. 2016, 47, 3394–3408. [Google Scholar] [CrossRef]
- Pham, T.N.; Nahavandi, S.; Hien, L.V.; Trinh, H.; Wong, K.P. Static output feedback frequency stabilization of time-delay power systems with coordinated electric vehicles state of charge control. IEEE Trans. Power Syst. 2016, 32, 3862–3874. [Google Scholar] [CrossRef]
- Wei, Y.L.; Qiu, J.B.; Shi, P.; Wu, L.G. A piecewise-Markovian Lyapunov approach to reliable output feedback control for fuzzy-affine systems with time-delays and actuator faults. IEEE Trans. Cybern. 2018, 48, 2723–2735. [Google Scholar] [CrossRef] [PubMed]
- Li, W.F.; Xie, Z.C.; Zhao, J.; Wong, P.K.; Wang, H.; Wang, X.-W. Static-output-feedback based robust fuzzy wheelbase preview control for uncertain active suspensions with time delay and finite frequency constraint. IEEE/CAA J. Autom. Sin. 2021, 8, 664–678. [Google Scholar] [CrossRef]
- Zhou, K.; Huang, T.M.; Zhao, T.; Gao, F.H. Membership-function-dependent stability and stabilization conditions for T-S fuzzy time-delay systems. IETE J. Res. 2019, 65, 351–364. [Google Scholar] [CrossRef]
- Lam, H.K.; Narimani, M. Stability analysis and performance design for fuzzy-model-based control system under imperfect premise matching. IEEE Trans. Fuzzy Syst. 2009, 17, 949–961. [Google Scholar] [CrossRef]
- Zhao, T.; Liu, J.H.; Dian, S.Y. Finite-time control for interval type-2 fuzzy time-delay systems with norm-bounded uncertainties and limited communication capacity. Inf. Sci. 2019, 483, 153–173. [Google Scholar] [CrossRef]
- Che, C.; Peng, J.Y.; Xiao, J.; Zhao, T.; Zhou, J. Membership-function-dependent stabilization conditions for interval type-2 fuzzy time-delay systems via static output feedback scheme. Int. J. Fuzzy Syst. 2018, 20, 1439–1450. [Google Scholar] [CrossRef]
- Li, X.M.; Merhan, K.; Bao, Z.Y. Membership Function, Time Delay-Dependent η-Exponential Stabilization of Positive Discrete Time Polynomial Fuzzy Model Control System. IEEE Trans. Fuzzy Syst. 2022, 30, 2197–2209. [Google Scholar] [CrossRef]
- Gu, K. An Integral Inequality in the Stability Problem of Time-Delay Systems. In Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, NSW, Australia, 12–15 December 2000; pp. 2805–2810. [Google Scholar]
- Park, P.G.; Ko, J.W.; Jeong, C. Reciprocally convex approach to stability of systems with time-varying delays. Automatica 2011, 47, 235–238. [Google Scholar] [CrossRef]
- Wang, Y.Y.; Xie, L.H.; de Souza, C.E. Robust control of a class of uncertain nonlinear systems. Syst. Control Lett. 1992, 19, 139–149. [Google Scholar] [CrossRef]
- De Souza, C.E. Robust stability and stabilization of uncertain discrete-time Markovian jump linear systems. IEEE Trans. Autom. Control 2006, 51, 836–841. [Google Scholar] [CrossRef]
- Xie, W.B.; Lim, C.C.; Zhang, J.; Huang, L. New approaches to observer design and stability analysis for T-S fuzzy system with multiplicative noise. J. Frankl. Inst. 2017, 354, 887–901. [Google Scholar] [CrossRef]
- Fang, C.H.; Liu, Y.S.; Kau, S.W.; Hong, L.; Lee, C.H. A new LMI-based approach to relaxed quadratic stabilization of T-S fuzzy control systems. IEEE Trans. Fuzzy Syst. 2006, 14, 386–397. [Google Scholar] [CrossRef]
- Che, C.; Peng, J.; Zhao, T.; Xiao, J.; Zhou, J. Improved stabilization conditions for nonlinear systems with input and state delays via T-S fuzzy model. Math. Probl. Eng. 2018, 2018, 3542352. [Google Scholar] [CrossRef] [Green Version]
- Tao, H.F.; Hu, S.S.; Cai, J.W. L∞ Static Output Feedback Control for T-S Fuzzy Systems with Time-Varying Delays. Acta Autom. Sin. 2008, 34, 453–459. [Google Scholar] [CrossRef]
- Chen, B.; Liu, X.P.; Tong, S.C. Delay-dependent stability analysis and control synthesis of fuzzy dynamic systems with time delay. Fuzzy Sets Syst. 2006, 157, 2224–2240. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, S.; Zhou, K.; Xu, S.; Gao, Y. New Relaxed Static Output Feedback Stabilization of T–S Fuzzy Systems with Time-Varying Delays. Processes 2023, 11, 121. https://doi.org/10.3390/pr11010121
Qi S, Zhou K, Xu S, Gao Y. New Relaxed Static Output Feedback Stabilization of T–S Fuzzy Systems with Time-Varying Delays. Processes. 2023; 11(1):121. https://doi.org/10.3390/pr11010121
Chicago/Turabian StyleQi, Shunan, Kun Zhou, Suan Xu, and Yanfeng Gao. 2023. "New Relaxed Static Output Feedback Stabilization of T–S Fuzzy Systems with Time-Varying Delays" Processes 11, no. 1: 121. https://doi.org/10.3390/pr11010121
APA StyleQi, S., Zhou, K., Xu, S., & Gao, Y. (2023). New Relaxed Static Output Feedback Stabilization of T–S Fuzzy Systems with Time-Varying Delays. Processes, 11(1), 121. https://doi.org/10.3390/pr11010121





