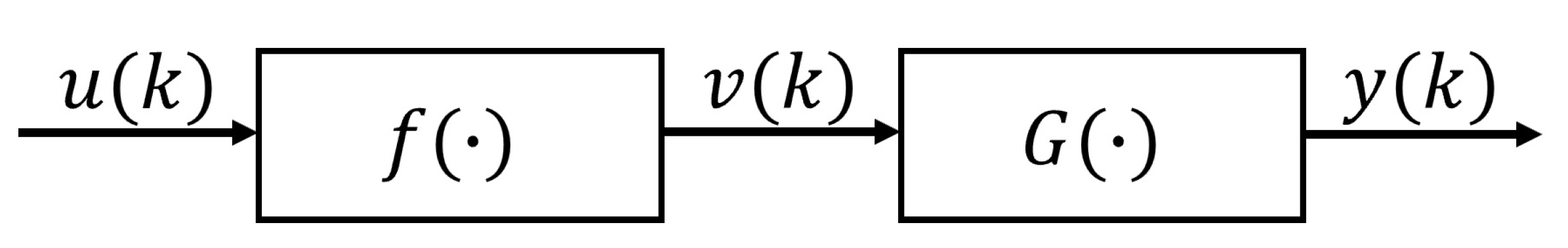Abstract
As the most critical equipment in the pre-calcination process of dry cement production, the temperature of the precalciner is an essential factor affecting the quality of cement. However, the cement calcination system is time-delayed, nonlinear, and multi-disturbance, which makes it difficult to predict and control the precalciner temperature. In this study, a deep learning-based Hammerstein model is proposed, and a model predictive control system is built to predict and control the precalciner temperature. In the prediction model, the CNN-GRU network architecture is used to extract the operating states of the precalciner, and an attention mechanism is employed to find and emphasize the important historical information in the extracted states. Then, an ARX model is built to predict the temperature of the precalciner using the extracted operating state information. The complex nonlinear model solution in the control system is formed into a linear control problem and an inverse solution problem. The generalized predictive control (GPC) is used for linear control, and the improved sparrow search algorithm (ISSA) is used for the problem of an inverse solution. Tested with data from a cement plant in Hebei, China, the prediction accuracy of the model proposed in this paper is 99%, and the established control algorithm has less overshoot compared to PID and better stability in anti-disturbance tests. It is demonstrated that the prediction model developed in this study has better accuracy and the control strategy based on this model has good robustness.
1. Introduction
Cement production plays a critical role in the national economy. However, as a high energy-consuming and polluting industry, the calcination process of cement production consumes lots of energy [1]. On the other hand, the quality of the calcination process affects the physical properties of cement and then affects its quality as a building material [2,3]. Currently, dry-process cement production technology has been adopted as the mainstream cement production technology. The unique feature of the dry process cement production technology is the addition of a precalciner system consisting of a preheater and a precalciner between the raw material silo and the rotary kiln [4]. The precalciner system is responsible for the carbonate decomposition, which is the most heat-consuming part of the cement clinker calcination process. The raw cement is first warmed in the preheater and then fed into the precalciner in suspension. It combines with the fuel and absorbs the heat from fuel combustion to quickly raise the temperature and decompose CaCO in the raw material [5]. The precalciner temperature is a crucial variable affecting the performance of the pre-calcination system. Suppose the temperature of the precalciner is too high. In that case, the raw meal is excessively decomposed in the cyclone, causing clogging of the preheater and increasing the coal consumption per unit of clinker, resulting in fuel waste [6,7]. Therefore, effective control of the precalciner temperature can significantly ensure the stable operation of the cement production system. However, the precalciner has nonlinearity, large time lag, parameter uncertainty, and multiple perturbations. The precalciner’s slow rate of fuel combustion and heat production, as well as the disruption of airflow and material brought on by the preheater and rotary kiln, are the causes that contribute to these features [8,9,10,11]. These factors create difficulties for the precalciner temperature and its control.
Traditional control methods such as PID and fuzzy control are fast in response but less effective when dealing with systems with large time delays [12]. Model Predictive Control (MPC) is a class of optimal control algorithms that can deal with multivariable, constrained systems and whose online computational effort is accepted by process control [13]. Since MPC was proposed, it has been widely used in chemical, petroleum, metallurgical industry, electric power, and other industrial fields [14]. Cheng used the fuzzy clustering approach to apply generalized predictive control to supercritical power plants, which improved boiler combustion efficiency compared with traditional PID [15]. Shi proposed a fuzzy generalized predictive control frame for a hydraulic turbine regulation system, and it was more robust than fuzzy control [16].
MPC is a model prediction-dependent control method. Although there is a feedback correction link in the control framework, the prediction accuracy of its model still largely affects the controller’s performance. Achieving accurate prediction for nonlinear time-delay systems is even more challenging. The traditional approach is to establish polynomial equations to approximate the nonlinear model generally. Bhagyesh established Bernstein polynomial equations to model nonlinear systems and used them as a basis for studying control methods for nonlinear systems [17]. R. Cordero also used polynomials as a reference object to study the use and improvement of MPC [18]. Unlike traditional methods, neural networks and machine learning have a better predictive effect. With good results, SVM was improved using PSO and applied to the temperature prediction in the calcination zone of a lime rotary kiln [19]. Further, a random forest model predictive control scheme for slurry thickening was proposed, with higher accuracy than the ARIMAX model [20]. Zheng used deep learning to construct a hybrid model for rotary kiln temperature prediction utilizing LSTM networks and machine models to handle nonlinearity and time delay [21]. Although neural networks and machine learning perform exceptionally well in prediction accuracy, their models cannot describe the system’s dynamics. Furthermore, when performing multi-step prediction and solution, model predictive control-based neural networks necessitate a large amount of computational resources.
The Hammerstein model consists of a nonlinear model and a linear model in series. It can describe a large class of industrial nonlinear processes [22]. The specificity of the Hammerstein model structure allows the Hammerstein model to be nonlinearized for the system while reflecting its dynamic properties [23]. Based on the detachability of the model, different methods can be used for different parts of the model in the control framework. Because the Hammerstein model solves the nonlinear problem first, the linear MPC can be used [24,25]. The linear MPC is much less computationally stressful than the direct use of nonlinear MPC. Zhang used the Hammerstein model to establish the predictive model of the turntable servo system, and the NMPC is used to control the turntable servo system effectively [26]. N. Kayedpour also used the Hammerstein model to research the operation of a floating offshore wind turbine and used quadratic programming to solve the objective function. Fast and stable control of the grid frequency is achieved [27].
For the nonlinear part of the Hammerstein model, one can define their nonlinear functions such as sigmoid networks [28], wavelet networks [29], fuzzy rule functions [30], or even deep learning network models [31] according to the control object. Machine learning and deep learning have made impressive advances in recent years. The accuracy of their predictions has been improving, but the complexity of their model structures leads to difficulties in solving the control quantities directly and applying them to control. The rise of intelligent optimization-solving algorithms in the last 20 years has made this possible. The Grey Wolf algorithm was applied to optimize the LSSVM parameters and solve the non-convex optimization problem of NMPC with success on the L-Lysine production system [32]. The differential evolution algorithm was used to solve the objective function of DBN-MPC and applied to a denitrification system in cement production to reduce ammonia consumption [33]. AlfarizI uses an ANN model to model the numerical reservoir simulation output of an injection well and solves it using a genetic algorithm to find the optimal control volume and thus improve efficiency [34]. However, the above intelligent optimization algorithm has the disadvantage of slow convergence and a tendency to fall into local optimum, which is also not conducive to stable and fast control of the system.
In this study, we use deep learning to extract the operating state characteristics of the precalciner and establish dynamic equations. The accurate prediction of the precalciner temperature is found in the form of the Hammerstein model, and effective control is realized based on the Hammerstein model. The contributions of this study are as follows:
- (1)
- To solve the time-delay and nonlinear problems of the precalciner system, the CNN-GRU network architecture is proposed to extract the operating states of the precalciner and an attention mechanism is employed to find and emphasize the important historical information in the extracted states.
- (2)
- To address the problem of poor dynamic properties of conventional neural networks, deep learning and dynamic equations are combined in the form of a Hammerstein model to achieve dynamic prediction of the precalciner temperature.
- (3)
- A model predictive control framework based on a deep learning Hammerstein model is proposed for precalciner systems whose volatility makes it difficult to control the temperature accurately.
- (4)
- To solve the problem of solving deep learning sessions with constraints in the Hammerstein model, an improved sparrow search algorithm is proposed.
2. Analysis of Cement Pre-Calcination Systems
In this section, the pre-calcination process in cement manufacturing is briefly described, and the input and output variables of the precalciner system are examined.
2.1. Cement Pre-Calcination Process
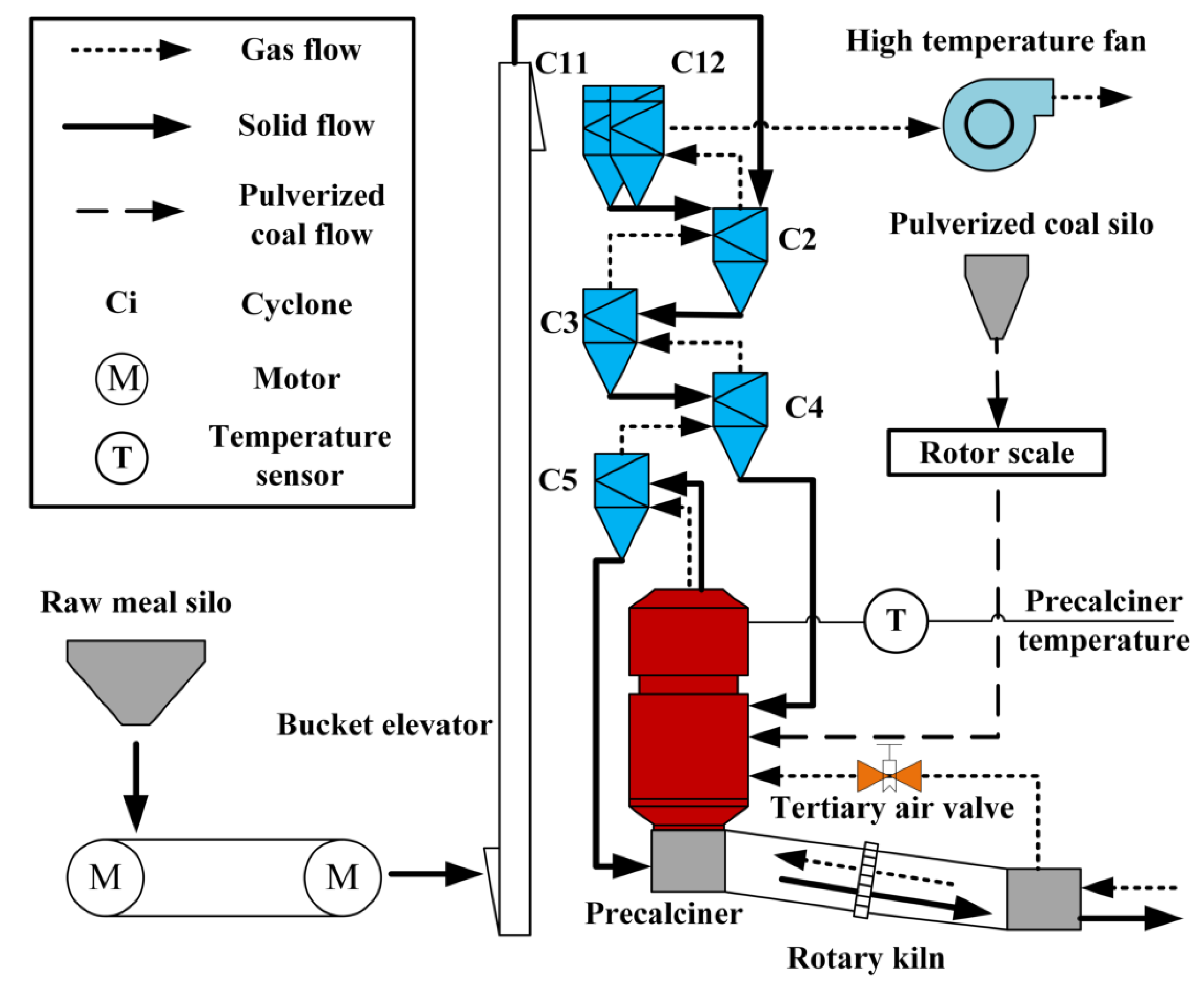
The pre-calcination system is one of the most critical steps in the dry process cement process. The exothermic reaction of the precalciner fuel and the heat-absorbing decomposition reaction of the cement raw meal occurs in this process. These reactions can increase the decomposition rate of cement raw meal. As shown in Figure 1, the pre-calcination process consists mainly of a cyclone preheater and a precalciner. The heat required for the pre-calcination process is mainly generated by the combustion of pulverized coal in the precalciner. The dashed, dotted, and solid lines in the diagram represent the coal, gas, and raw meal paths, respectively.
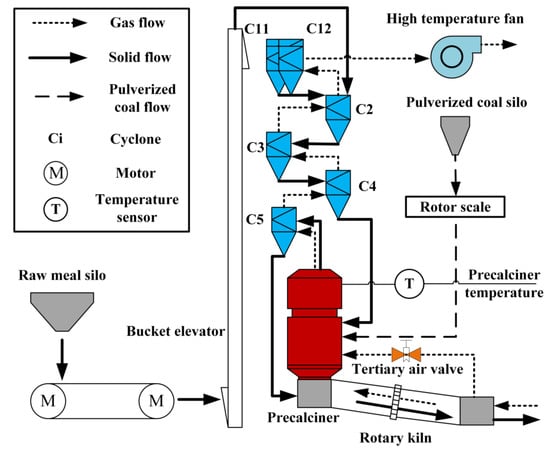
Figure 1.
Cement calcinations system.
The rotor scale weighs the pulverized coal from the pulverized coal bin after receiving the control signal and then enters the precalciner. The pulverized coal reacts chemically with the oxygen-rich air from the tertiary air valves in the precalciner, releasing a large amount of heat and generating a large amount of combustion exhaust gas. Together with the high-temperature exhaust gases from the rotary kiln calcination process, these combustion exhaust gases are pumped into the suspension preheater by the high-temperature fan above. Simultaneously, the raw cement material from the raw meal homogenizing silo is weighed by a belt scale and lifted by a bucket elevator to the highest stage of the suspension preheater into cyclones C2, C11, and C12. In the cyclones, the raw material is blown into uniform suspension by the spiraling exhaust gas stream, while the heat exchange with the high-temperature exhaust gas is rapidly completed. The raw material is then separated by gravity from the upward-flowing high-temperature exhaust gas and enters the next cyclone stage. The heat exchange is repeated until the raw meal leaves the C4 and enters the precalciner. The upward flow of the kiln exhaust gas blows the incoming raw meal out of the furnace and keeps it in suspension for a short time. The high-temperature environment created by pulverized coal combustion allows the raw meal to complete the decomposition reaction quickly in suspension or fluidized form. Finally, the decomposed material is sent to the rotary kiln for calcination via cyclone C5.
2.2. Internal Structure and Thermodynamic Analysis of the Precalciner
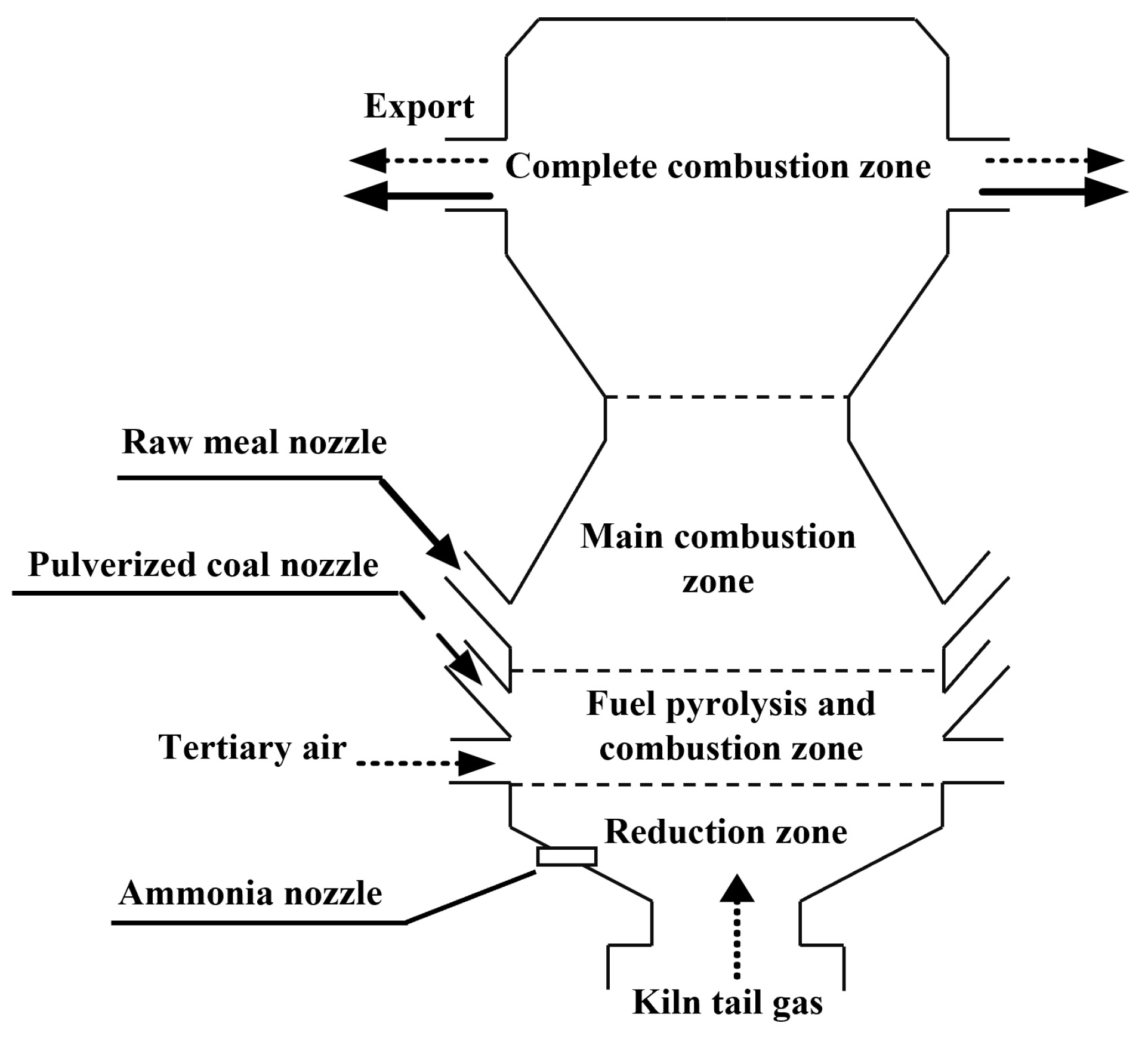
Precalciner is a crucial component of new dry cement precalcining technology. Important reactions such as pulverized coal combustion, carbonate decomposition, and nitrogen oxide reduction occur inside it. The precalciner has the advantages of improving the cement decomposition rate, reducing the heat load of the rotary kiln, and reducing kiln size and large-scale production. As shown in Figure 2, when the precalciner is working, its internal space can be divided into four areas: reduction area, fuel cracking and combustion area, main combustion area, and complete combustion area. The reduction zone is mainly used to reduce NOx in the exhaust gas of the kiln tail. The pulverized coal reacts with the high-temperature oxygen-enriched tertiary air in the fuel cracking and combustion zone. The coke is continuously cracked and burned, generating a lot of heat. The reaction generated in the main combustion zone is then transferred to the reduction zone. The raw meal and pulverized coal are uniformly mixed and burned. The raw meal is heat-absorbing and classified in this part, and its optimum temperature is 950–1000 °C. The function of the complete combustion zone is to complete the combustion of a small part of the unburned fuel and promote the raw meal. As the outlet of the precalciner, its maximum temperature should be maintained between 890 and 900 °C, so that the decomposition efficiency of the raw meal can be maintained above 90%.
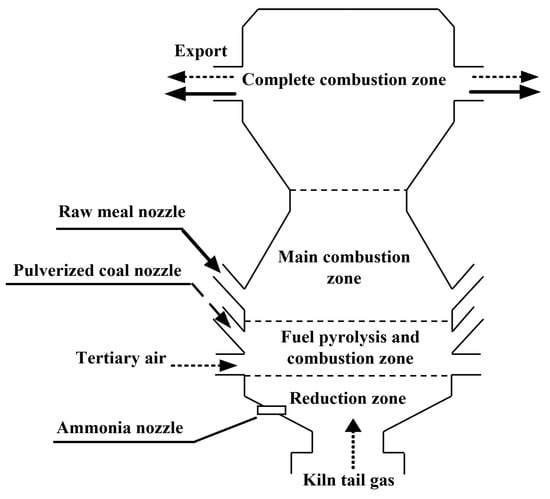
Figure 2.
Precalciner structure.
Most of the heat required by the system originates from the pulverized coal combustion in the precalciner. While the main source of heat consumption is the raw meal, the flow of air ensures both the full combustion of pulverized coal and the circulation and heat absorption of the raw meal in the cyclone. The most important indicator of the system is the exit temperature of the precalciner. The input of pulverized coal () determines the heat provided by the system and can be used as the main operating quantity. The amount of raw meal determines the heat consumption. From the point of view of the whole cement production system, the input of raw meal affects not only the pre-decomposition link but also the calcination link and the final output, so the quantity of raw meal () is regarded as the observable feedforward disturbance. The speed of the high-temperature fan () determines not only the speed of air circulation in the pre-calcination system, but also the speed of exhaust gas removal from the rotary kiln system. Because of this, the speed of the high-temperature fan is also used as an observable feedforward disturbance. In addition, the O content (), CO content (), and outlet temperature () of primary cyclone C11 also reflect, to some extent, the operating conditions of the precalciner. In addition, the opening of the feed baffle () and the speed of the EP fan () also influence the operating state of the precalciner, although the settings generally do not change significantly in industrial operation. Therefore, the selected variables can all be used as feedforward variables. The input, output, and disturbance variables of the system are shown in Table 1.

Table 1.
Variables of the temperature controller.
3. Prediction of Precalciner Temperature Based on the CGA-ARX Model
3.1. Basic Structure of Hammerstein Model
As shown in Figure 3, the most characteristic feature of the Hammerstein model is that its structure consists of a nonlinear static part and a linear dynamic part . The linear part is dominated by the ARX model, whereas the nonlinear part can be designed using functions based on the characteristics of the control object.
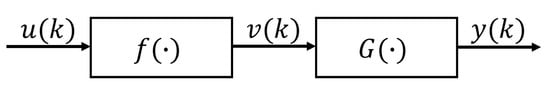
Figure 3.
Hammerstein model.
3.2. CGA-ARX Model
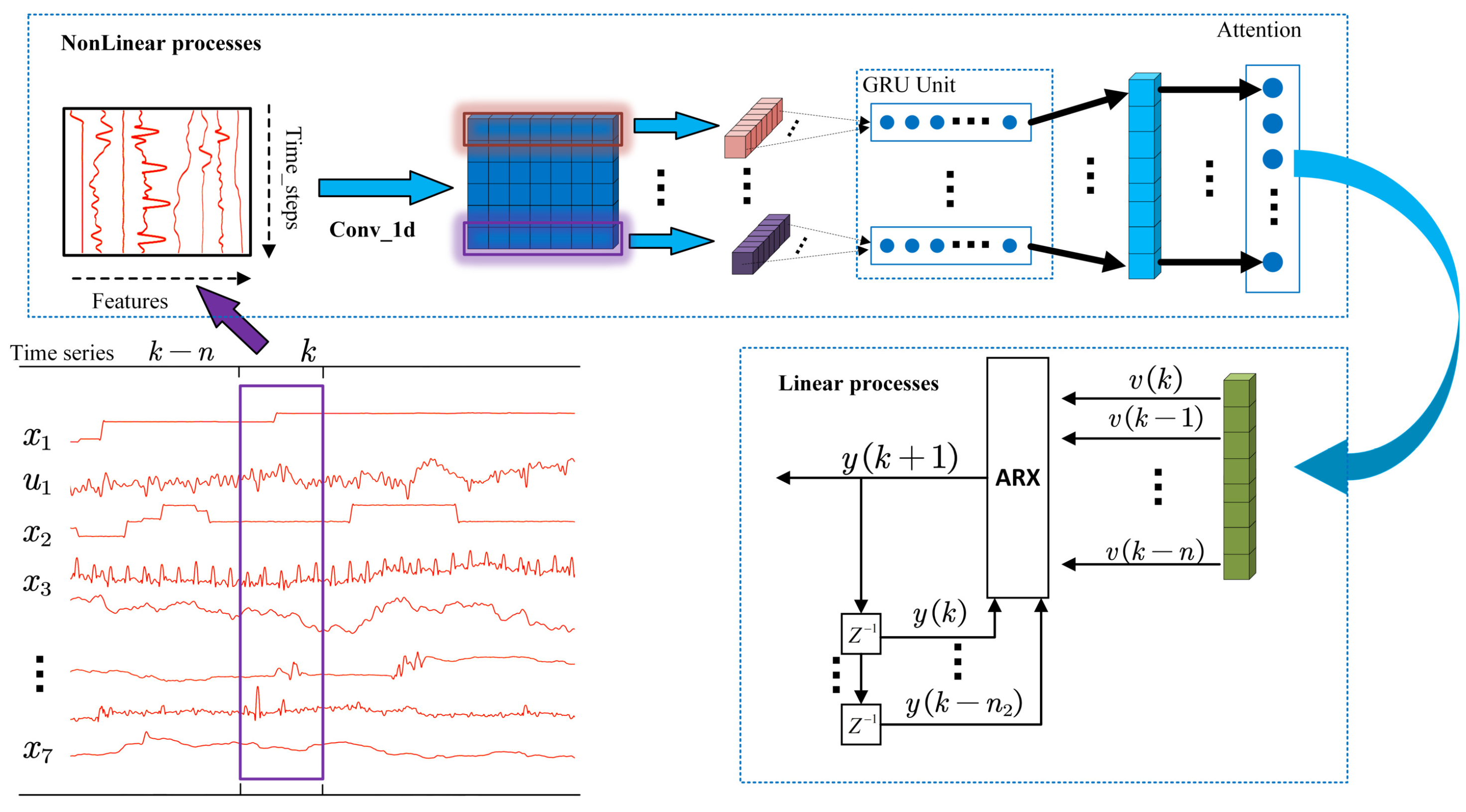
The CNN-GRU-Attention-ARX (CGA-ARX) consists of a CNN-GRU-Attention deep learning network that represents the nonlinear part and an ARX mode that represents the dynamic linear part, the specific structure of which is shown in Figure 4.
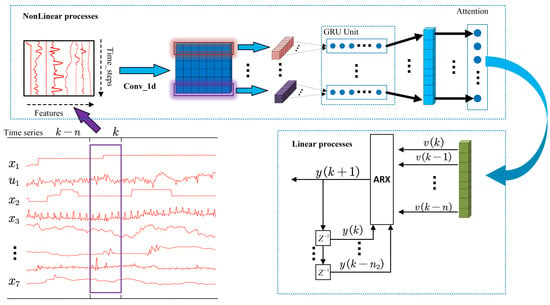
Figure 4.
CGA-ARX model.
As a method for processing multidimensional data, Convolutional Neural Network (CNN) has shown remarkable advantages in image processing and multidimensional time series processing [35]. For the different effects of different operating variables on the precalciner temperature at the same moment in the cement pre-calcination process, one-dimensional convolution is used to extract the temporal features of each input data. The output of the CNN layer is given by Equation (1).
where is the activation function, and and represent the weight matrix and bias vector of the CNN layer, respectively.
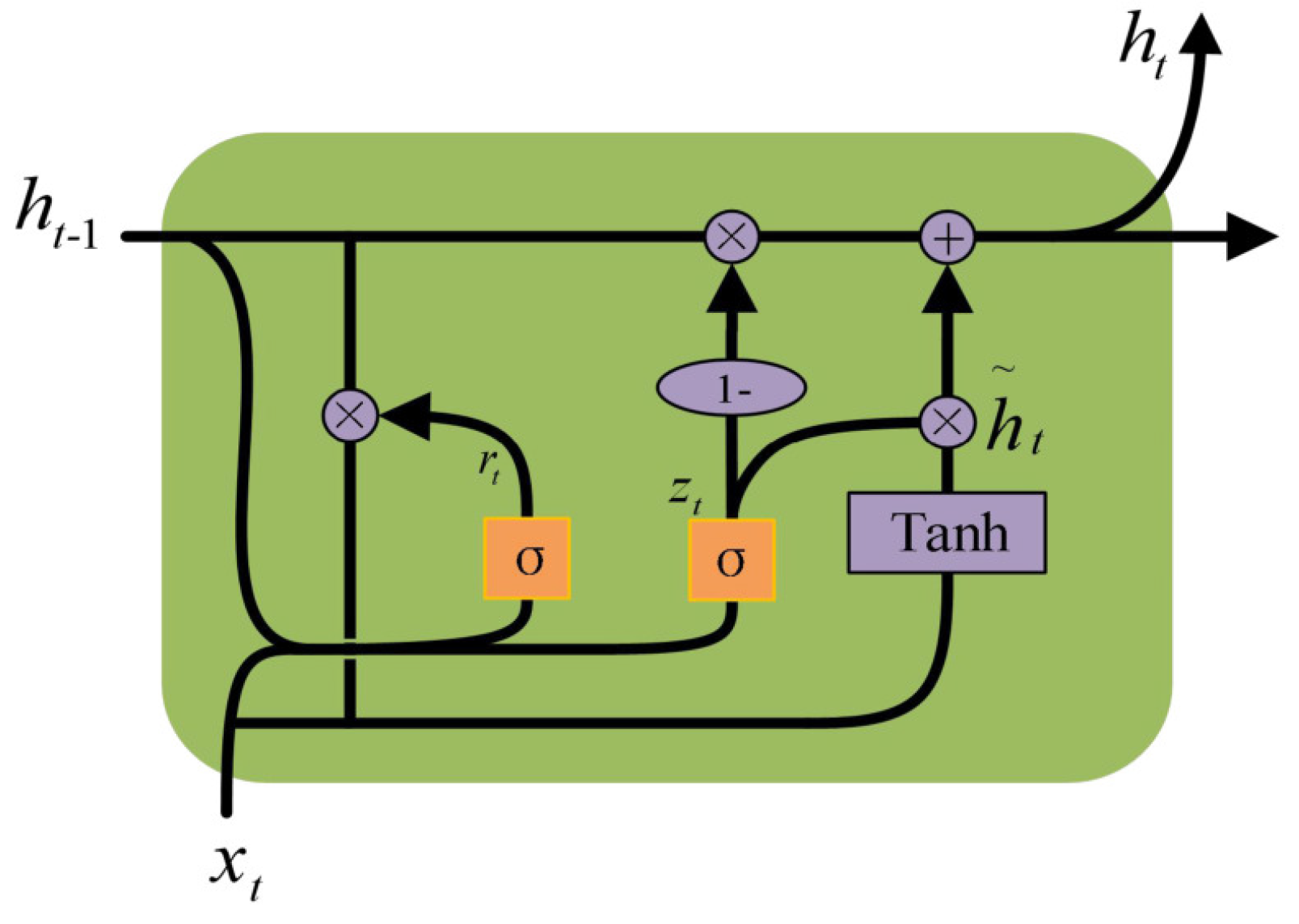
The GRU network is a variation of the LSTM network and performs better in processing time series than traditional recurrent neural networks [36]. The GRU unit is illustrated in Figure 5. A gated cyclic unit includes an update gate and a reset gate, which, owing to the design of the gates in the structure, allows the GRU network to capture the dynamics of the time series more effectively than traditional neural network features.
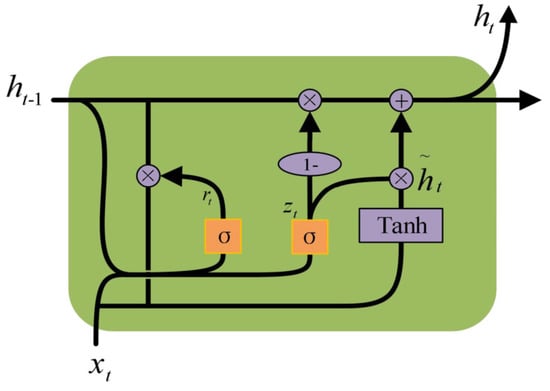
Figure 5.
GRU unit.
After CNN feature extraction, the data are used to capture the temporal characteristics of the data through a GRU network to address the time delay on the cement pre-calcination system. The formula used is as follows:
where , , and represent the weight matrix of the update gate, reset gate, and unit, respectively, , , and represent the bias vector of the update gate, reset gate, and unit, respectively, and represent the output of the update gate and reset gate, and are the activation functions, h represents the output of the hidden layer at the current moment, is the state of the hidden layer at the previous moment, and is the state of the cell at the current input.
The attention mechanism can effectively capture key information in time series and assign weights [37]. The current working state of the precalciner is highly correlated with its historical state. The attention mechanism can help us to determine the periods that have a strong influence on the current state and to give them greater weight to strengthen their role in the deep learning model. The specific formula for the attention mechanism is given in Equations (6) and (7):
where represents the hidden states output from the GRU units, w represents the weight of each GRU output, is the activation function used to calculate the score for each output from the GRU units after multiplying the weights, and represents the final status output.
Finally, the deep learning network refinement of the precalciner state in the form of ARX dynamic modeling to achieve accurate prediction of the decomposition furnace temperature, the specific formula is shown in Equation (8).
where represents the predicted output at the next moment, Ais a matrix, represents the historical precalciner temperature, and Bis a matrix. n and ’s exact values can be calculated using the Akaike information criterion (AIC) [38].
4. Control of Precalciner Temperature Based on CGA-ARX Model
Using the special characteristics of the Hammerstein model structure, a complex MIMO nonlinear system can be disassembled into a linear control part, and a nonlinear solution part, and a Hammerstein model predictive control system (HMPC) can be established. As predictive control requires multi-step prediction, the specificity of the structure of the Hammerstein model can be used to reduce the computational pressure by using the linear part for multi-step prediction.
4.1. Prediction and Control of Linear Part
Generalized predictive control (GPC) as a method of MPC has a good control effect on linear systems [39]. GPC typically uses the ARX model as the prediction model. In this study, one-step prediction can be expressed by Equation (8).
The objective function of the GPC is constructed as follows:
where is the setpoint at time , is the starting point of the controller calculation , N is the prediction step, is the control step and , is a weighting factor that constrains the control volume to prevent system oscillations, and is the amount of change in the intermediate variable.
MPC often uses a strategy of predicting multiple steps ahead and providing multiple steps of control to achieve optimal control. To obtain a j-step ahead prediction, we can convert Equation (8) to (10).
where represents the step ahead prediction, and are polynomials of order n and , respectively, and is the intermediate variable from the CGA model.
By introducing the Diophantine equation as follows:
We reintroduce Equation (13):
We can obtain the future N step prediction vector as follows:
where represents the amount of change in .
By using Equation (14), the objective function Equation (9) can be transformed into the following equation:
where is the prediction vector whose shape is , is the set value vector after softening whose shape is , and is the change in the intermediate variable.
In the end, we can obtain the optimal solution of control as follows:
The current control volume can be obtained via Equation (16) as follows:
where is the first-row vector from .
4.2. Optimal Solution Strategy for Nonlinear Complex Problem
Using GPC, we can derive the ideal intermediate variable for the next moment. To obtain the actual control quantity for the next moment, the problem can be transformed into an optimization problem to be solved. The specific expression is given by Equation (18).
where is the actual control quantity to be sought, represents disturbance variables and feedforward variables in Table 1, is the predicted value of the CGA model where the input is the actual control volume, is the weighting factor, is the lower limit of the actual control quantity to be sought, and is the high limit of the actual control quantity to be sought.
To solve an optimization problem containing complex functions, as shown in Equation (18), intelligent optimization algorithms can be used to solve this problem. Common intelligent optimization algorithms include PSO, GA, DE, and so on. As one of the newest intelligent optimization algorithms, SSA performs well in handling optimization problems with complex functions.
4.2.1. Principle of Sparrow Search Algorithm
The basic idea of SSA is to find the optimal solution to the problem by simulating the foraging and anti-predatory behavior of sparrows. Based on their foraging behavior, sparrows have three roles: finders, scroungers, and reporters [40].
The finder is responsible for finding food and providing directions to other individuals. The position is iteratively formulated as follows:
where t is the round of the current iteration, is the ith sparrow’s position in the jth dimension, is the maximum number of iterations, is a uniform random number with a range of , Q is a random number that satisfies the standard normal distribution, is a uniformly distributed random number within the range of , and is a threshold value within the range of .
The scroungers follow the finder foraging with the following iterative position formula:
where and are the global worst and best positions in the tth iteration, respectively, A is a matrix whose elements are randomly assigned to 1 or −1, and L is a matrix whose elements are all 1.
Reporters are responsible for providing safety warnings with the following iterative position formula:
where is the best global position of individuals for the tth iteration, is a random value that follows a standard normal distribution, K is a random value within the range , , , and are the best global fitness, individual fitness, and worst global fitness of current iteration process, respectively, and is the minimum constant to avoid the denominator being zero.
4.2.2. Principle of Improved Sparrow Search Algorithm
Although SSA has the advantages of powerful optimization ability and rapid convergence speed, it is likely to fall into the local optimization. It fails to find the best solution to the problem [41]. SSA uses a standard normal distribution to initialize populations, which limits the diversity of populations. The Tent chaotic map is stochastic and ergodic in nature. The use of the Tent chaos map allows for better diversity in the initial population and improves global search capabilities [42]. The formula is as follows:
where is the parameter within the range of ; in this paper, we set the value of as 0.5. is the mapping value of the mapping number.
A reporter search phase helps improve the algorithm’s global search capability. However, setting the number of reporters to a fixed value is not conducive to convergence in the later stages of the algorithm; therefore, a decreasing number of reporters is used to regulate the number of reporters in the iterative process. The number of reporters is large at the beginning of the iteration, and the number is reduced at the later stage of the iteration. The whole process of change ensures the global search capability while improving the convergence speed of the algorithm. The formula is as follows:
where is the maximum population size.
When a reporter appears, the original SSA uses a standard normal distribution random method for jumping, with a limited step size, which can easily fall into a local optimum. A weighted sine and cosine algorithm based on the growth function model can solve this problem [43]. The formula is as follows:
where and are e constants of 1.6 and 2, respectively, is a random number within range , and is a random number within range .
As shown in Equation (20), the population converges gradually to 0 when . The objective function is more efficient for certain optimally convergent solutions around 0, whereas in practical engineering applications, these individuals usually move toward lower fitness values overall. The crossover process is at the heart of the genetic algorithm and generates a new phase mask by mixing segments of the two selected phase masks from the previous generation. Using this approach to update scroungers’ positions is more in line with practical engineering applications [44]. The formula is as follows:
In addition, the mutation operation, which is at the heart of genetic algorithms, can bring diversity to populations. Get rid of the local optimum by performing a dynamic adaptive T-distribution mutation such as Equation (26) after updating the sparrow’s position [41].
where is the random number of the distribution as the parameter of the degree of freedom.
4.2.3. ISSA Specific Process
The ISSA calculation process is shown in the pseudo-code in Table 2. Based on this, we obtain the solution of the objective function in Equation (18).

Table 2.
Pseudo-code of ISSA algorithm.
4.3. Specific Control Process
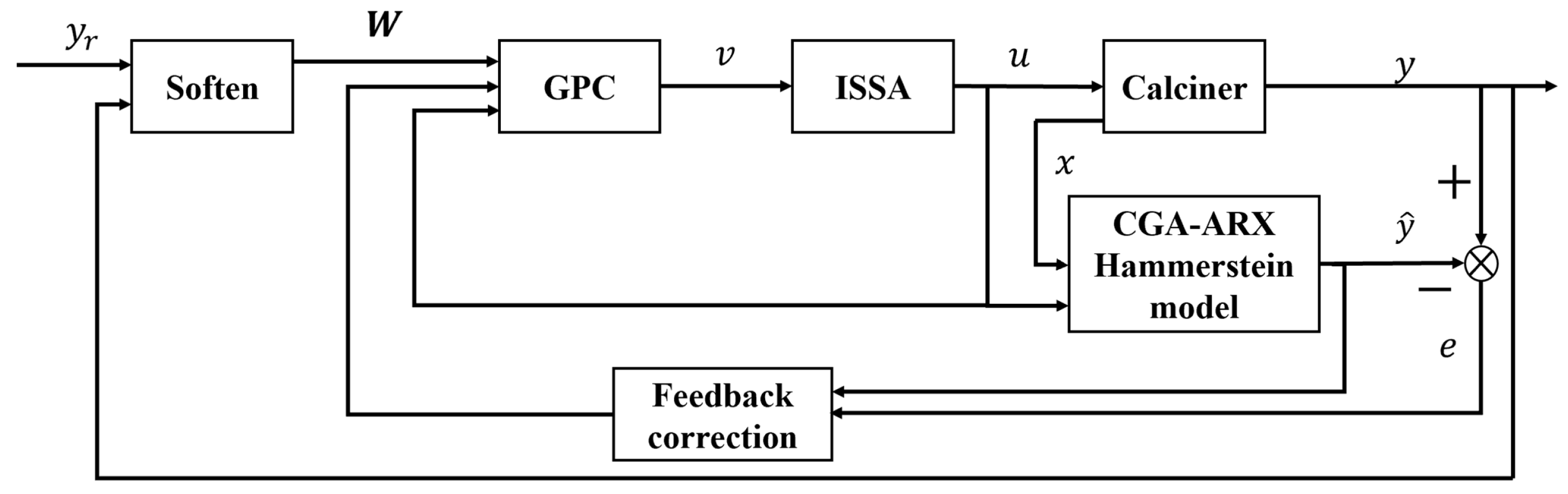
The control framework based on the CGA-ARX Hammerstein model is shown in Figure 6 CGA-ARX-HMPC structure, and its specific control flow is presented in Table 3.
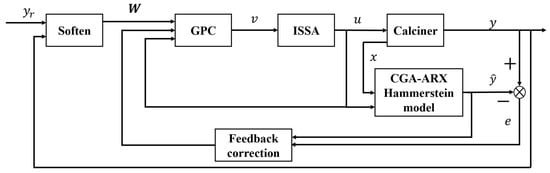
Figure 6.
CGA-ARX-HMPC structure.

Table 3.
Pseudo-code of CGA-ARX-HMPC algorithm.
5. Experimental Results and Analysis
In this section, we test the proposed CGA-ARX prediction model, ISSA, and constructed the HMPC framework. The data were provided by the Jidong Cement Plant in Hebei Province, China.
5.1. CGA-ARX Performance
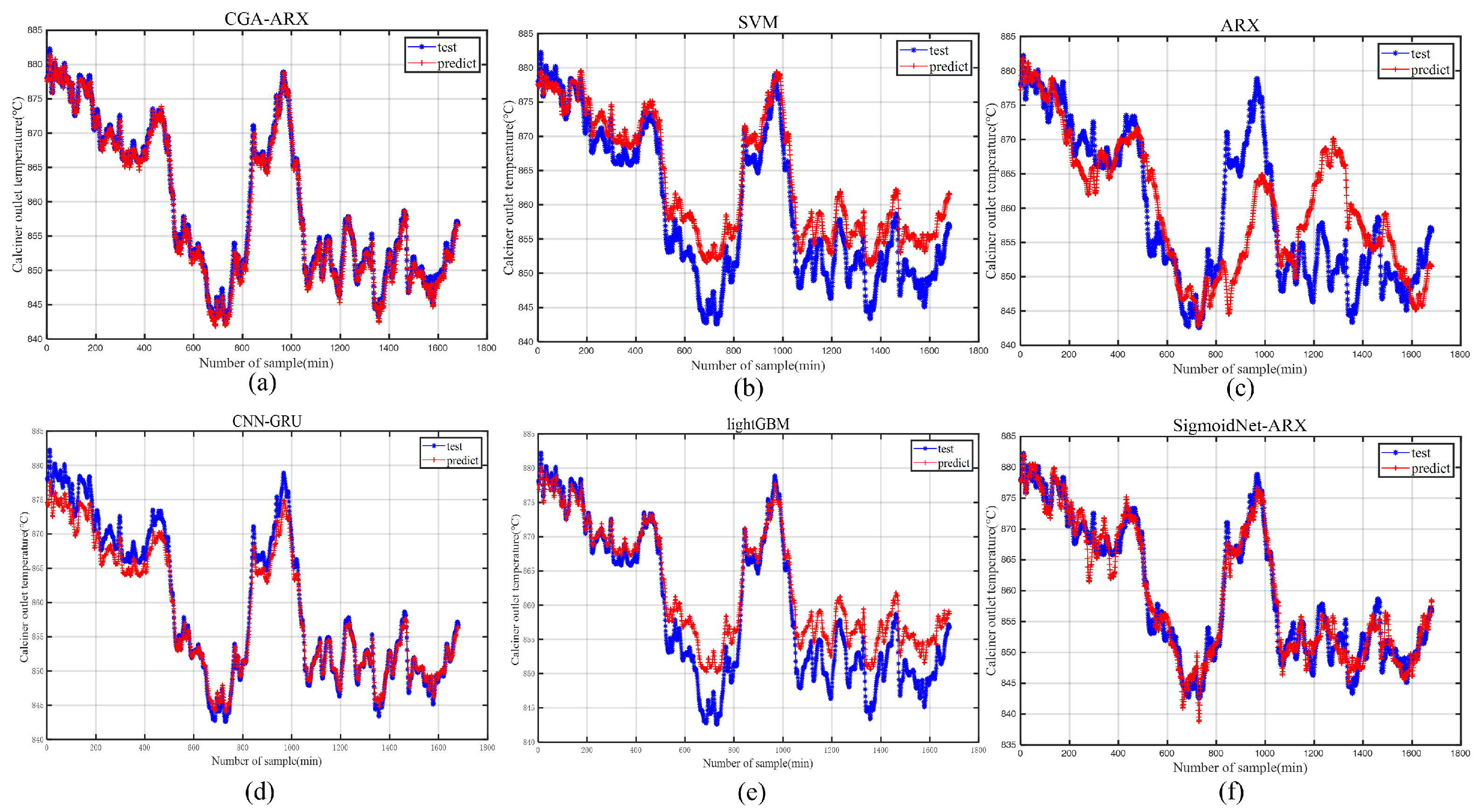
We extracted 10,000 sets of data from a 5000 t/d cement plant in Hebei Province, China, for March 2019 and processed the data. The final 25,000 sets of data were selected for training and 1680 sets of data for testing. The ARX model, sigmoid neural network Hammerstein model, CNN-GRU network, SVM, and lightGBM were also used for comparison, representing the traditional dynamic models, Hammerstein models, deep learning, and machine learning methods, respectively. Each model’s prediction results and errors are shown in Figure 7 and Figure 8.
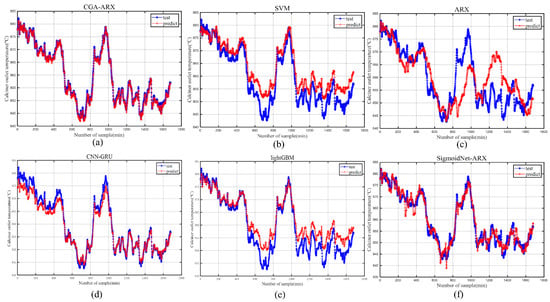
Figure 7.
Prediction results of the different methods.
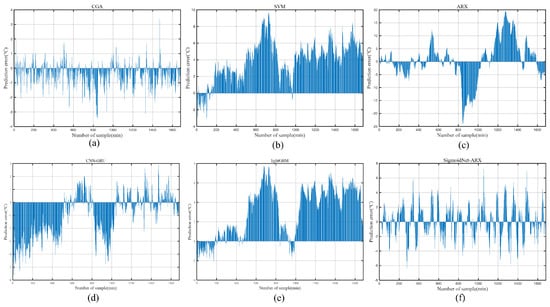
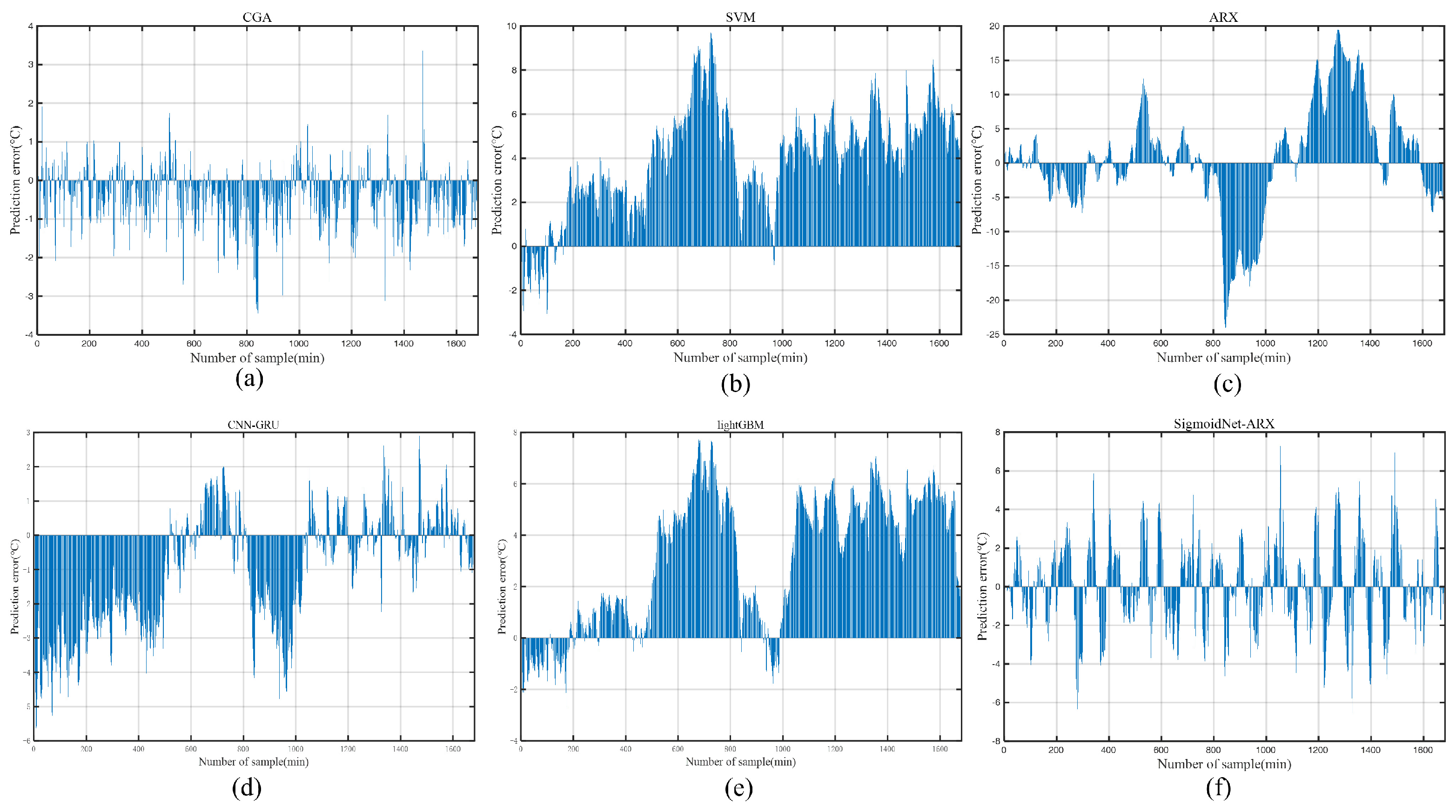
Figure 8.
Prediction errors.
As seen in Figure 7, the traditional linear ARX model for predicting precalciner temperature could be better, mainly because of the strong nonlinearity of the precalciner system. SigmoidNet-ARX is slightly better than ARX but still needs to be better. SVM and lightGBM are not initially suitable for time series forecasting with time delay but adding historical information to the input layer of the model allows the forecasts to trend approximately the same as the actual labeled values. However, as shown in Figure 8, the prediction errors are mostly positive, indicating poor generalization ability. Deep learning methods perform better than traditional modeling methods for precalciner temperature prediction. After introducing the attention mechanism, its prediction results are more accurate To visualize the superiority of the CGA-ARX prediction method, several error metrics and goodness-of-fit metrics are selected for illustration: mean absolute error (MAE) (Equation (27)), root mean square error (RMSE) (Equation (28)), mean absolute percentage error (SMAPE) (Equation (29)), and goodness of fit (R2) (Equation (30)), the equations for which are shown below. The results of the specific test indexes are listed in Table 4.

Table 4.
Evaluation indexes of the different models.
As shown in Table 4, the CGA-ARX model has a lower prediction error than the other methods, whereas the R2 metric, which provides an intuitive indication of the fit of the prediction results, is higher. The tests show that the CGA-ARX Hammerstein model proposed in this study is more reliable
5.2. ISSA Performance
To prove that ISSA has good convergence and global search capability, we selected some existing optimization algorithms, as shown in Table 5, and some common benchmark functions, as shown in Table 6, for the comparison test. Since intelligent search algorithms have a certain randomness, to ensure the experiment’s reliability, we run each algorithm on the benchmark function 30 times and take its optimal solution; the specific results are shown in Table 7.

Table 5.
The parameter settings of the chosen optimization algorithms.

Table 6.
Test function.

Table 7.
Benchmark function test optimization results.
Table 7 shows that ISSA performs better than the other optimization algorithm on the benchmark function test and that the optimal value found is the test function’s ideal optimal value. In multiple runs, the Mean metric is closer to the answer of the test function, and the Std metric is smaller, indicating the reliability of ISSA.
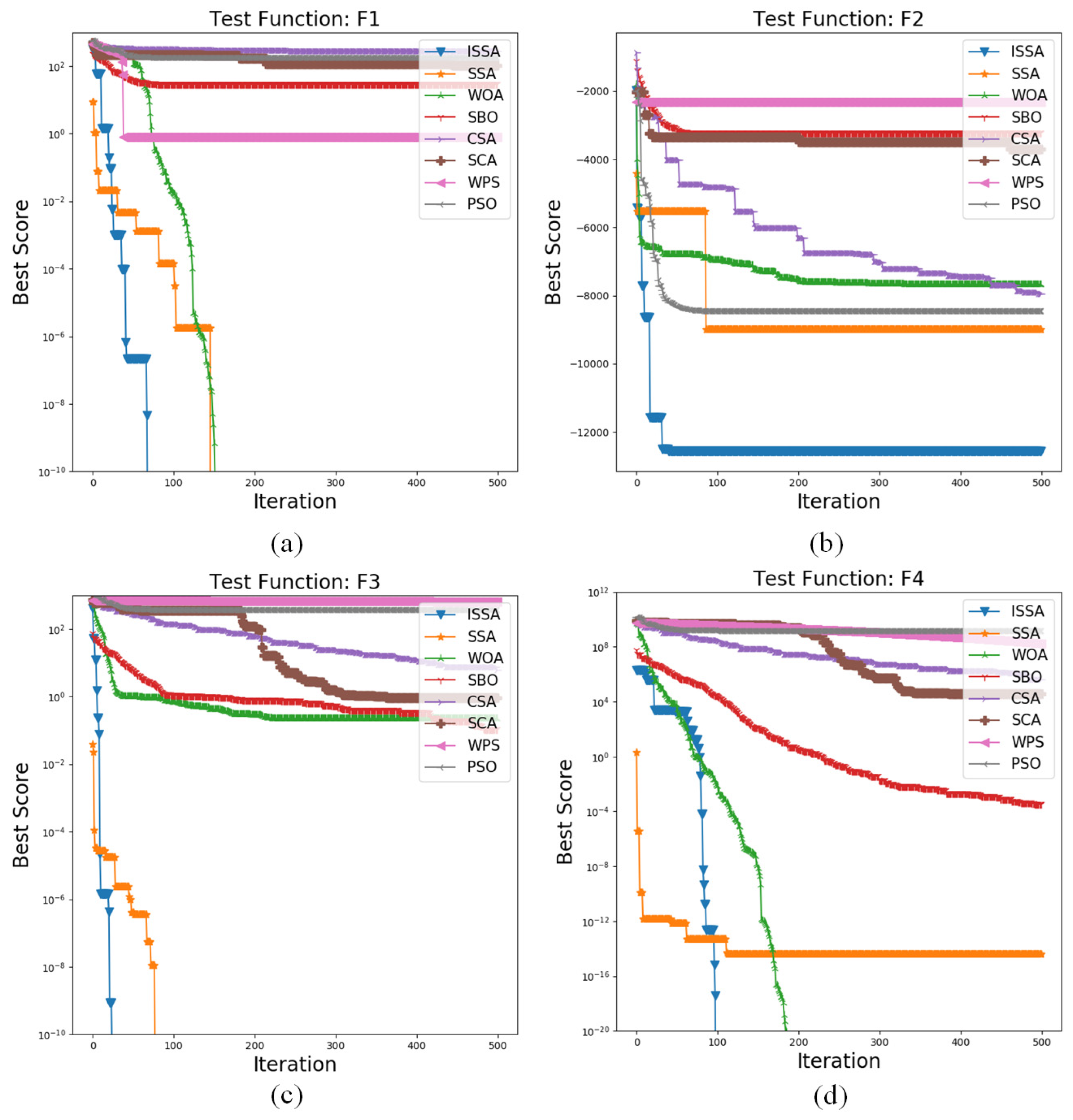
The convergence curve is an important index to evaluate the performance of an algorithm. Through the convergence curve, we can directly observe the algorithm’s convergence speed, convergence trend, and solution quality when solving the function. As shown in Figure 9, the ISSA proposed in this study has faster convergence speed and better global optimization ability than other optimization algorithms, which provides the basis for solving complex models in model predictive control.
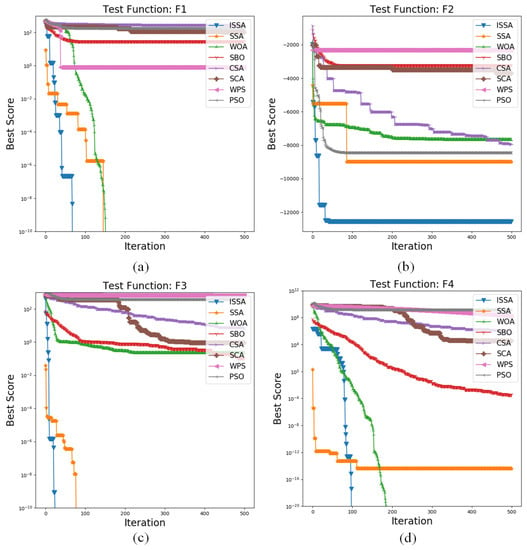
Figure 9.
Convergence curves of different algorithms on test functions.
5.3. CGA-ARX-HMPC Experiment Results
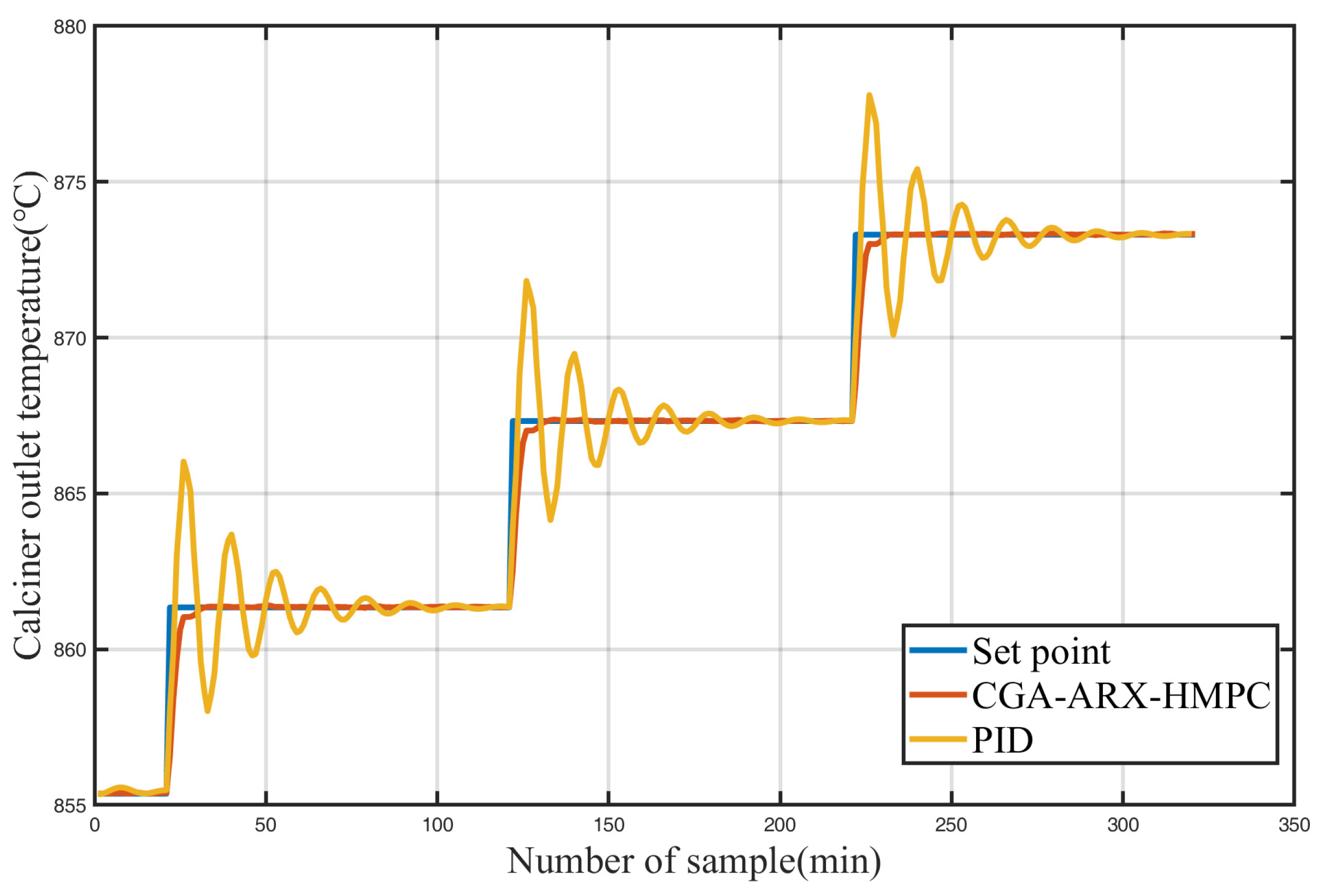
To demonstrate the superiority of the control system developed in this study, the operational data used for training the predictive model described above are introduced into the control system as a real-time operational state, and the PID method was tested for comparison. The results are shown in Figure 10. The CGA-ARX-HMPC control is significantly better than that of the PID controller. During dynamic changes, the CNN-ARX-HMPC performs faster and smoother in tracking the changing set point. However, the PID controller has large fluctuations during the dynamic process, with a large overshoot, and it takes longer to reach stable control.
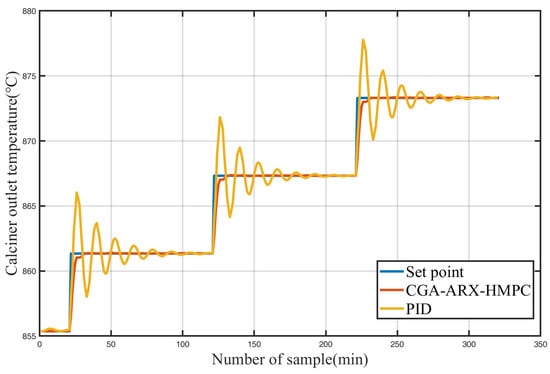
Figure 10.
Comparison chart of dynamic processes.
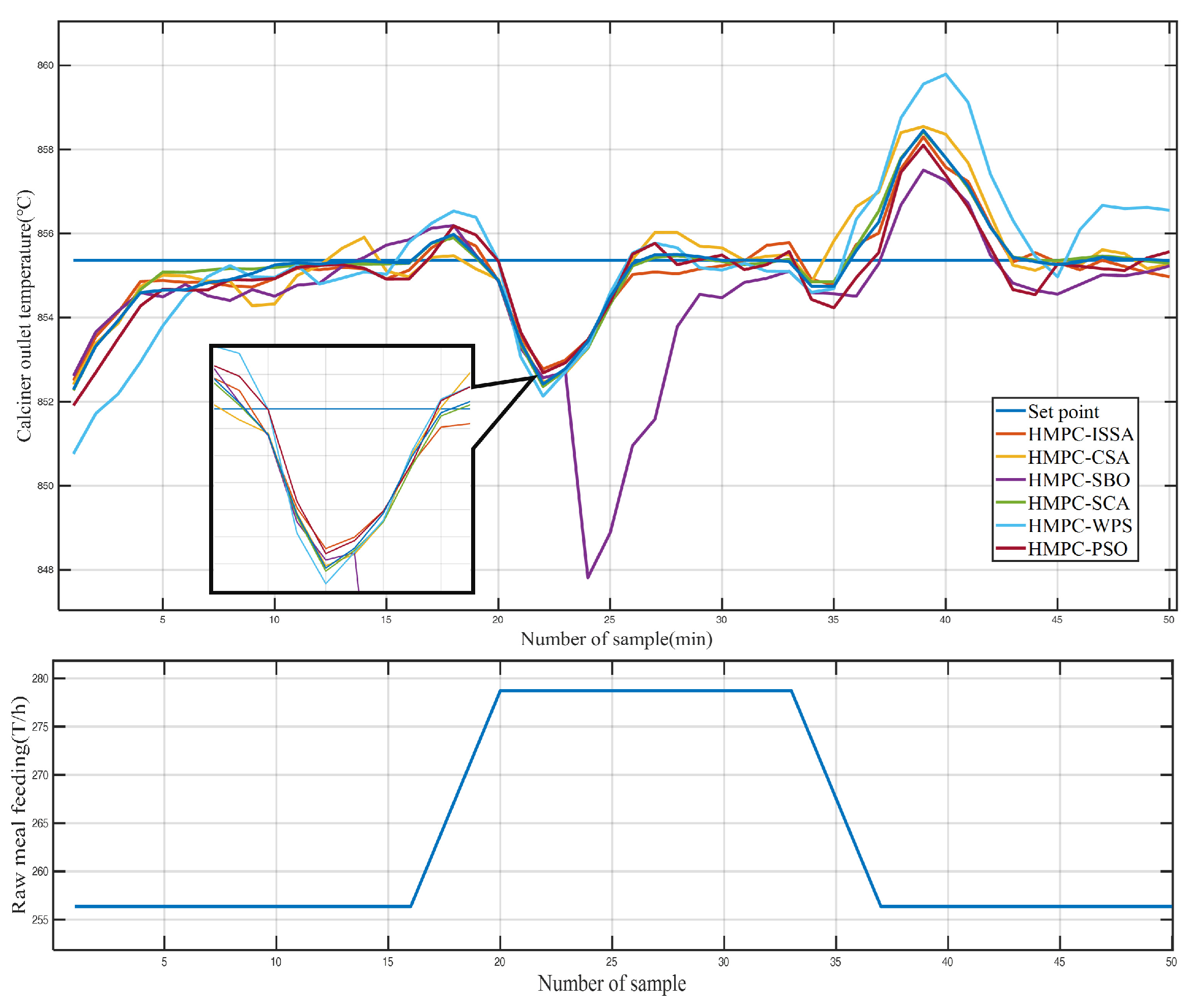
During the cement calcination process, the precalciner system experiences disturbances mainly from large variations in the feed rate. To evaluate the robustness of the control strategy proposed in this study, experiments on feed rate perturbations are designed, and the results are as follows:
As shown in Figure 11, the feeding volume of the system changes dramatically at the 16 and 33 min moments. The significant rise and fall in feed volume inevitably affect the system’s temperature. We tested the controller using different optimization algorithms in Table 5. During the tests, we found that the long calculation times required by WOA were not conducive to practical control applications. Therefore, we do not show the control effect using WOA anymore.
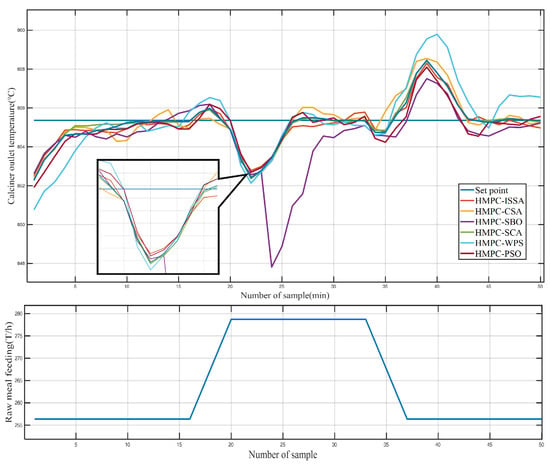
Figure 11.
Controller stability verification with ISSA.
Where the overall trends are broadly similar, we can analyze them by the absolute value of the errors. As shown in Table 8, the controller using ISSA has the lowest maximum absolute error and the lowest mean value of absolute error under disturbance relative to the controller using the other algorithms. This shows the reliability of the controllers designed in this study.

Table 8.
Error index.
6. Conclusions
For the nonlinear and large time delay features of the pre-calcination system in the cement production process, a CGA-ARX Hammerstein prediction model was proposed in this work. The CGA-ARX model has a superior prediction effect compared to the standard prediction model. The model predictive control framework is designed to take advantage of the unique features of the Hammerstein model structure, flawlessly merging the GPC and the intelligent optimization method. Simultaneously, the sparrow search algorithm is enhanced to improve its global search capability and convergence speed, and it is successfully used in the control framework developed in this study. The CGA-ARX-HMPC offers a superior control effect and robustness compared to typical control approaches, according to the experiments.
The CGA-ARX Hammerstein model proposed in this study is an offline model, based on which the model can be extended to an online model to optimize the parameters of the dynamic response part of the Hammerstein model online. In addition, the proposed ISSA and control framework can be used for both economic model predictive control and zone control.
Author Contributions
Conceptualization, C.S. and P.L.; methodology, C.S.; software, P.L.; validation, H.G.; formal analysis and investigation, Y.D.; resources, X.H.; data curation, Q.X.; writing—original draft preparation, P.L.; project administration, X.H.; funding acquisition, X.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported by the National Natural Science Foundation of China (Grant No. 62073281), the Hebei Provincial Natural Science Foundation (Grant No.F2022203088), the Hebei Provincial Science and Technology Plan Project (Grant No. 19211602D). The APC was funded by Chao Sun.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Adams, D.; Oh, D.H.; Kim, D.W.; Lee, C.H.; Oh, M. Prediction of SOx–NOx emission from a coal-fired CFB power plant with machine learning: Plant data learned by deep neural network and least square support vector machine. J. Clean. Prod. 2020, 270, 122310. [Google Scholar] [CrossRef]
- Ahmad, J.; Martinez-Garcia, R.; de Prado-Gil, J.; Irshad, K.; El-Shorbagy, M.A.; Fediuk, R.; Vatin, N.I. Concrete with Partial Substitution of Waste Glass and Recycled Concrete Aggregate. Materials 2022, 15, 430. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.A.; Imam, M.K.; Irshad, K.; Ali, H.M.; Hasan, M.A.; Islam, S. Comparative Overview of the Performance of Cementitious and Non-Cementitious Nanomaterials in Mortar at Normal and Elevated Temperatures. Nanomaterials 2021, 11, 911. [Google Scholar] [CrossRef] [PubMed]
- De Lena, E.; Arias, B.; Romano, M.C.; Abanades, J.C. Integrated Calcium Looping System with Circulating Fluidized Bed Reactors for Low CO2 Emission Cement Plants. Int. J. Greenh. Gas Control. 2022, 114, 103555. [Google Scholar] [CrossRef]
- Zhang, L.; Wei, X.; Zhang, Z.; Li, S. Modeling De-NOx by Injection Ammonia in High Temperature Zone of Cement Precalciner. J. Therm. Sci. 2020, 30, 636–643. [Google Scholar] [CrossRef]
- Qiao, J.; Chai, T. Intelligence-Based Temperature Switching Control for Cement Raw Meal Calcination Process. IEEE Trans. Control. Syst. Technol. 2015, 23, 644–661. [Google Scholar] [CrossRef]
- Kurdowski, W.; Jelito, E. Rotary kilns in current cement industry. Cem. Wapno Beton 2020, 25, 127–136. [Google Scholar] [CrossRef]
- Fellaou, S.; Harnoune, A.; Seghra, M.A.; Bounahmidi, T. Statistical modeling and optimization of the combustion efficiency in cement kiln precalciner. Energy 2018, 155, 351–359. [Google Scholar] [CrossRef]
- Santos, T.A.; Cilla, M.S.; Ribeiro, E.D.V. Use of asbestos cement tile waste (ACW) as mineralizer in the production of Portland cement with low CO2 emission and lower energy consumption. J. Clean. Prod. 2022, 335, 130061. [Google Scholar] [CrossRef]
- Yang, Y.; Zhang, Y.; Li, S.; Liu, R.; Duan, E. Numerical simulation of low nitrogen oxides emissions through cement precalciner structure and parameter optimization. Chemosphere 2020, 258, 127420. [Google Scholar] [CrossRef]
- Soni, A.; Das, P.K.; Yusuf, M.; Pasha, A.A.; Irshad, K.; Bourchak, M. Synergy of RHA and silica sand on physico-mechanical and tribological properties of waste plastic-reinforced thermoplastic composites as floor tiles. Environ. Sci. Pollut. Res. Int. 2022. [Google Scholar] [CrossRef]
- Zhao, J.; Li, J.; Shan, Y. Research on a forecasted load-and time delay-based model predictive control (MPC) district energy system model. Energy Build. 2021, 231, 110631. [Google Scholar] [CrossRef]
- Scattolini, R. Architectures for distributed and hierarchical Model Predictive Control—A review. J. Process. Control 2009, 19, 723–731. [Google Scholar] [CrossRef]
- Mayne, D.Q. Model predictive control: Recent developments and future promise. Automatica 2014, 50, 2967–2986. [Google Scholar] [CrossRef]
- Cheng, C.; Peng, C.; Zhang, T. Fuzzy K-Means Cluster Based Generalized Predictive Control of Ultra Supercritical Power Plant. IEEE Trans. Ind. Informatics 2021, 17, 4575–4583. [Google Scholar] [CrossRef]
- Shi, K.; Wang, B.; Chen, H. Fuzzy generalised predictive control for a fractional-order nonlinear hydro-turbine regulating system. IET Renew. Power Gener. 2018, 12, 1708–1713. [Google Scholar] [CrossRef]
- Patil, B.V.; Bhartiya, S.; Nataraj, P.S.V.; Nandola, N.N. Multiple-model based predictive control of nonlinear hybrid systems based on global optimization using the Bernstein polynomial approach. J. Process. Control. 2012, 22, 423–435. [Google Scholar] [CrossRef]
- Cordero, R.; Estrabis, T.; Gentil, G.; Batista, E.A.; Andrea, C.Q. Development of a Generalized Predictive Control System for Polynomial Reference Tracking. IEEE Trans. Circuits Syst. II: Express Briefs 2021, 68, 2875–2879. [Google Scholar] [CrossRef]
- Tian Zhongda, L.S.; Wang Yanhong, W.X. SVM predictive control for calcination zone temperature in lime rotary kiln with improved PSO algorithm. Trans. Inst. Meas. Control 2018, 40, 3134–3146. [Google Scholar] [CrossRef]
- Diaz, P.; Salas, J.C.; Cipriano, A.; Núñez, F. Random forest model predictive control for paste thickening. Miner. Eng. 2021, 163, 106760. [Google Scholar] [CrossRef]
- Zheng, J.; Zhao, L.; Du, W. Hybrid model of a cement rotary kiln using an improved attention-based recurrent neural network. ISA Trans. 2022, 129, 631–643. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Wang, H.; Liu, C. MILM hybrid identification method of fractional order neural-fuzzy Hammerstein model. Nonlinear Dyn. 2022, 108, 2337–2351. [Google Scholar] [CrossRef]
- Mehta, U.; Majhi, S. Identification of a class of Wiener and Hammerstein-type nonlinear processes with monotonic static gains. ISA Trans. 2010, 49, 501–509. [Google Scholar] [CrossRef] [PubMed]
- Ding, B.; Wang, J.; Su, B. Output feedback model predictive control for Hammerstein model with bounded disturbance. IET Control Theory Appl. 2022, 16, 1032–1041. [Google Scholar] [CrossRef]
- Cao, Q.; Tan, Y. Online Optimization Method for Nonlinear Model-Predictive Control in Angular Tracking for MEMS Micromirror. Micromachines 2022, 13, 1867. [Google Scholar] [CrossRef]
- Zhang, Q.; Wang, Q.; Li, G. Nonlinear modeling and predictive functional control of Hammerstein system with application to the turntable servo system. Mech. Syst. Signal Process. 2016, 72–73, 383–394. [Google Scholar] [CrossRef]
- Kayedpour, N.; Samani, A.E.; De Kooning, J.D.; Vandevelde, L.; Crevecoeur, G. Model Predictive Control with a Cascaded Hammerstein Neural Network of a Wind Turbine Providing Frequency Containment Reserve. IEEE Trans. Energy Convers. 2022, 37, 198–209. [Google Scholar] [CrossRef]
- Oleynik, A.; Ponosov, A.; Kostrykin, V.; Sobolev, A.V. Spatially localized solutions of the Hammerstein equation with sigmoid type of nonlinearity. J. Differ. Equat. 2016, 261, 5844–5874. [Google Scholar] [CrossRef]
- Chen, W.; Zhang, R.; Liu, H.; Xie, X.; Yan, L. A novel method for solar panel temperature determination based on a wavelet neural network and Hammerstein-Wiener model. Adv. Space Res. 2020, 66, 2035–2046. [Google Scholar] [CrossRef]
- Liutkevičius, R. Fuzzy Hammerstein Model of Nonlinear Plant. Nonlinear Anal. Model. Control. 2008, 2, 201–212. [Google Scholar] [CrossRef]
- Schulze, J.C.; Doncevic, D.T.; Mitsos, A. Identification of MIMO Wiener-type Koopman models for data-driven model reduction using deep learning. Comput. Chem. Eng. 2022, 161, 107781. [Google Scholar] [CrossRef]
- Wang, B.; Shahzad, M.; Zhu, X.; Rehman, K.U.; Uddin, S. A Non-linear Model Predictive Control Based on Grey-Wolf Optimization Using Least-Square Support Vector Machine for Product Concentration Control in L-Lysine Fermentation. Sensors 2020, 20, 3335. [Google Scholar] [CrossRef]
- Xu, Q.; Hao, X.; Shi, X.; Zhang, Z.; Sun, Q.; Di, Y. Control of denitration system in cement calcination process: A Novel method of Deep Neural Network Model Predictive Control. J. Clean. Prod. 2022, 332, 129970. [Google Scholar] [CrossRef]
- Alfarizi, M.G.; Stanko, M.; Bikmukhametov, T. Well control optimization in waterflooding using genetic algorithm coupled with Artificial Neural Networks. Upstream Oil Gas Technol. 2022, 9, 100071. [Google Scholar] [CrossRef]
- Zhao, Y.; Ding, B.; Zhang, Y.; Yang, L.; Hao, X. Online cement clinker quality monitoring: A soft sensor model based on multivariate time series analysis and CNN. ISA Trans. 2021, 117, 180–195. [Google Scholar] [CrossRef]
- Meng, X.; Zhu, T.; Li, C. Construction of perfect dispatch learning model based on adaptive GRU. Energy Rep. 2022, 8, 668–677. [Google Scholar] [CrossRef]
- Hou, L.; Zhang, J.; Wu, O.; Yu, T.; Yao, R. Method and Dataset Entity Mining in Scientific Literature: A CNN + Bi-LSTM Model with Self-attention. Artif. Intell. 2020, 235, 107621. [Google Scholar] [CrossRef]
- Dridi, N.; Hadzagic, M. Akaike and Bayesian Information Criteria for Hidden Markov Models. IEEE Signal Process. Lett. 2019, 26, 302–306. [Google Scholar] [CrossRef]
- Li, S.; Shi, Y.; Hu, L.; Sun, Z. A generalized model predictive control method for series elastic actuator driven exoskeleton robots. Comput. Electr. Eng. 2021, 94, 107328. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Hui, X.; Guangbin, C.; Shengxiu, Z.; Xiaogang, Y.; Mingzhe, H. Hypersonic reentry trajectory optimization by using improved sparrow search algorithm and control parametrization method. Adv. Space Res. 2022, 69, 2512–2524. [Google Scholar] [CrossRef]
- Li, Y.; Han, M.; Guo, Q. Modified Whale Optimization Algorithm Based on Tent Chaotic Mapping and Its Application in Structural Optimization. KSCE J. Civ. Eng. 2020, 24, 3703–3713. [Google Scholar] [CrossRef]
- Ma, J.; Hao, Z.; Sun, W. Enhancing sparrow search algorithm via multi-strategies for continuous optimization problems. Inf. Process. Manag. 2022, 59, 102854. [Google Scholar] [CrossRef]
- Zhou, S.; Xie, H.; Zhang, C.; Hua, Y.; Zhang, W.; Chen, Q.; Gu, G.; Sui, X. Wavefront-shaping focusing based on a modified sparrow search algorithm. Optik 2021, 244, 167516. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).