Discrete Element Simulations of Contact Heat Transfer on a Batch-Operated Single Floor of a Multiple Hearth Furnace
Abstract
:1. Introduction
2. Discrete Element Method and Contact Heat Transfer Model
2.1. DEM
2.2. Contact Heat Transfer Model
3. Experimental Setup
4. Results and Discussion
4.1. Validation of Particle Mechanics
4.2. Numerical Results after Correction for Heat Loss
5. Conclusions and Future Work
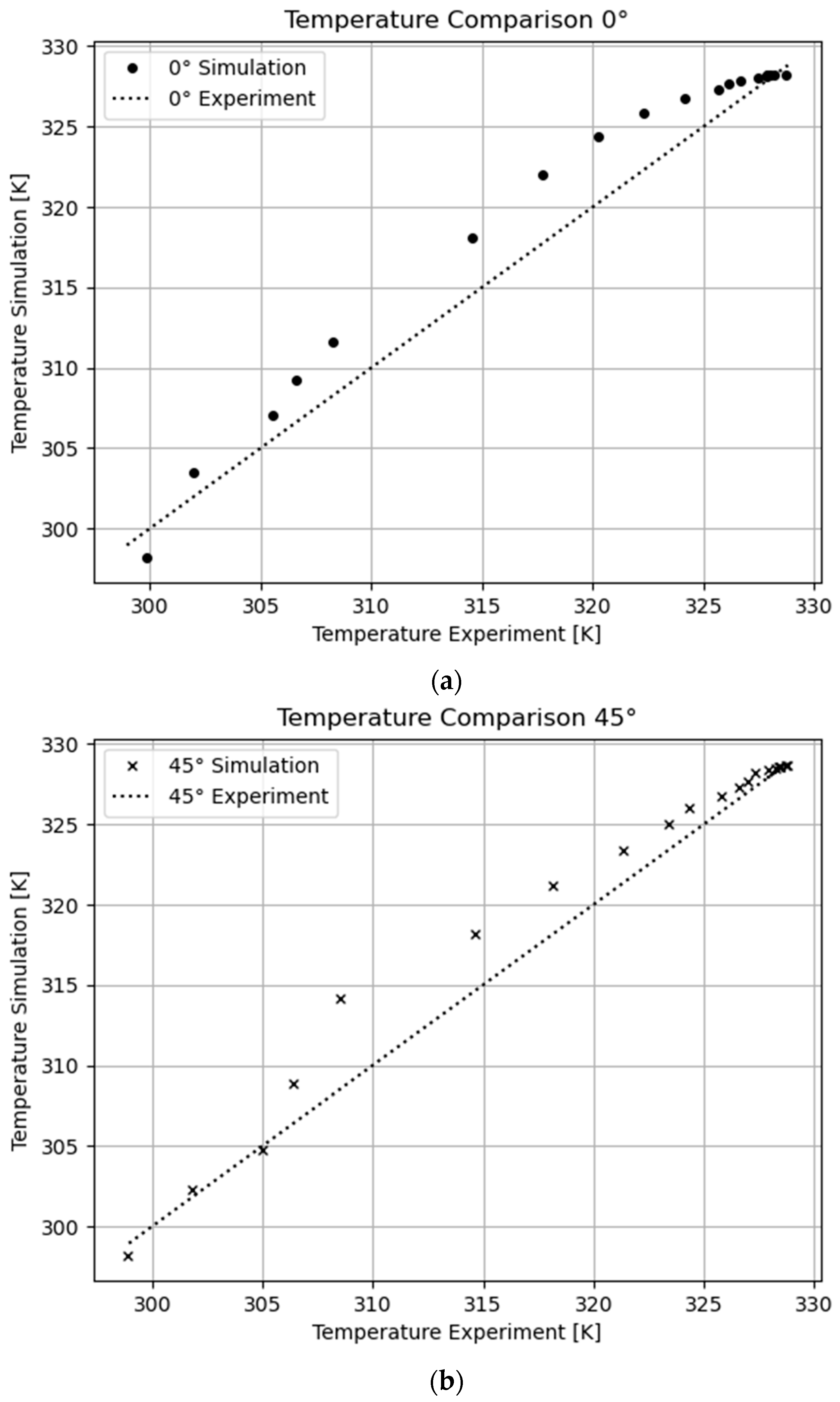
- A costly DEM-CFD coupling can be avoided for the present setup. The heat loss parameter derived for DEM allows us to predict the temperature evolution of the particles for all angular positions of the blades in good agreement with the values taken from the experiments.
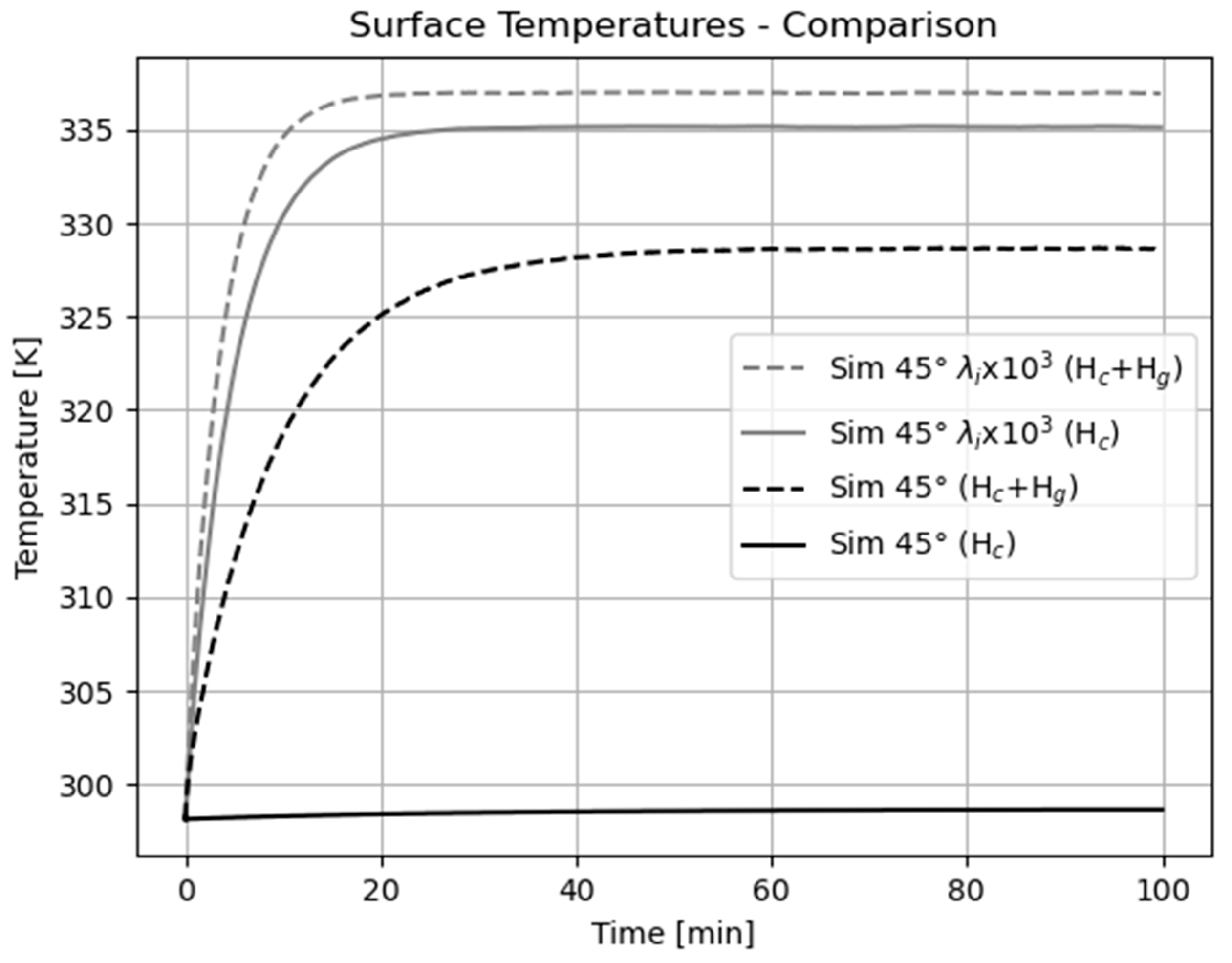
- Particle–floor contact heat transfer clearly dominates over particle–particle heat transfer. Furthermore, it turned out that for low thermal conductivity POM particles, the heat transfer through the gas layer in the vicinity of the contact point of the particles with the floor is much larger than the direct heat transfer through solid–solid contact. This behaviour changes for high thermal conductivity materials such as aluminium, where solid–solid-contact heat transfer cannot be neglected. Changes may also occur at higher temperatures when radiative transport becomes important.
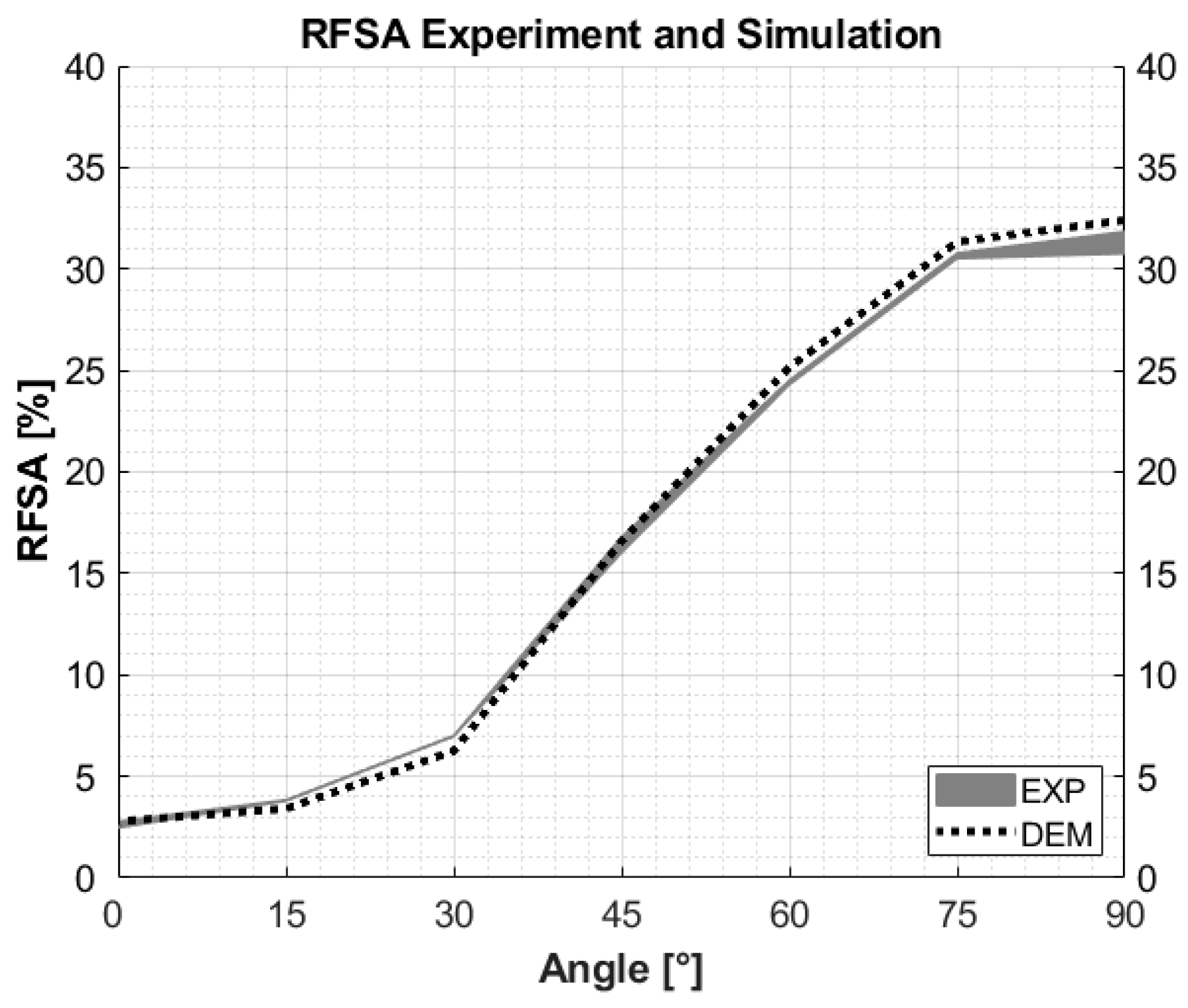
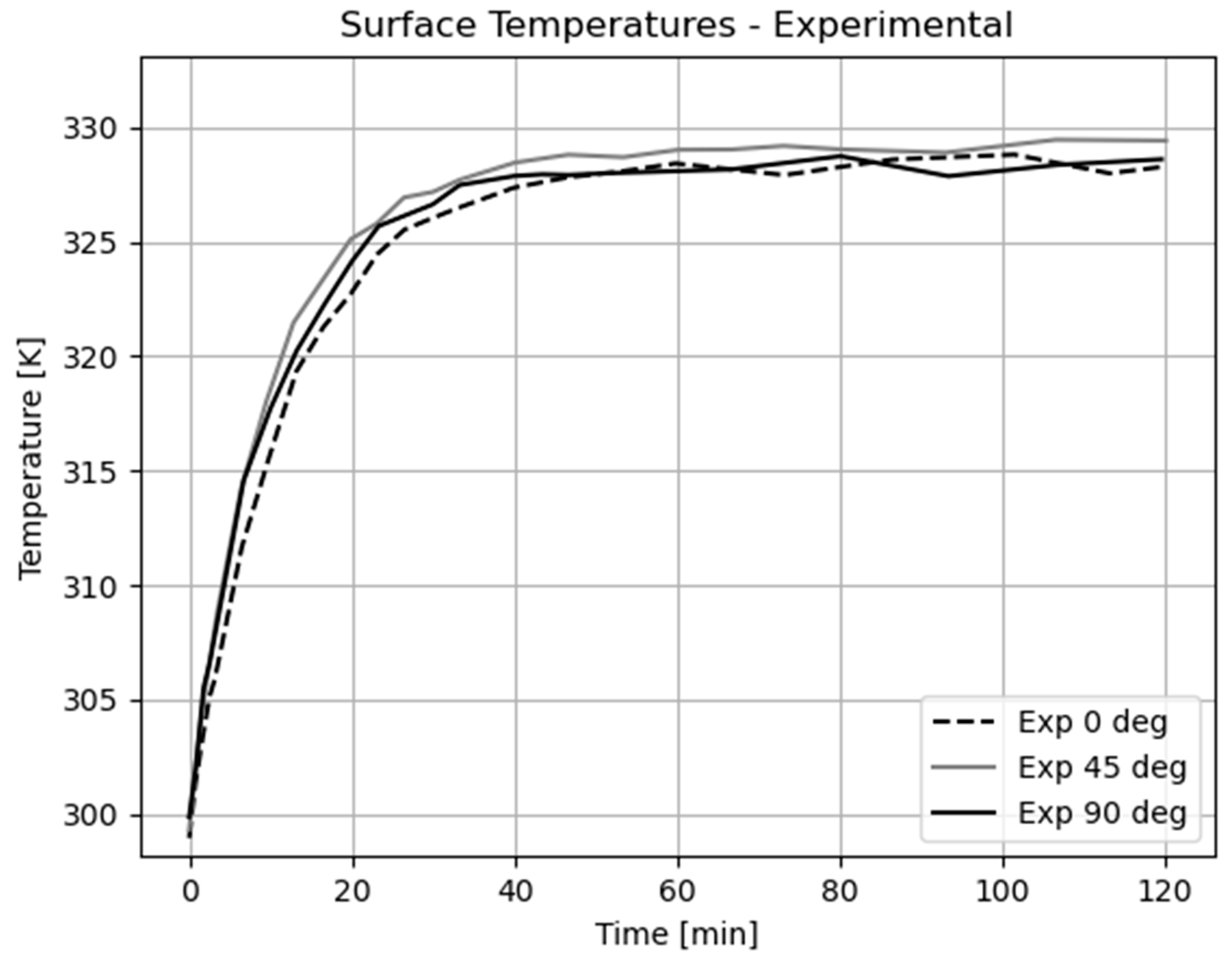
- The blade angle has hardly any influence on the temporal evolution of the particle temperatures. This is due to two opposite effects. As the blade angle increases, the heat transfer from the plate to the spheres is reduced, since the number of spheres in direct contact with the hot floor is smaller. This occurs due to the accumulation of the particles upstream of the blades. This accumulation simultaneously causes the convective heat loss to be reduced, as the surface area of the bulk exposed to the surrounding gas is reduced. These two effects seem to balance each other.
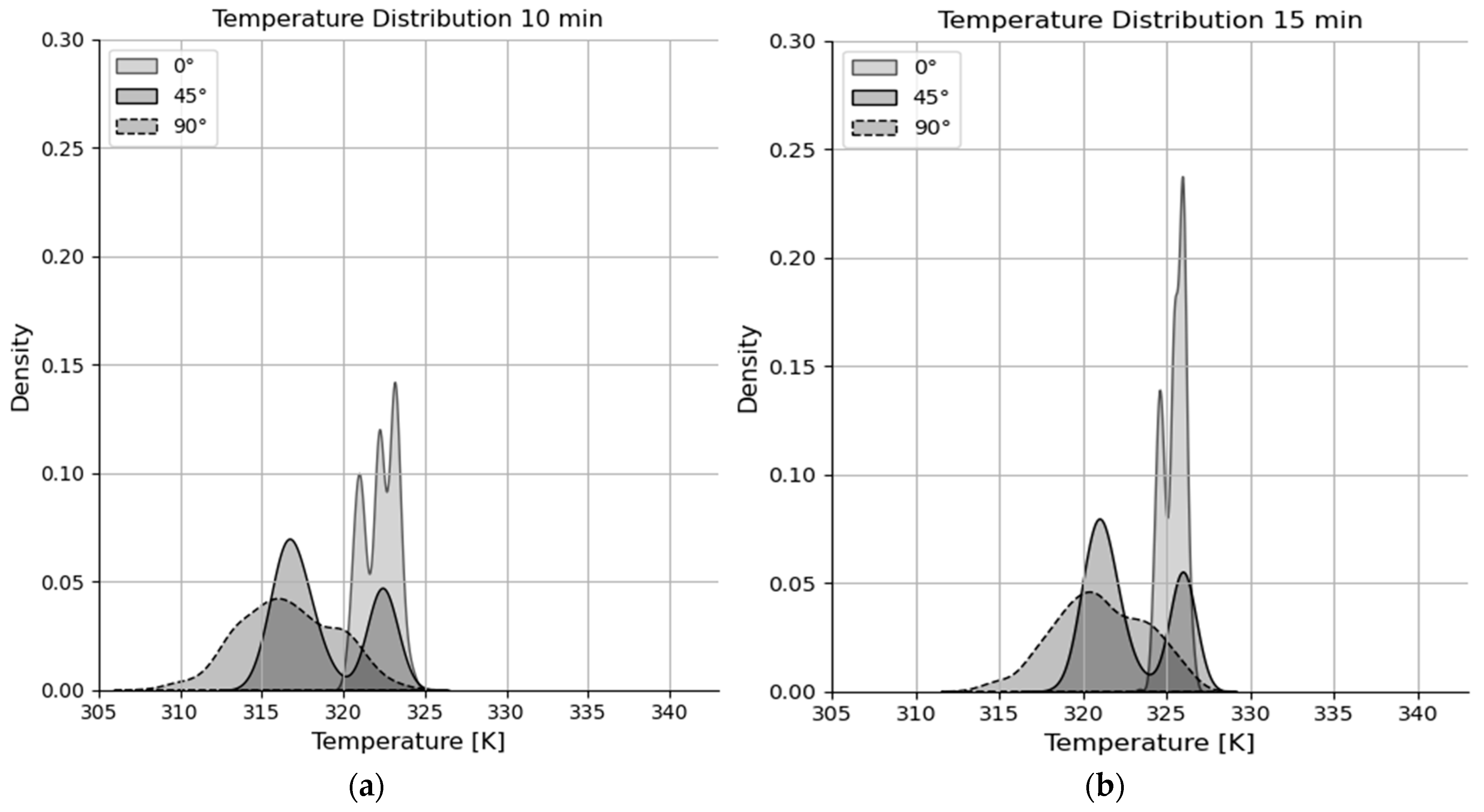
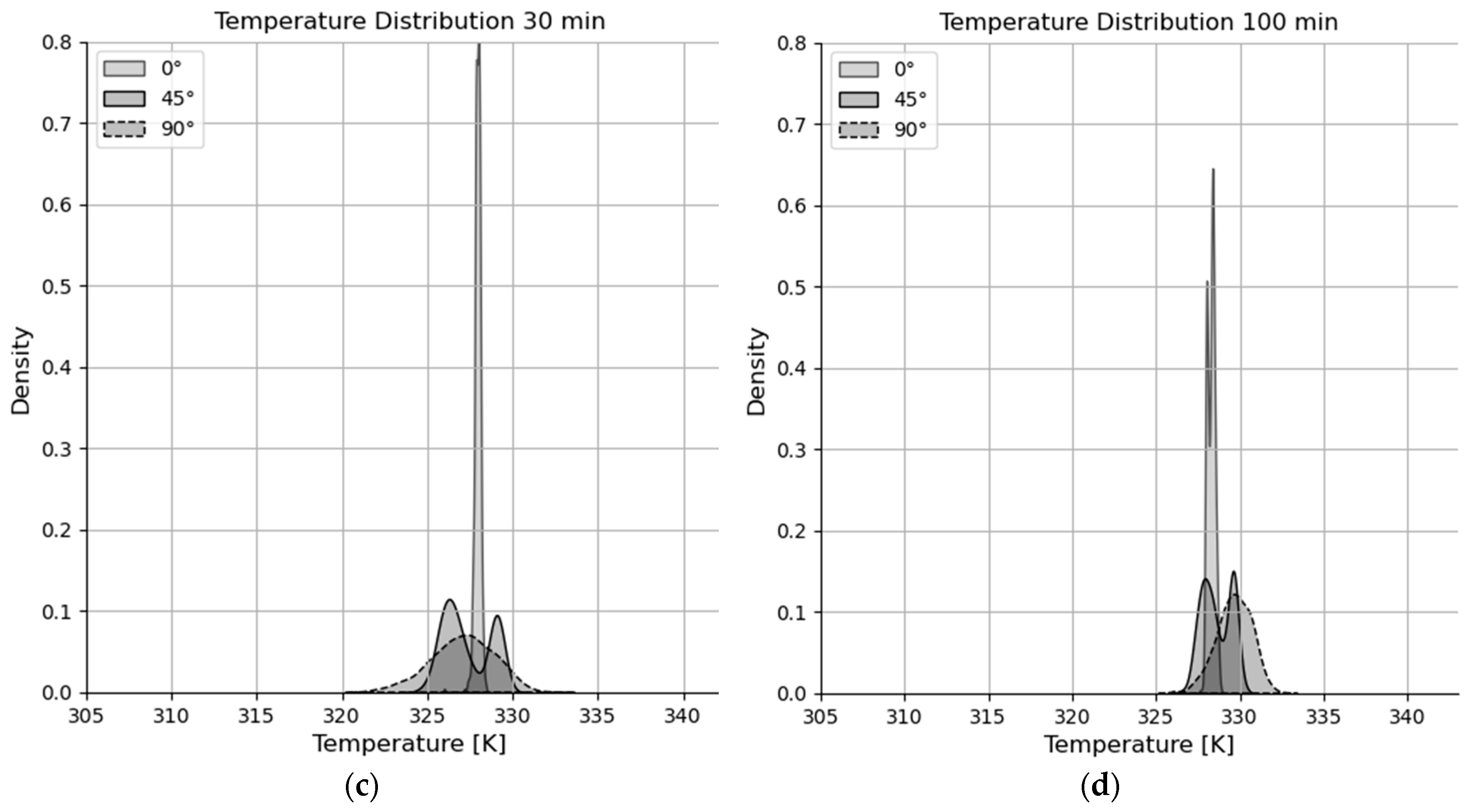
- The frequency distribution of particle temperature depends on the blade angle. The standard deviation increases with the blade angle, and for a 45° blade angle a bimodal frequency distribution develops, whereas for the 0° and 90° blade angles monodisperse frequency distributions prevail.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviations | ||
| CFD | computational fluid dynamics | |
| DEM | Discrete Element Method | |
| IR | infrared | |
| POM | polyoxymethylene | |
| RFSA | relative free surface area | |
| Latin Symbols | ||
| A | area | [m2] |
| ac | contact radius | [mm] |
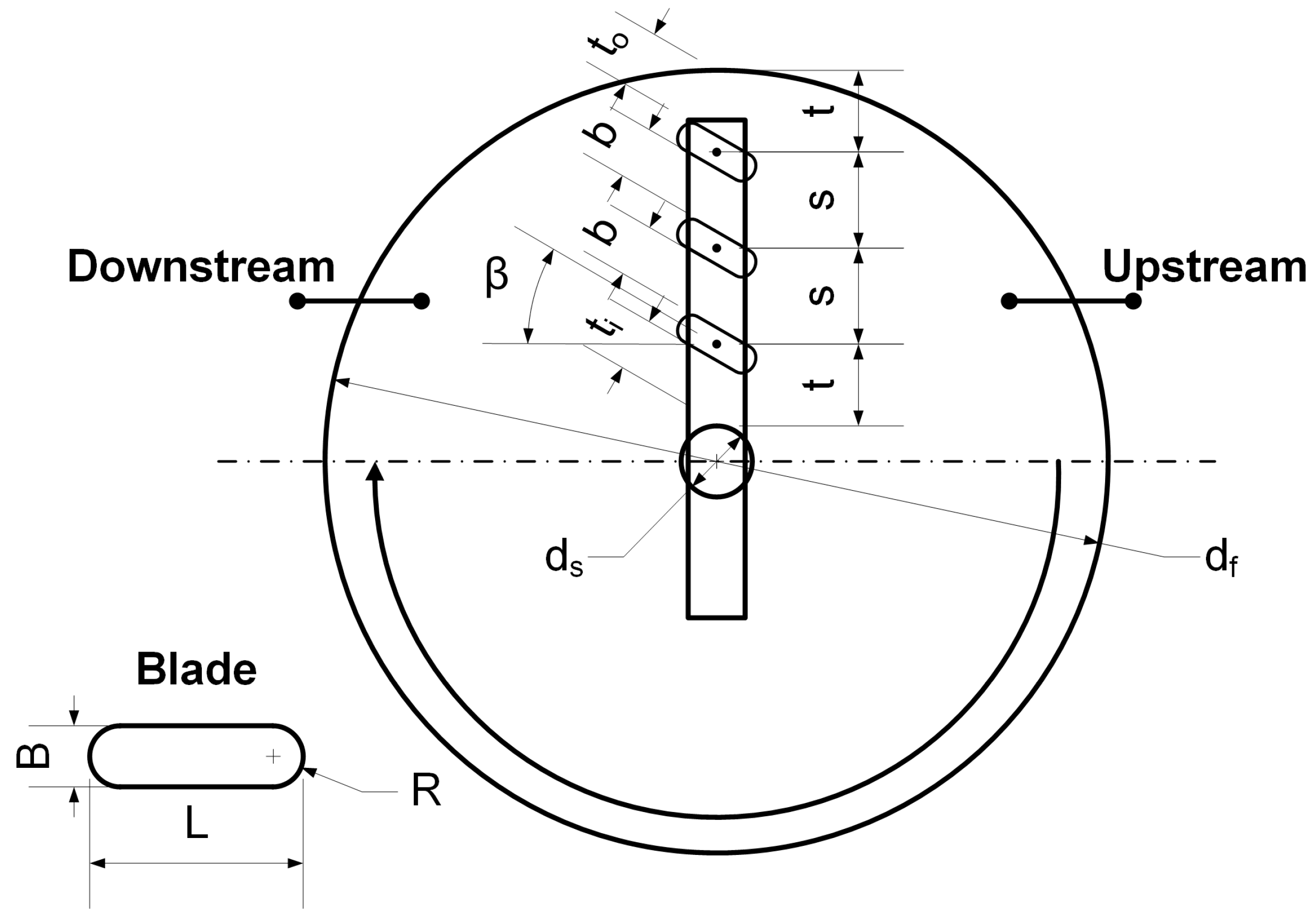
| B | blade thickness | [mm] |
| b | passage width between blades | [mm] |
| df | floor diameter | [mm] |
| dp | particle diameter | [mm] |
| ds | shaft diameter | [mm] |
| E | Young’s modulus | |
| en | coefficient of restitution | [-] |
| FA | visible floor surface area | [m2] |
| FA0 | initially visible floor surface area | [m2] |
| external force induced by particles/walls | [N] | |
| normal force | [N] | |
| tangential force | [N] | |
| G | shear modulus | |
| H | conductance | |
| k | linear spring stiffness | |
| L | blade length | [mm] |
| l | length | [mm] |
| external momentum induced by particles/walls | [Nm] | |
| rolling friction torque | [Nm] | |
| m | mass | [kg] |
| heat flow | [W] | |
| R | blade ends radius | [mm] |
| rolling radius | [mm] | |
| r | radius | [mm] |
| s | blade spacing distance | [mm] |
| t | spacing between blade—central shaft/blade—steel blanket | [mm] |
| tn | collision time | [s] |
| relative velocity | ||
| Greek Symbols | ||
| α | heat transfer coefficient | |
| β | blade angle | [degree] |
| γn | damping coefficient | [kg/s] |
| δ | virtual overlap | [mm] |
| emissivity | [-] | |
| Θ | moment of inertia | |
| thermal conductivity | ||
| Coulomb friction | [-] | |
| rolling friction | [-] | |
| Poisson’s ratio | [-] | |
| tangential displacement | [m] | |
| standard deviation | [K] | |
| relative angular velocity | ||
| Subscripts | ||
| c | contact | |
| eff | effective | |
| fl | floor | |
| g | gas | |
| i | index variable | |
| j | index variable | |
Appendix A. DEM Force Models
| Sphere– Sphere | Sphere– Plate/Wall | Sphere– Blade/Shaft | ||
|---|---|---|---|---|
| Coefficient of restitution | [-] | 0.85 | 0.75 | 0.75 |
| Collision time | [s] | 6 × 10−4 | 6 × 10−4 | 6 × 10−4 |
| Rolling friction | [-] | 0.015 | 0.02 | 0.02 |
| Sliding friction | [-] | 0.3 | 0.3 | 0.25 |
Appendix B. Simulated Quasi-Adiabatic Final Temperatures
| Blade Angle | RFSA [%] | Final Temperatures Quasi-Adiabatic [K] | Percentage of Temperature Decrease [%] |
|---|---|---|---|
| 0° | 2.5 | 343.15 | 0.00 |
| 15° | 3.9 | 342.36 | 1.13 |
| 30° | 6.2 | 341.99 | 1.66 |
| 45° | 16.8 | 341.85 | 1.86 |
| 60° | 25.1 | 341.60 | 2.21 |
| 75° | 30.5 | 341.31 | 2.63 |
| 90° | 30.5 | 341.31 | 2.63 |
References
- Eskelinen, A.; Zakharov, A.; Jämsä-Jounela, S.-L.; Hearle, J. Dynamic modeling of a multiple hearth furnace for kaolin calcination. AIChE J. 2015, 61, 3683–3698. [Google Scholar] [CrossRef]
- Thyssenkrupp: MULTIPOL—Multiple Hearth Furnace. Available online: https://ucpcdn.thyssenkrupp.com/_legacy/UCPthyssenkruppBAIS/assets.files/products___services/mineral_processing/pyroprocessing_systems/product_sheet-multipol-en-webview.pdf (accessed on 11 July 2023).
- Lampe, K.; Grund, G.; Erpelding, R.; Denker, J. Biocoal preparation—Biomass a sustainable fuel for industrial processes. In Proceedings of the 6th European Metallurgical Conference EMC 2011, Aachen, Germany, 26–29 June 2011; Volume 5, pp. 1623–1630. [Google Scholar]
- Liu, X.; Jiang, J. Mass and Heat Transfer in a Continuous Plate Dryer. Dry. Technol. 2004, 22, 1621–1635. [Google Scholar] [CrossRef]
- Siraj, M.S.; Radl, S.; Glasser, B.J.; Khinast, J.G. Effect of blade angle and particle size on powder mixing performance in a rectangular box. Powder Technol. 2011, 211, 100–113. [Google Scholar] [CrossRef]
- Kriegeskorte, M.; Hilse, N.; Spatz, P.; Scherer, V. Experimental study on influence of blade angle and particle size on particle mechanics on a batch-operated single floor of a multiple hearth furnace. Particuology 2023, 85, 224–240. [Google Scholar] [CrossRef]
- Jämsä-Jounela, S.-L.; Gomez Fuentes, J.V.; Hearle, J.; Moseley, D.; Smirnov, A. Control strategy for a multiple hearth furnace in kaolin production. Control Eng. Pract. 2018, 81, 18–27. [Google Scholar] [CrossRef]
- Gomez, F.J.V.; Jämsä-Jounela, S.L. Control Strategy for a Multiple Hearth Furnace. IFAC—PapersOnLine 2018, 51, 189–194. [Google Scholar] [CrossRef]
- Guatame-Garcia, A.; Buxton, M. Framework for Monitoring and Control of the Production of Calcined Kaolin. Minerals 2020, 10, 403. [Google Scholar] [CrossRef]
- Autogenous Roasting of Low-Grade Zinc in Multiple Hearth Furnace at Risdon. Available online: https://www.911metallurgist.com/autogenous-roasting-low-grade-zinc/ (accessed on 11 July 2023).
- Peng, Z.; Doroodchi, E.; Moghtaderi, B. Heat transfer modelling in Discrete Element Method (DEM)-based simulations of thermal processes: Theory and model development. Prog. Energy Combust. Sci. 2020, 79, 100847. [Google Scholar] [CrossRef]
- Tsotsas, E. Particle-particle heat transfer in thermal DEM: Three competing models and a new equation. Int. J. Heat Mass Transf. 2019, 132, 939–943. [Google Scholar] [CrossRef]
- Batchelor, G.K.; O’Brien, R.W. Thermal or electrical conduction through a granular material. Proc. R. Soc. Lond. Ser. A. Math. Phys. Sci. 1977, 355, 313–333. [Google Scholar] [CrossRef]
- Kruggel-Emden, H.; Simsek, E.; Rickelt, S.; Wirtz, S.; Scherer, V. Review and extension of normal force models for the Discrete Element Method. Powder Technol. 2007, 171, 157–173. [Google Scholar] [CrossRef]
- Sun, J.; Chen, M. A theoretical analysis of heat transfer due to particle impact. Int. J. Heat Mass Transf. 1988, 31, 969–975. [Google Scholar] [CrossRef]
- Shi, D.; Vargas, W.L.; McCarthy, J.J. Heat transfer in rotary kilns with interstitial gases. Chem. Eng. Sci. 2008, 63, 4506–4516. [Google Scholar] [CrossRef]
- Schlünder, E.U. Wärmeübergang an bewegte Kugelschüttungen bei kurzfristigem Kontakt. Chem. Ing. Tech. 1971, 43, 651–654. [Google Scholar] [CrossRef]
- Tsotsas, E. M6 Heat Transfer from a Wall to Stagnant and Mechanically Agitated Beds. In VDI Heat Atlas; VDI e. V.: Berlin/Heidelberg, Germany; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1311–1326. [Google Scholar] [CrossRef]
- Weigler, F. Diskrete Untersuchung des Aufheizverhaltens von Partikelschüttungen. Ph.D. Thesis, Otto-von-Guericke-Universität Magdeburg, Magdeburg, Germany, 2012. [Google Scholar] [CrossRef]
- Morris, A.B.; Pannala, S.; Ma, Z.; Hrenya, C.M. A conductive heat transfer model for particle flows over immersed surfaces. Int. J. Heat Mass Transf. 2015, 89, 1277–1289. [Google Scholar] [CrossRef]
- Wang, S.; Luo, K.; Hu, C.; Lin, J.; Fan, J. CFD-DEM simulation of heat transfer in fluidized beds: Model verification, validation, and application. Chem. Eng. Sci. 2019, 197, 280–295. [Google Scholar] [CrossRef]
- Vargas, W.L.; McCarthy, J.J. Heat conduction in granular materials. AIChE J. 2001, 47, 1052–1059. [Google Scholar] [CrossRef]
- Hou, Q.F.; Zhou, Z.Y.; Yu, A.B. Computational study of heat transfer in a bubbling fluidized bed with a horizontal tube. AIChE J. 2012, 58, 1422–1434. [Google Scholar] [CrossRef]
- Cheng, G.J.; Yu, A.B.; Zulli, P. Evaluation of effective thermal conductivity from the structure of a packed bed. Chem. Eng. Sci. 1999, 54, 4199–4209. [Google Scholar] [CrossRef]
- Illana, E.; Merten, H.; Wirtz, S.; Scherer, V. DEM/CFD Simulations of a Generic Oxy-Fuel Kiln for Lime Production. Therm. Sci. Eng. Prog. 2023, 45, 102076. [Google Scholar] [CrossRef]
- Vargas, W.L.; McCarthy, J. Conductivity of granular media with stagnant interstitial fluids via thermal particle dynamics simulation. Int. J. Heat Mass Transf. 2002, 45, 4847–4856. [Google Scholar] [CrossRef]
- Komossa, H.; Wirtz, S.; Scherer, V.; Herz, F.; Specht, E. Heat transfer in indirect heated rotary drums filled with monodisperse spheres: Comparison of experiments with DEM simulations. Powder Technol. 2015, 286, 722–731. [Google Scholar] [CrossRef]
- Beaulieu, C.; Vidal, D.; Yari, B.; Chaouki, J.; Bertrand, F. Impact of surface roughness on heat transfer through spherical particle packed beds. Chem. Eng. Sci. 2021, 231, 116256. [Google Scholar] [CrossRef]
- Hartmanshenn, C.; Chaksmithanont, P.; Leung, C.; Ghare, D.V.; Chakraborty, N.; Patel, S.; Halota, M.; Khinast, J.G.; Papageorgiou, C.D.; Mitchell, C.; et al. Infrared temperature measurements and DEM simulations of heat transfer in a bladed mixer. AIChE J. 2022, 68, e17636. [Google Scholar] [CrossRef]
- Hertz, H. Ueber die Berührung fester elastischer Körper. Crll 1882, 1882, 156–171. [Google Scholar] [CrossRef]
- Rickelt, S. Discrete Element Simulation and Experimental Validation of Conductive and Convective Heat Transfer in Moving Granular Material. In Berichte aus der Energietechnik; Shaker Verlag: Aachen, Germany, 2011. [Google Scholar]
- Fischer, J.; Rodrigues, S.; Kriegeskorte, M.; Hilse, N.; Illana, E.; Scherer, V.; Tsotsas, E. Particle-particle contact heat transfer models in thermal DEM: A model comparison and experimental validation. Powder Technol. 2023, 429, 118909. [Google Scholar] [CrossRef]
- Maxwell, J.C., IV. On the dynamical theory of gases. Philos. Trans. R. Soc. Lond. 1867, 157, 49–88. [Google Scholar] [CrossRef]
- Zhou, Y.C.; Wright, B.D.; Yang, R.Y.; Xu, B.H.; Yu, A.B. Rolling friction in the dynamic simulation of sandpile formation. Phys. A Stat. Mech. Its Appl. 1999, 269, 536–553. [Google Scholar] [CrossRef]






| POM | Aluminium | Steel | Air | ||
|---|---|---|---|---|---|
| Density | [kg/m3] | 1420 | 2700 | 7700 | - |
| Heat capacity | [J/(kgK)] | 1460 | 900 | 466 | - |
| Thermal conductivity | [W/(mK)] | 0.292 | 237 | 50 | 0.0262 |
| Young’s modulus | [Pa] | 3.2 × 109 | 7.0 × 1010 | 2.0 × 1011 | - |
| Poisson’s ratio | [-] | 0.44 | 0.33 | 0.27 | - |
| 4.04 | 3.69 | 3.52 | 2.66 | 2.07 | 1.77 | 1.77 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hilse, N.; Kriegeskorte, M.; Fischer, J.; Spatz, P.; Illana, E.; Schiemann, M.; Scherer, V. Discrete Element Simulations of Contact Heat Transfer on a Batch-Operated Single Floor of a Multiple Hearth Furnace. Processes 2023, 11, 3257. https://doi.org/10.3390/pr11123257
Hilse N, Kriegeskorte M, Fischer J, Spatz P, Illana E, Schiemann M, Scherer V. Discrete Element Simulations of Contact Heat Transfer on a Batch-Operated Single Floor of a Multiple Hearth Furnace. Processes. 2023; 11(12):3257. https://doi.org/10.3390/pr11123257
Chicago/Turabian StyleHilse, Nikoline, Max Kriegeskorte, Jonas Fischer, Phil Spatz, Enric Illana, Martin Schiemann, and Viktor Scherer. 2023. "Discrete Element Simulations of Contact Heat Transfer on a Batch-Operated Single Floor of a Multiple Hearth Furnace" Processes 11, no. 12: 3257. https://doi.org/10.3390/pr11123257
APA StyleHilse, N., Kriegeskorte, M., Fischer, J., Spatz, P., Illana, E., Schiemann, M., & Scherer, V. (2023). Discrete Element Simulations of Contact Heat Transfer on a Batch-Operated Single Floor of a Multiple Hearth Furnace. Processes, 11(12), 3257. https://doi.org/10.3390/pr11123257







