Influence of Positive Guide Vane Geometric Parameters on the Head-Flow Curve of the Multistage Pump as Turbine
Abstract
:1. Introduction
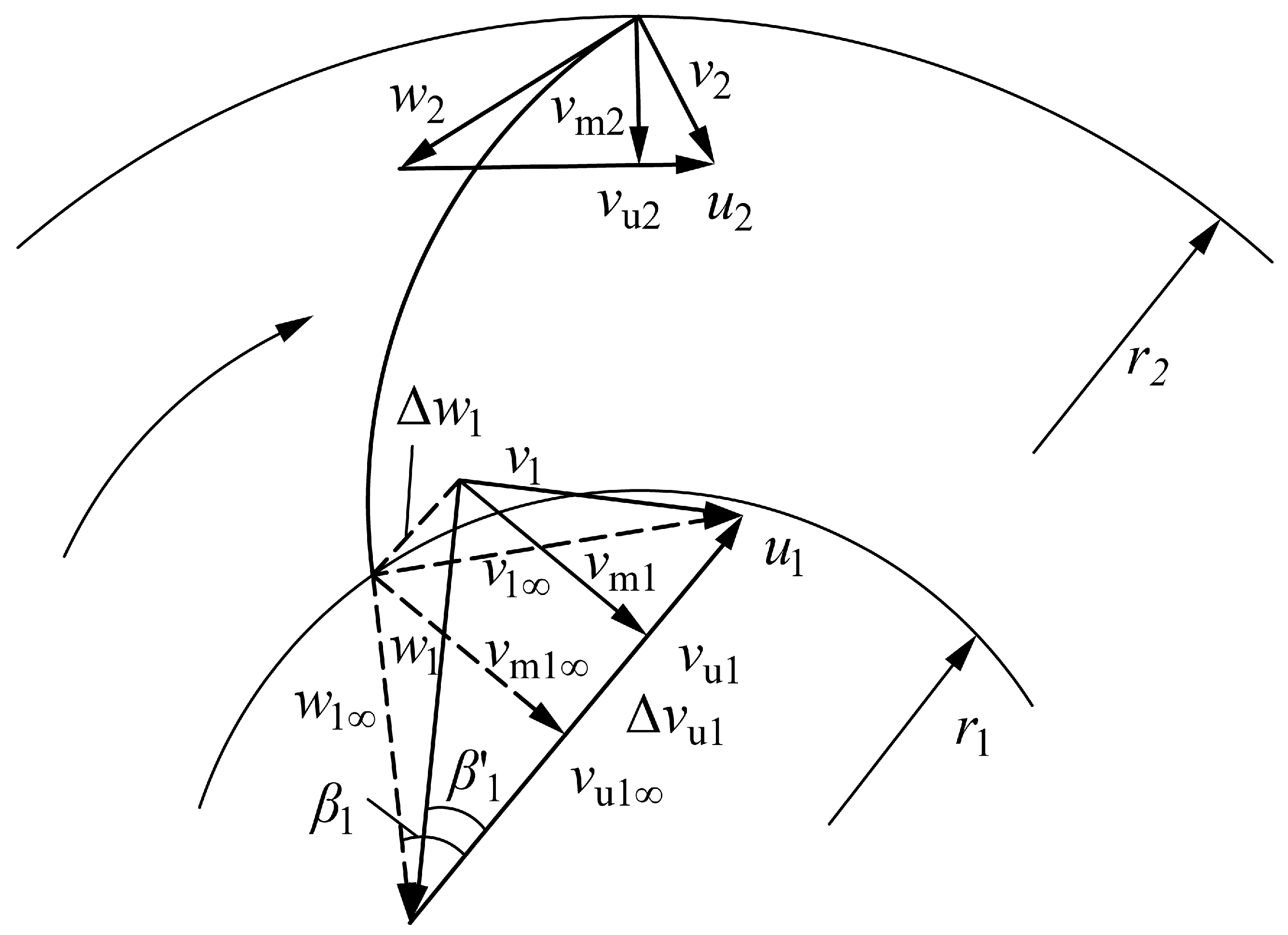
2. Theoretical Analysis
2.1. Derivation of the Theoretical Head of Guide Vane PAT
2.2. Flatness Analysis of H-Q Curve of Guide Aane PAT
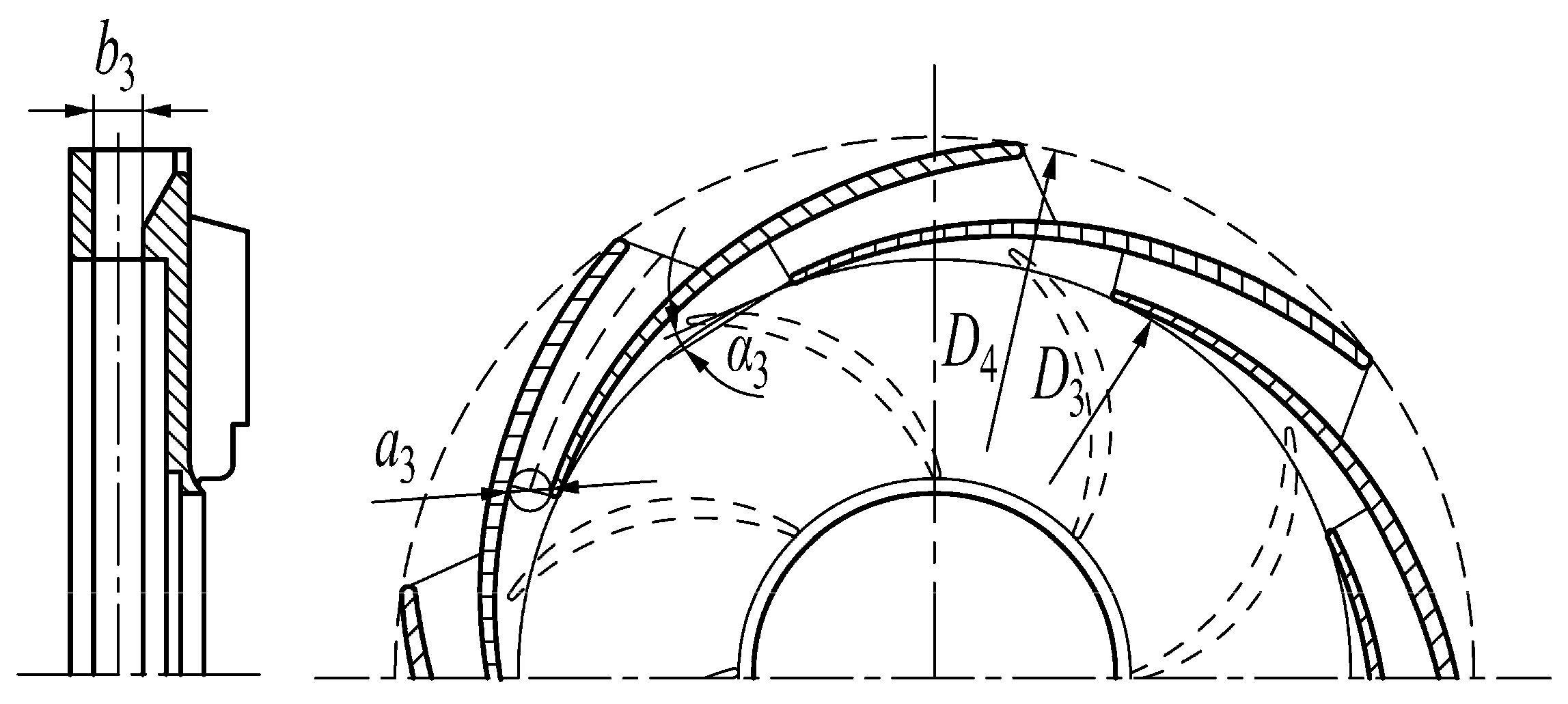
3. Original PAT and Scheme Design
4. Numerical Investigation
4.1. CFD Model
4.2. Solution Parameters
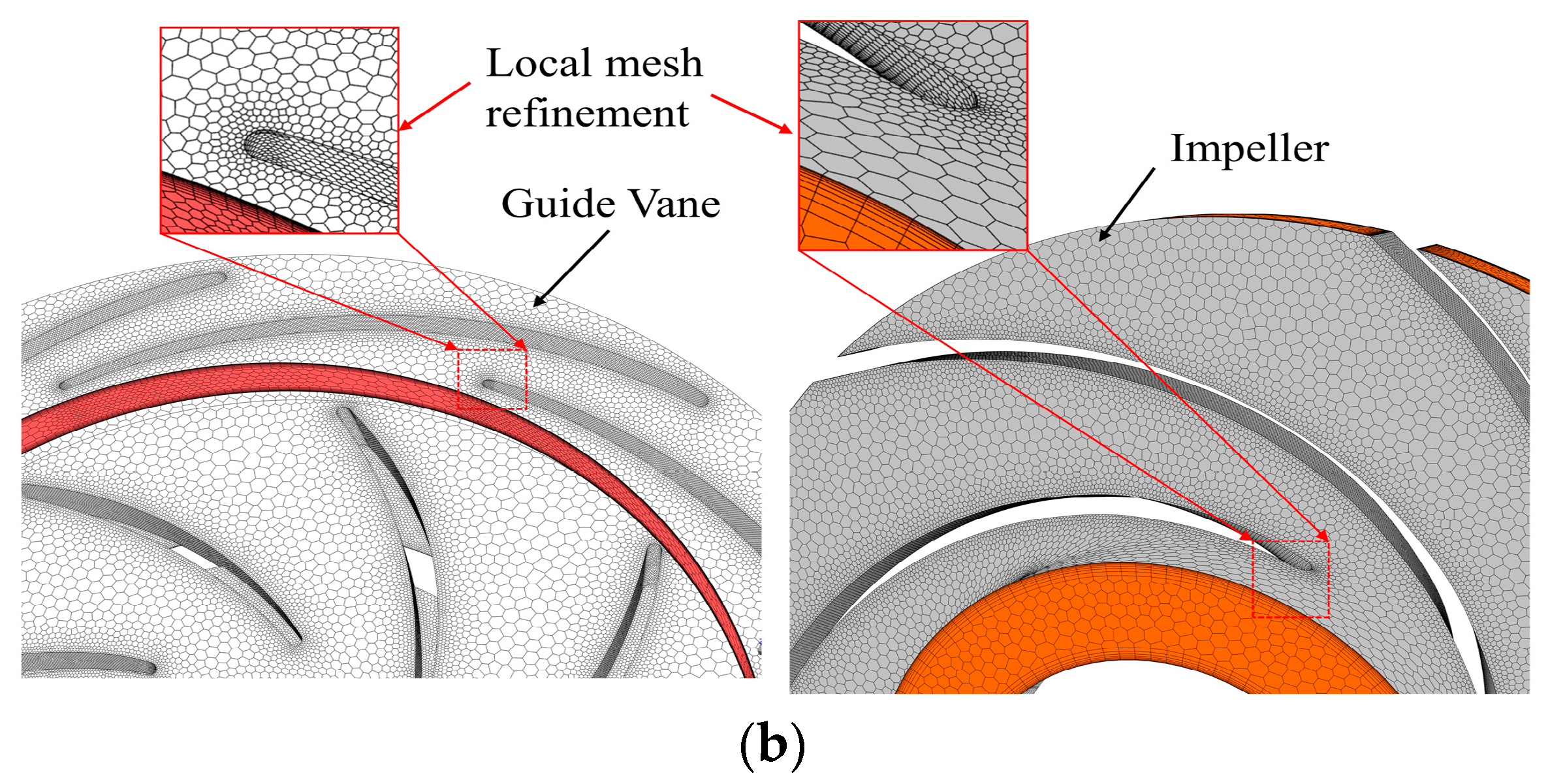
4.3. Mesh Independence Test
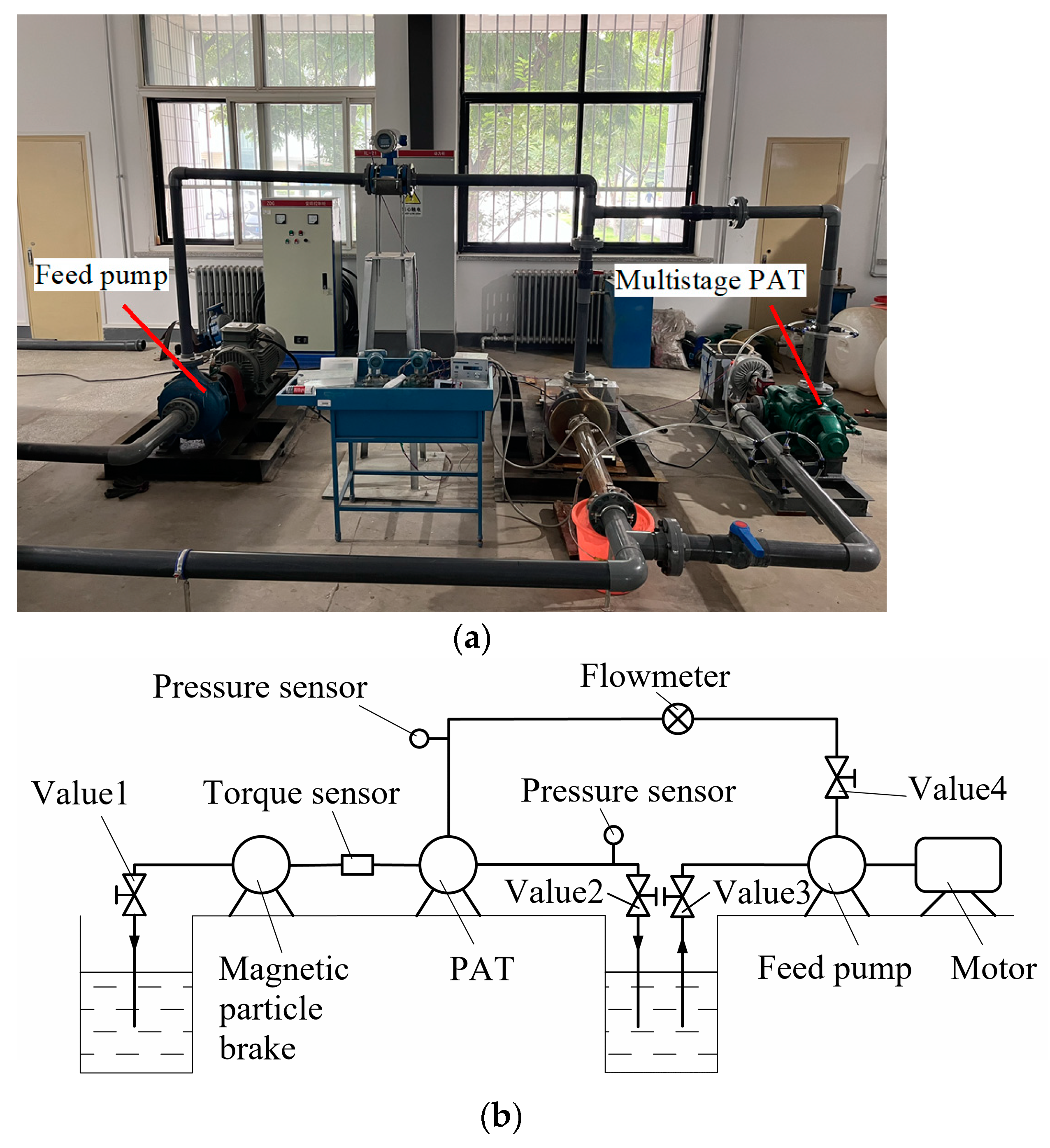
4.4. Experimental Research
5. Results and Discussion
6. Conclusions
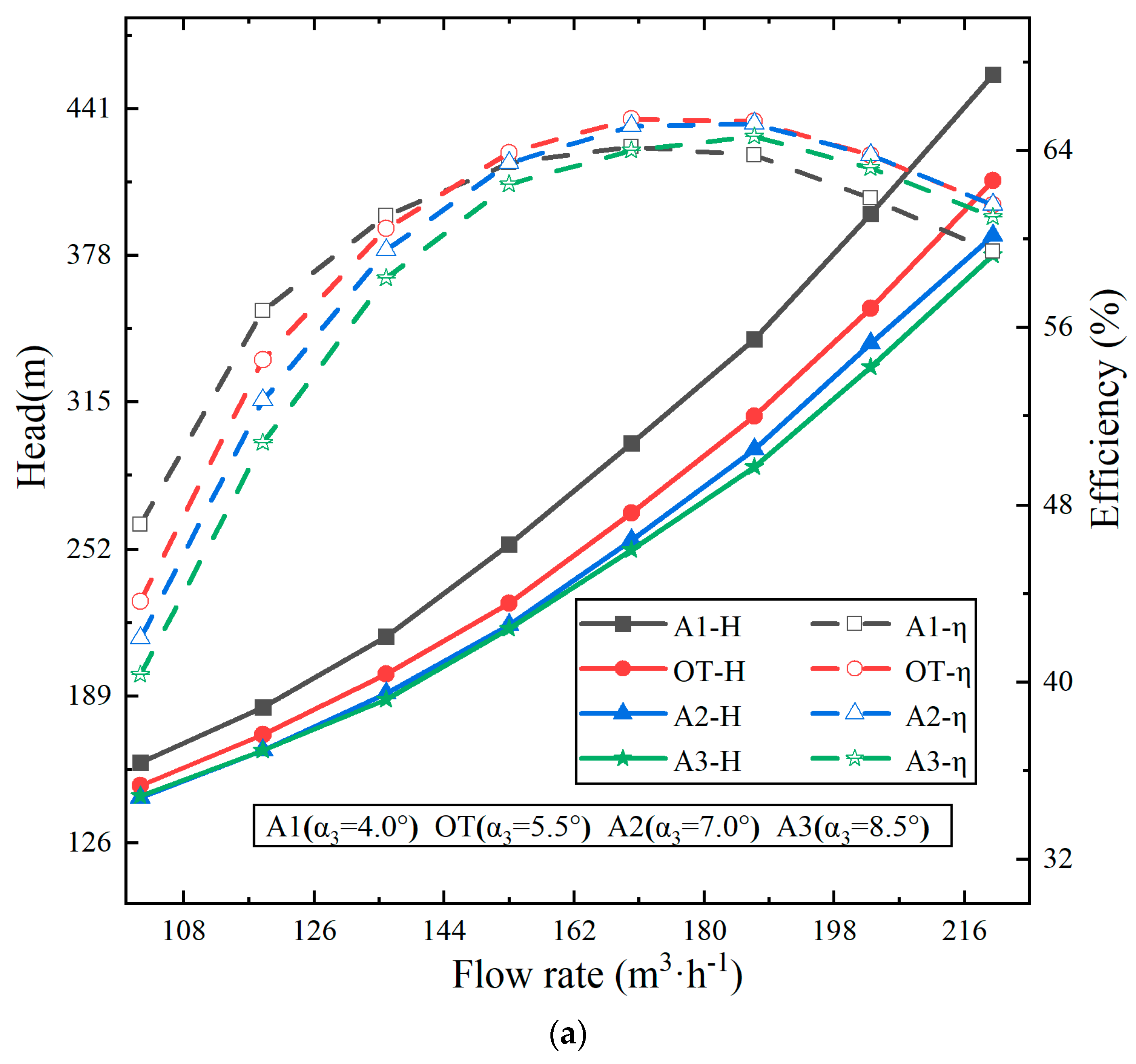
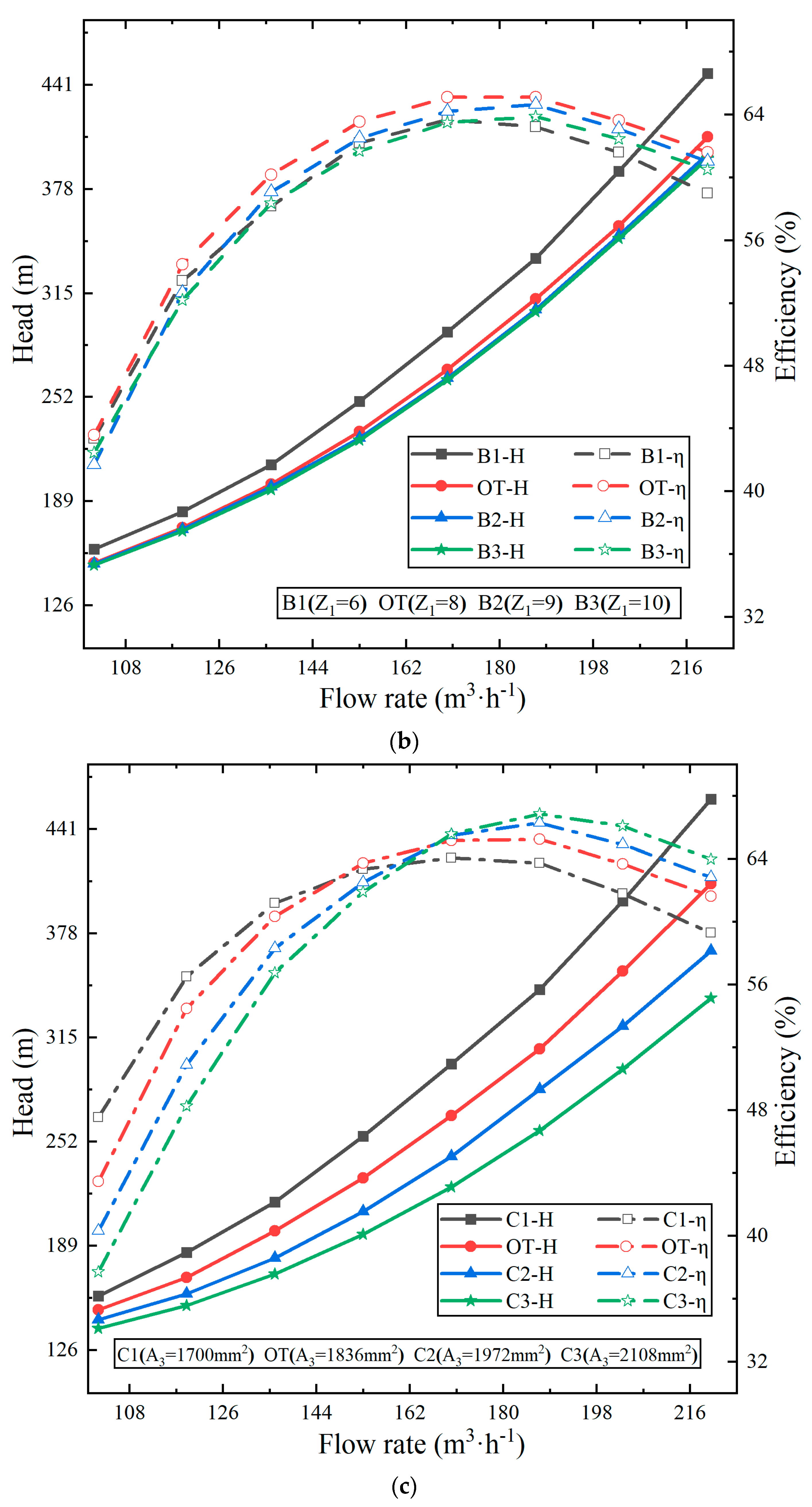
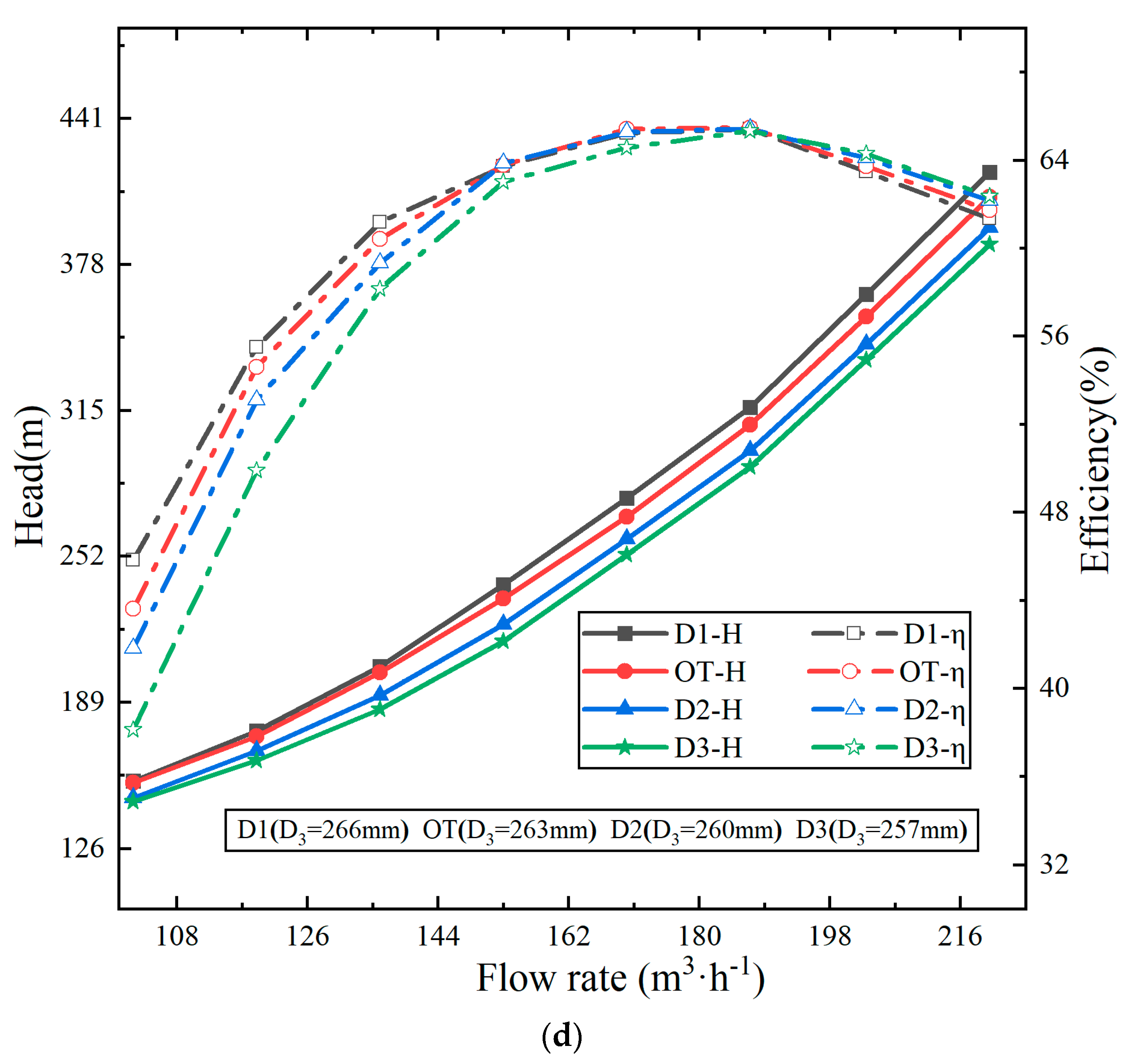
- As a result of the theoretical derivation, the turbine H-Q curve was able to be flattened by appropriately increasing the outlet placement angle, the number of blades and the throat area of the radial guide vane, or by reducing the base circle diameter of the guide vane.
- The positive guide vane throat area exerted the most significant impact on the slope of the H-Q curve, succeeded by the positive guide vane outlet angle, the positive guide vane blade number, and the diameter of the positive guide vane base circle. For the example of the two-stage PAT in this paper, the individual contributions to reducing the slope were 0.53, 0.24, 0.1, and 0.09.
- Increasing the positive guide vane throat area appropriately was able to enhance the efficiency of a multistage PAT, with the BEP shifting towards high flow rates. However, in other cases, the BEP all decreased.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A3 | Guide vane throat area (m2) |
| b | Flow passage width (m) |
| D | Diameter (m) |
| Z | Blade number |
| g | Gravitational acceleration (m/s2) |
| H | Head (m) |
| Q | Flow rate (m3/s) |
| Qd | Flow rate at design-point (m3/s) |
| r | Radius (m) |
| n | Rotation speed (rpm) |
| v | Absolute velocity (m/s) |
| w | Relative velocity (m/s) |
| Δw | Slip of w (m/s) |
| u | Peripheral velocity (m/s) |
| vu | Peripheral component of velocity (m/s) |
| vm | Meridian component of velocity (m/s) |
| Δvu | Slip of vu (m/s) |
| Su | Blade thickness |
| Z0 | Impeller blade number |
| Greeks | |
| α | Absolute flow angle (°) |
| β | Blade angle (°) |
| β′ | Relative flow angle (°) |
| λ | Slip factor |
| η | Efficiency |
| ψ | Blade crowding coefficient |
| Subscripts | |
| 1 | At the impeller outlet |
| 2 | At the impeller inlet |
| 3 | At the guide vane outlet |
| 4 | At the guide vane inlet |
| t | Theoretical |
| ∞ | Infinite blade number |
| Abbreviations | |
| CFD | Computational fluid dynamics |
| PAT | Pump as turbine |
| OT | Original pump as turbine |
References
- Renzi, M.; Rudolf, P.; Stefan, D.; Nigro, A.; Rossi, M. Installation of an axial Pump-as-Turbine (PaT) in a wastewater sewer of an oil refinery: A case study. Appl. Energy 2019, 250, 665–676. [Google Scholar] [CrossRef]
- Hayder, G.; Ramli, M.Z.; Malek, M.A.; Khamis, A.; Hilmin, N.M. Prediction model development for petroleum refinery wastewater treatment. J. Water Process Eng. 2014, 4, 1–5. [Google Scholar] [CrossRef]
- Williams, A. The turbine performance of centrifugal pumps: A comparison of prediction methods. Proc. Inst. Mech. Eng. Part A J. Power 1994, 208, 59–66. [Google Scholar] [CrossRef]
- Huang, S.; Qiu, G.; Su, X.; Chen, J.; Zou, W. Performance prediction of a centrifugal pump as turbine using rotor-volute matching principle. Renew. Energy 2017, 108, 64–71. [Google Scholar] [CrossRef]
- Tan, X.; Engeda, A. Performance of centrifugal pumps running in reverse as turbine: Part Ⅱ-systematic specific speed and specific diameter based performance prediction. Renew. Energy 2016, 99, 188–197. [Google Scholar] [CrossRef]
- Balacco, G. Performance Prediction of a Pump as Turbine: Sensitivity Analysis Based on Artificial Neural Networks and Evolutionary Polynomial Regression. Energies 2018, 11, 3497. [Google Scholar] [CrossRef]
- Derakhshan, S.; Nourbakhsh, A. Theoretical, numerical and experimental investigation of centrifugal pumps in reverse operation. Exp. Therm. Fluid Sci. 2008, 32, 1620–1627. [Google Scholar] [CrossRef]
- Liu, M.; Tan, L.; Cao, S. Theoretical model of energy performance prediction and BEP determination for centrifugal pump as turbine. Energy 2019, 172, 712–732. [Google Scholar] [CrossRef]
- Novara, D.; McNabola, A. A model for the extrapolation of the characteristic curves of pumps as turbines from a datum best efficiency point. Energy Convers. Manag. 2018, 174, 1–7. [Google Scholar] [CrossRef]
- Li, W.-G. Optimising prediction model of centrifugal pump as turbine with viscosity effects. Appl. Math. Model. 2017, 41, 375–398. [Google Scholar] [CrossRef]
- Wang, X.; Kuang, K.; Wu, Z.; Yang, J. Numerical Simulation of Axial Vortex in a Centrifugal Pump as Turbine with S-Blade Impeller. Processes 2020, 8, 1192. [Google Scholar] [CrossRef]
- Yang, S.-S.; Liu, H.-L.; Kong, F.-Y.; Dai, C.; Dong, L. Experimental, numerical, and theoretical research on impeller diameter influencing centrifugal pump-as-turbine. J. Energy Eng. 2013, 139, 299–307. [Google Scholar] [CrossRef]
- Jain, S.V.; Swarnkar, A.; Motwani, K.H.; Patel, R.N. Effects of impeller diameter and rotational speed on performance of pump running in turbine mode. Energy Convers. Manag. 2015, 89, 808–824. [Google Scholar] [CrossRef]
- Zhou, W.; Yu, D.; Wang, Y.; Shi, J.; Gan, B. Research on the fluid-induced excitation characteristics of the centrifugal pump considering the compound whirl effect. Facta Univ. Ser. Mech. Eng. 2023, 21, 223–238. [Google Scholar] [CrossRef]
- Shi, F.; Yang, J.; Wang, X. Analysis on the effect of variable guide vane numbers on the performance of pump as turbine. Adv. Mech. Eng. 2018, 10, 1687814018780796. [Google Scholar] [CrossRef]
- Doshi, A.; Channiwala, S.; Singh, P. Inlet impeller rounding in pumps as turbines: An experimental study to investigate the relative effects of blade and shroud rounding. Exp. Therm. Fluid Sci. 2017, 82, 333–348. [Google Scholar] [CrossRef]
- Yang, H.; Zhu, L.; Xue, H.; Duan, J.; Deng, F. A Numerical Analysis of the Effect of Impeller Rounding on Centrifugal Pump as Turbine. Processes 2021, 9, 1673. [Google Scholar] [CrossRef]
- Wang, K.J.; Wang, S.L.; Meng, P.Y.; Wang, C.P.; Li, Y.H.; Zheng, W.X.; Liu, J.; Kou, J.W. Strategies employed in the design and optimization of pump as turbine runner. Renew. Energy 2023, 216, 119080. [Google Scholar] [CrossRef]
- Jiang, B.X.; Yang, J.H.; Wang, X.H.; Miao, S.C.; Bai, X.B. Optimization of pumps as turbines blades based on SVM-HDMR model and PSO algorithm. Adv. Mech. Eng. 2021, 13, 16878140211034364. [Google Scholar] [CrossRef]
- Miao, S.C.; Zhang, H.B.; Wang, T.T.; Wang, X.H.; Shi, F.X. Optimal design of blade in pump as turbine based on multidisciplinary feasible method. Sci. Prog. 2020, 103, 0036850420982105. [Google Scholar] [CrossRef]
- Wang, T.; Wang, C.; Kong, F.; Gou, Q.; Yang, S. Theoretical, experimental, and numerical study of special impeller used in turbine mode of centrifugal pump as turbine. Energy 2017, 130, 473–485. [Google Scholar] [CrossRef]
- Madina, I.; Rollan, N.; Dimitar, K.; Abilikhair, Z.; Aysen, I. Computational and Experimental Study of the Composite Material for the Centrifugal Pump Impellers Manufacturing. J. Appl. Comput. Mech. 2022, 8, 2383–4536. [Google Scholar] [CrossRef]
- Yang, J.H.; Ma, Q.H.; Luo, Y.T.; Ji, Y.Y.; Lin, B.; Li, Z.F. Influence of geometrical parameters on head-flow curve of pump as turbine. Trans. Chin. Soc. Agric. Mach. 2019, 50, 167–172. [Google Scholar] [CrossRef]
- Charbonnier, V.; Enoki, H.; Asano, K.; Kim, H.; Sakaki, K. Tuning the hydrogenation properties of Ti1+yCr2−x MnX laves phase compounds for high pressure metal-hydride compressors. Int. J. Hydrogen Energy 2021, 46, 36369–36380. [Google Scholar] [CrossRef]
- Li, X.; Tao, O.; Lin, Y.; Zhu, Z. Interstage difference and deterministic decomposition of internal unsteady flow in a five-stage centrifugal pump as turbine. Phys. Fluids 2023, 35, 045136. [Google Scholar] [CrossRef]
- Mohammadi, M.; Yasi, M.; Jamali, S.; Hajikandi, H. Experimental Study on Single- and Multi-stage Pump as Turbine on Water Supply Pipelines. Iran. J. Sci. Technol. Trans. Civ. Eng. 2022, 46, 3307–3318. [Google Scholar] [CrossRef]
- Gülich, J.F. Centrifugal Pumps; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Memardezfouli, M.; Nourbakhsh, A. Experimental investigation of slip factors in centrifugal pumps. Exp. Therm. Fluid Sci. 2009, 33, 938–945. [Google Scholar] [CrossRef]
- Kan, K.; Zhang, Q.; Zheng, Y.; Xu, H.; Xu, Z.; Zhai, J.; Muhirwa, A. Investigation into Influence of Wall Roughness on the Hydraulic Characteristics of an Axial Flow Pump as Turbine. Sustainability 2022, 14, 8459. [Google Scholar] [CrossRef]



| Parameter | Value |
|---|---|
| Impeller inlet diameter D2(mm) | 252 |
| Impeller inlet width b2(mm) | 15.5 |
| Blade inlet placement angle βb2(°) | 24 |
| Blade outlet edge width b1(mm) | 19.8 |
| Intermediate streamline blade outlet diameter D1(mm) | 108.7 |
| Intermediate streamline blade outlet placement angle βb1(°) | 25 |
| Blade number Z0 | 7 |
| Positive guide vane number Z1 | 8 |
| Anti-guide vane number Z2 | 8 |
| Positive guide vane outlet placement angle α3 (°) | 5.5 |
| Diameter of base circle of positive guide vane D3(mm) | 263 |
| Radial width of the throat of positive guide vane a3(mm) | 13.5 |
| Axial width of the throat of positive guide vane b3(mm) | 17 |
| Scheme | α3 (°) | Z1 | A3 (mm2) | D3 (mm) | a3 (mm) | b3 (mm) | D4 (mm) |
|---|---|---|---|---|---|---|---|
| OT | 5.5 | 8 | 1836 | 263.0 | 13.5 | 17.0 | 324.0 |
| A1 | 4.0 | 8 | 1836 | 263.0 | 13.5 | 17.0 | 324.8 |
| A2 | 7.0 | 8 | 1836 | 263.0 | 13.5 | 17.0 | 323.2 |
| A3 | 8.5 | 8 | 1836 | 263.0 | 13.5 | 17.0 | 322.4 |
| B1 | 5.5 | 6 | 1836 | 263.0 | 20.6 | 14.9 | 324.0 |
| B2 | 5.5 | 9 | 1836 | 263.0 | 11.4 | 17.9 | 324.0 |
| B3 | 5.5 | 10 | 1836 | 263.0 | 9.8 | 18.7 | 324.0 |
| C1 | 5.5 | 8 | 1700 | 263.0 | 12.5 | 17.0 | 322.8 |
| C2 | 5.5 | 8 | 1972 | 263.0 | 14.5 | 17.0 | 325.2 |
| C3 | 5.5 | 8 | 2108 | 263.0 | 15.5 | 17.0 | 326.4 |
| D1 | 5.5 | 8 | 1836 | 266.0 | 13.5 | 17.0 | 327.0 |
| D2 | 5.5 | 8 | 1836 | 260.0 | 13.5 | 17.0 | 321.0 |
| D3 | 5.5 | 8 | 1836 | 257.0 | 13.5 | 17.0 | 318.0 |
| Case | Mesh Number | Head (m) |
|---|---|---|
| 1 | 3637854 | 260.18 |
| 2 | 5163348 | 267.58 |
| 3 | 6085721 | 268.27 |
| 4 | 7125813 | 267.96 |
| Scheme | dH/dQ | η (%) |
|---|---|---|
| OT | 2.30 | 65.27 |
| A1 | 2.53 | 64.17 |
| A2 | 2.15 | 65.21 |
| A3 | 2.06 | 64.48 |
| B1 | 2.47 | 63.82 |
| B2 | 2.21 | 64.79 |
| B3 | 2.19 | 64.03 |
| C1 | 2.57 | 64.13 |
| C2 | 1.98 | 66.27 |
| C3 | 1.77 | 66.92 |
| D1 | 2.31 | 65.26 |
| D2 | 2.22 | 65.52 |
| D3 | 2.21 | 65.21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Yang, J.; Xu, G. Influence of Positive Guide Vane Geometric Parameters on the Head-Flow Curve of the Multistage Pump as Turbine. Processes 2023, 11, 3393. https://doi.org/10.3390/pr11123393
Wang S, Yang J, Xu G. Influence of Positive Guide Vane Geometric Parameters on the Head-Flow Curve of the Multistage Pump as Turbine. Processes. 2023; 11(12):3393. https://doi.org/10.3390/pr11123393
Chicago/Turabian StyleWang, Shicheng, Junhu Yang, and Guobin Xu. 2023. "Influence of Positive Guide Vane Geometric Parameters on the Head-Flow Curve of the Multistage Pump as Turbine" Processes 11, no. 12: 3393. https://doi.org/10.3390/pr11123393
APA StyleWang, S., Yang, J., & Xu, G. (2023). Influence of Positive Guide Vane Geometric Parameters on the Head-Flow Curve of the Multistage Pump as Turbine. Processes, 11(12), 3393. https://doi.org/10.3390/pr11123393






