Experimental and Numerical Study for Gas Release and Dispersion on Offshore Platforms
Abstract
:1. Introduction
2. Offshore Platform Gas Release and Dispersion Experiments
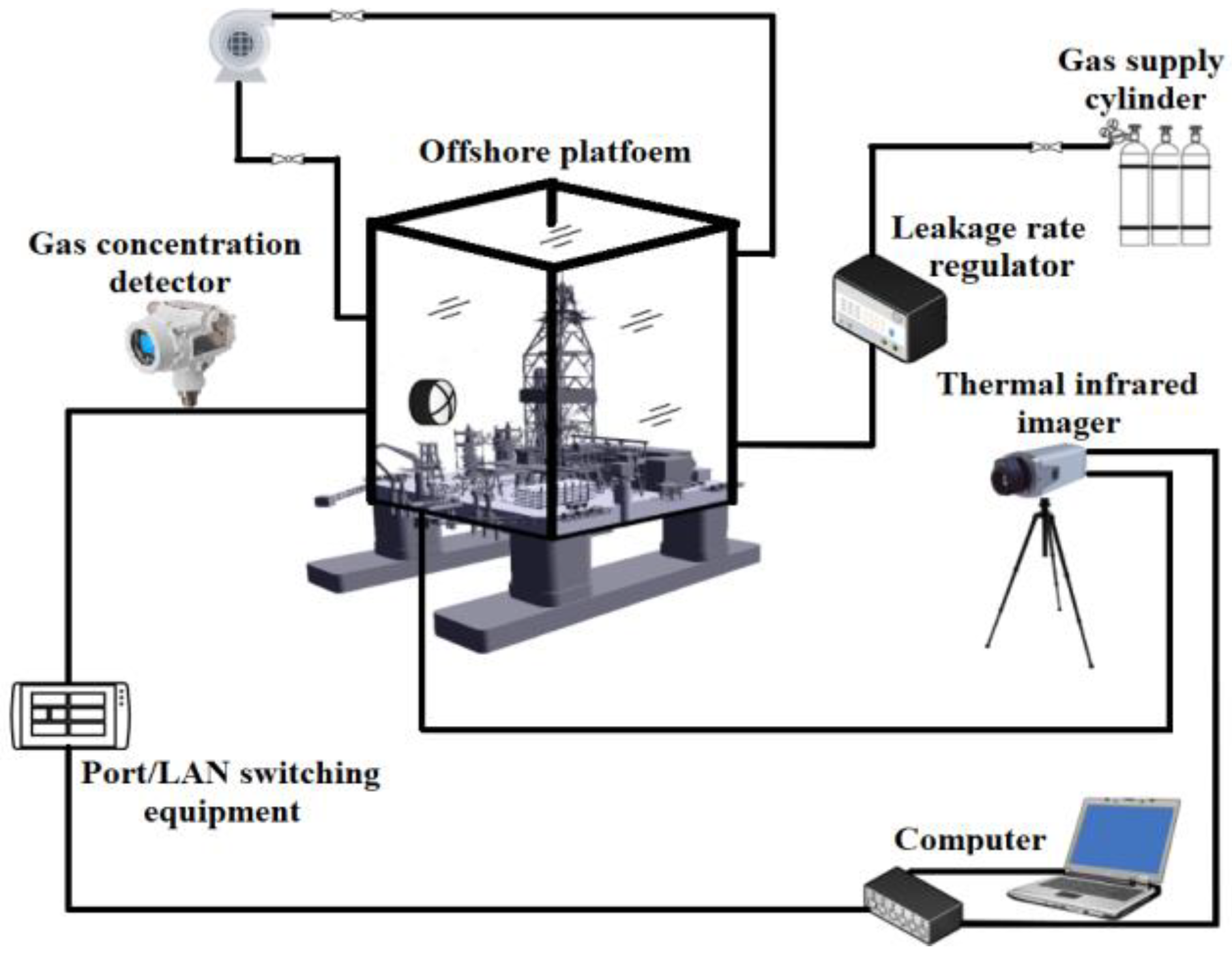
2.1. Experimental Details
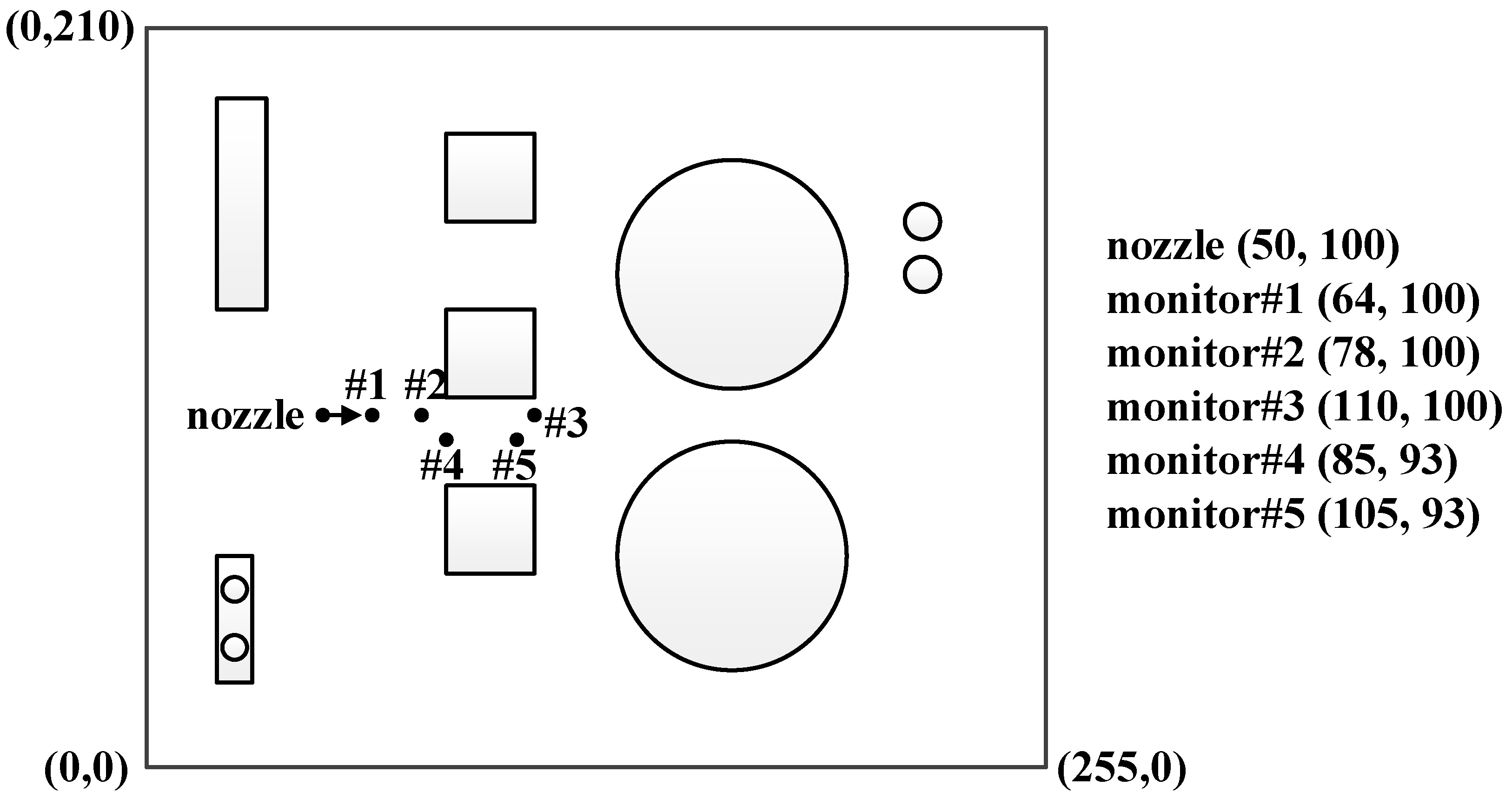
2.1.1. Gas Leakage Module
2.1.2. Data Acquisition Module
2.1.3. Other Experimental Details
2.2. Experimental Results and Discussions
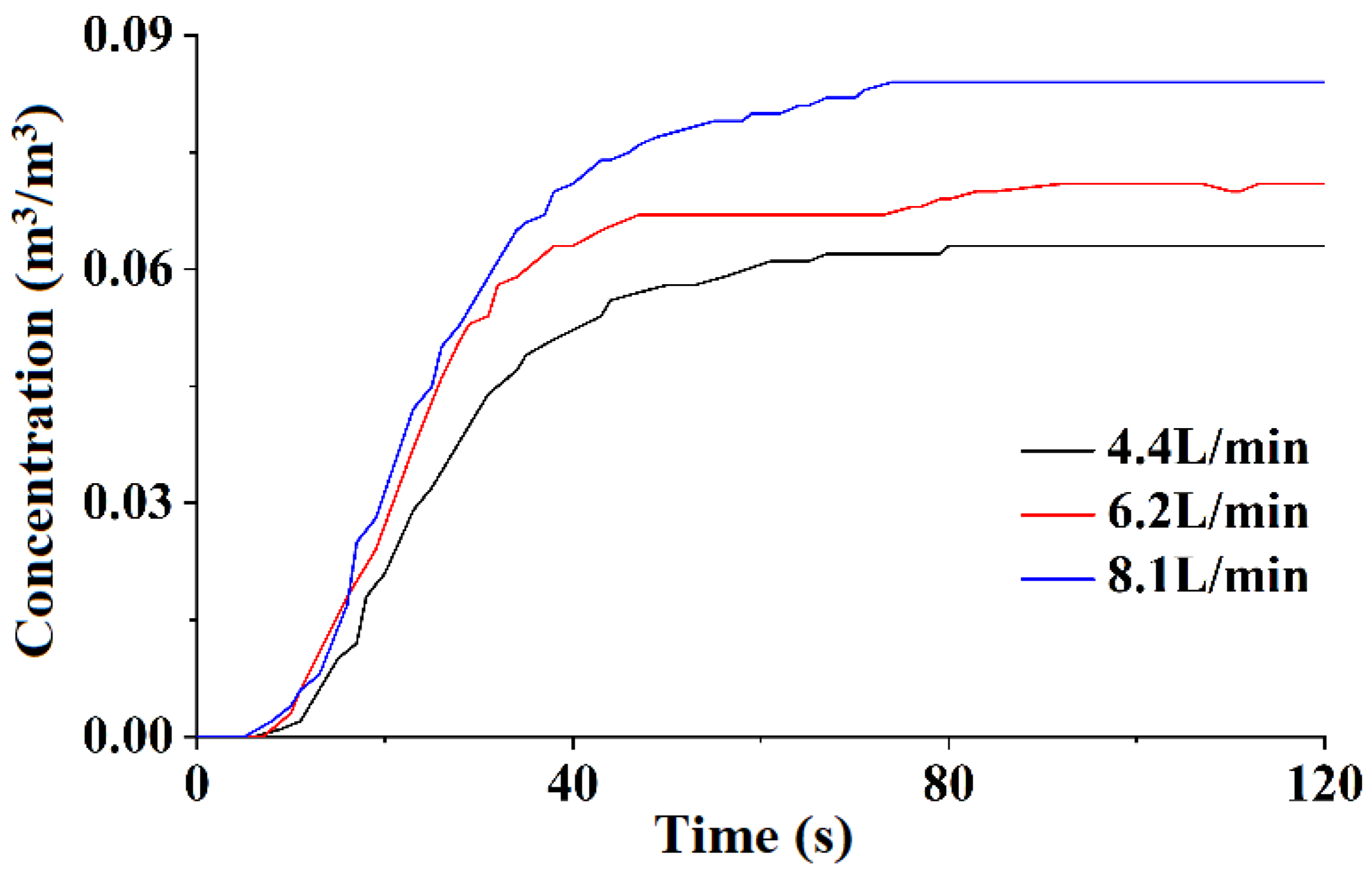
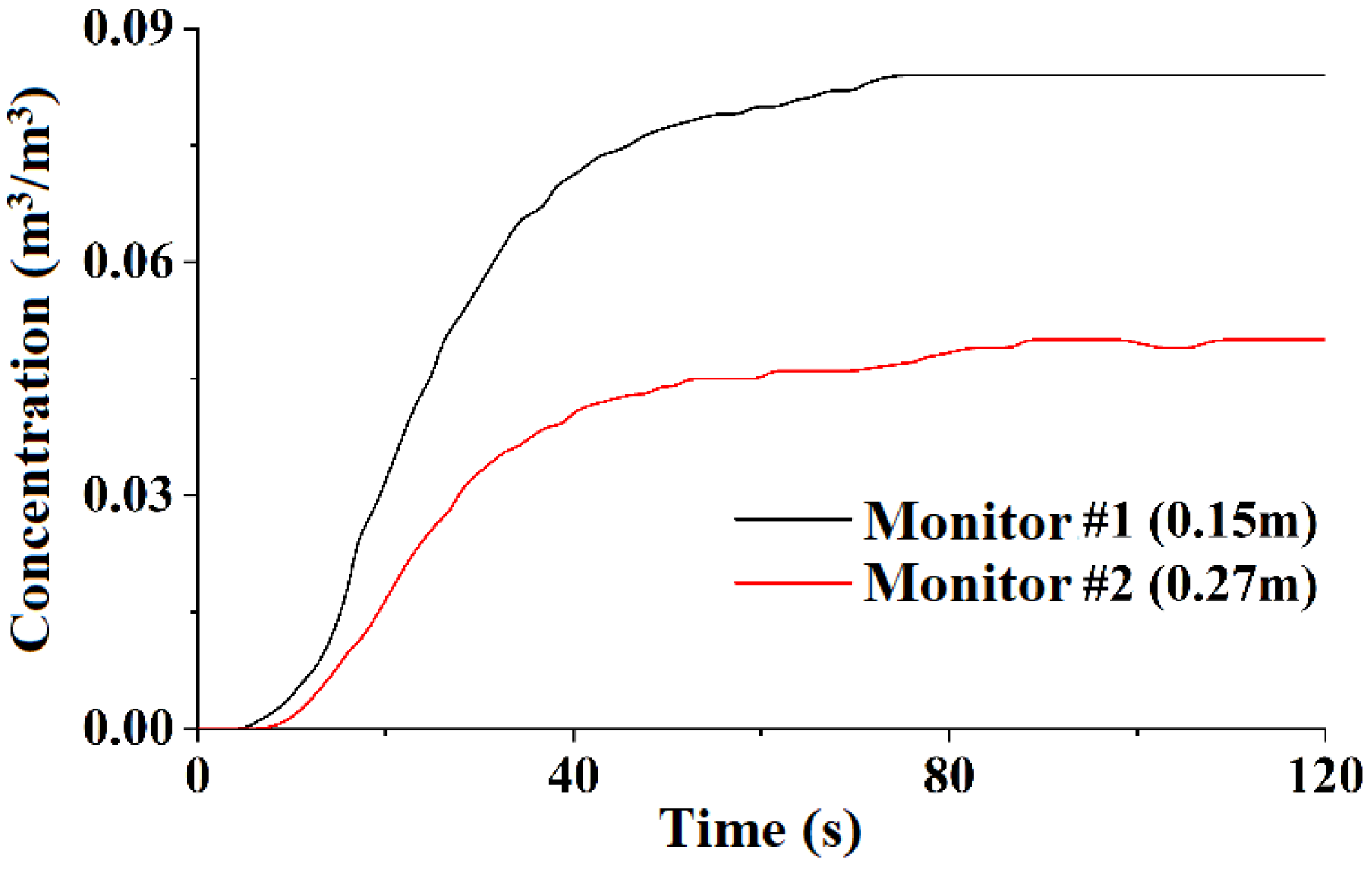
2.2.1. Constant Leakage Rates
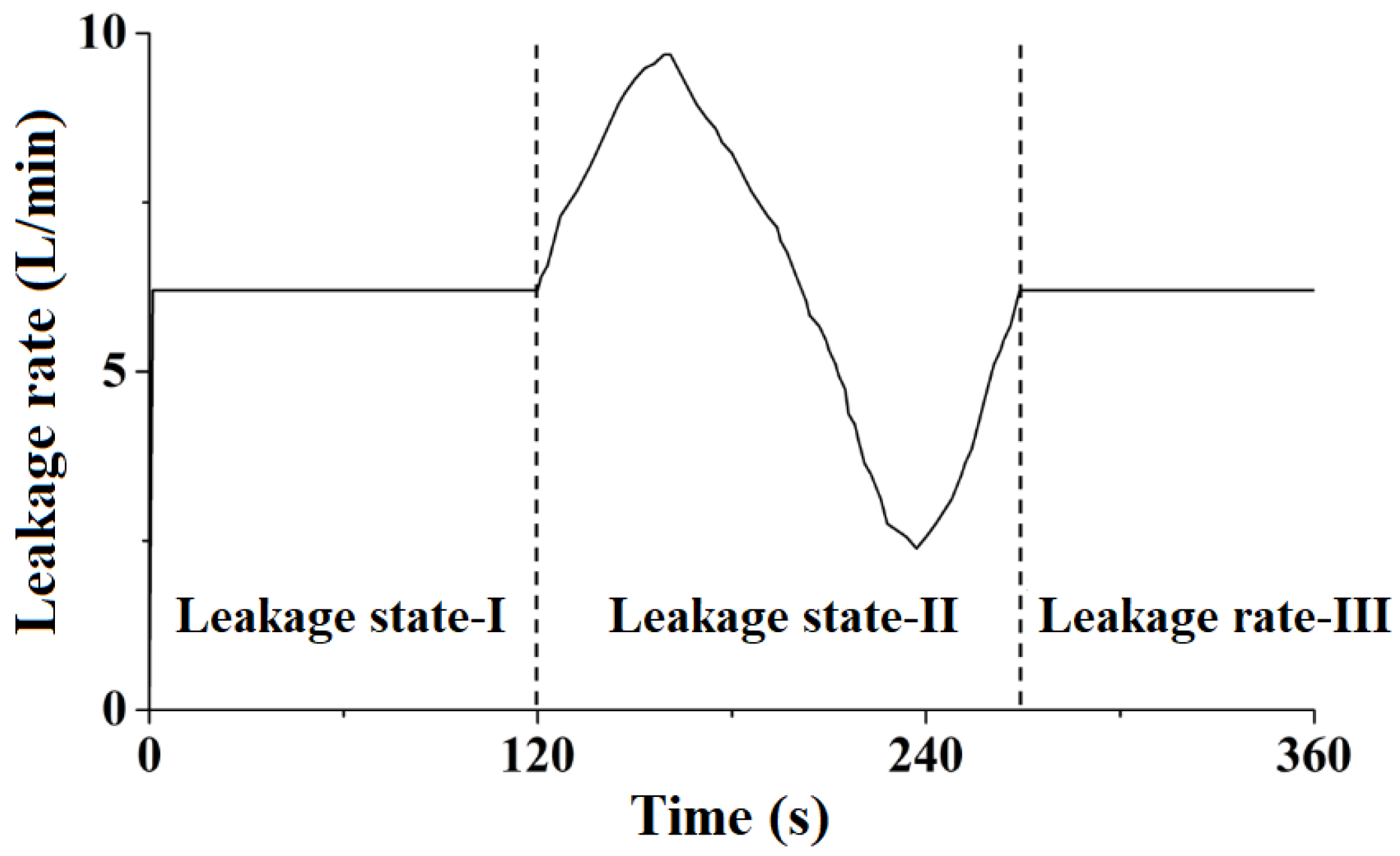
2.2.2. Time-Varying Leakage Rate
3. Model Verification
3.1. The Modeling Concept
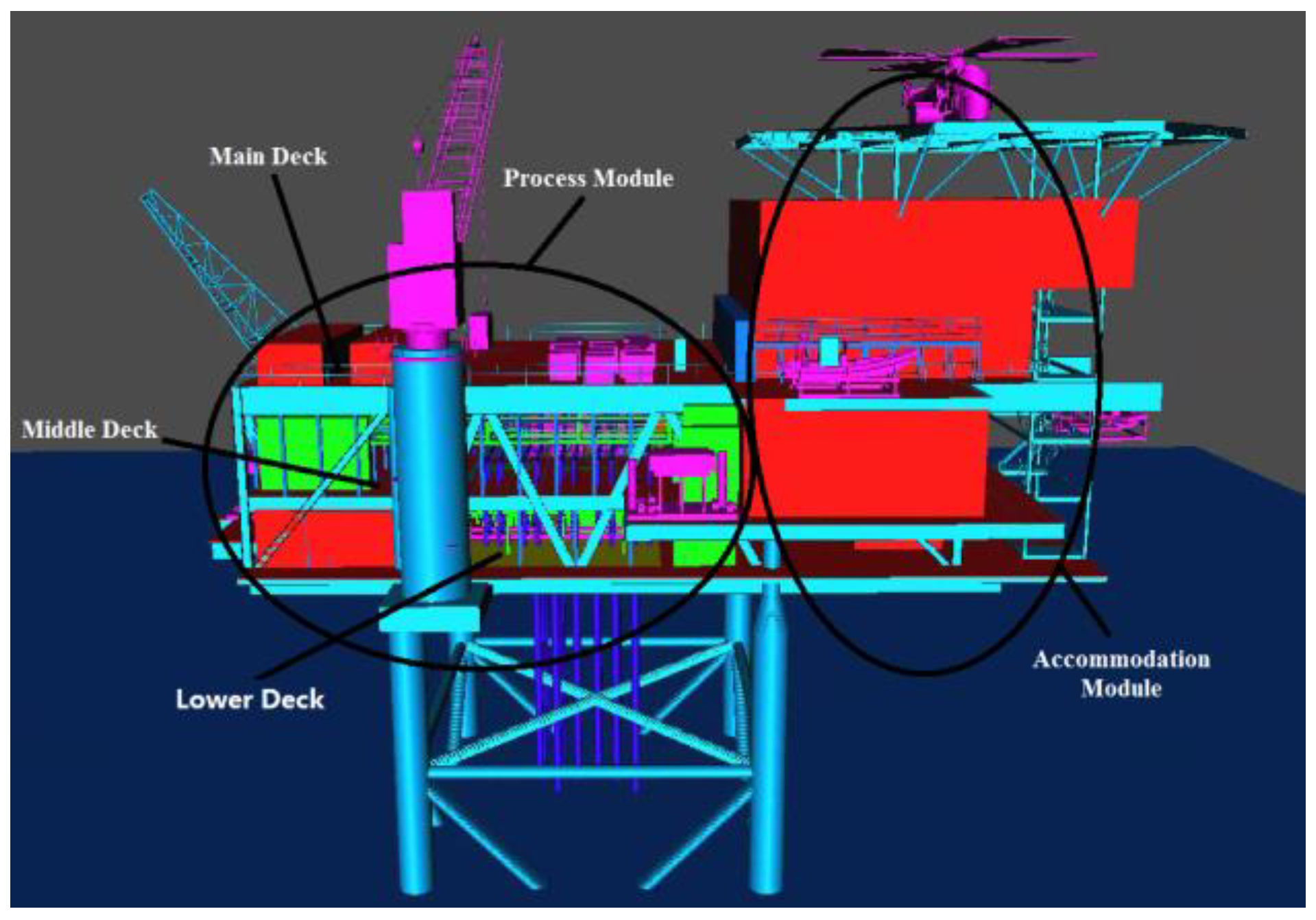
3.2. Geometric Model and Mesh Generation of an Offshore Platform
3.3. Basis of Validation of Numerical Calculation Results
3.4. Model Validation against Scenarios with Constant Leakage Rates
- (1)
- The difference in the geometry of the detector. The detectors are imaginary in the numerical simulation. Some hypothetical detectors are set so that no extra geometry is involved. In the experiment, the gas detector exists objectively which may affect the dispersion behavior of the released gas.
- (2)
- The difference in the sampling dimension of the gas detector. In the experiment, the appearance of the sampling chamber is a plane rather than a point, and thus it actually captures the released gas within an area. In the numerical simulation, the gas concentration is associated with an exact coordinate.
- (3)
- The difference in the boundary conditions. The leakage rate is so low that the performance of the anti-interference is poor. There may be disturbances that affect the intensity of the air turbulence in the experiment. Similar conditions will not occur in the numerical simulation.
- (4)
- The inherent error of the experimental instrument and the numerical calculation. There are inherent errors in the experimental instruments, including the gas detector and the leakage rate regulator. FLACS uses the Reynolds Averaged Navier–Stokes (RANS) equations and a k-ε model for turbulence. Some reasonable simplifications are made and some empirical parameters are employed, which inevitably lead to errors.
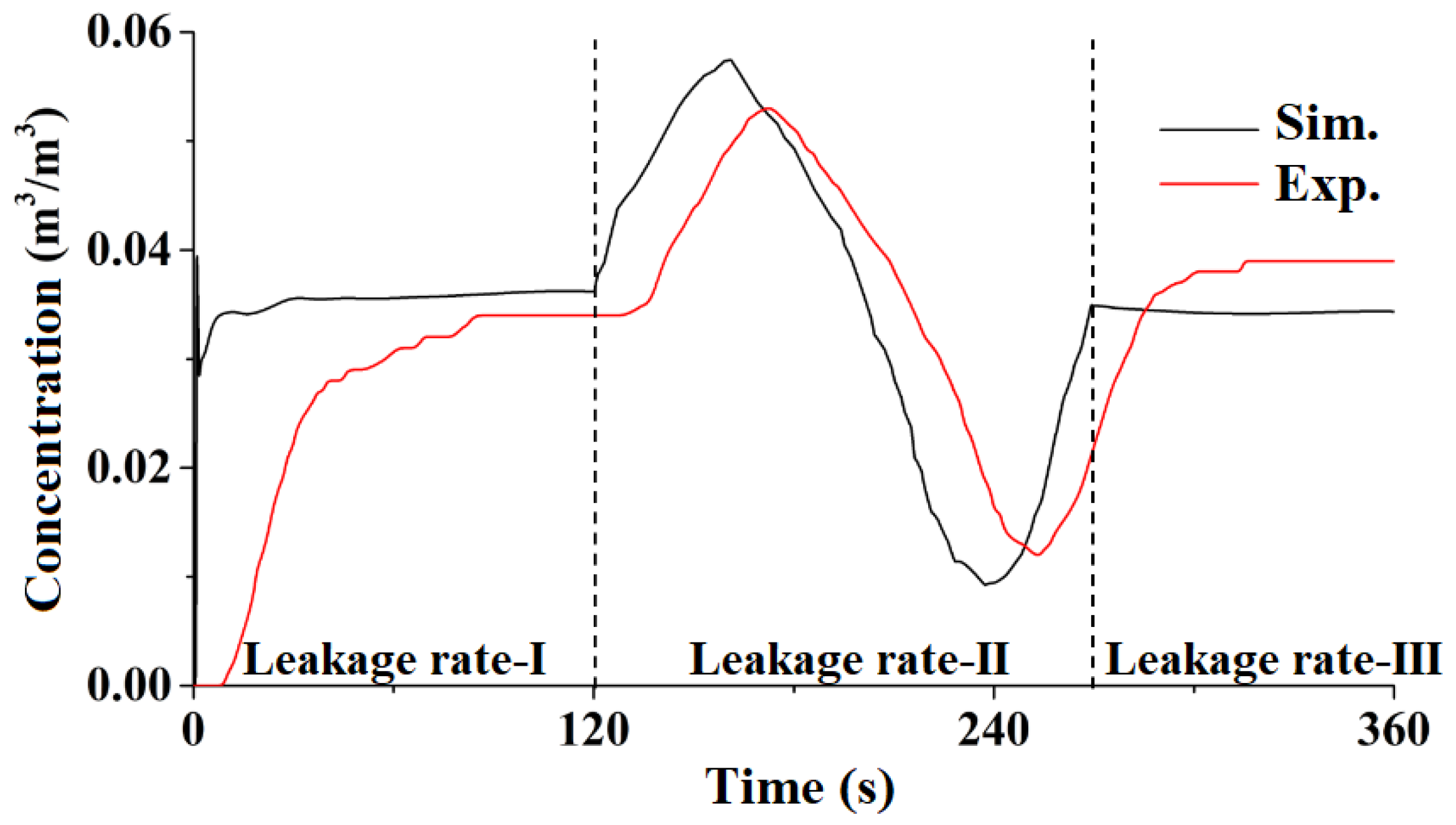
3.5. Model Validation against Scenarios with a Time-Varying Leakage Rate
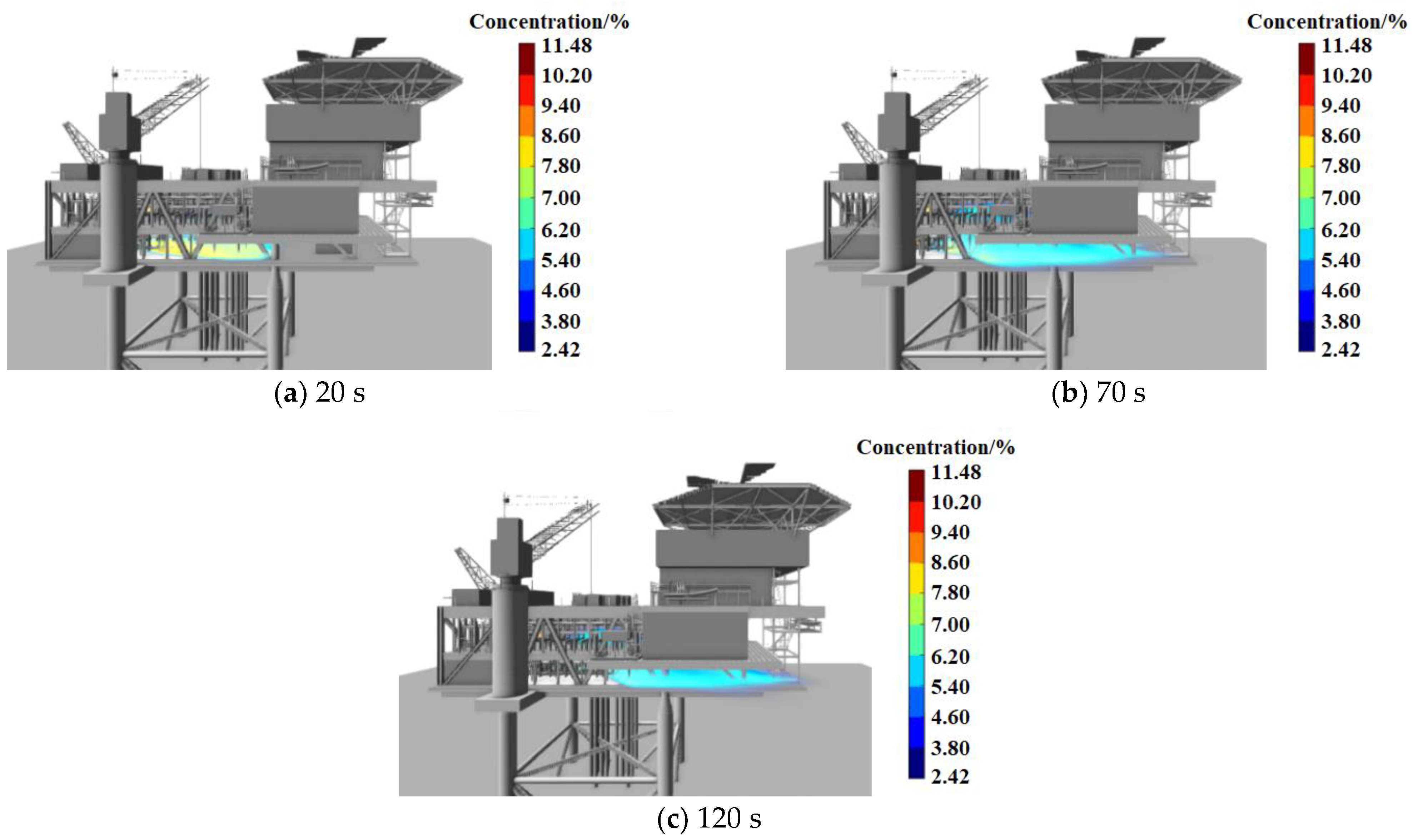
4. Model Application
5. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anjana, N.; Amarnath, A.; Nair, M. Toxic hazards of ammonia release and population vulnerability assessment using geographical information system. J. Environ. Manag. 2018, 10, 201–209. [Google Scholar]
- Bagheri, M.; Alamdari, A.; Davoudi, M. Quantitative risk assessment of sour gas transmission pipelines using CFD. J. Nat. Gas Sci. Eng. 2016, 31, 108–118. [Google Scholar]
- Huang, Y.; Ma, G. A grid-based risk screening method for fire and explosion events of hydrogen refueling stations. Int. J. Hydrog. Energy 2018, 43, 442–454. [Google Scholar]
- Dadashzadeh, M.; Khan, F.; Hawboldt, K.; Amyotte, P. An integrated approach for fire and explosion consequence modelling. Fire Saf. J. 2013, 61, 324–337. [Google Scholar]
- Dadashzadeh, M.; Abbassi, R.; Khan, F.; Hawboldt, K. Explosion modeling and analysis of BP Deepwater Horizon accident. Saf. Sci. 2013, 57, 150–160. [Google Scholar]
- Dadashzadeh, M.; Khan, F.; Abbassi, R.; Hawboldt, K. Combustion products toxicity risk assessment in an offshore installation. Process Saf. Environ. Prot. 2014, 92, 616–624. [Google Scholar]
- Gupta, S.; Chan, S. A CFD based explosion risk analysis methodology using time varying release rates in dispersion simulations. J. Loss Prev. Process Ind. 2016, 39, 59–67. [Google Scholar]
- Lucas, M.; Skjold, T.; Hiskem, H. Computational fluid dynamics simulations of hydrogen releases and vented deflagrations in large enclosures. J. Loss Prev. Process Ind. 2020, 63, 103999. [Google Scholar]
- Baalisampang, T.; Abbassi, R.; Garaniya, V.; Khan, F. Accidental release of liquefied natural gas in a processing facility: Effect of equipment congestion level on dispersion behaviour of the flammable vapour. J. Loss Prev. Process Ind. 2019, 61, 237–248. [Google Scholar]
- Mcquaid, J. Heavy Gas Dispersion Trials at Thorney Island; Elsevier: Amsterdam, The Netherlands, 1985; pp. 341–356. [Google Scholar]
- Hanna, S.; Chang, J. Use of the Kit Fox field data to analyze dense gas dispersion modeling issues. Atmos. Environ. 2001, 35, 2231–2242. [Google Scholar]
- Middha, P.; Hansen, O.; Storvik, I. Validation of CFD-model for hydrogen dispersion. J. Loss Prev. Process Ind. 2009, 22, 1034–1038. [Google Scholar]
- Middha, P.; Hansen, O.; Grune, J.; Kotchourko, A. CFD calculations of gas leak dispersion and subsequent gas explosions: Validation against ignited impinging hydrogen jet experiments. J. Hazard. Mater. 2010, 179, 84–94. [Google Scholar]
- Savvides, C.; Tam, V.; Kinnear, D. Dispersion of fuel in offshore modules: Comparison of predictions using FLACS and full-scale experiments. In Major Hazards Offshore; ERA Technology Ltd.: London, UK, 2001. [Google Scholar]
- Hansen, O.; Gavelli, F.; Ichard, M.; Davis, S. Validation of FLACS against experimental data sets from the model evaluation database for LNG vapor dispersion. J. Loss Prev. Process Ind. 2010, 23, 857–877. [Google Scholar]
- Spouge, J. A Guide to Quantitative Risk Assessment for Offshore Installations; CMPT: Aberdeen, SD, USA, 1999. [Google Scholar]
- Pan, X.; Jiang, J. Progress of accidental release source and mechanism models. J. Nnajing Univ. Technol. 2002, 24, 105–110. [Google Scholar]
- Yang, D.; Chen, G.; Fu, J.; Zhu, Y.; Dai, Z.; Wu, L. The mitigation performance of ventilation on the accident consequences of H2S-containing natural gas release. Process Saf. Environ. Prot. 2021, 148, 1327–1336. [Google Scholar]
- Yang, D.; Chen, G.; Shi, J.; Zhu, Y.; Dai, Z. A novel approach for hazardous area identification of toxic gas leakage accidents on offshore facilities. Ocean. Eng. 2020, 217, 107926. [Google Scholar]
- GexCon. FLACS v10.4 User’s Manual; GexCon: Bergen, Norway, 2015. [Google Scholar]
- API. Manufacturing, Distribution and Marketing Department. In Guide for Pressure-Relieving and Depressuring Systems; American petroleum Institute: Washington, WA, USA, 1997. [Google Scholar]









| Length (cm) | Width (cm) | Height (cm) | |
|---|---|---|---|
| The whole experimental offshore platform | 255 | 210 | 308 |
| The main deck | 255 | 210 | / |
| The middle deck | 255 | 210 | 046 |
| The lower deck | 255 | 210 | 046 |
| Item | Value or Value Range | Item | Value or Value Range |
|---|---|---|---|
| Molecular weight | 44.10 | Critical pressure (MPa) | 4.25 |
| Relative density | 1.56 | Minimus ignition energy (mJ) | 0.26 |
| Viscosity (kg/m·s) | 1.01 × 10−5 | Flashpoint (°C) | −104 |
| Saturated vapor pressure (kPa) | 53.32 (−55.6 °C) | Autoignition temperature (°C) | 450 |
| Critical Temperature (°C) | 96.8 | Explosion limit (%) | 2.1~9.5 |
| Grid Size (m) | 0.15 | 0.12 | 0.10 | 0.075 |
|---|---|---|---|---|
| Computation time (s) | 6259.29 | 8217.88 | 9872.21 | 18,834.57 |
| Max. FLAM (m3) | 0.289 | 0.248 | 0.237 | 0.234 |
| SPM | MRB | MRSE | FAC2 | MG | VG |
|---|---|---|---|---|---|
| Acceptance criteria | −0.4 < MRB < 0.4 | MRSE < 2.3 | 0.5 ≤ FAC2 | 0.67 < MG < 1.5 | VG < 3.3 |
| SPM | 4.4 L/min | 6.2 L/min | 8.1 L/min |
|---|---|---|---|
| −0.4 < MRB < 0.4 | 0.0129 | −0.0897 | −0.0877 |
| MRSE < 2.3 | 0.0025 | 0.0081 | 0.0077 |
| 0.5 ≤ FAC2 ≤ 2 | 0.9885 | 1.0940 | 1.0920 |
| 0.67 < MG < 1.5 | 1.014 | 0.9145 | 0.9160 |
| VG < 3.3 | 1.0026 | 1.0082 | 1.0078 |
| SPM | Max. Concentration | Min. Concentration |
|---|---|---|
| −0.4 < MRB < 0.4 | −0.0797 | 0.1724 |
| MRSE < 2.3 | 0.00635 | 0.02972 |
| 0.5 ≤ FAC2 | 1.083 | 0.841 |
| 0.67 < MG < 1.5 | 0.923 | 1.189 |
| VG < 3.3 | 1.0064 | 1.0303 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, F.; Li, Y.; Zhang, J.; Dong, H.; Yang, D.; Chen, G. Experimental and Numerical Study for Gas Release and Dispersion on Offshore Platforms. Processes 2023, 11, 3437. https://doi.org/10.3390/pr11123437
Xiao F, Li Y, Zhang J, Dong H, Yang D, Chen G. Experimental and Numerical Study for Gas Release and Dispersion on Offshore Platforms. Processes. 2023; 11(12):3437. https://doi.org/10.3390/pr11123437
Chicago/Turabian StyleXiao, Fengpu, Yanan Li, Jun Zhang, Hai Dong, Dongdong Yang, and Guoming Chen. 2023. "Experimental and Numerical Study for Gas Release and Dispersion on Offshore Platforms" Processes 11, no. 12: 3437. https://doi.org/10.3390/pr11123437
APA StyleXiao, F., Li, Y., Zhang, J., Dong, H., Yang, D., & Chen, G. (2023). Experimental and Numerical Study for Gas Release and Dispersion on Offshore Platforms. Processes, 11(12), 3437. https://doi.org/10.3390/pr11123437






