Random-Enabled Hidden Moving Target Defense against False Data Injection Alert Attackers
Abstract
:1. Introduction
1.1. Related Work
1.2. Research Gap
1.3. Contribution
- We summarize two alert attacker models against MTD in the literature: (i) a BDD-based alert attacker who uses Chi-square BDD to detect the existence of MTD; and (ii) a data-driven alert attacker who uses dimension reduction and unsupervised learning methods to detect the existence of MTD.
- We propose a novel alert attacker model, i.e., a model-based alert attacker, who uses the MTD operation model to calculate the dispatched line reactance and then uses Chi-square BDD to verify the correctness of the estimated reactance. This attacker model can use the estimated line reactance to construct stealthy FDI attacks against HMTD methods that lack randomness.
- We propose a novel RHMTD operation model in the DC power system model, which maximizes the weighted line reactance changes and integrates the derived MTD hiddenness operation condition as constraints. The weights of the line reactance in the objective function follow the uniform distribution for introducing the randomness.
- We theoretically prove the hiddenness of the proposed RHMTD method against three alert attacker models. We further analyze the attack detection effectiveness of the proposed method against three alert attacker models.
2. Alert Attacker Models
2.1. Notation
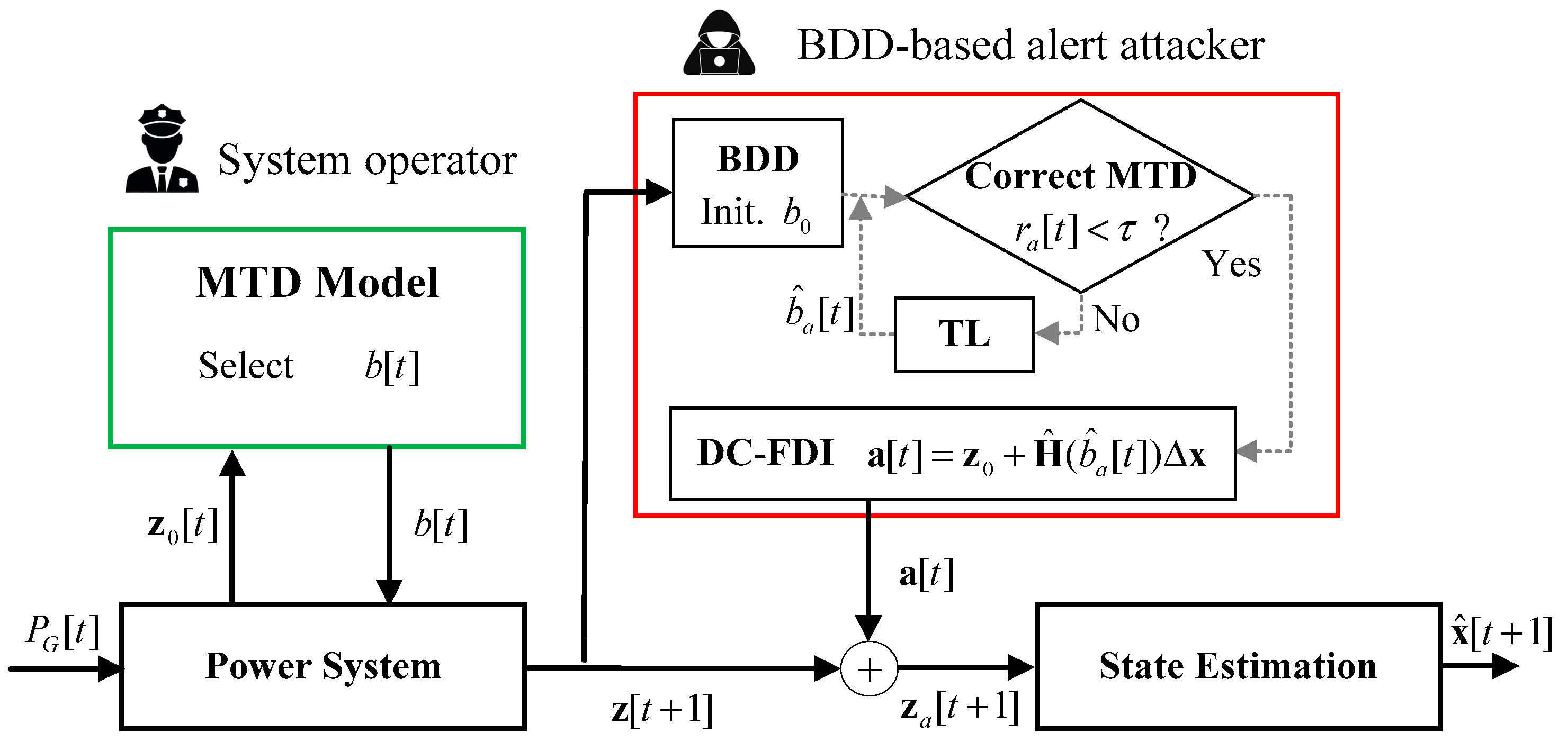
2.2. BDD-Based Alert Attacker Model
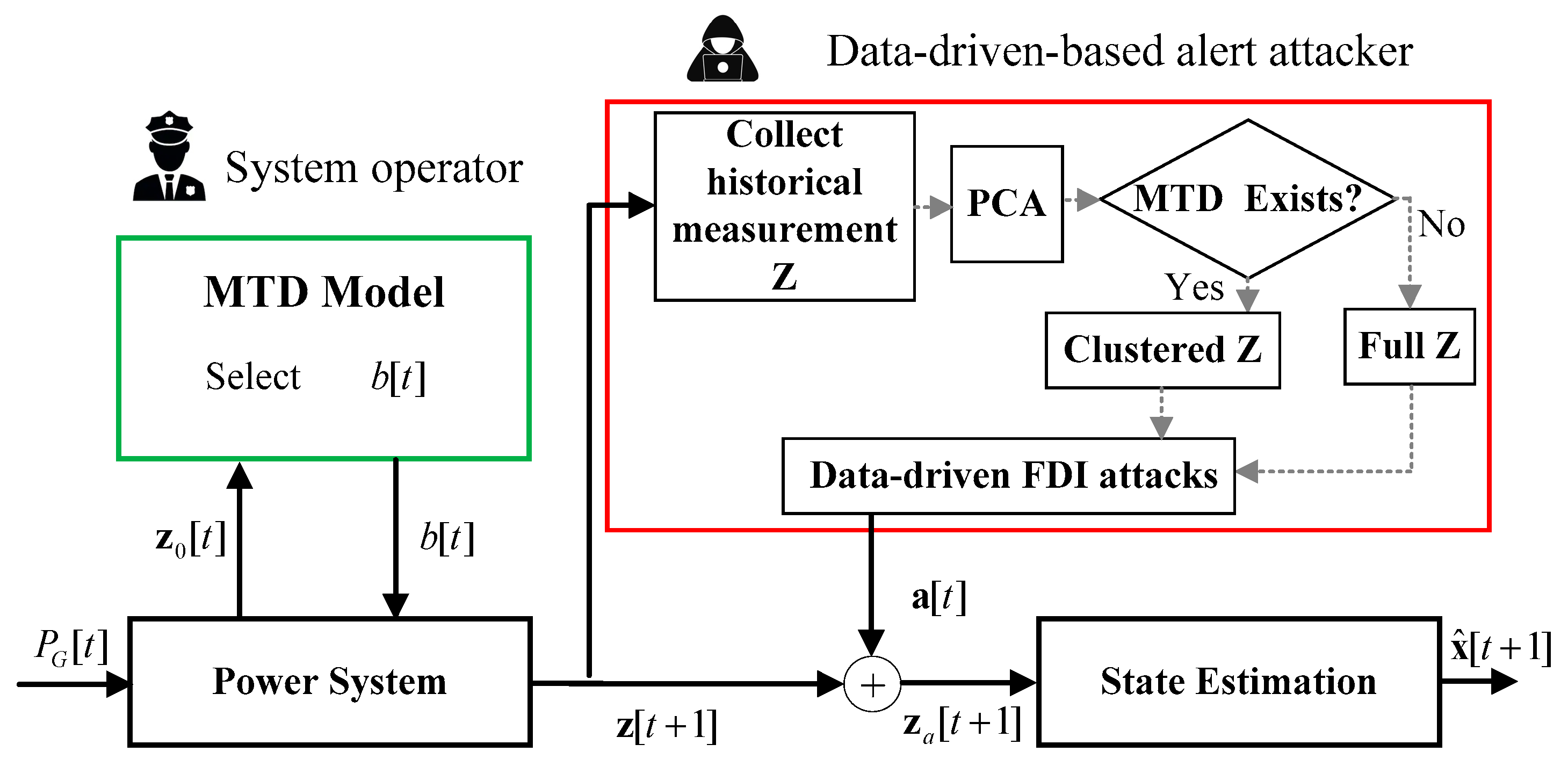
2.3. Data-Driven Alert Attacker Model
2.4. Model-Based Alert Attacker Model
3. Random-Enabled HMTD
3.1. Hiddenness Operation Condition
3.2. The Random-Enabled HMTD Model
3.3. Hiddenness of the RHMTD against Alert Attackers
3.4. Detection Effectiveness of the RHMTD against Alert Attackers
4. Numerical Results
4.1. Test Systems
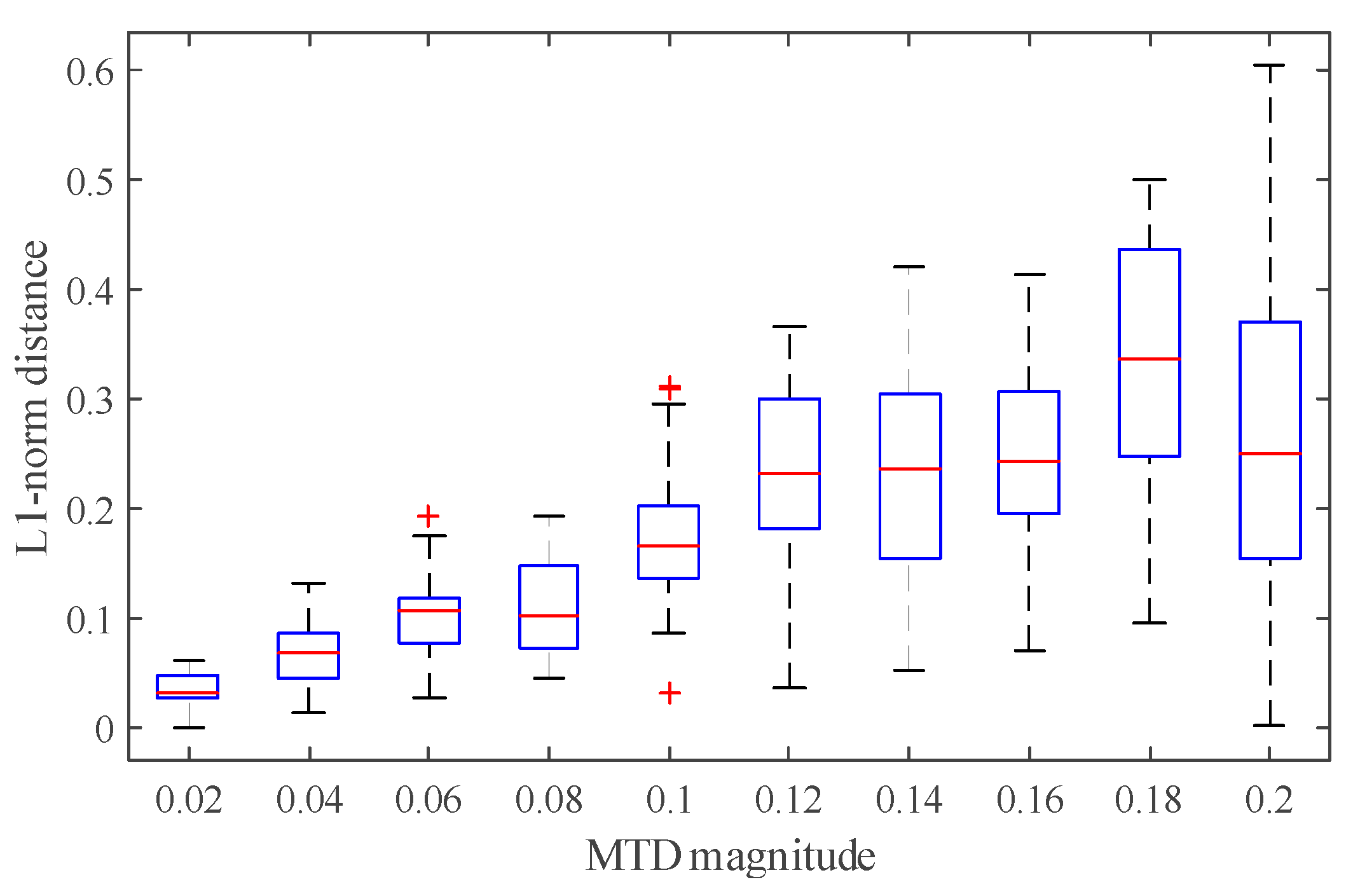
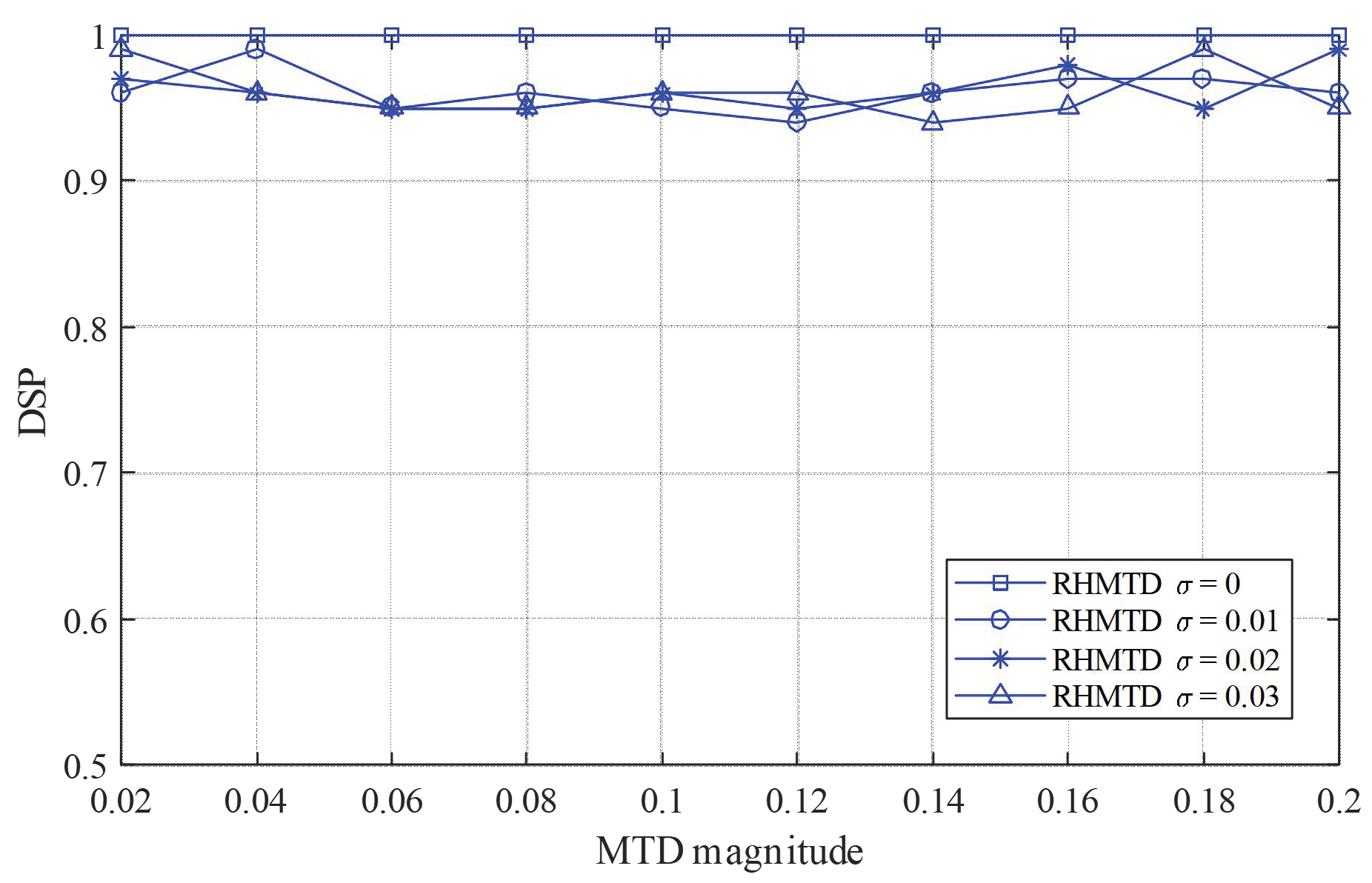
4.2. Uncertainties of RHMTD
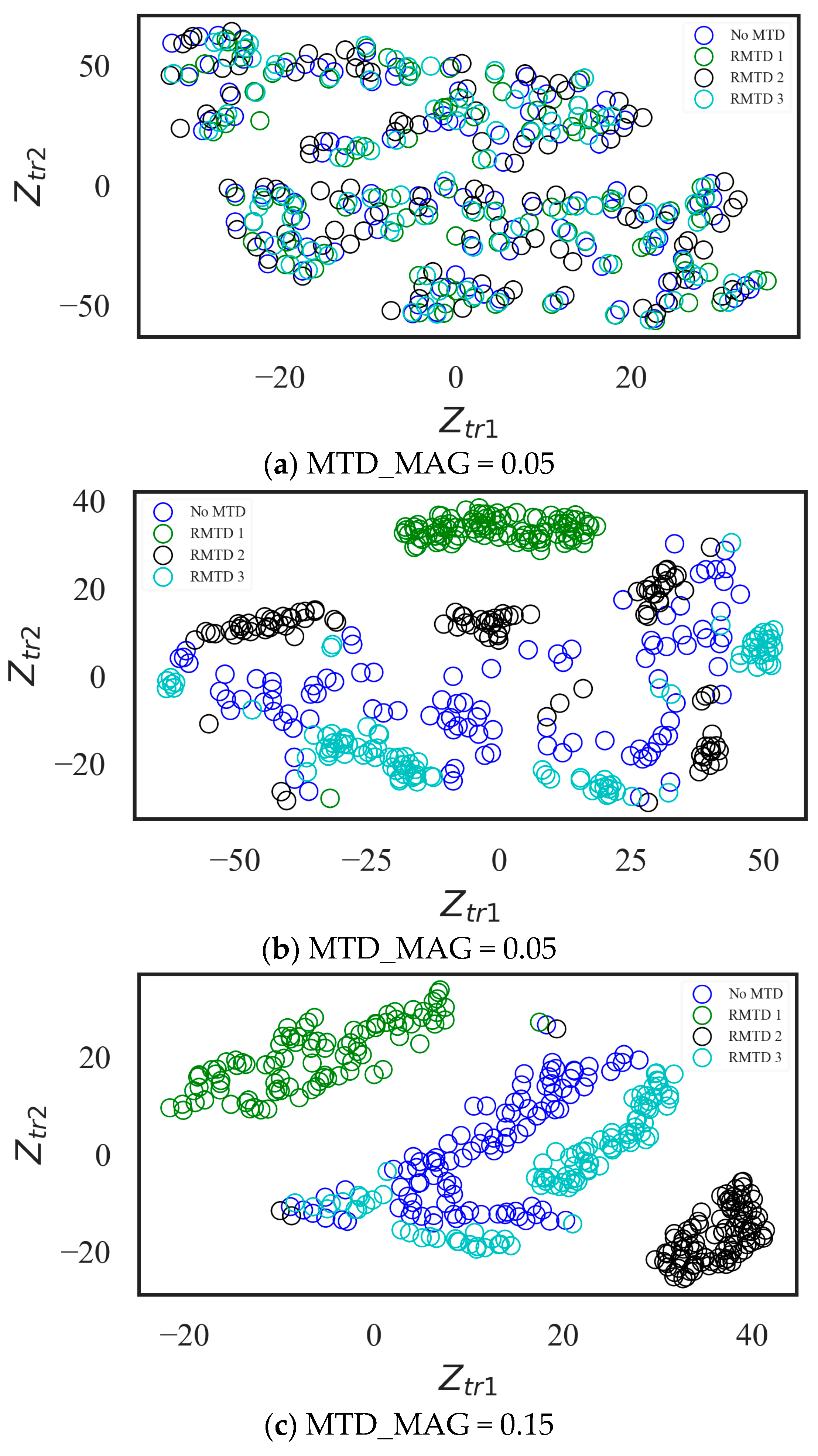
4.3. Hiddenness of RHMTD against Three Alert Attackers
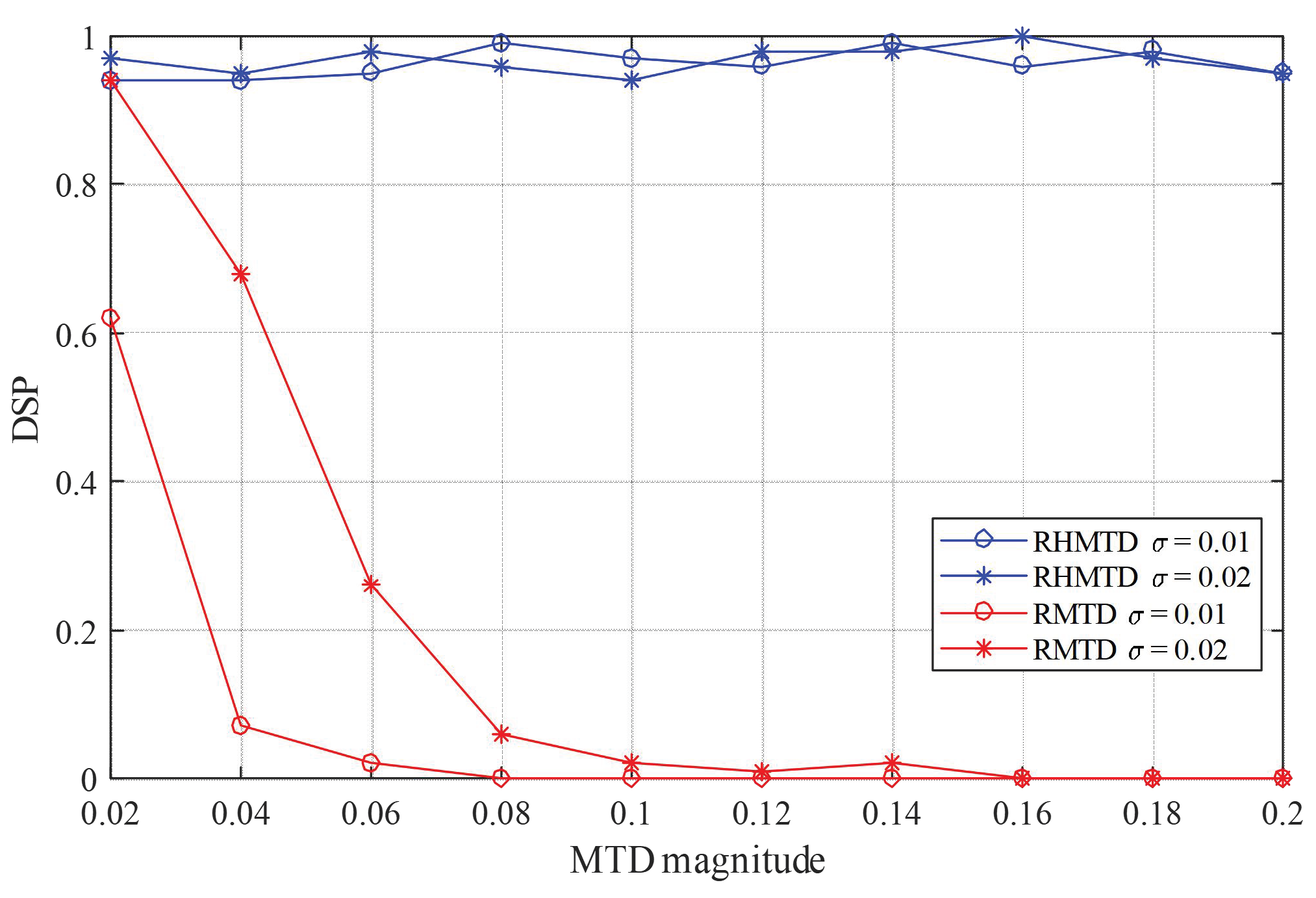
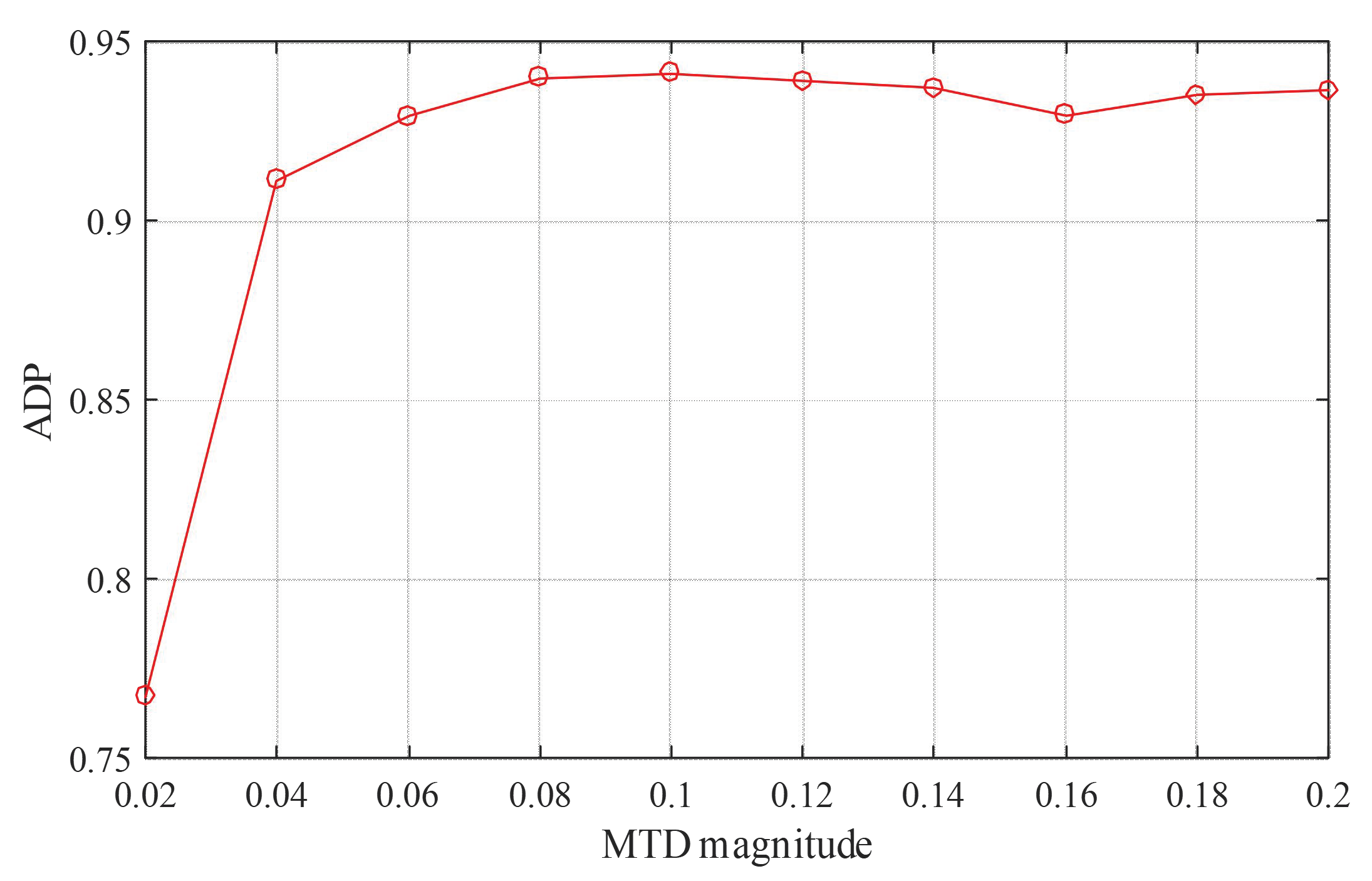
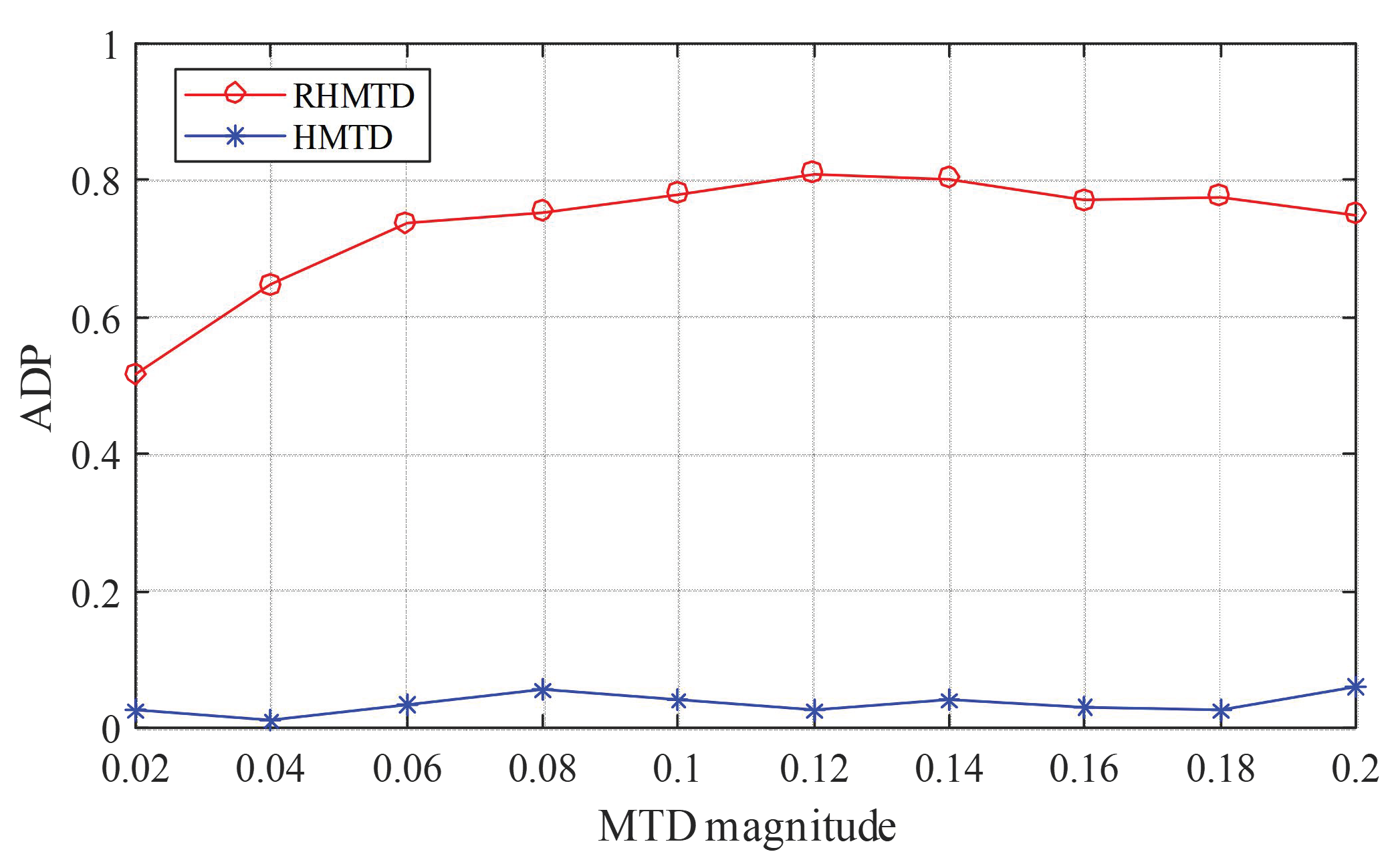
4.4. Attack Detection Effectiveness of the RHMTD against Three Alert Attackers
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
Nomenclature
| Symbol | Definition |
| θ | Voltage angle of buses excluding reference bus |
| z | Measurement vector |
| a | FDI attack vector |
| H0 | DC measurement matrix in SE before MTD |
| H | DC measurement matrix in SE after MTD |
| A | Incident matrix of power system graph |
| X | Diagonal line reactance matrix |
| xij | The reactance of line i–j (between bus i and j) |
| n | Total number of system buses |
| m | Total number of measurements |
| p | Total number of lines |
References
- Balouch, S.; Muhammad, A.; Muqeet, K.A.; Pansota, M.; Jamil, H.; Hamdi, M.; Malik, A.; Hamam, H. Optimal Scheduling of Demand Side Load Management of Smart Grid Considering Energy Efficiency. Front. Energy Res. 2022, 1. [Google Scholar] [CrossRef]
- Musleh, A.S.; Chen, G.; Dong, Z.Y. A Survey on the Detection Algorithms for False Data Injection Attacks in Smart Grids. IEEE Trans. Smart Grid 2020, 11, 2218–2234. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, B.; Wu, H. Smart Grid Cyber-Physical Attack and Defense: A Review. IEEE Access 2021, 9, 29641–29659. [Google Scholar] [CrossRef]
- Rahman, M.A.; Al-Shaer, E.; Bobba, R.B. Moving Target Defense for Hardening the Security of the Power System State Estimation. In Proceedings of the First ACM Workshop on Moving Target Defense; ACM: New York, NY, USA, 2014; pp. 59–68. [Google Scholar]
- Liu, B.; Wu, H. Optimal Planning and Operation of Hidden Moving Target Defense for Maximal Detection Effectiveness. IEEE Trans. Smart Grid 2021, 12, 4447–4459. [Google Scholar] [CrossRef]
- Tian, J.; Tan, R.; Guan, X.; Liu, T. Enhanced Hidden Moving Target Defense in Smart Grids. IEEE Trans. Smart Grid 2019, 10, 2208–2223. [Google Scholar] [CrossRef]
- Liu, M.; Zhao, C.; Zhang, Z.; Deng, R. Explicit Analysis on Effectiveness and Hiddenness of Moving Target Defense in AC Power Systems. IEEE Trans. Power Syst. 2022, 37, 4732–4746. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, B.; Liu, X.; Pahwa, A.; Wu, H. Voltage Stability Constrained Moving Target Defense against Net Load Redistribution Attacks. IEEE Trans. Smart Grid 2022, 13, 3748–3759. [Google Scholar] [CrossRef]
- Zhang, Z.; Tian, Y.; Deng, R.; Ma, J. A Double-Benefit Moving Target Defense Against Cyber–Physical Attacks in Smart Grid. IEEE Internet Things J. 2022, 9, 17912–17925. [Google Scholar] [CrossRef]
- Deng, R.; Zhuang, P.; Liang, H. CCPA: Coordinated Cyber-Physical Attacks and Countermeasures in Smart Grid. IEEE Trans. Smart Grid 2017, 8, 2420–2430. [Google Scholar] [CrossRef]
- Tian, J.; Tan, R.; Guan, X.; Xu, Z.; Liu, T. Moving Target Defense Approach to Detecting Stuxnet-Like Attacks. IEEE Trans. Smart Grid 2020, 11, 291–300. [Google Scholar] [CrossRef]
- Liu, B.; Wu, H. Optimal D-FACTS Placement in Moving Target Defense against False Data Injection Attacks. IEEE Trans. Smart Grid 2020, 11, 4345–4357. [Google Scholar] [CrossRef]
- Liu, C.; Wu, J.; Long, C.; Kundur, D. Reactance Perturbation for Detecting and Identifying FDI Attacks in Power System State Estimation. IEEE J. Sel. Top. Signal Process. 2018, 12, 763–776. [Google Scholar] [CrossRef]
- Zhang, Z.; Deng, R.; Cheng, P.; Chow, M.-Y. Strategic Protection Against FDI Attacks With Moving Target Defense in Power Grids. IEEE Trans. Control Netw. Syst. 2022, 9, 245–256. [Google Scholar] [CrossRef]
- Lakshminarayana, S.; Yau, D.K.Y. Cost-Benefit Analysis of Moving-Target Defense in Power Grids. IEEE Trans. Power Syst. 2020, 3, 1152–1163. [Google Scholar]
- Liu, B.; Yang, Q.; Zhang, H.; Wu, H. An Interior-Point Solver for AC Optimal Power Flow Considering Variable Impedance-Based FACTS Devices. IEEE Access 2021, 9, 154460–154470. [Google Scholar] [CrossRef]
- Zhang, Z.; Deng, R.; Yau, D.K.Y.; Cheng, P.; Chen, J. Analysis of Moving Target Defense Against False Data Injection Attacks on Power Grid. IEEE Trans. Inf. Forensics Secur. 2019, 15, 2320–2335. [Google Scholar] [CrossRef] [Green Version]
- Liu, M.; Zhao, C.; Zhang, Z.; Deng, R.; Cheng, P. Analysis of Moving Target Defense in Unbalanced and Multiphase Distribution Systems Considering Voltage Stability. In Proceedings of the 2021 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Aachen, Germany, 25–28 October 2021; pp. 207–213. [Google Scholar]
- Zhang, Z.; Deng, R.; Yau, D.K.Y.; Cheng, P.; Chow, M.-Y. Security Enhancement of Power System State Estimation With an Effective and Low-Cost Moving Target Defense. IEEE Trans. Syst. Man Cybern. Syst. 2022; 1–16, accepted. [Google Scholar]
- Liu, B.; Wu, H.; Pahwa, A.; Ding, F.; Ibrahim, E.; Liu, T. Hidden Moving Target Defense against False Data Injection in Distribution Network Reconfiguration. In Proceedings of the 2018 IEEE Power Energy Society General Meeting (PESGM), Portland, OR, USA, 5–10 August 2018; pp. 1–5. [Google Scholar]
- Higgins, M.; Teng, F.; Parisini, T. Stealthy MTD Against Unsupervised Learning-Based Blind FDI Attacks in Power Systems. IEEE Trans. Inf. Forensics Secur. 2021, 16, 1275–1287. [Google Scholar] [CrossRef]
- Murguia, C.; Ruths, J. CUSUM and chi-squared attack detection of compromised sensors. In Proceedings of the 2016 IEEE Conference on Control Applications (CCA), Buenos Aires, Argentina, 19–22 September 2016; IEEE: Buenos Aires, Argentina, 2016; pp. 474–480. [Google Scholar]
- Zhang, Z.; Deng, R.; Yau, D.K.Y.; Cheng, P.; Chen, J. On Hiddenness of Moving Target Defense against False Data Injection Attacks on Power Grid. ACM Trans. Cyber-Phys. Syst. 2020, 4, 1–29. [Google Scholar] [CrossRef] [Green Version]
- Zheng, J.; Namin, A.S. A Survey on the Moving Target Defense Strategies: An Architectural Perspective. J. Comput. Sci. Technol. 2019, 34, 207–233. [Google Scholar] [CrossRef]
- Lakshminarayana, S.; Sthapit, S.; Maple, C. A Comparison of Data-Driven Techniques for Power Grid Parameter Estimation. arXiv 2021. Available online: https://arxiv.org/pdf/2107.03762.pdf (accessed on 16 January 2023).
- Yang, H.; He, X.; Wang, Z.; Qiu, R.C.; Ai, Q. Blind False Data Injection Attacks Against State Estimation Based on Matrix Reconstruction. IEEE Trans. Smart Grid 2022, 13, 3174–3187. [Google Scholar] [CrossRef]
- Yu, Z.-H.; Chin, W.-L. Blind False Data Injection Attack Using PCA Approximation Method in Smart Grid. IEEE Trans. Smart Grid 2015, 6, 1219–1226. [Google Scholar] [CrossRef]
- Kim, J.; Tong, L.; Thomas, R.J. Subspace Methods for Data Attack on State Estimation: A Data Driven Approach. IEEE Trans. Signal Process. 2015, 63, 1102–1114. [Google Scholar] [CrossRef] [Green Version]
- Zimmerman, R.D.; Murillo-Sanchez, C.E.; Thomas, R.J. MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef] [Green Version]
- Liu, B.; Wu, H. Systematic planning of moving target defence for maximising detection effectiveness against false data injection attacks in smart grid. IET Cyber-Phys. Syst. Theory Appl. 2021, 6, 151–163. [Google Scholar] [CrossRef]






| Method | BDD-AA | DD-AA | M-AA | Characteristics |
|---|---|---|---|---|
| Watermarking HMTD [21] | Y/Y | Y/Y | Y/Y | Detection delay of FDI attacks |
| Secure-meter-based HMTD [23] | Y/Y | N/Y | Y/Y | Extra expensive protected meters |
| Model-based HMTD [5,20] | Y/Y | Y/Y | Y/N | Lack of randomness |
| This paper | Y/Y | Y/Y | Y/Y | No detection delay and no protected meters with randomness |
| Method | BDD-AA | DD-AA | M-AA |
|---|---|---|---|
| Watermarking HMTD | 94% | 100% | 83% |
| Model-based HMTD | 93% | 100% | 96% |
| RHMTD | 95% | 100% | 96% |
| Method | BDD-AA | M-AA | DD-AA |
|---|---|---|---|
| Watermarking HMTD | 37.8% | 47.3% | 33.0% |
| Model-based HMTD | 93.9% | 6.0% | 59.0% |
| RHMTD | 93.6% | 75.1% | 68.0% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, B.; Wu, H.; Yang, Q.; Zhang, H. Random-Enabled Hidden Moving Target Defense against False Data Injection Alert Attackers. Processes 2023, 11, 348. https://doi.org/10.3390/pr11020348
Liu B, Wu H, Yang Q, Zhang H. Random-Enabled Hidden Moving Target Defense against False Data Injection Alert Attackers. Processes. 2023; 11(2):348. https://doi.org/10.3390/pr11020348
Chicago/Turabian StyleLiu, Bo, Hongyu Wu, Qihui Yang, and Hang Zhang. 2023. "Random-Enabled Hidden Moving Target Defense against False Data Injection Alert Attackers" Processes 11, no. 2: 348. https://doi.org/10.3390/pr11020348
APA StyleLiu, B., Wu, H., Yang, Q., & Zhang, H. (2023). Random-Enabled Hidden Moving Target Defense against False Data Injection Alert Attackers. Processes, 11(2), 348. https://doi.org/10.3390/pr11020348








