A Semi-Analytical Model for Gas–Water Two-Phase Productivity Prediction of Carbonate Gas Reservoirs
Abstract
:1. Introduction
2. Establishment of Model
2.1. Physical Model
2.2. Mathematical Model
3. Semi-Analytical Solution of the Gas–Water Two-Phase Productivity Prediction
3.1. Solution of the Gas Phase Flow Equation
3.2. Solution of the Aqueous Phase Flow Equation
3.3. Establishment of the Fluid Mass Balance Equation
4. Dynamic Analysis of Gas–Water Two-Phase Production
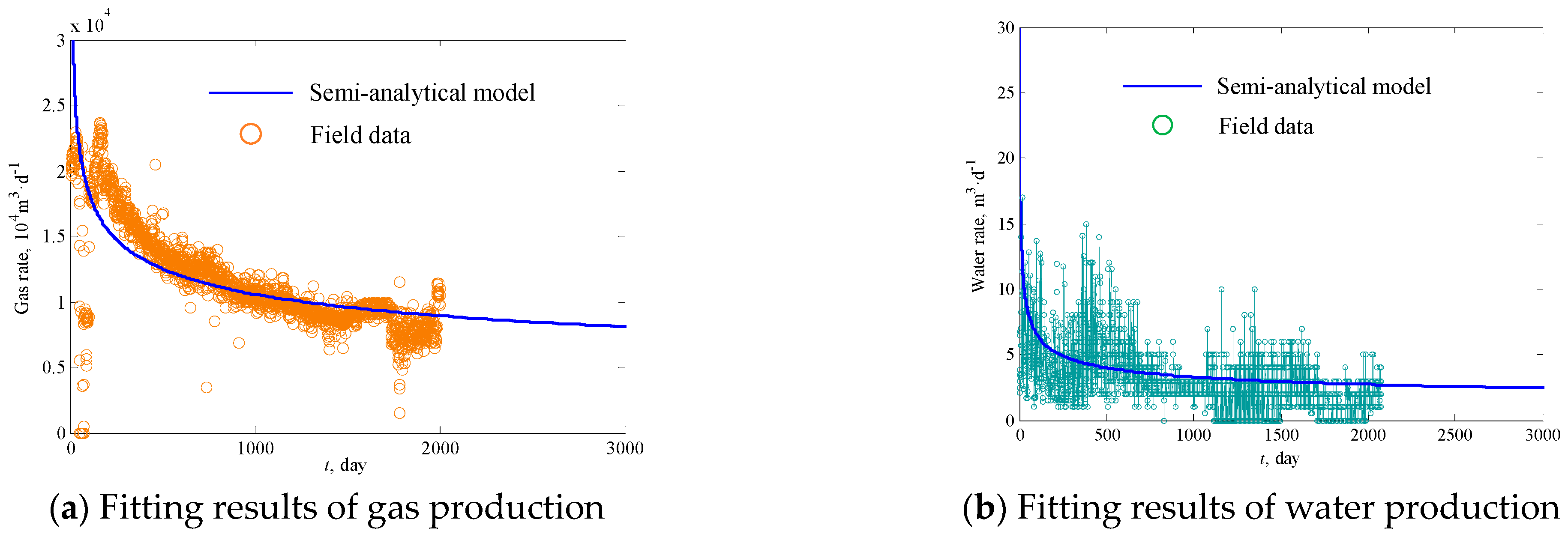
4.1. Model Validation
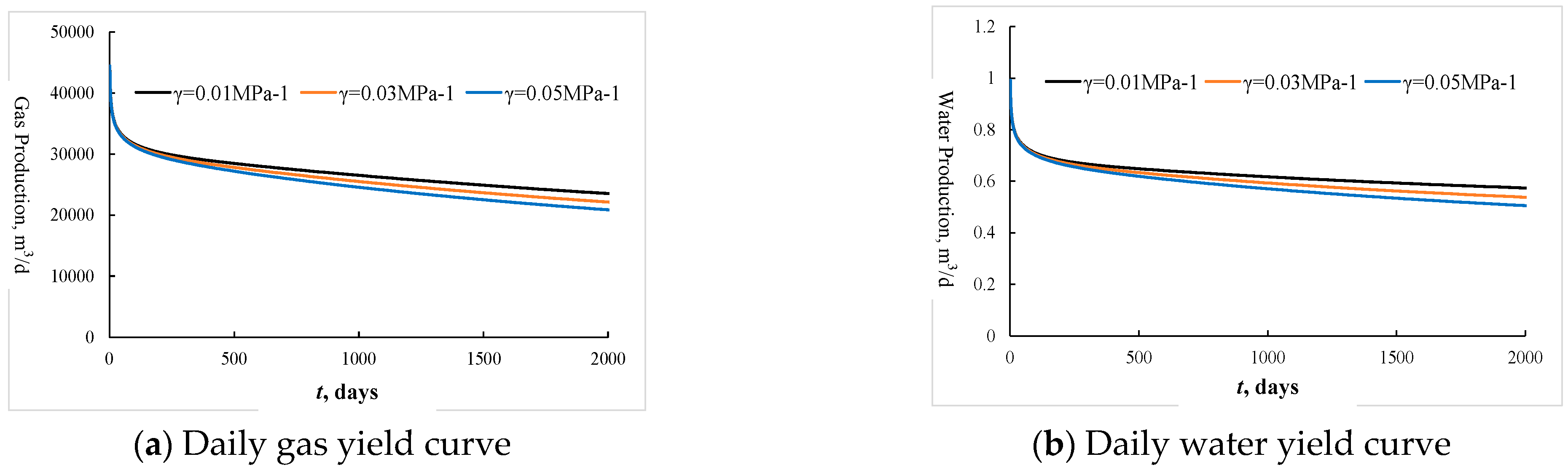
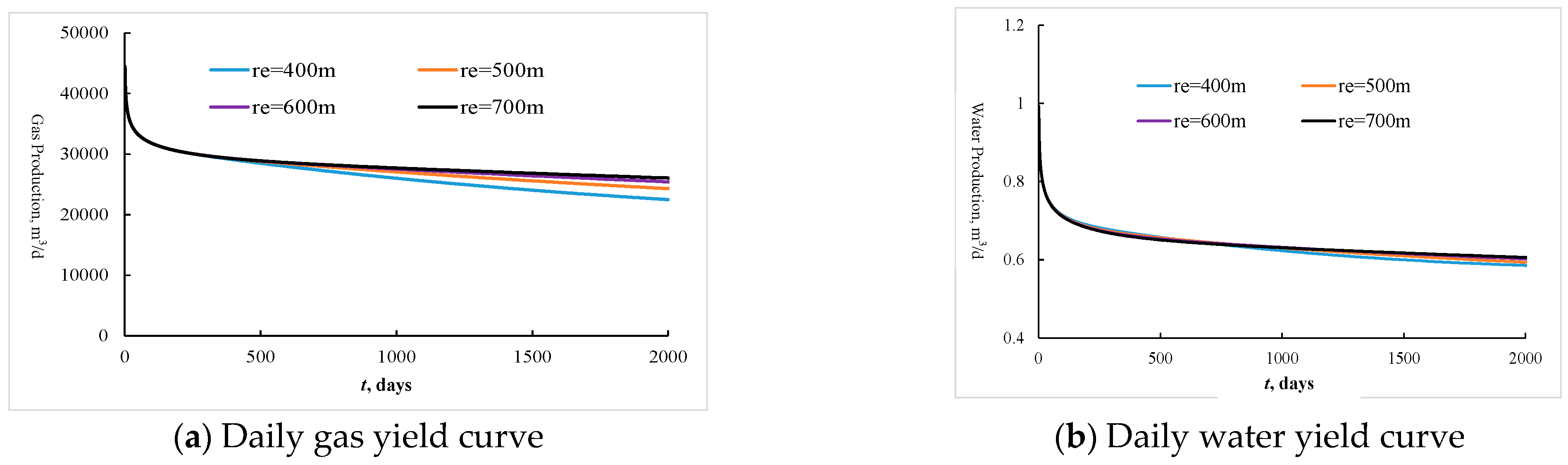
4.2. Analysis of Factors Affecting Production Dynamics
4.3. Case Analysis
5. Conclusions
- (1)
- The average pressure and average saturation of the reservoir are calculated using the flow material balance method, and the nonlinear parameters in the seepage model are updated step by step, which can deal with the gas–water two-phase nonlinear seepage problem with higher accuracy.
- (2)
- Validation work using the numerical model and field application showed that the semi-analytical method proposed in this paper has high prediction accuracy and can be used to predict the gas–water two-phase production of carbonate gas wells.
- (3)
- Fracture and key percolation parameters of the reservoir play important roles in gas–water two-phase production performance. Since the water production of carbonate gas reservoirs dramatically affects the productivity of a gas well, under the same reservoir and fracture parameters, the productivity with gas–water two-phase flow is significantly lower than that of single-phase flow.
- (4)
- The stress sensitivity of fractures affects the productivity of carbonate gas wells. In the production process, it is necessary to control the production pressure difference carefully to inhibit the negative impact of the stress sensitivity effect.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, Y.; Cheng, L.; Huang, S.; Fang, S.; Jia, P.; Wang, S. A semianalytical model for simulating fluid flow in naturally fractured reservoirs with non-homogeneous vugs and fractures. SPE J. 2019, 24, 334–348. [Google Scholar] [CrossRef]
- Jones, F.O. A Laboratory Study of the Effects of Confining Pressure on Fracture Flow and Storage Capacity in Carbonate Rocks. Soc. Pet. Eng. 1975, 27, 21–27. [Google Scholar]
- Duan, Y.; Meng, Y.; Luo, P.; Su, W. Stress Sensitivity of Naturally Fractured-porous Reservoir with Dual-porosity. In SPE International Oil and Gas Conference and Exhibition in China; OnePetro: Beijing, China, 1998. [Google Scholar]
- Ayala, L.F.; Kouassi, J.P. The similarity theory applied to the analysis of two-phase flow in gas-condensate reservoirs. Energy Fuels 2007, 21, 1592–1600. [Google Scholar] [CrossRef]
- Sheng, G.; Zhao, H.; Su, Y.; Javadpour, F.; Wang, C.; Zhou, Y.; Liu, J.; Wang, H. An analytical model to couple gas storage and transport capacity in organic matter with noncircular pores. Fuel 2020, 268, 117288. [Google Scholar] [CrossRef]
- Sheng, G.; Su, Y.; Wang, W. A new fractal approach for describing induced-fracture porosity/permeability/ compressibility in stimulated unconventional reservoirs. J. Pet. Sci. Eng. 2019, 179, 855–866. [Google Scholar] [CrossRef]
- Wang, S.; Cheng, L.; Huang, S.; Xue, Y.; Bai, M.; Wu, Y.; Wang, J. A semi-analytical method for modeling two-phase flow behavior in fractured carbonate oil reservoirs. J. Energy Resour. Technol. 2019, 141, 072902. [Google Scholar] [CrossRef]
- O’Sullivan, M.J. A similarity method for geothermal well test analysis. Water Resour. Res. 1981, 17, 390–398. [Google Scholar] [CrossRef]
- Pruess, K.; Narasimhan, T.N. Practical method for modeling fluid and heat flow in fractured porous media. Soc. Pet. Eng. J. 1985, 25, 14–26. [Google Scholar] [CrossRef] [Green Version]
- Qu, M.; Hou, J.; Zhao, F.; Song, Z.; Ma, S.; Wang, Q.; Li, M.; Yang, M. 3-D visual experiments on fluid flow behavior of water flooding and gas flooding in fractured-vuggy carbonate reservoir. In Proceedings of the Paper SPE-187273-MS Presented at SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 9–11 October 2017. [Google Scholar]
- Jia, P.; Cheng, L.; Huang, S.; Xue, Y.; Clarkson, C.R.; Williams-Kovacs, J.D.; Wang, S.; Wang, D. Dynamic coupling of analytical linear flow solution and numerical fracture model for simulating early-time flowback of fractured tight oil wells (planar fracture and complex fracture network). J. Pet. Sci. Eng. 2019, 177, 1–23. [Google Scholar] [CrossRef]
- Matthai, S.K.; Mezentsev, A.A.; Belayneh, M. Finite element-node-centered finite-volume two-phase-flow experiments with fractured rock represented by unstructured hybrid-element meshes. SPE Reserv. Eval. Eng. 2007, 10, 740–756. [Google Scholar] [CrossRef]
- Wu, Y.S.; Li, J.; Ding, D.Y.; Wang, C.; Di, Y. A Generalized Framework Model for Simulation of Gas Production in Unconventional Gas Reservoirs. SPE J. 2014, 19, 845–857. [Google Scholar] [CrossRef]
- Wu, Y.; Cheng, L.; Huang, S.; Jia, P. A green element method-based discrete fracture model for simulation of the transient flow in heterogeneous fractured porous media. Adv. Water Resour. 2020, 136, 103489. [Google Scholar] [CrossRef]
- Xu, Y.; Sheng, G.; Zhao, H.; Hui, Y.; Zhou, Y.; Ma, J.; Rao, X.; Zhong, X.; Gong, J. A new approach for gas-water flow simulation in multi-fractured horizontal wells of shale gas reservoirs. J. Pet. Sci. Eng. 2021, 199, 108292. [Google Scholar] [CrossRef]
- Wu, Y.; Cheng, L.; Ma, L.; Huang, S.; Fang, S.; Killough, J.E.; Jia, P.; Wang, S. Transient two-phase flow model for production prediction of tight gas wells with fracturing fluid-induced formation damage. J. Pet. Sci. Eng. 2021, 199, 108351. [Google Scholar] [CrossRef]
- De Swaan, A.O. Analytical solution for determining naturally fractured reservoir properties by well testing. SPE J. 1976, 16, 117–122. [Google Scholar]
- Sun, Z.; Li, X.; Liu, W.; Zhang, T.; He, M.; Nasrabadi, H. Molecular Dynamics of Methane Flow Behavior through Realistic Organic Nanopores under Geologic Shale Condition: Pore size and Kerogen Types. Chem. Eng. J. 2020, 398, 124341. [Google Scholar] [CrossRef]
- Zhou, W.; Banerjee, R.; Poe, B.; Spath, J.; Thambynayagam, M. Semi-analytical production simulation of complex hydraulic fracture networks. SPE J. 2014, 19, 6–18. [Google Scholar] [CrossRef]
- Jia, P.; Cheng, L.; Huang, S.; Liu, H. Transient behavior of complex fracture networks. J. Pet. Sci. Eng. 2015, 132, 1–17. [Google Scholar] [CrossRef]
- Stehfest, H. Numerical Inversion of Laplace Transforms. ACM Commun. 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Qanbari, F. A semi-analytical forecasting method for unconventional gas and light oil wells: A hybrid approach for addressing the limitations of existing empirical and analytical methods. SPE Reserv. Eval. Eng. 2014, 18, 260–263. [Google Scholar]
- Sun, Z.; Huang, B.; Liu, Y.; Jiang, Y.; Zhang, Z.; Hou, M.; Li, Y. Gas-phase production equation for CBM reservoirs: Interaction between hydraulic fracturing and coal orthotropic feature. J. Pet. Sci. Eng. 2022, 213, 110428. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, S.; Xiong, H.; Wu, K.; Shi, J. Optimal nanocone geometry for water flow. AIChE J. 2022, 68, e17543. [Google Scholar] [CrossRef]
- Wattenbarger, R.A.; El-Banbi, A.H.; Villegas, M.E.; Maggard, J.B. Production analysis of linear flow into fractured tight gas wells. Gas Field 1998. [Google Scholar]
- Clarkson, C.R.; Qanbari, F. History-matching and forecasting tight gas condensate and oil wells using the dynamic drainage area concept. In Proceedings of the SPE/CSUR Unconventional Resources Conference, Calgary, AB, Canada, 20–22 October 2015; Society of Petroleum Engineers: Calgary, AB, Canada, 2015. [Google Scholar]
- Wang, S.; Cheng, L.; Xue, Y.; Huang, S.; Wu, Y.; Jia, P.; Sun, Z. A semi-analytical method for simulating two-phase flow performance of horizontal volatile oil wells in fractured carbonate reservoirs. Energies 2018, 11, 2700. [Google Scholar] [CrossRef]

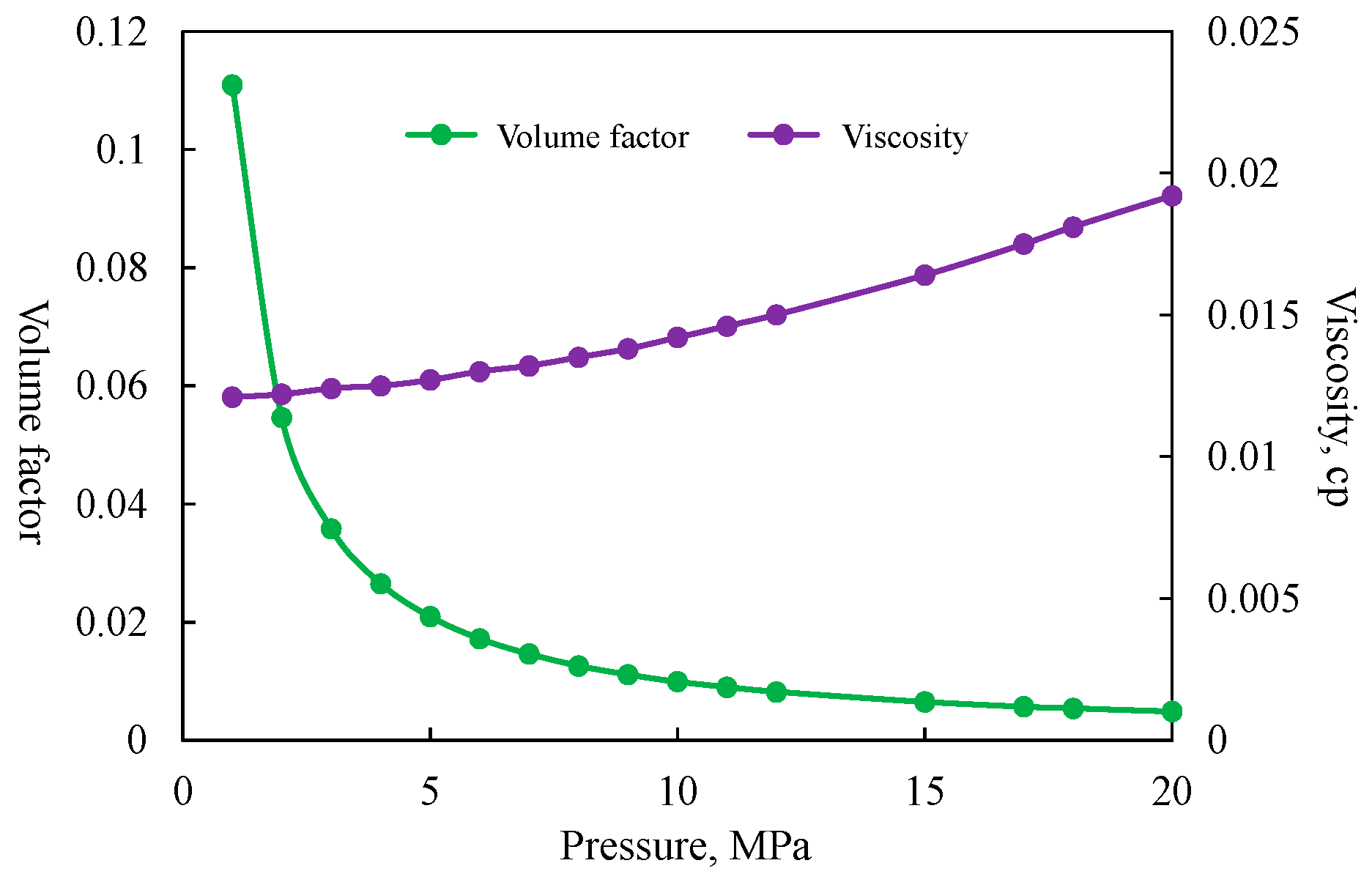
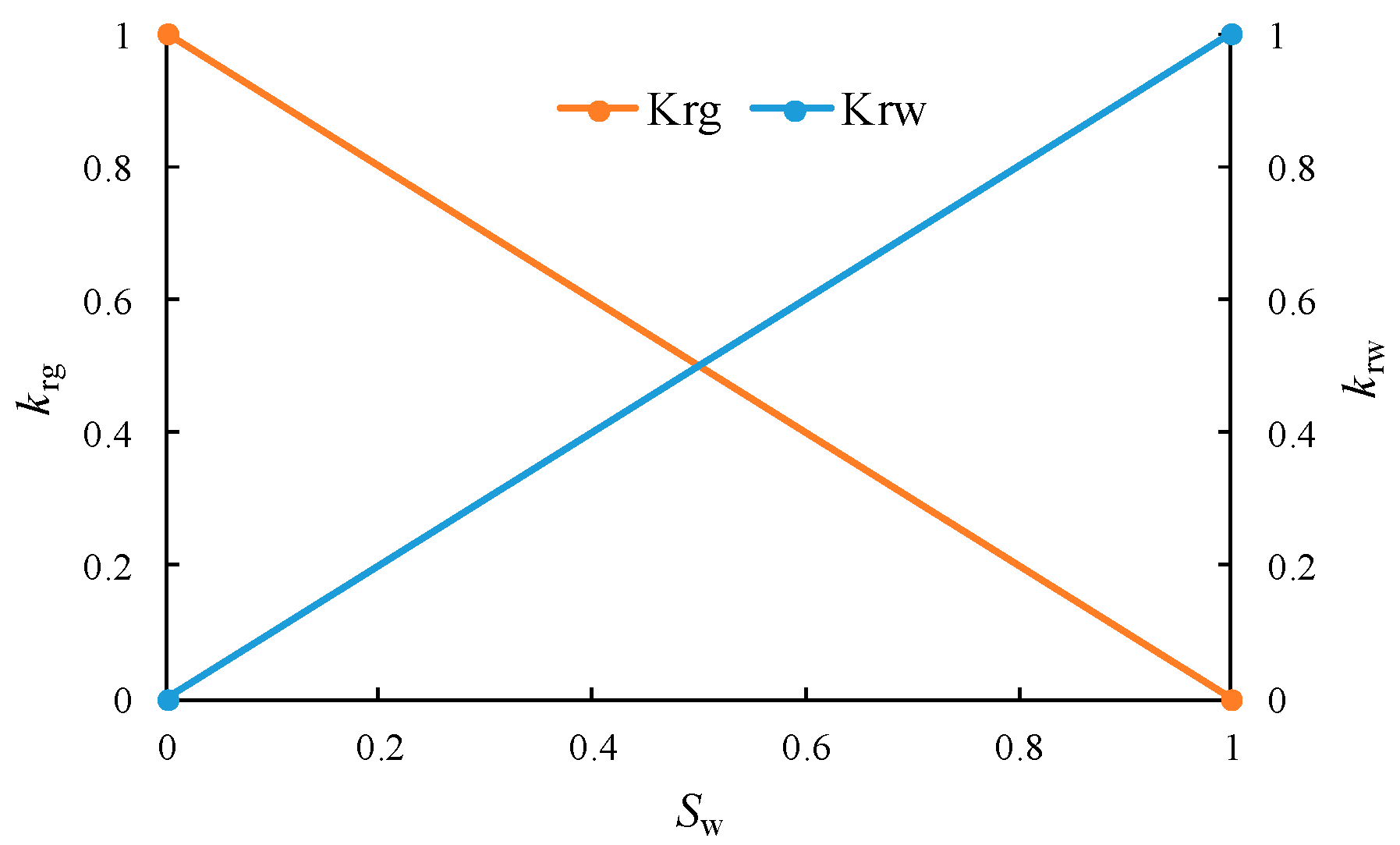
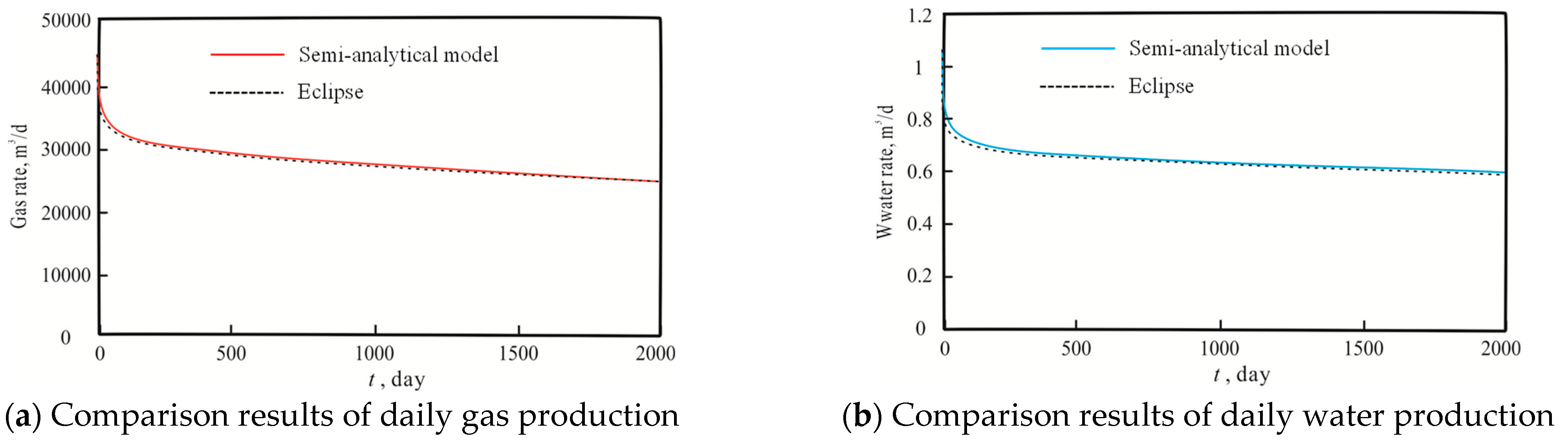
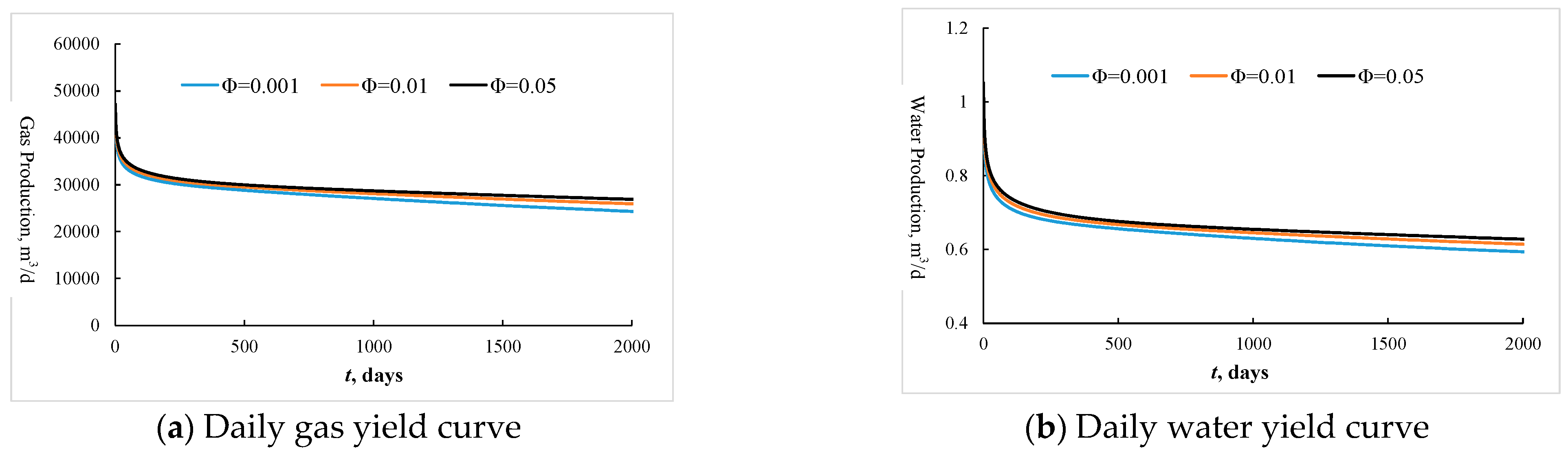
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Reservoir temperature, K | 373 K | Original formation pressure, MPa | 22 |
| Fracture permeability, mD | 50 | Reservoir radius, m | 500 |
| Bottom hole flow pressure, MPa | 6 | Initial gas saturation, % | 65 |
| Compressibility coefficient of rock, MPa−1 | 1 × 10−4 | Permeability modulus, MPa−1 | 0.02 |
| Matrix porosity, % | 9 | Matrix permeability, mD | 0.025 |
| Effective thickness of reservoir, m | 29 | Wellbore radius, m | 0.07 |
| Parameter | Value |
|---|---|
| Permeability modulus, MPa−1 | 0.01, 0.05, 0.1 |
| Fracture porosity, % | 0.1, 1, 5 |
| Outer boundary distance, m | 400, 500, 600 |
| Parameter | Value |
|---|---|
| Fracture porosity | 0.02 |
| Permeability modulus, MPa−1 | 0.035 |
| Outer boundary distance, m | 495 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Sun, Z. A Semi-Analytical Model for Gas–Water Two-Phase Productivity Prediction of Carbonate Gas Reservoirs. Processes 2023, 11, 591. https://doi.org/10.3390/pr11020591
Chen D, Sun Z. A Semi-Analytical Model for Gas–Water Two-Phase Productivity Prediction of Carbonate Gas Reservoirs. Processes. 2023; 11(2):591. https://doi.org/10.3390/pr11020591
Chicago/Turabian StyleChen, Dayong, and Zheng Sun. 2023. "A Semi-Analytical Model for Gas–Water Two-Phase Productivity Prediction of Carbonate Gas Reservoirs" Processes 11, no. 2: 591. https://doi.org/10.3390/pr11020591
APA StyleChen, D., & Sun, Z. (2023). A Semi-Analytical Model for Gas–Water Two-Phase Productivity Prediction of Carbonate Gas Reservoirs. Processes, 11(2), 591. https://doi.org/10.3390/pr11020591






