A Casing Deformation Prediction Model Considering the Properties of Cement
Abstract
:1. Introduction
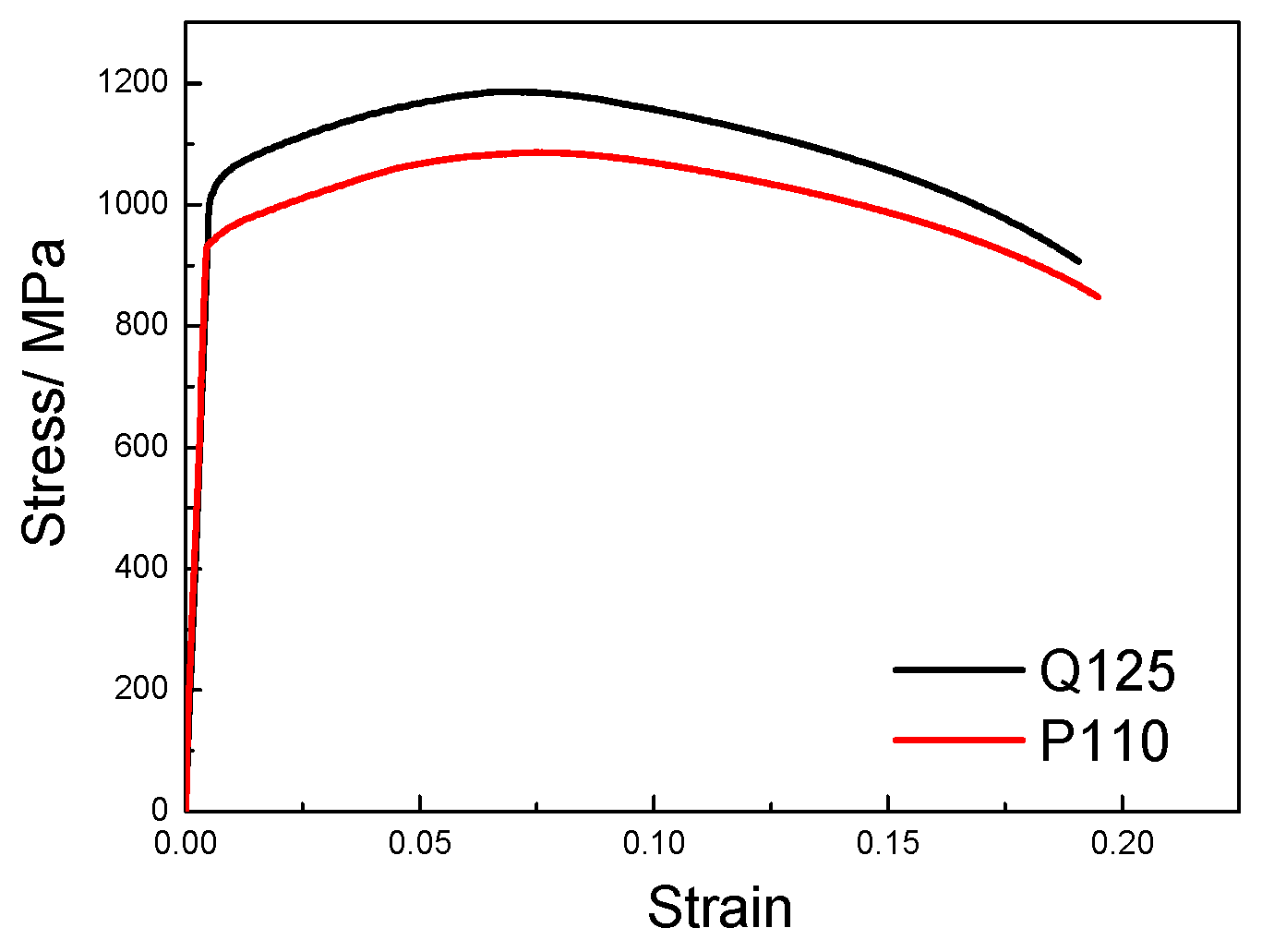
2. Materials and Methods
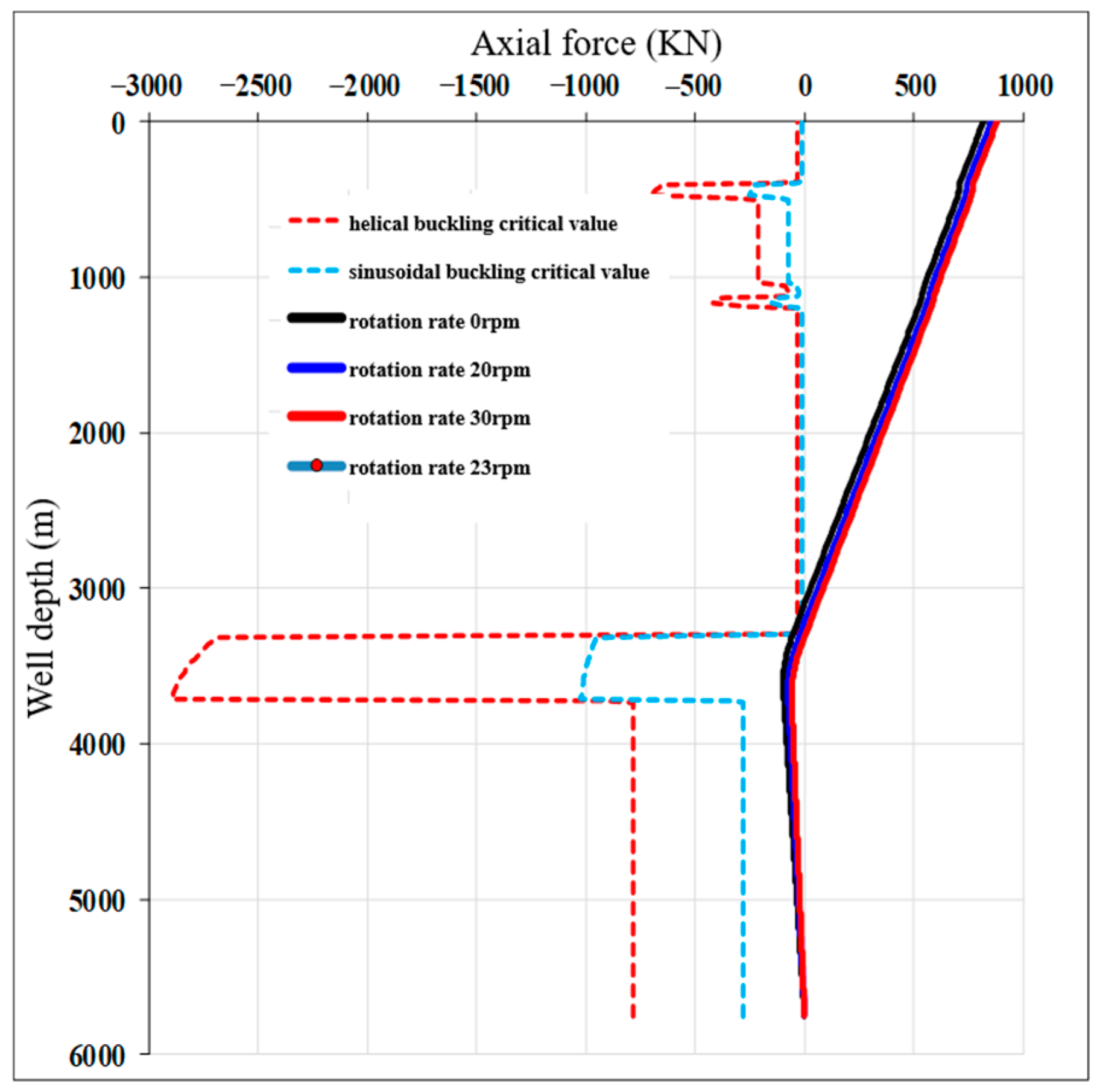
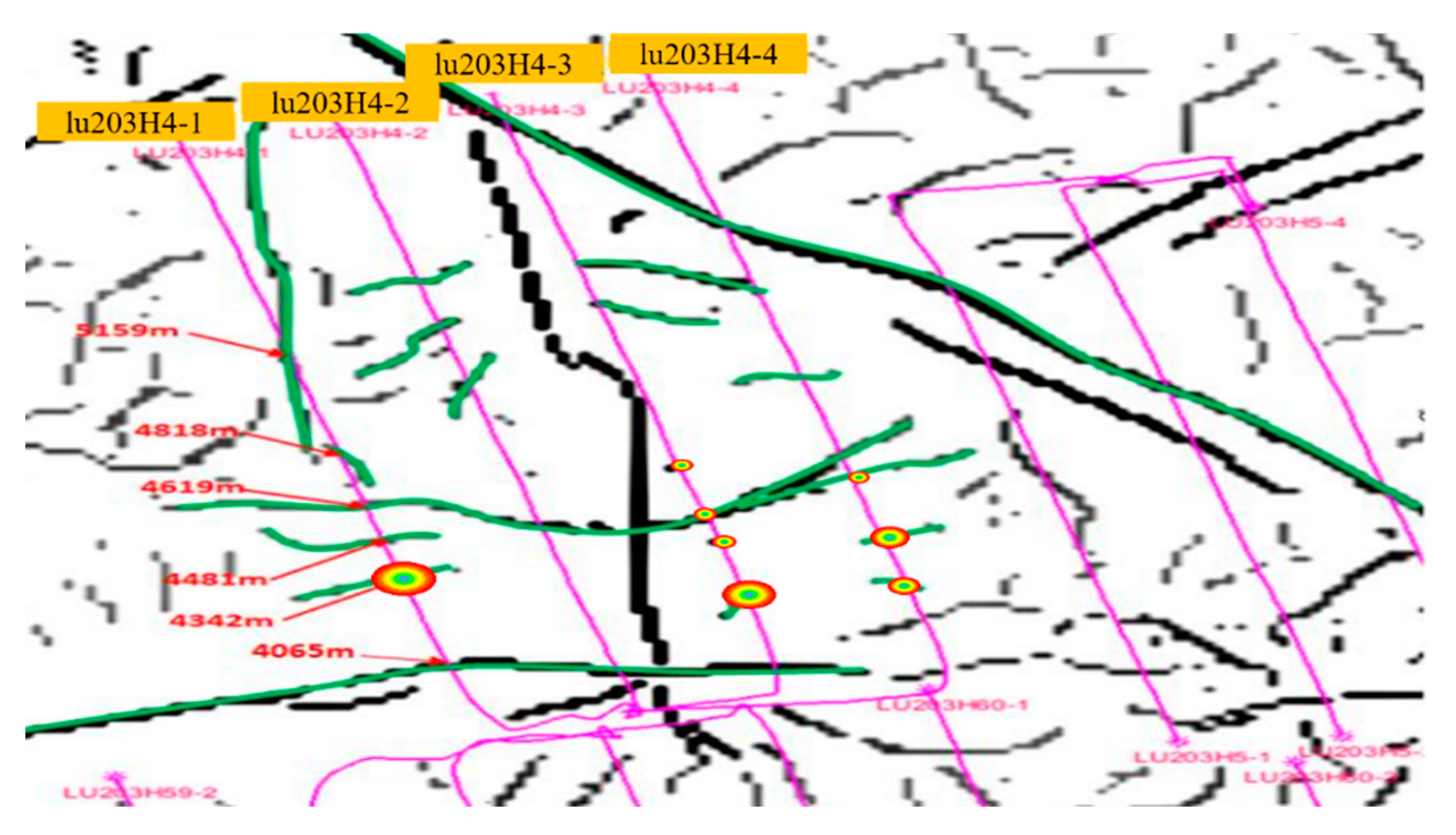
3. Casing Deformation Mechanism and Boundary Conditions of Shale Gas Wells
4. Protective Effect and Influence Law of Cement Sheath on Casing
4.1. Protective Effect of Cement Sheath on Casing
4.2. Influence of Elastic Modulus of Cement Sheath on Casing Deformation
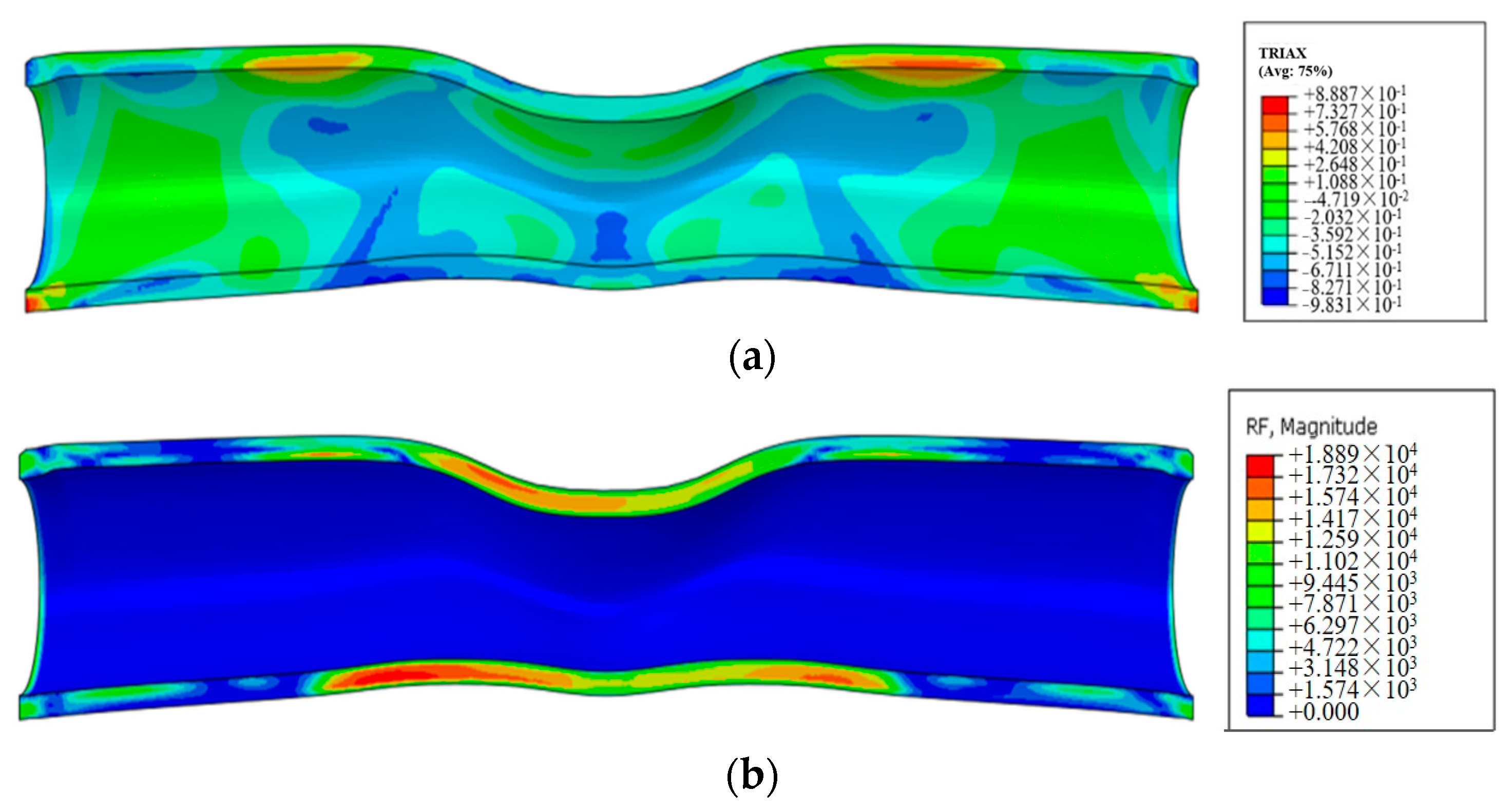
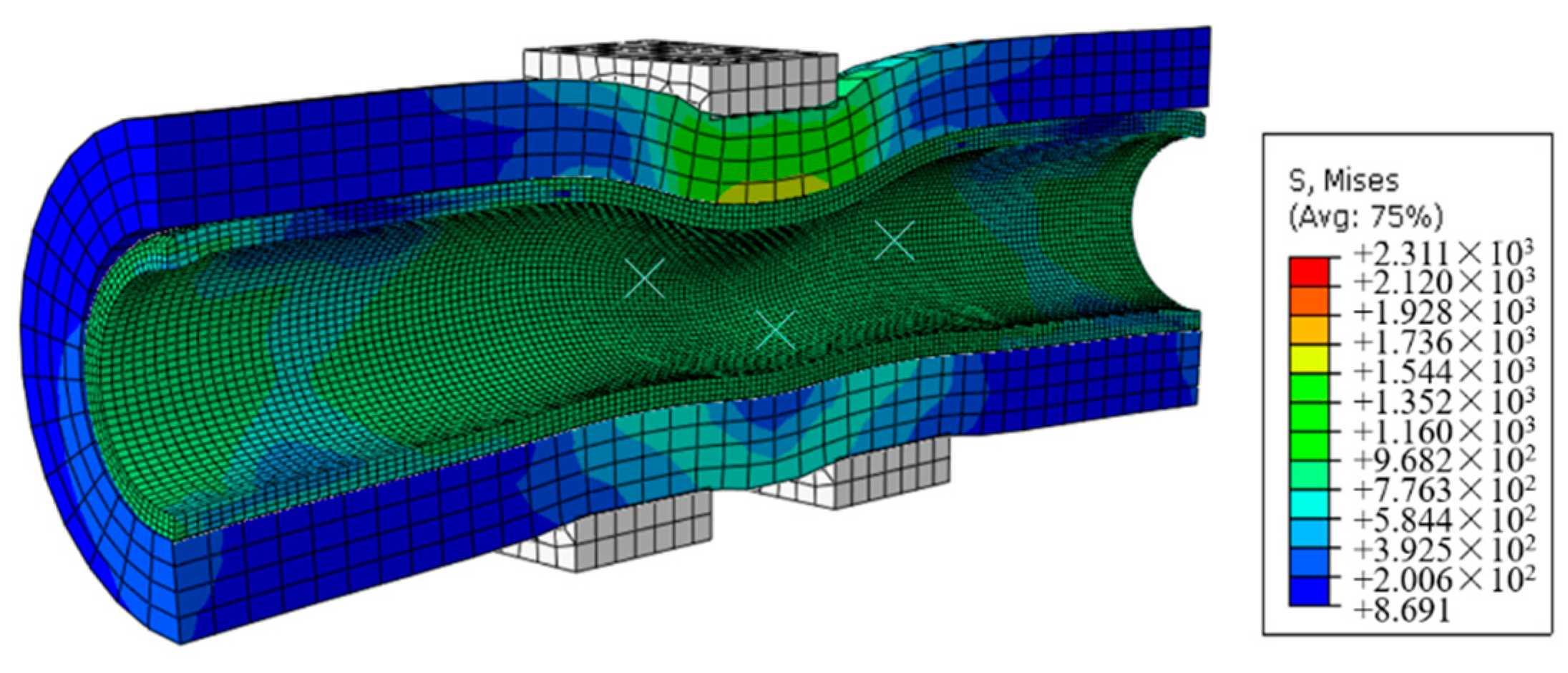
4.3. Influence of Cement Sheath Wall Thickness on Casing Deformation
5. Establishment and Verification of Prediction Model for Casing Minimum Drift Diameter
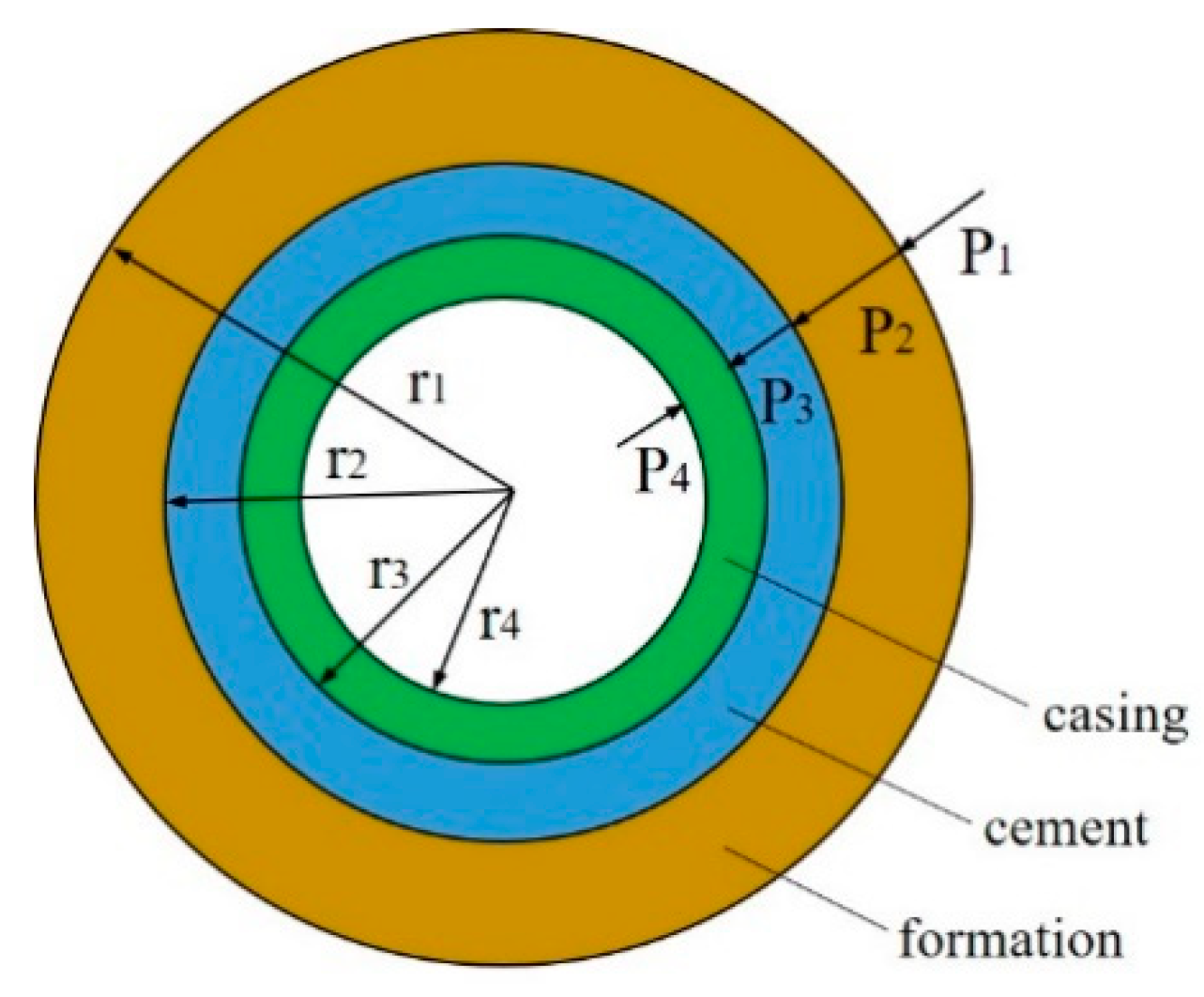
5.1. Casing Outer Wall Displacement
5.2. Displacement of Inner and Outer Walls of Cement Sheath
5.3. Displacement of Inner Wall of Borehole Surrounding Rock
5.4. Establishment and Verification of Prediction Model for Casing Minimum Drift Diameter
6. Conclusions
- (1)
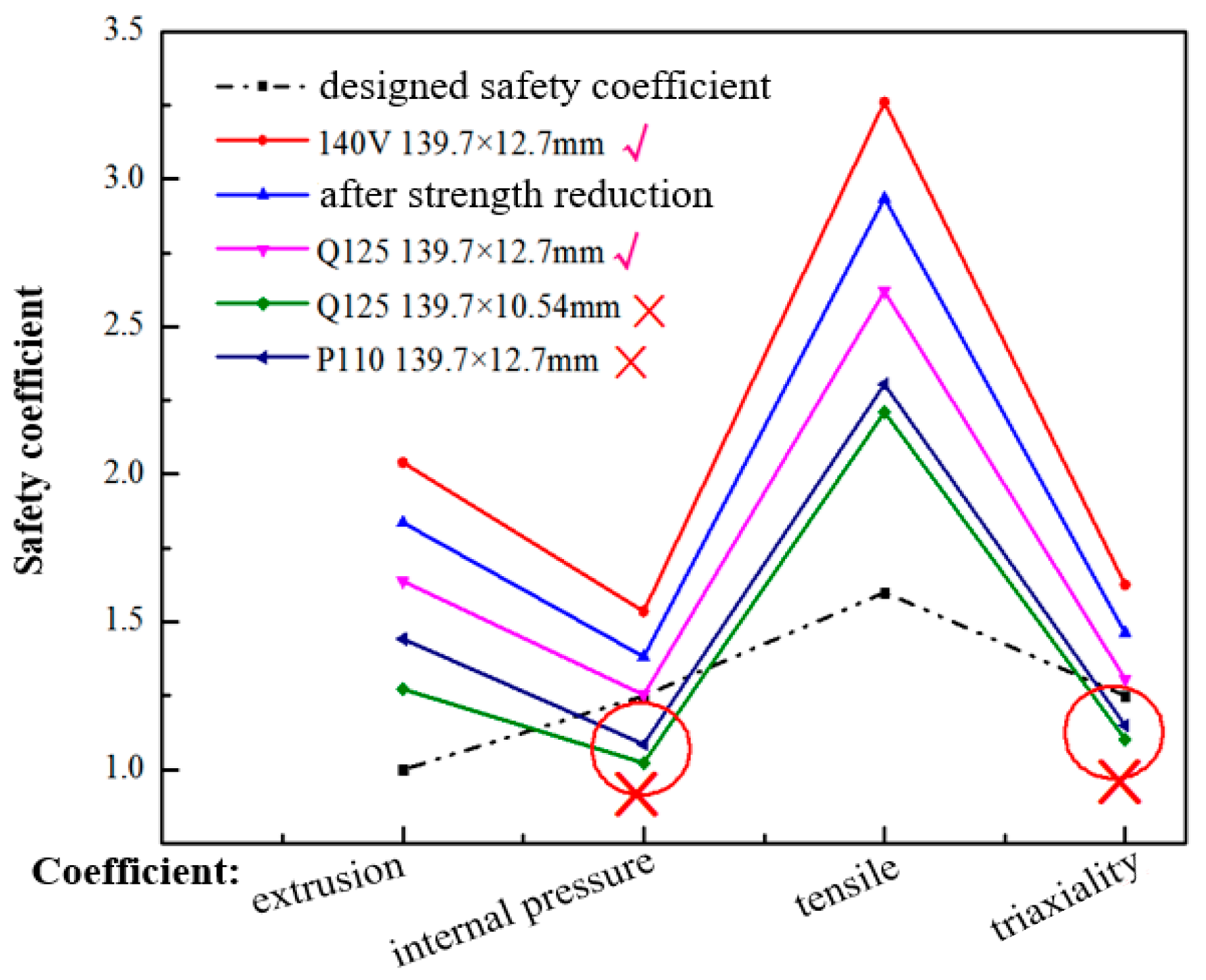
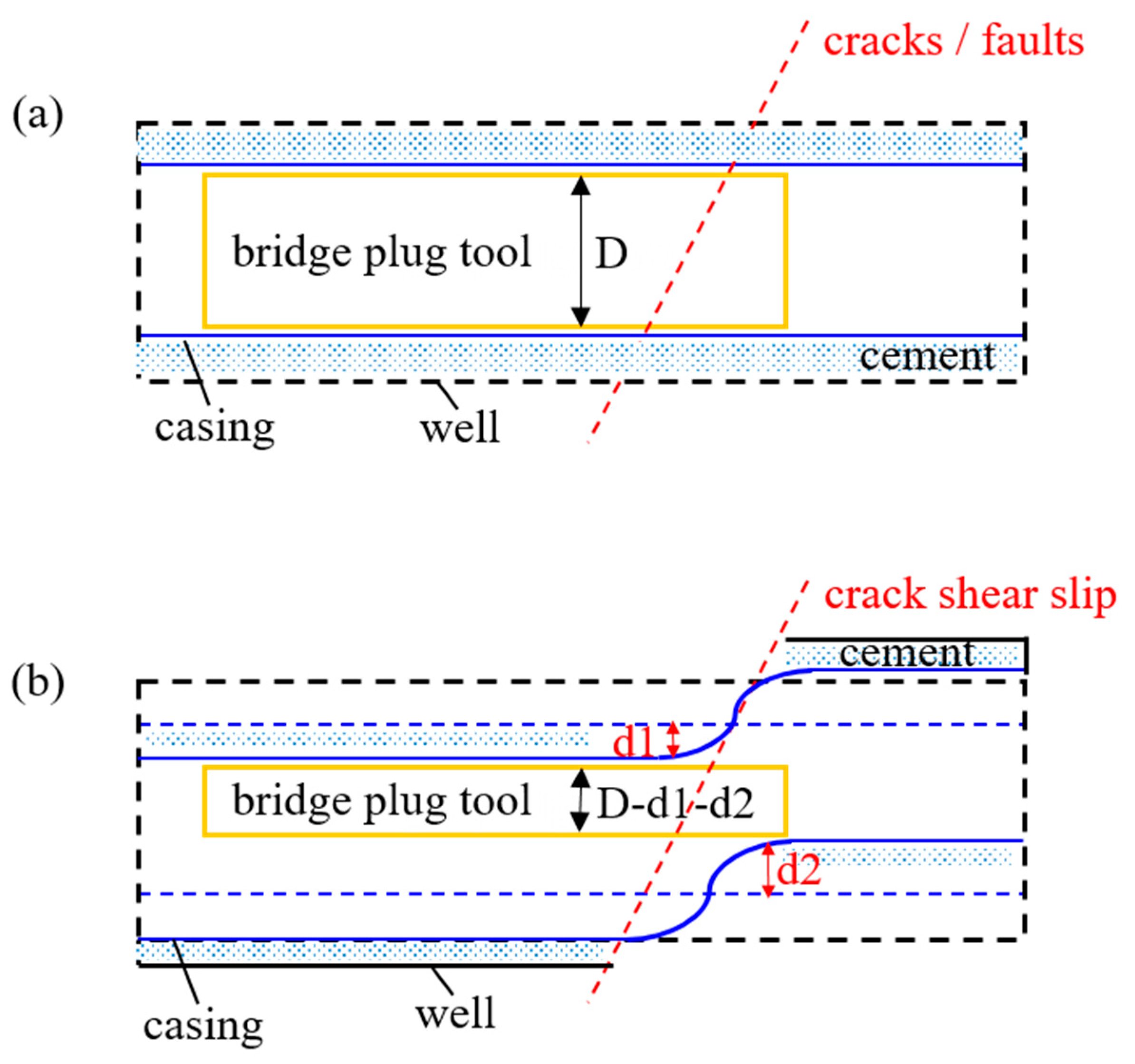
- The main control factor of complex fracturing casing deformation in shale gas wells is displacement control, the mode is shear dominated, and the formation slip boundary condition is less than 40 mm, which provides a basis for casing deformation prevention.
- (2)
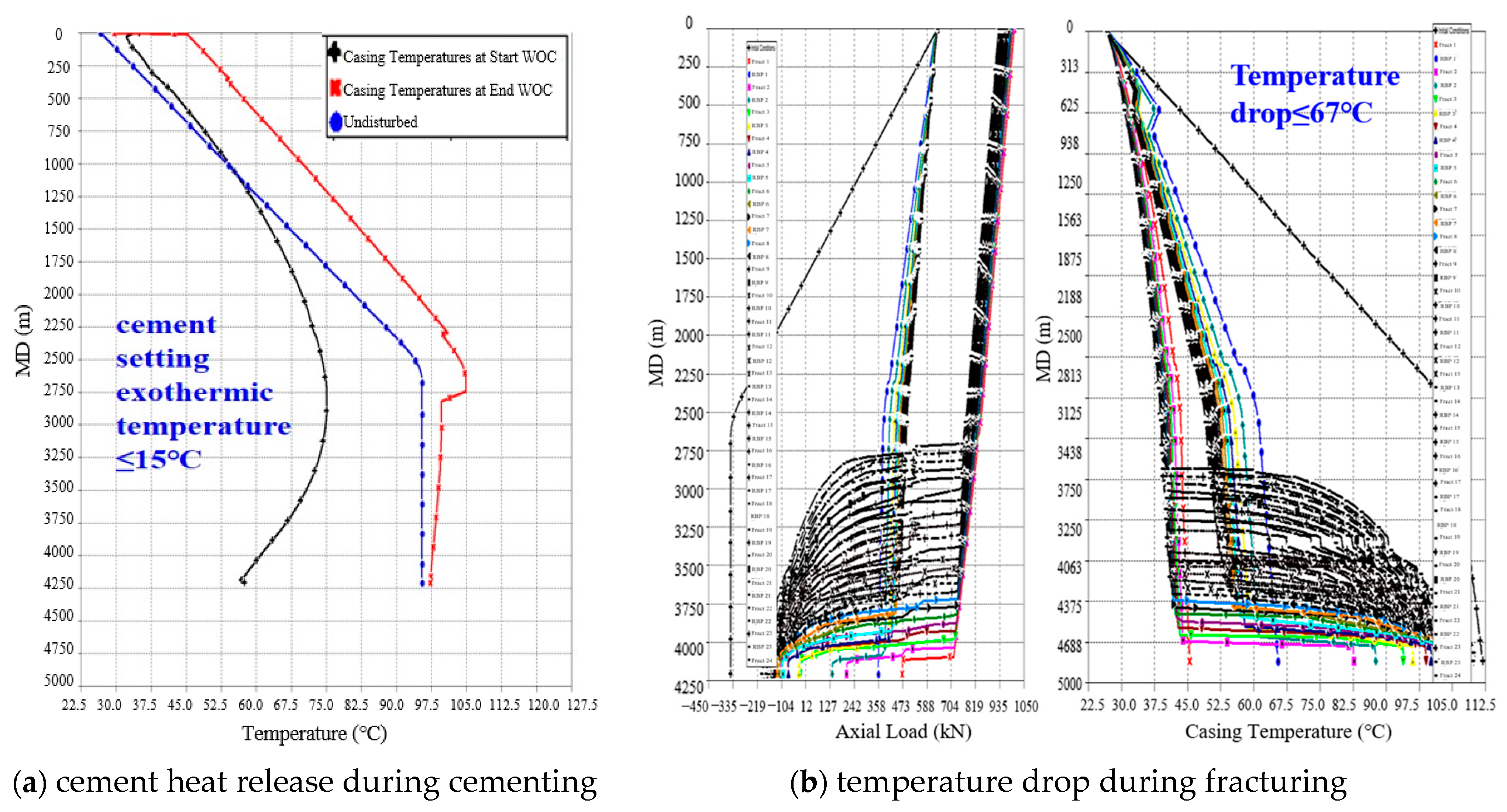
- Considering the rotating speed under casing running condition, the heat release of cement solidification under cementing condition, and the temperature drop of fracturing fluid under fracturing condition comprehensively, the safe service margin of the casing is large, meeting the requirements of working conditions.
- (3)
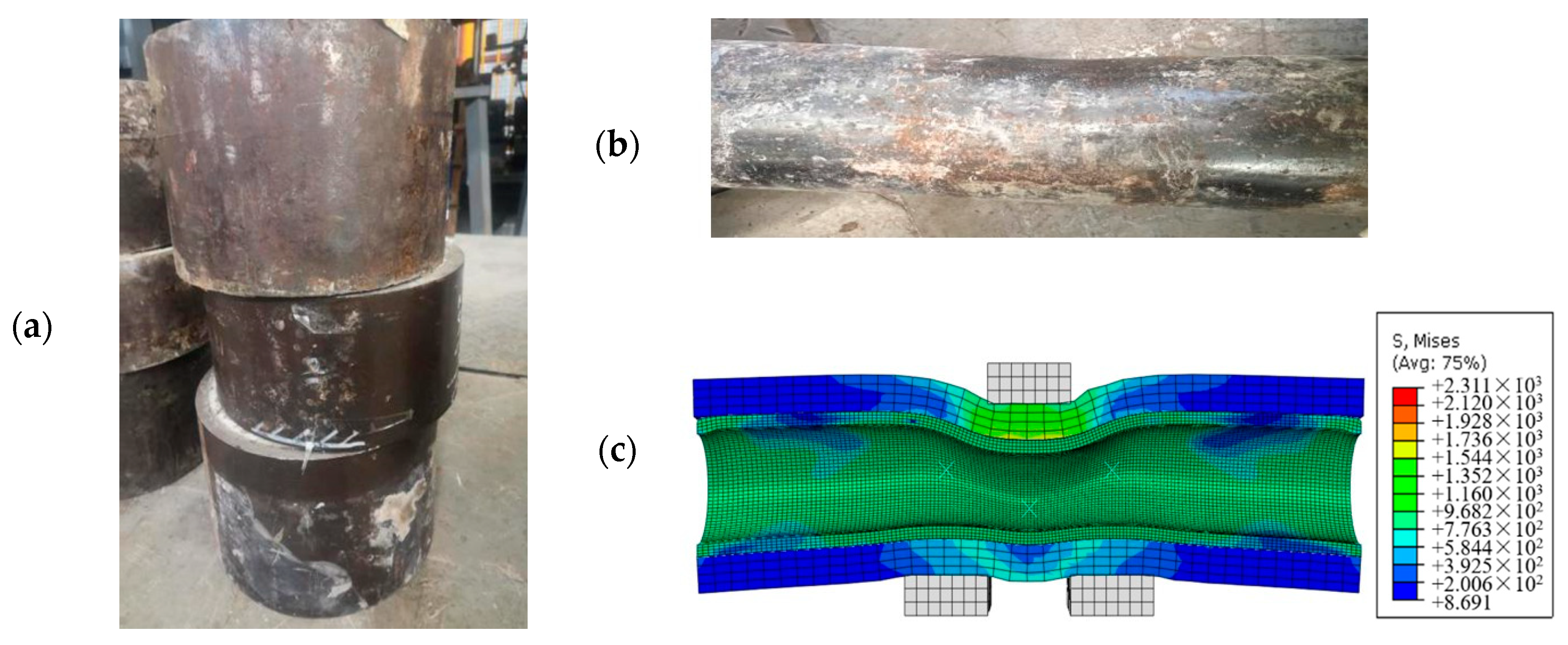
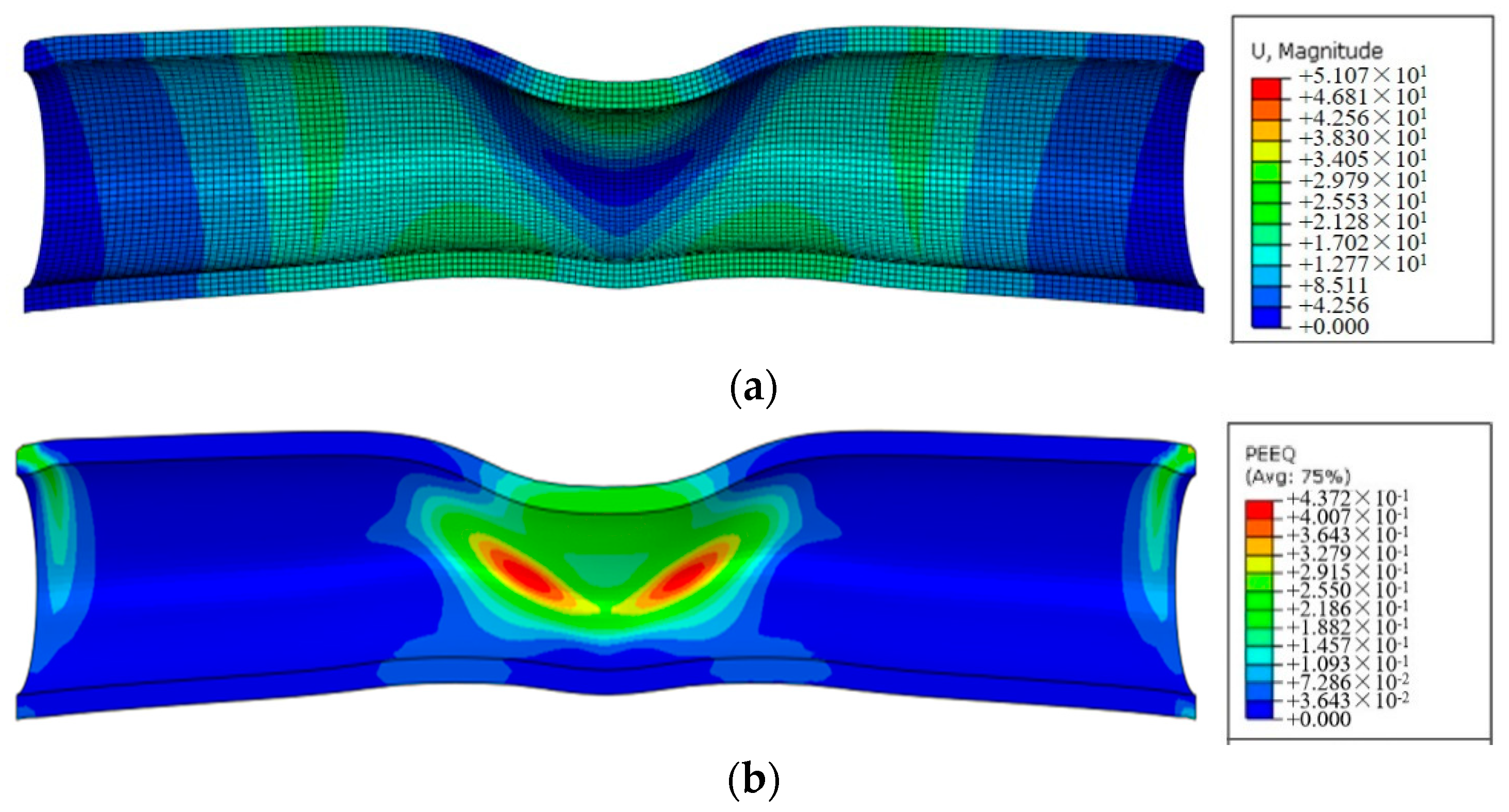
- By using the method of unconventional oil and gas well casing string simulation tests and numerical simulation, the mechanical response of the whole wellbore and the mechanism of bridge plug resistance are studied. An analytical model of the casing minimum drift diameter under the effect of formation slip is established, which provides a technical support for the cement parameter selection and the measures to prevent casing deformation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Landry, G.; Welty, R.D.; Thomas, M.; Vaughan, M.L.; Tatum, D. Bridging the gap: An integrated approach to solving sustained casing pressure in the cana woodford shale. In Proceedings of the SPE Well Integrity Symposium, Galveston, TX, USA, 2–3 June 2015; p. 174525. [Google Scholar]
- Blake, R. Extending lateral length using casing floatation to reduce field development cost in shale gas plays. In Proceedings of the SPE Annual Technical Conference and Exhibition, Amsterdam, The Netherlands, 27 October 2014; p. 170888-MS. [Google Scholar]
- Yin, H.; Zhang, Y.Y. A quantitative evaluation method for the effect of temperature on casing collapsing strength: A case study of large-scale hydraulic fracturing in shale gas horizontal wells. Nat. Gas Ind. 2016, 36, 73–77. [Google Scholar]
- Tian, Z.L.; Shi, L.; Qiao, L. Research of and countermeasure for wellbore integrity of shale gas horizontal well. Natur. Gas Ind. 2015, 35, 70–76. [Google Scholar]
- Lian, W.; Li, J.; Liu, G.H.; Xi, Y.; Wu, L.H.; Chen, L.P. Analysis of casing stress difference at different positions in horizontal segment of shale gas well during fracturing process. Drill. Prod. Technol. 2020, 43, 11–14. [Google Scholar]
- Chen, Z.W.; Xiang, D.G.; Zhang, F.Z.; Mengke, A.; Zirui, Y.; Zhenyuan, J. Fault slip and casing deformation caused by hydraulic fracturing in Changning-Weiyuan Blocks, Sichuan: Mechanism and prevention strategy. Pet. Sci. Bull. 2019, 4, 364–377. [Google Scholar]
- Sugden, C.; Johnson, J.; Chambers, M.; Ring, G.; Suryanarayana, P.V. Special considerations in the design optimization of high rate, Multistage Fractured Shale Wells. In Proceedings of the IADC/SPE Drilling Conference and Exhibition, San Diego, CA, USA, 6–8 March 2012. SPE-151470-MS. [Google Scholar]
- Deenadayalu, C.; Suarez-Rivera, R. The effect of horizontal completions on the breakdown pressures of anisotropic gas shales. Am. Rock Mech. Assoc. 2010, 10, 27–35. [Google Scholar]
- Wang, X.Z.; Qu, Z.; Dou, Y.H. Influence of Geometrical and Physical Parameters of Cement on Loads of Casing and Cement. Adv. Mater. Res. 2013, 634–638, 3591–3594. [Google Scholar] [CrossRef]
- Qu, Z.; Wang, X.Z.; Dou, Y.H. Analytic and Numerical Solutions of Load and Stress of Casing and Cement in Cementing Section. Appl. Mech. Mater. 2013, 268–270, 721–724. [Google Scholar] [CrossRef]
- Deng, J.G.; Tian, H.; Wang, Z.Z.; Zhou, J.L. Laboratory study of casing strength under nonuniform load. Rock Soil Mech. 2005, 26, 855–858. [Google Scholar]
- Zou, L.Z.; Deng, J.Z.; Zeng, Y.J.; Li, J.; Dong, W.Z. Investigation of casing load calculation and casing design for deep salt formation. Pet. Drill. Tech. 2008, 36, 23–27. [Google Scholar]
- Han, L.H.; Yang, S.Y.; Wei, F.Q.; Ye, X.Q.; Wang, J.J. Casing Deformation Mechanism and Controlling Method for Shale Gas Well under Complex Fracture Environment. Pet. Tubul. Goods Instrum. 2020, 6, 16–23. [Google Scholar]
- Li, Y.; Liu, S.Q.; Wang, Z.H. Effect of cement thickness and its mechanical parameters on cement stress. Oil Drill. Prod. Technol. 2010, 32, 37–40. [Google Scholar]


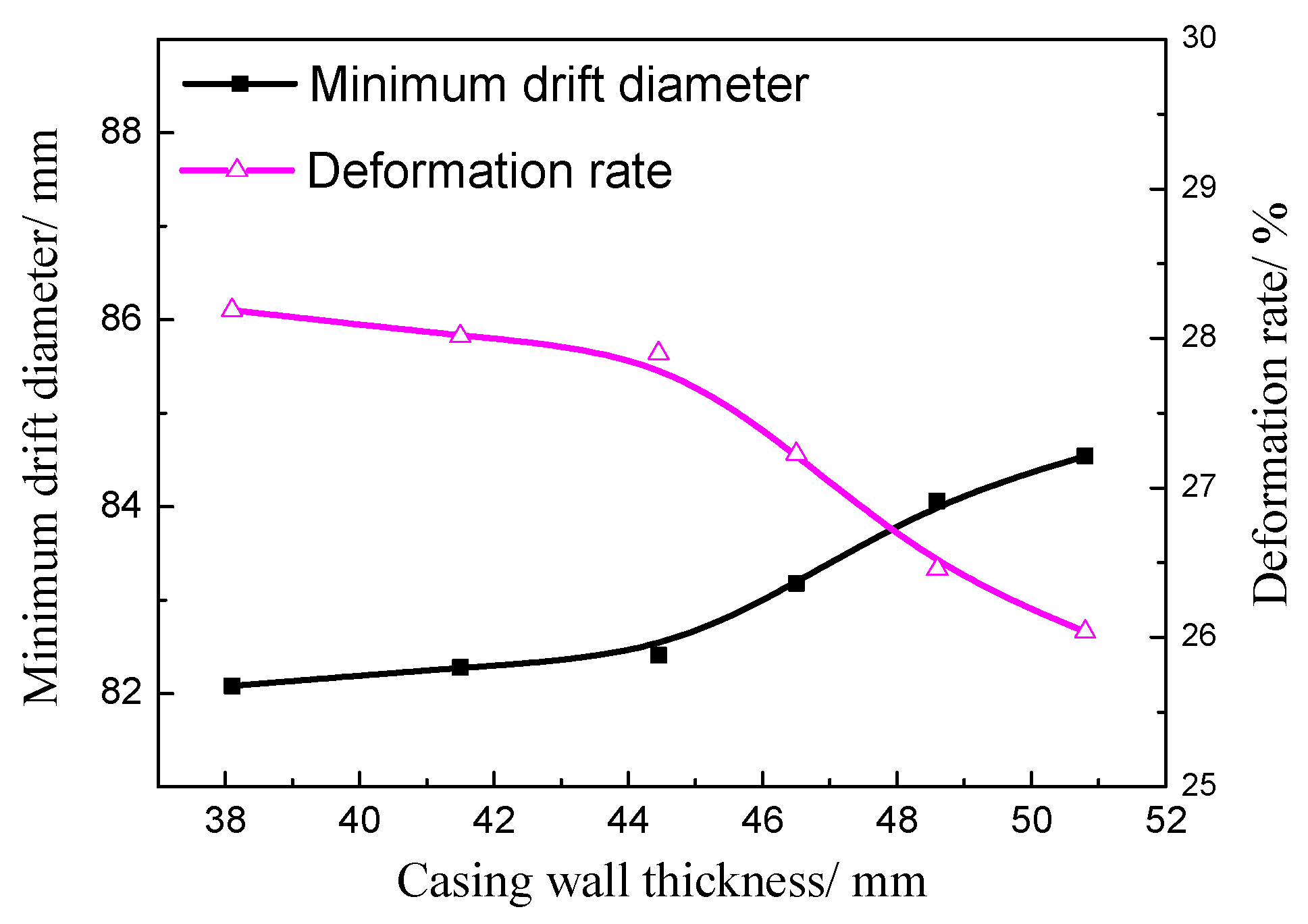

| Wall Thickness/mm | H1/mm | H2/mm | Hmin/mm | ∆H/mm |
|---|---|---|---|---|
| 50.80 | 87.7 | 3.16 | 84.54 | 29.76 |
| 48.60 | 87.38 | 3.32 | 84.06 | 30.24 |
| 46.50 | 86.77 | 3.59 | 83.18 | 31.12 |
| 44.45 | 86.49 | 4.08 | 82.41 | 31.89 |
| 41.50 | 86.44 | 4.16 | 82.28 | 32.02 |
| 38.10 | 86.29 | 4.21 | 82.08 | 32.22 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, B.; Zhou, X.; Cao, J.; Zhou, F.; Wang, Y.; Wang, Y.; Song, Y.; Hu, J.; Du, Y. A Casing Deformation Prediction Model Considering the Properties of Cement. Processes 2023, 11, 695. https://doi.org/10.3390/pr11030695
Zeng B, Zhou X, Cao J, Zhou F, Wang Y, Wang Y, Song Y, Hu J, Du Y. A Casing Deformation Prediction Model Considering the Properties of Cement. Processes. 2023; 11(3):695. https://doi.org/10.3390/pr11030695
Chicago/Turabian StyleZeng, Bo, Xiaojin Zhou, Jing Cao, Feng Zhou, Yao Wang, Yezhong Wang, Yi Song, Junjie Hu, and Yurou Du. 2023. "A Casing Deformation Prediction Model Considering the Properties of Cement" Processes 11, no. 3: 695. https://doi.org/10.3390/pr11030695
APA StyleZeng, B., Zhou, X., Cao, J., Zhou, F., Wang, Y., Wang, Y., Song, Y., Hu, J., & Du, Y. (2023). A Casing Deformation Prediction Model Considering the Properties of Cement. Processes, 11(3), 695. https://doi.org/10.3390/pr11030695






