Parametric Analysis of a Double Shaft, Batch-Type Paddle Mixer Using the Discrete Element Method (DEM)
Abstract
1. Introduction
2. Materials and Methods
2.1. Modelling Approach
2.2. Simulation Setup
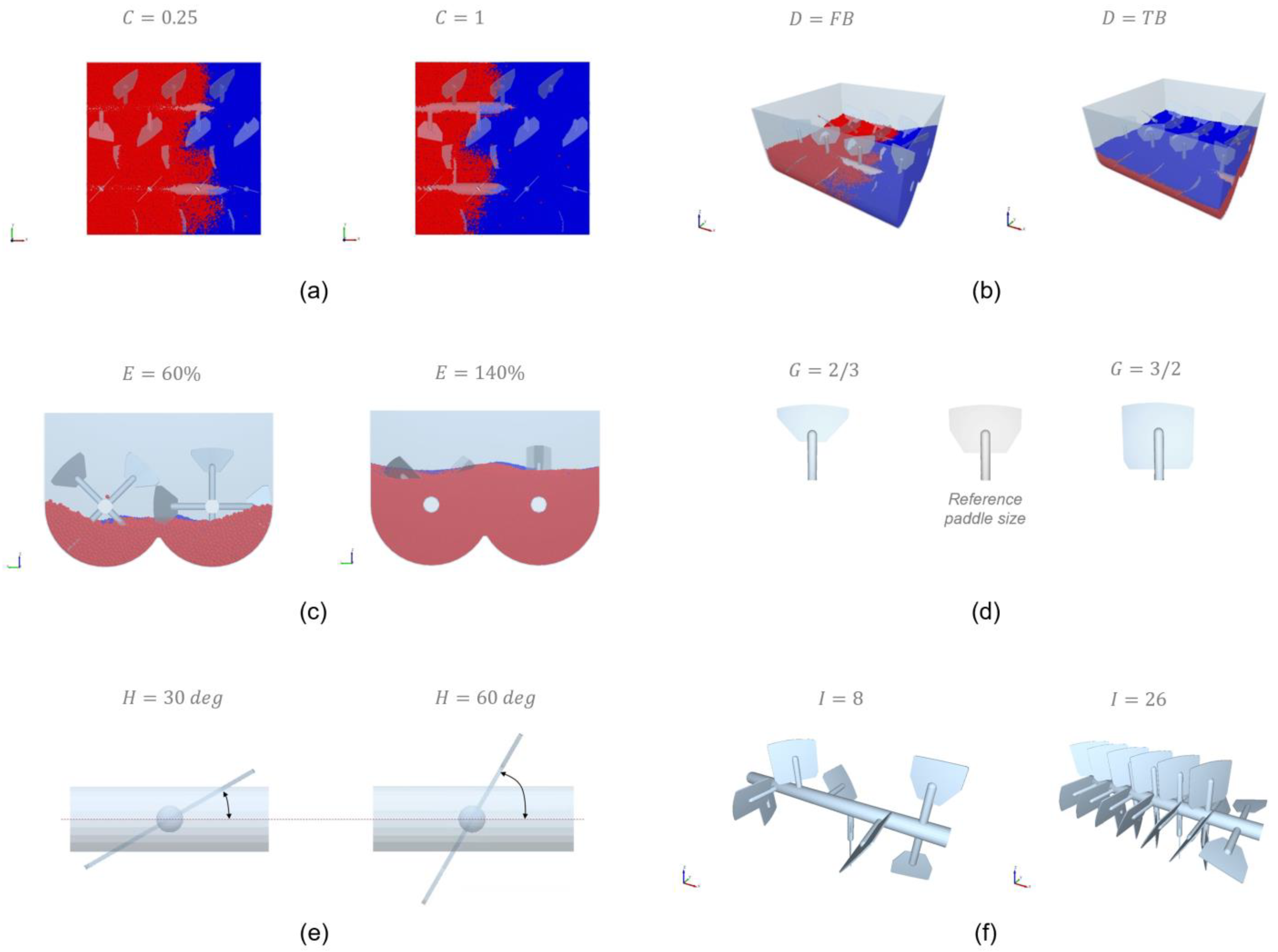
2.3. Plackett–Burman (P–B)
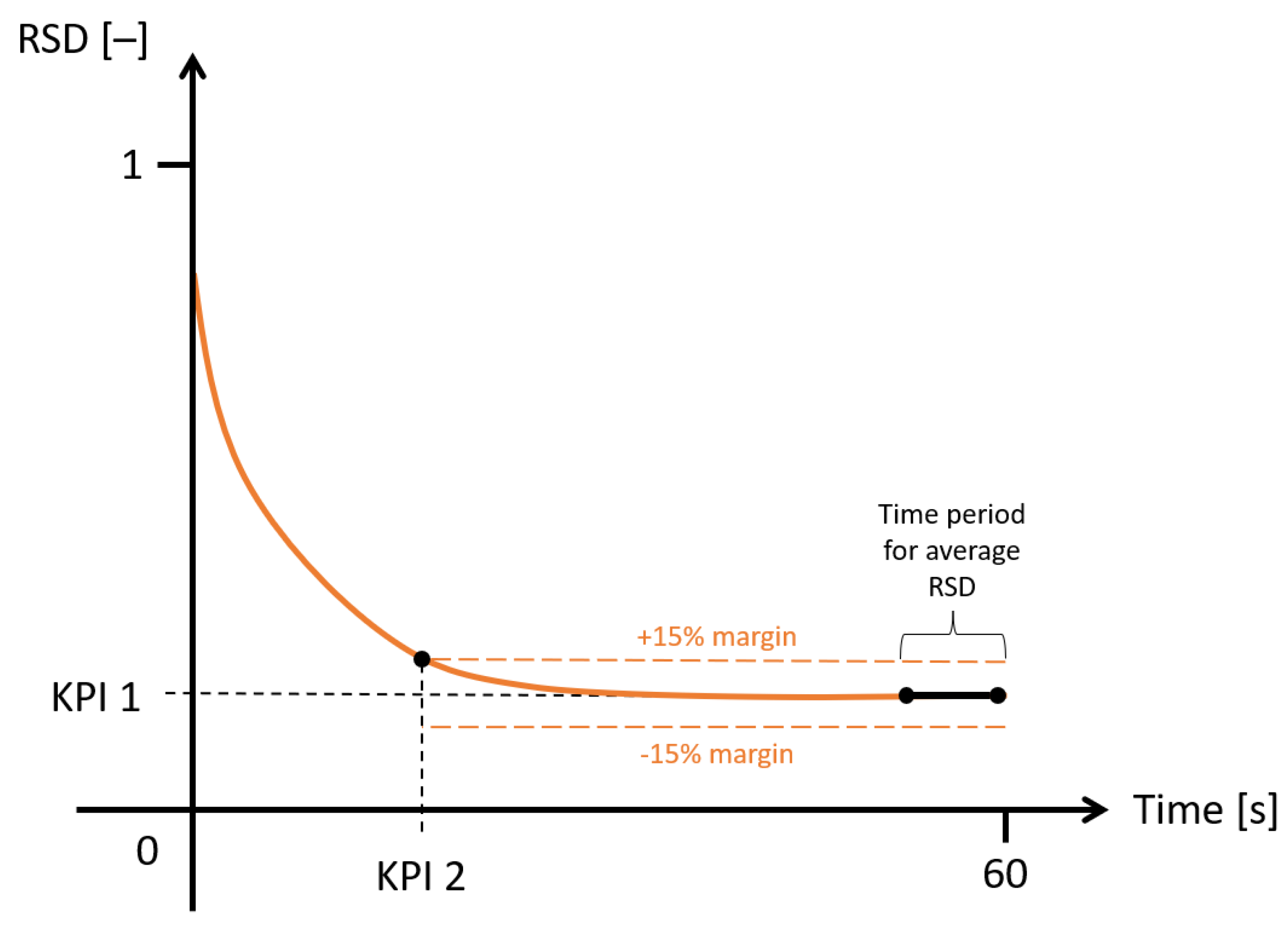
- KPI 1 (-) Mixing quality—Average steady-state RSD;
- KPI 2 (s) Mixing time—Time required to reach a steady-state RSD;
- KPI 3 (W/kg) Normalized average power—Average energy per second per kilogram over a full mixing period;
- KPI 4 (J/kg) Total energy consumption—Required energy to reach a steady state RSD.
2.4. Grid System
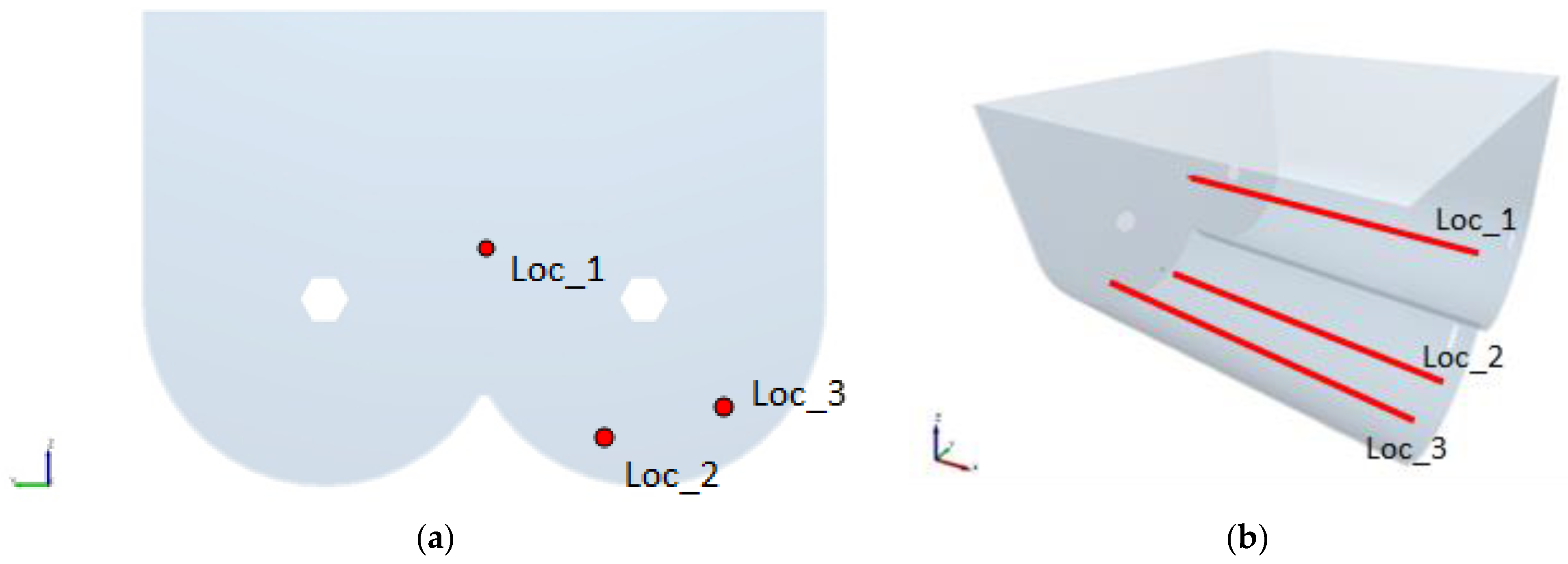
2.5. Granular Temperature
3. Results and Discussion
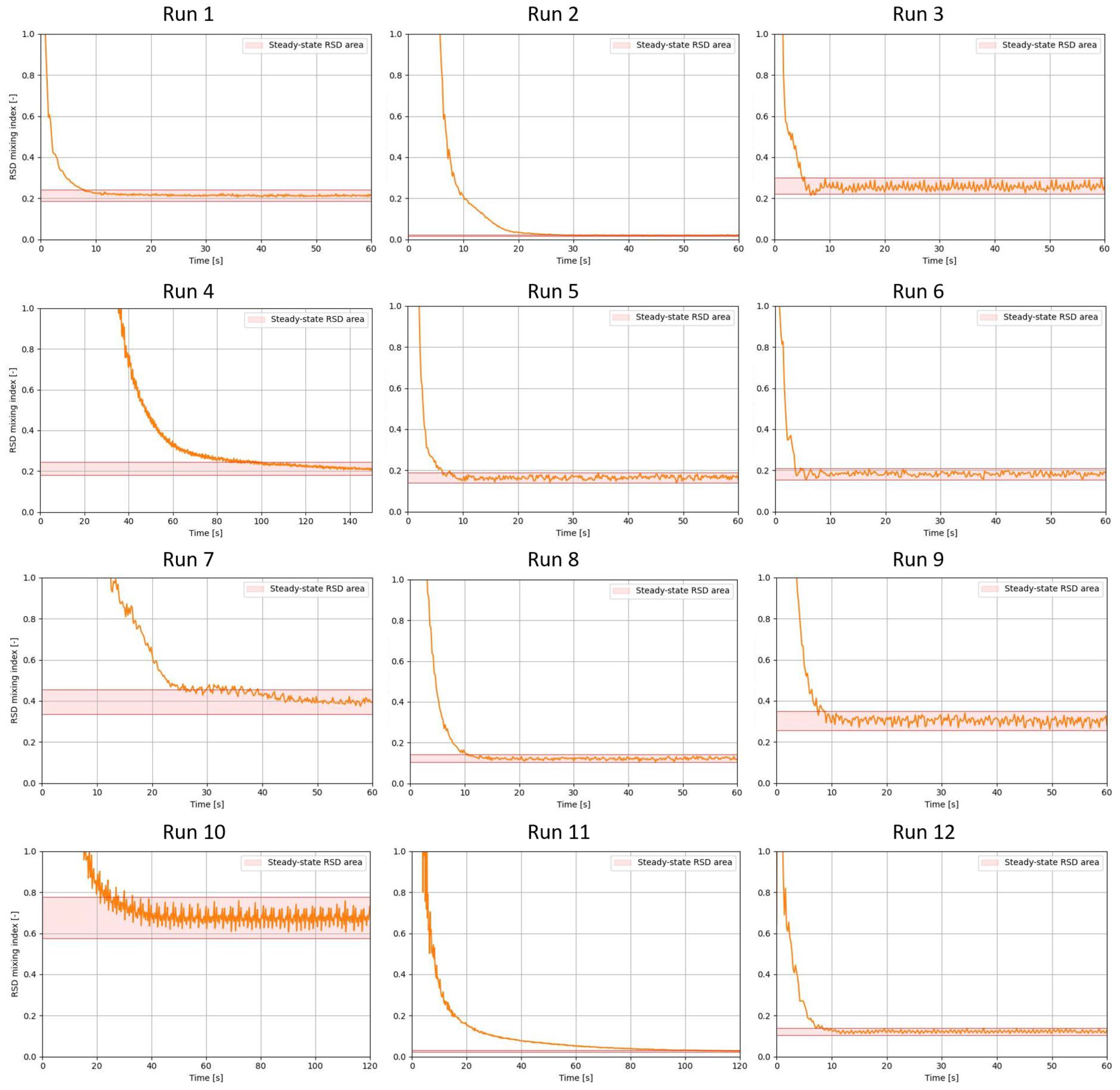
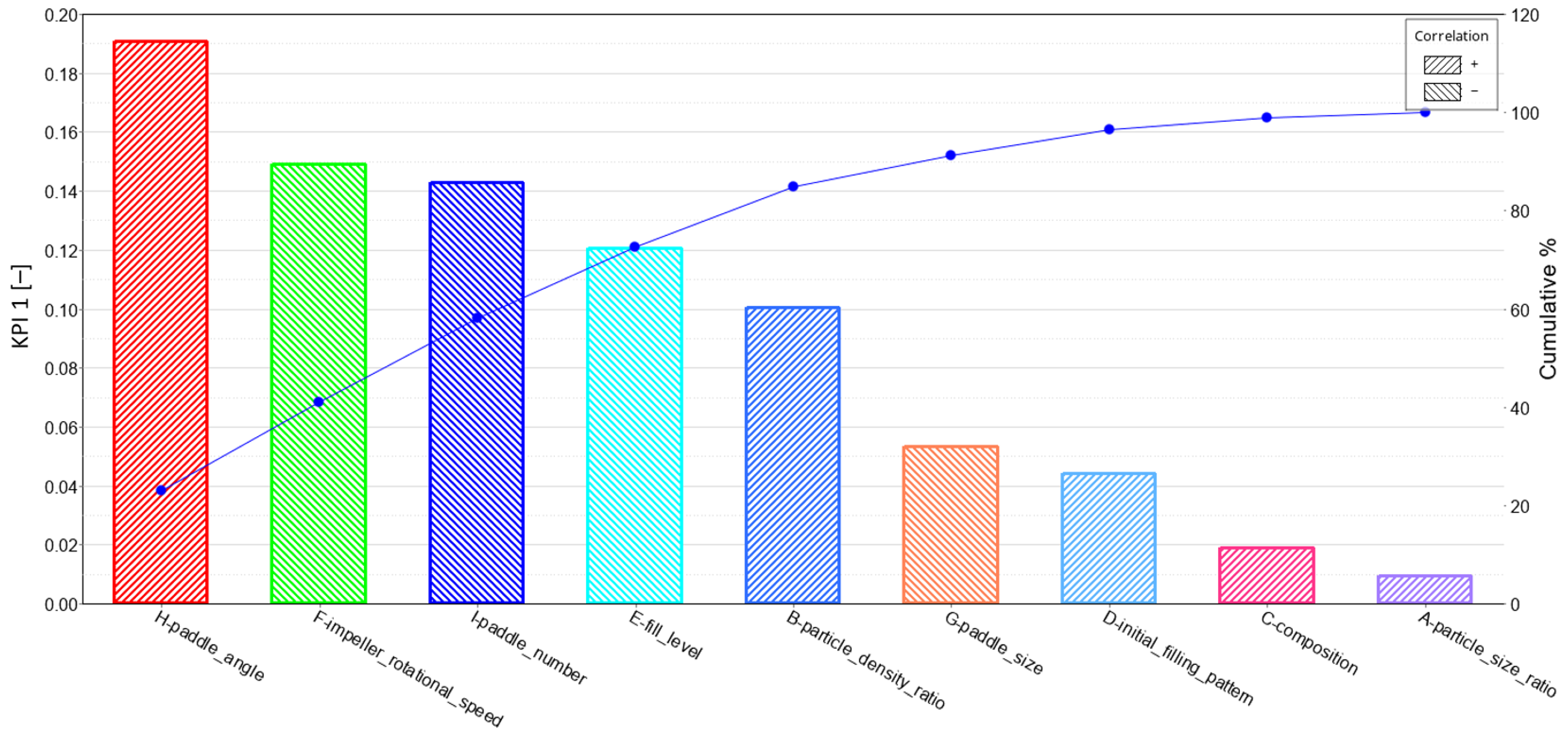
3.1. KPI 1: Mixing Quality
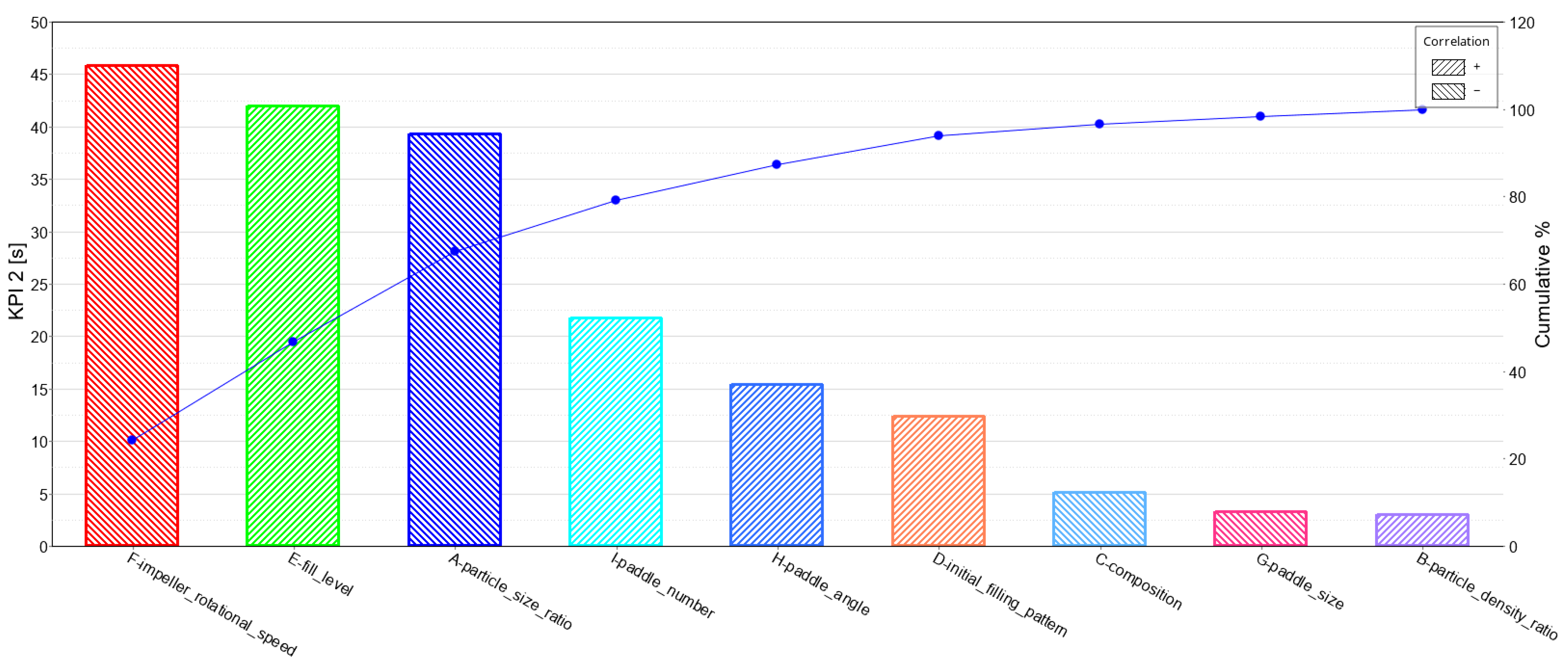
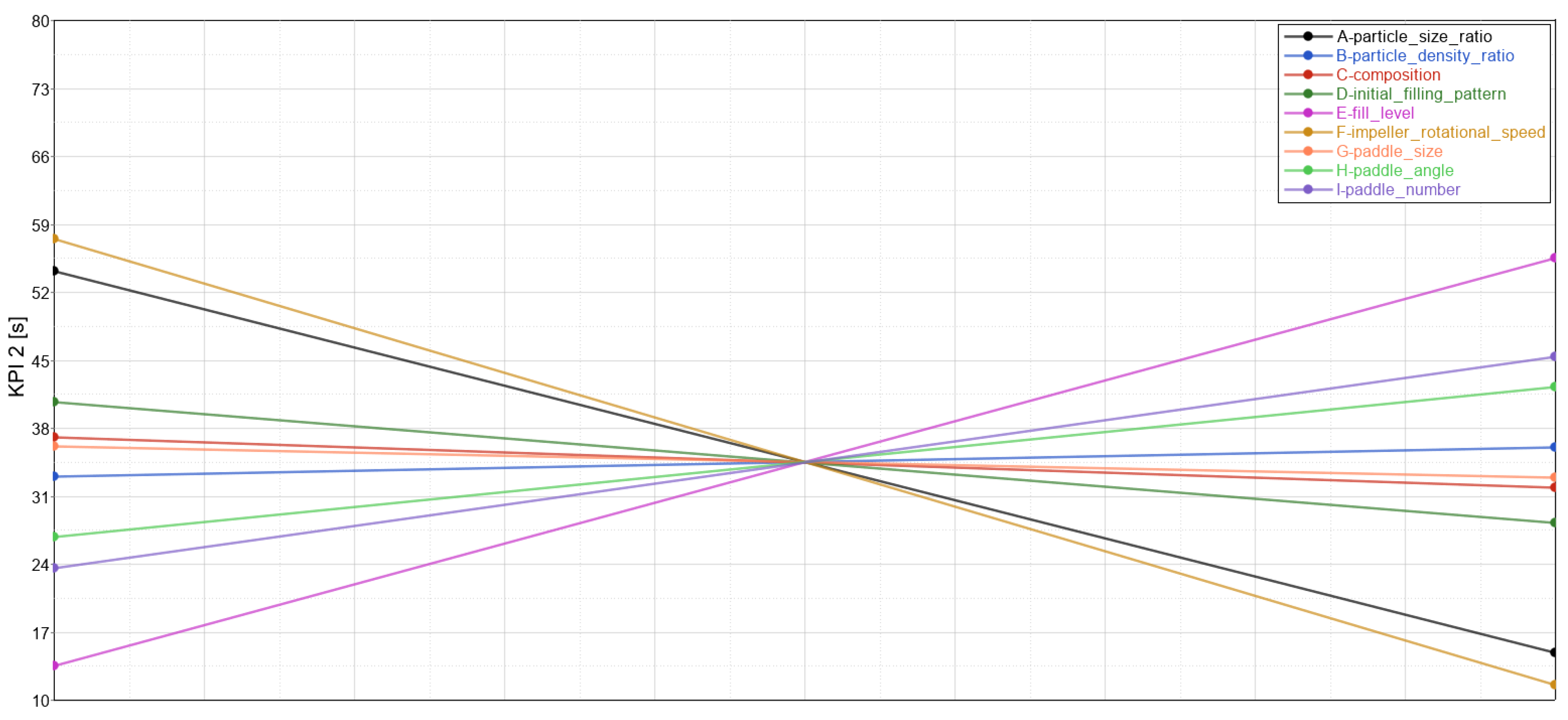
3.2. KPI 2: Mixing Time
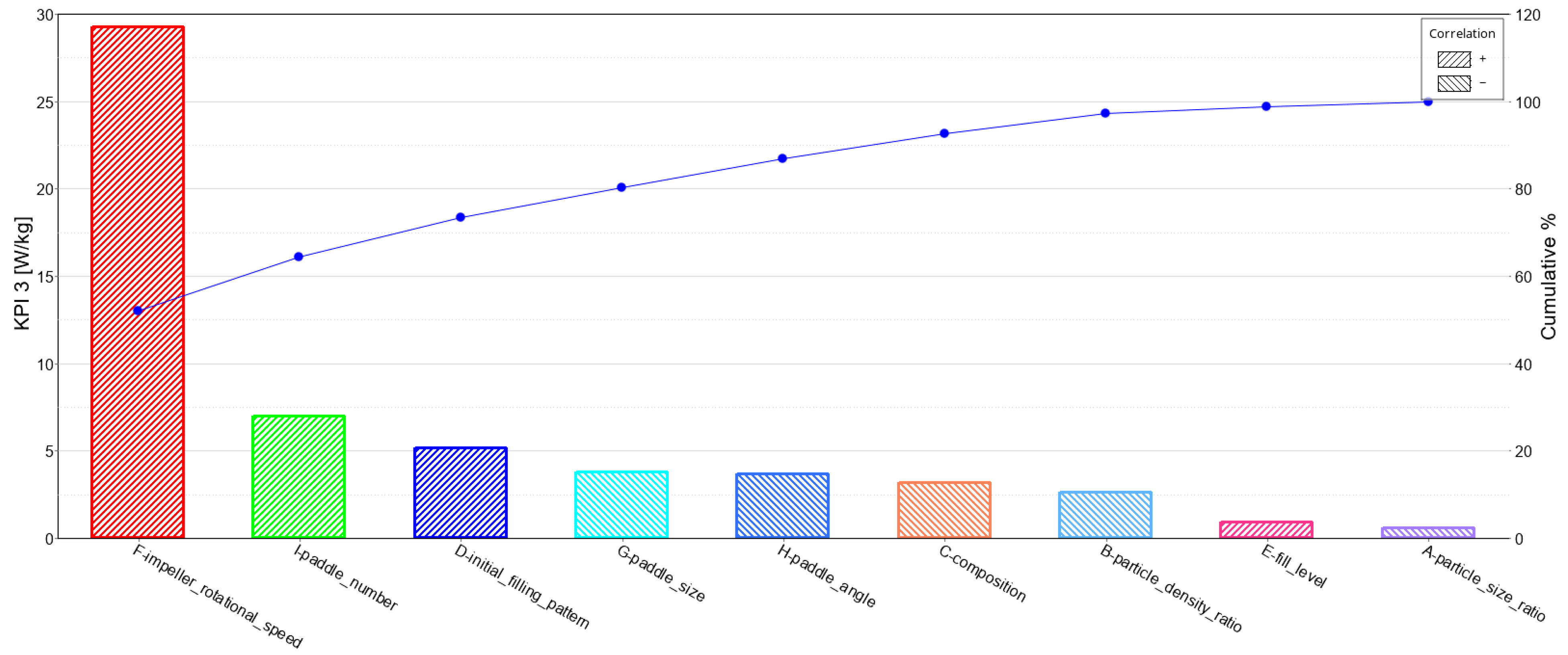
3.3. KPI 3: Average Mixing Power Per Kilogram
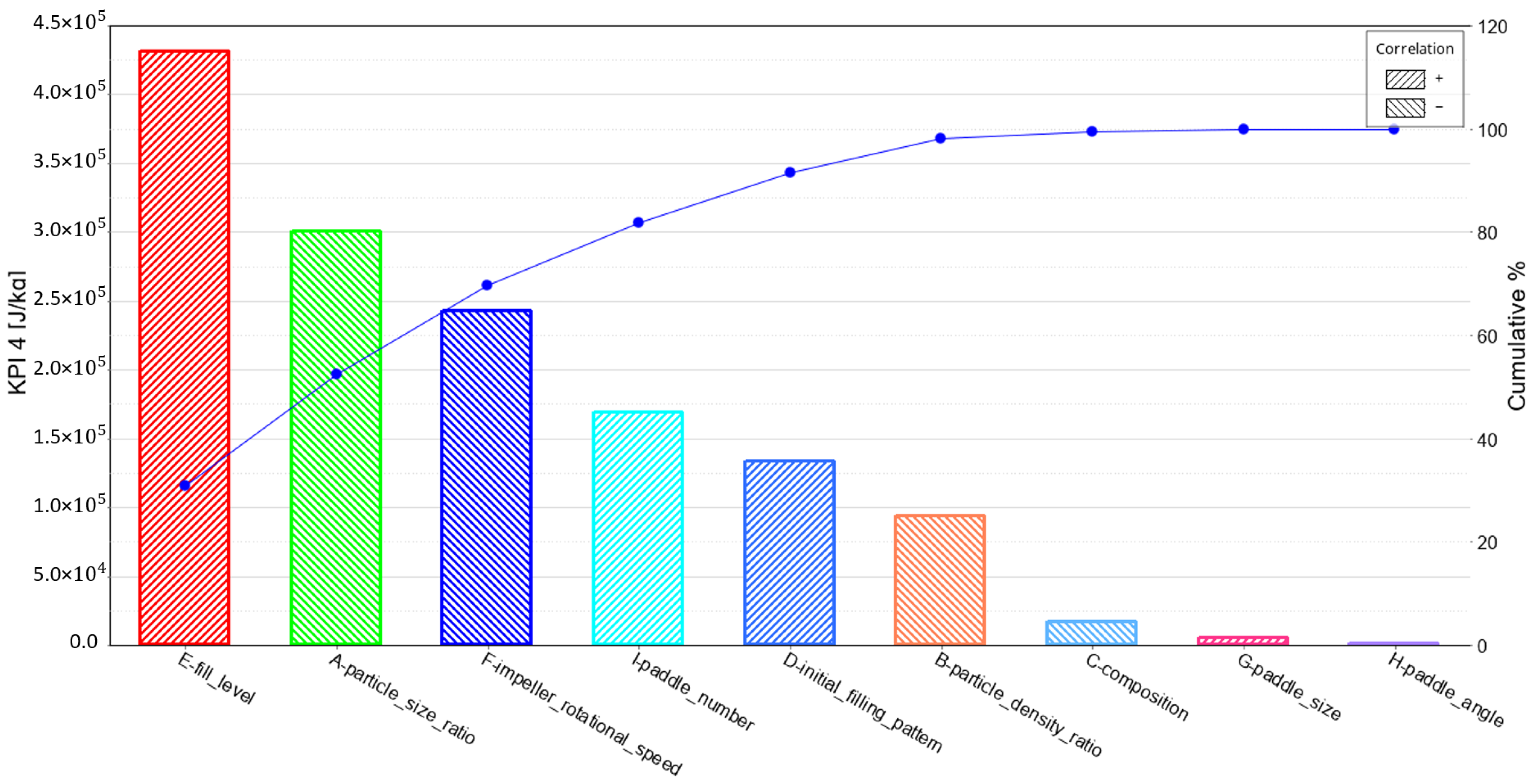
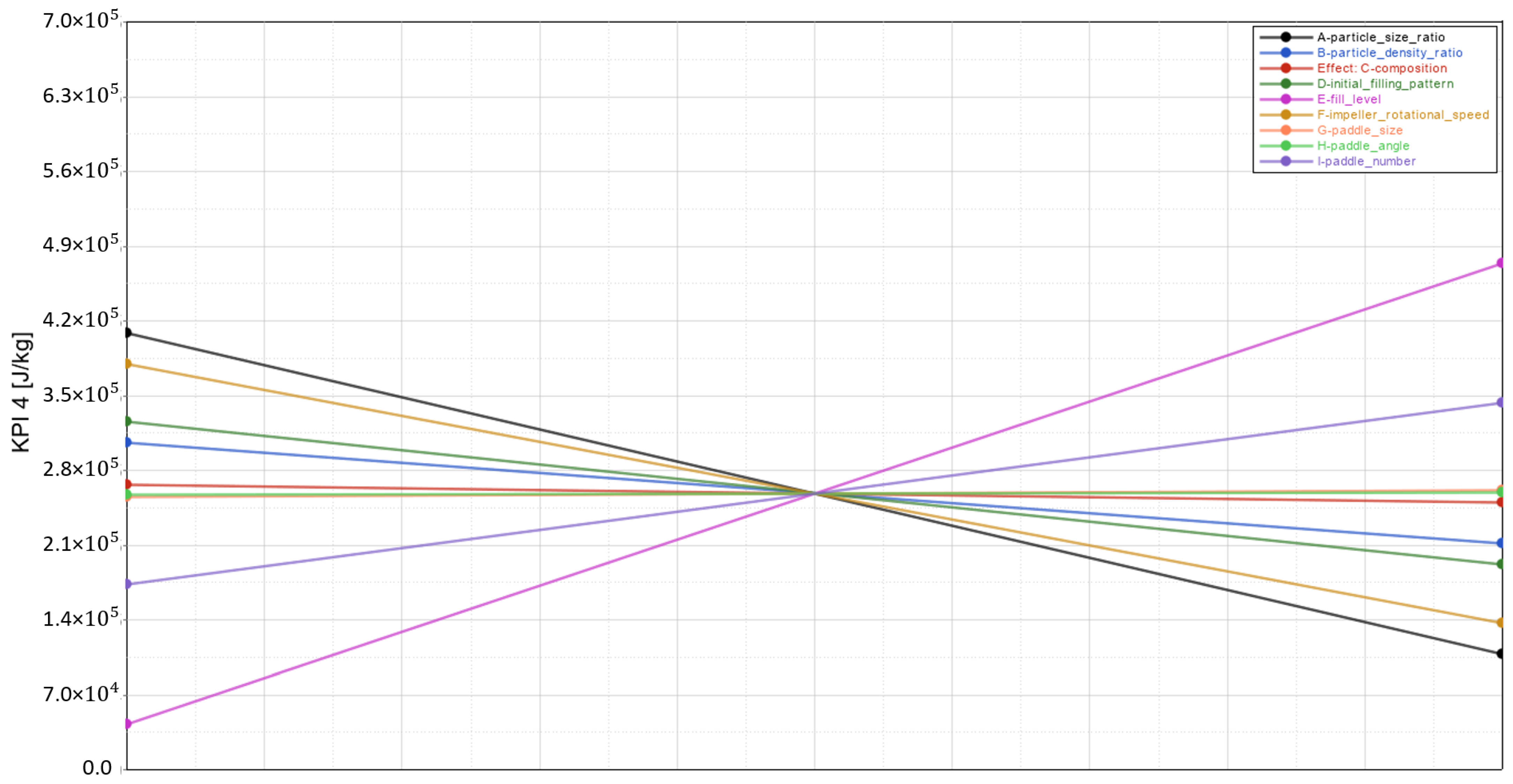
3.4. KPI 4: Total Mixing Energy Required to Reach a Steady-State RSD
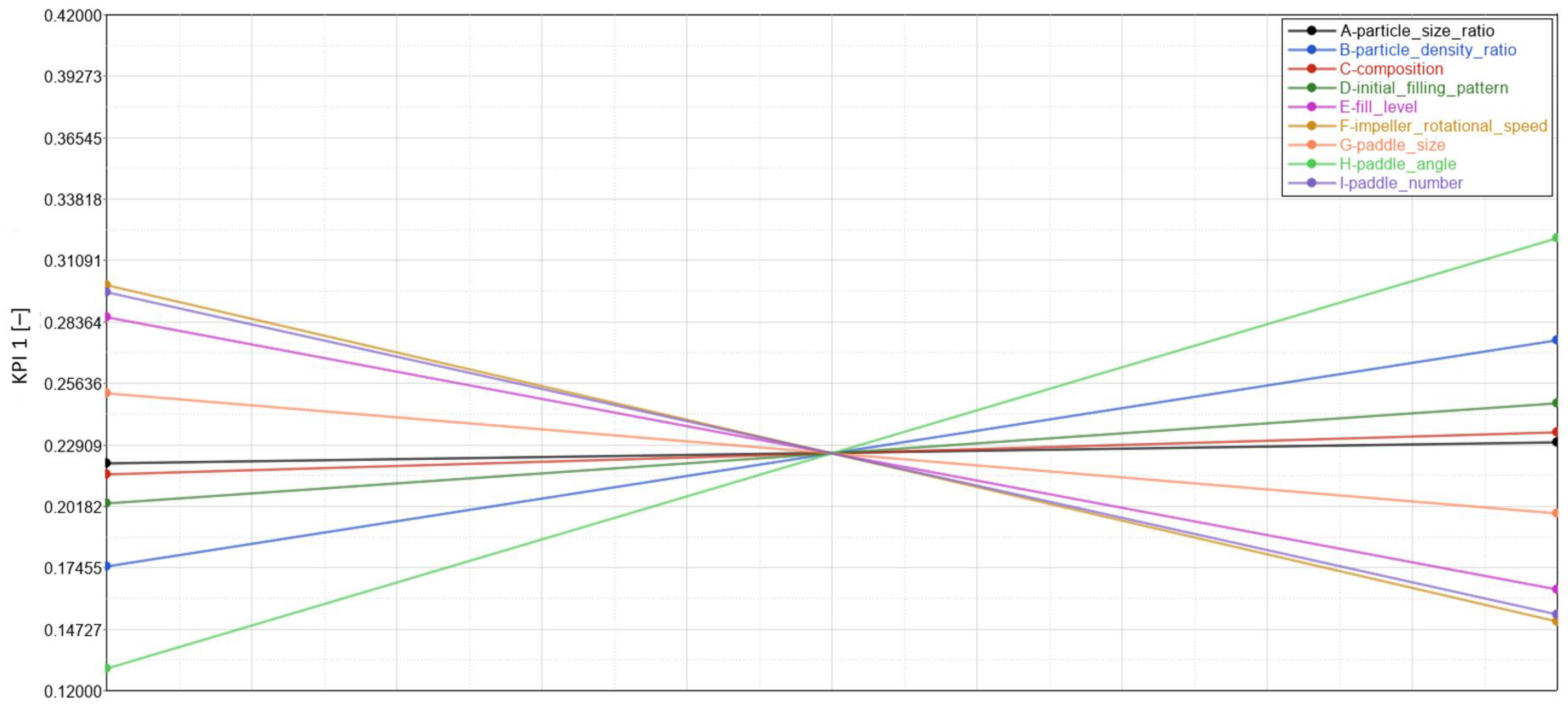
3.5. Summary of Results of the P–B Design
3.6. Granular Temperature
4. Conclusions
- Taking all KPIs into account, it can be generally concluded that material properties in the range investigated here do not significantly influence the mixer performance. In other words, when a mixer is well-designed, it will perform equally well in the range of material properties explored in this work. Nevertheless, it was found that a 50/50 volume ratio between components 1 and 2 needs less average mixing power (i.e., KPI 3) compared to an 20/80 composition.
- Increasing the fill level enhances the mixing quality, but at the same time sacrifices a fast mixing time and a low total energy consumption. In addition, an increase in the impeller rotational speed leads to a mixing quality improvement, higher mixing time and lower total energy consumption. In short, a lower fill level in combination with a high rotational speed could lead to improved mix qualities, achieved in a faster and more sustainable way.
- With respect to geometric parameters, the paddle angle is the most influential, where a decrease in the paddle angle significantly improves the mixing quality without compromising the mixing time or total energy consumption. Additionally, the paddle number seems to affect the mixing quality, but more research is required to confirm the aforementioned relation.
- While increasing the paddle size significantly decreases the energy consumption, it does not greatly affect the mixing quality and mixing time, meaning that this factor holds great potential to be optimised for both efficient and sustainable double paddle mixers.
- A granular temperature analysis showed an interesting relation between mixing time (KPI 2) and diffusivity in the fluidized zone of the paddle mixer. It was found that the mixing time is affected negatively when the fluidized zone is characterized by a low diffusive mixing mechanism.
- Overall, one should focus on operational conditions and geometric parameters when all the KPIs, including the mixing quality, mixing time and energy consumption, are of interest for the purpose of process optimisation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Rhodes, M.J. Introduction to Particle Technology; John Wiley & Sons: Hoboken, HJ, USA, 2008. [Google Scholar]
- Paul, E.L.; Atiemo-Obeng, V.A.; Kresta, S.M. Handbook of Industrial Mixing: Science and Practice; John Wiley & Sons: Hoboken, HJ, USA, 2003. [Google Scholar]
- Ebrahimi, M.; Yaraghi, A.; Jadidi, B.; Ein-Mozaffari, F.; Lohi, A. Assessment of bi-disperse solid particles mixing in a horizontal paddle mixer through experiments and DEM. Powder Technol. 2021, 381, 129–140. [Google Scholar] [CrossRef]
- Jadidi, B.; Ebrahimi, M.; Ein-Mozaffari, F.; Lohi, A. Mixing performance analysis of non-cohesive particles in a double paddle blender using DEM and experiments. Powder Technol. 2022, 397, 117122. [Google Scholar] [CrossRef]
- Bagster, D.; Bridgwater, J. The measurement of the force needed to move blades through a bed of cohesionless granules. Powder Technol. 1967, 1, 189–198. [Google Scholar] [CrossRef]
- Bagster, D.; Bridgwater, J. The flow of granular material over a moving blade. Powder Technol. 1969, 3, 323–338. [Google Scholar] [CrossRef]
- Stewart, R.; Bridgwater, J.; Parker, D. Granular flow over a flat-bladed stirrer. Chem. Eng. Sci. 2001, 56, 4257–4271. [Google Scholar] [CrossRef]
- Conway, S.L.; Lekhal, A.; Khinast, J.G.; Glasser, B.J. Granular flow and segregation in a four-bladed mixer. Chem. Eng. Sci. 2005, 60, 7091–7107. [Google Scholar] [CrossRef]
- Lekhal, A.; Conway, S.L.; Glasser, B.J.; Khinast, J.G. Characterization of granular flow of wet solids in a bladed mixer. AIChE J. 2006, 52, 2757–2766. [Google Scholar] [CrossRef]
- Boonkanokwong, V.; Remy, B.; Khinast, J.G.; Glasser, B.J. The effect of the number of impeller blades on granular flow in a bladed mixer. Powder Technol. 2016, 302, 333–349. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Alian, M.; Ein-Mozaffari, F.; Upreti, S.R. Analysis of the mixing of solid particles in a plowshare mixer via discrete element method (DEM). Powder Technol. 2015, 274, 77–87. [Google Scholar] [CrossRef]
- Chandratilleke, G.; Dong, K.; Shen, Y. DEM study of the effect of blade-support spokes on mixing performance in a ribbon mixer. Powder Technol. 2018, 326, 123–136. [Google Scholar] [CrossRef]
- Ebrahimi, M.; Yaraghi, A.; Ein-Mozaffari, F.; Lohi, A. The effect of impeller configurations on particle mixing in an agitated paddle mixer. Powder Technol. 2018, 332, 158–170. [Google Scholar] [CrossRef]
- Laurent, B.; Cleary, P. Comparative study by PEPT and DEM for flow and mixing in a ploughshare mixer. Powder Technol. 2012, 228, 171–186. [Google Scholar] [CrossRef]
- Gao, W.; Liu, L.; Liao, Z.; Chen, S.; Zang, M.; Tan, Y. Discrete element analysis of the particle mixing performance in a ribbon mixer with a double U-shaped vessel. Granul. Matter 2019, 21, 12. [Google Scholar] [CrossRef]
- Hassanpour, A.; Tan, H.; Bayly, A.; Gopalkrishnan, P.; Ng, B.; Ghadiri, M. Analysis of particle motion in a paddle mixer using Discrete Element Method (DEM). Powder Technol. 2011, 206, 189–194. [Google Scholar] [CrossRef]
- Qi, F.; Heindel, T.J.; Wright, M.M. Numerical study of particle mixing in a lab-scale screw mixer using the discrete element method. Powder Technol. 2017, 308, 334–345. [Google Scholar] [CrossRef]
- Jadidi, B.; Ebrahimi, M.; Ein-Mozaffari, F.; Lohi, A. Investigation of impacts of particle shape on mixing in a twin paddle blender using GPU-based DEM and experiments. Powder Technol. 2023, 417, 118259. [Google Scholar] [CrossRef]
- Jadidi, B.; Ebrahimi, M.; Ein-Mozaffari, F.; Lohi, A. Mixing and segregation assessment of bi-disperse solid particles in a double paddle mixer. Particuology 2023, 74, 184–199. [Google Scholar] [CrossRef]
- Jadidi, B.; Ebrahimi, M.; Ein-Mozaffari, F.; Lohi, A. A comprehensive review of the application of DEM in the investigation of batch solid mixers. Rev. Chem. Eng. 2022. [Google Scholar] [CrossRef]
- Pantaleev, S.; Yordanova, S.; Janda, A.; Marigo, M.; Ooi, J.Y. An experimentally validated DEM study of powder mixing in a paddle blade mixer. Powder Technol. 2017, 311, 287–302. [Google Scholar] [CrossRef]
- Tsunazawa, Y.; Soma, N.; Sakai, M. DEM study on identification of mixing mechanisms in a pot blender. Adv. Powder Technol. 2022, 33, 103337. [Google Scholar] [CrossRef]
- Yuan, Q.; Xu, L.; Ma, S.; Niu, C.; Yan, C.; Zhao, S. The effect of paddle configurations on particle mixing in a soil-fertilizer continuous mixing device. Powder Technol. 2021, 391, 292–300. [Google Scholar] [CrossRef]
- Alchikh-Sulaiman, B.; Ein-Mozaffari, F.; Lohi, A. Evaluation of poly-disperse solid particles mixing in a slant cone mixer using discrete element method. Chem. Eng. Res. Des. 2015, 96, 196–213. [Google Scholar] [CrossRef]
- Shenoy, P.; Xanthakis, E.; Innings, F.; Jonsson, C.; Fitzpatrick, J.; Ahrné, L. Dry mixing of food powders: Effect of water content and composition on mixture quality of binary mixtures. J. Food Eng. 2015, 149, 229–236. [Google Scholar] [CrossRef]
- Grima, A. Quantifying and Modelling Mechanisms of Flow in Cohesionless and Cohesive Granular Materials. Ph.D. Thesis, University of Wollongong, Wollongong, Australia, January 2011. Available online: https://ro.uow.edu.au/theses/3425 (accessed on 9 March 2022).
- Forberg, H.G. Twin Horizontal Axled Inwardly Rotating Paddle Mixer for Dry Ingredients. Canada Patent CA1143372 (A), 22 March 1983. [Google Scholar]
- AZO Materials, ‘Stainless Steel–Grade 304 (UNS S30400)’, AZoM.com. 23 October 2001. Available online: https://www.azom.com/article.aspx?ArticleID=965 (accessed on 7 December 2022).
- Lommen, S.; Schott, D.; Lodewijks, G. DEM speedup: Stiffness effects on behavior of bulk material. Particuology 2014, 12, 107–112. [Google Scholar] [CrossRef]
- Poux, M.; Fayolle, P.; Bertrand, J.; Bridoux, D.; Bousquet, J. Powder mixing: Some practical rules applied to agitated systems. Powder Technol. 1991, 68, 213–234. [Google Scholar] [CrossRef]
- Bhalode, P.; Ierapetritou, M. A review of existing mixing indices in solid-based continuous blending operations. Powder Technol. 2020, 373, 195–209. [Google Scholar] [CrossRef]
- Emmerink, J. Parametric Analysis of a Double Shaft Batch-Type Paddle Mixer: A DEM Study. 2022. Available online: https://repository.tudelft.nl/islandora/object/uuid%3A940bb90b-183a-4e00-bd1c-aee2f455b3f9 (accessed on 1 February 2023).
- Basinskas, G.; Sakai, M. Numerical study of the mixing efficiency of a ribbon mixer using the discrete element method. Powder Technol. 2016, 287, 380–394. [Google Scholar] [CrossRef]
- Tsugeno, Y.; Sakai, M.; Yamazaki, S.; Nishinomiya, T. DEM simulation for optimal design of powder mixing in a ribbon mixer. Adv. Powder Technol. 2021, 32, 1735–1749. [Google Scholar] [CrossRef]
- Antony, J. Design of Experiments for Engineers and Scientists; Elsevier: London, UK, 2014. [Google Scholar]
- Boukouvala, F.; Gao, Y.; Muzzio, F.; Ierapetritou, M.G. Reduced-order discrete element method modeling. Chem. Eng. Sci. 2013, 95, 12–26. [Google Scholar] [CrossRef]
- Remy, B.; Khinast, J.G.; Glasser, B.J. Discrete element simulation of free flowing grains in a four-bladed mixer. AIChE J. 2009, 55, 2035–2048. [Google Scholar] [CrossRef]
- Altair EDEM 2022. Available online: https://2022.help.altair.com/2022.1/EDEM/index.htm#t=Getting_Started.htm (accessed on 6 February 2023).
- Fang, M.; Yu, Z.; Zhang, W.; Cao, J.; Liu, W. Friction coefficient calibration of corn stalk particle mixtures using Plackett-Burman design and response surface methodology. Powder Technol. 2021, 396, 731–742. [Google Scholar] [CrossRef]
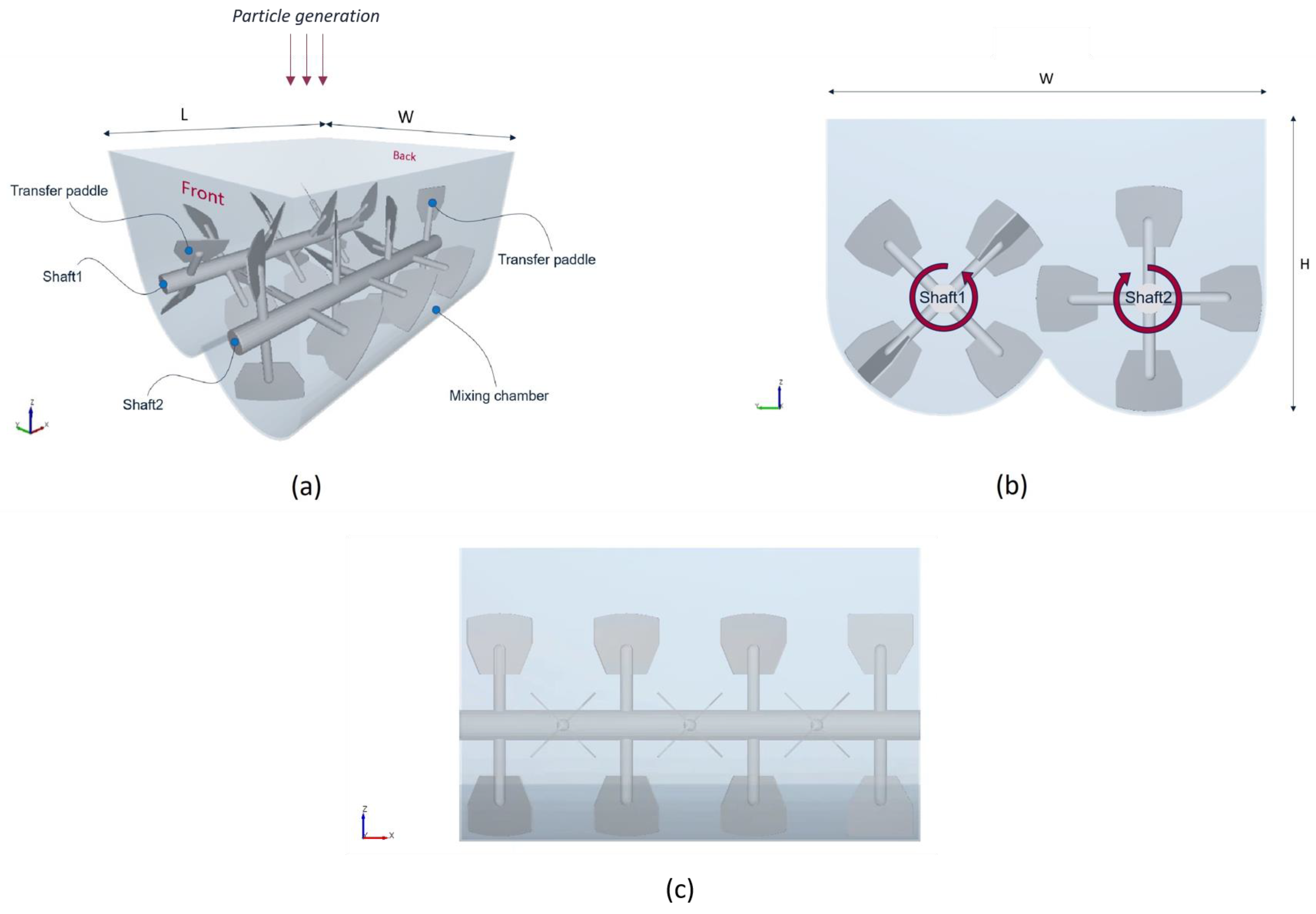

| Parameter | Unit | Value |
|---|---|---|
| L | mm | 900 |
| W | mm | 850 |
| H | mm | 570 |
| Parameter | Unit | Value |
|---|---|---|
| Poisson’s ratio, | - | 0.3 |
| Shear modulus, | Pa | 1 × 106 |
| Particle-particle coefficient of restitution, | - | 0.75 |
| Particle-particle coefficient of static friction, | - | 0.5 |
| Particle-particle coefficient of rolling friction, | - | 0.01 |
| Geometry density, | kg m−3 | 7850 |
| Poisson’s ratio, | - | 0.265 |
| Shear modulus, | Pa | 7.4 × 1010 |
| Particle-geometry coefficient of restitution, | - | 0.75 |
| Particle-geometry coefficient of static friction, | - | 0.35 |
| Particle-geometry coefficient of rolling friction, | - | 0.005 |
| Simulation time, | s | 60 |
| Time step, | s | 4.74378 × 10−5 |
| Factor | Description | Type of the Factor | Low Level (−1) | High Level (+1) |
|---|---|---|---|---|
| A | Particle size ratio | Material property | 1 | 3 |
| B | Particle density ratio | Material property | 1 | 20 |
| C | Composition (volume-based) | Material property | 0.25 | 1 |
| D | Initial filling pattern | Operational condition | FB | TB |
| E | Fill level | Operational condition | 60% | 140% |
| F | Impeller rotational speed | Operational condition | 40 rpm | 80 rpm |
| G | Paddle size | Geometric parameter | 0.67 | 1.5 |
| H | Paddle angle | Geometric parameter | 30 deg | 60 deg |
| I | Paddle number | Geometric parameter | 8 | 26 |
| Grid Size | Cell Size Factor | Number of Bins | Average Number of Particles in the Bin | KPI 1 |
|---|---|---|---|---|
| 4 × 4 × 3 | 13 | 48 | 4288 | 0.099 |
| 5 × 5 × 3 | 11 | 75 | 2744 | 0.131 |
| 6 × 6 × 4 | 9 | 144 | 1439 | 0.134 |
| 7 × 7 × 4 | 8 | 169 | 1060 | 0.160 |
| 8 × 8 × 5 | 7 | 320 | 675 | 0.166 |
| 9 × 9 × 6 | 6 | 486 | 448 | 0.180 |
| 11 × 11 × 7 | 5 | 847 | 243 | 0.210 |
| 14 × 14 × 9 | 4 | 1764 | 117 | 0.258 |
| Run | A | B | C | D | E | F | G | H | I | X1 | X2 | KPI 1 (-) | KPI 2 (s) | KPI 3 (W/kg) | KPI 4 (J/kg) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0.213 | 8.0 | 43.4 | 62,550 |
| 2 | −1 | −1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | 1 | −1 | 0.020 | 26.8 | 49.9 | 457,408 |
| 3 | −1 | −1 | −1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | 1 | 0.261 | 7.6 | 42.5 | 47,529 |
| 4 | −1 | 1 | −1 | −1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | 0.212 | 140.0 * | 25.0 | 968,404 |
| 5 | 1 | −1 | 1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | −1 | 0.165 | 7.8 | 56.0 | 64,200 |
| 6 | 1 | −1 | −1 | 1 | −1 | −1 | 1 | −1 | 1 | 1 | −1 | 0.182 | 5.8 | 24.1 | 20,576 |
| 7 | 1 | −1 | −1 | −1 | 1 | −1 | −1 | 1 | −1 | 1 | 1 | 0.395 | 50 * | 22.0 | 375,731 |
| 8 | −1 | 1 | −1 | −1 | −1 | 1 | −1 | −1 | 1 | 1 | 1 | 0.124 | 10.8 | 59.0 | 75,879 |
| 9 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | −1 | −1 | 1 | 0.304 | 9.0 | 15.6 | 10,777 |
| 10 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | −1 | 0.679 | 40 * | 12.0 | 36,812 |
| 11 | −1 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | 1 | −1 | 1 | 0.028 | 100 | 25.4 | 867,287 |
| 12 | 1 | 1 | −1 | 1 | 1 | 1 | −1 | −1 | −1 | −1 | −1 | 0.122 | 8.4 | 49.0 | 113,798 |
| Factor | Description | Sum of Squares | F-Value | p-Value | Order of Significance |
|---|---|---|---|---|---|
| A | Particle size ratio | 2.71 × 10−4 | 0.0236751 | 0.8918379 | 9 |
| B | Particle density ratio | 0.0303008 | 2.6495741 | 0.2451139 | 5 |
| C | Composition | 0.0010641 | 0.0930461 | 0.7891567 | 8 |
| D | Initial filling pattern | 0.0058521 | 0.5117209 | 0.5486319 | 7 |
| E | Fill level | 0.0438021 | 3.8301648 | 0.1894715 | 4 |
| F | Impeller rotational speed | 0.0667521 | 5.8369707 | 0.1369824 | 2 |
| G | Paddle size | 0.0085868 | 0.7508471 | 0.4775527 | 6 |
| H | Paddle angle | 0.1092521 | 9.5532780 | 0.0906657 | 1 |
| I | Paddle number | 0.0612041 | 5.3518396 | 0.1467947 | 3 |
| Total | 0.3499569 | ||||
| R2 = 0.9346429 |
| Factor | Description | Sum of Squares | F-Value | p-Value | Order of Significance |
|---|---|---|---|---|---|
| A | Particle size ratio | 4649.2033 | 5.8268239 | 0.1371741 | 3 |
| B | Particle density ratio | 27.603333 | 0.0345951 | 0.8696027 | 9 |
| C | Composition | 80.083333 | 0.1003681 | 0.7814001 | 7 |
| D | Initial filling pattern | 463.76333 | 0.5812323 | 0.5254726 | 6 |
| E | Fill level | 5300.4033 | 6.6429696 | 0.1233028 | 2 |
| F | Impeller rotational speed | 6320.4300 | 7.9213641 | 0.1064594 | 1 |
| G | Paddle size | 32.670000 | 0.0409452 | 0.8583601 | 8 |
| H | Paddle angle | 714.56333 | 0.8955587 | 0.4438642 | 5 |
| I | Paddle number | 1421.3633 | 1.7813877 | 0.3136374 | 4 |
| Total | 20,605.877 | ||||
| R2 = 0.9225564 |
| Factor | Description | Sum of Squares | F-Value | p-Value | Order of Significance |
|---|---|---|---|---|---|
| A | Particle size ratio | 1.1408333 | 0.3639989 | 0.6076023 | 9 |
| B | Particle density ratio | 21.067500 | 6.7218825 | 0.1221095 | 7 |
| C | Composition | 31.040833 | 9.9040149 | 0.0878654 | 6 |
| D | Initial filling pattern | 80.600833 | 25.716831 | 0.0367546 | 3 |
| E | Fill level | 2.5208333 | 0.8043074 | 0.4644522 | 8 |
| F | Impeller rotational speed | 2572.5408 | 820.80537 | 0.0012161 | 1 |
| G | Paddle size | 43.700833 | 13.943366 | 0.0648230 | 4 |
| H | Paddle angle | 40.700833 | 12.986174 | 0.0691167 | 5 |
| I | Paddle number | 146.30083 | 46.679341 | 0.0207580 | 2 |
| Total | 2945.8825 | ||||
| R2 = 0.9978722 | |||||
| Factor | Description | Sum of Squares | F-Value | p-Value | Order of Significance |
|---|---|---|---|---|---|
| A | Particle size ratio | 2.72 × 1011 | 5.7354659 | 0.1389247 | 2 |
| B | Particle density ratio | 2.66 × 1010 | 0.5605637 | 0.5321090 | 6 |
| C | Composition | 8.82 × 108 | 0.0186198 | 0.9039582 | 7 |
| D | Initial filling pattern | 5.38 × 1010 | 1.1366536 | 0.3980218 | 5 |
| E | Fill level | 5.59 × 1011 | 11.794572 | 0.0753296 | 1 |
| F | Impeller rotational speed | 1.77 × 1011 | 3.7405109 | 0.1927832 | 3 |
| G | Paddle size | 9.37 × 107 | 0.0019783 | 0.9685645 | 8 |
| H | Paddle angle | 7.52 × 104 | 0.000159 | 0.9910893 | 9 |
| I | Paddle number | 8.62 × 1010 | 1.8188166 | 0.3098714 | 4 |
| Total | 1.27 × 1012 | ||||
| R2 = 0.9253936 | |||||
| Factor | Description | KPI 1 [-] Mixing Quality | KPI 2 [s] Mixing Speed | KPI 3 [W/kg] Normalized Average Power | KPI 4 [J/kg] Total Energy Consumption |
|---|---|---|---|---|---|
| A | Particle size ratio | + | − − | − | − − |
| B | Particle density ratio | + | − | − − | − |
| C | Composition | + | − | − − − | − |
| D | Initial filling pattern | + | + | + + + | + |
| E | Fill level | − − | + + | + | + + + |
| F | Impeller rotational speed | − − | − − | + + + | − − |
| G | Paddle size | − | − | − − − | + |
| H | Paddle angle | + + + | + | − − − | + |
| I | Paddle number | − − | + | + + + | + |
| Run | KPI 2 (s) | Loc_1 (K) | Loc_2 (K) | Loc_3 (K) |
|---|---|---|---|---|
| 1 | 8.0 | 0.2552 | 0.03783 | 0.1722 |
| 2 | 26.8 | 0.0145 | 0.00231 | 0.0016 |
| 3 | 7.6 | 0.1074 | 0.02129 | 0.1300 |
| 4 | 140.0 | 0.0049 | 0.00127 | 0.0018 |
| 5 | 7.8 | 0.2220 | 0.01209 | 0.1509 |
| 6 | 5.8 | 0.0385 | 0.00674 | 0.3320 |
| 7 | 50 | 0.0037 | 0.00109 | 0.0007 |
| 8 | 10.8 | 0.0469 | 0.06964 | 0.1496 |
| 9 | 9.0 | 3.8086 | 0.06466 | 1.1007 |
| 10 | 40 | 0.0777 | 0.00396 | 0.0044 |
| 11 | 100 | 0.0026 | 0.00056 | 0.0006 |
| 12 | 8.4 | 0.8287 | 0.14147 | 0.1706 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Emmerink, J.; Hadi, A.; Jovanova, J.; Cleven, C.; Schott, D.L. Parametric Analysis of a Double Shaft, Batch-Type Paddle Mixer Using the Discrete Element Method (DEM). Processes 2023, 11, 738. https://doi.org/10.3390/pr11030738
Emmerink J, Hadi A, Jovanova J, Cleven C, Schott DL. Parametric Analysis of a Double Shaft, Batch-Type Paddle Mixer Using the Discrete Element Method (DEM). Processes. 2023; 11(3):738. https://doi.org/10.3390/pr11030738
Chicago/Turabian StyleEmmerink, Jeroen, Ahmed Hadi, Jovana Jovanova, Chris Cleven, and Dingena L. Schott. 2023. "Parametric Analysis of a Double Shaft, Batch-Type Paddle Mixer Using the Discrete Element Method (DEM)" Processes 11, no. 3: 738. https://doi.org/10.3390/pr11030738
APA StyleEmmerink, J., Hadi, A., Jovanova, J., Cleven, C., & Schott, D. L. (2023). Parametric Analysis of a Double Shaft, Batch-Type Paddle Mixer Using the Discrete Element Method (DEM). Processes, 11(3), 738. https://doi.org/10.3390/pr11030738








