Evaluation of Relative Permeability Curves in Sandstone Core Flooding Using Computational Fluid Dynamics
Abstract
:1. Introduction
2. Materials and Methods
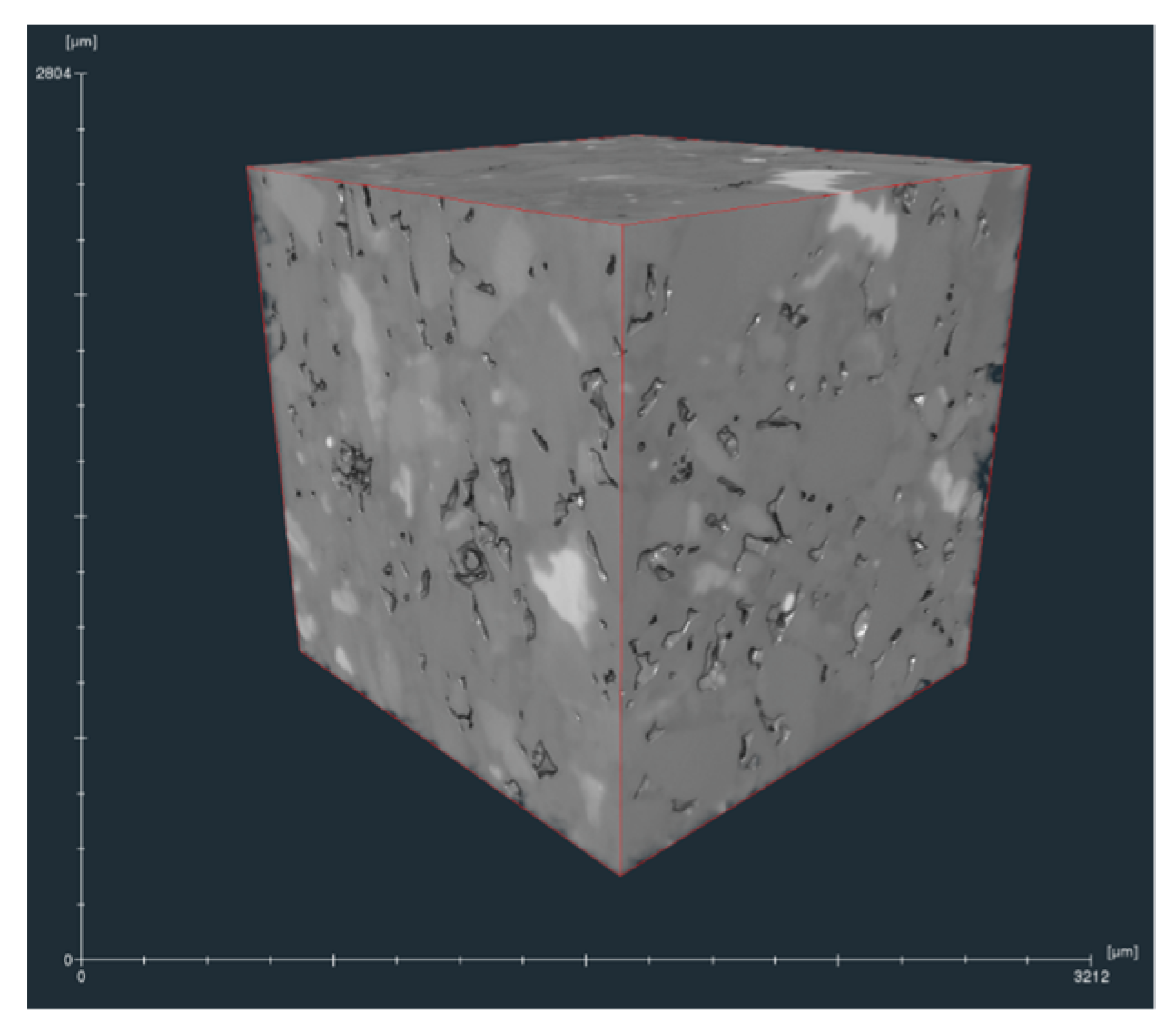
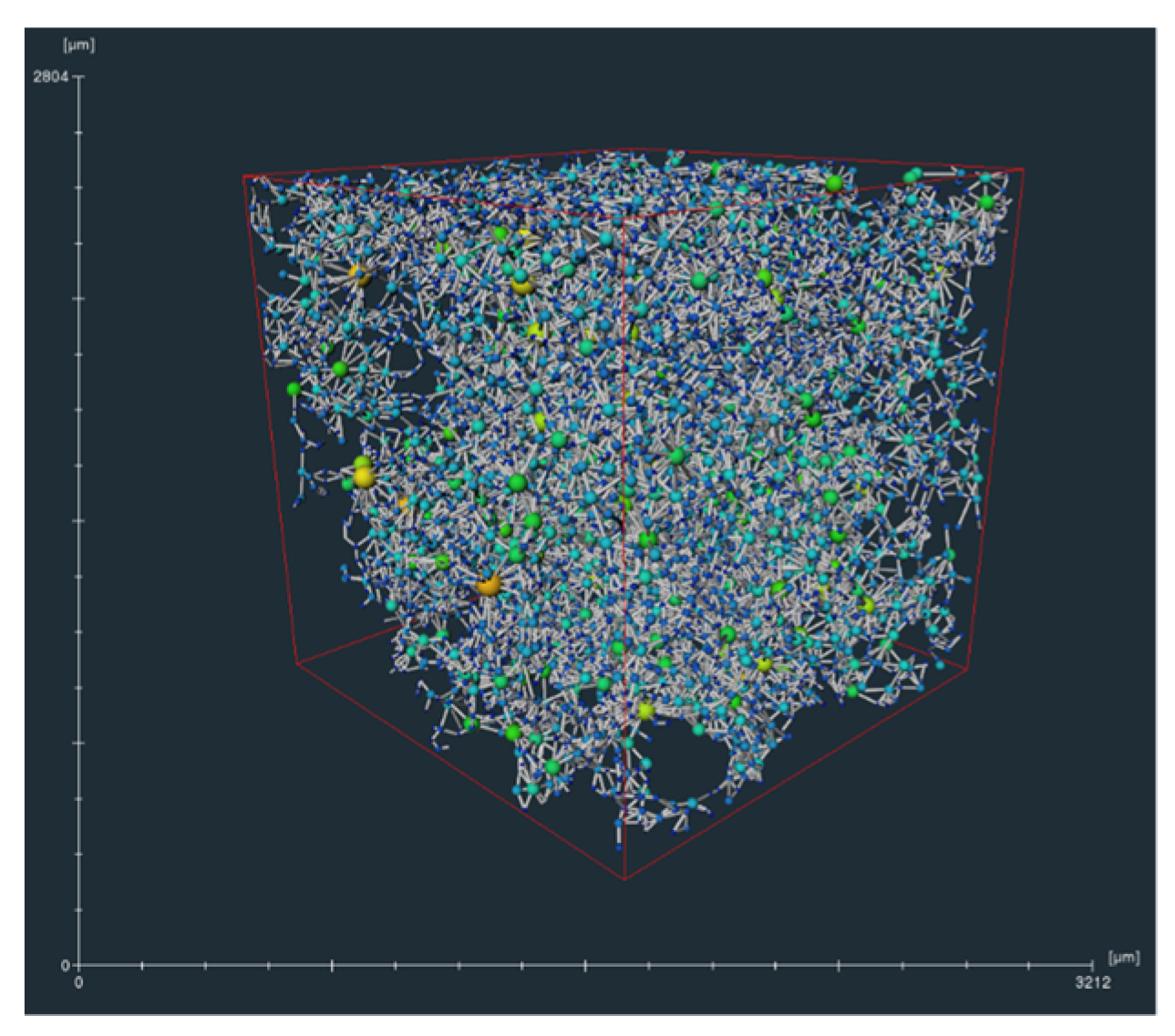
2.1. Micro-CT Scan and Image Processing Methods
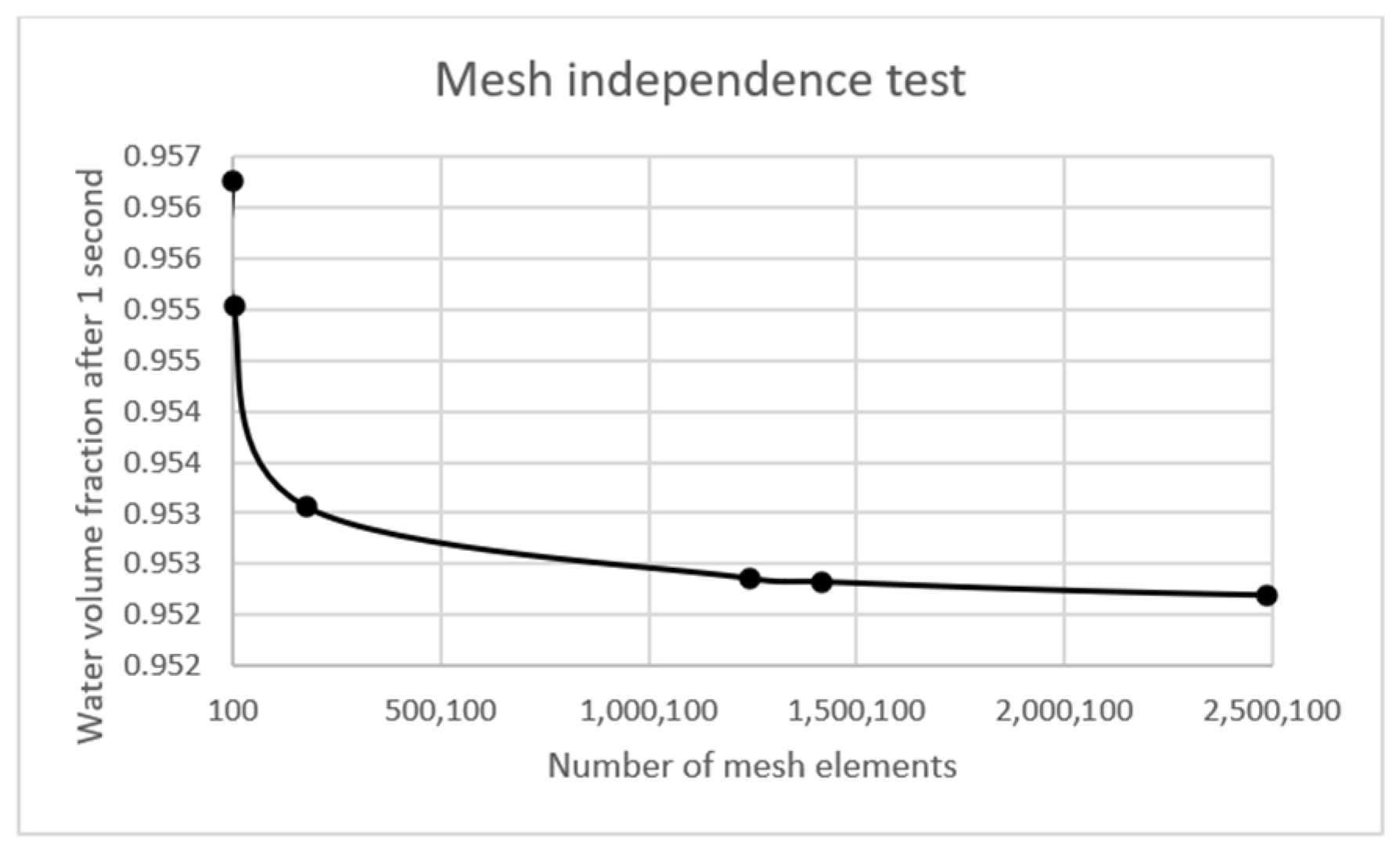
2.2. Numerical Method
3. Results and Discussion
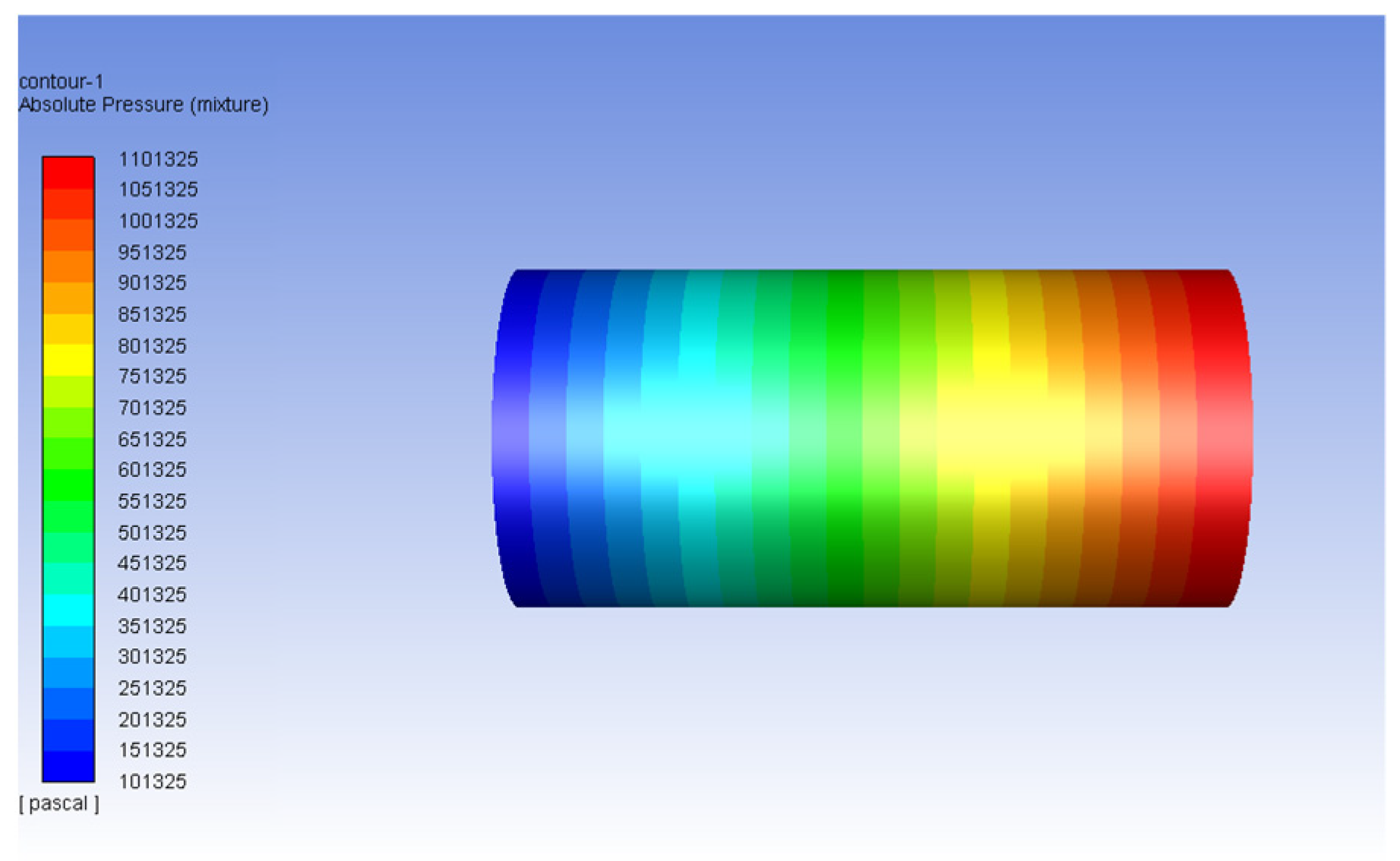
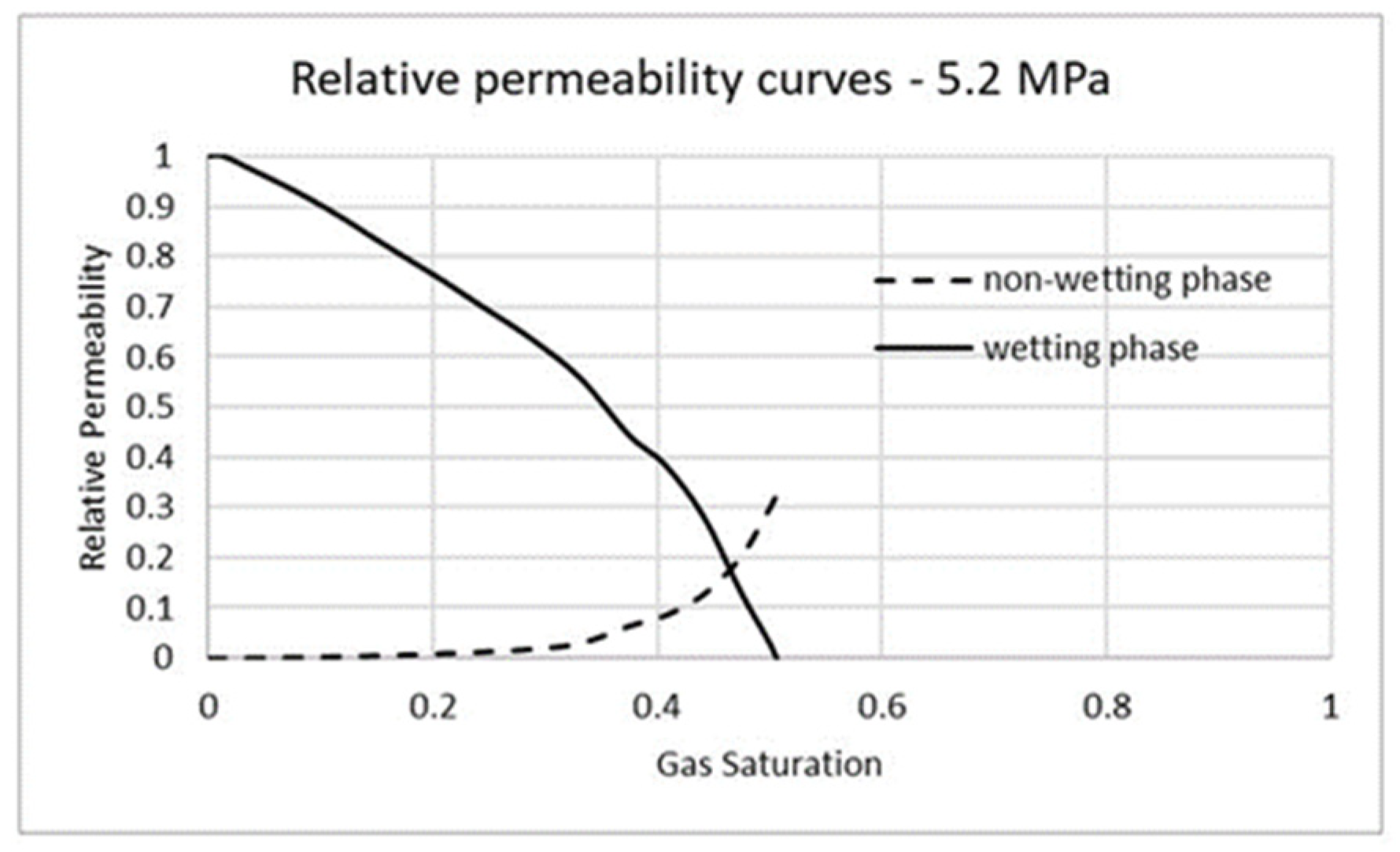
3.1. Validation
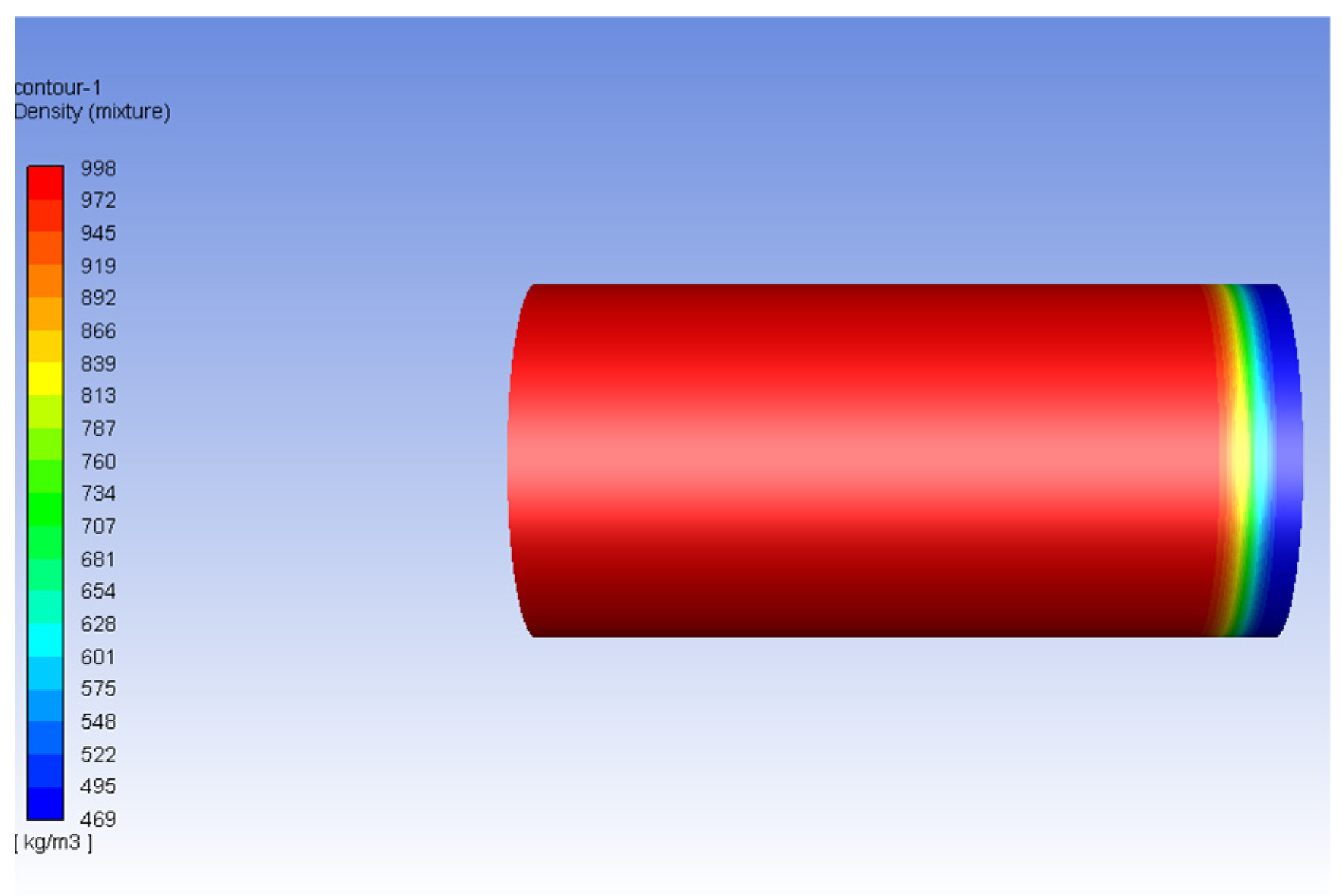
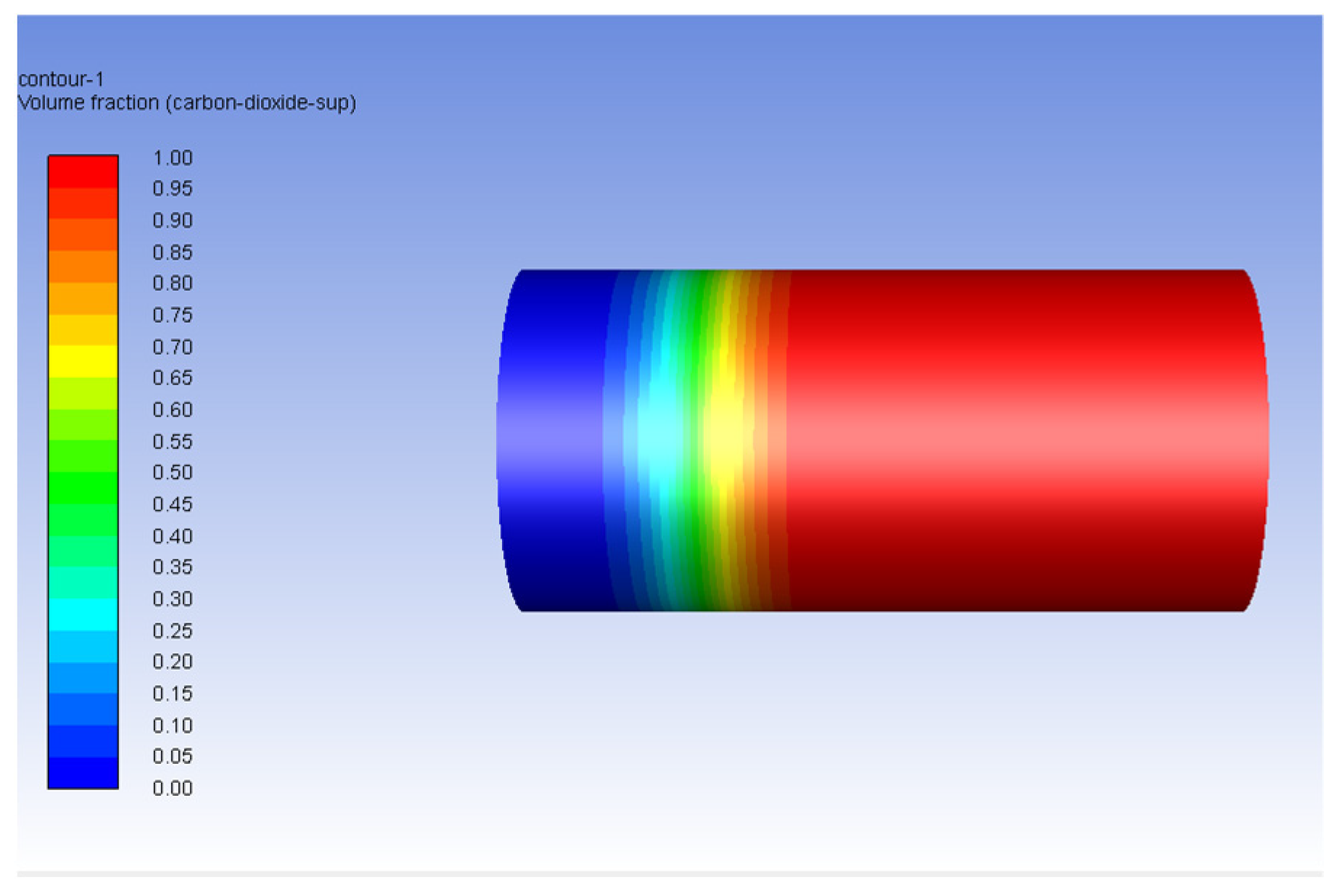
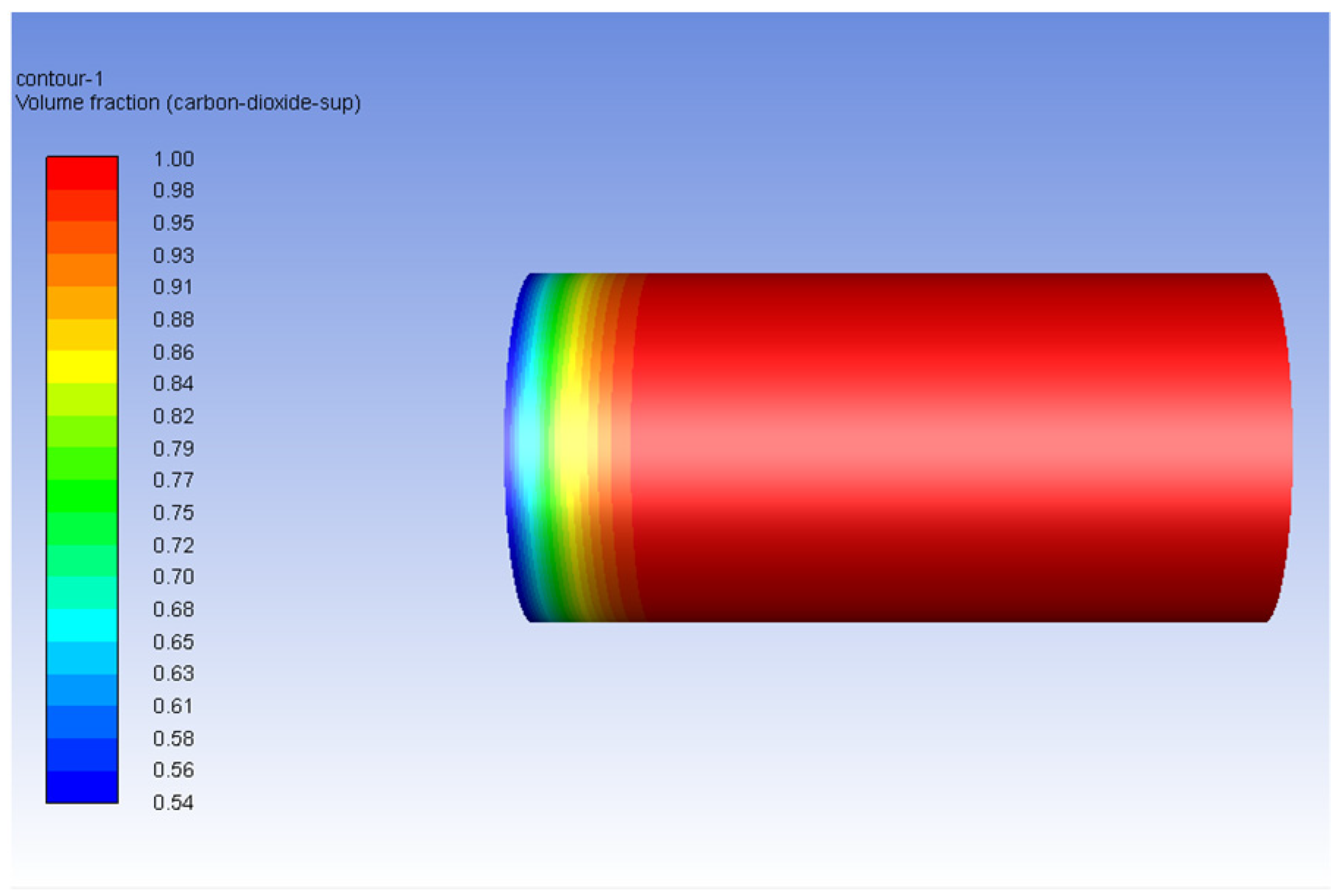
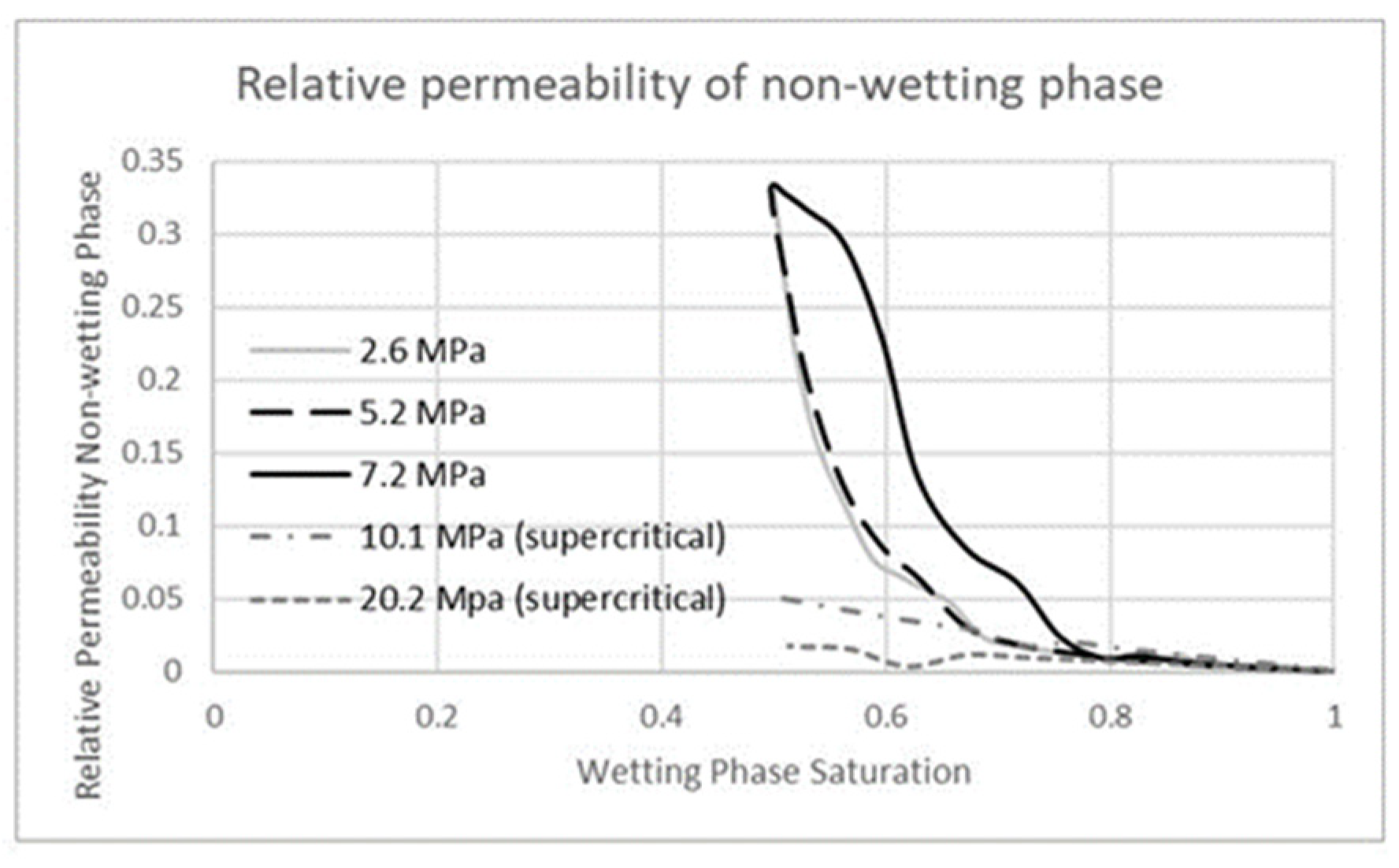
3.2. Carbon Dioxide in Gas Phase Versus Water
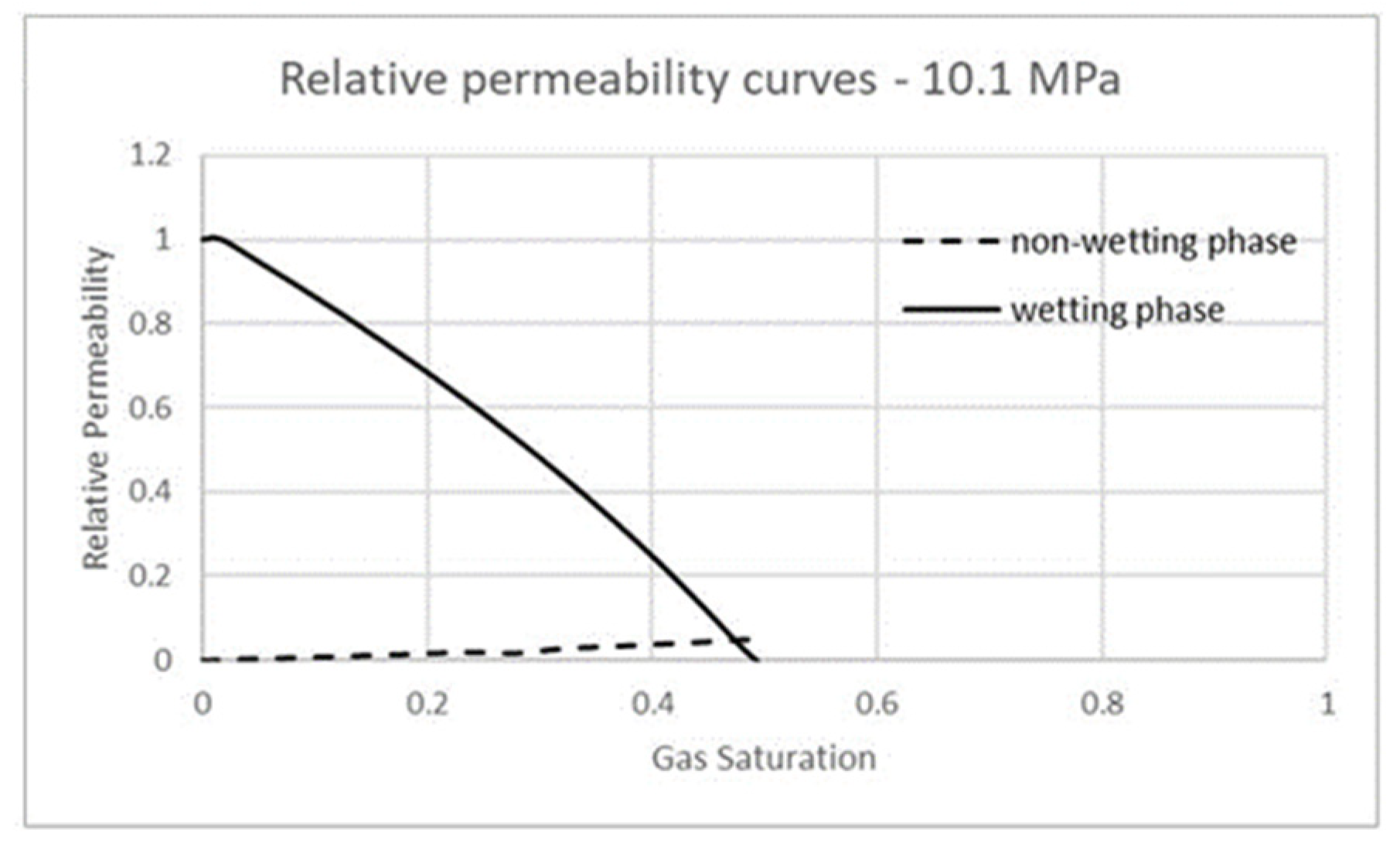
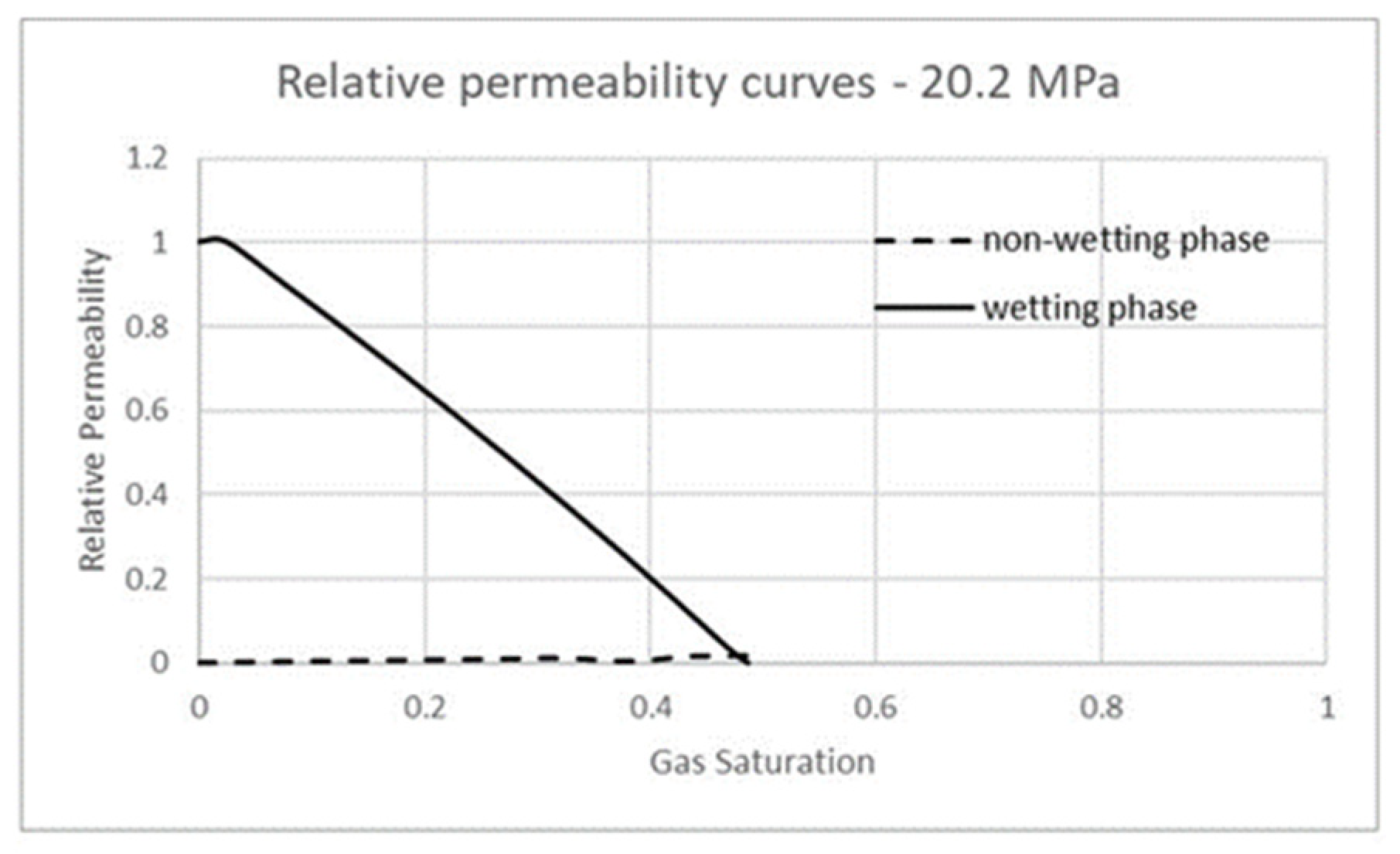
3.3. Carbon Dioxide in Supercritical Phase Versus Water
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- CO2 and Greenhouse Gas Emissions. Available online: https://ourworldindata.org/co2-and-other-greenhouse-gas-emissions (accessed on 7 January 2023).
- Global Greenhouse Gas Emissions Data. Available online: https://www.epa.gov/ghgemissions/global-greenhouse-gas-emissions-data (accessed on 7 January 2023).
- Zhang, D.; Song, J. Mechanisms for geological carbon sequestration. Procedia IUTAm. 2014, 10, 319–327. [Google Scholar] [CrossRef] [Green Version]
- Friedmann, S.J. Geological carbon dioxide sequestration. Elements 2007, 3, 179–184. [Google Scholar] [CrossRef]
- Lal, R. Carbon sequestration. Philos. Trans. R. Soc. B Biol. Sci. 2008, 363, 815–830. [Google Scholar] [CrossRef] [PubMed]
- Blomberg, A.E.; Waarum, I.K.; Totland, C.; Eek, E. Marine Monitoring for Offshore Geological Carbon Storage—A Review of Strategies, Technologies and Trends. Geosciences 2021, 11, 383. [Google Scholar] [CrossRef]
- DePaolo, D.J.; Cole, D.R. Geochemistry of geologic carbon sequestration: An overview. Rev. Mineral. Geochem. 2013, 77, 1–14. [Google Scholar] [CrossRef]
- Abidoye, L.K.; Khudaida, K.J.; Das, D.B. Geological carbon sequestration in the context of two-phase flow in porous media: A review. Crit. Rev. Environ. Sci. Technol. 2015, 45, 1105–1147. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Edwards, I.M.; Clarens, A.F. Wettability phenomena at the CO2–brine–mineral interface: Implications for geologic carbon sequestration. Environ. Sci. Technol. 2013, 47, 234–241. [Google Scholar] [CrossRef]
- Cao, S.C.; Dai, S.; Jung, J. Supercritical CO2 and brine displacement in geological carbon sequestration: Micromodel and pore network simulation studies. Int. J. Greenh. Gas Control. 2016, 44, 104–114. [Google Scholar] [CrossRef]
- Cannone, S.F.; Lanzini, A.; Santarelli, M. A review on CO2 capture technologies with focus on CO2-enhanced methane recovery from hydrates. Energies 2021, 14, 387. [Google Scholar] [CrossRef]
- Christopoulou, M.A.; Koutsovitis, P.; Kostoglou, N.; Paraskevopoulou, C.; Sideridis, A.; Petrounias, P.; Rogkala, A.; Stock, S.; Koukouzas, N. Evaluation of the CO2 Storage Capacity in Sandstone Formations from the Southeast Mesohellenic trough (Greece). Energies 2022, 15, 3491. [Google Scholar] [CrossRef]
- Pini, R.; Benson, S.M. Simultaneous determination of capillary pressure and relative permeability curves from core-flooding experiments with various fluid pairs. Water Resour. Res. 2013, 49, 3516–3530. [Google Scholar] [CrossRef]
- Medici, G.; West, L.J. Review of groundwater flow and contaminant transport modelling approaches for the Sherwood Sandstone aquifer, UK; insights from analogous successions worldwide. Q. J. Eng. Geol. Hydrogeol. 2022, 55, 2021–2176. [Google Scholar] [CrossRef]
- Tellam, J.H.; Barker, R.D. Towards prediction of saturated-zone pollutant movement in groundwaters in fractured permeable-matrix aquifers: The case of the UK Permo-Triassic sandstones. Geol. Soc. Spec. Publ. 2006, 263, 1–48. [Google Scholar] [CrossRef]
- Botset, H.G. Flow of gas-liquid mixtures through consolidated sand. Trans. Am. Inst. 1940, 136, 91–105. [Google Scholar] [CrossRef]
- Bachu, S.; Bennion, B. Effects of in-situ conditions on relative permeability characteristics of CO2-brine systems. Environ. Geol. 2008, 54, 1707–1722. [Google Scholar] [CrossRef]
- Benion, B.; Stefan, B. Relative Permeability Characteristics for Supercritical CO2 Displacing Water in a Variety of Potential Sequestration Zones in the West Canada Sedimentary Basin; SPE Annual Technical Conference and Exhibition: Dallas, TX, USA, 2005. [Google Scholar]
- Müller, N. Supercritical CO2-brine relative permeability experiments in reservoir rocks—Literature review and recommendations. Transport. Porous Med. 2011, 87, 367–383. [Google Scholar] [CrossRef]
- Reynolds, C.A.; Krevor, S. Characterizing flow behavior for gas injection: Relative permeability of CO2-brine and N2-water in heterogeneous rocks. Water Resour. Res. 2015, 51, 9464–9489. [Google Scholar] [CrossRef] [Green Version]
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of Porous Media; Hydrology Paper No. 3; Civil Engineering Department, Colorado State University: Fort Collins, CO, USA, 1964. [Google Scholar]
- Richardson, J.G.; Kerver, J.K.; Hafford, J.A.; Osoba, J.S. Laboratory determination of relative permeability. J. Pet. Technol. 1952, 4, 187–196. [Google Scholar] [CrossRef]
- Oak, M.J.; Baker, L.E.; Thomas, D.C. Three-phase relative permeability of Berea sandstone. J. Pet. Technol. 1990, 42, 1054–1061. [Google Scholar] [CrossRef]
- He, D.; Jiang, P.; Lun, Z.; Liu, X.; Xu, R. Pore scale CFD simulation of supercritical carbon dioxide drainage process in porous media saturated with water. Energ. Source. Part A 2019, 41, 1791–1799. [Google Scholar] [CrossRef]
- Garimella, S.S.; Ahmed, S.; Hossain, M. Comparison of different models for predicting drainage relative permeability using pore scale numerical simulation of supercritical carbon dioxide and brine flow. IOP Conf. Ser. Mater. Sci. Eng. 2019, 495, 012111. [Google Scholar] [CrossRef]
- Jahan, F. Pore-Scale, Computational Fluid Dynamics-Based Simulation of Supercritical CO2-Brine Flow through Porous Media; Curtin University: Perth, Australia, 2018. [Google Scholar]
- Jahan, F.; Ahmed, S.; Hossain, M. Investigating the Influence of Wettability and Direction on Supercritical CO2 Trapping for Supercritical CO2-Brine Imbibition Process at Pore Scale for Bentheimer Sandstone. In Proceedings of the SPE Asia Pacific Oil and Gas Conference and Exhibition, Brisbane, Australia, 23 October 2018. [Google Scholar]
- Xu, R.; Luo, S.; Jiang, P. Pore scale numerical simulation of supercritical CO2 injecting into porous media containing water. Energy Procedia 2011, 4, 4418–4424. [Google Scholar] [CrossRef] [Green Version]
- Dullien, F.A.L. Porous Media Fluid Transport and Pore Structure; Academic: San Diego, CA, USA, 1992. [Google Scholar]
- Lake, L.W. Enhanced Oil Recovery; Prentice Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Craig, F.F. The reservoir engineering aspects of waterflooding. In SPE Monograph Series 3; Society of Petroleum Engineers: New York, NY, USA, 1971. [Google Scholar]
- Krevor, S.; Pini, R.; Zuo, L.; Benson, S. Relative permeability and trapping of CO2 and water in sandstone rocks at reservoir conditions. Water Resour. Res. 2012, 48, 1–16. [Google Scholar] [CrossRef]
- Perrin, J.C.; Benson, S. An experimental study on the influence of sub-core scale heterogeneities on CO2 distribution in reservoir rocks. Transport Porous Med. 2010, 82, 93–109. [Google Scholar] [CrossRef]
- Morteza, A.; Piri, M. Relative permeability hysteresis and capillary trapping characteristics of supercritical CO2/brine systems: An experimental study at reservoir conditions. Adv. Water Resour. 2013, 52, 190–206. [Google Scholar]
- Chenot, P.E.; David, W. Round Mountain Field, Short Radius Lateral Drilling in the Vedder Sand Round Mountain Field, California (No. DOE/BC/15258-1); National Energy Technology Lab. (NETL): Tulsa, OK, USA; National Petroleum Technology Office (NPTO): Tulsa, OK, USA, 2002. [Google Scholar]
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20 June 2005. [Google Scholar]
- Bakke, S.; Øren, P.E. 3-D pore-scale modelling of sandstones and flow simulations in the pore networks. SPE J. 1997, 2, 136–149. [Google Scholar] [CrossRef] [Green Version]
- Fluent 14.5 User Guide; Fluent Inc.: New York, NY, USA, 2002.
- Cole, J.; Rasouli, V. Numerical simulations of CO2 injection into a porous sandstone formation. WIT Trans. Eng. Sci. 2012, 81, 59–69. [Google Scholar]
- Baozhi, P.; Lei, J.; Zhang, L.; Guo, Y. Research on the physical properties of supercritical CO2 and the log evaluation of CO2-bearing volcanic reservoirs. J. Geophys. Eng. 2017, 14, 1052–1060. [Google Scholar]
- Deng, J.; Zhao, G.; Zhang, L.; Ma, H.; Song, F.; Cao, Q.; Zhang, X. Simple and accurate calculation model of viscosity for supercritical CO2. J. Phys. Conf. Ser. 2021, 2076, 012030. [Google Scholar] [CrossRef]


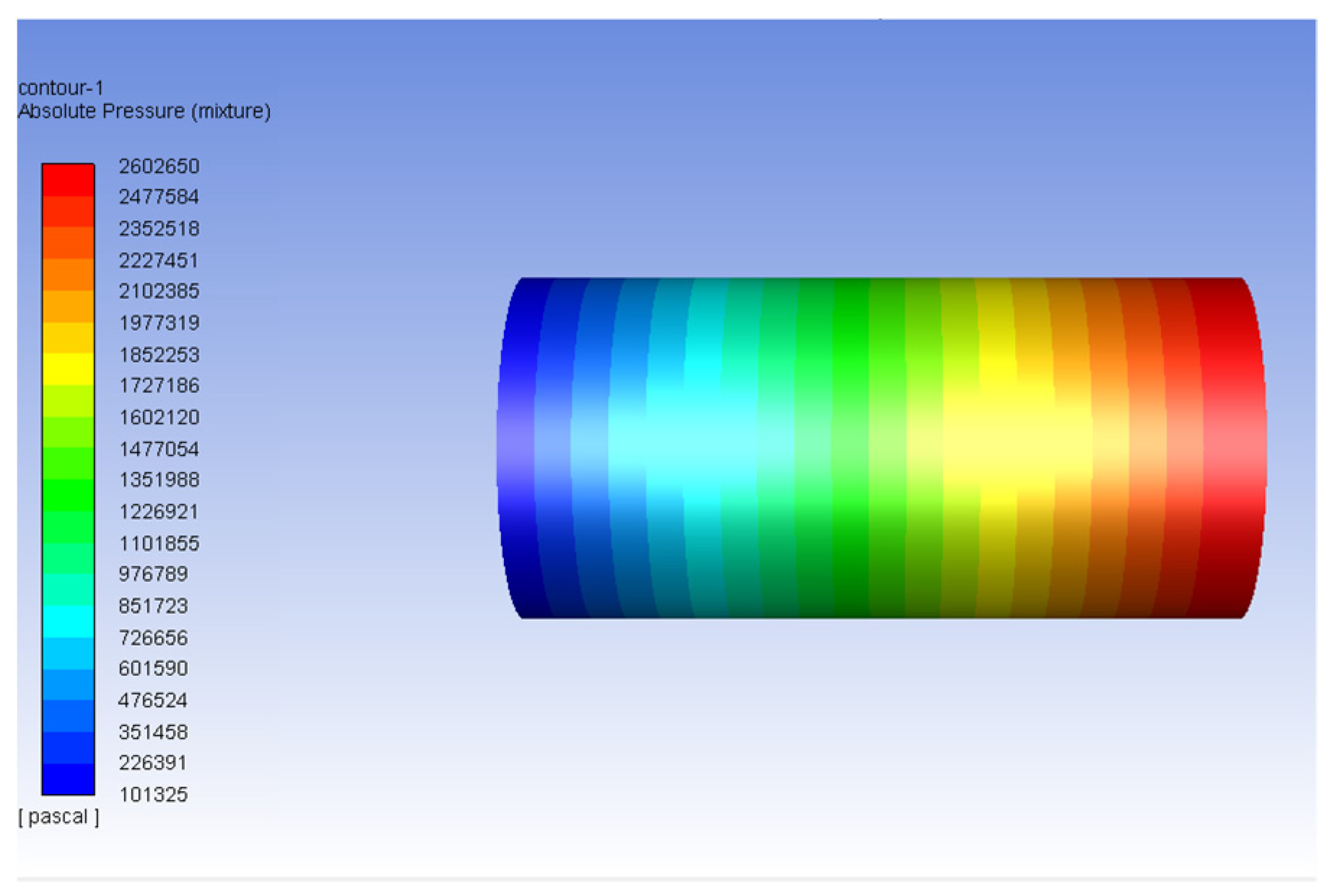
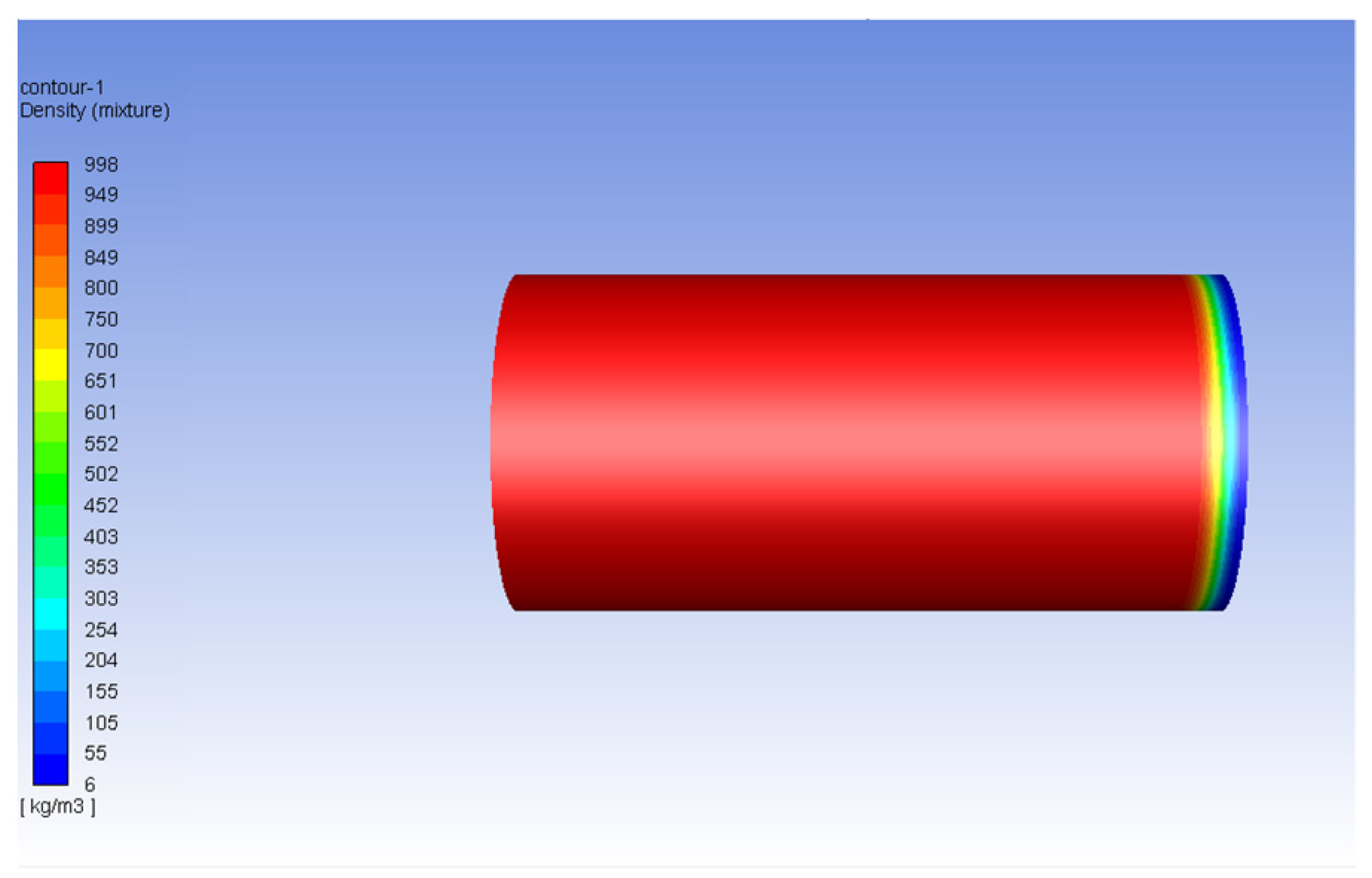
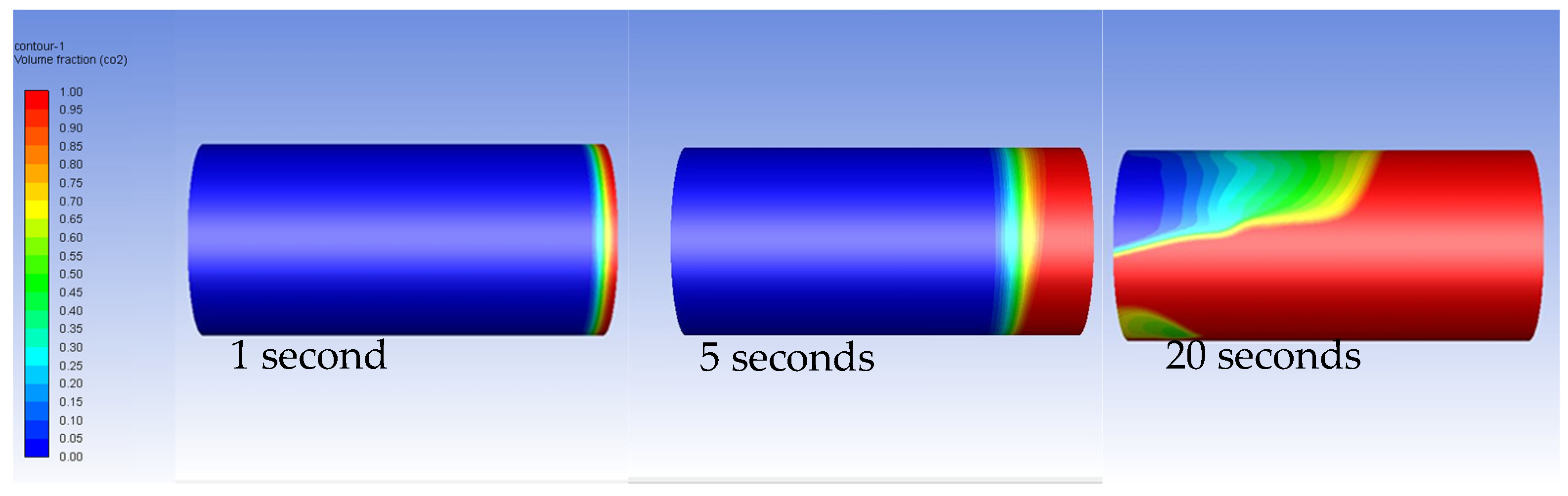
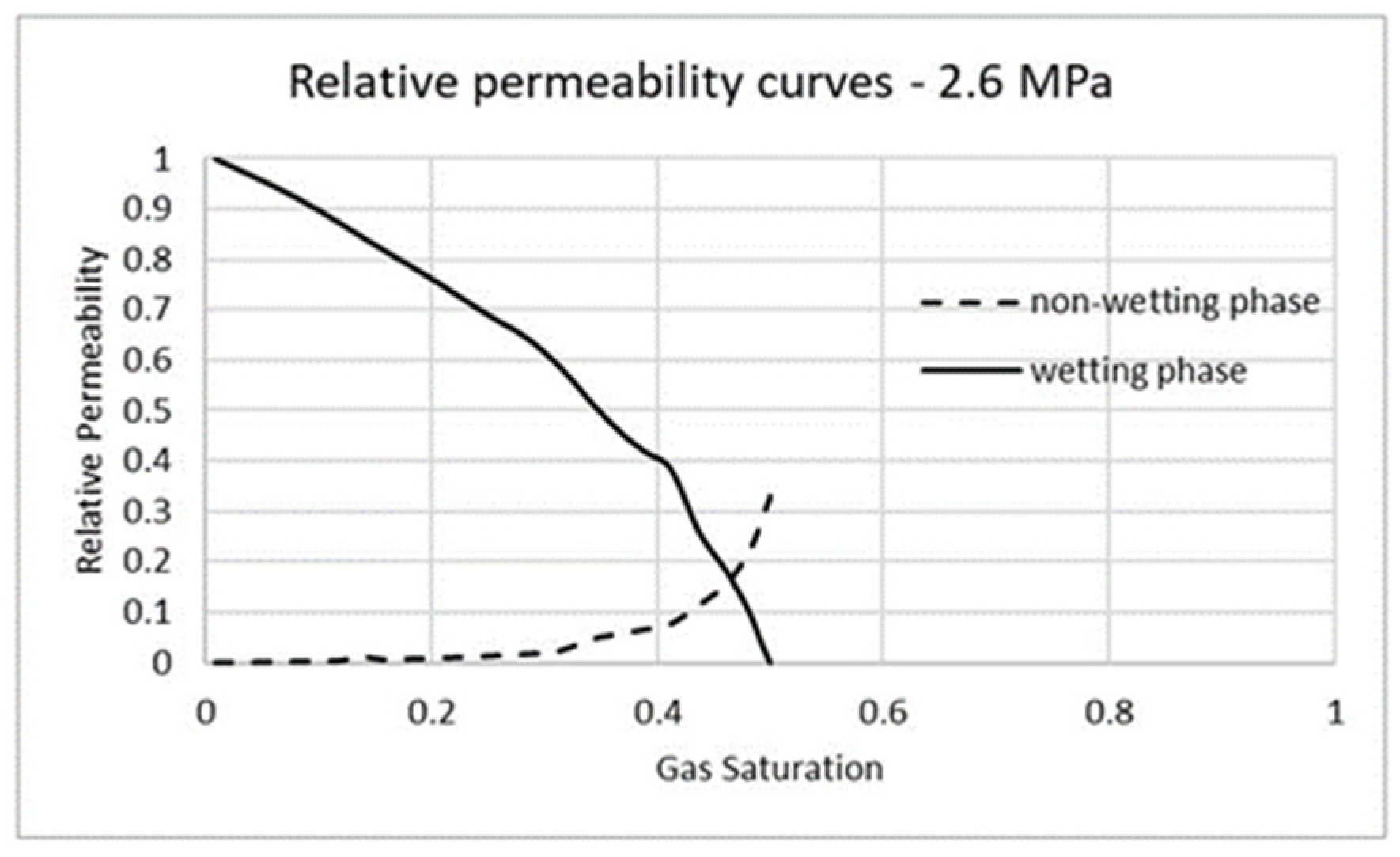


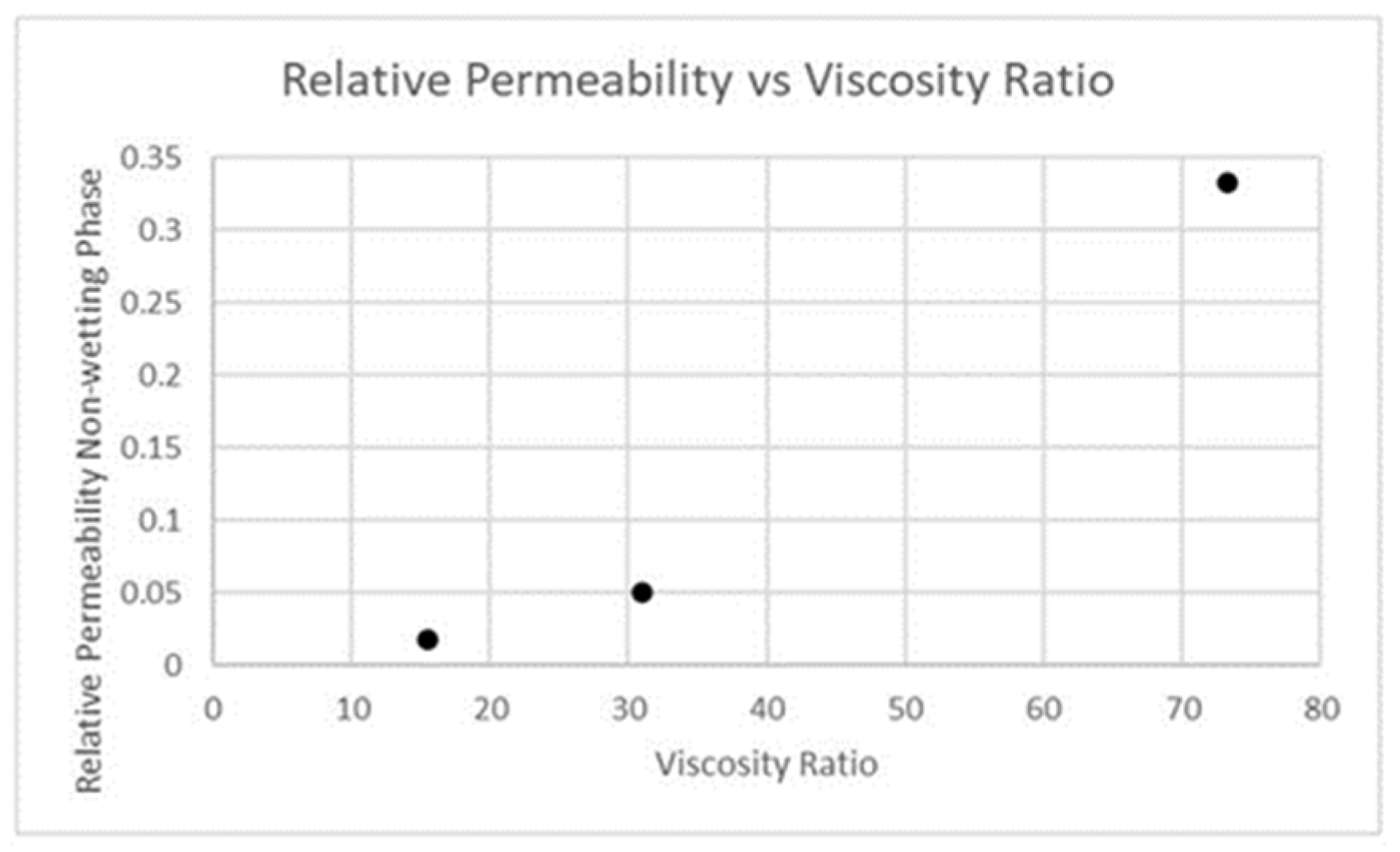
| Fluid | Density (kg/m3) | Viscosity (Pa-s) | Viscosity Ratio |
|---|---|---|---|
| carbon dioxide (gas) | 1.7878 | 1.37 × 10−5 | 73.21 |
| carbon dioxide (supercritical at 10.1 MPa) | 469 | 3.239 × 10−5 | 30.97 |
| carbon dioxide (supercritical at 20.2 MPa) | 750 | 6.5 × 10−5 | 15.44 |
| water | 998.2 | 0.001003 | ------- |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acharya, T.; Song, L.; Duginski, E.; Goodwin, A. Evaluation of Relative Permeability Curves in Sandstone Core Flooding Using Computational Fluid Dynamics. Processes 2023, 11, 780. https://doi.org/10.3390/pr11030780
Acharya T, Song L, Duginski E, Goodwin A. Evaluation of Relative Permeability Curves in Sandstone Core Flooding Using Computational Fluid Dynamics. Processes. 2023; 11(3):780. https://doi.org/10.3390/pr11030780
Chicago/Turabian StyleAcharya, Tathagata, Liaosha Song, Elizabeth Duginski, and Andrew Goodwin. 2023. "Evaluation of Relative Permeability Curves in Sandstone Core Flooding Using Computational Fluid Dynamics" Processes 11, no. 3: 780. https://doi.org/10.3390/pr11030780
APA StyleAcharya, T., Song, L., Duginski, E., & Goodwin, A. (2023). Evaluation of Relative Permeability Curves in Sandstone Core Flooding Using Computational Fluid Dynamics. Processes, 11(3), 780. https://doi.org/10.3390/pr11030780







