Variable-Coefficient Dynamic Modeling Method for a Ball Screw Feed System in the No-Extra-Load Running State
Abstract
1. Introduction
2. Materials and Methods
2.1. Equivalent Dynamic Model
2.2. Variable-Coefficient Dynamic Equation
2.3. Determination of the Variable-Coefficient of the Dynamic Equation
2.3.1. Stiffness and Mass Matrices of the Equivalent Beam Element
2.3.2. Equivalent Axial Stiffness of the Screw Nut Joints
2.3.3. Equivalent Axial Stiffness of the Bearing Joints
2.3.4. Total Stiffness and Mass Matrices of the System Based on Changes in the No-Extra-Load Running State
3. Dynamic Measurement of a Ball Screw Feed System in Different Running States
4. Results and Discussion
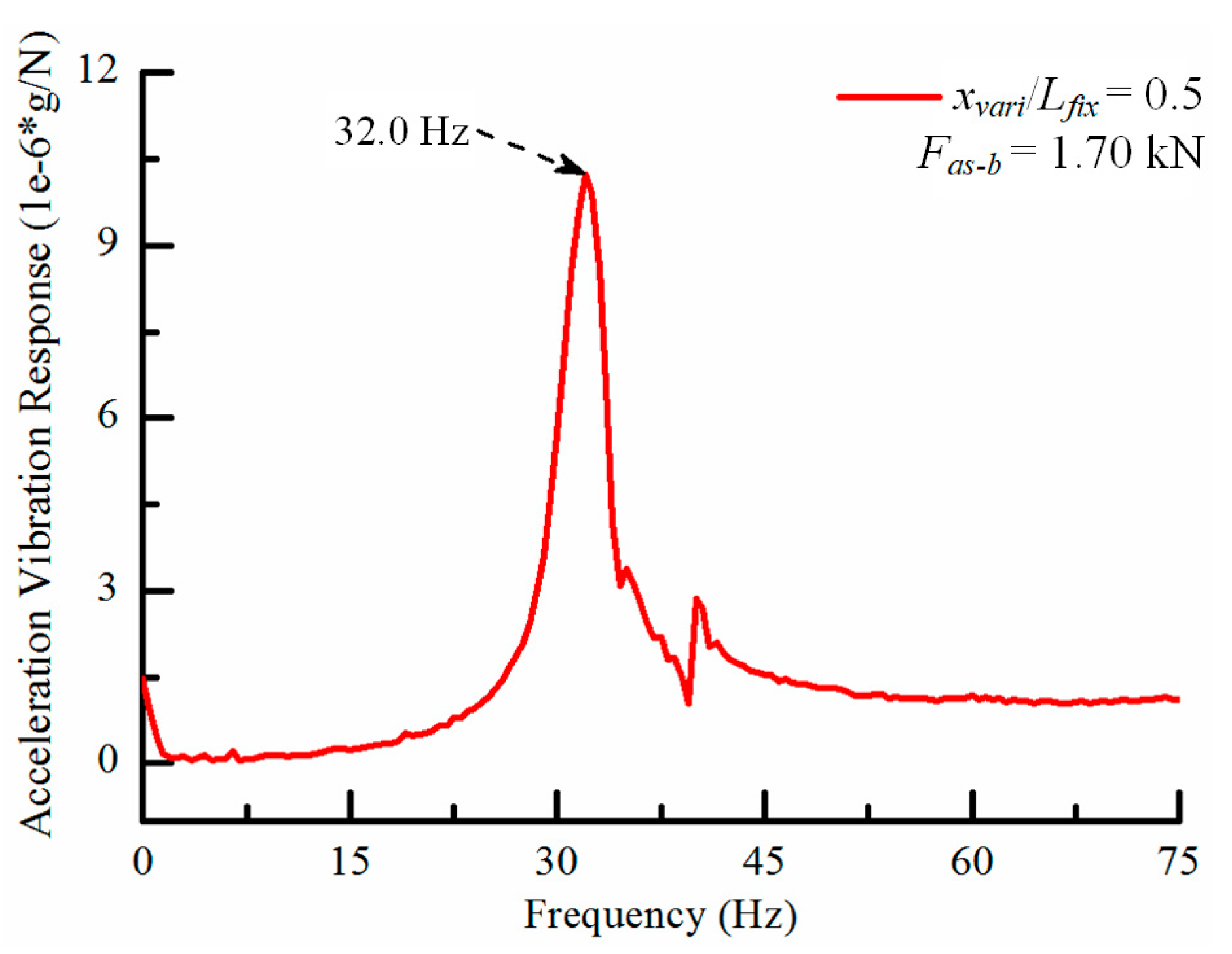
4.1. Comparison of the Theoretical and Experimental Results Based on the Worktable Position
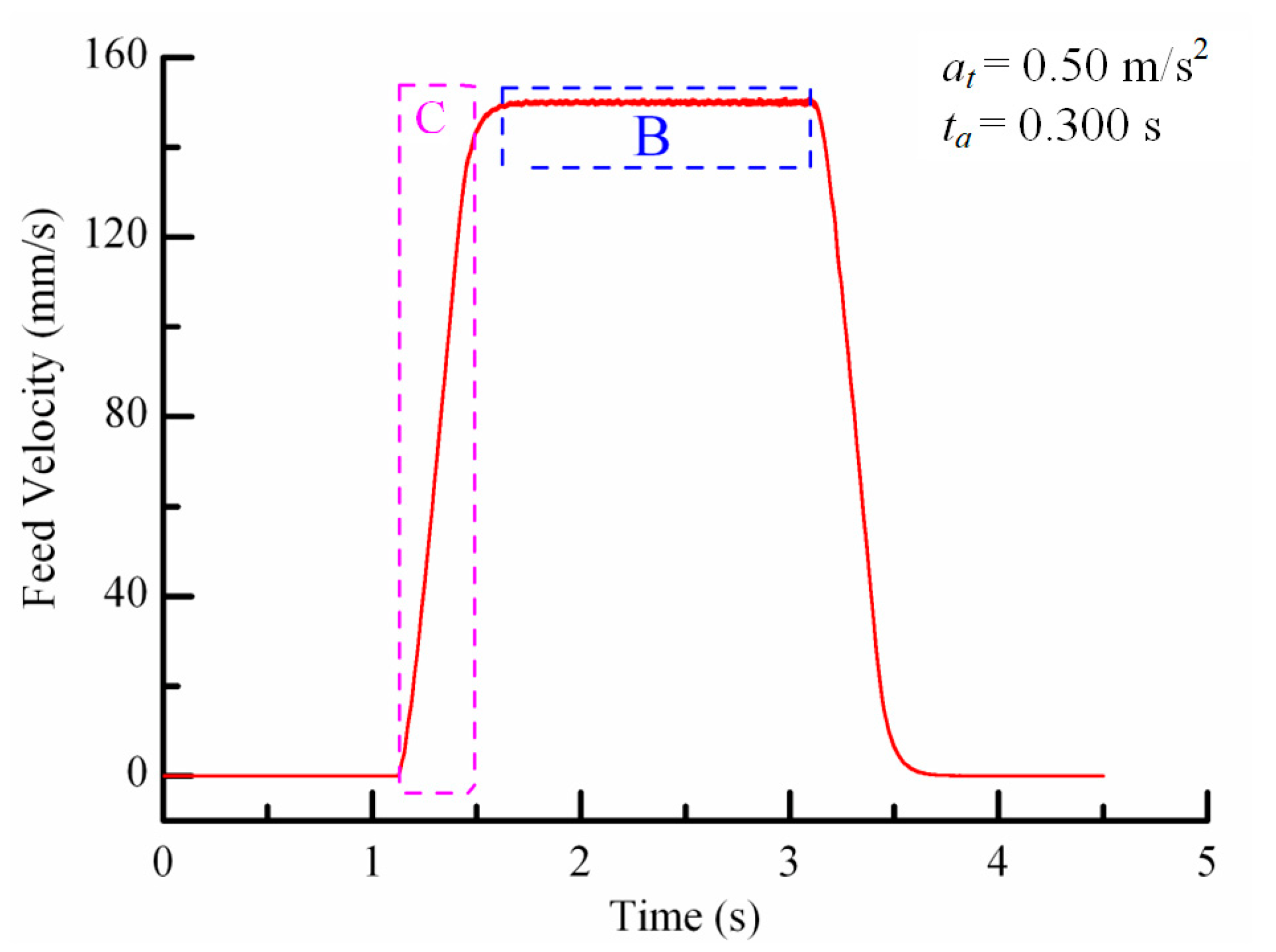
4.2. Comparison of the Theoretical and Experimental Results Based on the Feed Speed of the Worktable
4.3. Comparison of the Theoretical and Experimental Results Based on the Feed Acceleration of the Worktable
5. Conclusions
6. Future Directions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kim, M.S.; Chung, S.C. A systematic approach to design high-performance feed drive systems. Int. J. Mach. Tools Manuf. 2005, 45, 1421–1435. [Google Scholar] [CrossRef]
- Altintas, Y.; Verl, A.; Brecher, C.; Uriarte, L.; Pritschow, G. Machine tool feed drives. CIRP Ann. 2011, 60, 779–796. [Google Scholar] [CrossRef]
- Kamalzadeh, A.; Erkorkmaz, K. Compensation of Axial Vibrations in Ball Screw Drives. CIRP Ann. 2007, 56, 373–378. [Google Scholar] [CrossRef]
- Erkorkmaz, K.; Kamalzadeh, A. High Bandwidth Control of Ball Screw Drives. CIRP Ann. 2006, 55, 393–398. [Google Scholar] [CrossRef]
- Du, F.; Zhang, M.; Wang, Z.; Yu, C.; Feng, X.; Li, P. Identification and compensation of friction for a novel two-axis differential micro-feed system. Mech. Syst. Signal Process. 2018, 106, 453–465. [Google Scholar] [CrossRef]
- Yang, X.; Lu, D.; Liu, H.; Zhao, W. Integrated modeling and analysis of the multiple electromechanical couplings for the direct driven feed system in machine tools. Mech. Syst. Signal Process. 2018, 106, 140–157. [Google Scholar] [CrossRef]
- Kamalzadeh, A.; Erkorkmaz, K. Accurate tracking controller design for high-speed drives. Int. J. Mach. Tools Manuf. 2007, 47, 1393–1400. [Google Scholar] [CrossRef]
- Toh, C. Vibration analysis in high speed rough and finish milling hardened steel. J. Sound Vib. 2004, 278, 101–115. [Google Scholar] [CrossRef]
- Chanal, H.; Duc, E.; Ray, P. A study of the impact of machine tool structure on machining processes. Int. J. Mach. Tools Manuf. 2006, 46, 98–106. [Google Scholar] [CrossRef]
- Law, M.; Altintas, Y.; Phani, A.S. Rapid evaluation and optimization of machine tools with position-dependent stability. Int. J. Mach. Tools Manuf. 2013, 68, 81–90. [Google Scholar] [CrossRef]
- Law, M.; Ihlenfeldt, S.; Wabner, M.; Altintas, Y.; Neugebauer, R. Position-dependent dynamics and stability of serial-parallel kinematic machines. CIRP Ann. 2013, 62, 375–378. [Google Scholar] [CrossRef]
- Weck, M.; Krüger, P.; Brecher, C. Limits for controller settings with electric linear direct drives. Int. J. Mach. Tools Manuf. 2001, 41, 65–88. [Google Scholar] [CrossRef]
- Poignet, P.; Gautier, M.; Khalil, W. Modeling, control and simulation of high speed machine tool axes. In Proceedings of the Conference on Advanced Intelligent Mechatronics, Atlanta, GE, USA, 19–23 September 1999; pp. 617–622. [Google Scholar]
- Okwudire, C.E.; Altintas, Y. Hybrid Modeling of Ball Screw Drives with Coupled Axial, Torsional, and Lateral Dynamics. J. Mech. Des. 2009, 131, 071002. [Google Scholar] [CrossRef]
- Whalley, R.; Ebrahimi, M.; Abdul-Ameer, A.A. Machine Tool Axis Dynamics. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2006, 220, 403–419. [Google Scholar] [CrossRef]
- Zaeh, M.; Oertli, T.; Milberg, J. Finite Element Modelling of Ball Screw Feed Drive Systems. CIRP Ann. 2004, 53, 289–292. [Google Scholar] [CrossRef]
- Law, M.; Phani, S.; Altintas, Y. Position-Dependent Multibody Dynamic Modeling of Machine Tools Based on Improved Reduced Order Models. J. Manuf. Sci. Eng. 2013, 135, 021008. [Google Scholar] [CrossRef]
- Domblesky, J.P.; Feng, F. Two-dimensional and three-dimensional finite element models of external thread rolling. J. Eng. Manuf. 2002, 216, 507–517. [Google Scholar] [CrossRef]
- Feng, G.-H.; Pan, Y.-L. Investigation of ball screw preload variation based on dynamic modeling of a preload adjustable feed-drive system and spectrum analysis of ball-nuts sensed vibration signals. Int. J. Mach. Tools Manuf. 2012, 52, 85–96. [Google Scholar] [CrossRef]
- Zhou, Y.; Peng, F.Y.; Cao, X.H. Parameter sensitivity analysis of axial vibration for lead-screw feed drives with time-varying framework. Mechanika 2011, 17, 523–528. [Google Scholar] [CrossRef]
- Mi, L.; Yin, G.-F.; Sun, M.-N.; Wang, X.-H. Effects of preloads on joints on dynamic stiffness of a whole machine tool structure. J. Mech. Sci. Technol. 2012, 26, 495–508. [Google Scholar] [CrossRef]
- Feng, G.-H.; Pan, Y.-L. Establishing a cost-effective sensing system and signal processing method to diagnose preload levels of ball screws. Mech. Syst. Signal Process. 2012, 28, 78–88. [Google Scholar] [CrossRef]
- Tsai, P.; Cheng, C.; Hwang, Y. Ball screw preload loss detection using ball pass frequency. Mech. Syst. Signal Process. 2014, 48, 77–91. [Google Scholar] [CrossRef]
- Liu, H.; Zhang, J.; Xu, B.; Xu, X.; Zhao, W. Prediction of microstructure gradient distribution in machined surface induced by high speed machining through a coupled FE and CA approach. Mater. Des. 2020, 196, 109133. [Google Scholar] [CrossRef]
- Liu, H.; Birembaux, H.; Ayed, Y.; Rossi, F.; Poulachon, G. Recent advances on cryogenic assistance in drilling operation: A critical review. J. Manuf. Sci. Eng. 2022, 144, 100801. [Google Scholar] [CrossRef]
- Armstrong-Hélouvry, B.; Dupont, P.; De Wit, C.C. A survey of models, analysis tools and compensation methods for the control of machines with friction. Automatica 1994, 30, 1083–1138. [Google Scholar] [CrossRef]
- Awrejcewicz, J.; Olejnik, P. Analysis of Dynamic Systems with Various Friction Laws. Appl. Mech. Rev. 2005, 58, 389–411. [Google Scholar] [CrossRef]
- Reuss, M.; Dadalau, A.; Verl, A. Friction Variances of Linear Machine Tool Axes. Procedia CIRP 2012, 4, 115–119. [Google Scholar] [CrossRef]
- Verl, A.; Frey, S. Correlation between feed velocity and preloading in ball screw drives. CIRP Ann. 2010, 59, 429–432. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, H.; Du, C.; Zhao, W. Research on the dynamics of ball screw feed system with high acceleration. Int. J. Mach. Tools Manuf. 2016, 111, 9–16. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, J.; Liu, H.; Liang, T.; Zhao, W. Dynamic modeling and analysis of the high-speed ball screw feed system. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2014, 229, 870–877. [Google Scholar] [CrossRef]
- Lee, K.; Ibaraki, S.; Matsubara, A.; Kakino, Y.; Suzuki, Y.; Arai, S.; Braasch, J. A servo parameter tuning method for high-speed NC machine tools based on contouring error measurement. WIT Trans. Eng. Sci. 2003, 44, 12. [Google Scholar]
- Frey, S.; Dadalau, A.; Verl, A. Expedient modeling of ball screw feed drives. Prod. Eng. 2012, 6, 205–211. [Google Scholar] [CrossRef]
- Dhatt, G.; Touzot, G. Finite Element Method; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Okamoto. Design and Calculation of Ball Bearings; Huang, Z.Q., Ed.; China Machine Press: Beijing, China, 2003. [Google Scholar]
- Brewe, D.E.; Hamrock, B.J. Simplified solution for elliptical-contact deformation between two elastic solids. J. Lubr. Technol. 1977, 99, 485–487. [Google Scholar] [CrossRef]
- Greenwood, J.A. Analysis of elliptical Hertzian contacts. Tribol. Int. 1997, 30, 235–237. [Google Scholar] [CrossRef]
- He, W.X. Permanent Magnet Motor; China Power Press: Beijing, China, 2007. [Google Scholar]
- Zirn, O. Machine Tool Analysis: Modelling, Simulation and Control of Machine Tool Manipulators; ETH Zurich, Institute of Machine Tools and Manufacturing: Zurich, Switzerland, 2008. [Google Scholar]


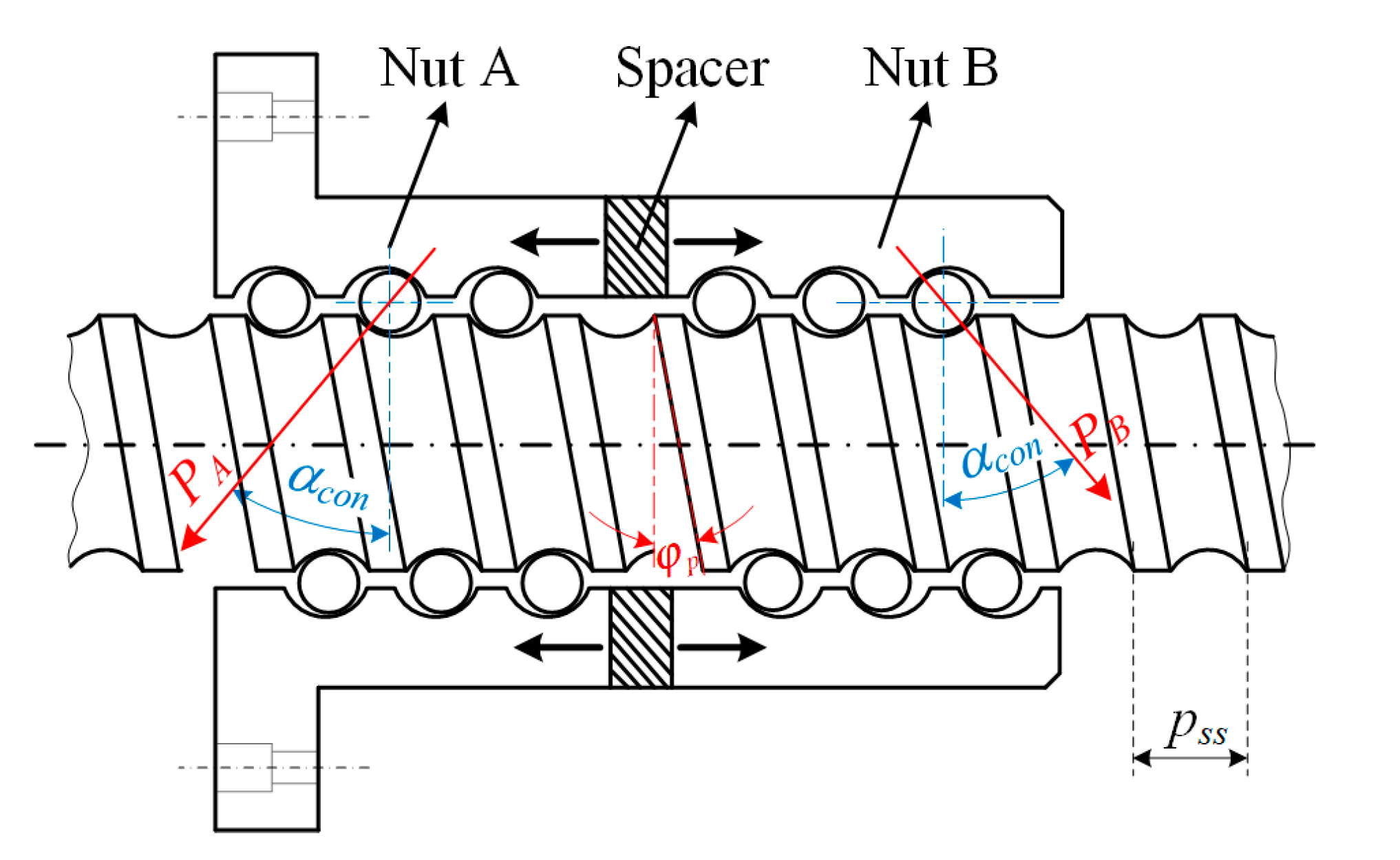
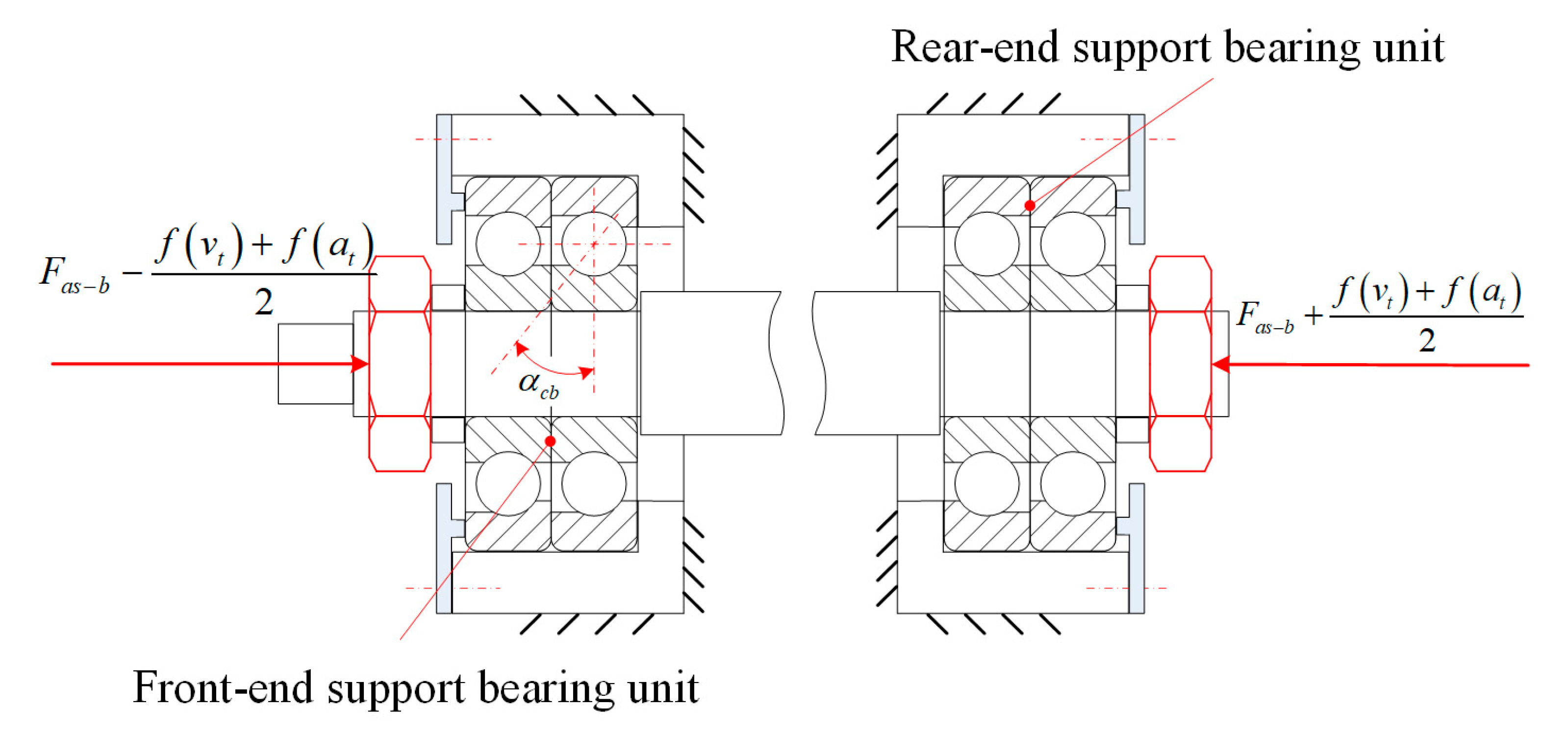




| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| Fas−b/kN | 1.70 | Pd/kN | 163.4 | Aess/m2 | 4.8 × 10−3 |
| αcb/° | 60 | Cp | 0.10 | Ass/m2 | 4.2 × 10−3 |
| ib/nb | 2/29 | αcon/° | 60 | Ess/(N/m2) | 2.1 × 1011 |
| cwb/cwn | 0.8 | φp/° | 3.643 | Gss/(N/m2) | 0.8 × 1011 |
| mt/kg | 7400 | isn | 2.5 | ρss/(kg/m3) | 7.85 × 103 |
| d0/mm | 80 | dsb/mm | 9.525 | Iρss/m4 | 3.6 × 10−6 |
| pss/mm | 16 | Lfix/m | 5.3 |
| Type | Number | Sensitivity (mV/g) | ||
|---|---|---|---|---|
| X | Y | Z | ||
| 356A66 | SN 190783 | 9.99 | 9.85 | 10.33 |
| SN 190788 | 9.96 | 10.08 | 10.11 | |
| SN 190789 | 9.95 | 9.78 | 9.82 | |
| SN 190791 | 9.76 | 10.01 | 10.08 | |
| fthe (Hz) | fexp1 (Hz) | Error (%) | |
|---|---|---|---|
| fthe0 | 35.9 | 32.0 | 12.19 |
| fthe1 | 33.7 | 32.0 | 5.31 |
| fthe (Hz) | fexp2 (Hz) | Error (%) | |
|---|---|---|---|
| fthe1 | 33.7 | 35.2 | 4.26 |
| fthe2 | 34.1 | 35.2 | 3.13 |
| fthe (Hz) | fexp3 (Hz) | Error (%) | |
|---|---|---|---|
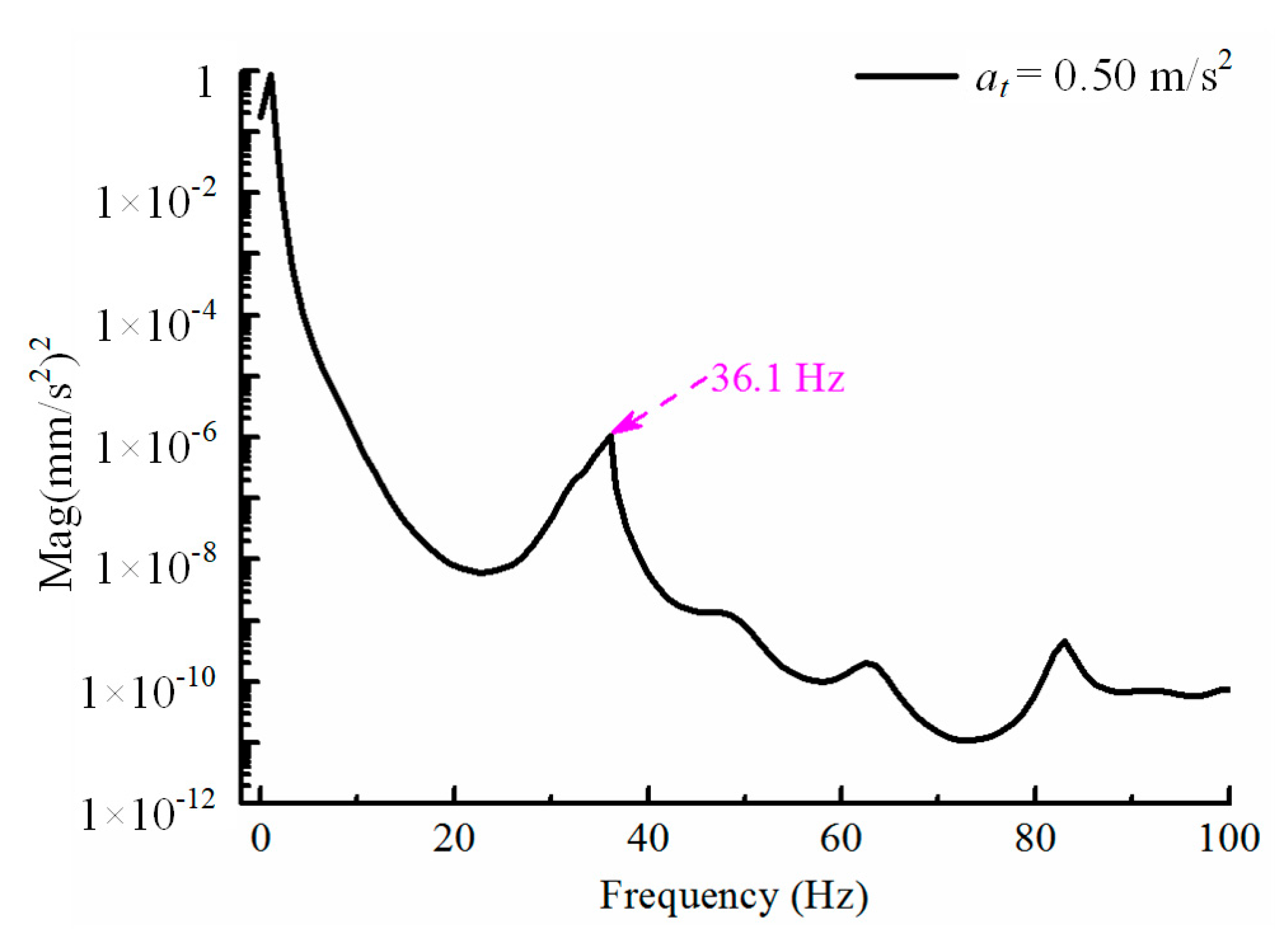
| fthe1 | 33.7 | 36.1 | 6.57 |
| fthe3 | 34.7 | 36.1 | 3.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Zha, J.; Du, C.; Liu, H.; Li, Y.; Lv, D. Variable-Coefficient Dynamic Modeling Method for a Ball Screw Feed System in the No-Extra-Load Running State. Processes 2023, 11, 793. https://doi.org/10.3390/pr11030793
Zhang H, Zha J, Du C, Liu H, Li Y, Lv D. Variable-Coefficient Dynamic Modeling Method for a Ball Screw Feed System in the No-Extra-Load Running State. Processes. 2023; 11(3):793. https://doi.org/10.3390/pr11030793
Chicago/Turabian StyleZhang, Huijie, Jun Zha, Chao Du, Hui Liu, Yang Li, and Dun Lv. 2023. "Variable-Coefficient Dynamic Modeling Method for a Ball Screw Feed System in the No-Extra-Load Running State" Processes 11, no. 3: 793. https://doi.org/10.3390/pr11030793
APA StyleZhang, H., Zha, J., Du, C., Liu, H., Li, Y., & Lv, D. (2023). Variable-Coefficient Dynamic Modeling Method for a Ball Screw Feed System in the No-Extra-Load Running State. Processes, 11(3), 793. https://doi.org/10.3390/pr11030793






