Transformer Aided Adaptive Extended Kalman Filter for Autonomous Vehicle Mass Estimation
Abstract
:1. Introduction
- A novel estimator based on transformer is introduced to provide an accurate pre-estimation of vehicle mass by learning nonlinear dynamics from vehicle data under diverse conditions, thus acting as a virtual observation for EKF.
- A fast confidence level calculation method is designed for weight adjustment based on the conformity level between the real-time input and the training data, to adaptively determine the impact of transformer pre-estimation.
- TA-AEKF is proposed to integrate the transformer pre-estimation into EKF with the adaptive weight adjustment in order to precisely and stably estimate vehicle mass.
2. Transformer Aided Adaptive Extended Kalman Filter
2.1. Framework
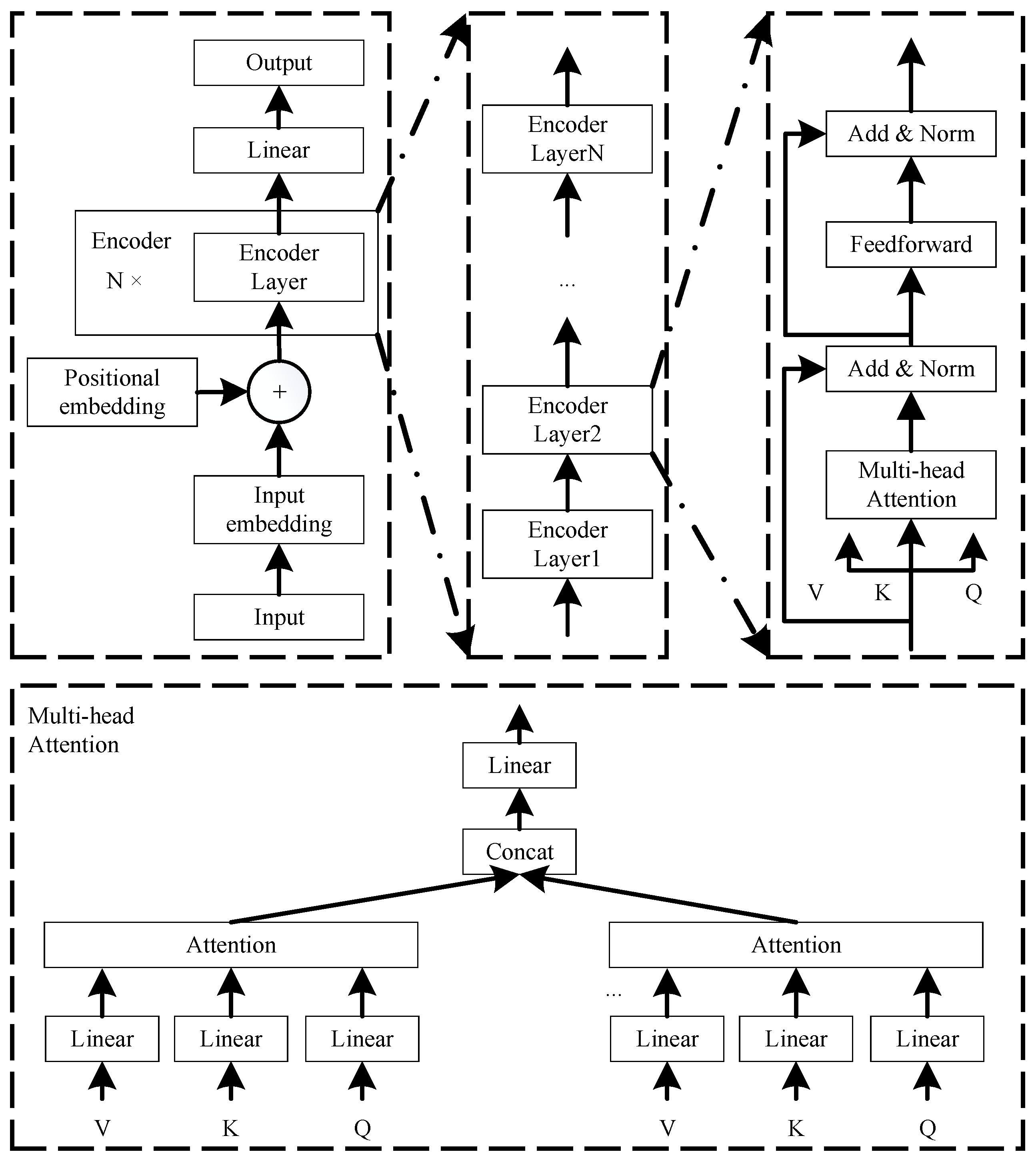
2.2. Transformer-Based Vehicle Mass Pre-Estimation
2.2.1. Preliminaries
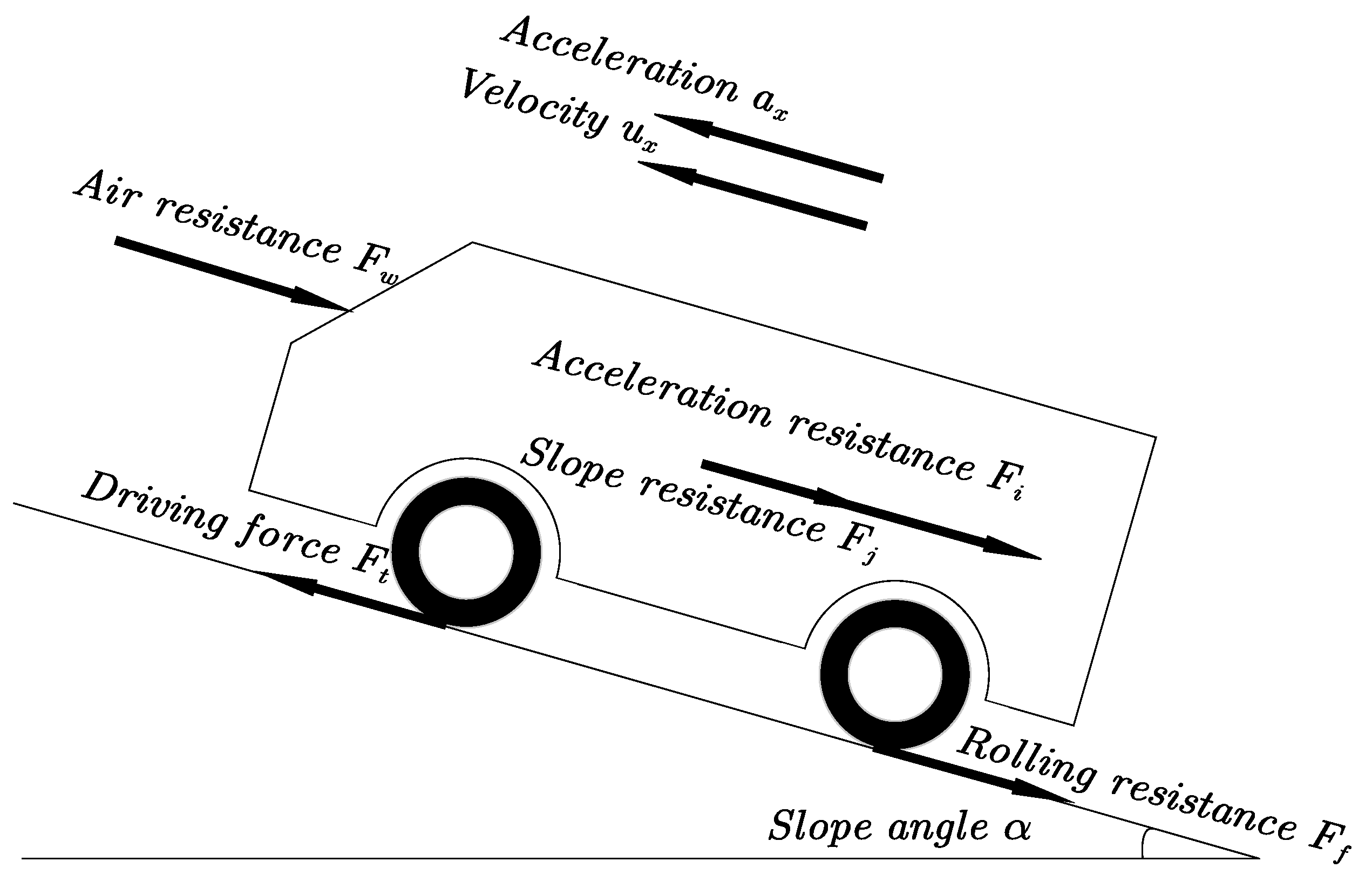
2.2.2. Input Feature Selection
2.2.3. Neural Network Architecture
2.3. Confidence Level for Weight Adjustment
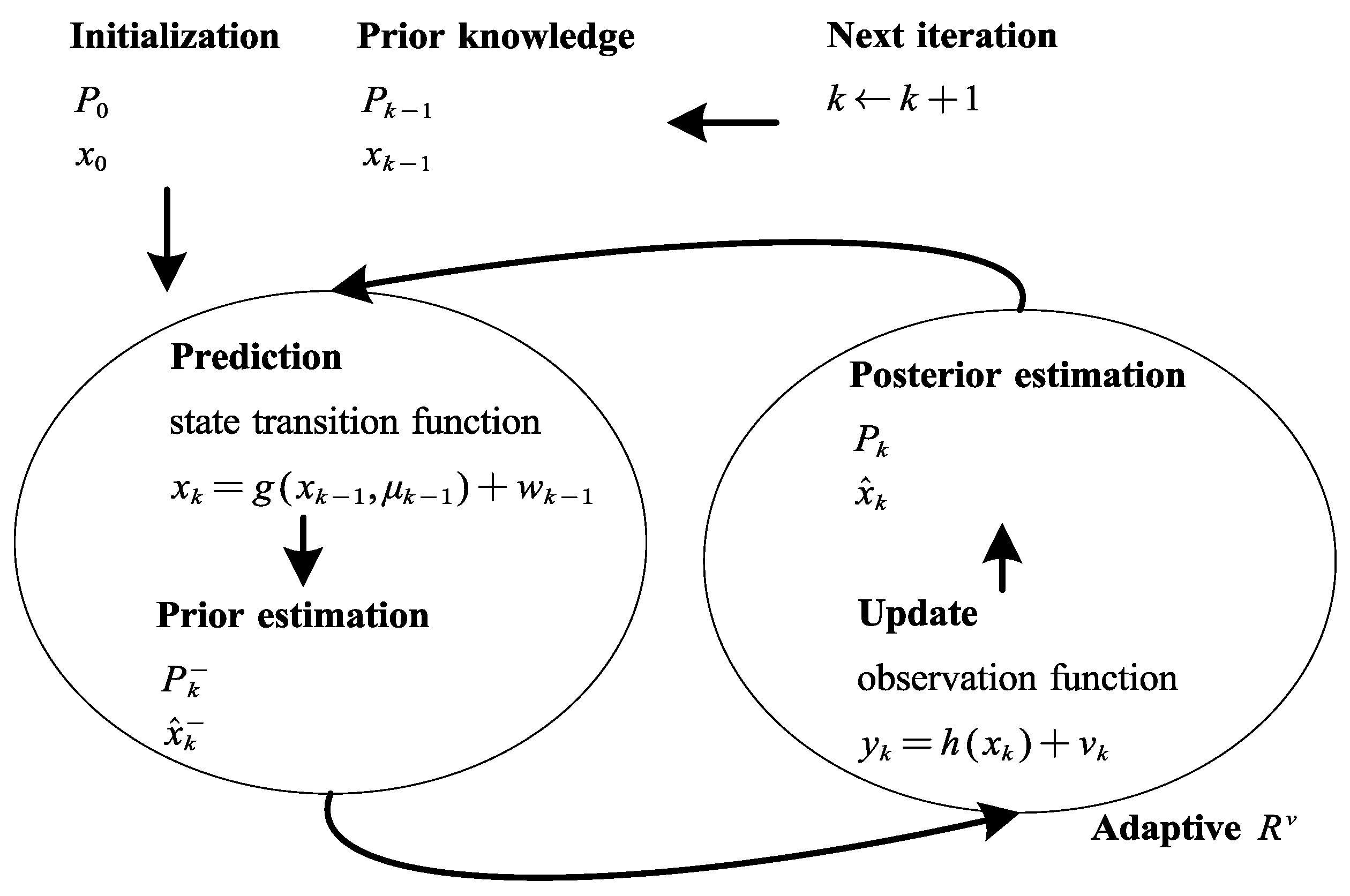
2.4. AEKF
| Algorithm 1 Transformer Aided Adaptive Extended Kalman Filter |
|
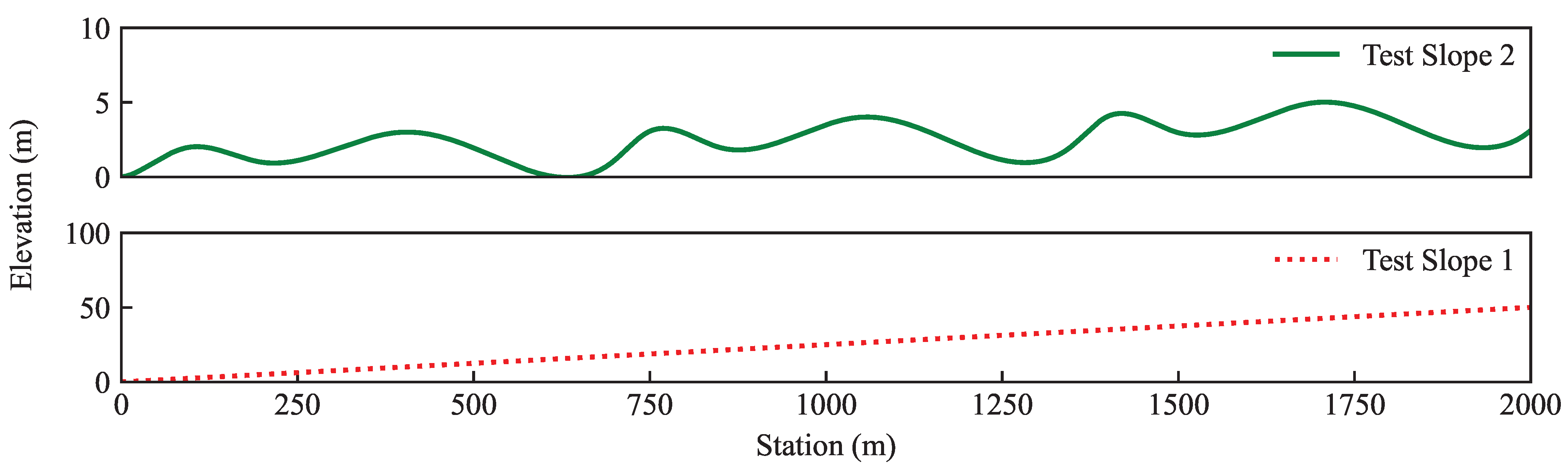
3. Data Acquisition
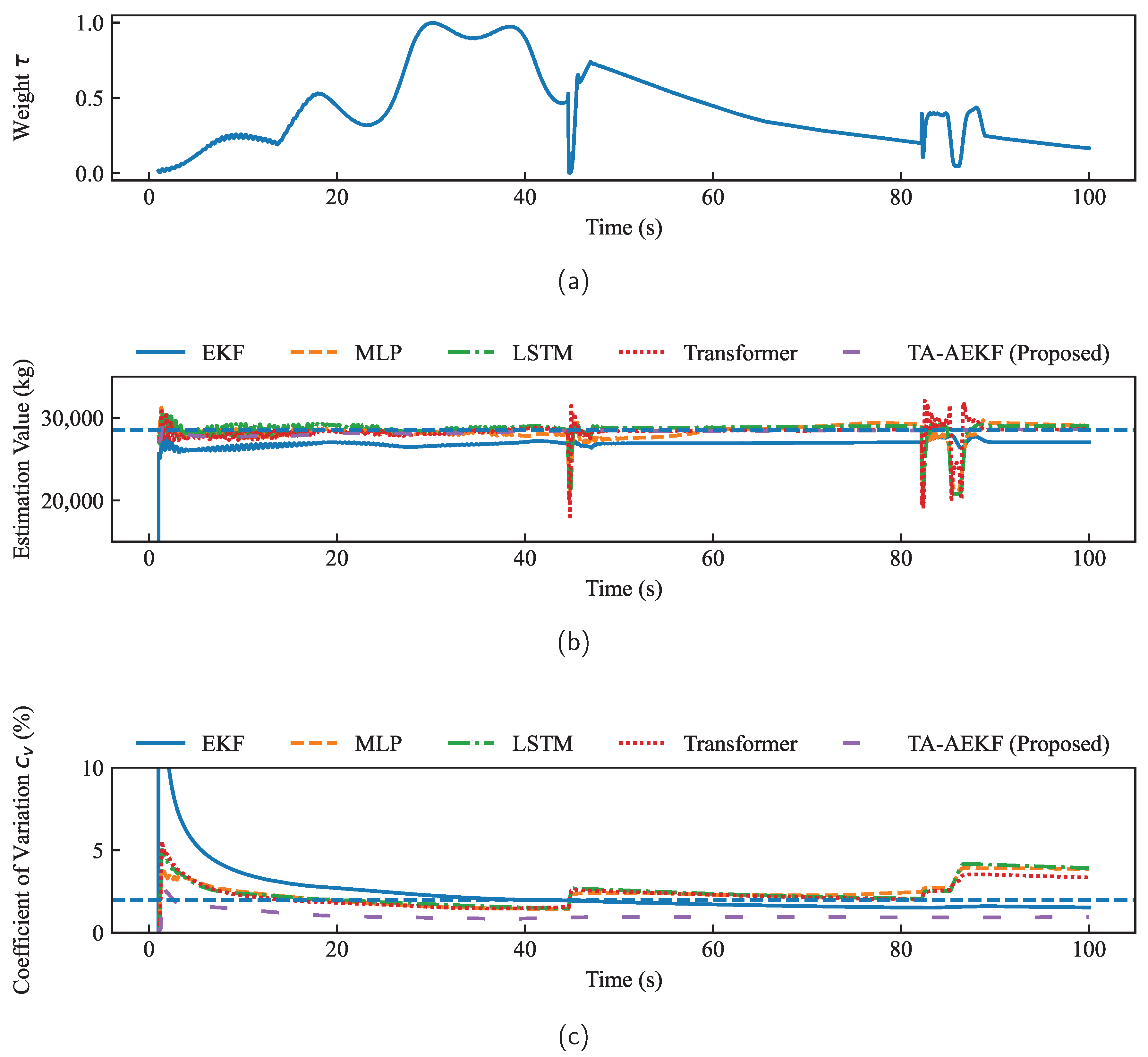
4. Results
4.1. Evaluation Metrics
4.2. Performance Evaluation
4.3. Input Feature Demonstration
4.4. Confidence Level Demonstration
4.4.1. Calculation Speed Demonstration
4.4.2. Improtance Demonstration
4.5. Real Time Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Singh, K.B.; Arat, M.A.; Taheri, S. Literature Review and Fundamental Approaches for Vehicle and Tire State Estimation. Veh. Syst. Dyn. 2019, 57, 1643–1665. [Google Scholar] [CrossRef]
- Xiong, H.; Tan, Z.; Zhang, R.; He, S. A New Dual Axle Drive Optimization Control Strategy for Electric Vehicles Using Vehicle-to-Infrastructure Communications. IEEE Trans. Ind. Inform. 2020, 16, 2574–2582. [Google Scholar] [CrossRef]
- Xiong, H.; Zhu, X.; Zhang, R. Energy Recovery Strategy Numerical Simulation for Dual Axle Drive Pure Electric Vehicle Based on Motor Loss Model and Big Data Calculation. Complexity 2018, 2018, e4071743. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.; Xiong, L.; Xia, X.; Lu, Y.; Gao, L.; Song, S. Vision-Aided Intelligent Vehicle Sideslip Angle Estimation Based on a Dynamic Model. IET Intell. Transp. Syst. 2020, 14, 1183–1189. [Google Scholar] [CrossRef]
- Xia, X.; Hashemi, E.; Xiong, L.; Khajepour, A. Autonomous Vehicle Kinematics and Dynamics Synthesis for Sideslip Angle Estimation Based on Consensus Kalman Filter. IEEE Trans. Control. Syst. Technol. 2023, 31, 179–192. [Google Scholar] [CrossRef]
- Yang, S.K.; Liu, T.S.; Cheng, Y.C. Automatic Measurement of Payload for Heavy Vehicles Using Strain Gages. Measurement 2008, 41, 491–502. [Google Scholar] [CrossRef]
- AG, C. Continental In-Tire Sensors Read Tread Depth. 2014. Available online: https://www.continental.com/en/press/press-releases/2014-05-07-tpms-profile-104542 (accessed on 14 April 2021).
- Zhang, Y.; Zhang, Y.; Ai, Z.; Feng, Y.; Zhang, J.; Murphey, Y.L. Estimation of Electric Mining Haul Trucks’ Mass and Road Slope Using Dual Level Reinforcement Estimator. IEEE Trans. Veh. Technol. 2019, 68, 10627–10638. [Google Scholar] [CrossRef]
- Torabi, S.; Wahde, M.; Hartono, P. Road Grade and Vehicle Mass Estimation for Heavy-duty Vehicles Using Feedforward Neural Networks. In Proceedings of the 2019 4th International Conference on Intelligent Transportation Engineering (ICITE), Singapore, 5–7 September 2019; IEEE: Singapore, 2019; pp. 316–321. [Google Scholar] [CrossRef]
- Wang, H.; Zheng, Y.; Yu, Y. Joint Estimation of SOC of Lithium Battery Based on Dual Kalman Filter. Processes 2021, 9, 1412. [Google Scholar] [CrossRef]
- Feng, W.; Dong, W.; Zhai, S.; Zhang, G.; Sun, X.; Ji, Y. A Deep Reinforcement Learning Method for Freight Train Driving Based on Domain Knowledge and Mass Estimation Network. In Proceedings of the 2021 6th International Conference on Machine Learning Technologies, Jeju Island, Republic of Korea, 23–25 April 2021; ACM: New York, NY, USA, 2021; pp. 41–46. [Google Scholar] [CrossRef]
- Ritter, A.; Widmer, F.; Vetterli, B.; Onder, C.H. Optimization-Based Online Estimation of Vehicle Mass and Road Grade: Theoretical Analysis and Experimental Validation. Mechatronics 2021, 80, 102663. [Google Scholar] [CrossRef]
- Li, X.; Ma, J.; Zhao, X.; Wang, L. Intelligent Two-Step Estimation Approach for Vehicle Mass and Road Grade. IEEE Access 2020, 8, 218853–218862. [Google Scholar] [CrossRef]
- Zhang, F.; Wang, Y.; Hu, J.; Yin, G.; Chen, S.; Zhang, H.; Zhou, D. A Novel Comprehensive Scheme for Vehicle State Estimation Using Dual Extended H-Infinity Kalman Filter. Electronics 2021, 10, 1526. [Google Scholar] [CrossRef]
- Mei, C.; Peng, J.; Yuhui, H. An Online Mass Estimation Algorithm for Single-shaft Parallel Hybrid Commercial Vehicle. Acta Armamentarii 2021, 42, 1838–1846. [Google Scholar] [CrossRef]
- Zhang, Z.; Yin, G.; Wu, Z. Joint Estimation of Mass and Center of Gravity Position for Distributed Drive Electric Vehicles Using Dual Robust Embedded Cubature Kalman Filter. Sensors 2022, 22, 10018. [Google Scholar] [CrossRef]
- Rajamani, R.; Hedrick, J.K. Adaptive Observers for Active Automotive Suspensions: Theory and Experiment. IEEE Trans. Control. Syst. Technol. 1995, 3, 86–93. [Google Scholar] [CrossRef]
- Jensen, K.M.; Santos, I.F.; Clemmensen, L.K.H.; Theodorsen, S.; Corstens, H.J.P. Mass Estimation of Ground Vehicles Based on Longitudinal Dynamics Using IMU and Can-Bus Data. Mech. Syst. Signal Process. 2022, 162, 107982. [Google Scholar] [CrossRef]
- Reina, G.; Paiano, M.; Blanco-Claraco, J.L. Vehicle Parameter Estimation Using a Model-Based Estimator. Mech. Syst. Signal Process. 2017, 87, 227–241. [Google Scholar] [CrossRef] [Green Version]
- Jeong, D.; Kim, S.; Lee, J.; Choi, S.B.; Kim, M.; Lee, H. Estimation of Tire Load and Vehicle Parameters Using Intelligent Tires Combined With Vehicle Dynamics. IEEE Trans. Instrum. Meas. 2020, 70, 1–12. [Google Scholar] [CrossRef]
- Cai, L.; Wang, H.; Jia, T.; Peng, P.; Pi, D.; Wang, E. Two-Layer Structure Algorithm for Estimation of Commercial Vehicle Mass. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 378–389. [Google Scholar] [CrossRef]
- Jin, X.; Yang, J.; Li, Y.; Zhu, B.; Wang, J.; Yin, G. Online Estimation of Inertial Parameter for Lightweight Electric Vehicle Using Dual Unscented Kalman Filter Approach. IET Intell. Transp. Syst. 2020, 14, 412–422. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, N.; Walker, P.; Lin, C. Intelligent Estimation for Electric Vehicle Mass with Unknown Uncertainties Based on Particle Filter. IET Intell. Transp. Syst. 2020, 14, 463–467. [Google Scholar] [CrossRef]
- Chen, J.; Feng, X.; Jiang, L.; Zhu, Q. State of Charge Estimation of Lithium-Ion Battery Using Denoising Autoencoder and Gated Recurrent Unit Recurrent Neural Network. Energy 2021, 227, 120451. [Google Scholar] [CrossRef]
- Barati, K.; Shen, X.; Li, N.; Carmichael, D.G. Automatic Mass Estimation of Construction Vehicles by Modeling Operational and Engine Data. J. Constr. Eng. Manag. 2022, 148, 04021208. [Google Scholar] [CrossRef]
- Xiong, H.; Wang, Z.; Wu, G.; Pan, Y.; Yang, Z.; Long, Z. Steering Actuator Fault Diagnosis for Autonomous Vehicle With an Adaptive Denoising Residual Network. IEEE Trans. Instrum. Meas. 2022, 71, 1–13. [Google Scholar] [CrossRef]
- Korayem, A.H.; Khajepour, A.; Fidan, B. Trailer Mass Estimation Using System Model-Based and Machine Learning Approaches. IEEE Trans. Veh. Technol. 2020, 69, 12536–12546. [Google Scholar] [CrossRef]
- Sieberg, P.M.; Blume, S.; Reicherts, S.; Maas, N.; Schramm, D. Hybrid State Estimation-A Contribution Towards Reliability Enhancement of Artificial Neural Network Estimators. IEEE Trans. Intell. Transp. Syst. 2022, 23, 6337–6346. [Google Scholar] [CrossRef]
- Hannan, M.A.; How, D.N.T.; Lipu, M.S.H.; Mansor, M.; Ker, P.J.; Dong, Z.Y.; Sahari, K.S.M.; Tiong, S.K.; Muttaqi, K.M.; Mahlia, T.M.I.; et al. Deep Learning Approach towards Accurate State of Charge Estimation for Lithium-Ion Batteries Using Self-Supervised Transformer Model. Sci. Rep. 2021, 11, 19541. [Google Scholar] [CrossRef]
- Pang, H.; Liu, F.; Xu, Z. Variable Universe Fuzzy Control for Vehicle Semi-Active Suspension System with MR Damper Combining Fuzzy Neural Network and Particle Swarm Optimization. Neurocomputing 2018, 306, 130–140. [Google Scholar] [CrossRef]
- Xing, Y.; Lv, C. Dynamic State Estimation for the Advanced Brake System of Electric Vehicles by Using Deep Recurrent Neural Networks. IEEE Trans. Ind. Electron. 2020, 67, 9536–9547. [Google Scholar] [CrossRef]
- Lin, C.; Wang, H.; Fu, M.; Yuan, J.; Gu, J. A Gated Recurrent Unit-Based Particle Filter for Unmanned Underwater Vehicle State Estimation. IEEE Trans. Instrum. Meas. 2020, 70, 1–12. [Google Scholar] [CrossRef]
- Wang, M.; Pang, H.; Luo, J.; Liu, M. On an Enhanced Back Propagation Neural Network Control of Vehicle Semi-Active Suspension with a Magnetorheological Damper. Trans. Inst. Meas. Control. 2023, 45, 512–523. [Google Scholar] [CrossRef]
- Zerveas, G.; Jayaraman, S.; Patel, D.; Bhamidipaty, A.; Eickhoff, C. A Transformer-Based Framework for Multivariate Time Series Representation Learning. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Singapore, 14–18 August 2021; ACM: New York, NY, USA, 2021; pp. 2114–2124. [Google Scholar] [CrossRef]
- Hong, S.; Lee, C.; Borrelli, F.; Hedrick, J.K. A Novel Approach for Vehicle Inertial Parameter Identification Using a Dual Kalman Filter. IEEE Trans. Intell. Transp. Syst. 2015, 16, 151–161. [Google Scholar] [CrossRef]
- Xiong, L.; Xia, X.; Lu, Y.; Liu, W.; Gao, L.; Song, S.; Yu, Z. IMU-Based Automated Vehicle Body Sideslip Angle and Attitude Estimation Aided by GNSS Using Parallel Adaptive Kalman Filters. IEEE Trans. Veh. Technol. 2020, 69, 10668–10680. [Google Scholar] [CrossRef]
- Xiong, H.; Liu, J.; Zhang, R.; Zhu, X.; Liu, H. An Accurate Vehicle and Road Condition Estimation Algorithm for Vehicle Networking Applications. IEEE Access 2019, 7, 17705–17715. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, S.; Li, W.; Miao, Q. State-of-Charge Estimation of Lithium-Ion Batteries Using LSTM and UKF. Energy 2020, 201, 117664. [Google Scholar] [CrossRef]
- Liu, W.; Xia, X.; Xiong, L.; Lu, Y.; Gao, L.; Yu, Z. Automated Vehicle Sideslip Angle Estimation Considering Signal Measurement Characteristic. IEEE Sens. J. 2021, 21, 21675–21687. [Google Scholar] [CrossRef]
- Oguiza, I. tsai - A State-of-the-Art Deep Learning Library for Time Series and Sequential Data; Github: San Francisco, CA, USA, 2022. [Google Scholar]
- Kidambi, N.; Harne, R.L.; Fujii, Y.; Pietron, G.M.; Wang, K.W. Methods in Vehicle Mass and Road Grade Estimation. SAE Int. J. Passeng. Cars-Mech. Syst. 2014, 7, 981–991. [Google Scholar] [CrossRef] [Green Version]





| Parameter | Value |
|---|---|
| vehicle curb weight | 6042 kg |
| vehicle payload | 4000 to 40,000 per 4000 kg |
| Frontal area | 6.8 |
| efficiency | 0.99 |
| sample time | 0.01 s |
| Method | MAPE (%) | MAE (kg) | RMSE (kg) | CR (steps) |
|---|---|---|---|---|
| EKF | 5.85 | 1669.77 | 1719.58 | 3790 |
| MLP | 2.28 | 652.05 | 1117.12 | nan |
| LSTM | 1.80 | 514.51 | 1124.30 | nan |
| Transformer | 1.42 | 404.91 | 972.35 | nan |
| TA-AEKF (Proposed) | 0.89 | 255.41 | 356.42 | 156 |
| Method | MAPE (%) | MAE (kg) | RMSE (kg) | CR (steps) |
|---|---|---|---|---|
| EKF | 5.98 | 1706.40 | 1745.78 | 3338 |
| MLP | 3.57 | 1018.14 | 2031.73 | nan |
| LSTM | 2.95 | 843.07 | 2018.19 | nan |
| Transformer | 2.15 | 613.11 | 1068.24 | nan |
| TA-AEKF (Proposed) | 0.90 | 257.53 | 357.61 | 212 |
| Method | MAPE (%) | MAE (kg) | RMSE (kg) | CR (steps) |
|---|---|---|---|---|
| EKF | 5.91 | 1688.08 | 1732.68 | 3564 |
| MLP | 2.93 | 835.09 | 1574.42 | nan |
| LSTM | 2.38 | 678.79 | 1571.25 | nan |
| Transformer | 1.78 | 509.01 | 1020.29 | nan |
| TA-AEKF (Proposed) | 0.90 | 256.47 | 357.01 | 184 |
| Method | Computing Time (s) | ||
|---|---|---|---|
| Test1 | Test2 | Average of Test1 & Test2 | |
| Method 1 ([28]) | 280.21 | 293.68 | 286.94 |
| Method 2 (Proposed) | 1.00 | 0.99 | 1.00 |
| Method | MAPE (%) | MAE (kg) | RMSE (kg) | CR (steps) |
|---|---|---|---|---|
| 8.06 | 2301.15 | 2305.04 | 154 | |
| 1.42 | 404.91 | 972.35 | nan | |
| 0.89 | 255.41 | 356.42 | 156 |
| Method | Computing Time (s) | ||
|---|---|---|---|
| Test1 | Test2 | Average of Test1 & Test2 | |
| EKF | 0.53 | 0.57 | 0.55 |
| MLP | 0.17 | 0.21 | 0.19 |
| LSTM | 0.17 | 0.18 | 0.17 |
| Transformer | 0.44 | 0.46 | 0.45 |
| TA-AEKF (Proposed) | 1.07 | 1.09 | 1.08 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Yang, Z.; Xiong, H.; Zhu, T.; Long, Z.; Wu, W. Transformer Aided Adaptive Extended Kalman Filter for Autonomous Vehicle Mass Estimation. Processes 2023, 11, 887. https://doi.org/10.3390/pr11030887
Zhang H, Yang Z, Xiong H, Zhu T, Long Z, Wu W. Transformer Aided Adaptive Extended Kalman Filter for Autonomous Vehicle Mass Estimation. Processes. 2023; 11(3):887. https://doi.org/10.3390/pr11030887
Chicago/Turabian StyleZhang, Hui, Zichao Yang, Huiyuan Xiong, Taohong Zhu, Zhineng Long, and Weibin Wu. 2023. "Transformer Aided Adaptive Extended Kalman Filter for Autonomous Vehicle Mass Estimation" Processes 11, no. 3: 887. https://doi.org/10.3390/pr11030887
APA StyleZhang, H., Yang, Z., Xiong, H., Zhu, T., Long, Z., & Wu, W. (2023). Transformer Aided Adaptive Extended Kalman Filter for Autonomous Vehicle Mass Estimation. Processes, 11(3), 887. https://doi.org/10.3390/pr11030887







