1. Introduction
A confined impinging jet reactor is a typical mixing device in a process requiring quick mixing, which is due to the intensified local energy dissipation, resulting in excellent mass transfer capacity [
1,
2,
3]. However, the operation of confined impinging jet reactors usually requires streams with equal momentum or jet diameter, or the deviation of stagnation point will lead to an obvious decline in micro-mixing, which is not beneficial to a quick or instantaneous reaction [
4]. Apparently, the confined impinging jet reactor is not easily applicable for mixing between unequal flows. For example, in the Beckmann rearrangement reaction, an important step in the production of caprolactam, the flow ratio between the cyclohexanone oxime and the strongly acidic can be as low as 0.7 [
5], where the confined impinging jet rector will not be so appropriate.
Hence, a reactor which can be applied to the mixing with unequal flows is required in such a process, such as the Venturi tube mixer (VTM) [
6]. The very first VTM was proposed and designed by Eric Haliburn, based on the Venturi effect, to rapidly mix cementitious grout [
7]. Then, it was widely used in the production of liquid insecticides and the irrigation of agriculture [
8]. A further understanding of the flow and mixing characteristics of VTM can promote its industrial value.
In the investigation of the flow and mixing characteristics in VTM, two typical flow phenomena in VTM are noteworthy, including the Venturi effect induced by fluid flow in the Venturi tube (VT) and the cross-flow generated by passive or active jetting fluid into the VT. Much research has been carried out on these two aspects in recent decades. Goharzadeh et al. [
9] investigated the velocity field in VT using Particle Image Velocimetry (PIV), and the results showed the pressure drop caused by viscosity mainly existed at the divergent region outlet. Vijay et al. [
10] numerically simulated the velocity, pressure and turbulence kinetic energy distributions in the VT, and found at most 5% relative error between the simulated and experimental results, indicating the accuracy and feasibility of Computational Fluid Dynamics (CFD). Sanghani et al. [
11] explored the effects of convergent ratio, length of throat, convergent angle and divergent angle on the pressure distribution in the VT using numerical simulation, and the convergent ratio was found to be the most influential factor among all parameters. Shi et al. [
12] explored fluid flow in the VT by simulation and experiment, and the convergent angle was found to greatly affect the cavitation phenomena in the VT. As for the cross-flow, Luo et al. [
13] used Planar Lase-Induced Fluorescence (PLIF) and the Large Eddy Simulation (LES) method to investigate the mixing process of cross-flow and revealed the effect of the interaction between two fluids on flow vortex. Kartaev et al. [
14] investigated macroscopic mixing in the cross-flow by both experiment and numerical simulation and calculated the axial penetration depth of countercurrent jetting flow.
In addition to the research method, many researchers have concentrated on how the structural and operating conditions affect the flow and mixing characteristics in VTM. Li et al. [
15] researched the hydraulic characteristics in VTM using CFD, and the results showed that the pressure at the throat region is more difficult to accurately predict than that at other regions, resulting in the requirement of refined mesh at the throat region. Simpson et al. [
16] investigated the cavitation characteristics of VTM with different operating conditions. The effect of throat length, convergent angle and geometric parameters on the occurrence and degree of cavitation were quantitatively discussed. Sundararaj et al. [
17,
18] investigated the effects of jetting angle and operating conditions on the mixing characteristics of VTM, and the results showed that increasing the jetting angle and velocity ratio of jetting flow to motive flow can promote the mixing quality. Wang et al. [
19] researched the flow field in VTM using PIV, and the results revealed that with the increase in jetting flow rate, reverse flow will appear in the downstream near the wall. Manzano et al. [
20] used the CFD method to investigate the relationship between the configuration of VTM and pressure drop, which showed that the diameter of the throat was an important factor affecting the pressure drop.
However, the present research is mainly focused on the flow characteristics inside the VTM without the mixing, along with a few works on the optimization of VTM structure and understanding the relationship between the structural characteristics and the resulting flow and mixing behavior. In the present work, the CFD method will be used to reveal how structural configurations affect the flow and mixing in the VTM. Before the optimization of VTM, firstly, two typical phenomena, namely Venturi flow and cross-flow, are simulated with different meshing schemes and turbulence models. By comparing the simulated results with experimental and theoretical results, a suitable meshing scheme and a turbulence model in simulating the flow in the VT and VTM are determined. Secondly, the effect of structural parameters on the flow in VT are investigated, which includes the convergent ratio, length-diameter ratio of the throat, convergent angle and divergent angle. In the research of VTM, a jetting tube is added at the throat region of previously optimized VT to construct a VTM. Then, the research focuses on the effect of structural parameters and operating conditions on the flow and mixing characteristics in VTM, including the pore-throat diameter ratio, jetting angle, jetting position ratio and so on. Finally, a flow optimized and lower energy consumption VTM configuration is proposed.
Hence, the highlights of this work are as follows: firstly, we compare the accuracy and feasibility of different turbulence models; then, these are employed to optimize the configuration of this mixing device from VT to VTM using a two-step method, with comprehensive structural analysis, which provides a meaningful guide for the design of such a mixing device.
2. Geometry of Venturi Tube Mixer and Numerical Simulation Method
2.1. Geometry of Venturi Mixer
There are generally four regions in a Venturi tube mixer (VTM), namely the convergent region, throat region, divergent region and jetting region, as shown in
Figure 1, where it is the Venturi tube (VT) if there is no jetting region.
In the operation of VTM, fluid A (motive flow or motive stream) flows from the convergent region to the divergent region through the throat region; meanwhile, fluid B (jetting flow or jetting stream) is injected from the jetting region, and then there is the mixture stream A + B flowing out of the VTM. If the jetting flow B is sucked into the throat region due to the pressure difference between the throat and jetting entrance, it is called a passive operation; when extra energy is inputted for fluid B, it is an active operation. For convenience,
Figure 1 shows all the nomenclatures representing key dimensions of the VTM. An additional straight tube, whose length is 10 times the throat region diameter
d, is added at convergent inlet and divergent outlet to ensure the sufficient development of turbulence.
2.2. Governing Equations in Numerical Simulation
The mixing of two or more fluid streams is the main operation purpose in a VTM. In this work, those equations are solved using ANSYS Fluent 2020R1, based on the finite volume method. The mathematical equations governing the flow and mixing are below.
2.2.1. Fluid Flow
In this work, incompressible Newtonian fluid, water at room temperature, is used as the material. The continuity equation and momentum equation are described below.
where
is the velocity vector,
θ is the time,
fB is the mass force acting on the fluid per unit mass,
ρ is the fluid density,
P is the pressure,
υ is the fluid kinematic viscosity.
2.2.2. Fluid Mixing
In describing the mixing process between two miscible fluids, species transport is a common model. For species
i in the mixing, the conservation equation is described below.
where
φi is the mass fraction of species
i,
Dm is the diffusion rate of species
i,
Si is the source term of species
i. There is
Si = 0 when species
i is not consumed or generated by reaction in the system.
In this work, the fluids A and B described in
Figure 1 are both water but are marked with different labels to distinguish their concentrations.
2.3. Boundary Condition and Solution Strategy
In this work, there are several types of boundary conditions, where the boundary for the incoming fluid was mainly the velocity inlet, and the exit for the fluid was mainly the pressure outlet according to the specific pressure conditions in the VTM. The entire solid wall in the simulated domain was set as the no-slip wall condition.
In this work, all the simulations were carried out in pressure-based and steady states. The solution method was the SIMPLE algorithm with second-order upwind for the momentum equation, first-order upwind for the turbulent kinetic energy and turbulence dissipation rate, and second-order for the pressure. Convergence criteria for all simulation runs was 10−5.
2.4. Mesh Sensitivity Analysis
In this work, according to the research scheme, there are mainly two aspects in the flow and mixing characteristics of VTM, including the flow in VT and the mixing induced from the cross-flow, where the cross-flow phenomenon needs refined mesh due to highly turbulent shearing. Therefore, there were two tests in the mesh sensitivity analysis.
2.4.1. Mesh Sensitivity of Venturi Tube
In this section, a 3D model of the Venturi tube was established based on the model of Caetano et al. [
21], of which the dimensional details of this Venturi tube are shown in
Table 1.
In this work, all meshes are structured meshes generated in the software ICEM. There were five meshing schemes in the mesh sensitivity analysis, where the total number of grid cells were about 0.02 million, 0.09 million, 0.13 million, 0.29 million and 0.58 million, respectively. In this section, the fluid velocity at the convergent inlet boundary and the pressure at the divergent outlet boundary are vcon = 1.106 m/s and Pdiv = 6.2 × 104 Pa, respectively.
2.4.2. Mesh Sensitivity of Cross-Flow
Figure 2a,b shows a typical schematic diagram of cross-flow and the corresponding 3D model. In this cross-flow, the motive stream flows into the cubic domain from left to right; meanwhile, a jetting stream is injected from the jetting tube, which is the same as the experimental device by Sherif [
22]. The dimensional details are shown in
Table 2. Four meshing schemes were used in this test, with grid cells numbering about 0.96 million, 1.39 million, 2.61 million and 8.5 million, respectively. The values of the boundary conditions are given in
Table 3.
2.5. Evaluation and Selection of Turbulence Model
In the numerical simulation of fluid flow, an appropriate turbulence model is vital for describing the turbulence characteristics, where the RANS (Reynolds-Averaged Navier-Stokes) method is popular in the design of industrial devices due to its relatively low computational resource requirement and high efficiency. In the RANS method, standard -, RNG - and Realizable - are three typical models, which should be evaluated before the numerical investigation of VT and VTM.
In this section, the selection of the turbulence model is divided into two parts, namely VT and cross-flow. With regard to the selection of the turbulence model in the simulation of VT, the configuration of VT is the same as that in the mesh sensitivity analysis (
Section 2.4.1). The boundary conditions are given in
Table 4.
The simulated pressure drop along the VT is compared with that of the theoretical value and the literature from Caetano et al. [
21] under different Reynolds numbers. The theoretical value of the pressure drop and the Reynolds number can be calculated, respectively, using Equations (4), (5) and (7).
where Δ
Pcon-thr and Δ
Pcon-div are the pressure difference between
Pcon and
Pthr,
Pcon and
Pdiv, respectively.
K1 and
K2 are the local pressure loss coefficients of the convergent region and the divergent region, respectively, where
K1 = 0.04 and
K2 ≈ 0.32 for
β = 13.7° [
23],
vcon,
vdiv and
vthr are the fluid velocities at the convergent inlet, divergent outlet and throat out boundaries, respectively. The energy loss caused by viscous resistance can be ignored because the VT is short.
As for the turbulence model in the simulation of cross-flow, the physical geometry and the boundary conditions are both the same as that in the mesh sensitivity analysis.
2.6. Numerical Simulation Schemes of VT and VTM
An efficient VTM is desired, and in this work, there are two steps in the optimization of VTM. The parameters, which are to be optimized in this work, are the core structures of VT and VTM, including the convergent ratio, the length-diameter ratio, the convergent and divergent angles, the pore-throat diameter ratio and the jetting angle. The convergent ratio (
γ1 =
d/
Din) presents the compressed degree of fluid flowing from the convergent region to the throat region, thereby affecting the pressure drop between the convergent and throat regions of VT. The length-diameter ratio (
δ =
lthr/
d) can affect the residence time of flow in the throat region. The convergent angle (
α) and divergent angle (
β) define the intensification of flow in the VT being compressed and developed. The pore-throat diameter ratio has an effect on the flow resistance of the jetting tube and then affects the suction capacity of VTM. The change of jetting angle can affect the impingement intensification between jetting flow and motive flow, thereby affecting the mixing quality and energy consumption. The jetting position ratio determines the position where jetting flow and motive flow begin to mix. In addition, the number of jetting influences the flow rate of jetting directly, then it affects the mixing quality. Firstly, the influences of the convergent ratio (
γ1 =
d/
Din), length-diameter ratio of throat (
δ =
lthr/
d), convergent angle (
α) and divergent angle (
β) on the flow in VT are briefly discussed to access an optimized configuration of VT. The structural parameters in the optimization of VT are shown in
Table 5.
Subsequently, the flow and mixing characteristics in VTM are simulated based on the optimized VT, where the structural parameters’ pore-throat diameter ratio
γ2 (=
djet/
d), jetting angle (
θ1), jetting position ratio
m (=
ljet-con/
lthr) and the number of jetting
N, and the operating conditions, including the passive suction and active injection, are discussed, where
Re is only changed in the operation of passive suction, and
R (=
vjet/
vcon) is only changed in the active injection operation. These structural parameters in this step are shown in
Table 6. The operating conditions with passive suction are given in
Table 7, and the operating conditions with active injection are given in
Table 8. In the optimization work of VT and VTM, the total number of simulation cases is 70.
2.7. Evaluation of the Flow and Mixing Quality in VT and VTM
In the evaluation of flow in the VT and VTM, variables including the pressure at the throat
Pthr, the pressure drop coefficient (
λ) and the vacuum transfer coefficient (
T) are commonly used. The suction capacity of VTM is directly affected by
Pthr, and the suction capacity increases with
Pthr. The pressure drop coefficient (
λ) can be used to evaluate the energy consumption, which is calculated using Equation (8).
Generally, the energy consumption in the VT is used to conquer the pressure drop between the convergent and divergent regions. To quantify the pressure drop, a dimensionless number lambda is defined as the pressure drop divided by the kinetic energy of the fluid. It is a great convenience to use lambda to characterize the pressure drop even under a different structure of the VT, and that is why lambda can also be named as the energy consumption coefficient. In this work, the fluid material is water with low viscosity, and it can be regarded as an ideal fluid in the case of a rather large Reynolds number; therefore, the energy consumption generated by viscous dissipation is neglected. The vacuum transfer coefficient
T is the ratio of vacuum degree to Δ
Pcon-div, and the larger the value of
T, the better the performance of the Venturi tube. The value of
T can be calculated using Equation (9).
When evaluating the flow and mixing in the VTM, Δ
Pcon-div, ejecting ratio (
σ) and mixing quality (
M) are usually used, in which Δ
Pcon-div can be used to evaluate the energy consumption, and ejecting ratio
σ can be used to evaluate the suction capacity, calculated using Equation (10).
where
Qe is the volume flow rate of the motive flow, and
Qc is the volume flow rate of the jetting flow.
Because the main application of VTM is mixing, the mixing quality of VTM should be considered, which can be characterized by the variable
M [
24]
, calculated using Equation (11).
where
n is the number of sampling points on the concerned plane (for example, the divergent outlet),
kj is the mole fraction of species at the sampling point
j, and
k0 is the species average mole fraction on the plane of the divergent outlet. Apparently, the mixing quality
M is between 0 and 1, where there is complete mixing if
M = 1 and non-mixing if
M = 0. Meanwhile, the secondary index
δm [
25] is used to evaluate mixing quality, calculated using Equation (12).
where
σb is the standard deviation of the liquid volumetric flow, which can be calculated using the following expression.
where the
ux is the velocity component in the
x direction, and
is the bulk mass fraction evaluated as the following formula.
The maximum value of σ
b is σ
max, which can be calculated using Equation (15).
4. Conclusions
A Venturi tube mixer is a typical process-intensification device, where fast mixing can be achieved by intensive shearing in its throat region. In this work, in order to discover the flow and mixing characteristics of a Venturi tube mixer and thereby its optimization, a two-step method was used, where we firstly optimized the configuration of the Venturi tube without jetting tube by changing the convergent ratio γ1, length-diameter ratio of throat δ, convergent angle α and divergent angle β of the Venturi tube. Then, based on the optimized Venturi tube, the effects of pore-throat diameter ratio γ2, jetting angle θ1, jetting position ratio m, jetting tube number N and the operation mode of jetting flow on the flow and mixing in the Venturi tube mixer were discussed.
In the description of flow in the Venturi tube and the cross-flow, the Realizable k-ε model is an appropriate choice, with a similar average relative error as the LES model but more efficient.
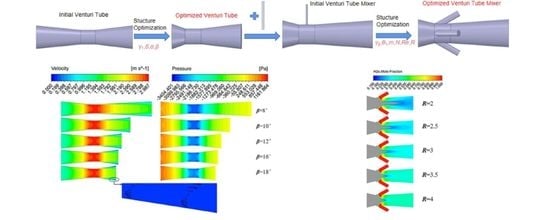
Among all the structural parameters of the Venturi tube mentioned in this work, the convergent ratio is the most influential factor on the flow and the pressure drop in the Venturi tube, while the effects of length-diameter ratio of the throat is not as much as expected. The effects of convergent angle and divergent angle on the flow and pressure drop in the Venturi tube are opposite. Therefore, an optimized configuration of the Venturi tube is proposed, where above parameters are γ1 = 0.71, δ = 0.8, α = 28° and β = 8°. After the optimization of VT, the pressure drop coefficient of optimized VT reduces by 61.6%, while the vacuum transfer coefficient improves by 44.1%.
Based on the optimized configuration of the Venturi tube, a jetting tube is introduced to generate cross-flow to realize a Venturi tube mixer. To a reasonable extent, the pore-throat diameter ratio can be beneficial to suction capacity of the Venturi tube mixer. Jetting angle has a significant effect on mixing quality, where a large jetting angle can contribute to the mixing at the cost of energy consumption (pressure drop) in the Venturi tube mixer. The jetting position is a weak factor in affecting the flow and mixing in the Venturi tube mixer, while increasing the number of jetting tubes from single to quadplex can be a positive factor in the mixing quality. Compared with passive suction, active injection can promote mixing more efficiently. As a result, an optimized configuration of Venturi tube mixer (in passive operation) is proposed, where above parameters are γ2 = 0.3, θ1 = 150°, m = 0.1 and N = 4. The energy consumption of optimized VTM has decreased by 85.6%, and the mixing quality has increased by 4.8%.
In the chemical industry, VTM plays an important role in some specific processes, for example, the mixing of fluid and fine powders, the generation of micro bubbles to intensify mass transfer, the premixing of ingredients in hydrogenation reaction, etc. According to the research of the mixing characteristics of VTM in this work, help and suggestions in the design of an excellent VTM for industrial applications have been provided.