Experimental and Simulation Study on the Direct Contact Condensation of Saturated Steam on Moving Droplets at Sub-Atmospheric Pressure
Abstract
:1. Introduction
2. Experiment
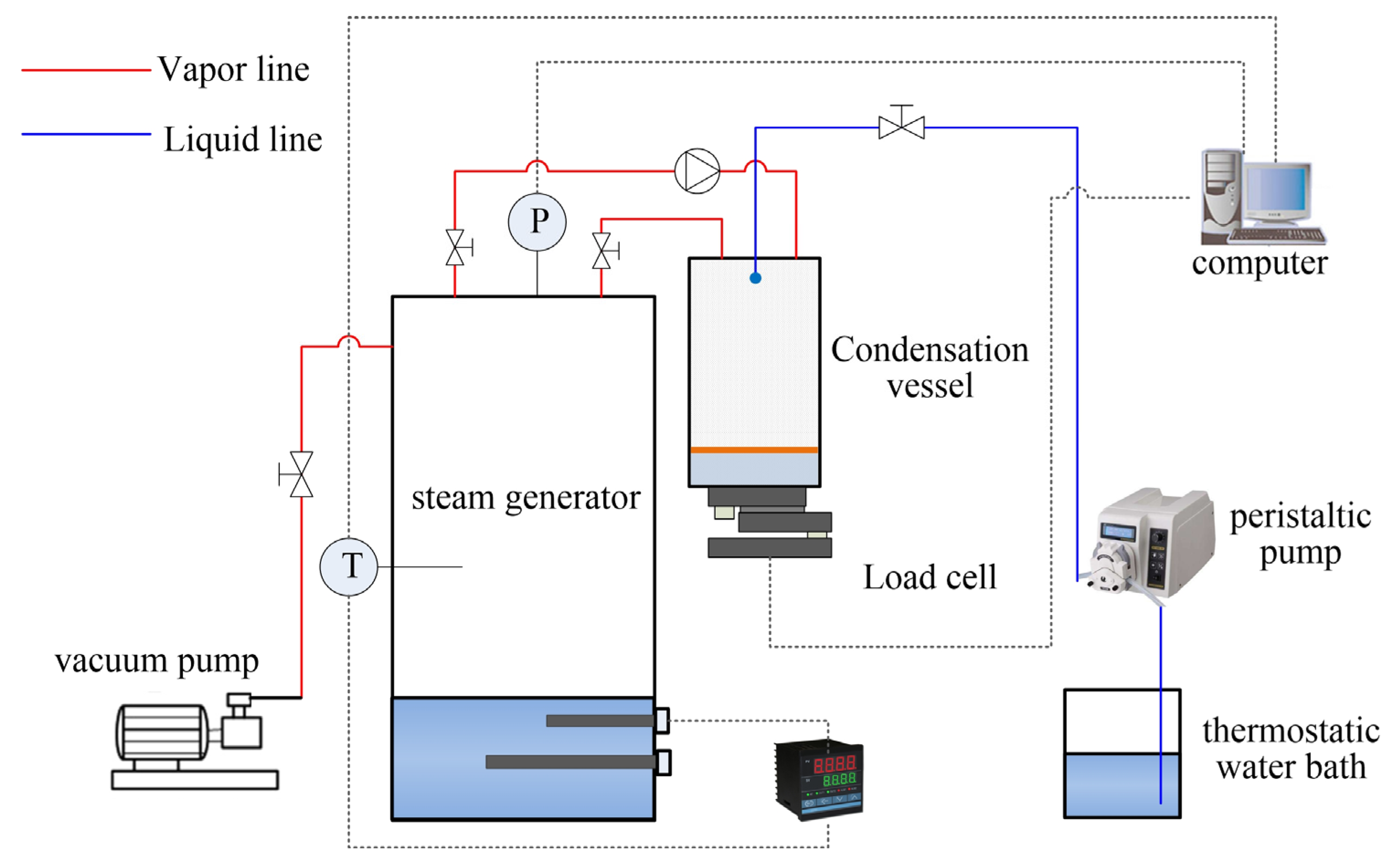
2.1. Experimental Apparatus and Procedure
2.2. Analysis Approach
2.2.1. Heat Transfer Rate
2.2.2. The Transient Heat Transfer Coefficient
2.2.3. The Optimum Condensation Distance
2.3. Uncertainty Analysis
3. Simulation
3.1. Mesh and Boundary Conditions
3.2. Numerical Methods
4. Results and Discussion
4.1. Evolution of the Droplet during Heat Transfer
4.2. Effect of Initial Diameter on the DCC Process
4.3. Optimization
4.4. Heat Transfer Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Q | heat release ratio of vapor, kW |
| mc | mass flow rate of condensate, kg/s |
| min | mass flow rate of inlet water, kg/s |
| mL | mass flow rate of droplets, kg/s |
| γ | latent heat of condensation, kJ/kg |
| h | heat transfer coefficient, kW/m2 °C |
| ΔT | heat transfer difference, °C |
| Ts | saturated vapor temperature, °C |
| Td | droplet temperature, °C |
| Ti | inlet temperature, °C |
| Cp | specific heat, kJ/(kg °C) |
| ρ | water density, kg/m3 |
| d | diameter of the droplet, m |
| d* | characteristic diameter, m |
| Abbreviations | |
| DCC | direct contact condensation |
| DCCV | direct contact condensation vessel |
References
- Pasamehmetoglu, K.O.; Nelson, R.A. Transient direct-contact condensation on liquid droplets. In Proceedings of the National Heat Transfer Conference and Exhibition, Pittsburgh, PA, USA, 9 August 1987; Volume 3, pp. 7–10. [Google Scholar]
- Apriyanti, V.; Adriansyah, W.; Abdurrachim; Pasek, A.D. A review of direct contact condensation of steam on water droplets. AIP Conf. Proc. 2018, 1984, 020035. [Google Scholar]
- Weinberg, S. Heat transfer to low pressure sprays of water in steam atmosphere. Proc. Inst. Mech. 1953, 1, 240–258. [Google Scholar] [CrossRef]
- Bron, G. Heat transmission by condensation of steam on a spray of water drops. Proc. Gen. Discuss. Heat Transf. 1951, 1, 49–52. [Google Scholar]
- Celeta, G.P.; Cumo, M.; Annibale, F.D.; Farello, G.E. Direct contact condensation of steam on droplets. Int. J. Multiph. Flow. 1991, 2, 191–211. [Google Scholar] [CrossRef]
- Lekic, A.; Ford, J.D. Direct contact condensation of vapour on a spray of subcooled liquid droplets. Int. J. Heat Mass Transf. 1980, 23, 1531–1537. [Google Scholar] [CrossRef]
- Gumruk, S.; Aktas, M.K.; Kasap, F. Experimental investigation of spray dehumidification process in moist air. Int. Commun. Heat Mass 2018, 97, 163–171. [Google Scholar] [CrossRef]
- Lee, S.Y.; Tankin, R.S. Study of liquid spray(water) in a non-condensable environment(air). Int. J. Heat Mass Transf. 1983, 27, 351–361. [Google Scholar] [CrossRef]
- Lu, W.; Chen, Y. A study on direct contact condensation of a droplet falling through a saturated vapor atmosphere. J. Chin. Inst. Eng. 1980, 3, 95–103. [Google Scholar] [CrossRef]
- Skelland, A.H.P.; Wellek, R.M. Resistance to mass transfer inside droplets. AIChE J. 1964, 10, 491–496. [Google Scholar] [CrossRef]
- Rose, P.M.; Kintner, R.C. Mass transfer from large oscillating drops. AIChE J. 1966, 12, 531–534. [Google Scholar] [CrossRef]
- Ford, J.D.; Lekic, A. Rate of growth of drops during condensation. Int. J. Heat Mass Transf. 1973, 16, 61–64. [Google Scholar] [CrossRef]
- Pasamehmetoglu, K.O.; Nelson, R.A. Direct-Contact Condensation on Liquid Droplets during Rapid Depressuri-Zation Part; American Society of Mechanical Engineers: New York, NY, USA, 1987. [Google Scholar]
- Ohba, K.; Kitada, H.; Nishiguchi, A. Direct Contact Condensation of Steam on a High Speed Spray Jet of Subcooled Water. Proceeding Int. Cent. Heat Mass Transfer. 1982, 17, 289–300. [Google Scholar]
- Huang, L.J.; Ayyaswamy, P.S. Drag Coefficients Associated With a Moving Drop Experiencing Condensation. J. Heat Transf. T Asme 1987, 109, 1003–1006. [Google Scholar] [CrossRef]
- Ayyaswamy, P.S. Direct-Contact Transfer Processes with Moving Liquid Droplets. Adv. Heat Transf. 1995, 26, 33–35. [Google Scholar]
- Chung, J.N.; Ayyaswamy, P.S. Laminar condensation heat and mass transfer to a moving drop. AIChE J. 1981, 27, 372–377. [Google Scholar] [CrossRef]
- Yang, Z.; Ma, X.; Duan, Y.; Chen, Y. Internal flow and heat transfer of a condensing water droplet in steam flow. Chem. Eng. Sci. 2013, 94, 54–59. [Google Scholar] [CrossRef]
- Bochkareva, E.M.; Nemtsev, V.A.; Sorokin, V.V.; Terekhov, V.V.; Terekhov, V.I. Reduction in the Vapor Pressure in Condensation on Cold Droplets of a Liquid. J. Eng. Phys. Thermophys. 2016, 89, 553–558. [Google Scholar] [CrossRef]
- Orazzo, A.; Tanguy, S. Direct numerical simulations of droplet condensation. Int. J. Heat Mass Transf. 2019, 129, 432–448. [Google Scholar] [CrossRef] [Green Version]
- Ding, H.; Luo, Y.; Yuan, X. Numerical investigation of heat transfer in direct contact condensation of steam to subcooled water spray. Chem. Eng. Process. 2019, 140, 52–63. [Google Scholar] [CrossRef]
- Ying, Z.; Yulong, L. Nonequilibrium molecular dynamics simulations of mass transfer on transient direct-contact condensation. Int. J. Heat Mass Transf. 2022, 184, 184. [Google Scholar] [CrossRef]
- Boziuk, T.R.; Smith, M.K.; Glezer, A. Enhanced Two-Phase Heat Transfer by Direct-Contact Condensation Using Directional Acoustic Actuation. In Proceedings of the 25th International Workshop on Thermal Investigations of ICs and Systems (THERMINIC), Lecco, Italy, 25–27 September 2019. [Google Scholar]
- Viswanath, V.; Peter, J.; Agarwal, D.K. Direct Contact Condensation of Subsonic, Inversely Buoyant Steam Jet in a stagnant Pool of Water, In Proceedings of the 8th International and 47th National Conference on Fluid Mechanics and Fluid Power, Guwahati, India, 9–11 December 2020.
- Bureš, L.; Sato, Y. Direct numerical simulation of phase change in the presence of non-condensable gases. Int. J. Heat Mass Transf. 2020, 151, 119400. [Google Scholar] [CrossRef]
- Kvlic, E.; Rhodes, E. Direct Contact Condensation from Air-steam Mixtures on a Single Droplet. Can. J. Chem. Eng. 1977, 55, 131–137. [Google Scholar]
- Hijikata, K.; Mori, Y.; Kawaguchi, S. Direct contact condensation of vapor to falling cooled droplets. Int. J. Heat Mass Transfer. 1984, 27, 1631–1640. [Google Scholar] [CrossRef]
- Celata, G.P.; Cumo, M.; Farello, G.E.; Focardi, G. A comprehensive analysis of direct contact condensation of saturated steam on subcooled liquid jets. Int. J. Heat Mass Transf. 1989, 32, 639–654. [Google Scholar] [CrossRef]
- Takahashi, M.; Nayak, A.K.; Kitagawa, S.I.; Murakoso, H. Heat Transfer in Direct Contact Condensation of Steam to Subcooled Water Spray. J. Heat Transfer. 2001, 123, 703–711. [Google Scholar] [CrossRef]
- Chavez, A.; Gebhard, P.; Mayinger, F. Measurement of Direct-Contact Condensation of Pure Saturated Vapour on an Injection Spray by Applying Pulsed Laser Holography. Int. J. Heat Mass Transf. 1993, 35, 691–702. [Google Scholar]
- Lu, Q.Z.; Melton, L.A. Measurement of transient temperature field within a falling droplet. AIAA J. 2000, 38, 95–101. [Google Scholar] [CrossRef]
- Luo, Q.; Ma, R.; Dong, B.; Li, W.; Gong, J. Simulation on heat and mass transfer for a subcooled droplet falling freely in saturated steam by the lattice Boltzmann method. Int. J. Heat Mass Transf. 2016, 101, 226–239. [Google Scholar] [CrossRef] [Green Version]
- Lekic, A.; Bajramovic, R.; James, D.F. Droplet size distribution-an improved method for fitting experimental data. Can. J. Chem. Eng. 1976, 54, 399–402. [Google Scholar] [CrossRef]
- Isachenko, V.P.; Kushnyrev, V.I. Condensation Heat Transfer in Dispersed Liquid Spray; Begel House Inc.: Danbury, CT, USA, 1974. [Google Scholar]
- Mugele, R.A.; Evans, H.D. Droplet Size Distribution in Sprays. Ind. Eng. Chem. 1951, 43, 1317–1324. [Google Scholar] [CrossRef]
- Jing, Y.; Guo, F.; Wang, Y.; Huang, Q. Influence of Piping on On-Line Continuous Weighing of Materials inside Process Equipment: Theoretical Analysis and Experimental Verification. Appl. Sci. 2021, 11, 5246. [Google Scholar] [CrossRef]









| Parameter | Parameter Symbol | Value | Error |
|---|---|---|---|
| Vapor temperature, °C | Ts | 40–60 | ±0.2% |
| Pressure, kPa | P | 7.3–19.9 | ±0.2% |
| Droplet temperature, °C | Ti | 10/15/20/25/30 | ±0.05% |
| Inlet water mass flow rate, g/s | min | 1–20 | ±1% |
| Condensate mass flow rate, g/s | mc | - | ±1% |
| Droplet diameter, mm | d | - | ±0.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jing, Y.; Wang, Y.; Huang, Q. Experimental and Simulation Study on the Direct Contact Condensation of Saturated Steam on Moving Droplets at Sub-Atmospheric Pressure. Processes 2023, 11, 1097. https://doi.org/10.3390/pr11041097
Jing Y, Wang Y, Huang Q. Experimental and Simulation Study on the Direct Contact Condensation of Saturated Steam on Moving Droplets at Sub-Atmospheric Pressure. Processes. 2023; 11(4):1097. https://doi.org/10.3390/pr11041097
Chicago/Turabian StyleJing, Yuanlin, Yiping Wang, and Qunwu Huang. 2023. "Experimental and Simulation Study on the Direct Contact Condensation of Saturated Steam on Moving Droplets at Sub-Atmospheric Pressure" Processes 11, no. 4: 1097. https://doi.org/10.3390/pr11041097
APA StyleJing, Y., Wang, Y., & Huang, Q. (2023). Experimental and Simulation Study on the Direct Contact Condensation of Saturated Steam on Moving Droplets at Sub-Atmospheric Pressure. Processes, 11(4), 1097. https://doi.org/10.3390/pr11041097





