Research on the Effect of Crucial Parameters on Ice Borehole Deformations Using a Proposed Computation Model
Abstract
1. Introduction
2. Modelling
2.1. Basis and Assumption
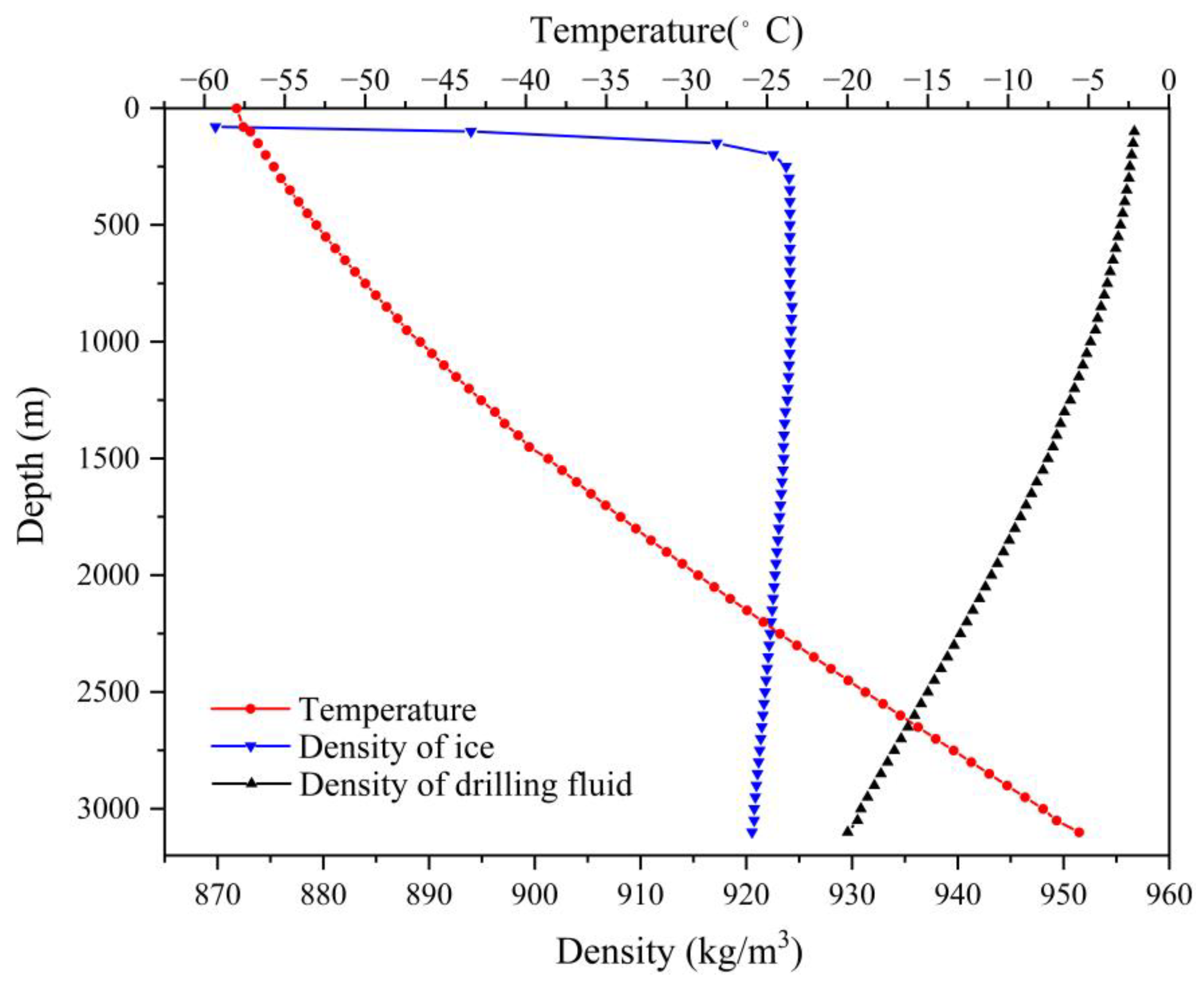
2.2. Ice Temperature and Density Variation
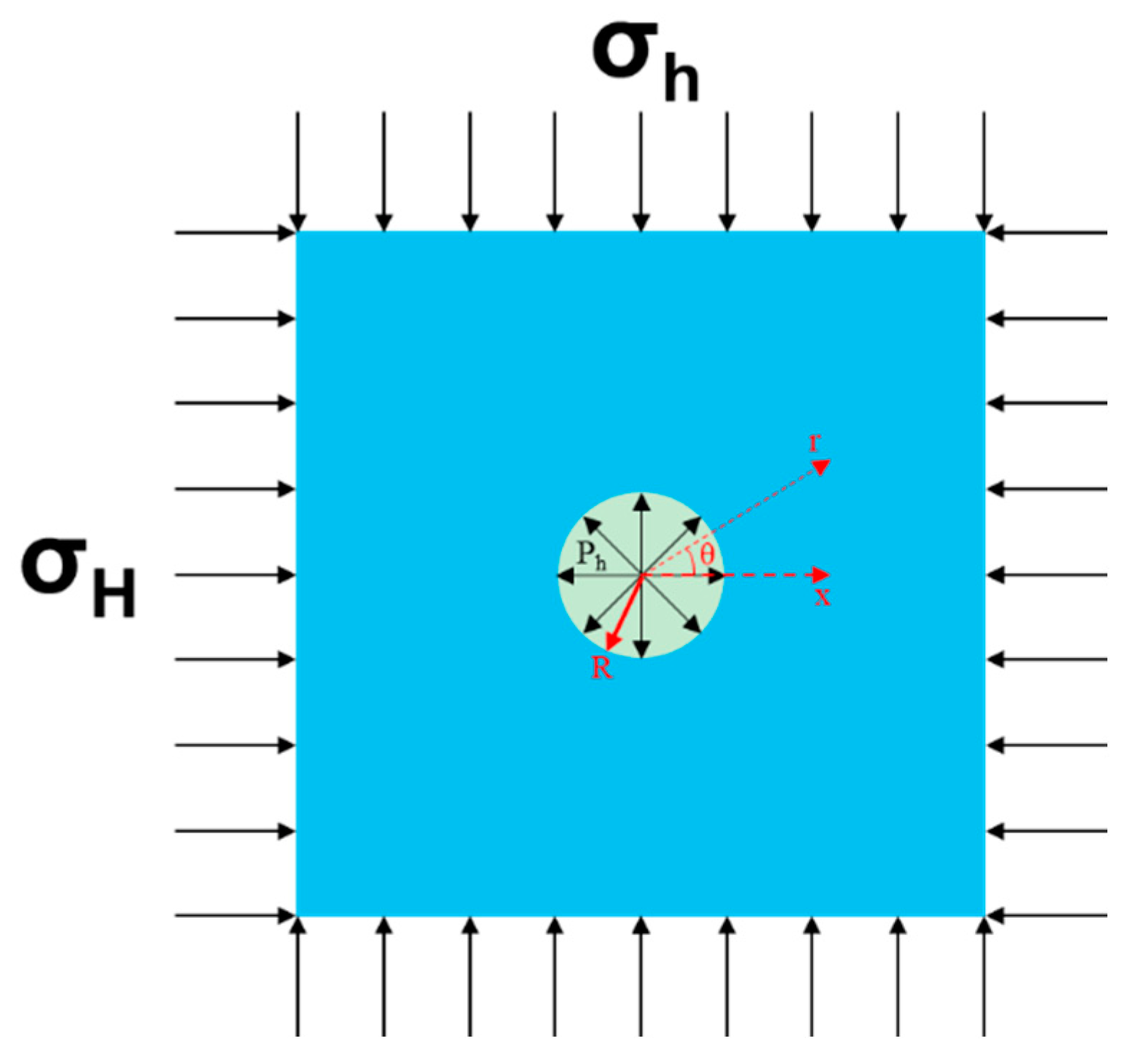
2.3. In Situ Ice Pressure
2.4. Hydrostatic Pressure and Density Variation
2.5. Stress Distribution
2.6. Unbalanced Differential Pressure
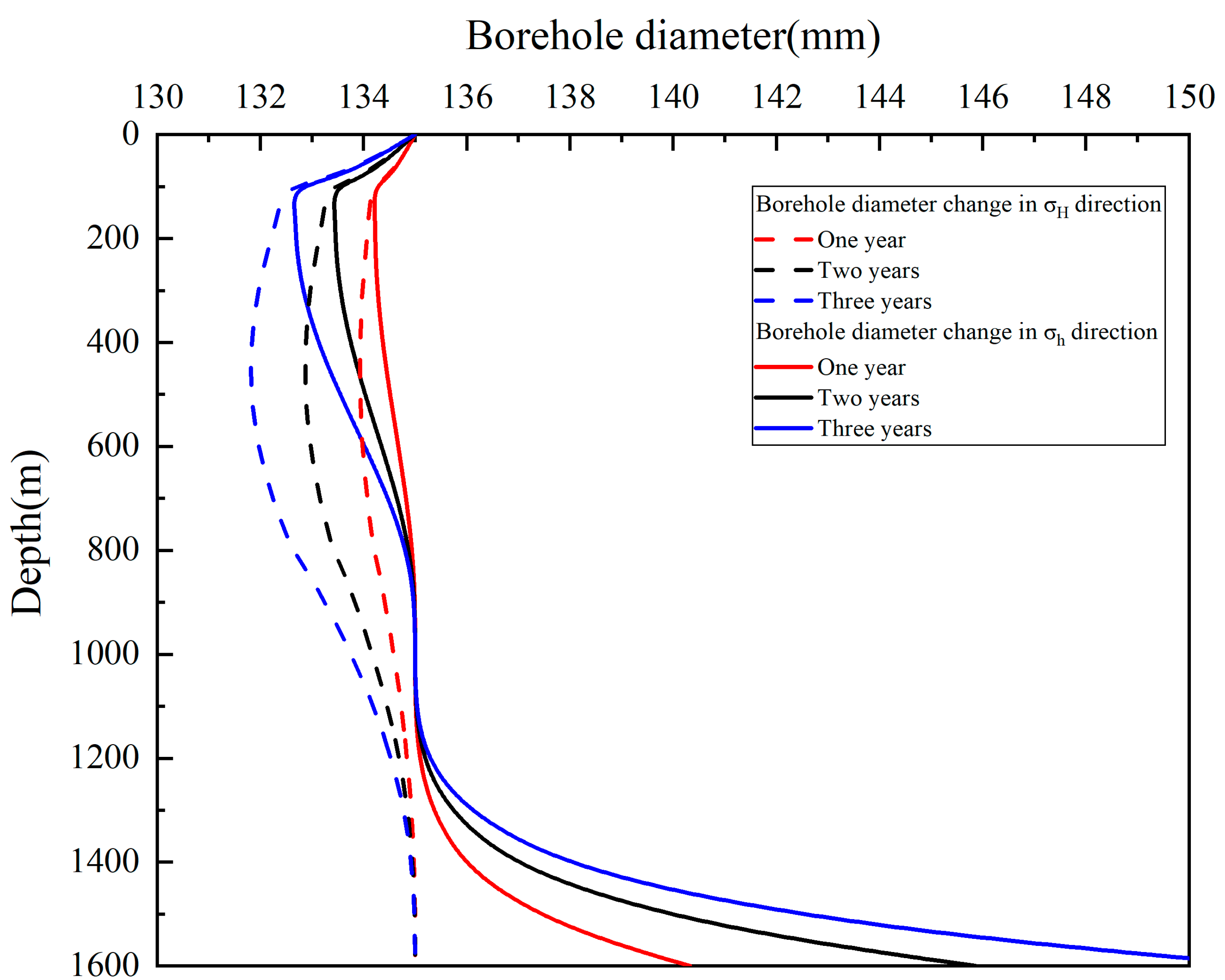
3. Borehole Deformation in Dome A
3.1. Parameter Values
3.2. Deformation at the Dome A Ice Borehole
3.2.1. Temperature and Density Distribution at Dome A
3.2.2. Change in Borehole Diameter at the Dome A Ice Borehole
4. Analysis of Factors Influencing Ice Borehole Deformation
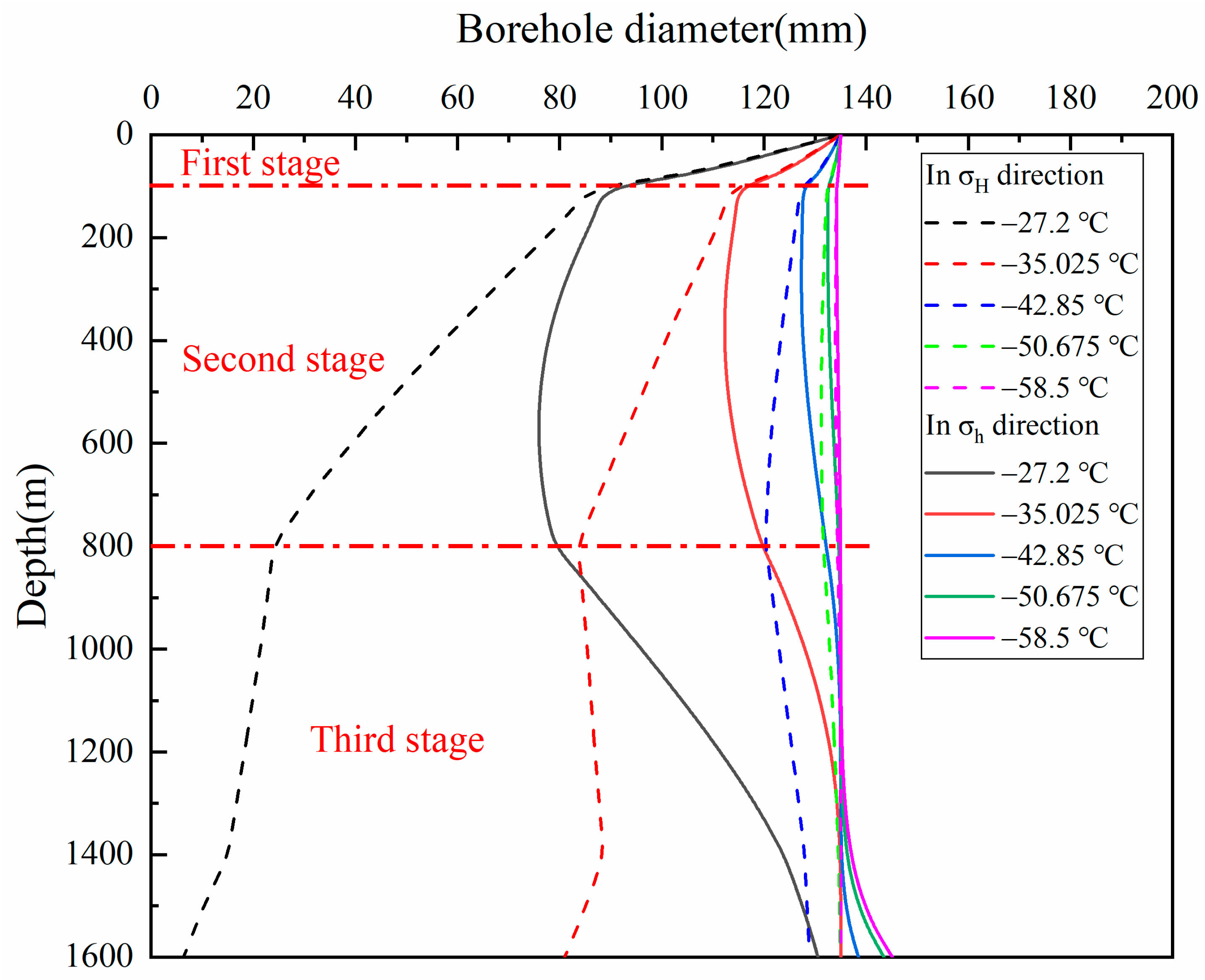
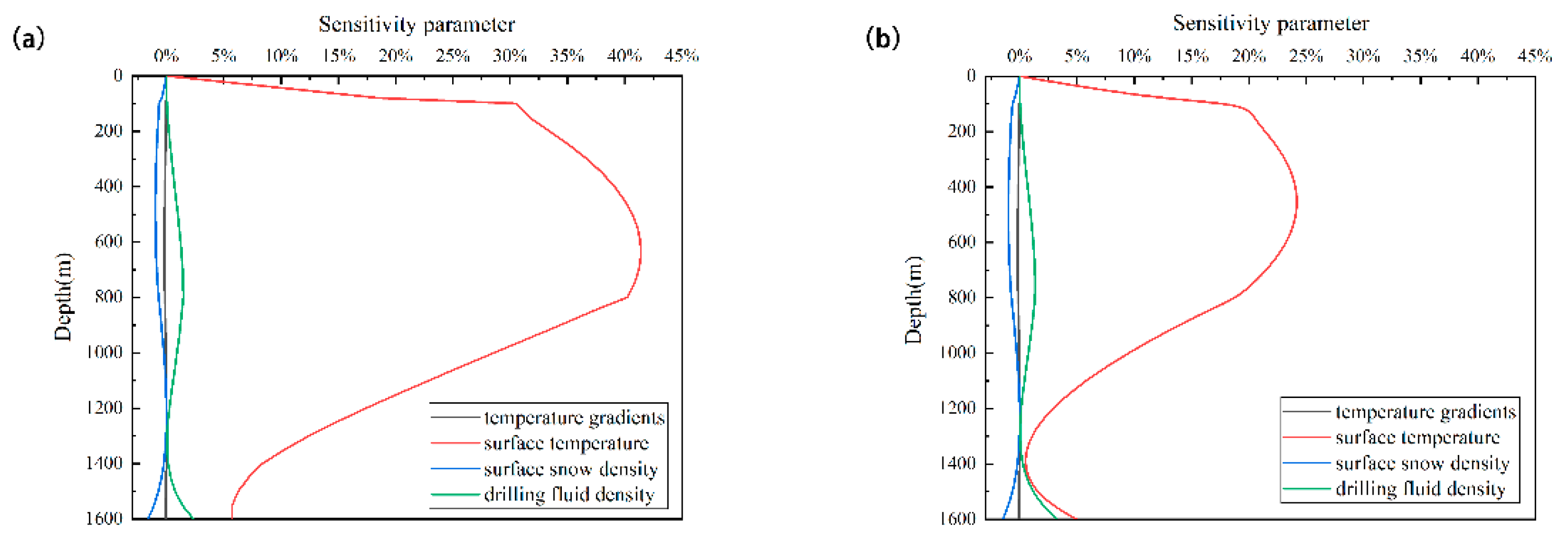
4.1. Effect of Surface Temperature
4.2. Effect of Temperature Gradients
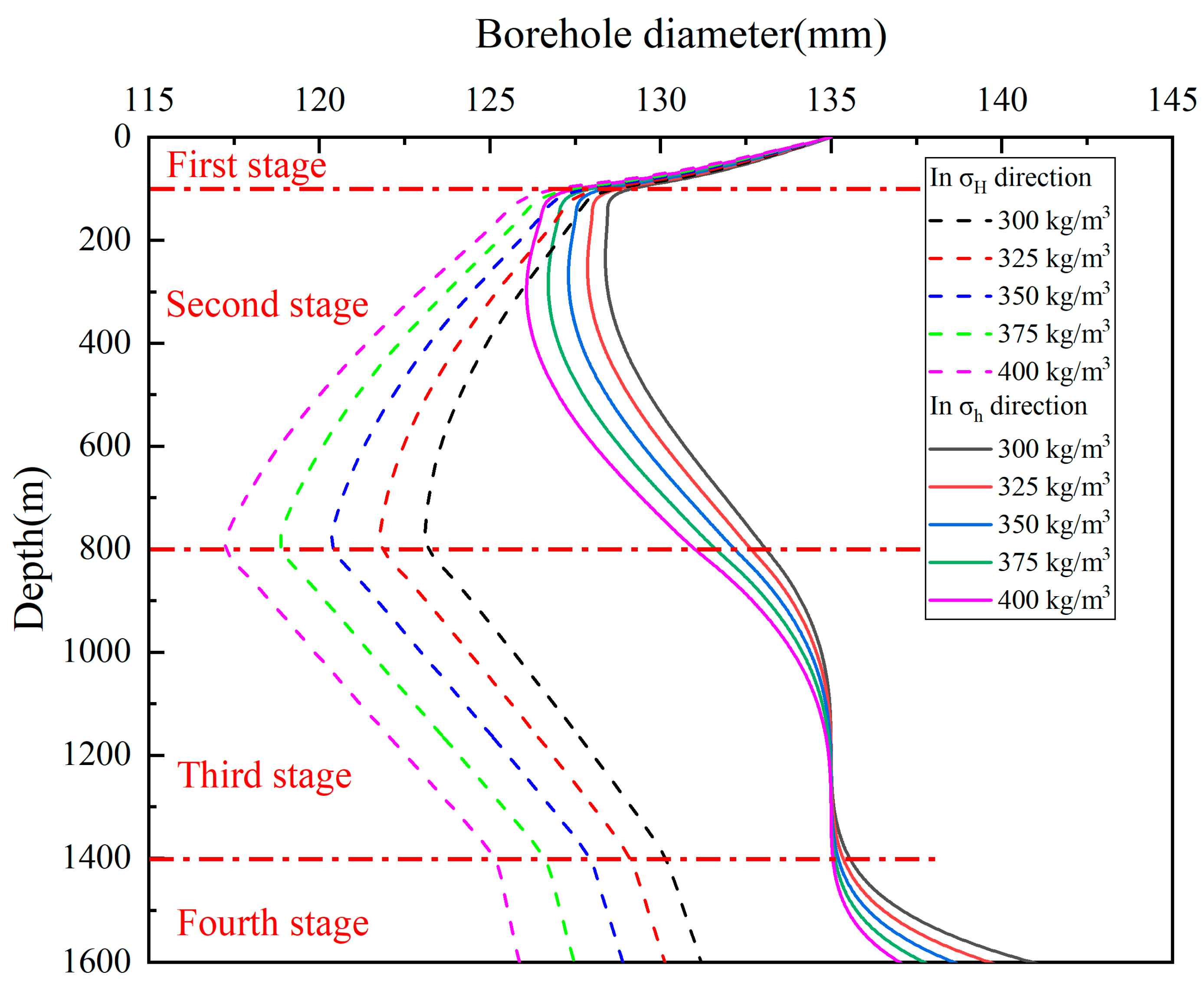
4.3. Effect of Surface Snow Density
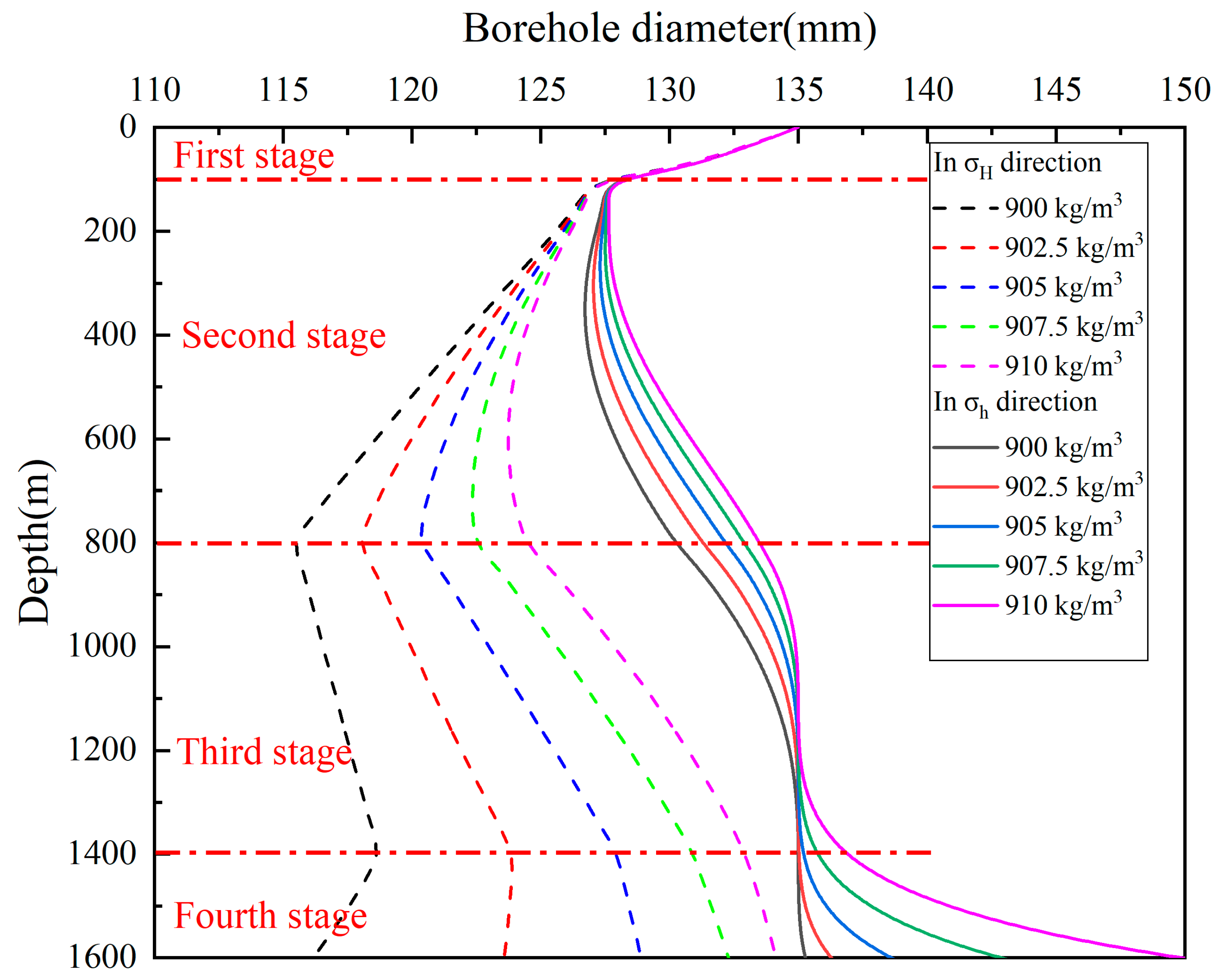
4.4. Effect of Drilling Fluid Density
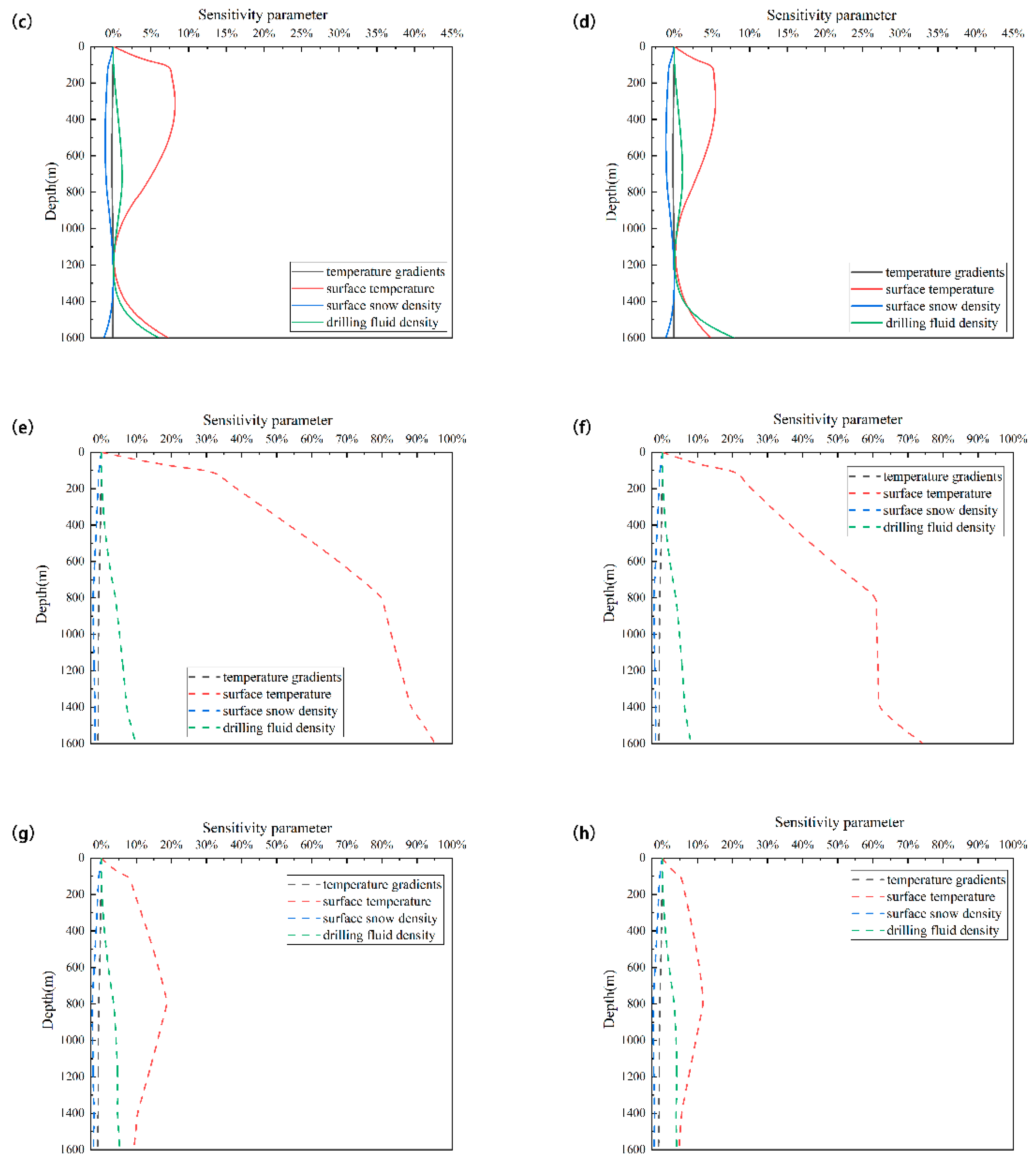
4.5. Multivariate Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gautier, D.L.; Bird, K.J.; Charpentier, R.R.; Grantz, A.; Houseknecht, D.W.; Klett, T.R.; Moore, T.E.; Pitman, J.K.; Schenk, C.J.; Schuenemeyer, J.H.; et al. Assessment of Undiscovered Oil and Gas in the Arctic. Science 2009, 324, 1175–1179. [Google Scholar] [CrossRef]
- Lodolo, E.; Camerlenghi, A.; Madrussani, G.; Tinivella, U.; Rossi, G. Assessment of gas hydrate and free gas distribution on the South Shetland margin (Antarctica) based on multichannel seismic reflection data. Geophys. J. Int. 2002, 148, 103–119. [Google Scholar] [CrossRef]
- Schulson, E.; Duval, P. Creep and Fracture of Ice; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Duval, P.; Ashby, M.F.; Anderman, I. Rate-controlling processes in the creep of polycrystalline ice. J. Phys. Chem. 1983, 87, 4066–4074. [Google Scholar] [CrossRef]
- Glen, J. The Creep of Polycrystalline Ice. Proc. R. Soc. A Math. Phys. Eng. Sci. 1955, 228, 519–538. [Google Scholar] [CrossRef]
- Hooke, R.L.; Mellor, M.; Budd, W.F.; Glen, J.W.; Higashi, A.; Jacka, T.H.; Jones, S.J.; Lile, R.C.; Martin, R.T.; Meier, M.F.; et al. Mechanical properties of polycrystalline ice: An assessment of current knowledge and priorities for research: Report prepared for the International Commission on Snow and Ice, with support from the U.S. National Science Foundation. Cold Reg. Sci. Technol. 1980, 3, 263–275. [Google Scholar] [CrossRef]
- Mellor, M.; Cole, D.M. Deformation and failure of ice under constant stress or constant strain-rate. Cold Reg. Sci. Technol. 1982, 5, 201–219. [Google Scholar] [CrossRef]
- Fujii, Y.; Azuma, N.; Tanaka, Y.; Nakayama, Y.; Kameda, T.; Shinbori, K.; Katagiri, K.; Fujita, S.; Takahashi, A.; Kawada, K.; et al. Deep ice core drilling to 2503 m depth at Dome Fuji, Antarctica. Mem. Natl. Inst. Polar Res 2002, 56, 103–116. [Google Scholar]
- Ueda, H.; Talalay, P. Fifty Years of Soviet and Russian Drilling Activity in Polar and Non-Polar Ice: A Chronological History; Cold Regions Research and Engineering Laboratory: Hanover, NH, USA, 2007; p. 145. [Google Scholar]
- Talalay, P.; Fan, X.; Xu, H.; Yu, D.; Han, L.; Han, J.; Sun, Y. Drilling fluid technology in ice sheets: Hydrostatic pressure and borehole closure considerations. Cold Reg. Sci. Technol. 2014, 98, 47–54. [Google Scholar] [CrossRef]
- Fisher, D.A.; Koerner, R.M. On the Special Rheological Properties of Ancient Microparticle-Laden Northern Hemisphere Ice as Derived from Bore-Hole and Core Measurements. J. Glaciol. 1986, 32, 501–510. [Google Scholar] [CrossRef]
- Paterson, W.S.B. Secondary and tertiary creep of glacier ice as measured by borehole closure rates. Rev. Geophys. 1977, 15, 47. [Google Scholar] [CrossRef]
- Talalay, P.; Hooke, R. Closure of deep boreholes in ice sheets: A discussion. Ann. Glaciol. 2007, 47, 125–133. [Google Scholar] [CrossRef]
- Hooke, R.L. Principles of Glacier Mechanics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Ghassemi, A.; Diek, A. Linear chemo-poroelasticity for swelling shales: Theory and application. J. Pet. Sci. Eng. 2003, 38, 199–212. [Google Scholar] [CrossRef]
- Bradley, W.B. Failure of Inclined Boreholes. J. Energy Resour. Technol. 1979, 101, 232–239. [Google Scholar] [CrossRef]
- Karimi-Khajelangi, B.; Noorian-Bidgoli, M. Numerical study of the effect of rock anisotropy on stresses around an opening located in the fractured rock mass. J. Pet. Sci. Eng. 2022, 208, 109593. [Google Scholar] [CrossRef]
- Budd, W.; Jacka, T.; Jenssen, D.; Radok, U.; Young, N. Derived Physical Characteristics of the Greenland Ice Sheet; University of Melbourne: Melbourne, Australia, 1982. [Google Scholar]
- Schytt, V. Snow Studies at Maudheim; Scientific Results; Norwegian British Swedish Antarctic Expedition,1949–1952; scientific results; Norsk Polarinstitutt: Oslo, Norway, 1958. [Google Scholar]
- Cuffey, K.M.; Paterson, W.S.B. Physics of Glaciers; Academic Press: Cambridge, MA, USA, 2010. [Google Scholar]
- Talalay, P.; Gundestrup, N. Hydrostatic pressure and fluid density profile in deep ice bore-holes. Mem. Natl. Inst. Polar Res. 2002, 56, 171–180. [Google Scholar]
- Hongkui, G.; Yingsong, L. Distribution of In-Situ Stresses in Oilfield. Fault-Block Oil Gas Field 1998, 5, 1–5. [Google Scholar]
- Joussineau, G.d.; Petit, J.-P.; Gauthier, B.D.M. Photoelastic and numerical investigation of stress distributions around fault models under biaxial compressive loading conditions. Tectonophysics 2003, 363, 19–43. [Google Scholar] [CrossRef]
- Zhang, N.; An, C.; Fan, X.; Shi, G.; Li, C.; Liu, J.; Hu, Z.; Talalay, P.; Sun, Y.; Li, Y. Chinese First Deep Ice-Core Drilling Project DK-1 at Dome A, Antarctica (2011–2013): Progress and performance. Ann. Glaciol. 2014, 55, 88–98. [Google Scholar] [CrossRef]
- Wang, B.; Tian, G.; Cui, X.; Zhang, X. The internal COF features in Dome A of Antarctica revealed by multi-polarization-plane RES. Appl. Geophys. 2008, 5, 230–237. [Google Scholar] [CrossRef]
- Guo, Y.; Li, G.; Jia, C.; Chang, T.; Cui, H.; MARKOV, A. Study of ultrasonic test in the measurements of mechanical properties of ice. Chin. J. Polar Res. 2016, 28, 152–157. [Google Scholar]
- Hou, S.; Li, Y.; Xiao, C.; Ren, J. Recent accumulation rate at Dome A, Antarctica. Chin. Sci. Bull. 2007, 52, 428–431. [Google Scholar] [CrossRef]
- Wang, Y.; Sodemann, H.; Hou, S.; Masson-Delmotte, V.; Jouzel, J.; Pang, H. Snow accumulation and its moisture origin over Dome Argus, Antarctica. Clim. Dyn. 2013, 40, 731–742. [Google Scholar] [CrossRef]
- Hooke, R.L.; Hudleston, P.J. Ice Fabrics in a Vertical Flow Plane, Barnes Ice Cap, Canada. J. Glaciol. 1980, 25, 195–214. [Google Scholar] [CrossRef]
- Baker, R.W. Textural and crystal-fabric anisotropies and the flow of ice masses. Science 1981, 211, 1043–1044. [Google Scholar] [CrossRef] [PubMed]
- Baker, R.W. A flow equation for anisotropic ice. Cold Reg. Sci. Technol. 1982, 6, 141–148. [Google Scholar] [CrossRef]
- Russell-Head, D.S.; Budd, W.F. Ice-Sheet Flow Properties Derived from Bore-Hole Shear Measurements Combined with Ice-Core Studies. J. Glaciol. 1979, 24, 117–130. [Google Scholar] [CrossRef]
- Hooke, R.; Dahlin, B.; Kauper, M. Creep of Ice Containing Dispersed Fine Sand. J. Glaciol. 1972, 11, 327–336. [Google Scholar] [CrossRef]
- Durham, W.B.; Kirby, S.H.; Stern, L.A. Effects of dispersed particulates on the rheology of water ice at planetary conditions. J. Geophys. Res. 1992, 97, 20883. [Google Scholar] [CrossRef]
- De La Chapelle, S.; Milsch, H.; Castelnau, O.; Duval, P. Compressive creep of ice containing a liquid intergranular phase: Rate-controlling processes in the dislocation creep regime. Geophys. Res. Lett. 1999, 26, 251–254. [Google Scholar] [CrossRef]
- Mangold, N.; Allemand, P.; Duval, P.; Geraud, Y.; Thomas, P. Experimental and theoretical deformation of ice–rock mixtures: Implications on rheology and ice content of Martian permafrost. Planet. Space Sci. 2002, 50, 385–401. [Google Scholar] [CrossRef]
- Eisen, O.; Hamann, I.; Kipfstuhl, S.; Steinhage, D.; Wilhelms, F. Direct evidence for continuous radar reflector originating from changes in crystal-orientation fabric. Cryosphere 2007, 1, 1–10. [Google Scholar] [CrossRef]
- Matsuoka, K.; Furukawa, T.; Fujita, S.; Maeno, H.; Uratsuka, S.; Naruse, R.; Watanabe, O. Crystal orientation fabrics within the Antarctic ice sheet revealed by a multipolarization plane and dual-frequency radar survey. J. Geophys. Res. Solid Earth 2003, 108, 1–10. [Google Scholar] [CrossRef]
- Tang, X.; Sun, B.; Zhang, Z.; Zhang, X.; Cui, X.; Li, X. Structure of the internal isochronous layers at Dome A, East Antarctica. Sci. China Earth Sci. 2011, 54, 445–450. [Google Scholar] [CrossRef]
- Sun, B.; Moore, J.C.; Zwinger, T.; Zhao, L.; Steinhage, D.; Tang, X.; Zhang, D.; Cui, X.; Martín, C. How old is the ice beneath Dome A, Antarctica? Cryosphere 2014, 8, 1121–1128. [Google Scholar] [CrossRef]
- Zhao, L.; Moore, J.C.; Sun, B.; Tang, X.; Guo, X. Where is the 1-million-year-old ice at Dome A? Cryosphere 2018, 12, 1651–1663. [Google Scholar] [CrossRef]
- Morris, E.M.; Vaughan, D.G. Snow surface temperatures in West Antarctica. Antarct. Sci. 1994, 6, 529–535. [Google Scholar] [CrossRef]
- Wang, Y.; Hou, S. Spatial distribution of 10 m firn temperature in the Antarctic ice sheet. Sci. China Earth Sci. 2011, 54, 655–666. [Google Scholar] [CrossRef]
- Ding, M.; Xiao, C.; Jin, B.; Ren, J.; Qin, D.; Sun, W. Distribution of δ 18O in surface snow along a transect from Zhongshan Station to Dome A, East Antarctica. Chin. Sci. Bull. 2010, 55, 2709–2714. [Google Scholar] [CrossRef]
- Ma, Y.; Bian, L.; Xiao, C.; Allison, I.; Zhou, X. Near surface climate of the traverse route from Zhongshan Station to Dome A, East Antarctica. Antarct. Sci. 2010, 22, 443–459. [Google Scholar] [CrossRef]




| Parameters | Description | Value | Unit | Reference |
|---|---|---|---|---|
| Density of pure ice | 916.8 | [10] | ||
| Firn correction parameter | 34 | m | [20] | |
| Poisson’s ratio of ice | 0.331 | [26] | ||
| n | Creep exponent | 3 | [10] | |
| B | Coefficient of viscosity | 0.14 | MPa a1/n | [14] |
| Longitudinal strain rate | 0.1 | a−1 | [14] | |
| Accumulation rate | 0.023 | ma−1 | [27] | |
| Thermal diffusivity | 37.2 | m2a−1 | [14] | |
| Q | Activation energy for creep | 60 | kJmol−1 | [13] |
| R | Universal gas constant | 8.314 | Jmol−1k−1 | |
| Temperature gradients | 0.0226 | Km−1 | [18] | |
| Annual temperature at 10 m depth of the ice layer | −58.5 | °C | [27] | |
| Density of surface snow | 350 | [28] | ||
| Density of drilling fluid at 0 °C | 901.2 | kg/m3 | [10] |
| Depth (m) | Value of E |
|---|---|
| 0–800 | 1–4 |
| 800–1400 | 4–2.4 |
| 1400–2000 | 2.4 |
| Parameters | Description | Value | Unit | Reference |
|---|---|---|---|---|
| Temperature gradients | 0.0226–0.0264 | Km−1 | [18] | |
| Temperature at 10 m of the ice layer | −27.2– −58.5 | °C | [27,44] | |
| Density of surface snow | 300–400 | [45] | ||
| Density of drilling fluid at 0 °C | 900–910 | kg/m3 | (Personal communication) |
| −1 | −0.5 | 0 | 0.5 | 1 | |
|---|---|---|---|---|---|
| Temperature gradient | 0.0226 | 0.02355 | 0.0245 | 0.02545 | 0.0264 |
| Surface temperature | −27.2 | −35.025 | −42.85 | −50.675 | −58.5 |
| Surface snow density | 300 | 325 | 350 | 375 | 400 |
| Drilling fluid density | 900 | 902.5 | 905 | 907.5 | 910 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Zhong, X.; Nie, S.; Zhu, Y.; Chen, C. Research on the Effect of Crucial Parameters on Ice Borehole Deformations Using a Proposed Computation Model. Processes 2023, 11, 1150. https://doi.org/10.3390/pr11041150
Wang Y, Zhong X, Nie S, Zhu Y, Chen C. Research on the Effect of Crucial Parameters on Ice Borehole Deformations Using a Proposed Computation Model. Processes. 2023; 11(4):1150. https://doi.org/10.3390/pr11041150
Chicago/Turabian StyleWang, Yafei, Xiuping Zhong, Shuaishuai Nie, Ying Zhu, and Chen Chen. 2023. "Research on the Effect of Crucial Parameters on Ice Borehole Deformations Using a Proposed Computation Model" Processes 11, no. 4: 1150. https://doi.org/10.3390/pr11041150
APA StyleWang, Y., Zhong, X., Nie, S., Zhu, Y., & Chen, C. (2023). Research on the Effect of Crucial Parameters on Ice Borehole Deformations Using a Proposed Computation Model. Processes, 11(4), 1150. https://doi.org/10.3390/pr11041150







