Cogeneration of Fresh Water and Electricity with High-Temperature Power Cycles: Comparative Assessment of Multi-Effect Distillation and Reverse Osmosis
Abstract
:1. Introduction
2. System Description
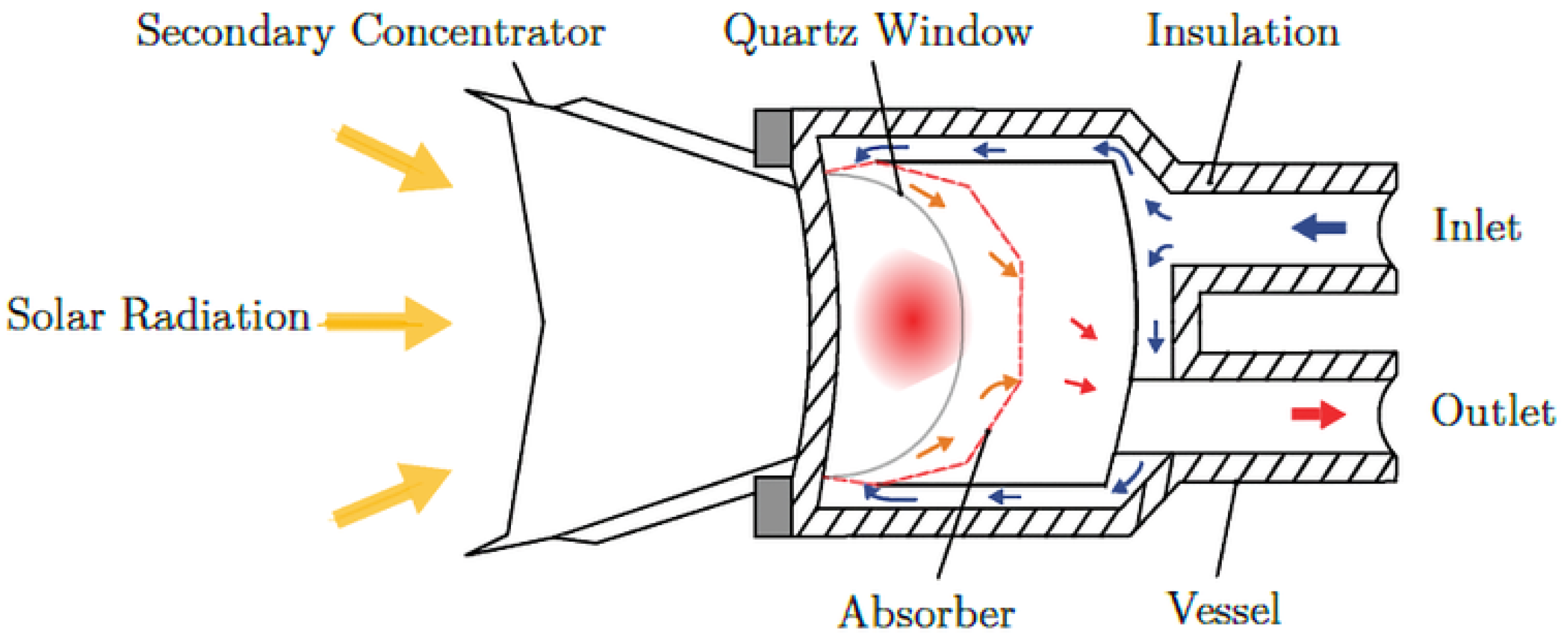
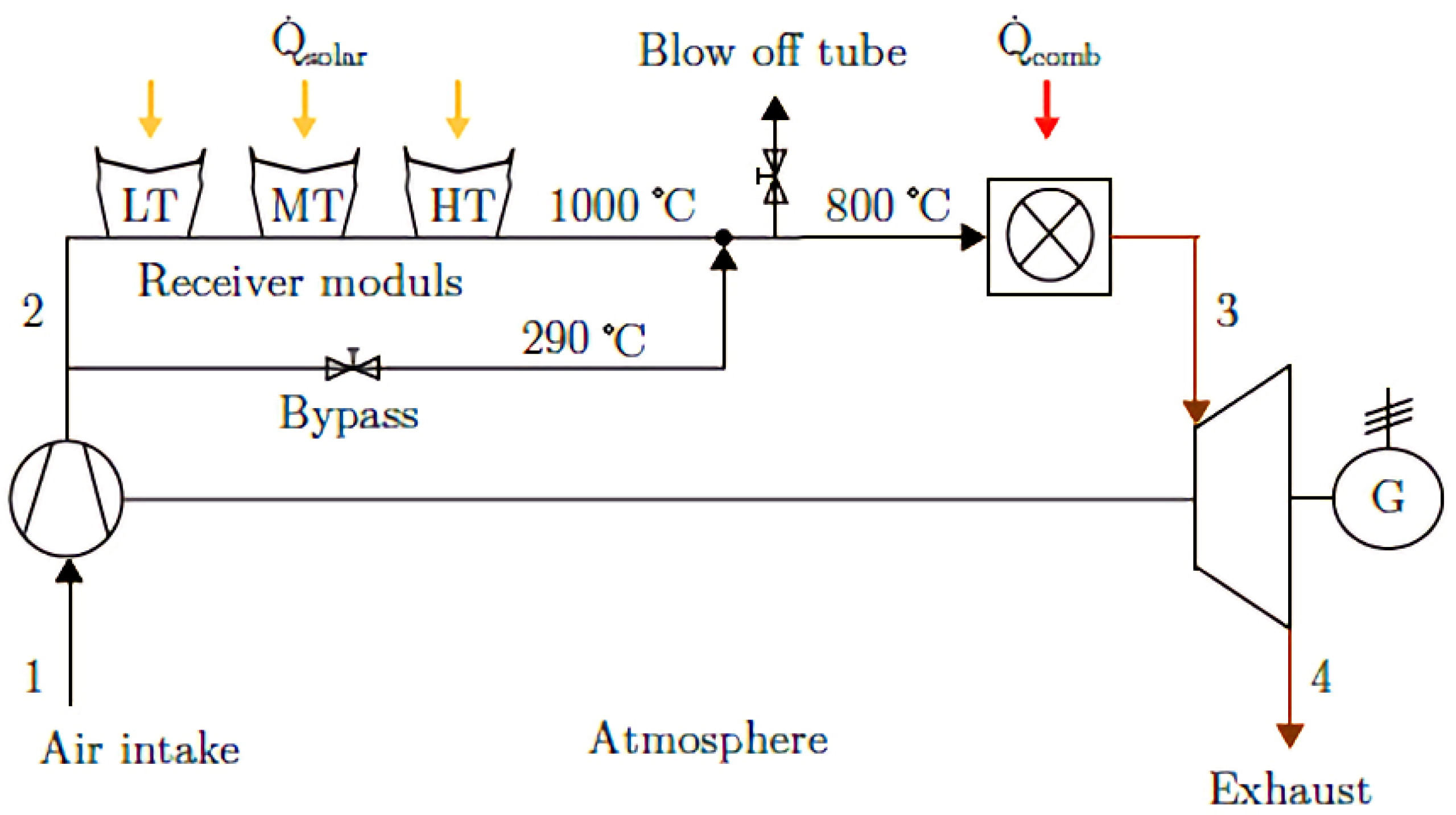
2.1. Central Receiver Solar
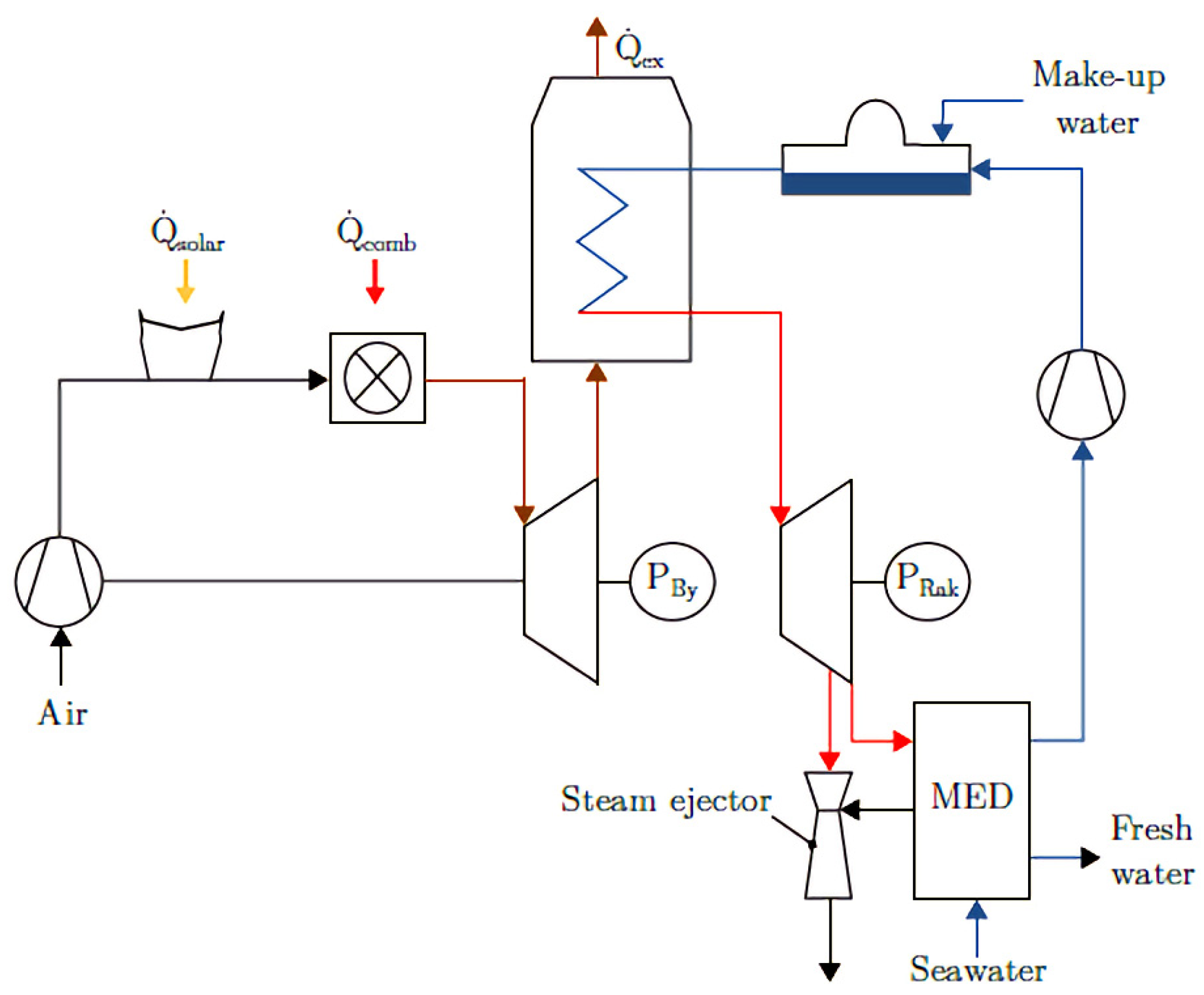
2.2. LT-MED Coupled with a Central Receiver Solar Plant
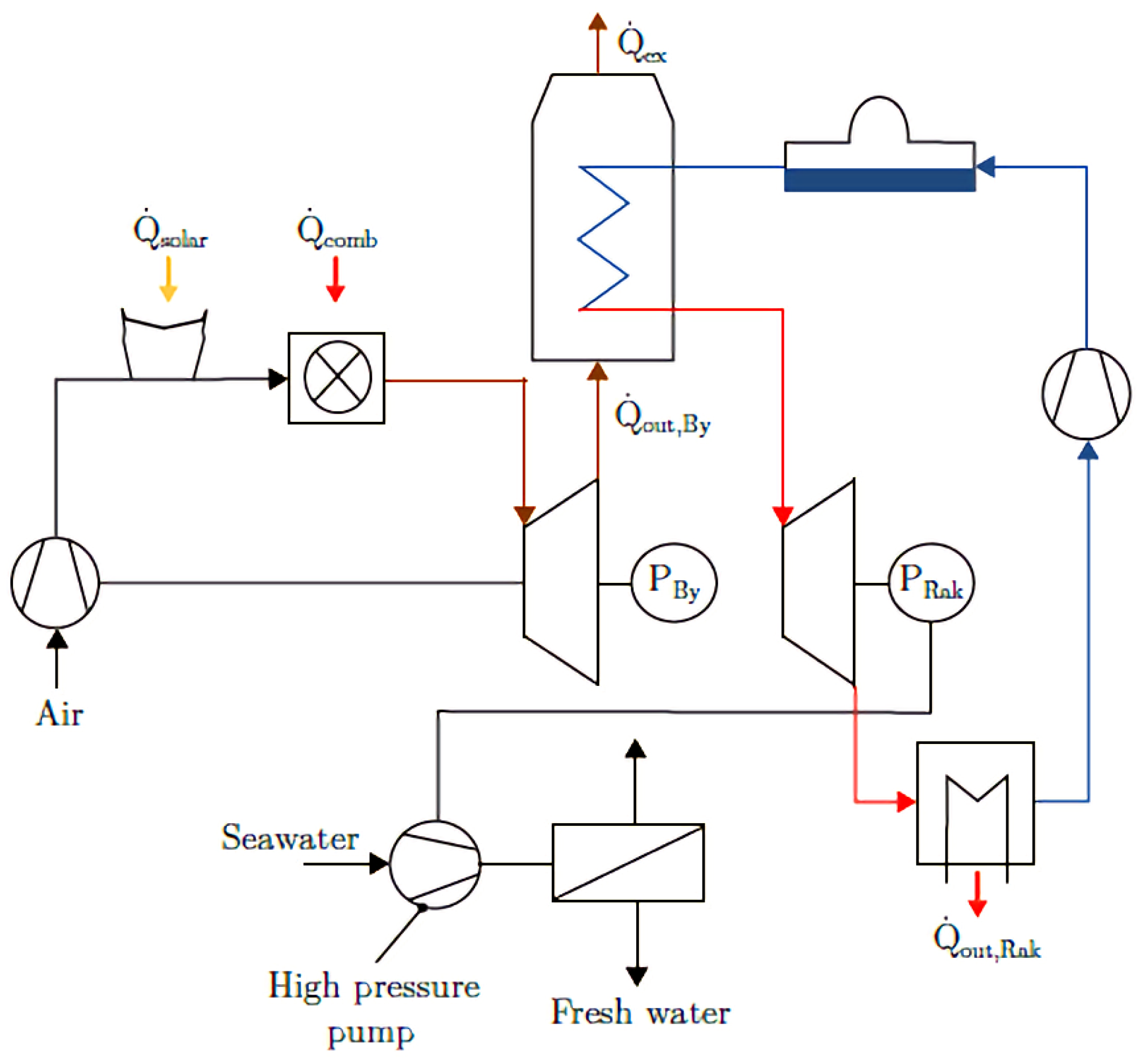
2.3. Reverse Osmosis Coupled with a Central Receiver Solar Plant
3. Modeling
3.1. Central Receiver Solar Plant
3.1.1. Solar Field
3.1.2. Receiver
3.1.3. Power Block
3.2. Reverse Osmosis
3.3. Multi-Effect Distillation
Design of the Vacuum System
3.4. Simulation
3.4.1. RO Model
3.4.2. MED Model
3.4.3. CRS + Desalination Model
4. Results and Discussion
4.1. Solar Field
4.2. CRS Plant with RO
4.3. CRS Plant with LT-MED
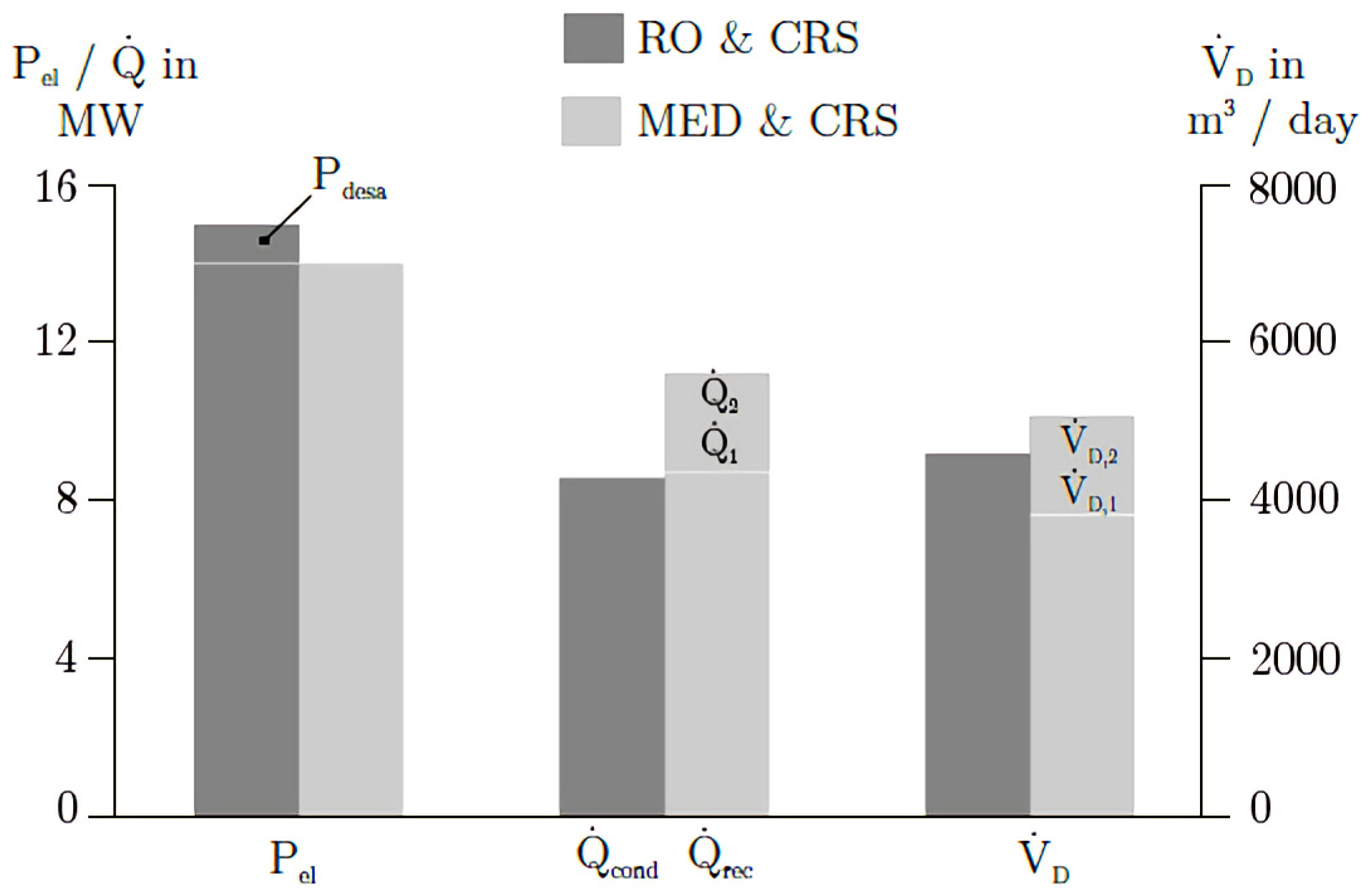
4.4. Comparative Assessment of the CRS Plant with RO & LT-MED
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Greek Symbols | |
| Heat loss convective coefficient, W/m2K | |
| Nominal pressure drop in the receiver, bar | |
| Pressure drop over the turbine of the ERS, bar | |
| Evaporator high-temperature difference, °C | |
| Evaporator low-temperature difference, °C | |
| Factor for atmospheric extinction | |
| Efficiency reduction due to blocking | |
| Cleanliness factor | |
| Compressor efficiency | |
| Cosine efficiency | |
| Efficiency of the generator | |
| Solar field efficiency | |
| Efficiency reduction due to parasitic losses | |
| Efficiency of the pump | |
| Efficiency reduction due to shadowing | |
| Efficiency of the turbine | |
| Thermal efficiency of the combined cycle | |
| Optical solar field efficiency | |
| Receiver efficiency | |
| Efficiency reduction due to spillage | |
| Average solar field reflectivity | |
| Receiver emissivity | |
| Latent heat of evaporation inside the 1st effect of the MED unit, kJ/kg | |
| Latent heat of condensation in the 1st effect of the MED unit, kJ/kg | |
| Latent heat of condensation in effect i of the MED unit, kJ/kg | |
| Osmotic pressure, bar | |
| Osmotic pressure of the concentrate, bar | |
| Osmostic pressure of the feed, bar | |
| Pressure ratio, Brayton | |
| Recovery Ratio for the RR | |
| Density of the feed water, kg/m3 | |
| Roman Symbols | |
| Aperture area, m2 | |
| Heat transfer area of the effect i in the MED unit, m2 | |
| Total area of the heliostat solar field, m2 | |
| Membrane area, m2 | |
| Specific heat, kJ/kg °C | |
| Concentration of the component “i” in the solution, mol/m3 | |
| Fouling factor | |
| Gain Output Ratio | |
| Direct normal irradiation, W/m2 | |
| Permeability coefficient, m3/hm2bar | |
| Distillate mass flow rate leaving each effect of the MED unit, kg/s | |
| Feedwater mass flow rate sprayed in the 1st effect of the MED unit, kg/s | |
| Total vapor mass flow rate generated in the 1st effect, kg/s | |
| Mass flow rate of the total distillate produced in the MED unit, kg/s | |
| Steam mass flow rate supplied in the 1st effect of the MED unit, kg/s | |
| Vapor mass flow rate generated in effect i of the MED unit, kg/s | |
| Pressure, bar | |
| Net power produced by the Brayton cycle, W | |
| Boiler low pressure, bar | |
| Boiler high pressure, bar | |
| Net power produced by the Rankine cycle, W | |
| Receiver losses due to conduction, W | |
| Receiver losses due to convection, W | |
| Thermal energy supplied in the 1st effect of MED plant, W | |
| Design intercept power, kW | |
| Thermal energy input of the Brayton cycle, W | |
| Thermal energy input of the Rankine cycle, W | |
| Receiver losses due to radiation, W | |
| Receiver losses due to reflection, W | |
| Intercepted thermal flow at the receiver, W | |
| Output heat flow from the receiver to the power block, W | |
| Universal gas constant, J/molK | |
| Recovery Ratio | |
| Temperature, °C | |
| Temperature of brine in the 1st effect of the MED after evaporation, °C | |
| Temperature of the feedwater sprayed in the 1st effect of the MED, °C | |
| Gas turbine inlet temperature, °C | |
| Surface temperature, °C | |
| Vapor temperature in the effect i of the MED unit, °C | |
| Volume of air, m3 | |
| Total permeate/distillate flow rate, m3/day | |
| Concentrate flow rate, m3/s | |
| Volume flow rate of feed water, m3/s | |
| Feedwater flow rate in the RO, m3/s | |
| Power consumed by the desalination processes, W | |
| Power consumed by the pretreatment, W | |
| Power consumed by the RO process, W | |
| Specific Energy Consumption of the RO process, Wh/m3 | |
| Specific Thermal Energy Consumption of the MED process, Wh/m3 | |
| Heat transfer coefficient, kW/m2 °C | |
| CSP | Concentrating Solar Power |
| CSP+D | Concentrating Solar Power and Desalination |
| CR | Central Receiver |
| CRS | Central Solar Receiver |
| ISCC | Integrated solar gas turbine-steam turbine combined cycle |
| LT-MED | Low-temperature multi-effect distillation |
| MED | Multi-effect distillation |
| MENA | Middle East and North Africa |
| MSF | Multistage flash |
| PSA | Plataforma Solar de Almería |
| PT | Parabolic Trough |
| RO | Reverse Osmosis |
| ROSA | Reverse Osmosis System Analysis |
| SDI | Silt Density Index |
| TDS | Total Dissolved Solids |
References
- Micale, G.; Cipollina, A.; Rizzuti, L. Seawater Desalination: Conventional and Renewable Energy Processes. In Seawater Desalination: Conventional and Renewable Energy Processes; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-642-01149-8. [Google Scholar] [CrossRef]
- Lozán, J.L. Global Change: Enough Water for All? Wissenschaftliche Auswertungen: Frankfurt am Main, Germany, 2007; ISBN 3980966828. [Google Scholar]
- Alrobaei, H. Novel Integrated Gas Turbine Solar Cogeneration Power Plant. Desalination 2008, 220, 574–587. [Google Scholar] [CrossRef]
- UNESCO; World Water Assessment Programme. The United Nations World Water Development Report 2014: Water and Energy; UNESCO: Paris, France, 2014. [Google Scholar]
- The Glasgow Climate Pact—UN Climate Change Conference (COP26) at the SEC—Glasgow 2021. Available online: https://ukcop26.org/the-glasgow-climate-pact/ (accessed on 9 February 2023).
- Boretti, A.; Castelletto, S. Techno-economic performances of future concentrating solar power plants in Australia. Humanit. Soc. Sci. Commun. 2021, 8, 326. [Google Scholar] [CrossRef]
- Palenzuela, P.; Ortega-Delgado, B.; Alarcón-Padilla, D.-C. Comparative assessment of the annual electricity and water production by concentrating solar power and desalination plants: A case study. Appl. Therm. Eng. 2020, 177, 115485. [Google Scholar] [CrossRef]
- Ortega-Delgado, B.; Palenzuela, P.; Alarcón-Padilla, D.C. Analysis of the Time Step Influence in the Yearly Simulation of Integrated Seawater Multi-Effect Distillation and Parabolic trough Concentrating Solar Thermal Power Plants. Processes 2022, 10, 573. [Google Scholar] [CrossRef]
- Palenzuela, P.; Zaragoza, G.; Alarcón-Padilla, D.C.; Guillén, E.; Ibarra, M.; Blanco, J. Assessment of Different Configurations for Combined Parabolic-Trough (PT) Solar Power and Desalination Plants in Arid Regions. Energy 2011, 36, 4950–4958. [Google Scholar] [CrossRef]
- Palenzuela, P.; Zaragoza, G.; Alarcón, D.; Blanco, J. Simulation and Evaluation of the Coupling of Desalination Units to Parabolic-Trough Solar Power Plants in the Mediterranean Region. Desalination 2011, 281, 379–387. [Google Scholar] [CrossRef]
- Palenzuela, P.; Alarcón-Padilla, D.C.; Zaragoza, G. Large-Scale Solar Desalination by Combination with CSP: Techno-Economic Analysis of Different Options for the Mediterranean Sea and the Arabian Gulf. Desalination 2015, 366, 130–138. [Google Scholar] [CrossRef]
- Palenzuela, P.; Zaragoza, G.; Alarcón-Padilla, D.C. Characterisation of the Coupling of Multi-Effect Distillation Plants to concentrating Solar Power Plants. Energy 2015, 82, 986–995. [Google Scholar] [CrossRef]
- Ortega-Delgado, B.; García-Rodríguez, L.; Alarcón-Padilla, D.C. Thermoeconomic Comparison of Integrating Seawater Desalination Processes in a Concentrating Solar Power Plant of 5 MWe. Desalination 2016, 392, 102–117. [Google Scholar] [CrossRef]
- Ortega-Delgado, B.; Palenzuela, P.; Bonilla, J.; Berenguel, M.; Roca, L.; Alarcón-Padilla, D.C. Dynamic Modeling of a Multi-Effect Vertical Falling-Film Evaporator for Water Reuse in CSP Plants. Desalination 2022, 529, 115623. [Google Scholar] [CrossRef]
- Ortega-Delgado, B.; Palenzuela, P.; Alarcón-Padilla, D.C. Parametric Study of a Multi-Effect Distillation Plant with Thermal Vapor Compression for Its Integration into a Rankine Cycle Power Block. Desalination 2016, 394, 18–29. [Google Scholar] [CrossRef]
- Sharan, P.; Neises, T.; McTigue, J.D.; Turchi, C. Cogeneration using multi-effect distillation and a solar-powered supercritical carbon dioxide Brayton cycle. Desalination 2019, 459, 20–33. [Google Scholar] [CrossRef]
- Maia, C.B.; Silva, F.V.M.; Cabezas-Gómez, L. A CSP-desalination system using a supercritical carbon dioxide Brayton cycle in Brazil. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 154. [Google Scholar] [CrossRef]
- Yuan, L.; Zhu, Q.; Zhang, T.; Duan, R.; Zhu, H. Performance evaluation of a co-production system of solar thermal power generation and seawater desalination. Renew. Energy 2021, 169, 1121–1133. [Google Scholar] [CrossRef]
- Hoffmann, J.E.; Dall, E.P. Integrating desalination with concentrating solar thermal power: A Namibian case study. Renew. Energy 2018, 115, 423–432. [Google Scholar] [CrossRef]
- Wellmann, J.; Meyer-Kahlen, B.; Morosuk, T. Exergoeconomic evaluation of a CSP plant in combination with a desalination unit. Renew. Energy 2018, 128, 586–602. [Google Scholar] [CrossRef]
- Ait Lahoussine Ouali, H.; Soomro, M.I.; Touili, S.; Eltaweel, M.; Alami Merrouni, A. Performance investigation of seawater desalination system powered by central receiver concentrated solar thermal plant. Appl. Therm. Eng. 2023, 225, 120165. [Google Scholar] [CrossRef]
- Frantz, C.; Seifert, B. Thermal Analysis of a Multi Effect Distillation Plant Powered by a Solar Tower Plant. Energy Procedia 2015, 69, 1928–1937. [Google Scholar] [CrossRef] [Green Version]
- Trieb, F.; Müller-Steinhagen, H.; Kern, J.; Scharfe, J.; Kabariti, M.; Al Taher, A. Technologies for Large Scale Seawater Desalination Using Concentrated Solar Radiation. Desalination 2009, 235, 33–43. [Google Scholar] [CrossRef]
- Eveloy, V.; Rodgers, P.; Qiu, L. Hybrid Gas Turbine–Organic Rankine Cycle for Seawater Desalination by Reverse Osmosis in a Hydrocarbon Production Facility. Energy Convers. Manag. 2015, 106, 1134–1148. [Google Scholar] [CrossRef]
- Shaaban, S. Performance Optimization of an Integrated Solar Combined Cycle Power Plant Equipped with a Brine Circulation MSF Desalination Unit. Energy Convers. Manag. 2019, 198, 111794. [Google Scholar] [CrossRef]
- Rensonnet, T.; Uche, J.; Serra, L. Simulation and Thermoeconomic Analysis of Different Configurations of Gas Turbine (GT)-Based Dual-Purpose Power and Desalination Plants (DPPDP) and Hybrid Plants (HP). Energy 2007, 32, 1012–1023. [Google Scholar] [CrossRef]
- Khademi, M.; Ahmadi, A.; Dashti, R.; Shirmohammadi, R. Thermoeconomic optimization of a solar-assisted supercritical CO2 Brayton cycle, organic Rankine cycle and multi-effect distillation system. Energy Rep. 2022, 8, 13494–13503. [Google Scholar] [CrossRef]
- European Commission, Directorate-General for Research and Innovation. SOLGATE, Solar Hybrid Gas Turbine Electric Power System; Publications Office of the European Union: Luxembourg, 2005. [Google Scholar]
- STEAG. Energy Services GmbH EBSILON Professional. Available online: https://www.steag-systemtechnologies.com/en/products/ebsilon-professional/ (accessed on 4 August 2021).
- Kaltschmitt, M.; Streicher, W.; Wiese, A. (Eds.) Erneuerbare Energien—Systemtechnik · Wirtschaftlichkeit · Umweltaspekte; Springer: Berlin/Heidelberg, Germany, 2020; ISBN 978-3-662-61189-0. [Google Scholar] [CrossRef]
- Singer, C. Solarturmreceiver für Überkritische Dampfprozesse und Ihre Technische und Ökonomische Bewertung; Springer Fachmedien: Wiesbaden, Germany, 2013; ISBN 978-3-658-02210-5. [Google Scholar] [CrossRef]
- WAVE Water Treatment Design Software. Available online: https://www.dupont.com/water/resources/design-software.html (accessed on 10 January 2023).
- Strathmann, H. Introduction to Membrane Science and Technology; Wiley-VCH: Weinheim, Germany, 2011; ISBN 9783527324514. [Google Scholar]
- Final Report Summary—SOLHYCO (Solar-Hybrid Power and Cogeneration Plants)|FP6|CORDIS|European Commission. Available online: https://cordis.europa.eu/project/id/19830/reporting (accessed on 20 February 2023).
- Green, D.W.; Perry, R.H. Perry’s Chemical Engineers’ Handbook, 8th ed.; McGraw-Hill Education: New York, NY, USA, 2008; ISBN 9780071422949. [Google Scholar]
- Melin, T.; Rautenbach, R. Membranverfahren: Grundlagen der Modul- und Anlagenauslegung, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 9783540343288. [Google Scholar] [CrossRef]
- Pearce, G.K. UF/MF Pre-Treatment to RO in Seawater and Wastewater Reuse Applications: A Comparison of Energy Costs. Desalination 2008, 222, 66–73. [Google Scholar] [CrossRef]
- FilmTecTM SW30HR-380 Wet. Available online: https://www.dupont.com/products/filmtecsw30hr380wet.html (accessed on 20 February 2023).
- Palenzuela, P.; Alarcón, D.; Zaragoza, G.; Blanco, J.; Ibarra, M. Parametric Equations for the Variables of a Steady-State Model of a Multi-Effect Desalination Plant. Desalin. Water Treat. 2013, 51, 1229–1241. [Google Scholar] [CrossRef]
- Palenzuela, P.; Hassan, A.S.; Zaragoza, G.; Alarcón-Padilla, D.-C. Steady State Model for Multi-Effect Distillation Case Study: Plataforma Solar de Almería MED Pilot Plant. Desalination 2014, 337, 31–42. [Google Scholar] [CrossRef]
- El-Dessouky, H.T.; Ettouney, H.M. Fundamentals of Salt Water Desalination; Elsevier: Amsterdam, The Netherlands, 2002; ISBN 9780444508102. [Google Scholar] [CrossRef]
- Aigner, D.; Bollrich, G. Bauwesen Wissen: Handbuch der Hydraulik: Für Wasserbau und Wasserwirtschaft; Beuth Verlag GmbH: Berlin, Germany, 2015; ISBN 9783410213413. [Google Scholar]
- Greenlee, L.F.; Lawler, D.F.; Freeman, B.D.; Marrot, B.; Moulin, P. Reverse Osmosis Desalination: Water Sources, Technology, and Today’s Challenges. Water Res. 2009, 43, 2317–2348. [Google Scholar] [CrossRef]



| Parameter | Value | Unit | |
|---|---|---|---|
| Fixed | pH | 7.6 | - |
| Operating temperature, T | 25 | °C | |
| Concentration | 8 | mg/L | |
| Permeability coefficient, L | 1.0979 × 10−3 | m/(h bar) | |
| Variable | Feed flow, | 200 | m3/day |
| Recovery Ratio, | 40 | % | |
| Fouling Factor, | 0.85 | - |
| Component | Concentration in mg/L |
|---|---|
| Cl− | 23,000 |
| Na+ | 12,000 |
| SO42− | 2670 |
| Mg2+ | 1550 |
| Ca2+ | 670 |
| HCO3− | 142 |
| CO32− | 8 |
| Sr2+ | 7.5 |
| B | 5.3 |
| TDS | 40,052.8 |
| Parameter | Value | Unit |
|---|---|---|
| Initial temp. diff. in the 1st effect (brine–feedwater) | 3 | °C |
| Recovery Ratio, | 37 | % |
| Number of effects, | 15 | - |
| Number of preheaters, | 14 | - |
| Heating steam temperature, | 70.6 | °C |
| Vapor temperature in the last effect, | 35 | °C |
| Temperature increase in the condenser | 7 | °C |
| Parameter | Unit |
|---|---|
| Heat transfer area, | m2 |
| Total distillate production, | m3/day |
| Gain Output Ratio, | - |
| Feedwater flow rate, | m3/day |
| Feedwater temperature, | °C |
| Seawater mass flow rate, | kg/s |
| Specific Thermal Consumption, | kWh/m3 |
| Parameter | Value | Unit |
|---|---|---|
| Aperture area, | 19.63 | m2 |
| Design intercept power, | 16,130 | kW |
| Efficiency, | 0.74 | - |
| Emissivity, | 0.84 | - |
| Heat loss convective coefficient, | 12 | W/m2K |
| Surface temperature, | 830 | °C |
| Nominal pressure drop, | 1 | bar |
| Parameter | Value | Unit |
|---|---|---|
| Pressure ratio, Brayton, | 16 | - |
| Gas turbine inlet temperature, | 1256 | °C |
| Low-pressure, Boiler, | 5 | bar |
| High-pressure, Boiler, | 121 | bar |
| High-temperature difference, Evaporator, | 20 | K |
| Low-temperature difference, Evaporator, | 15 | K |
| Compressor efficiency, | 85 | % |
| Generator efficiency, | 98 | % |
| Design Parameter | Value | Unit |
|---|---|---|
| Total reflective area | 25,458.6 | m2 |
| Number of heliostats | 220 | - |
| Heliostat reflective area | 115.72 | m2 |
| Efficiency | 0.74 | - |
| Average field reflectivity | 0.88 | - |
| Field density | 0.22 | - |
| Design Parameter | Value | Unit | |
|---|---|---|---|
| Power plant performance | Gross Power Brayton | 10 | MWe |
| Gross Power Rankine | 5 | MWe | |
| Parasitic energy losses | 0.1 | MWe | |
| Thermal efficiency | Brayton cycle | 35.9 | % |
| Rankine cycle | 27.8 | % | |
| Combined cycle | 53.3 | % | |
| Solar fraction | 41 | % |
| RO Unit | Variable | Value | Unit |
|---|---|---|---|
| Power for desalination | 900 | kWe | |
| No energy recovery system | Power for pretreatment MF/UF | 87 | kWe |
| Power for RO | 813 | kWe | |
| Fresh water production | 3200 | m3/day | |
| Number of modules | 40 | - | |
| RO process | 6.07 | kWh/m3 | |
| With energy recovery system | Power for pretreatment MF/UF | 126 | kWe |
| Power for RO | 774 | kWe | |
| Fresh water production | 4640 | m3/day | |
| Number of modules | 58 | - | |
| RO process | 3.98 | kWh/m3 |
| CRS Plant with LT-MED | Variable | Value | Unit |
|---|---|---|---|
| Power plant performance | Gross Power Brayton | 10 | MWe |
| Gross Power Rankine | 4.4 | MWe | |
| Parasitic energy losses | 0.09 | MWe | |
| Electric Consumption MED | 0.31 | MWe | |
| Thermal efficiency | Brayton cycle | 35.9 | % |
| Rankine cycle | 24.5 | % | |
| Combined cycle | 50.2 | % | |
| Solar fraction | 41 | % | |
| Brayton cycle | 35.9 | % |
| (kg/s) | (kW) | (kW) | (m3/Day) | (kWh/m3) | |
|---|---|---|---|---|---|
| 4.249 | 10,080 | 8831 | 3831 | 10.33 | 63.1 |
| 4.829 | 11,633 | 10,214 | 4562 | 10.82 | 61.2 |
| 5.231 | 12,658 | 11,120 | 4942 | 10.82 | 61.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palenzuela, P.; Alarcón-Padilla, D.-C.; Ortega-Delgado, B.; Zaragoza, G. Cogeneration of Fresh Water and Electricity with High-Temperature Power Cycles: Comparative Assessment of Multi-Effect Distillation and Reverse Osmosis. Processes 2023, 11, 1181. https://doi.org/10.3390/pr11041181
Palenzuela P, Alarcón-Padilla D-C, Ortega-Delgado B, Zaragoza G. Cogeneration of Fresh Water and Electricity with High-Temperature Power Cycles: Comparative Assessment of Multi-Effect Distillation and Reverse Osmosis. Processes. 2023; 11(4):1181. https://doi.org/10.3390/pr11041181
Chicago/Turabian StylePalenzuela, Patricia, Diego-César Alarcón-Padilla, Bartolomé Ortega-Delgado, and Guillermo Zaragoza. 2023. "Cogeneration of Fresh Water and Electricity with High-Temperature Power Cycles: Comparative Assessment of Multi-Effect Distillation and Reverse Osmosis" Processes 11, no. 4: 1181. https://doi.org/10.3390/pr11041181
APA StylePalenzuela, P., Alarcón-Padilla, D.-C., Ortega-Delgado, B., & Zaragoza, G. (2023). Cogeneration of Fresh Water and Electricity with High-Temperature Power Cycles: Comparative Assessment of Multi-Effect Distillation and Reverse Osmosis. Processes, 11(4), 1181. https://doi.org/10.3390/pr11041181







