Non-Newtonian Mixed Convection Magnetized Flow with Heat Generation and Viscous Dissipation Effects: A Prediction Application of Artificial Intelligence
Abstract
:1. Introduction
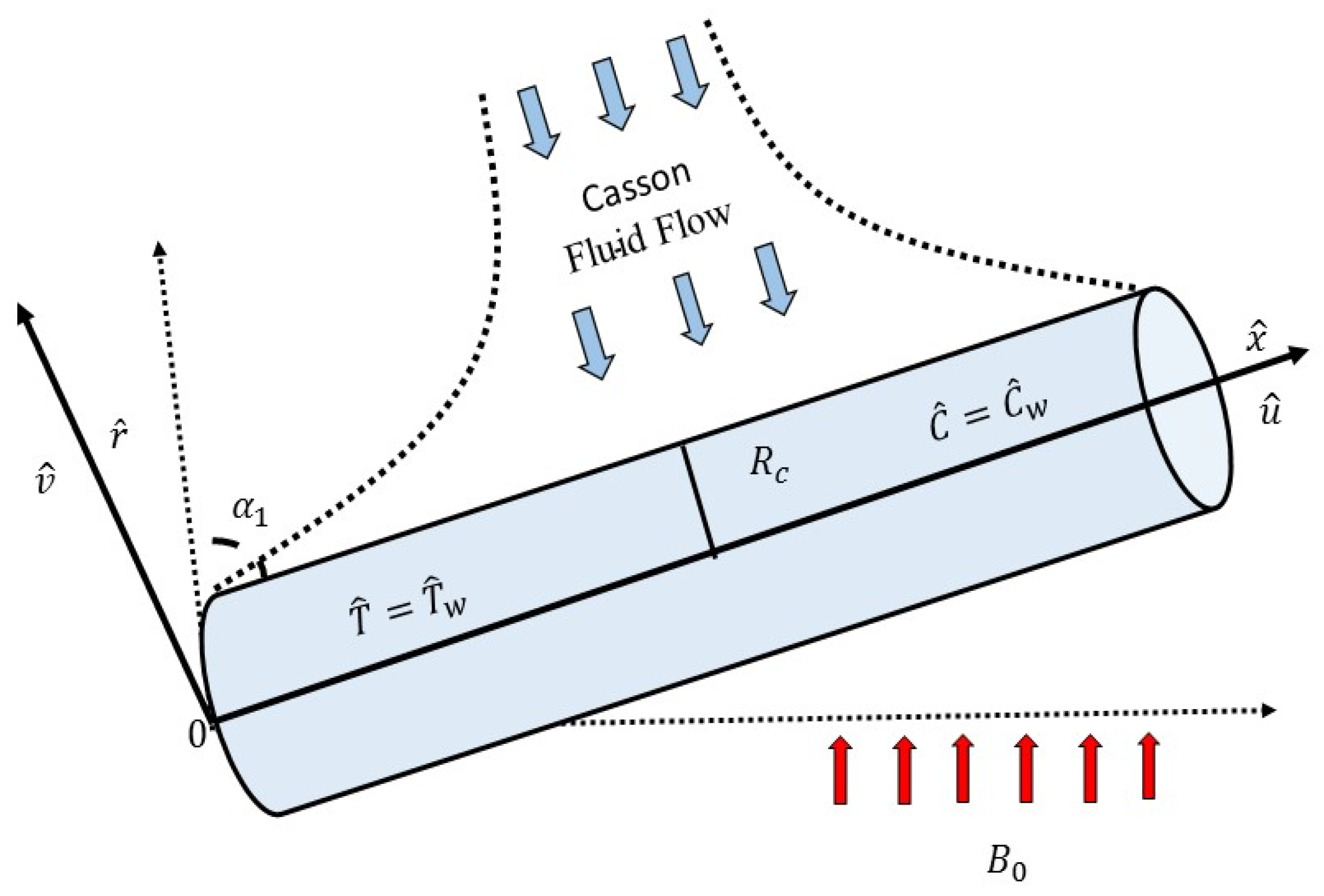
2. Mathematical Formulation
3. Solution Scheme
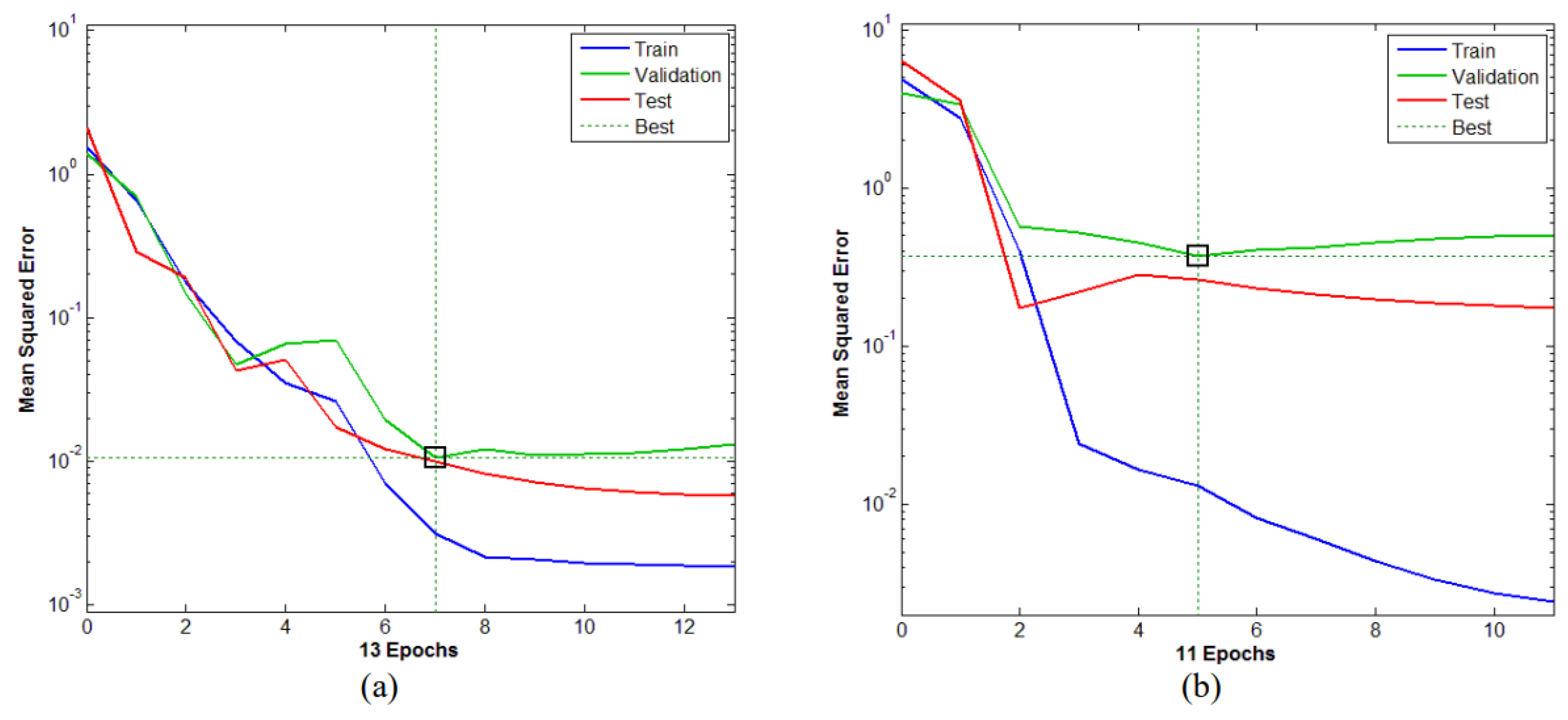
4. Construction of Artificial Neural Networking Model
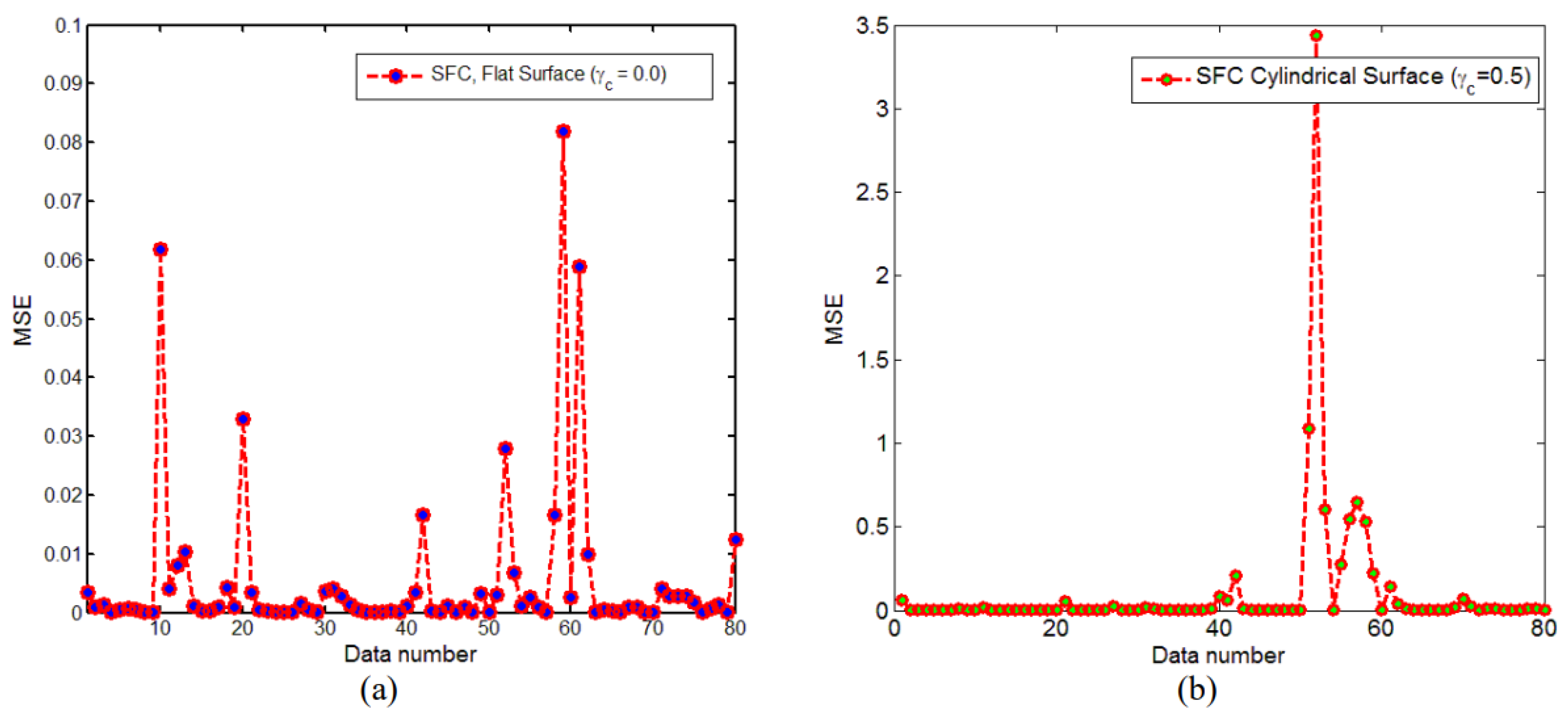
5. Results and Discussion
6. Conclusions
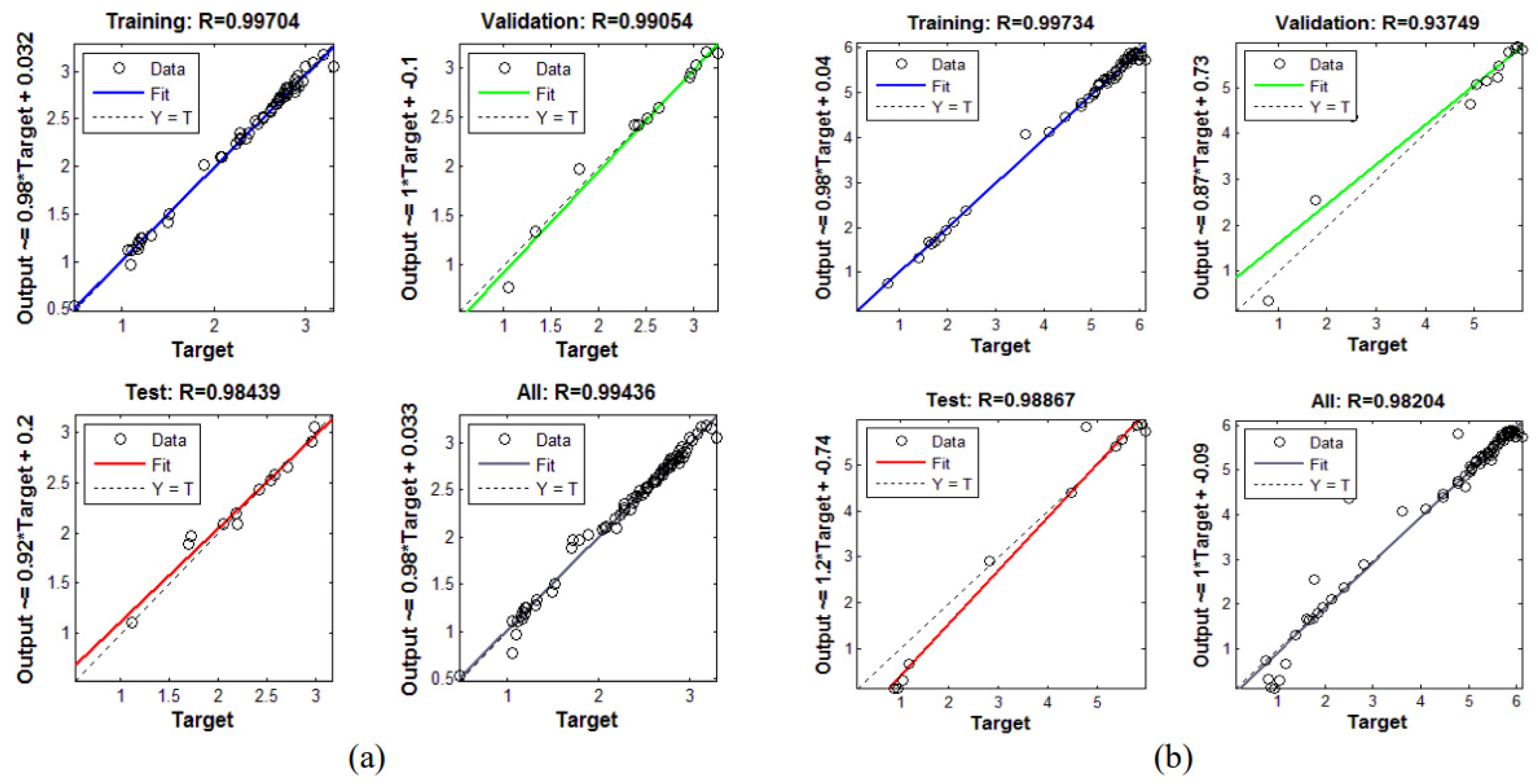
- The values of the coefficient of determination are in support of the best artificial neural networking to predict the SFC at the surface.
- The average mean square error (MSE) value for the ANN model towards a flat stretched surface was 0.51666569% and it was quite satisfactory.
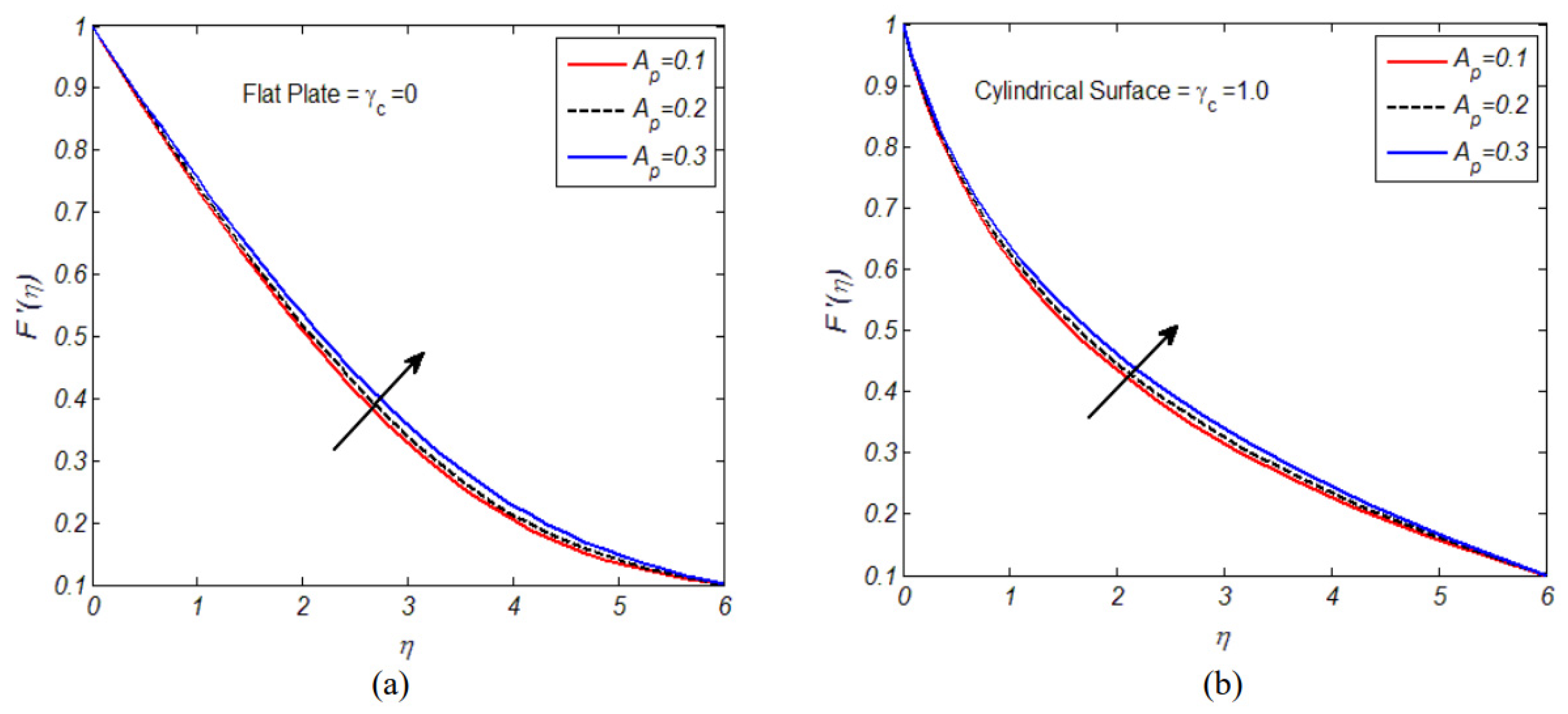
- Owning to a prediction by ANN models, we observed that, compared to a flat surface, the strength of the SFC was larger in the case of cylindrical surfaces.
- SFC showed decline values for the velocity ratio parameter, the concentration Grashof number, the Casson fluid parameter, and the solutal Grashof number.
- Casson fluid velocity showed increasing trends towards the velocity ratio parameter; the opposite was the case for the Casson fluid parameter and magnetic field parameter.
- One can extend this study to examine the non-Newtonian fluid models (namely Power Law, the Carreau, and the Generalized Power Law) subject to stretched surfaces having engineering standpoints.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Cylindrical coordinates | |
| Kinematic viscosity | |
| Velocity components | |
| Casson fluid parameter | |
| Gravitational acceleration | |
| Thermal expansion coefficient | |
| Angle of inclination | |
| Solutal expansion coefficient | |
| Temperature of fluid | |
| Ambient temperature | |
| Magnetic field constant | |
| Ambient concentration | |
| Concentration of fluid | |
| Free stream velocity | |
| Specific heat at constant pressure | |
| Fluid electrical conductivity | |
| Fluid density | |
| Variable thermal conductivity | |
| Radiative heat flux | |
| Dynamic viscosity | |
| Characteristic length | |
| Heat generation coefficient | |
| Small parameter | |
| Surface concentration | |
| Reference velocity | |
| Mass diffusivity | |
| Surface temperature | |
| Radius of cylinder | |
| Fluid concentration | |
| Fluid velocity | |
| Fluid temperature | |
| Concentration Grashof number | |
| Temperature Grashof number | |
| Pr | Prandtl number |
| Radiation parameter | |
| Velocities ratio parameter | |
| Magnetic field parameter | |
| Coefficient of mean absorption | |
| Curvature parameter | |
| Eckert number | |
| Stefan–Boltzmann constant | |
| Sc | Schmidt number |
| Heat generation parameter |
References
- Rohlf, K.; Tenti, G. The role of the Womersley number in pulsatile blood flow: A theoretical study of the Casson model. J. Biomech. 2001, 34, 141–148. [Google Scholar] [CrossRef]
- Mernone, A.; Mazumdar, J.; Lucas, S. A mathematical study of peristaltic transport of a Casson fluid. Math. Comput. Model. 2002, 35, 895–912. [Google Scholar] [CrossRef]
- Joye, D.D. Shear rate and viscosity corrections for a Casson fluid in cylindrical (Couette) geometries. J. Colloid Interface Sci. 2003, 267, 204–210. [Google Scholar] [CrossRef] [PubMed]
- Raja Ramesh, H.; You, Z. Application of the augmented Lagrangian method to steady pipe flows of Bingham, Casson and Herschel–Bulkley fluids. J. Non-Newton. Fluid Mech. 2005, 128, 126–143. [Google Scholar]
- Kelessidis, V.; Maglione, R. Modeling rheological behavior of bentonite suspensions as Casson and Robertson–Stiff fluids using Newtonian and true shear rates in Couette viscometry. Powder Technol. 2006, 168, 134–147. [Google Scholar] [CrossRef]
- Mahanta, G.; Shaw, S. 3D Casson fluid flow past a porous linearly stretching sheet with convective boundary condition. Alex. Eng. J. 2015, 54, 653–659. [Google Scholar] [CrossRef]
- Akbar, N.S.; Tripathi, D.; Bég, O.A.; Khan, Z. MHD dissipative flow and heat transfer of Casson fluids due to metachronal wave propulsion of beating cilia with thermal and velocity slip effects under an oblique magnetic field. Acta Astronaut. 2016, 128, 1–12. [Google Scholar] [CrossRef]
- Thammanna, G.; Kumar, K.G.; Gireesha, B.; Ramesh, G.; Prasannakumara, B. Three dimensional MHD flow of couple stress Casson fluid past an unsteady stretching surface with chemical reaction. Results Phys. 2017, 7, 4104–4110. [Google Scholar] [CrossRef]
- Siddiqa, S.; Begum, N.; Ouazzi, A.; Hossain, A.; Gorla, R.S.R. Heat transfer analysis of Casson dusty fluid flow along a vertical wavy cone with radiating surface. Int. J. Heat Mass Transf. 2018, 127, 589–596. [Google Scholar] [CrossRef]
- Mahmood, A.; Jamshed, W.; Aziz, A. Entropy and heat transfer analysis using Cattaneo-Christov heat flux model for a boundary layer flow of Casson nanofluid. Results Phys. 2018, 10, 640–649. [Google Scholar] [CrossRef]
- Madhu, A.; Chandra, A.; Sharma, S. Natural convection in a partially heated porous cavity to Casson fluid. Int. Commun. Heat Mass Transf. 2020, 114, 104555. [Google Scholar]
- Anantha Kumar, K.; Sugunamma, V.; Sandeep, N. Effect of thermal radiation on MHD Casson fluid flow over an exponentially stretching curved sheet. J. Therm. Anal. Calorim. 2020, 140, 2377–2385. [Google Scholar] [CrossRef]
- Banerjee, A.; Mahato, S.K.; Bhattacharyya, K.; Chamkha, A.J. Divergent channel flow of Casson fluid and heat transfer with suction/blowing and viscous dissipation: Existence of boundary layer. Partial. Differ. Equ. Appl. Math. 2021, 4, 100172. [Google Scholar] [CrossRef]
- Parvin, S.; Mohamed Isa, S.S.; Arifin, N.M.; Md Ali, F. The inclined factors of magnetic field and shrinking sheet in Casson fluid flow, heat and mass transfer. Symmetry 2021, 13, 373. [Google Scholar] [CrossRef]
- Obalalu, A.M.; Ajala, A.O.; Akindele, A.O.; Oladapo, O.A.; Adepoju, O.; Jimoh, M.O. Unsteady squeezed flow and heat transfer of dissipative casson fluid using optimal homotopy analysis method: An application of solar radiation. Partial. Differ. Equ. Appl. Math. 2021, 4, 100146. [Google Scholar] [CrossRef]
- Raza, A.; Khan, S.U.; Farid, S.; Khan, M.I.; Sun, T.-C.; Abbasi, A.; Malik, M. Thermal activity of conventional Casson nanoparticles with ramped temperature due to an infinite vertical plate via fractional derivative approach. Case Stud. Therm. Eng. 2021, 27, 101191. [Google Scholar] [CrossRef]
- Saeed, A.; Algehyne, E.A.; Aldhabani, M.S.; Dawar, A.; Kumam, P.; Kumam, W. Mixed convective flow of a magnetohydrodynamic Casson fluid through a permeable stretching sheet with first-order chemical reaction. PLoS ONE 2022, 17, e0265238. [Google Scholar] [CrossRef]
- Priam, S.S.; Nasrin, R. Numerical appraisal of time-dependent peristaltic duct flow using Casson fluid. Int. J. Mech. Sci. 2022, 233, 107676. [Google Scholar] [CrossRef]
- Prameela, M.; Gangadhar, K.; Reddy, G.J. MHD free convective non-Newtonian Casson fluid flow over an oscillating vertical plate. Partial. Differ. Equ. Appl. Math. 2022, 5, 100366. [Google Scholar] [CrossRef]
- Hussain, S.; Zeeshan, M.; Sagheer, D.-E. Irreversibility analysis for the natural convection of Casson fluid in an inclined porous cavity under the effects of magnetic field and viscous dissipation. Int. J. Therm. Sci. 2022, 179, 107699. [Google Scholar] [CrossRef]
- Rehman, K.U.; Shatanawi, W.; Yaseen, S. A Comparative Numerical Study of Heat and Mass Transfer Individualities in Casson Stagnation Point Fluid Flow Past a Flat and Cylindrical Surfaces. Mathematics 2023, 11, 470. [Google Scholar] [CrossRef]
- Nawaz, Y.; Arif, M.S.; Abodayeh, K.; Mansoor, M. Finite difference schemes for MHD mixed convective Darcy–forchheimer flow of Non-Newtonian fluid over oscillatory sheet: A computational study. Front. Phys. 2023, 11, 1072296. [Google Scholar] [CrossRef]
- Sadaf, H.; Asghar, Z.; Iftikhar, N. Cilia-driven flow analysis of cross fluid model in a horizontal channel. Comput. Part. Mech. 2022, 9, 1–8. [Google Scholar] [CrossRef]
- Nawaz, Y.; Arif, M.S.; Abodayeh, K. Predictor–Corrector Scheme for Electrical Magnetohydrodynamic (MHD) Casson Nanofluid Flow: A Computational Study. Appl. Sci. 2023, 13, 1209. [Google Scholar] [CrossRef]
- Fatima, N.; Kousar, N.; Rehman, K.U.; Shatanawi, W. Magneto-thermal convection in partially heated novel cavity with multiple heaters at bottom wall: A numerical solution. Case Stud. Therm. Eng. 2023, 43, 102781. [Google Scholar] [CrossRef]
- Atashafrooz, M.; Sajjadi, H.; Delouei, A.A. Simulation of Combined Convective-Radiative Heat Transfer of Hybrid Nanofluid Flow inside an Open Trapezoidal Enclosure Considering the Magnetic Force Impacts. J. Magn. Magn. Mater. 2023, 567, 170354. [Google Scholar] [CrossRef]
- Salahuddin, T. Carreau fluid model towards a stretching cylinder: Using Keller box and shooting method. Ain Shams Eng. J. 2020, 11, 495–500. [Google Scholar] [CrossRef]
- Muhammad, K.; Abdelmohsen, S.A.; Abdelbacki, A.M.; Ahmed, B. Ahmed. Darcy-Forchheimer flow of hybrid nanofluid subject to melting heat: A comparative numerical study via shooting method. Int. Commun. Heat Mass Transf. 2022, 135, 106160. [Google Scholar] [CrossRef]
- Shafiq, A.; Çolak, A.B.; Sindhu, T.N.; Muhammad, T.; Shafiq, A.; Çolak, A.B.; Sindhu, T.N.; Muhammad, T. Optimization of Darcy-Forchheimer squeezing flow in nonlinear stratified fluid under convective conditions with artificial neural network. Heat Transf. Res. 2022, 53, 67–89. [Google Scholar] [CrossRef]
- Said, Z.; Sharma, P.; Elavarasan, R.M.; Tiwari, A.K.; Rathod, M.K. Exploring the specific heat capacity of water-based hybrid nanofluids for solar energy applications: A comparative evaluation of modern ensemble machine learning techniques. J. Energy Storage 2022, 54, 105230. [Google Scholar] [CrossRef]
- Acikgoz, O.; Çolak, A.B.; Camci, M.; Karakoyun, Y.; Dalkilic, A.S. Machine learning approach to predict the heat transfer coefficients pertaining to a radiant cooling system coupled with mixed and forced convection. Int. J. Therm. Sci. 2022, 178, 107624. [Google Scholar] [CrossRef]
- Rehman, K.U.; Shatanawi, W.; Çolak, A.B. Artificial Neural Networking Magnification for Heat Transfer Coefficient in Convective Non-Newtonian Fluid with Thermal Radiations and Heat Generation Effects. Mathematics 2023, 11, 342. [Google Scholar] [CrossRef]
- Hayat, T.; Asad, S.; Alsaedi, A. Flow of variable thermal conductivity fluid due to inclined stretching cylinder with viscous dissipation and thermal radiation. Appl. Math. Mech. 2014, 35, 717–728. [Google Scholar] [CrossRef]
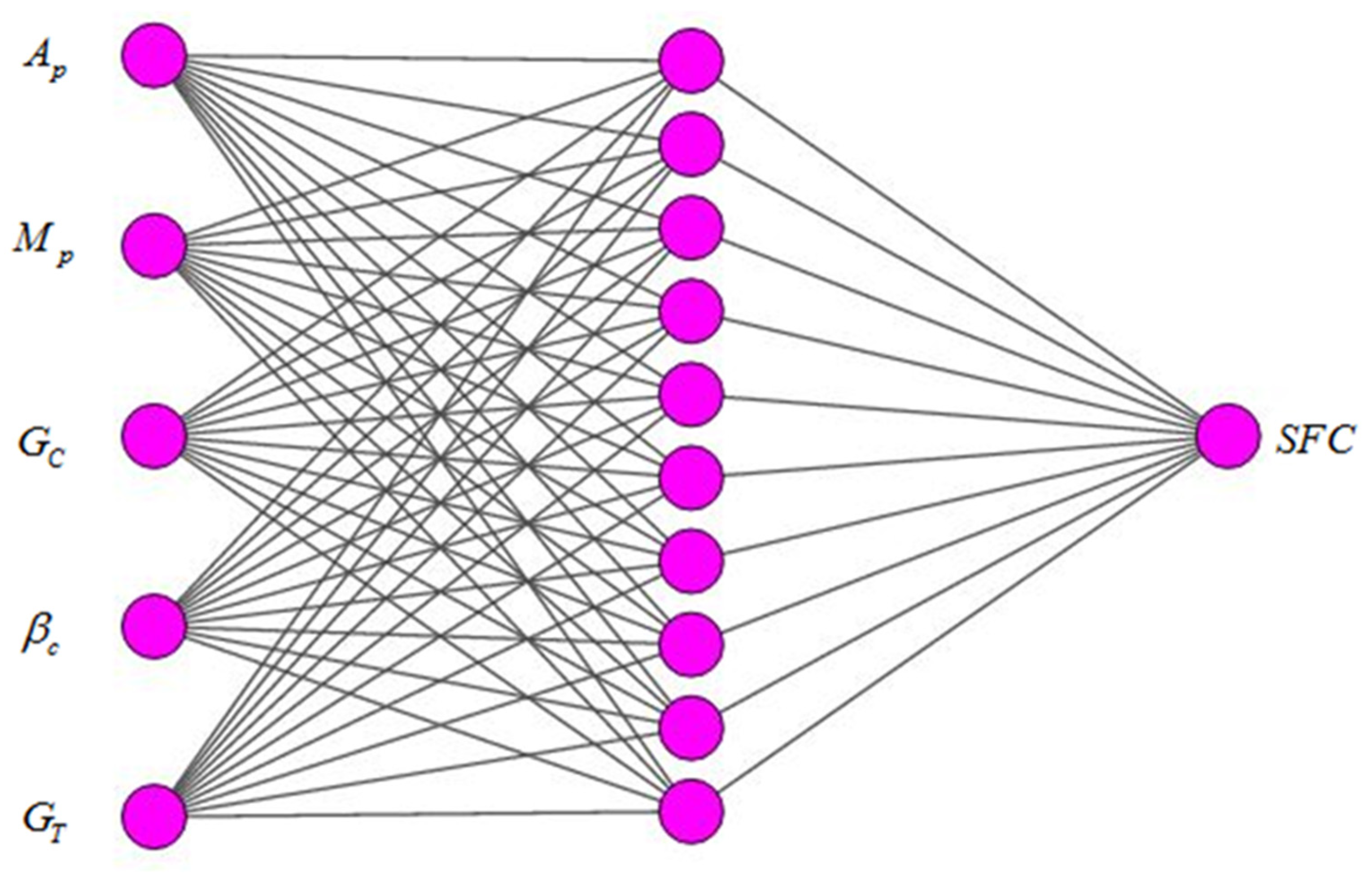




| Model | Surface | Input | Output | ||||
|---|---|---|---|---|---|---|---|
| ANN Model-I | SFC | ||||||
| ANN Model-II | SFC | ||||||
| Samples | Model-I | Model-II |
|---|---|---|
| Data for training | 56 | 56 |
| Data for validation | 12 | 12 |
| Data for test Data | 12 | 12 |
| Total | 80 | 80 |
(Plate) | (Cylinder) | (Plate) | (Cylinder) | |
|---|---|---|---|---|
| 0.1 | −0.2724 | −0.5437 | −2.9964 | −5.9807 |
| 0.2 | −0.2654 | −0.5389 | −2.9194 | −5.9279 |
| 0.3 | −0.2538 | −0.5297 | −2.7918 | −5.8267 |
| 0.4 | −0.2463 | −0.5176 | −2.7093 | −5.6936 |
| 0.5 | −0.2376 | −0.5021 | −2.6136 | −5.5231 |
| 0.6 | −0.2277 | −0.4832 | −2.5047 | −5.3152 |
| 0.7 | −0.2163 | −0.4609 | −2.3793 | −5.0699 |
| 0.8 | −0.2041 | −0.4354 | −2.2451 | −4.7894 |
| 0.9 | −0.1901 | −0.4065 | −2.0911 | −4.4715 |
| 1.0 | −0.1567 | −0.3743 | −1.7237 | −4.1173 |
(Plate) | (Cylinder) | (Plate) | (Cylinder) | |
|---|---|---|---|---|
| 0.1 | −0.2695 | −0.5419 | −2.9645 | −5.9609 |
| 0.2 | −0.2666 | −0.5367 | −2.9326 | −5.9037 |
| 0.3 | −0.2626 | −0.5282 | −2.8886 | −5.8102 |
| 0.4 | −0.2513 | −0.5162 | −2.7643 | −5.6782 |
| 0.5 | −0.2439 | −0.5009 | −2.6829 | −5.5099 |
| 0.6 | −0.2353 | −0.4822 | −2.5883 | −5.3042 |
| 0.7 | −0.2255 | −0.4601 | −2.4805 | −5.0611 |
| 0.8 | −0.2144 | −0.4347 | −2.3584 | −4.7817 |
| 0.9 | −0.1882 | −0.4054 | −2.0702 | −4.4594 |
| 1.0 | −0.1548 | −0.3739 | −1.7028 | −4.1129 |
(Plate) | (Cylinder) | (Plate) | (Cylinder) | |
|---|---|---|---|---|
| 0.1 | −0.2724 | −0.5423 | −2.9964 | −5.9653 |
| 0.2 | −0.2625 | −0.5319 | −2.8875 | −5.8509 |
| 0.3 | −0.2552 | −0.5215 | −2.8072 | −5.7365 |
| 0.4 | −0.2514 | −0.5110 | −2.7654 | −5.6210 |
| 0.5 | −0.2475 | −0.5006 | −2.7225 | −5.5066 |
| 0.6 | −0.2434 | −0.4901 | −2.6774 | −5.3911 |
| 0.7 | −0.2391 | −0.4979 | −2.6301 | −5.4769 |
| 0.8 | −0.2301 | −0.4692 | −2.5311 | −5.1612 |
| 0.9 | −0.2199 | −0.4588 | −2.4189 | −5.0468 |
| 1.0 | −0.2080 | −0.4483 | −2.2880 | −4.9313 |
(Plate) | (Cylinder) | (Plate) | (Cylinder) | |
|---|---|---|---|---|
| 0.1 | −0.2695 | −0.5419 | −2.9645 | −5.9609 |
| 0.2 | −0.2625 | −0.5315 | −2.8875 | −5.8465 |
| 0.3 | −0.2551 | −0.5210 | −2.8061 | −5.731 |
| 0.4 | −0.2473 | −0.5106 | −2.7203 | −5.6166 |
| 0.5 | −0.2390 | −0.5001 | −2.629 | −5.5011 |
| 0.6 | −0.2299 | −0.4897 | −2.5289 | −5.3867 |
| 0.7 | −0.2197 | −0.4792 | −2.4167 | −5.2712 |
| 0.8 | −0.2077 | −0.4688 | −2.2847 | −5.1568 |
| 0.9 | −0.1993 | −0.4583 | −2.1923 | −5.0413 |
| 1.0 | −0.1863 | −0.4478 | −2.0493 | −4.9258 |
(Plate) | (Cylinder) | (Plate) | (Cylinder) | |
|---|---|---|---|---|
| 0.1 | −0.2724 | −0.5437 | −2.9964 | −5.9807 |
| 0.2 | −0.3153 | −0.6033 | −1.8918 | −3.6198 |
| 0.3 | −0.3505 | −0.6489 | −1.5188 | −2.8119 |
| 0.4 | −0.3803 | −0.6850 | −1.33105 | −2.3975 |
| 0.5 | −0.4059 | −0.7146 | −1.2177 | −2.1438 |
| 0.6 | −0.4480 | −0.7393 | −1.1946 | −1.9714 |
| 0.7 | −0.4814 | −0.7602 | −1.16911 | −1.8462 |
| 0.8 | −0.4957 | −0.7782 | −1.1153 | −1.7509 |
| 0.9 | −0.5010 | −0.7939 | −1.0576 | −1.6760 |
| 1.0 | −0.5825 | −0.8077 | −1.1650 | −1.6154 |
(Plate) | (Cylinder) | (Plate) | (Cylinder) | |
|---|---|---|---|---|
| 0.1 | −0.2688 | −0.4341 | −2.9568 | −4.7751 |
| 0.2 | −0.2995 | −0.4186 | −1.797 | −2.5116 |
| 0.3 | −0.3457 | −0.4083 | −1.4980 | −1.7693 |
| 0.4 | −0.3747 | −0.4011 | −1.31145 | −1.40385 |
| 0.5 | −0.3997 | −0.3959 | −1.1991 | −1.1877 |
| 0.6 | −0.4407 | −0.3920 | −1.1752 | −1.0453 |
| 0.7 | −0.4578 | −0.3889 | −1.1118 | −0.9444 |
| 0.8 | −0.4872 | −0.3865 | −1.0962 | −0.8696 |
| 0.9 | −0.4999 | −0.3846 | −1.0553 | −0.8119 |
| 1.0 | −0.2414 | −0.3831 | −0.4828 | −0.7662 |
(Plate) | (Cylinder) | (Plate) | (Cylinder) | |
|---|---|---|---|---|
| 0.1 | −0.2998 | −0.5554 | −3.2978 | −6.1094 |
| 0.2 | −0.2949 | −0.5488 | −3.2439 | −6.0368 |
| 0.3 | −0.2899 | −0.5423 | −3.1889 | −5.9653 |
| 0.4 | −0.2850 | −0.5357 | −3.1350 | −5.8927 |
| 0.5 | −0.2801 | −0.5292 | −3.0811 | −5.8212 |
| 0.6 | −0.2752 | −0.5227 | −3.0272 | −5.7497 |
| 0.7 | −0.2703 | −0.5162 | −2.9733 | −5.6782 |
| 0.8 | −0.2654 | −0.5097 | −2.9194 | −5.6067 |
| 0.9 | −0.2605 | −0.5033 | −2.8655 | −5.5363 |
| 1.0 | −0.2557 | −0.4968 | −2.8127 | −5.4648 |
(Plate) | (Cylinder) | (Plate) | (Cylinder) | |
|---|---|---|---|---|
| 0.1 | −0.2695 | −0.5429 | −2.9645 | −5.9719 |
| 0.2 | −0.2617 | −0.5335 | −2.8787 | −5.8685 |
| 0.3 | −0.2539 | −0.5252 | −2.7929 | −5.7772 |
| 0.4 | −0.2462 | −0.5170 | −2.7082 | −5.6870 |
| 0.5 | −0.2385 | −0.5087 | −2.6235 | −5.5957 |
| 0.6 | −0.2308 | −0.5004 | −2.5388 | −5.5044 |
| 0.7 | −0.2231 | −0.4922 | −2.4541 | −5.4142 |
| 0.8 | −0.2155 | −0.4840 | −2.3705 | −5.3240 |
| 0.9 | −0.2078 | −0.4758 | −2.2858 | −5.2338 |
| 1.0 | −0.2002 | −0.4676 | −2.2022 | −5.1436 |
| MSE | R | ||||||
|---|---|---|---|---|---|---|---|
| Model | Surface | Training | Validation | Test | Training | Validation | Test |
| Model-I | 0.0031 | 0.0107 | 0.0099 | 0.9970 | 0.9905 | 0.9844 | |
| Model-II | 0.0130 | 0.3709 | 0.2642 | 0.9973 | 0.9375 | 0.9887 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehman, K.U.; Shatanawi, W. Non-Newtonian Mixed Convection Magnetized Flow with Heat Generation and Viscous Dissipation Effects: A Prediction Application of Artificial Intelligence. Processes 2023, 11, 986. https://doi.org/10.3390/pr11040986
Rehman KU, Shatanawi W. Non-Newtonian Mixed Convection Magnetized Flow with Heat Generation and Viscous Dissipation Effects: A Prediction Application of Artificial Intelligence. Processes. 2023; 11(4):986. https://doi.org/10.3390/pr11040986
Chicago/Turabian StyleRehman, Khalil Ur, and Wasfi Shatanawi. 2023. "Non-Newtonian Mixed Convection Magnetized Flow with Heat Generation and Viscous Dissipation Effects: A Prediction Application of Artificial Intelligence" Processes 11, no. 4: 986. https://doi.org/10.3390/pr11040986
APA StyleRehman, K. U., & Shatanawi, W. (2023). Non-Newtonian Mixed Convection Magnetized Flow with Heat Generation and Viscous Dissipation Effects: A Prediction Application of Artificial Intelligence. Processes, 11(4), 986. https://doi.org/10.3390/pr11040986








