Next Article in Journal
Review of Two-Dimensional MXenes (Ti3C2Tx) Materials in Photocatalytic Applications
Previous Article in Journal
HPLC-UV Analysis of Chrysophanol in Senna occidentalis Extract Obtained by Using the RSM-Optimized Ultrasonic Extraction Process
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Processes
Volume 11
Issue 5
10.3390/pr11051411
processes-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Dissipative Particle Dynamics Simulation and Microscopic Experimental Study of Emulsification Performance of Surfactant/Polymer Flooding

by
Biao Zhang
1,*,
Baoshan Guan
1,2,
Weidong Liu
2,
Baoliang Peng
2 and
Sunan Cong
2
1
Research Institute of Percolation Fluids Mechanics, Chinese Academy of Sciences, Beijing 100010, China
2
Research Institute of Petroleum Exploration and Development, Beijing 100010, China
*
Author to whom correspondence should be addressed.
Processes 2023, 11(5), 1411; https://doi.org/10.3390/pr11051411
Submission received: 3 April 2023 / Revised: 18 April 2023 / Accepted: 30 April 2023 / Published: 6 May 2023
(This article belongs to the Section Chemical Processes and Systems)
Browse Figures
Versions Notes

Abstract

:
Polymers can increase the viscosity of water, reduce the relative permeability of the water phase, and enhance the flowability of the oil phase; surfactants can form molecular films at the oil–water interface boundaries, thereby reducing interfacial tension. Surfactant/polymer (S/P) flooding technology for enhancing oil recovery has become a major way to increase crude oil production. This study used dissipative particle dynamics (DPD) technology to simulate the emulsification process of a four-component composite system consisting of oil, water, sodium dodecylbenzene sulfonate (SDBS), and partially hydrolyzed polyacrylamide (HPAM). By changing the concentration of the S/P system, the effect on emulsification behavior was analyzed. Combined with particle distribution diagrams and interfacial tension parameters, the effect of the emulsification behavior on the performance of the S/P binary system was analyzed. On this basis, the effect of different emulsion performances on the recovery factor was evaluated using micro-experiments. The study found that the S/P system that produced stable emulsification had a lower interfacial tension and relatively good effect on improving the recovery factor. Increasing the concentration of the polymer and surfactant may cause changes in the interfacial film of the emulsion, thereby affecting the ability of the S/P system to reduce interfacial tension and may not improve the oil recovery factor. The research results help to better analyze and screen the S/P system used for oil extraction and improve crude oil recovery.

1. Introduction

In primary and secondary oil recovery processes, a mere 20% to 40% of potential crude oil reserves can be extracted [1,2]. Therefore, it is necessary to use tertiary oil recovery methods to improve the oil recovery [3]. Common techniques for enhancing oil recovery include steam injection, steam flooding, polymer flooding, immiscible flooding, and nanoparticles [4,5,6]. Binary combination flooding technology has emerged as a vital means of enhancing oil recovery, thereby increasing crude oil production [7,8]. Incorporating polymers into the binary composite system augments the water’s viscosity, diminishes the water phase’s relative permeability, and bolsters the oil phase’s flow capabilities [9,10]. Additionally, this approach reduces the likelihood of viscous fingering while enhancing the sweep efficiency via the polymer solution’s viscoelastic properties [11]. The integration of surfactants substantially elevates the water phase’s sweeping and displacement efficiency [12,13,14]. As amphiphilic interfacial active substances, surfactants can form molecular films at the oil–water interface boundaries, thereby reducing interfacial tension [15]. The binary composite system generates ultra-low interfacial tension while utilizing the polymer’s viscoelastic properties [16,17]. This system transports residual oil from various types of water flooding in the microscopic model in the form of “oil wires” and “emulsions”, ultimately inducing emulsification [18]. In the binary system, the polymer’s synergistic action results in complex oil–water interface characteristics, with varying conditions leading to diverse effects [19]. Oil-in-water emulsions are advantageous for increasing the viscosity of the water phase to improve the sweep efficiency while simultaneously reducing the fluid’s flow resistance to enhance oil recovery [20,21]. Nevertheless, there are potential drawbacks. Inappropriate emulsification may cause formation plugging in low-permeability formations, leading to pressure surges [22]. Moreover, stable emulsions can exacerbate the demulsification challenges associated with the subsequent produced liquid [23,24]. An increasing number of studies are employing interfacial rheometers to measure the properties of interfacial films during the oil–water emulsification processes. Based on these findings, researchers have analyzed the stability of the oil–water interface and investigated the emulsification mechanisms of polymers and surfactants in combination [25,26,27]. In addition, researchers have investigated changes in parameters such as conductivity and interfacial tension in emulsion fluids during the oil–water emulsification process with the aim to explore the influence of various surfactants and polymers on emulsification [28,29]. In a binary system, the addition of surfactants helps enhance the performance and stability of the emulsification interfacial films formed by polymers, thereby improving the emulsification efficiency of the system [30,31]. A growing body of research has focused on analyzing the emulsification mechanisms and predicting the emulsification outcomes. Gaining insights into these processes and mechanisms is essential to optimize the oil recovery techniques and tackle the challenges associated with emulsification in the oil industry.
Emulsification occurs at the microscopic level, and conventional methods can only observe the phenomenon. With the rapid advancement of computer technology, molecular simulation has emerged as an increasingly important research tool [32]. A growing number of scholars are turning their attention to molecular simulation methods as they enable the calculation of various molecular properties through computer technology [33]. Molecular simulation is an important research method for studying the structure and properties of molecules or a molecular system through computer simulations. This approach includes techniques such as Monte Carlo (MC), molecular dynamics (MD), and dissipative particle dynamics (DPD). An increasing number of scholars are adopting molecular simulation techniques to investigate the emulsification behavior of a binary system consisting of polymers and surfactants at the oil–water interface. Leveraging the analytical tools provided by computer technology, parameter changes throughout the entire reaction process can be accurately and efficiently analyzed. The DPD method was first introduced by Hoogerbrugge and Koelman [34]. This method utilizes Newtonian mechanics, coarse-grained atoms, [35] and forces to reduce computational demands, and has been widely employed in the simulation of mesoscale systems [36]. In traditional molecular dynamics simulations, computational limitations often restrict the spatial scale to around 100 Å and the molecular simulation model to tens of thousands of atoms within the system [37]. In mesoscopic simulations, the conversion of numerous coarse-grained atoms into a single bead significantly improves the simulation scale, while the reasonable integration of the action field in DPD also enables the realization of larger simulation scales [38]. DPD allows for the exploration of properties at a much lower computational cost compared to molecular dynamics. Consequently, DPD is well-suited for simulating the emulsification behavior of polymers and surfactants. DPD has established a complete set of research methods from real parameter transformation, performance simulation, and results analysis, and has been widely used in the research of emulsification and other behaviors: Mayoral and Nahmad-Achar [39] studied the effect of temperature on the oil–water interface by calculating the solubility parameters at different temperatures; Fernando Alvarez [40] constructed a crude oil emulsion based on the crude oil four-component coarse-grained model.
In the present study, DPD was employed to investigate the emulsification behavior of a surfactant/polymer system in contact with oil and water. The evaluation of emulsification in the binary system was conducted by examining the interface morphology of the emulsion, the interfacial film integrity, and alterations in interfacial tension and density distribution. Microscopic experiments were performed to assess enhanced oil recovery in a S/P system, encompassing various emulsification and interfacial tension characteristics. Subsequently, a comprehensive analysis was carried out to establish the correlation between the emulsification behavior and enhanced oil recovery.

2. Materials and Methods

2.1. Materials

The surfactant and polymer were dissolved in formation water with a salinity of 1000 mg/L at 25 °C. Partially hydrolyzed polyacrylamide (HPAM, Mn ≈ 180 × 105 KDa) and sodium dodecyl benzene sulfonate (SBDS) was purchased from a company in Daqing, China. The oil sample was diesel (#0, η25 °C = 5.43 mPa·s; ρ25 °C = 0.825 g·cm−3) and only contained light components corresponding to the short-chain light components in the simulation. The diesel oil was stained with Sudan red to improve its microscopic visual effect.

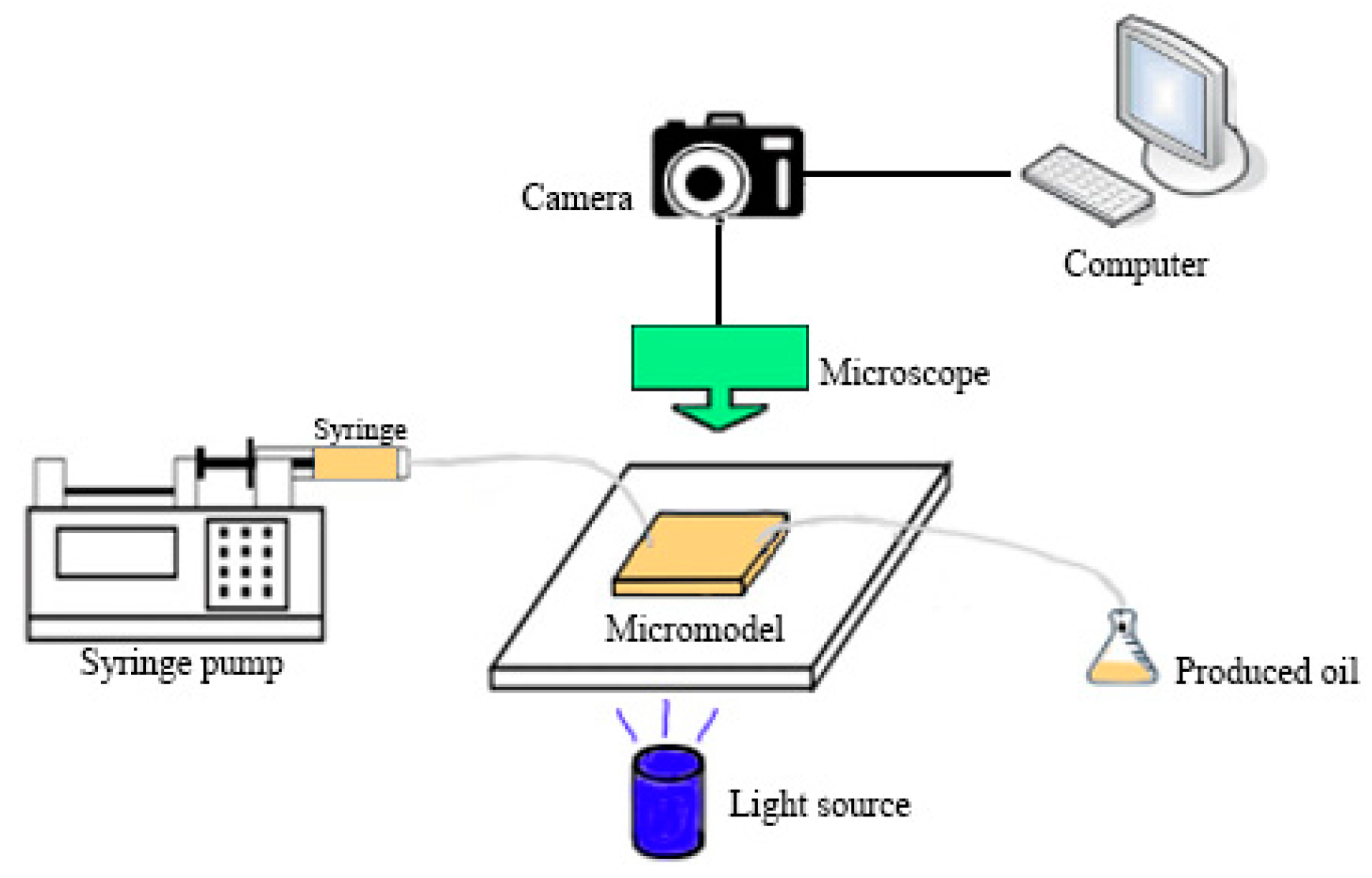
2.2. Microscopic Experiment

As shown in Figure 1, a microscopic displacement experiment was conducted utilizing a triple-layered heterogeneous micromodel. This approach enabled the analysis of the recovery efficiency for various emulsion S/P systems. Within the micromodel, the pore radii of the low-permeability, medium-permeability, and high-permeability layers were 20 μm, 50 μm, and 100 μm, respectively.
The main research object of the micro simulation model is the pore network. According to the different production process, this can be divided into the designated pore network model and rock etching model. This model is not the real pore of the core, but is based on the research needs to make the designated pore network model or according to the pore structure characteristics of the reservoir under a microscope [41,42]. The microscopic visual system was used to conduct the displacement, as shown in Figure 2.
The experimental process was as follows. ① After the airtightness of the model was tested, the water bath was turned on and set to 25 °C to prepare for displacement. ② The micropump was used to inject oil at a speed of 0.001 mL/min into the microscopic model until the model was fully saturated with crude oil. ③ Brine was injected into the micromodel at a speed of 0.001 mL/min until there was no more oil recovery, recording the data. ④ The S/P solution was injected at a speed of 0.001 mL/min until the oil production ceased. ⑤ Image processing [43] was used to calculate the recovery efficiency.

2.3. Molecular Simulation Method

2.3.1. Dissipative Particle Dynamics Parametrization Method

The main parametrization strategies including the Flory–Huggins parameters and matching infinite dilution activity coefficients [44,45] and the Flory–Huggins theory can be used to simulate multicomponent systems such as binary liquid mixtures. Based on statistical mechanics, DPD can simulate complex fluid motions for large spaces and long timescales on a mesoscopic scale. In the DPD simulation, the molecular structure of the complex were coarse-grained into discrete beads, ignoring the details of the molecular structure and degree of freedom. Each bead is a carrier with mass attributes, reflecting the motion change of the fluid.
In a DPD system, coarse-grained beads follow the Newtonian Equation (1) of motion:
d r → i d t = v i , m i d v → i d t = f i →
where r → i , v → i , and f → i represent the vector, velocity, and total force at the position of the i position bead, respectively.
The superposition of the three forces and their subsequent motions is the force equation on the mesoscopic level for the coarse-grained model [37]. There are mutual forces between the coarse-grained beads, as shown in the Equation (2) [34,46]:
  F   → = ∑ i ≠ j   F → i j D + F → i j C + F → i j R
where F → i j D refers to the dissipative force, which describes the friction dissipation between the structural system in the simulated bead. F → i j C is the conservative force that describes the repulsive properties between coarse grained beads. F → i j R is the random force that simulates Brownian random motion at ambient temperatures.
The dispersive and random forces act as a heat sink and source, respectively, consequently, their combined effect is a thermostat. The conservative forces are in the form of [47]:
F → i j C = a i j 1 − r R c ; r ≤ R c   0   ; r > R c
where r is the distance between the bead i and j. Rc is the interaction radius on the dimensions of the simulation system. The parameter aij is the hydrodynamic interaction parameter that contains the physical-chemical information relevant to the atomic group.
We can use the Flory–Huggins model to calculate the aij parameter in DPD.
k − 1 = 1 + 2 α a i i ρ ¯
where k − 1 is the dimensionless isothermal compressibility; a i i is the self-repulsive conservative parameter; α is the correction coefficient; ρ ¯ is the density of system. Groot and Warren [48] established a link between the aij and the Flory–Huggins parameter χ i j .
a i j = 25 + 3.5 χ i j
In this emulsification simulation system, χ i j is the Flory–Huggins parameter, so the obtained χ i j can establish that the force field is under dissipative particle dynamics [49].
χ i j = v b k b T δ i − δ j 2
where δ i and δ j are the solubility parameters of the coarse grained beads i and j, respectively. k b T is the environment value of the system.

2.3.2. Coarse-Grained Model Construction

Each system was modeled using the Materials Visualizer modeling tool, and coarse-grained division was carried out according to different structures [50]. As shown in Table 1, referring to the method of Yosadara Ruiz-Morales [35], three water molecules were coarse-grained into one mesoscopic bead. Four acrylamide monomers of a polyacrylamide long chain were grained into a mesoscopic polymer bead, and the parameter χ was calculated. Thirty polymer beads were connected to form a mesoscopic polymer long chain. The crude oil of heptane (short chain of seven carbons) was coursed into an oil bead, and the light crude oil component involved in emulsification was simulated in the system. Due to the different lipophilic and hydrophobic properties of the structure of SDBS, the hydrophobic chain was divided into oil-wet beads, and the hydrophilic benzene ring and functional group were divided into hydrophilic beads [51]. By calculating the parameter χ of the two types of beads and connecting it, it is possible to show the amphiphilic properties of surfactant molecules.

2.3.3. Calculation of Solubility Parameters

The Flory–Huggins parameter χ for conventional polymer structures can be obtained through the solubility handbook [52]. However, the solubility parameters of the system can be obtained by using molecular dynamics to a high level of numerical accuracy and computational efficiency [53]. All of the simulation processes were completed by Materials Studio, and the selected force field was COMPASS III [54]. An annealing simulation was used to optimize the design, with a temperature range between 300 K and 600 K, and the structure was analyzed every 50 K to eliminate any unreasonable forms. The specific procedures were as follows: (1) 100 ps NVT-MD simulation at 298.15 K; (2) 100 ps NPT-MD simulation at 1 bar and 298.15 K; (3) 100 ps NVT-MD simulation; (4) using cohesive energy density (CED) [55], task calculation was carried out to obtain the coarse-graining structure of the solubility parameters [56].

2.3.4. System Details

The conservative force parameters of the coarse-grained beads for each system were put into a DPD field file, building a force field of the S/P system. This is shown in Table 2.
The dimensions of the simulation box were (35 × 35 × 60) r c 3 . The simulation was carried out at ambient temperature, T = 1.0(298.15 K); The density of the system was ρ = 3. The number of beads in a simulated system was 4.8 × 105. In the system, the water content or concentration is the change of the proportion in the system, so this will only change the number of different beads in the system, but not the total number of beads in the system. Periodic boundaries were used to eliminate the impact of the box boundary on the results [57].

2.3.5. Interfacial Tension Measurement

In our present work, we utilized interfacial tension data to evaluate the emulsification of the S/P system. Interfacial tension was used to evaluate the oil and water emulsification performance [58]. The oil–water interfacial tension in each model was calculated by the Mesocite calculation script [49]. The principle of the calculation can be obtained from Equation (7).
γ D P D = ∫ 〈 P ¯ X X 〉 − 0.5 〈 P ¯ Y Y 〉 − 〈 P ¯ Z Z 〉 d x ¯
where γ D P D is the interfacial tension in the DPD model; P ¯ X X is the pressure perpendicular to the interface direction; P ¯ Z Z and P ¯ Y Y are parallel to the interface direction; x is the length of the box along the perpendicular of the interface.

3. Results and Discussion

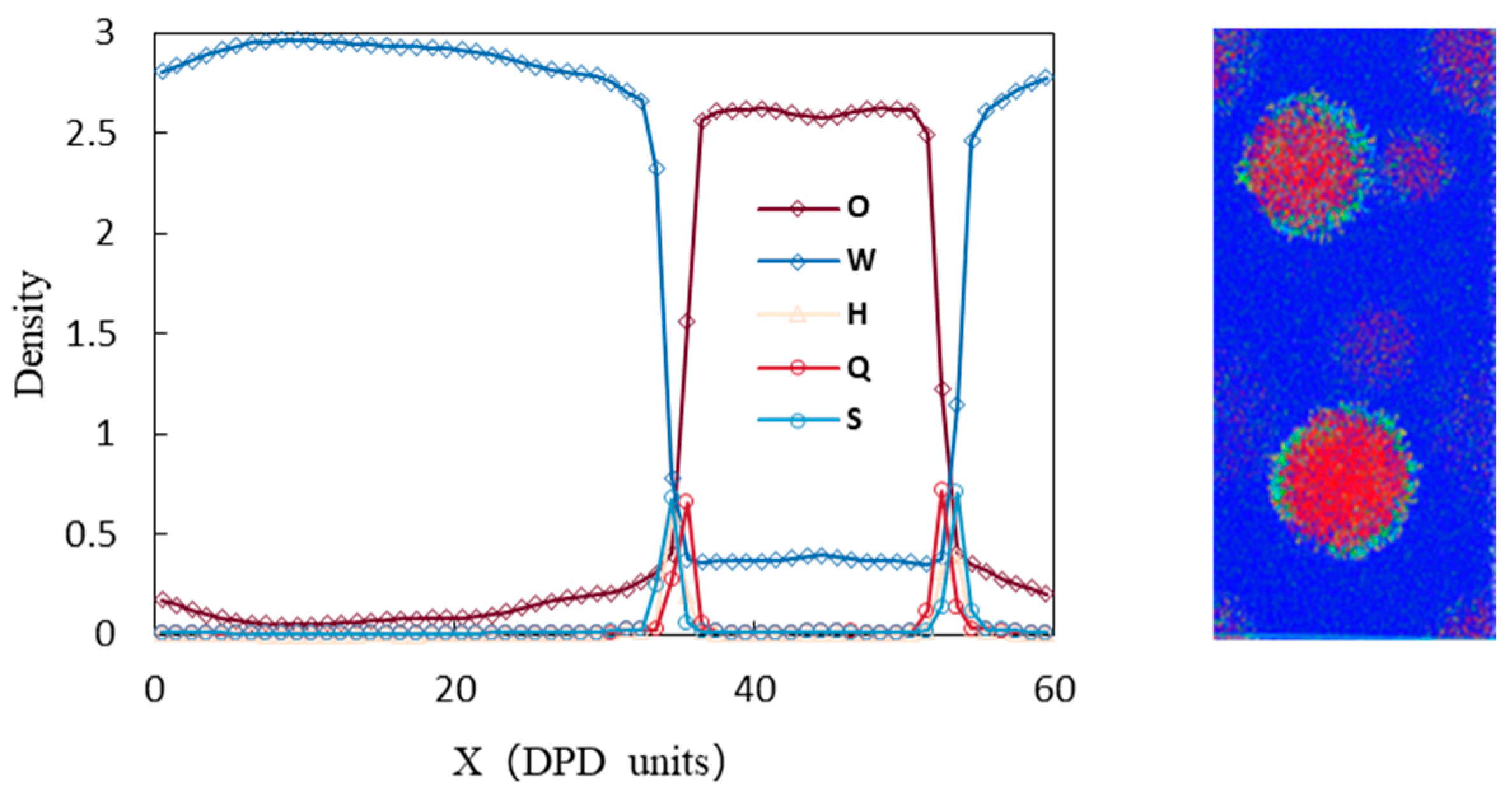
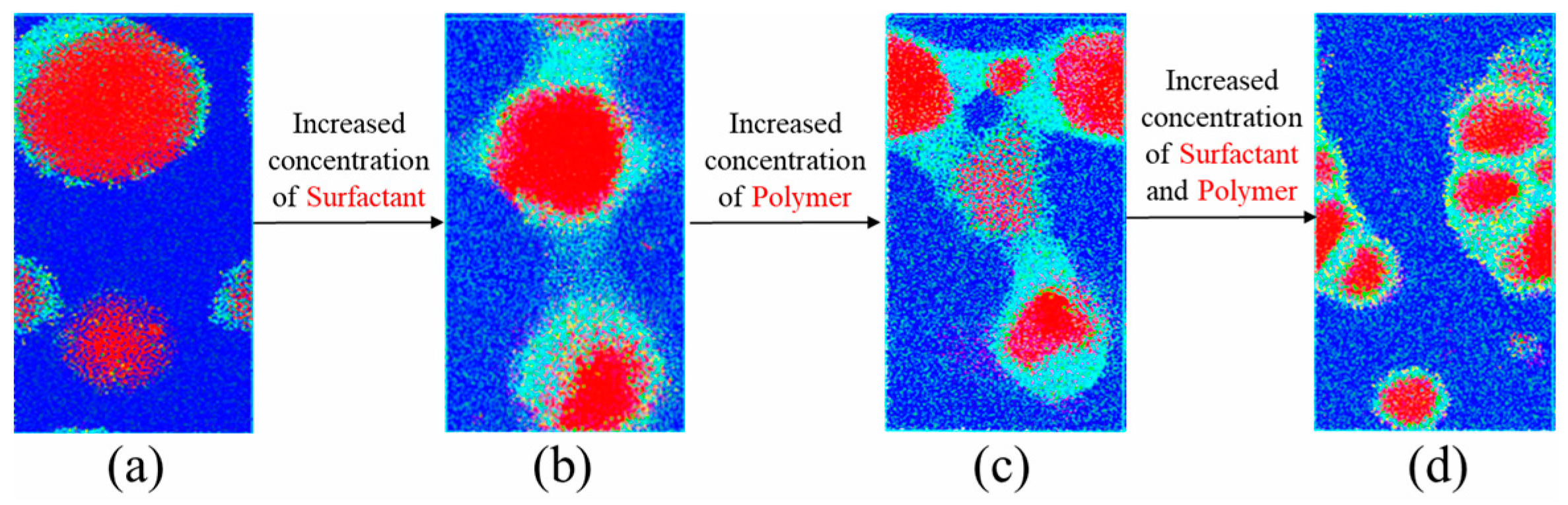
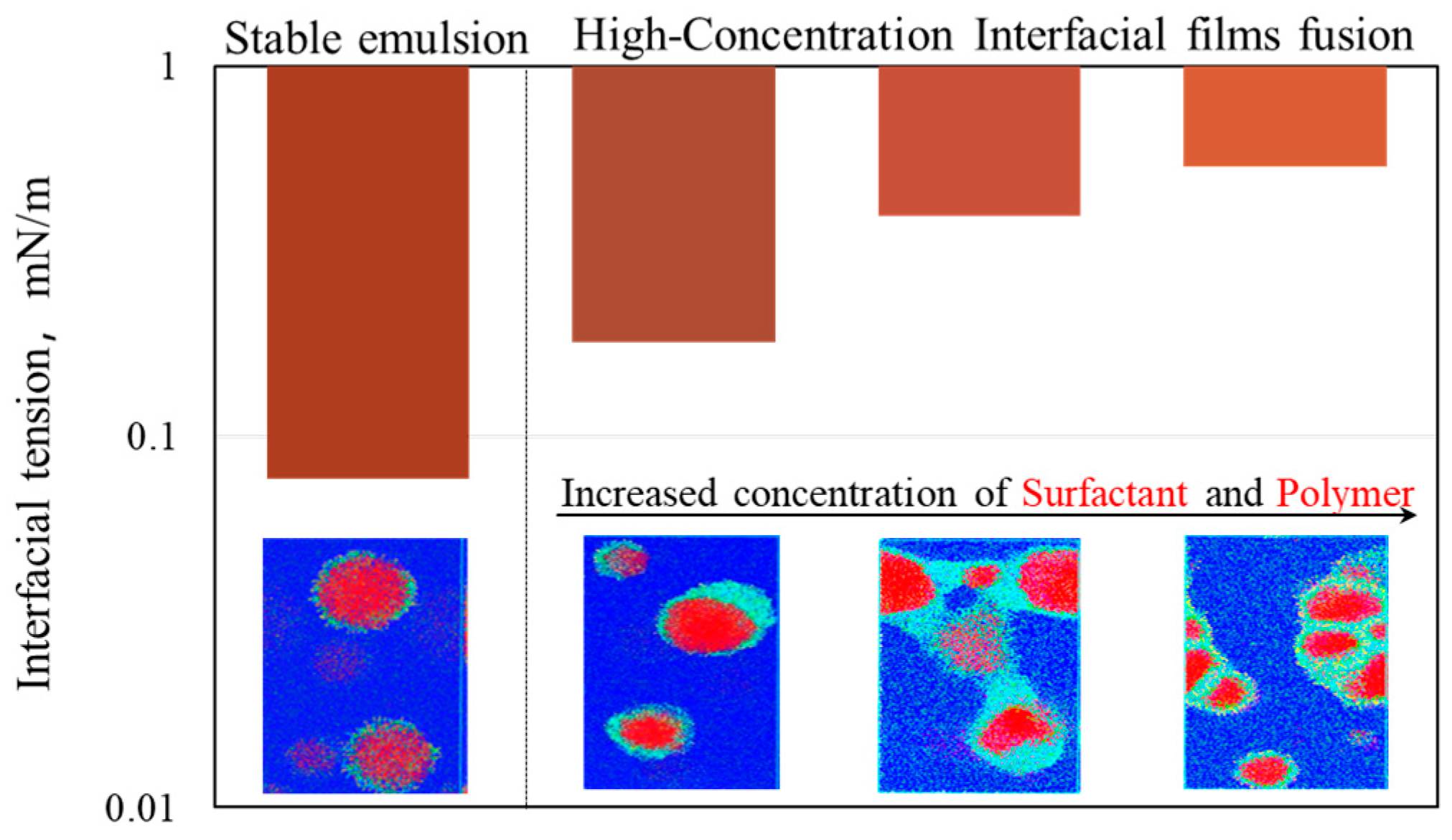
3.1. Analysis of Emulsification Behavior

When water is dispersed as phases, the system generates an oil-in-water emulsion. Figure 3 shows the different morphologies of the oil–water emulsions formed by the polymer and the surfactant. Water and oil are continuous and dispersed phases are surrounded by an interfacial film of polymers and surfactants. Surfactants are attached to the polymer to stabilize the emulsion and prevent oil–water separation. As can be seen from the particle interface distribution plots, polymer beads were clustered at the oil–water boundary, while lipophilic and hydrophilic beads of the surfactant were clustered in the direction of the oil and water phases, respectively, and uniformly distributed over the interface film.
Changes in the surfactant and polymer concentrations result in changes in the emulsion interfacial film morphology. As shown in Figure 4, the different proportions of the polymer and surfactant resulted in different morphology, integrity degree, and thickness of the interfacial film. Combined with interfacial film integrity, the emulsion can be divided into the following three types, as shown in Figure 4:
Figure 4 illustrates the different types of interfacial film emulsions formed by different degrees of interfacial film integrity. The binary system at 0.05% polymer and 0.05% surfactant produced an interfacial film that was completely intact, encapsulating the oil droplets in water. This type of interfacial film had the highest stability. As shown in the particle distribution diagram, the polymer and surfactant were uniformly distributed on both sides of the oil–water interface, forming a uniform emulsion interfacial film. In Figure 4b, with an increase in polymer concentration, the interfacial film was partially broken and exposed some of the oil–water contact areas. This type of interfacial film had lower stability and caused deformation of the oil droplets. The particle density diagram shows that the polymer and surfactant had an uneven distribution on one side of the oil–water interface due to the fracture. In Figure 4c, the interfacial film was mostly damaged and formed an unstable interfacial film emulsion. This type of interfacial film occurs when the polymer concentration is high (c ≥ 0.05%) and the surfactant concentration is low (c ≤ 0.03%). The excess polymer cannot form a uniform layer around the water and migrates to the oil region, increasing the oil–water relative motion and reducing the emulsion stability. The particle density diagram shows that there was a cluster of polymer and surfactant particles on one side of the oil–water interface, but none on the other side.
Figure 5 shows the change in the emulsion morphology, where the water content of the system was the same, and the proportion of the polymer and surfactant concentration resulted in the change in the emulsion morphology: the system generates a stable oil in water emulsion at low polymer and surfactant concentrations. The increase in the polymer concentration led to the increase in the thickness of the interfacial film, which diffused outward in some areas, extended into the water phase, and made contact with other emulsified areas. The interaction of the polymer and surfactant concentration led to the interfacial film fusion. With the increase in surfactant concentration, the oil phase further dispersed under the influence of high-concentration surfactants, resulting in a greater number of smaller emulsification cores. The reduced interfacial film size led to the diffusion of a larger number of polymer long chains. Under the influence of surfactants, interfacial films formed, which subsequently underwent mutual fusion. Upon further increasing the concentrations of both the polymer and the surfactant, the interfacial film fusion phenomenon intensified. Furthermore, multiple water-in-oil emulsions with their interfacial films could merge, leading to the formation of water-in-oil emulsions with multiple cores.

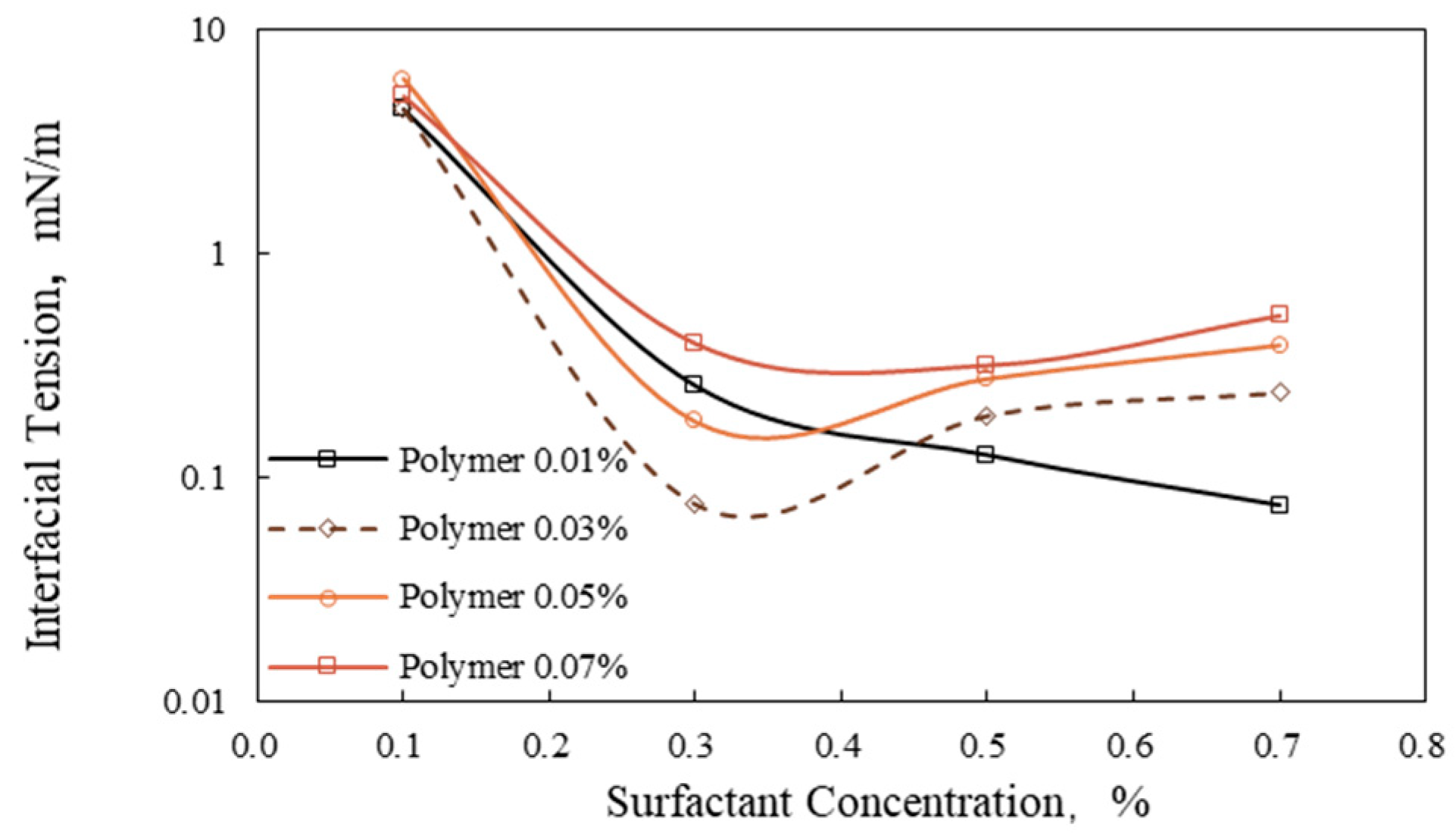
3.2. Interfacial Tension of Surfactant/Polymer Flooding

The influence of the surfactant concentration on the interfacial tension in the emulsion system is contingent upon both the polymer concentration present within the system. As depicted in Figure 6, at low surfactant concentrations ranging from 0.01% to 0.03%, the interfacial tension exhibited a decrease, which is in line with the expectations. Conversely, when the surfactant concentration surpassed 0.03%, the interfacial tension experienced an increase. This particular phenomenon was more pronounced under conditions of high polymer concentration. When the surfactant concentration exceeded the critical micelle concentration (CMC), the surfactant molecules started to aggregate on the polymer chain, leading to a reduction in the polymer’s interfacial activity. This aggregation resulted in the formation of thicker interfacial films, which weakened the surfactant’s ability to reduce the interfacial tension.
As shown in Figure 7, the morphology of the emulsions has a direct relationship with changes in the interfacial tension in a binary system. Stable emulsions have a lower interfacial tension, while unstable emulsions with higher polymer concentrations and the same surfactant concentration can only reduce the interfacial tension between oil and water to a level of 10−1 mN/m. As the concentrations of the surfactant and polymer increase, the interfaces’ film of emulsions begin to fuse, leading to a further increase in the interfacial tension between oil and water. However, high concentrations of polymer and surfactant damage the ability of the binary system to reduce interfacial tension, which is higher than that of unstable emulsions but lower than that of stable emulsions.

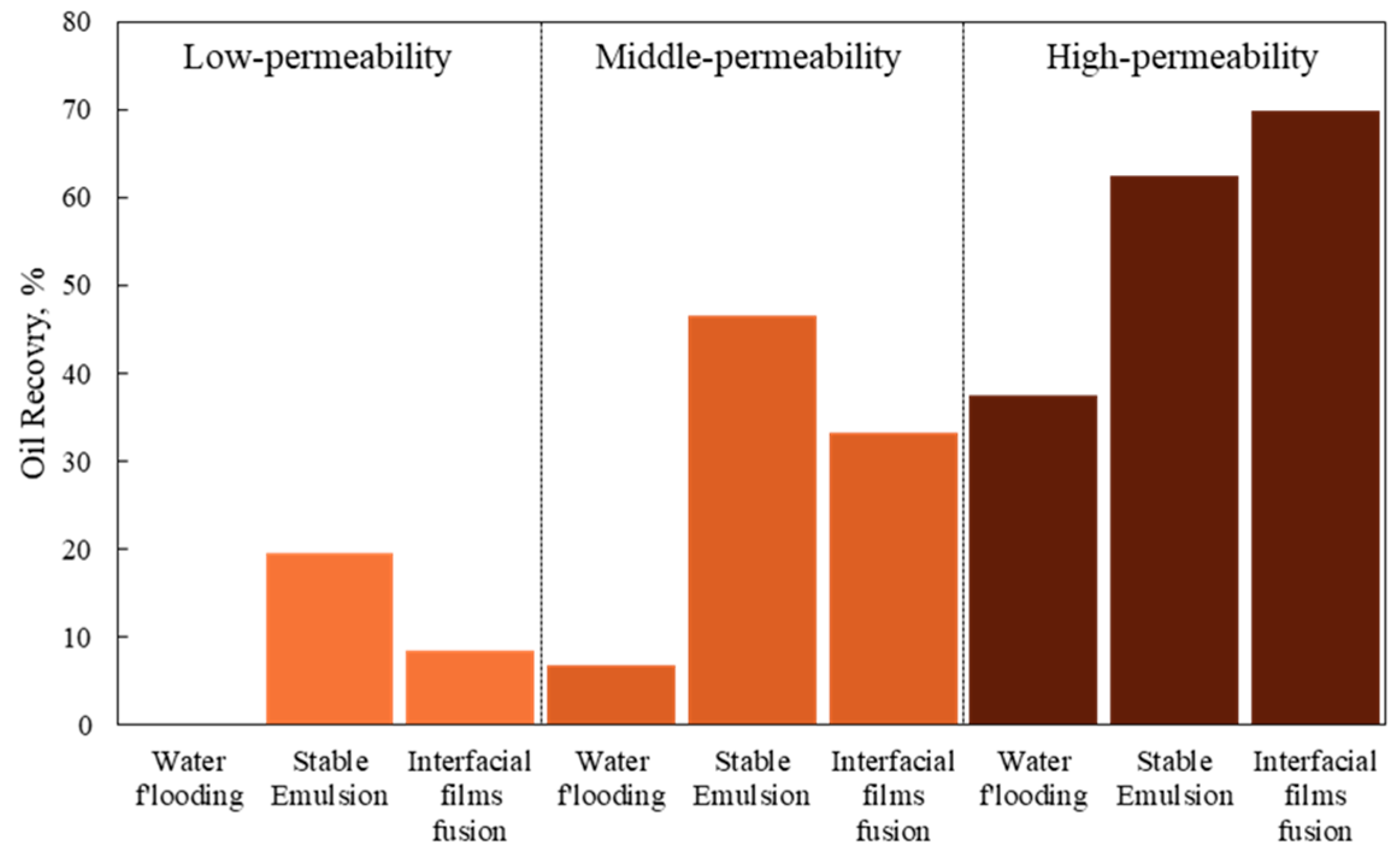
3.3. Emulsification and Oil Recovery in Microscale Experiments

Therefore, we conducted microscopic displacement experiments on the group with the stable emulsified and interfacial tension in the simulation, the group with higher concentration (generate interface film fusion), and a group of water flooding as a control group. The experimental results are shown in Figure 8 below.
As illustrated in Figure 8, during the water flooding process, the water drive replacement was utilized until no further crude oil was recovered from the model. It is evident that water penetrated the microscopic pore space, primarily flowing in the high permeability layer and establishing the main flow channel in this layer. Due to water’s low viscosity, it can only marginally infiltrate the medium permeability at the injection end because of the elevated injection pressure. However, it is fundamentally incapable of displacing crude oil in the medium and low permeability layers, resulting in an insignificant increase in the water flooding recovery factor.
Upon completing the water flooding process, further displacement experiments were conducted on microscopic pores using stable emulsion and high-concentration systems, respectively, until no oil was recovered. In contrast to water flooding, both surfactant/polymer systems established main flow channels in high permeability layers. The increased viscosity of the surfactant/polymer system expanded these dominant flow channels, enhancing the swept volume.
The low interfacial tension induced by stable emulsions efficiently displaces the irreducible oil trapped within the pores. As illustrated in Figure 9, in both the low and medium permeability pores, the stable emulsion surfactant/polymer (S/P) system left significantly less residual oil after displacement compared to the high-concentration S/P system. This finding highlights the importance of optimizing the surfactant/polymer system for different permeability regions to maximize the oil recovery factor and minimize the residual oil.
Figure 10 displays the recovery factor of the water flooding, stable emulsion system, and high-concentration system in models with varying permeabilities.
Figure 10 reveals that high concentrations of polymers and surfactants achieved the highest recovery factor in high permeability regions. The image demonstrates that the high-concentration surfactant/polymer system provided a substantially larger swept volume compared to the water flooding and stable emulsion systems. Nevertheless, a considerable amount of residual oil remained within the pores, suggesting that the interfacial tension reduction capability of the high concentration system was weakened, resulting in a lower displacement efficiency than the stable emulsion S/P system. Therefore, the advantages of increasing the polymer and surfactant concentrations in high permeability are limited.
In contrast, in low and medium permeability regions, the stable emulsion S/P system exhibited a higher recovery factor than the high-concentration S/P system. The low interfacial tension of the stable emulsion S/P system led to a more effective displacement efficiency, enabling the establishment of stable dominant flow channels, even in medium permeability regions.

4. Conclusions

For the binary system composed of HPAM and SDBS, at chemical concentrations below 0.7%, it is unwise to reduce the interfacial tension and increase the recovery factor by increasing the concentration of the S/P system. The increase in polymer and surfactant concentration will result in the change in the emulsion morphology. The increase in the concentration of the interface film fusion will lead to the decrease in interfacial activity, an increase in interfacial tension, and a decrease in the recovery efficiency of the low and medium permeability. Therefore, excessive increases to the polymer concentration does not enhance oil recovery. The change in the ratio of the polymer to surfactant will lead to the change in the interfacial membrane integrity. The decrease in the integrity of the interfacial film will lead to the increase in the interfacial tension, thereby reducing the recovery efficiency of the binary system. The above analysis provides a theoretical basis for the design of a polymer and surfactant system.

Author Contributions

Conceptualization, B.Z.; Investigation, B.Z.; Review and editing, B.G. and W.L.; Supervision, B.P. and S.C.; Funding acquisition, W.L. and B.P. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (22008263), and the PetroChina Scientific Research and Technology Development Project (2021DJ1602).

Data Availability Statement

The data presented in this study are available on request from the corresponding author.

Acknowledgments

The authors would like to thank Research Institute of Petroleum Exploration and Development.

Conflicts of Interest

The authors declare that they have no known competing financial interest or personal relationship that could have appeared to influence the work reported in this paper.

References

  1. Abidin, A.; Puspasari, T.; Nugroho, W. Polymers for Enhanced Oil Recovery Technology. Procedia Chem. 2012, 4, 11–16. [Google Scholar] [CrossRef]
  2. Nazar, M.F.; Shah, S.S.; Khosa, M.A. Microemulsions in enhanced oil recovery: A review. Pet. Sci. Technol. 2011, 29, 1353–1365. [Google Scholar] [CrossRef]
  3. Pogaku, R.; Fuat, N.H.M.; Sakar, S.; Cha, Z.W.; Musa, N.; Tajudin, D.N.A.A. Polymer flooding and its combinations with other chemical injection methods in enhanced oil recovery. Polym. Bull. 2018, 75, 1753–1774. [Google Scholar] [CrossRef]
  4. Khormali, A.; Koochi, M.R.; Varfolomeev, M.A.; Ahmadi, S. Experimental study of the low salinity water injection process in the presence of scale inhibitor and various nanoparticles. J. Pet. Explor. Prod. Technol. 2022, 13, 903–916. [Google Scholar] [CrossRef]
  5. Pratama, R.A.; Babadagli, T. A review of the mechanics of heavy-oil recovery by steam injection with chemical additives. J. Pet. Sci. Eng. 2021, 208, 109717. [Google Scholar] [CrossRef]
  6. Tao, L.; Chen, Y.; Wang, Y.; Zhang, N.; Li, S.; Yang, Y.; Hu, Z. Optimization of hydrophilic SiO2/SDS dispersions in decentralized system: Experiments and RSM/CCD. J. Nanoparticle Res. 2022, 24, 138. [Google Scholar] [CrossRef]
  7. Tackie-Otoo, B.N.; Mohammed, M.A.A.; Yekeen, N.; Negash, B.M. Alternative chemical agents for alkalis, surfactants and polymers for enhanced oil recovery: Research trend and prospects. J. Pet. Sci. Eng. 2019, 187, 106828. [Google Scholar] [CrossRef]
  8. Sheng, J.J. A Comprehensive Review of Alkaline-Surfactant-Polymer (ASP) Flooding. Asia-Pac. J. Chem. Eng. 2014, 9, 471–489. [Google Scholar] [CrossRef]
  9. Yang, H.; Kang, W.; Yin, X.; Tang, X. A Low Elastic-microsphere/surfactant/polymer Combined Displacing Method after Polymer Flooding. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 24–27 April 2017. [Google Scholar] [CrossRef]
  10. Louis, H.; Bauyrzhan, S.; Aziz, O.; Henri, B. Transport of polymer stabilized foams in porous media: Associative polymer versus pam. J. Pet. Ence Eng. 2018, 169, 602–609. [Google Scholar]
  11. Karnanda, W.; Benzagouta, M.S.; AlQuraishi, A.; Amro, M.M. Effect of temperature, pressure, salinity, and surfactant concentration on IFT for surfactant flooding optimization. Arab. J. Geosci. 2012, 6, 3535–3544. [Google Scholar] [CrossRef]
  12. Kurnia, I.; Zhang, G.; Han, X.; Yu, J. Zwitterionic-anionic surfactant mixture for chemical enhanced oil recovery without alkali. Fuel 2020, 259, 116236. [Google Scholar] [CrossRef]
  13. Clarke, A.; Howe, A.M.; Mitchell, J.; Staniland, J.; Hawkes, L.A. How Viscoelastic-Polymer Flooding Enhances Displacement Efficiency. SPE J. 2016, 21, 0675–0687. [Google Scholar] [CrossRef]
  14. Xia, H.; Pan, J.; Niu, L.; Xu, T. Mechanism research on starting residual oil migration in ASP flooding with different Alkali concentration. IOP Conf. Series: Earth Environ. Sci. 2018, 121, 022043. [Google Scholar] [CrossRef]
  15. AfzaliTabar, M.; Rashidi, A.; Alaei, M.; Koolivand, H.; Pourhashem, S.; Askari, S. Hybrid of quantum dots for interfacial tension reduction and reservoir alteration wettability for enhanced oil recovery (EOR). J. Mol. Liq. 2020, 307, 112984. [Google Scholar] [CrossRef]
  16. Lotfollahi, M.; Koh, H.; Li, Z.; Delshad, M.; Pope, G.A. Mechanistic Simulation of Residual Oil Saturation in Viscoelastic Polymer Floods. In Proceedings of the SPE EOR Conference at Oil and Gas West Asia, Muscat, Oman, 21–23 March 2016. [Google Scholar] [CrossRef]
  17. Erincik, M.Z.; Qi, P.; Balhoff, M.T.; Pope, G.A. New Method To Reduce Residual Oil Saturation by Polymer Flooding. SPE J. 2018, 23, 1944–1956. [Google Scholar] [CrossRef]
  18. Yuan, C.D.; Pu, W.F.; Wang, X.C.; Sun, L.; Zhang, Y.C.; Cheng, S. Effects of interfacial tension, emulsification, and sur-factant concentration on oil recovery in surfactant flooding process for high temperature and high salinity reservoirs. Energy Fuels 2015, 29, 6165–6176. [Google Scholar] [CrossRef]
  19. Dicharry, C.; Arla, D.; Sinquin, A.; Graciaa, A.; Bouriat, P. Stability of water/crude oil emulsions based on interfacial dila-tational rheology. J. Colloid Interface Sci. 2006, 297, 785–791. [Google Scholar] [CrossRef]
  20. Torrealba, V.A.; Hoteit, H. Conformance improvement in oil reservoirs by use of microemulsions. In Proceedings of the SPE Kingdom of Saudi Arabia Annual Technical Symposium and Exhibition, Dammam, Saudi Arabia, 23–26 April 2018. [Google Scholar]
  21. Yu, L.; Dong, M.; Ding, B.; Yuan, Y. Emulsification of heavy crude oil in brine and its plugging performance in porous media. Chem. Eng. Sci. 2018, 178, 335–347. [Google Scholar] [CrossRef]
  22. Alwi, N.B.; Salleh, I.K.B.; Ibrahim, J.M.; Carpenter, I.; Dyer, S.J.; Simpson, C.; Frigo, D.M.; Graham, G.M. Development of Improved Chemical Formulations for Scale Control for Alkaline Surfactant Polymer Flood in a Seawater Flooded Reservoir. In Proceedings of the Spe International Oilfield Scale Conference & Exhibition, Aberdeen, UK, 11–12 May 2016. [Google Scholar] [CrossRef]
  23. Yi, M.; Huang, J.; Wang, L. Research on crude oil demulsification using the combined method of ultrasound and chemical demulsifier. J. Chem. 2017, 2017, 9147926. [Google Scholar] [CrossRef]
  24. Phukan, M.; Koczo, K.; Falk, B.; Palumbo, A. New Silicon Copolymers for Efficient Demulsification. In Proceedings of the SPE Oil and Gas India Conference and Exhibition, Mumbai, India, 20–22 January 2010. [Google Scholar] [CrossRef]
  25. Tadros, T.; Vandamme, A.; Booten, K.; Levecke, B.; Stevens, C. Stabilisation of emulsions using hydrophobically modified inulin (polyfructose). Colloids Surfaces A: Physicochem. Eng. Asp. 2004, 250, 133–140. [Google Scholar] [CrossRef]
  26. Jiang, J.; Kang, X.; Wu, H.; Lu, Y.; Li, Z.; Xu, D.; Ma, T.; Yang, H.; Kang, W. Spontaneous emulsification induced by a novel surfactant-polymer compound system and its application to enhance oil recovery. J. Mol. Liq. 2021, 337, 116399. [Google Scholar] [CrossRef]
  27. Shi, W.; Xu, L.; Tao, L.; Zhu, Q.; Bai, J. Flow behaviors and residual oil characteristics of water flooding assisted by multi-effect viscosity reducer in extra heavy oil reservoir. Pet. Sci. Technol. 2022, 41, 1231–1249. [Google Scholar] [CrossRef]
  28. Nedjhioui, M.; Moulai-Mostefa, N.; Morsli, A.; Bensmaili, A. Combined effects of polymer/surfactant/oil/alkali on physical chemical properties. Desalination 2005, 185, 543–550. [Google Scholar] [CrossRef]
  29. Iyi, D.; Balogun, Y.; Oyeneyin, B.; Faisal, N. Numerical modelling of the effect of wettability, interfacial tension and tem-perature on oil recovery at pore-scale level. J. Pet. Sci. Eng. 2021, 201, 108453. [Google Scholar] [CrossRef]
  30. Førdedal, H.; Nodland, E.; Sjöblom, J.; Kvalheim, O.M. A Multivariate Analysis of W/O Emulsions in High External Electric Fields as Studied by Means of Dielectric Time Domain Spectroscopy. J. Colloid Interface Sci. 1995, 173, 396–405. [Google Scholar] [CrossRef]
  31. Pei, H.; Zhang, G.; Ge, J.; Jiang, P.; Zhang, J.; Zhong, Y. Study of polymer-enhanced emulsion flooding to improve viscous oil recovery in waterflooded heavy oil reservoirs. Colloids Surfaces A Physicochem. Eng. Asp. 2017, 529, 409–416. [Google Scholar] [CrossRef]
  32. Zimmerman, M.I.; Porter, J.R.; Ward, M.D.; Singh, S.; Bowman, G.R. SARS-CoV-2 simulations go exascale to predict dramatic spike opening and cryptic pockets across the proteome. Nat. Chem. 2021, 13, 651–659. [Google Scholar] [CrossRef] [PubMed]
  33. Fu, L.; Gu, F.; Liao, K.; Wen, X.; Huang, W.; Li, X.; Ren, Z.; Xie, L. Application of molecular simulation in tertiary oil recovery: A systematic review. J. Pet. Sci. Eng. 2022, 212, 110196. [Google Scholar] [CrossRef]
  34. Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating Microscopic Hydrodynamic Phenomena with Dissipative Particle Dynamics. EPL Europhys. Lett. 1992, 19, 155–160. [Google Scholar] [CrossRef]
  35. Ruiz-Morales, Y.; Mullins, O.C. Coarse-Grained Molecular Simulations to Investigate Asphaltenes at the Oil–Water Interface. Energy Fuels 2015, 29, 1597–1609. [Google Scholar] [CrossRef]
  36. Lin, S.L.; Xu, M.Y.; Yang, Z.R. Dissipative particle dynamics study on the mesostructures of n-octadecane/water emulsion with alternating styrene–maleic acid copolymers as emulsifier. Soft Matter 2011, 8, 375–384. [Google Scholar] [CrossRef]
  37. Noid, W.G. Perspective: Coarse-grained models for biomolecular systems. J. Chem. Phys. 2013, 139, 090901. [Google Scholar] [CrossRef]
  38. Bian, X.; Litvinov, S.; Qian, R.; Ellero, M.; Adams, N.A. Multiscale modeling of particle in suspension with smoothed dis-sipative particle dynamics. Phys. Fluids 2012, 24, 147. [Google Scholar] [CrossRef]
  39. Mayoral, E.; Goicochea, A.G. Modeling the temperature dependent interfacial tension between organic solvents and water using dissipative particle dynamics. J. Chem. Phys. 2013, 138, 094703. [Google Scholar] [CrossRef]
  40. Alvarez, F.; Flores, E.A.; Castro, L.V.; Hernández, J.G.; López, A.; Vázquez, F. Dissipative Particle Dynamics (DPD) Study of Crude Oil−Water Emulsions in the Presence of a Functionalized Co-polymer. Energy Fuels 2010, 25, 562–567. [Google Scholar] [CrossRef]
  41. Al-Shalabi, E.W.; Ghosh, B. Effect of Pore-Scale Heterogeneity and Capillary-Viscous Fingering on Commingled Waterflood Oil Recovery in Stratified Porous Media. J. Pet. Eng. 2016, 2016, 1–14. [Google Scholar] [CrossRef]
  42. Jamaloei, B.Y.; Asghari, K.; Kharrat, R.; Ahmadloo, F. Pore-scale two-phase filtration in imbibition process through porous media at high- and low-interfacial tension flow conditions. J. Pet. Sci. Eng. 2010, 72, 251–269. [Google Scholar] [CrossRef]
  43. Meybodi, H.E.; Kharrat, R.; Araghi, M.N. Experimental studying of pore morphology and wettability effects on micro-scopic and macroscopic displacement efficiency of polymer flooding. J. Pet. Sci. Eng. 2011, 78, 347–363. [Google Scholar] [CrossRef]
  44. Mingtsung, L.; Runfang, M.; Aleksey, V.; Neimark, A.V. Parametrization of chain molecules in dissipative particle dynamics. J. Phys. Chem. B 2016, 120, 4980. [Google Scholar]
  45. Steinmetz, D.; González, K.R.A.; Lugo, R.; Verstraete, J.; Lachet, V.; Mouret, A.; Creton, B.; Nieto-Draghi, C. Experimental and Mesoscopic Modeling Study of Water/Crude Oil Interfacial Tension. Energy Fuels 2021, 35, 11858–11868. [Google Scholar] [CrossRef]
  46. Koelman, J.M.V.A.; Hoogerbrugge, P.J. Dynamic Simulations of Hard-Sphere Suspensions Under Steady Shear. EPL Europhys. Lett. 1993, 21, 363–368. [Google Scholar] [CrossRef]
  47. Groot, R.D.; Madden, T.J. Dynamic simulation of diblock copolymer microphase separation. J. Chem. Phys. 1998, 108, 8713–8724. [Google Scholar] [CrossRef]
  48. Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
  49. Shi, K.; Lian, C.; Bai, Z.; Zhao, S.; Liu, H. Dissipative particle dynamics study of the water/benzene/caprolactam system in the absence or presence of non-ionic surfactants. Chem. Eng. Sci. 2015, 122, 185–196. [Google Scholar] [CrossRef]
  50. Quann, R.; Jaffe, S. Building useful models of complex reaction systems in petroleum refining. Chem. Eng. Sci. 1996, 51, 1615–1635. [Google Scholar] [CrossRef]
  51. Meng, S.; Zhang, J.; Wu, C.; Zhang, Y.; Xiao, Q.; Lu, G. Dissipative particle dynamics simulations of surfactant CTAB in ethanol/water Mixture. Mol. Simul. 2013, 40, 1052–1058. [Google Scholar] [CrossRef]
  52. Jamali, S.; Boromand, A.; Khani, S.; Wagner, J.; Yamanoi, M.; Maia, J. Generalized mapping of multi-body dissipative particle dynamics onto fluid compressibility and the Flory-Huggins theory. J. Chem. Phys. 2015, 142, 164902. [Google Scholar] [CrossRef]
  53. Keaveny, E.E.; Pivkin, I.G.; Maxey, M.; Karniadakis, G.E. A comparative study between dissipative particle dy-namics and molecular dynamics for simple- and complex-geometry flows. J. Chem. Phys. 2005, 123, 104107. [Google Scholar] [CrossRef]
  54. Santo, K.P.; Neimark, A.V. Dissipative particle dynamics simulations in colloid and Interface science: A review. Adv. Colloid Interface Sci. 2021, 298, 102545. [Google Scholar] [CrossRef]
  55. Maiti, A.; Mcgrother, S. Bead–bead interaction parameters in dissipative particle dynamics: Relation to bead-size, solubility parameter, and surface tension. J. Chem. Phys. 2004, 120, 1594–1601. [Google Scholar] [CrossRef]
  56. Rezaei, H.; Modarress, H. Dissipative particle dynamics (DPD) study of hydrocarbon–water interfacial tension (IFT). Chem. Phys. Lett. 2015, 620, 114–122. [Google Scholar] [CrossRef]
  57. Zhang, D.; Shangguan, Q.; Wang, Y. An easy-to-use boundary condition in dissipative particle dynamics system. Comput. Fluids 2018, 166, 117–122. [Google Scholar] [CrossRef]
  58. Paredes, R.; Fariñas-Sánchez, A.I.; Medina-Rodríguez, B.; Samaniego, S.; Aray, Y.; Álvarez, L.J. Dynamics of Surfactant Clustering at Interfaces and Its Influence on the Interfacial Tension: Atomistic Simulation of a Sodium Hexadecane–Benzene Sulfonate–Tetradecane–Water System. Langmuir 2018, 34, 3146–3157. [Google Scholar] [CrossRef] [PubMed]
Processes 11 01411 g001 550
Figure 1. Triple-layer microscopic displacement model.
Figure 1. Triple-layer microscopic displacement model.
Processes 11 01411 g001
Processes 11 01411 g002 550
Figure 2. The microscopic visual system.
Figure 2. The microscopic visual system.
Processes 11 01411 g002
Processes 11 01411 g003 550
Figure 3. Oil–water emulsification and interface film details, In the picture, red beads are the oil, dark blue beads are the water, light blue beads are the polymer (HPAM), and yellow and green beads are the lipophilic and hydrophilic end of the surfactant (SDBS).
Figure 3. Oil–water emulsification and interface film details, In the picture, red beads are the oil, dark blue beads are the water, light blue beads are the polymer (HPAM), and yellow and green beads are the lipophilic and hydrophilic end of the surfactant (SDBS).
Processes 11 01411 g003
Processes 11 01411 g004 550
Figure 4. Particle distribution diagram of the emulsion interface and interfacial films with different integrity. In order, three system with a 30% water content, the emulsification in picture (a) was generated by the binary system under the conditions of polymer 0.05%, surfactant 0.05%; in (b), emulsification was generated by a binary system at polymer 0.05%, surfactant 0.07%; in (c), emulsification was generated by a binary system under polymer 0.05%, surfactant 0.1%. In the picture, red is the O bead, dark blue is the W bead, light blue is the H bead, yellow is the Q bead and green is the S bead.
Figure 4. Particle distribution diagram of the emulsion interface and interfacial films with different integrity. In order, three system with a 30% water content, the emulsification in picture (a) was generated by the binary system under the conditions of polymer 0.05%, surfactant 0.05%; in (b), emulsification was generated by a binary system at polymer 0.05%, surfactant 0.07%; in (c), emulsification was generated by a binary system under polymer 0.05%, surfactant 0.1%. In the picture, red is the O bead, dark blue is the W bead, light blue is the H bead, yellow is the Q bead and green is the S bead.
Processes 11 01411 g004
Processes 11 01411 g005 550
Figure 5. Microemulsions formed in the S/P system under a 70% water content condition: (a) polymer concentration at 0.03% and surfactant concentration at 0.03%; (b) polymer concentration at 0.03% and surfactant concentration at 0.05%; (c) polymer concentration at 0.05% and surfactant concentration at 0.05%; (d) polymer concentration at 0.07% and surfactant concentration at 0.7%. In the picture, red is the O bead, dark blue is the W bead, light blue is the H bead, yellow is the Q bead and green is the S bead.
Figure 5. Microemulsions formed in the S/P system under a 70% water content condition: (a) polymer concentration at 0.03% and surfactant concentration at 0.03%; (b) polymer concentration at 0.03% and surfactant concentration at 0.05%; (c) polymer concentration at 0.05% and surfactant concentration at 0.05%; (d) polymer concentration at 0.07% and surfactant concentration at 0.7%. In the picture, red is the O bead, dark blue is the W bead, light blue is the H bead, yellow is the Q bead and green is the S bead.
Processes 11 01411 g005
Processes 11 01411 g006 550
Figure 6. Interfacial tension of different polymer concentration systems with the surfactant concentration.
Figure 6. Interfacial tension of different polymer concentration systems with the surfactant concentration.
Processes 11 01411 g006
Processes 11 01411 g007 550
Figure 7. Changes in the interfacial tension in different emulsions. In order, the emulsification in picture (A) was under the conditions of polymer 0.03%, surfactant 0.03%; in (B), emulsification was generated under polymer 0.05%, surfactant 0.03%; in (C), emulsification was generated under polymer 0.05%, surfactant 0.07%; in (D), under polymer 0.07%, surfactant 0.07%. In the picture, red is the O bead, dark blue is the W bead, light blue is the H bead, yellow is the Q bead and green is the S bead.
Figure 7. Changes in the interfacial tension in different emulsions. In order, the emulsification in picture (A) was under the conditions of polymer 0.03%, surfactant 0.03%; in (B), emulsification was generated under polymer 0.05%, surfactant 0.03%; in (C), emulsification was generated under polymer 0.05%, surfactant 0.07%; in (D), under polymer 0.07%, surfactant 0.07%. In the picture, red is the O bead, dark blue is the W bead, light blue is the H bead, yellow is the Q bead and green is the S bead.
Processes 11 01411 g007
Processes 11 01411 g008 550
Figure 8. Images from the microscopy experiment. (a) Water flooding until no oil recovery. (b) Stable emulsified S/P system with 0.03% polymer and 0.03% surfactant concentrations. (c) Interfacial film-fusion S/P system with 0.07% polymer and 0.07% surfactant concentrations. The area circled in red is the main flow path.
Figure 8. Images from the microscopy experiment. (a) Water flooding until no oil recovery. (b) Stable emulsified S/P system with 0.03% polymer and 0.03% surfactant concentrations. (c) Interfacial film-fusion S/P system with 0.07% polymer and 0.07% surfactant concentrations. The area circled in red is the main flow path.
Processes 11 01411 g008
Processes 11 01411 g009 550
Figure 9. Microscopic pore-scale images. (a) High-permeability image during the microscopy experiment with a stable emulsified S/P system (0.03% polymer and 0.03% surfactant). (b) High-permeability image during the microscopy experiment with S/P system (0.07% polymer and 0.07% surfactant). (c) Low-permeability image during microscopic experiment with a stable emulsified S/P system (0.03% polymer and 0.03% surfactant). (d) Low-permeability image during the microscopy experiment with the interfacial film fusion S/P system (0.07% polymer and 0.07% surfactant).
Figure 9. Microscopic pore-scale images. (a) High-permeability image during the microscopy experiment with a stable emulsified S/P system (0.03% polymer and 0.03% surfactant). (b) High-permeability image during the microscopy experiment with S/P system (0.07% polymer and 0.07% surfactant). (c) Low-permeability image during microscopic experiment with a stable emulsified S/P system (0.03% polymer and 0.03% surfactant). (d) Low-permeability image during the microscopy experiment with the interfacial film fusion S/P system (0.07% polymer and 0.07% surfactant).
Processes 11 01411 g009
Processes 11 01411 g010 550
Figure 10. The oil recovery factor with different permeabilities.
Figure 10. The oil recovery factor with different permeabilities.
Processes 11 01411 g010
Table
Table 1. Chemical structures and coarse-grained model.
Table 1. Chemical structures and coarse-grained model.
MoleculeBead TypeMolecule StructureMolecule Dynamics ModelCoarse-grained Model
H2OW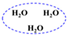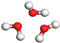Processes 11 01411 i001Processes 11 01411 i002Processes 11 01411 i003
PAMH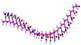Processes 11 01411 i004Processes 11 01411 i005Processes 11 01411 i006
OilO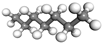Processes 11 01411 i007Processes 11 01411 i008Processes 11 01411 i009
Surfactant
(Pro-oil base group)		Q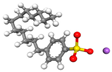Processes 11 01411 i010Processes 11 01411 i011Processes 11 01411 i012
Surfactant
(Hydrophilic group)		S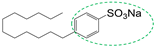Processes 11 01411 i013
Table
Table 2. The DPD simulation field parameters.
Table 2. The DPD simulation field parameters.
Field Parameters (Reduce Type)OWHQS
O25.45
W161.625.82
H102.478.2427.62
Q26.15151.7232.5425
S148.7325.9326.56177.325
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Zhang, B.; Guan, B.; Liu, W.; Peng, B.; Cong, S. Dissipative Particle Dynamics Simulation and Microscopic Experimental Study of Emulsification Performance of Surfactant/Polymer Flooding. Processes 2023, 11, 1411. https://doi.org/10.3390/pr11051411

AMA Style

Zhang B, Guan B, Liu W, Peng B, Cong S. Dissipative Particle Dynamics Simulation and Microscopic Experimental Study of Emulsification Performance of Surfactant/Polymer Flooding. Processes. 2023; 11(5):1411. https://doi.org/10.3390/pr11051411

Chicago/Turabian Style

Zhang, Biao, Baoshan Guan, Weidong Liu, Baoliang Peng, and Sunan Cong. 2023. "Dissipative Particle Dynamics Simulation and Microscopic Experimental Study of Emulsification Performance of Surfactant/Polymer Flooding" Processes 11, no. 5: 1411. https://doi.org/10.3390/pr11051411

APA Style

Zhang, B., Guan, B., Liu, W., Peng, B., & Cong, S. (2023). Dissipative Particle Dynamics Simulation and Microscopic Experimental Study of Emulsification Performance of Surfactant/Polymer Flooding. Processes, 11(5), 1411. https://doi.org/10.3390/pr11051411

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop