Multi-Period Production Optimization Decision Models under Net-Zero Transformation
Abstract
:1. Introduction
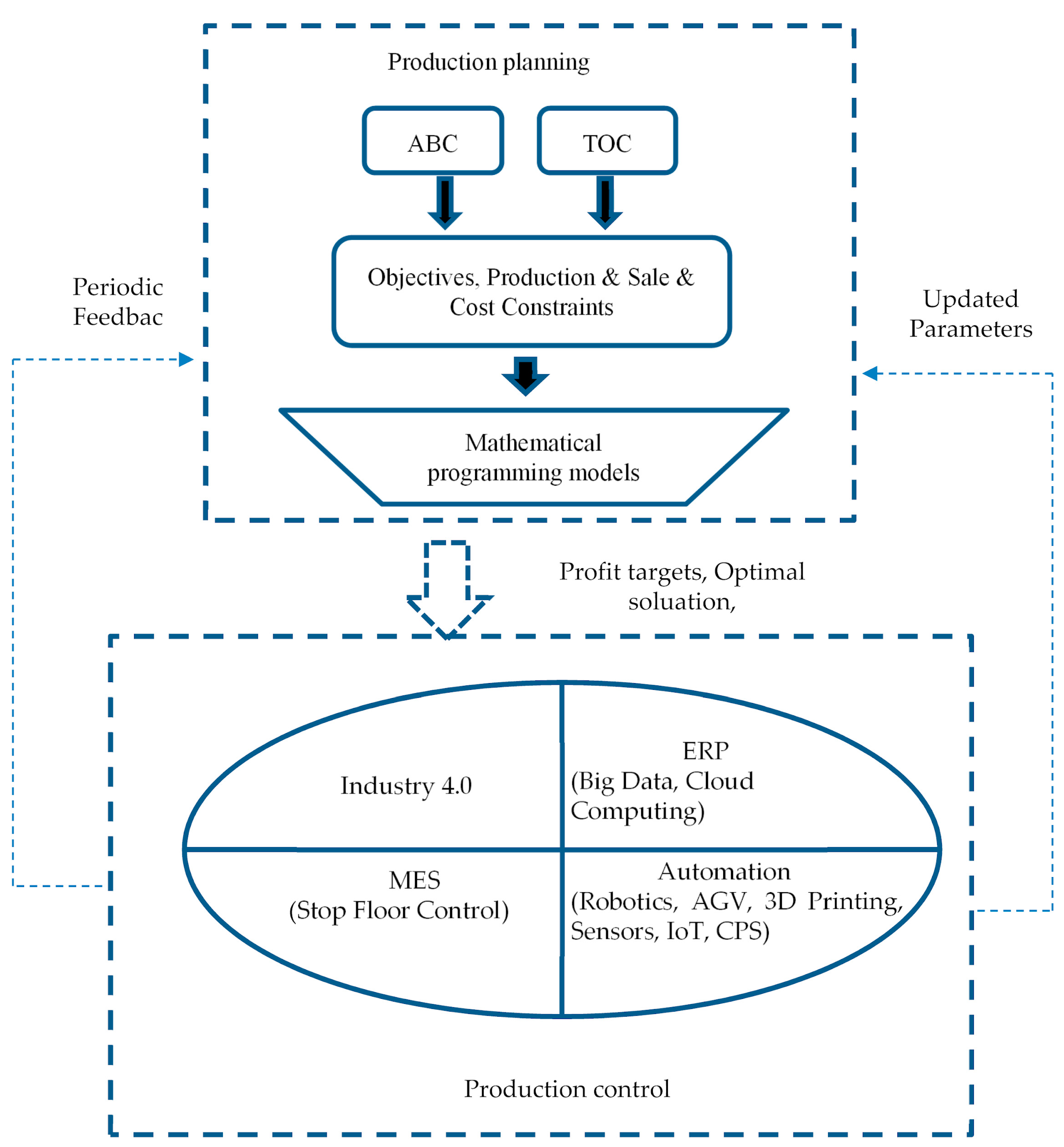
2. Research Background
3. Research Model
3.1. Multi-Phase Model of the Basic Production Model
3.1.1. Objective Function
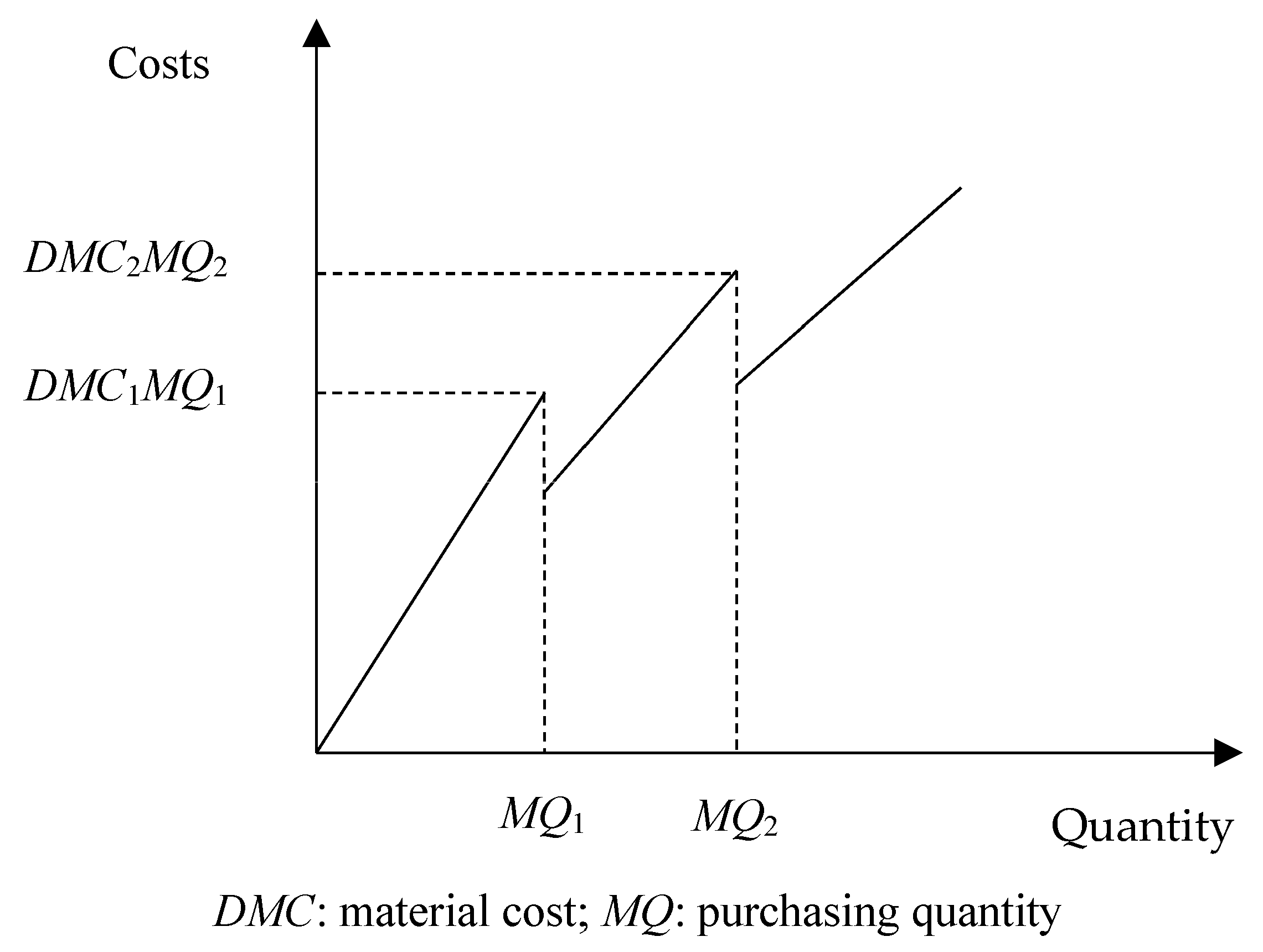
3.1.2. Direct Material Discount Function
3.1.3. Unit-Level Operations: Direct Labor Cost Function
3.2. Multi-Phase Models without Allowance
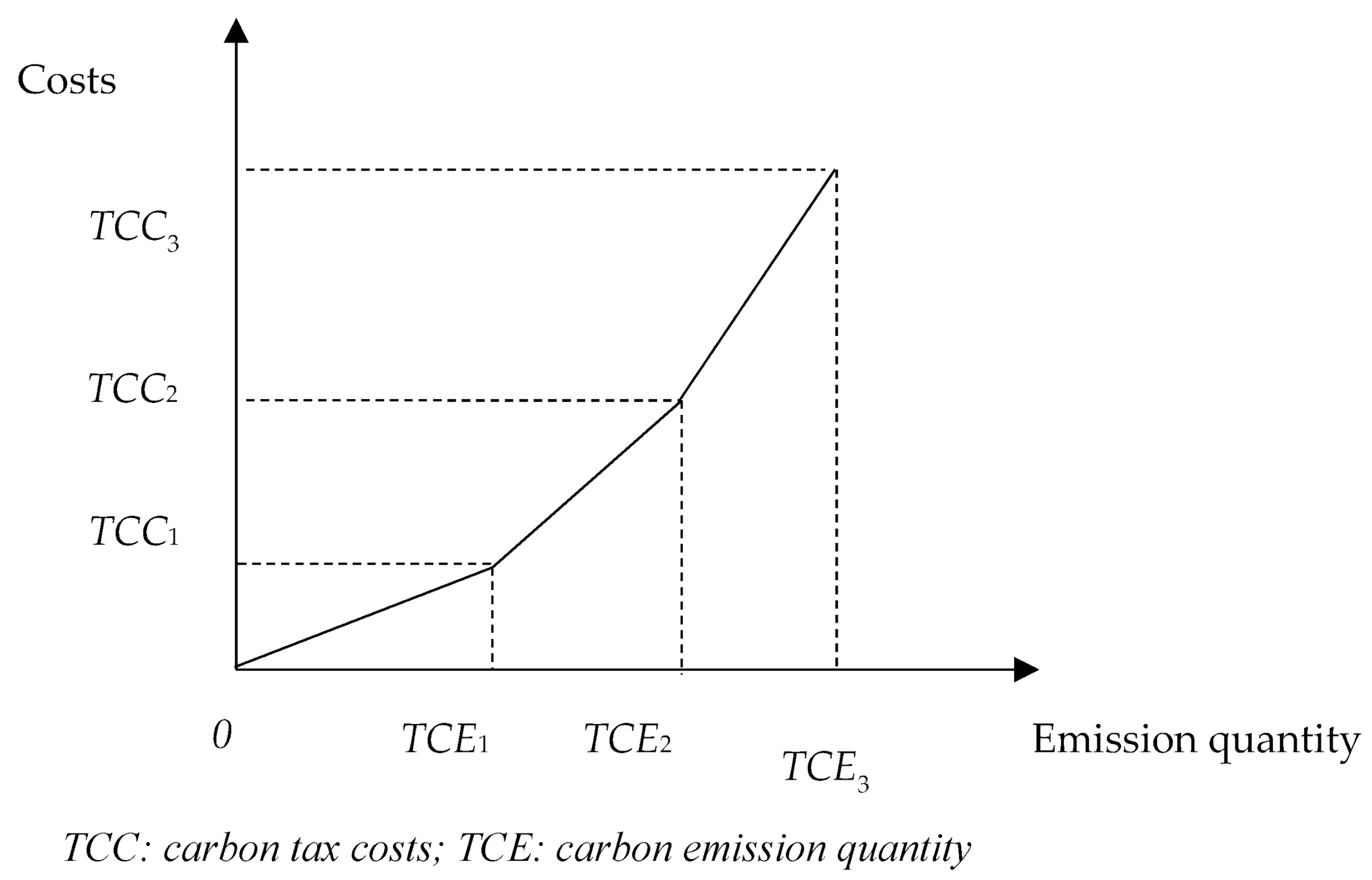
3.2.1. Carbon Tax Function with Incremental Tax Rate without Allowance (Model A)
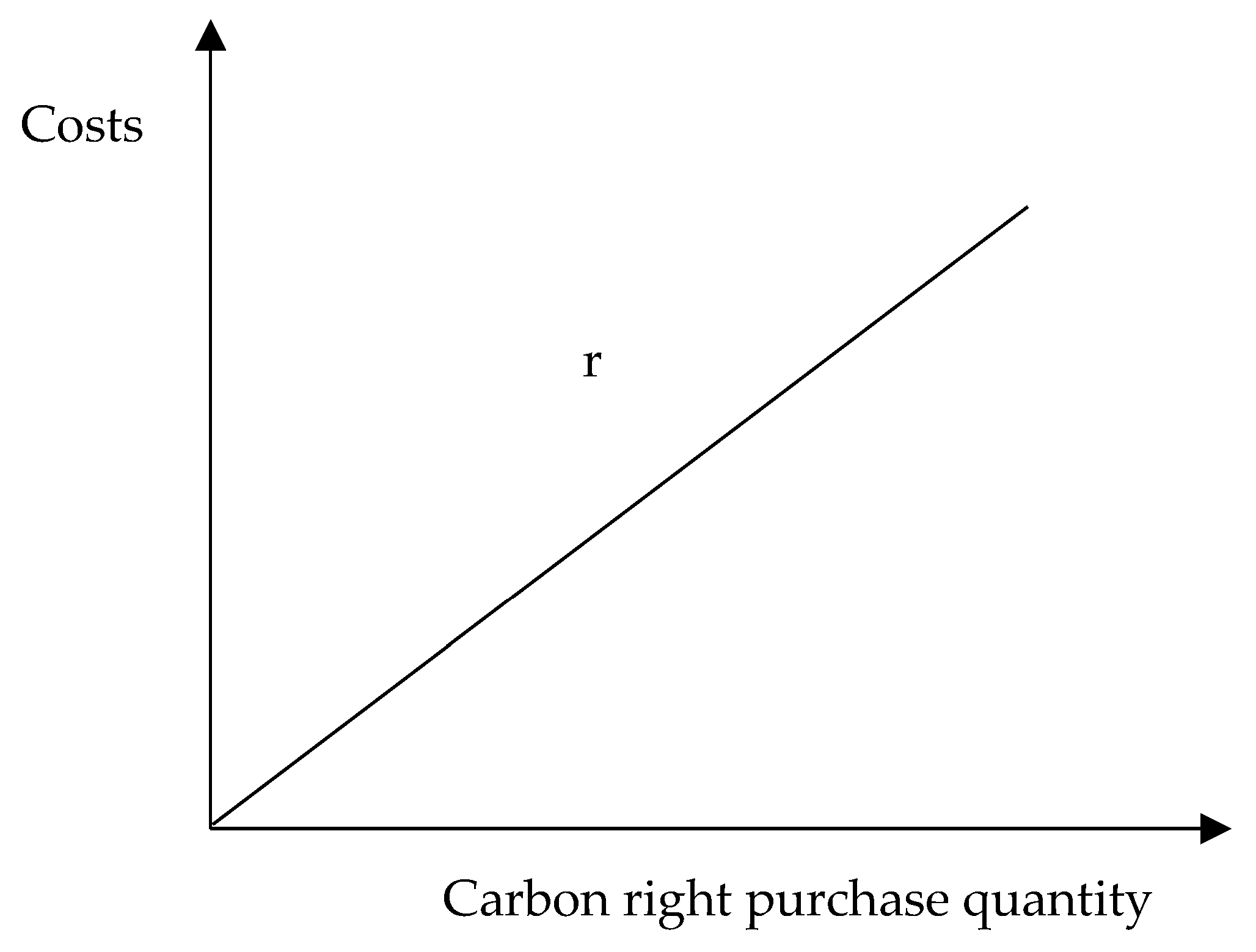
3.2.2. Carbon Tax Function with Incremental Tax Rate without Allowance (with Carbon Trading) (Model B)
3.3. Multi-Phase Modes with Allowance
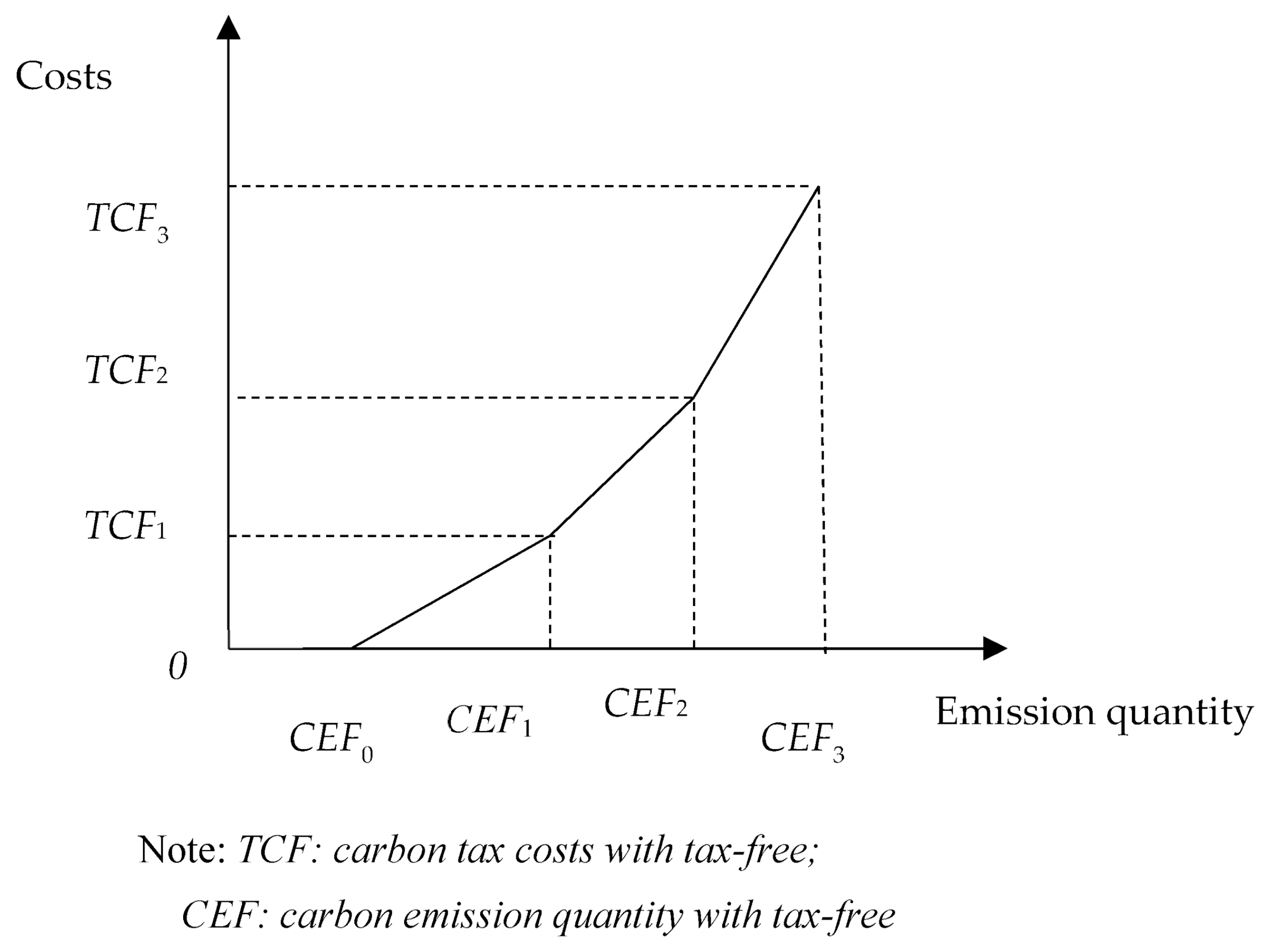
3.3.1. Carbon Tax Function with Incremental Incremental Tax Rate with Allowance (Model C)
3.3.2. Carbon Tax Function with Incremental Incremental Tax Rate with Allowance (with Carbon Trading) (Model D)
4. Research Analysis
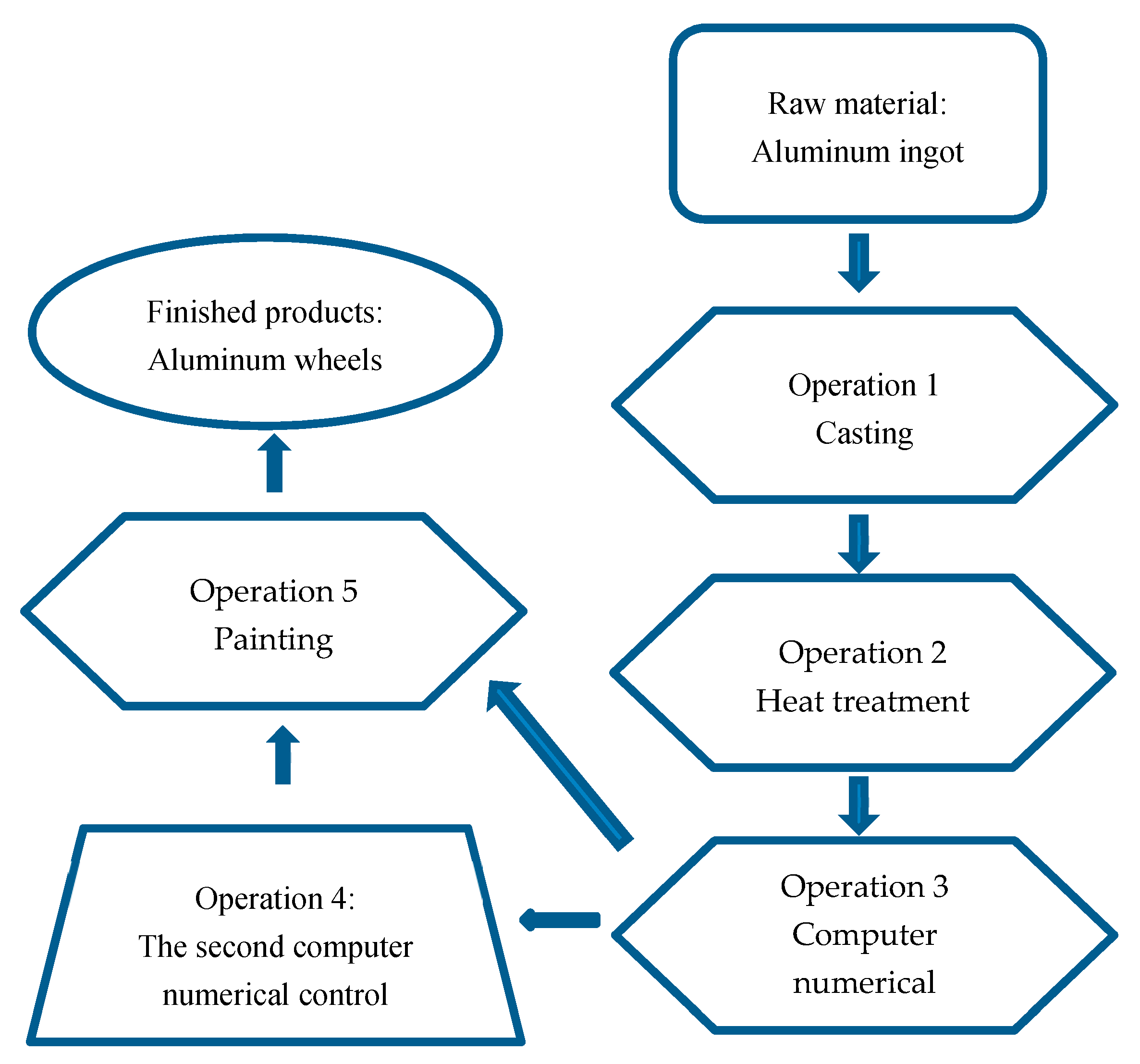
4.1. Sample Data
4.2. Data Analysis
4.2.1. Carbon Tax Function with Incremental Incremental Tax Rate without Allowance (Model A)
4.2.2. Carbon Tax Function with Incremental Incremental Tax Rate with Allowance (Model C)
4.2.3. Model Comparison
4.3. Multi-Period Sensitivity Analysis
4.4. Review
5. Conclusions and Suggestion
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Definition |
| π | Company’s maximum profit |
| Si | Unit sales price of the i-th product |
| Pi | The output of the i-th product |
| DMC1,DMC2, DMC3 | Under normal circumstances, the unit cost of materials (DMC1), the first-stage discounted cost (DMC2) |
| DQ1, DQ2, DQ3 | The quantity consumed under normal conditions (DQ1), the quantity of the first segment of the discount section (DQ2) |
| MCj | j material unit cost |
| qij | When producing a unit of product i, the amount of material j consumed |
| HR1,HR2, HR3 | Direct labor costs under normal circumstances (HR1), the first period of overtime cost (HR2), the second period of overtime cost (HR3) |
| ω0, ω1, ω2 | SOS2 variable, must be a set of positive variables, at most two variables can be non-zero |
| do | When performing a unit of operation o operation cost |
| Bo | Number of batch operations under material handling operations (o ∈ B) |
| MQ | Equivalent to the sum of GCE1 + GCE2 +…GCEt |
| TMBR | Maximum number of carbon rights purchased in multi-period model |
| λ1, λ2, | SOS1 variables |
| ACQ1 | In the multi-period model, it is decided whether the company wants to purchase carbon rights |
| Sio | i product demand under setting operation (o ∈ B) |
| Bio | The batch quantity of the i product under the set operation (o ∈ B) |
| F | Other fixed costs of example company |
References
- Atwoli, L.; Erhabor, G.E.; Gbakima, A.A.; Haileamlak, A.; Kayembe Ntumba, J.-M.; Kigera, J.; Mulaudzi, F.M. COP27 Climate Change Conference: Urgent action needed for Africa and the worldWealthy nations must step up support for Africa and vulnerable countries in addressing past, present and future impacts of climate change. Nutr. Rev. 2022, 23, 19–21. [Google Scholar] [CrossRef]
- Nag, A.K.; Joshi, R. COP 26: Accelerating Efforts Towards Emission Reduction And Net Zero Pledge. Manag. Account. J. 2022, 57, 68–70. [Google Scholar] [CrossRef]
- O’riordan, T. COP 26 and Sustainability Science. Environ. Sci. Policy Sustain. Dev. 2022, 64, 2–3. [Google Scholar] [CrossRef]
- Ohlendorf, N.; Jakob, M.; Minx, J.C.; Schröder, C.; Steckel, J.C. Distributional Impacts of Carbon Pricing: A Meta-Analysis. Environ. Resour. Econ. 2021, 78, 1–42. [Google Scholar] [CrossRef]
- Stavins, R.N. The Relative Merits of Carbon Pricing Instruments: Taxes versus Trading. Rev. Environ. Econ. Policy 2022, 16, 62–82. [Google Scholar] [CrossRef]
- Folkens, L.; Schneider, P. Responsible Carbon Resource Management through Input-Oriented Cap and Trade (IOCT). Sustainability 2022, 14, 5503. [Google Scholar] [CrossRef]
- Carmona, R.; Fehr, M.; Hinz, J.; Porchet, A. Market Design for Emission Trading Schemes. SIAM Rev. 2010, 52, 403–452. [Google Scholar] [CrossRef]
- Kara, M.; Syri, S.; Lehtilä, A.; Helynen, S.; Kekkonen, V.; Ruska, M.; Forsström, J. The impacts of EU CO2 emissions trading on electricity markets and electricity consumers in Finland. Energy Econ. 2008, 30, 193–211. [Google Scholar] [CrossRef]
- Hervert-Escobar, L.; López-Pérez, J.F. Production planning and scheduling optimization model: A case of study for a glass container company. Ann. Oper. Res. 2020, 286, 529–543. [Google Scholar] [CrossRef]
- Lin, B.; Wu, W.; Song, M. Industry 4.0: Driving factors and impacts on firm’s performance: An empirical study on China’s manufacturing industry. Ann. Oper. Res. 2019. [Google Scholar] [CrossRef]
- Tsai, W.-H.; Chu, P.-Y.; Lee, H.-L. Green Activity-Based Costing Production Planning and Scenario Analysis for the Aluminum-Alloy Wheel Industry under Industry 4.0. Sustainability 2019, 11, 756. [Google Scholar] [CrossRef]
- Quesado, P.; Silva, R. Activity-Based Costing (ABC) and Its Implication for Open Innovation. J. Open Innov. Technol. Mark. Complex. 2021, 7, 41. [Google Scholar] [CrossRef]
- Al-Dhubaibi, A.A.S. Optimizing the value of activity based costing system: The role of successful implementation. Manag. Sci. Lett. 2021, 11, 179–186. [Google Scholar] [CrossRef]
- Ruidas, S.; Seikh, M.R.; Nayak, P.K. A Production Inventory Model for Green Products with Emission Reduction Technology Investment and Green Subsidy. Process. Integr. Optim. Sustain. 2022, 6, 863–882. [Google Scholar] [CrossRef]
- Chen, X.; Yang, H.; Wang, X.; Choi, T.-M. Optimal carbon tax design for achieving low carbon supply chains. Ann. Oper. Res. 2020. [Google Scholar] [CrossRef]
- Ruidas, S.; Seikh, M.R.; Nayak, P.K. A production inventory model with interval-valued carbon emission parameters under price-sensitive demand. Comput. Ind. Eng. 2021, 154, 107154. [Google Scholar] [CrossRef]
- Holmen, J.S. ABC vs. TOC: It’s a matter of time. Strateg. Financ. 1995, 76, 37. [Google Scholar]
- Shapiro, J.F. Modeling and IT Perspectives on Supply Chain Integration. Inf. Syst. Front. 2001, 3, 455–464. [Google Scholar] [CrossRef]
- Das, S.K.; Green, J.A.S.; Kaufman, J.G. The development of recycle-friendly automotive aluminum alloys. JOM 2007, 59, 47–51. [Google Scholar] [CrossRef]
- Association, A. Aluminum: The Element of Sustainability—A North American Aluminum Industry Sustainability Report; Retrieved 30 April 2013; The Aluminum Association: Arlington, VA, USA, 2011. [Google Scholar]
- Liu, G.; Bangs, C.E.; Müller, D.B. Unearthing Potentials for Decarbonizing the U.S. Aluminum Cycle. Environ. Sci. Technol. 2011, 45, 9515–9522. [Google Scholar] [CrossRef]
- Sarkar, B.; Kar, S.; Basu, K.; Guchhait, R. A sustainable managerial decision-making problem for a substitutable product in a dual-channel under carbon tax policy. Comput. Ind. Eng. 2022, 172, 108635. [Google Scholar] [CrossRef]
- Luo, R.; Zhou, L.; Song, Y.; Fan, T. Evaluating the impact of carbon tax policy on manufacturing and remanufacturing decisions in a closed-loop supply chain. Int. J. Prod. Econ. 2022, 245, 108408. [Google Scholar] [CrossRef]
- Cooper, R.; Kaplan, R.S. Profit priorities from activity-based costing. Harv. Bus. Rev. 1991, 69, 130–135. [Google Scholar]
- Malmi, T. Activity-based costing diffusion across organizations: An exploratory empirical analysis of Finnish firms. Account. Organ. Soc. 1999, 24, 649–672. [Google Scholar] [CrossRef]
- Toyabe, S.; Kurashima, S.; Okada, M.; Akazawa, K.; Cao, P. A Modified Method of Activity-based Costing for Objectively Reducing Cost Drivers in Hospitals. Methods Inf. Med. 2006, 45, 462–469. [Google Scholar] [CrossRef]
- Lin, B.Y.-J.; Chao, T.-H.; Yao, Y.; Tu, S.-M.; Wu, C.-C.; Chern, J.-Y.; Chao, S.-H.; Shaw, K.-Y. How can activity-based costing methodology be performed as a powerful tool to calculate costs and secure appropriate patient care? J. Med. Syst. 2007, 31, 85–90. [Google Scholar]
- Tsai, W.-H.; Lai, S.-Y.; Hsieh, C.-L. Exploring the impact of different carbon emission cost models on corporate profitability. Ann. Oper. Res. 2022, 322, 41–74. [Google Scholar] [CrossRef]
- Kee, R.; Schmidt, C. A comparative analysis of utilizing activity-based costing and the theory of constraints for making product-mix decisions. Int. J. Prod. Econ. 2000, 63, 1–17. [Google Scholar] [CrossRef]
- Rand, G.K. Critical chain: The theory of constraints applied to project management. Int. J. Proj. Manag. 2000, 18, 173–177. [Google Scholar] [CrossRef]

| Researchers | Research Topic |
|---|---|
| Hervert-Escobar and López-Pérez, 2020 [9] | Production planning and scheduling optimization model: a case of study for a glass container company. |
| Ruidas et al., 2021 [16] | A production inventory model with interval-valued carbon emission parameters under price-sensitive demand. |
| Al-Dhubaibi, 2021 [13] | Optimizing the value of activity-based costing system: The role of successful implementation. |
| Quesado and Silva, 2021 [12] | Activity-based costing (ABC) and its implication for open innovation. |
| Ruidas et al., 2022 [14] | A Production Inventory Model for Green Products with Emission Reduction Technology Investment and Green Subsidy. |
| Product Item | Pi | Si | Direct Materials at the Unit Level | Quantity Cost | |
|---|---|---|---|---|---|
| Maximum /Minimum Production Volume | Selling Price | qi1 Aluminum Ingot (m = 1) | qi2 Coating (m = 2) | ||
| Car rim | >2000 | 4000 | 10 | 2 | MQ1 = 80,000D DMC1 = $70 |
| Truck rim | >1000 | 6000 | 20 | 3 | MQ2 = 250,000 DMC2 = $69 |
| Custom rims | >2000, <6000 | 8000 | 10 | 4 | >250,000 DMC3 = $67 |
| Product Item | c Material Handling | d Setting | Direct Labor Cost | Other Fixed Costs | Decision-Making Mode of Multi-Phase Production | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| H6 | ρ6 | Si7 | τi7 | Cost | Labor Hours | Salary Rate | The Upper Limit of Three-Phase Carbon Emission | The Upper Limit of Three-Phase Material | ||
| Car rim | 1 | 70 | 1 | 2 | HR1 = $7,022,400 HR2 = $14,018,400 HR3 = $23,337,600 | CH1 = 52,800 CH2 = 79,200 CH3 = 105,600 | $133/h $177/h $221 /h | F = 10,000,000 | GCE1 = 28,000 GCE2 = 25,200 GCE3 = 22,400 | UDQ=39,000 |
| Truck rim | 1 | 2 | ||||||||
| Custom rims | 2.5 | 1 | ||||||||
| Available capacity | A6 = 8800 | A7 = 17,600 | ||||||||
| Product Item | Machine Hours | Labor Hours | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| rhi1 Casting | rhi2e Heat treatment | rhi3 a CNC | rhi4 b CNC 2nd | Painting | ui1 Casting | ui2 Heat treatment | ui3 a CNC | ui4 b CNC 2nd | ui5 Painting | |
| Car rim | 2 | 3 | 2 | 0 | 0.1 | 1.2 | 1.5 | 1 | 0 | 0.3 |
| Truck rim | 3 | 4 | 3 | 0 | 0.1 | 1.7 | 2 | 1 | 0 | 0.3 |
| Custom rims | 2 | 4 | 1 | 0.9 | 0.2 | 1.2 | 1.5 | 1.6 | 1 | 0.7 |
| Available capacity | CP1 = 46,200 | CP2 = 50,400 | CPCNC =18,900 | CP5 = 2070 | ||||||
| Product Item | Available | |||||||
|---|---|---|---|---|---|---|---|---|
| o | Car Rim | Truck Rim | Custom Rims | Capacity | ||||
| Carbon tax with incremental tax rate without allowance (Model 1) | ei | 1.5 | 2 | 3 | ||||
| Cost | TCC1 = $2,500,000 | TCC2 = $5,500,000 | TCC3 = $9,000,000 | |||||
| Quantity | TCE1 = 10,000 | TCE2 = 20,000 | TCE3 = 30,000 | |||||
| Tax rate | cr1 = $250/unit | cr2 = $300/unit | cr3 = $350/unit | |||||
| Carbon tax with incremental incremental tax rate with allowance (Model 2) | ei | 1.5 | 2 | 3 | ||||
| Cost | TCF1 = $2,500,000 | TCF2 = $5,500,000 | TCF3 = $9,000,000 | |||||
| Quantity | CEF0 = 5000 | CEF1 = 15,000 | CEF2 = 25,000 | CEF3 = 35,000 | ||||
| Tax rate | crf1 = $250/unit | crf2 = $300/unit | crf3 = $350/unit | |||||
| Linear carbon right cost | ||||||||
| Carbon right cost | r = $250/unit | Maximum carbon emissions cap set by the government | GCE = 28,000 | |||||
| Quantity | MBR = 100,000 | |||||||
| [Optimal solution] | |
| π = 28,088,110; P1 = 2006; P2 = 3624; P3 = 5914; DQ1 = 0; DQ2 = 151,680; DQ3 = 0; ω0 = 0.6656061; ω1 = 0.3343939; ω2 = 0; B6 = 2167; B17 = 1003; B27 = 1812; B37 = 5914; φ0 = 0; φ1 = 0; φ2 = 0.2001; φ3 = 0.7999; α1 = 0; α2 = 1; α3 = 0; β1 = 1; β2 = 0; γ1 = 0; γ2 = 0; γ3 = 1; CCE = 27,999 | |
| [Objective function] | |
| Maximum π = 4000*P1 + 6000*P2 + 8000*P3 − (70*DQ1 + 69*DQ2 + 67*DQ3 − 100*P1 + 150*P2 + 200*P3) − [7,022,400 + ω1*6,996,000 + ω2*16,315,200] − 2500*B6 − 200*B17 − 200*B27 − 500*B37 −(2,500,000*φ1 + 5,500,000*φ1 + 9,000,000*φ2) – 10,000,000 | |
| [Constraints] | |
| Direct material discount: | Direct labor: |
| 10*P1 + 20*P2 + 10*P3 = DQ1 + DQ2 + DQ3 | 4*P1 + 5*P2 + 6*P3 = 52,800 − ω1*26,400 − ω2*52,800 |
| 0 ≤ DQ1 ≤ α0*200,000 | ω0 − β1 ≤ 0 |
| α1*200,000 < DQ2 ≤ α1*500,000 | ω1 − β1 − β2 ≤ 0 |
| α2*500,000 < DQ3 | ω2 − β2 ≤ 0 |
| α0 + α1 + α2 = 1 | ω0 + ω1 + ω2 = 1 |
| β1 + β2 = 1 | |
| Batch Level: Material Handling | |
| 10*P1 + 20*P2 + 10*P3 ≤ 70*B6 | Batch Level: Settings |
| 1*B6 ≤ 8800 | P1 ≤ 2*B17 |
| P2 ≤ 2*B27 | |
| Machine hours: | P3 ≤ 1*B37 |
| o = 1 : 2*P1 + 3*P2 + 2*P3 ≤ 46,200 | 1*B17 + 1*B27 + 2.5*B37 ≤ 17,600 |
| o = 2 : 3*P1 + 4*P2 + 3*P3 ≤ 50,400 | |
| o = 3, 4 : 1*P1 + 1*P2 + 1.9*P3 ≤ 18,900 | Min/Max demand: |
| o = 5 : 0.1*P1 + 0.1*P2 + 0.2*P3 ≤ 2070 | P1 > 2000; P2 > 1000; 6000 > P3 > 2000 |
| Carbon tax with incremental incremental tax rate without allowance: | |
| 1.5*P1 + 2*P2 + 3*P3 = φ1*10,000 + φ2*20,000 + φ3*30,000 | |
| 1.5*P1 + 2*P2 + 3*P3 ≤ 28,000 | |
| φ0 – γ1 ≤ 0 | |
| φ1 – γ1 – γ2 ≤ 0 | |
| φ2 – γ2 – γ3 ≤ 0 | |
| φ3 – γ3 ≤ 0 | |
| φ0 + φ1 + φ2 + φ3 = 1 | |
| γ1 + γ2 + γ3 = 1 | |
| [Optimal solution] | |
| π = 28,886,270; P1 = 2000; P2 = 5058; P3 = 5628; DQ1 = 0; DQ2 = 177,440; DQ3 = 0; ω0 = 0.4599242; ω1 = 0.5400758; ω2 = 0; B6 = 2535; B17 = 1000; B27 = 2529; B37 = 5628; φ0 = 0; φ1 = 0; φ2 = 0; φ3 =1; α1 = 0;α2 = 1; α3 = 0; β1 = 1; β2 = 0;γ1 = 0;γ2 = 0; γ3 = 1; GCE = 28,000; Ø1 = 0; Ø2 = 1; CQ1 = 0; CQ2 = 30,000 | |
| [Objective function] | |
| Maximum π = 4000*P1 + 6000*P2 + 8000*P3 – (70*DQ1 + 69*DQ2 + 67*DQ3 – 100*P1 + 150*P2 + 200*P3) – [7,022,400 + ω1*6,996,000 + ω2*16,315,200] – 2500*B6 – 200*B17 – 200*B27 – 500*B37 – (2,500,000*φ1 + 5,500,000*φ1 +9,000,000*φ2 – 250*(GCE – CCE))* Ø1 – (2,500,000*φ1 + 5,500,000*φ1 + 9,000,000*φ2 + 250*(CCE – GCE))* Ø2 – 10,000,000 | |
| [Constraints] | |
| Direct material discount: | Direct labor: |
| 10*P1 + 20*P2 + 10*P3 = DQ1 + DQ2 + DQ3 | 4*P1 + 5*P2 + 6*P3 = 52,800 – ω1*26,400 – ω2*52,800 |
| 0 ≤ DQ1 ≤ α0*200,000 | ω0 – β1 ≤ 0 |
| α1*200,000 < DQ2 ≤ α1*500,000 | ω1 – β1 – β2 ≤ 0 |
| α2*500,000 < DQ3 | ω2 – β2 ≤ 0 |
| α0 + α1 + α2 = 1 | ω0 + ω1 + ω2 = 1 |
| β1 + β2 = 1 | |
| Batch Level: Material Handling | |
| 10*P1 + 20*P2 + 10*P3 ≤ 70*B6 | Batch Level: Settings |
| 1*B6 ≤ 8800 | P1 ≤ 2*B17 |
| P2 ≤ 2*B27 | |
| Machine hours: | P3 ≤ 1*B37 |
| o = 1 : 2*P1 + 3*P2 + 2*P3≤ 46,200 | 1*B17 + 1*B27 + 2.5*B37 ≤ 17,600 |
| o = 2 : 3*P1 + 4*P2 + 3*P3 ≤ 50,400 | |
| o = 3, 4 : 1*P1 + 1*P2 + 1.9*P3 ≤ 18,900 | Min/Max demand: |
| o = 5 : 0.1*P1 + 0.1*P2 + 0.2*P3 ≤ 2070 | P1 > 2000; P2 > 1000; 6000 > P3 > 2000 |
| Linear carbon rights: | Carbon tax with incremental incremental tax rate without allowance: |
| 1.5*P1 + 2*P2 + 3*P3 = CQ1 + CQ2 = CCE | 1.5*P1 + 2*P2 + 3*P3 = φ1*10,000 + φ2*20,000 + φ3*30,000 |
| 0 ≤ CQ1 ≤ 28,000*Ø1 | 1.5*P1 + 2*P2 + 3*P3 ≤ 28,000 |
| 28,000*Ø1 < CQ2 ≤ 128,000*Ø2 | φ0 − γ1 ≤ 0 |
| Ø1 + Ø2 = 1 | φ1 − γ1 − γ2 ≤ 0 |
| φ2 − γ2 − γ3 ≤ 0 | |
| φ3 − γ3 ≤ 0 | |
| φ0 + φ1 + φ2 + φ3 = 1 | |
| γ1 + γ2 + γ3 = 1 | |
| [Optimal solution] | |
| π = 29,838,110; P1 = 2006; P2 = 3624; P3 = 5914; DQ1 = 0; DQ2 = 151,680; DQ3 = 0;ω0 = 0.6656061; ω1 = 0.3343939; ω2 = 0; B6 = 2167; B17 = 1003; B27 = 1812; B37 = 5914; σ0 = 0; σ1 = 0; σ2 = 0.7001; σ3 = 0.2999; α1 = 0; α2 = 1; α3 = 0; β1 = 1; β2 = 0; μ1 = 0; μ2 = 0; μ3 = 1; CCE = 27,999 | |
| [Objective function] | |
| Maximum π = 4000*P1 + 6000*P2 + 8000*P3 − (70*DQ1 + 69*DQ2 + 67*DQ3 − 100*P1 + 150*P2 + 200*P3) − [7,022,400 + ω1*6,996,000 + ω2*16,315,200] − 2500*B6 − 200*B17 − 200*B27 − 500*B37 − (2,500,000*σ1 + 5,500,000*σ1 + 9,000,000*σ2) − 10,000,000 | |
| [Constraints] | |
| Direct material discount: | Direct labor: |
| 10*P1 + 20*P2 + 10*P3 = DQ1 + DQ2 + DQ3 | 4*P1 + 5*P2 + 6*P3 = 52,800 − ω1*26,400 − ω2*52,800 |
| 0 ≤ DQ1 ≤ α0*200,000 | ω0 − β1 ≤ 0 |
| α1*200,000 < DQ2 ≤ α1*500,000 | ω1 − β1 − β2 ≤ 0 |
| α2*500,000 < DQ3 | ω2 − β2 ≤ 0 |
| α0 + α1 + α2 = 1 | ω0 + ω1 + ω2 = 1 |
| β1 + β2 = 1 | |
| Batch Level: Material Handling | |
| 10*P1 + 20*P2 + 10*P3 ≤ 70*B6 | Batch Level: Settings |
| 1*B6 ≤ 8800 | P1 ≤ 2*B17 |
| P2 ≤ 2*B27 | |
| Machine hours: | P3 ≤ 1*B37 |
| o = 1: 2*P1 + 3*P2 + 2*P3 ≤ 46,200 | 1*B17 + 1*B27 + 2.5*B37 ≤ 17,600 |
| o = 2: 3*P1 + 4*P2 + 3*P3 ≤ 50,400 | |
| o = 3, 4: 1*P1 + 1*P2 + 1.9*P3 ≤ 18,900 | Min/Max demand: |
| o = 5: 0.1*P1 + 0.1*P2 + 0.2*P3 ≤ 2070 | P1 > 2000; P2 > 1000; 6000 > P3 > 2000 |
| Carbon tax with incremental incremental tax rate with allowance: | |
| 1.5*P1 + 2*P2 + 3*P3 ≤ 5000 + σ1*10,000 + σ2*20,000 + σ3*30,000 | |
| 1.5*P1 + 2*P2 + 3*P3 ≤ 28,000 | |
| σ0 − μ1 ≤ 0 | |
| σ1 − μ1 − μ2 ≤ 0 | |
| σ2 − μ2 − μ3 ≤ 0 | |
| σ3 − μ3 ≤ 0 | |
| σ0 + σ1 + σ2 + σ3 = 1 | |
| μ1 + μ2 + μ3 = 1 | |
| [Optimal solution] | |
| π = 31,668,590; P1 = 2000; P2 = 6910; P3 = 5257; DQ1 = 0; DQ2 = 210,770; DQ3 = 0;ω0 = 0.1934848; ω1= 0.8065152; ω2 = 0; B6 = 3011; B17 = 1000; B27 = 3455; B37 = 5257; σ0 = 0; σ1 =0; σ2 = 0.2409; σ3 = 0.7591; α1 = 0;α2 = 1; α3 = 0; β1 = 1; β2 = 0; μ1 = 0; μ2 = 0; μ3 = 1; GCE = 28,000 ;Ø1 = 0; Ø2 = 1;CQ1 = 0;CQ2 = 32,591 | |
| [Objective function] | |
| Maximum π = 4000*P1 + 6000*P2 + 8000*P3 − (70*DQ1 + 69*DQ2 + 67*DQ3 − 100*P1 + 150*P2 + 200*P3) − [7,022,400 + ω1*6,996,000 + ω2*16,315,200] − 2500*B6 − 200*B17 − 200*B27 − 500*B37 − (2,500,000*σ1 + 5,500,000*σ1 +9,000,000*σ2 − 250*(GCE − CCE))*Ø1 − (2,500,000*σ1 + 5,500,000*σ1 +9,000,000*σ2 +250*(CCE-GCE))*Ø2 −10,000,000 | |
| [Constraints] | |
| Direct material discount: | Direct labor: |
| 10*P1 + 20*P2 + 10*P3 = DQ1 + DQ2 + DQ3 | 4*P1 + 5*P2 + 6*P3 = 52,800 − ω1*26,400 − ω2*52,800 |
| 0 ≤ DQ1 ≤ α0*200,000 | ω0 − β1 ≤ 0 |
| α1*200,000 < DQ2 ≤ α1*500,000 | ω1 − β1 − β2 ≤ 0 |
| α2*500,000 < DQ3 | ω2 − β2 ≤ 0 |
| α0 + α1 + α2 = 1 | ω0 + ω1 + ω2 = 1 |
| β1 + β2 = 1 | |
| Batch Level: Material Handling | |
| 10*P1 + 20*P2 + 10*P3 ≤ 70*B6 | Batch Level: Settings |
| 1*B6 ≤ 8800 | P1 ≤ 2*B17 |
| P2 ≤ 2*B27 | |
| Machine hours: | P3 ≤ 1*B37 |
| o = 1: 2*P1 + 3*P2 + 2*P3 ≤ 46,200 | 1*B17 + 1*B27 + 2.5*B37 ≤ 17,600 |
| o = 2: 3*P1 + 4*P2 + 3*P3 ≤ 50,400 | |
| o = 3, 4: 1*P1 + 1*P2 + 1.9*P3 ≤ 18,900 | Min/Max demand: |
| o = 5: 0.1*P1 + 0.1*P2 + 0.2*P3 ≤ 2070 | P1 > 2000; P2 > 1000; 6000 > P3 > 2000 |
| Linear carbon rights: | Carbon tax with incremental incremental tax rate with allowance: |
| 1.5*P1 + 2*P2 + 3*P3 = CQ1 + CQ2 = CCE | 1.5*P1 + 2*P2 + 3*P3 ≤ 5000 + σ1*10,000 + σ2*20,000 + σ3*30,000 |
| 0 ≤ CQ1 ≤ 28,000*Ø1 | 1.5*P1 + 2*P2 + 3*P3 ≤ 28,000 |
| 28,000*Ø1 < CQ2 ≤ 128,000*Ø2 | σ0 − μ1 ≤ 0 |
| Ø1 + Ø2 = 1 | σ1 − μ1 − μ2 ≤ 0 |
| σ2 − μ2 − μ3 ≤ 0 | |
| σ3 − μ3 ≤ 0 | |
| σ0 + σ1 + σ2 + σ3 = 1 | |
| μ1 + μ2 + μ3 = 1 | |
| Model | Profit | Quantity of Goods | Carbon Emission | Carbon Tax | Carbon Rights | The Cost of Carbon Rights | Quantity of Material Purchased | Labor Cost | Labor Hours |
|---|---|---|---|---|---|---|---|---|---|
| A1 | 28,088,110 | P1 = 2006; P2 = 3624; P3 = 5914 | 27,999 | 8,299,650 | 0 | 0 | 151,680 | 9,361,820 | 61,628 |
| A2 | 28,886,270 | P1 = 2000; P2 = 5058; P3 = 5628 | 30,000 | 9,000,000 | 2000 | 50,000 | 177,440 | 10,800,770 | 67,058 |
| B1 | 29,838,110 | P1 = 2006; P2 = 3624; P3 = 5914 | 27,999 | 6,549,650 | 0 | 0 | 151,680 | 9,361,820 | 61,628 |
| B2 | 31,668,590 | P1 = 2000; P2 = 6910; P3 = 5257 | 32,591 | 8,156,850 | 4591 | 1,147,750 | 210,770 | 12,664,780 | 74,092 |
| Period | Profit | Quantity of Goods | Carbon Emission | Carbon Tax | Carbon Rights | The Cost of Carbon Rights | Quantity of MATERIAL | Cost of Material | Labor Hours | Labor Cost | Batch Cost |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Carbon emission caps set for each period | |||||||||||
| 1 | 28,923,600 | P1 = 4000 P2 = 1200 P3 = 6000 | 26,400 | 5,990,000 | (1600) | (400,000) | 124,000 | 10,336,000 | 58,000 | 8,400,400 | 7,950,000 |
| 2 | 28,557,480 | P1 = 3016 P2 = 2184 P3 = 6000 | 26,892 | 6,162,200 | 1692 | 423,000 | 133,840 | 11,064,160 | 58,984 | 8,661,160 | 8,300,000 |
| 3 | 27,800,720 | P1 = 3184 P2 = 2016 P3 = 6000 | 26,808 | 6,132,800 | 4408 | 1,102,000 | 132,160 | 10,939,840 | 58,816 | 8,616,640 | 8,240,000 |
| Lump sum | 85,281,800 | 80,100 | 18,285,000 | 4500 | 1,125,000 | 390,000 | 32,340,000 | 175,800 | 25,678,200 | 24,490,000 | |
| Carbon emissions that can be stored or borrowed per period | |||||||||||
| 1 | 29,091,930 | P1 = 3506 P2 = 1694 P3 = 6000 | 26,647 | 6,076,450 | (1353) | (338,250) | 128,940 | 10,701,560 | 58,494 | 8,531,310 | 8,125,000 |
| 2 | 28,492,930 | P1 = 3206 P2 = 1994 P3 = 6000 | 26,797 | 6,128,950 | 1597 | 399,250 | 131,940 | 10,923,560 | 58,794 | 8,610,810 | 8,232,500 |
| 3 | 27,696,940 | P1 = 3488 P2 = 1694 P3 = 6000 | 26,656 | 6,079,600 | 4256 | 1,064,000 | 129,120 | 10,714,880 | 58,422 | 8,536,080 | 8,132,500 |
| Lump sum | 85,281,800 | 80,100 | 18,285,000 | 4500 | 1,125,000 | 390,000 | 32,340,000 | 175,710 | 25,678,200 | 24,490,000 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsai, W.-H. Multi-Period Production Optimization Decision Models under Net-Zero Transformation. Processes 2023, 11, 1439. https://doi.org/10.3390/pr11051439
Tsai W-H. Multi-Period Production Optimization Decision Models under Net-Zero Transformation. Processes. 2023; 11(5):1439. https://doi.org/10.3390/pr11051439
Chicago/Turabian StyleTsai, Wen-Hsien. 2023. "Multi-Period Production Optimization Decision Models under Net-Zero Transformation" Processes 11, no. 5: 1439. https://doi.org/10.3390/pr11051439
APA StyleTsai, W.-H. (2023). Multi-Period Production Optimization Decision Models under Net-Zero Transformation. Processes, 11(5), 1439. https://doi.org/10.3390/pr11051439





