Research on New Energy Power System Stability Situation Awareness Based on Index Screening and Dynamic Evaluation
Abstract
1. Introduction
- In this paper, an index screening method based on Measure of Sampling Adequacy (MSA) and Kaiser–Meyer–Olkin (KMO) test statistics is proposed to screen the existing power system operation indexes and establish a stable operation situation awareness (SA) index system with low information overlap according to multiple operation criteria;
- The dynamic variable weight formula is proposed to dynamically change the weights according to the index values and to dynamically evaluate the operation status of the system by constructing a comprehensive evaluation method combining the intuitive fuzzy analysis hierarchy process and improved CRITIC;
- The effectiveness of the situational awareness framework in this paper is verified through simulation;
- This paper compares the state identification results of the comprehensive evaluation before and after the improvement of index screening and dynamic assignment, as well as the state identification results and sensitivity analysis results of the comprehensive evaluation methods proposed in the recent literature, and it verifies the superiority of the improved method proposed in this paper.
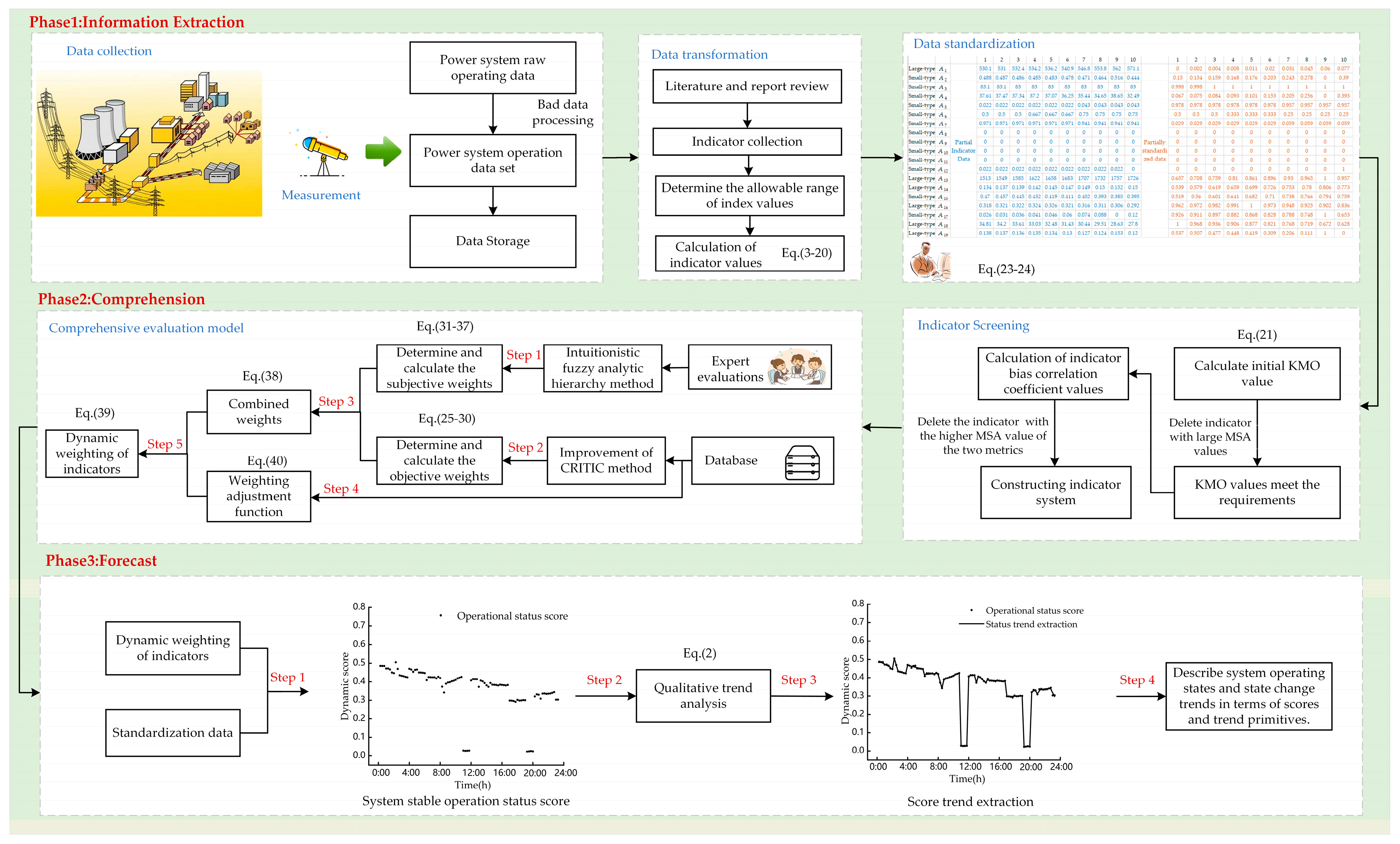
2. Situational Awareness Framework for Power Systems
2.1. Theoretical Framework of Situational Awareness
2.2. Qualitative Trend Analysis
2.2.1. Data Interception Based on Adaptive Sliding Time Window
2.2.2. Trend Identification
2.3. The Main Symbols Used in This Paper
3. Establishment of Index System
3.1. Index Definition
3.1.1. Steady-State Security Distance
3.1.2. Load Level
3.1.3. N − 1 Safety Criterion
3.1.4. Power Quality
3.1.5. Cleanliness Requirements
3.1.6. Safety Margin
3.2. Allowable Fluctuation Range of Indicators
3.3. Evaluation Index Screening Based on MSA and KMO
4. Dynamic Integrated Evaluation Model
4.1. Improvement of CRITIC Objective Empowerment Method
4.2. Intuitionistic Fuzzy Analytic Hierarchy Process
- (1)
- The intuitionistic fuzzy judgment matrix B = (bij)n×n is used to construct the product-type consistency judgment matrix .
- (2)
- Set the threshold coefficient to . Generally, is selected as 0.1 [37]. If and satisfy , the intuitionistic fuzzy judgment matrix is considered to meet the requirements. Further, is the distance-measure formula of and :
4.3. Subjective and Objective Dynamic Integrated Empowerment
4.4. Evaluation Score
4.5. The Flow of the Situational Awareness
4.6. Data Acquisition Intervals for Situational Awareness
5. Example Analysis
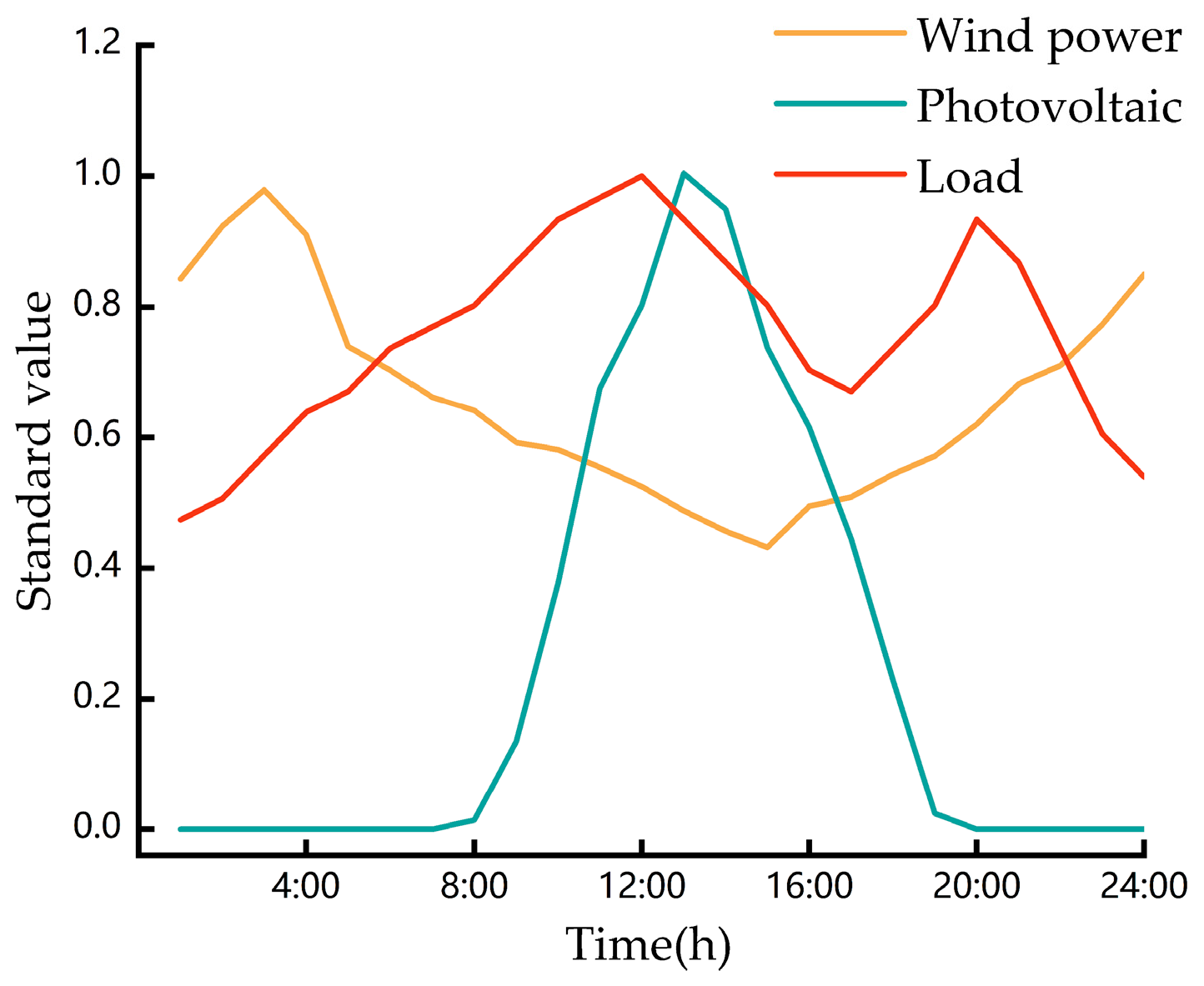
5.1. Stable Operational SA under the “Source Load” Fluctuation
5.2. Comparison of Situational Awareness Results under Different Evaluation Methods
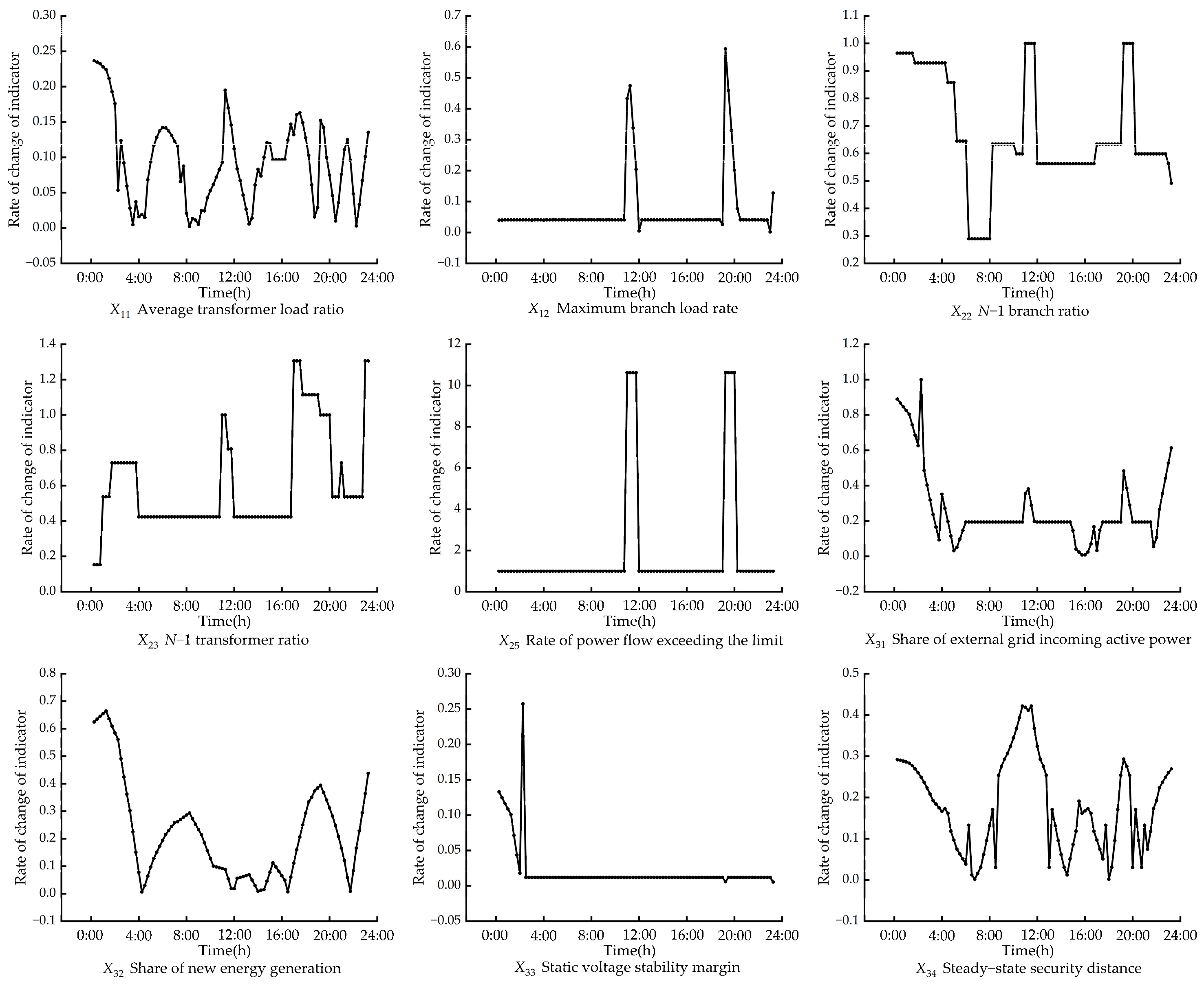
5.3. Sensitivity Analysis of Comprehensive Evaluation Methods in Texts
6. Conclusions
- (1)
- Starting from a situational awareness framework, we describe the process of applying situational awareness theory to the identification of the operational state of a power system;
- (2)
- A comprehensive evaluation method is used to identify the stable operating state of the system, and an indicator screening method combining KMO and MSA is proposed to screen current indicators. Additionally, a comprehensive evaluation method is proposed to adjust indicator weights according to the rate of change of indicator data, and a qualitative trend analysis method is introduced to improve visualization;
- (3)
- The effectiveness of the situational awareness method in this paper is verified through simulation analysis. A comparison with the operational status identification results of the pre-improvement method and the different evaluation methods recently proposed verifies the high sensing accuracy of the comprehensive evaluation method in this paper. A sensitivity analysis of the comprehensive evaluation model in this paper verifies that the evaluation scores of the model are also sensitive to indicators with small initial weights.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Liu, D.W.; Zhang, D.X.; Sun, H.D.; Ma, S.Y.; Li, B.Q. Construction of stability situation quantitative assessment and adaptive control system for large-scale power grid in the spatiotemporal big data environment. Proc. CSEE 2015, 35, 268–276. [Google Scholar]
- Liu, Y.; Mili, L.; Xu, Y.; Zhao, J.; Kamwa, I.; Srinivasan, D.; Mehrizi-Sani, A.; Arboleya, P.; Terzija, V. Guest editorial: Special issue on data-analytics for stability analysis, control, and situational awareness of power system with high-penetration of renewable energy. Int. J. Electr. Power Energy Syst. 2022, 137, 107773. [Google Scholar] [CrossRef]
- Liu, D.; Sheng, W.X.; Wang, Y.; Lu, Y.; Sun, C. Key technologies and trends of cyber physical system for power grid. Proc. CSEE 2015, 35, 3522–3531. [Google Scholar]
- Ge, L.; Li, Y.; Li, S.; Zhu, J.; Yan, J. Evaluation of the situational awareness effects for smart distribution networks under the novel design of indicator framework and hybrid weighting method. Front. Energy 2021, 15, 143–158. [Google Scholar] [CrossRef]
- Endsley, M.R. Toward a Theory of Situation Awareness in Dynamic Systems. Hum. Factors J. Hum. Factors Ergon. Soc. 1995, 37, 32–64. [Google Scholar] [CrossRef]
- Saunders, C.S.; Liu, G.; Yu, Y.; Zhu, W. Data-driven distributed analytics and control platform for smart grid situational awareness. CSEE J. Power Energy Syst. 2016, 2, 51–58. [Google Scholar] [CrossRef]
- Sun, W.Q.; Wang, C.M.; Zhang, Y. Flexibility evaluation and flexible comprehensive optimization in power systems. Euro. Trans. Electr. Power 2012, 22, 846–865. [Google Scholar]
- Porretta, B.; Kiguel, D.; Hamoud, G.; Neudorf, E. A comprehensive approach for adequacy and security evaluation of bulk power systems. IEEE Trans. Power Syst. 1991, 6, 433–441. [Google Scholar] [CrossRef]
- Xia, S.; Song, L.; Wu, Y.; Ma, Z.; Jing, J.; Ding, Z.; Li, G. An Integrated LHS–CD Approach for Power System Security Risk Assessment with Consideration of Source–Network and Load Uncertainties. Processes 2019, 7, 900. [Google Scholar] [CrossRef]
- Zhou, X.; Li, X.; Liu, F.; Ge, W.; Ma, X.; Tian, Y.; Li, G.; Zhang, J.; Qiu, Y. The comprehensive evaluation model of power supply capacity for regional-oriented distribution network. Neural Comput. Appl. 2020, 32, 5163–5171. [Google Scholar] [CrossRef]
- Ai, X.; Zhao, X.Z.; Hu, H.Y.; Wang, Z.D.; Peng, D.; Zhao, L. G1-entropy-independence Weight Method in Situational Awareness of Power Grid Development. Power Syst. Technol. 2020, 44, 3481–3487. [Google Scholar]
- Maihemuti, S.; Wang, W.; Wu, J.; Wang, H. New energy power system operation security evaluation based on the SWOT analysis. Sci. Rep. 2022, 12, 12680. [Google Scholar] [CrossRef]
- Song, R.J.; Ding, J.L.; Bai, L.; Liu, P.; Guannan, L.I. Fuzzy comprehensive evaluation of distribution network based on cooperative game theory and trapezoidal cloud model. Power Syst. Prot. Control. 2017, 45, 1–8. [Google Scholar]
- Zhang, S.; Wang, T.; Gu, X.Q. Synthetic Evaluation of Power Grid Operating States Based on Intuitionistic Fuzzy Analytic Hierarchy Process. Autom. Electr. Power Syst. 2016, 40, 41–49. [Google Scholar]
- Qian, J.X.; Wu, J.H.; Yao, L.; Mahmut, S.; Zhang, Q. Comprehensive performance evaluation of Wind- Solar- CCHP system based on energy analysis and multi-objective decision method. Energy 2021, 230, 120779. [Google Scholar] [CrossRef]
- Li, J.; Li, J.G.; Jiangang, Y.; Tangbing, L.I. Application of attribute recognition and G1-Entropy method in evaluation of power quality. Power Syst. Technol. 2009, 33, 56–61. [Google Scholar]
- Zhen, W.; Guang, X.; Heng, W. Distributed energy system for sustainability transition: A comprehensive assessment under uncertainties based on interval multicriteria decision making method by coupling interval DEMATEL and interval VIKOR. Energy 2019, 169, 750–761. [Google Scholar]
- Snežana, T.; Slobodan, Z.; Mladen, K. A novel hybrid MCDM model based on fuzzy DEMATEL, fuzzy ANP and fuzzy VIKOR for city logistics concept selection. Expert Sys. Appl. 2014, 41, 8112–8128. [Google Scholar]
- Fu, Z.; Xu, W.; Ming, K. Sustainable recycling partner selection using fuzzy DEMATEL-AEW-FVIKOR: A case study in small-and-medium enterprises (SMEs). J. Clean. Produc. 2018, 196, 489–504. [Google Scholar]
- Xiao, X.; Huang, J.; Lin, Z.; Wen, F. Multiple-criteria decision-making of distribution system planning considering distributed generation. In Proceedings of the International Conference on Sustainable Power Generation and Supply, Hangzhou, China, 8–9 September 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Wang, P.; Zhu, Z.; Wang, Y. A novel hybrid MCDM model combining the SAW, TOPSIS and GRA methods based on experimental design. Inf. Sci. 2016, 345, 27–45. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, Y.; Zhang, K.; Liu, Y.; Qiang, W.; Han Wen, Q. Artificial Intelligent Power Forecasting for Wind Farm Based on Multi-Source Data Fusion. Processes 2023, 11, 1429. [Google Scholar] [CrossRef]
- Hu, J.; Ma, D.; Liu, C.; Shi, Z.; Yan, H.; Hu, C. Network Security Situation Prediction Based on MR-SVM. IEEE Access 2019, 7, 130937–130945. [Google Scholar] [CrossRef]
- Fragkos, G.; Johnson, J.; Tsiropoulou, E.E. Dynamic Role-Based Access Control Policy for Smart Grid Applications: An Offline Deep Reinforcement Learning Approach. IEEE Trans. Hum.-Mach. Syst. 2022, 52, 761–773. [Google Scholar] [CrossRef]
- Messina, A.R.; Vittal, V. A structural time series approach to modeling dynamic trends in power system data. In Proceedings of the IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar] [CrossRef]
- Wang, T.; Zhang, S.; Gu, X. A trend-based approach for situation awareness in power systems. Int. Trans. Electr. Energy Syst. 2017, 27, e2446. [Google Scholar] [CrossRef]
- Basu, C.; Padmanaban, M.; Guillon, S.; Cauchon, L.; De Montigny, M.; Kamwa, I. Situational awareness for the electrical power grid. IBM J. Res. Dev. 2016, 60, 10: 1–10: 11. [Google Scholar] [CrossRef]
- Wu, J.; Ota, K.; Dong, M.; Li, J.; Wang, H. Big Data Analysis-Based Security Situational Awareness for Smart Grid. IEEE Trans. Big Data 2016, 4, 408–417. [Google Scholar] [CrossRef]
- Khan, I.A.; Akber, A.; Xu, Y. Sliding Window Regression based Short-Term Load Forecasting of a Multi-Area Power System. In Proceedings of the IEEE Canadian Conference of Electrical and Computer Engineering (CCECE), Edmonton, AB, Canada, 5–8 May 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Maurya, M.R.; Rengaswamy, R.; Venkatasubramanian, V. Fault diagnosis using dynamic trend analysis: A review and recent developments. Eng. Appl. Artif. Intell. 2007, 20, 133–146. [Google Scholar] [CrossRef]
- Chen, S.J.; Chen, Q.X.; Xia, Q. Steady-state Security Distance: Concept, Model and Meaning. Proc. CSEE 2015, 35, 600–608. [Google Scholar]
- Bhadane, K.V.; Ballal, M.S.; Nayyar, A.; Patil, D.P.; Jaware, T.H.; Shukla, H.P. A Comprehensive Study of Harmonic Pollution in Large Penetrated Grid-Connected Wind Farm. Mapan 2020, 36, 729–749. [Google Scholar] [CrossRef]
- Mendes, T.M.; Duque, C.A.; da Silva, L.R.M.; Ferreira, D.D.; Meyer, J.; Ribeiro, P.F. Comparative analysis of the measurement methods for the supraharmonic range. Int. J. Electr. Power Energy Syst. 2020, 118, 105801. [Google Scholar] [CrossRef]
- Krishnan, A.R.; Kasim, M.M.; Hamid, R.; Ghazali, M.F. A Modified CRITIC Method to Estimate the Objective Weights of Deci-sion Criteria. Symmetry 2021, 13, 973. [Google Scholar] [CrossRef]
- Lin, Z.; Wen, F.; Wang, H.; Lin, G.; Mo, T.; Ye, X. CRITIC-Based Node Importance Evaluation in Skeleton-Network Reconfiguration of Power Grids. IEEE Trans. Circuits Syst. II Express Briefs 2018, 65, 206–210. [Google Scholar] [CrossRef]
- Li, X.S.; Jiang, Y.L.; Xu, W.; Wang, Y.; Ding, Y. A Comprehensive Evaluation Method for Market Power of Generation Companies Based on Improved Critic-G1 Algorithm. Electr. Power 2021, 54, 59–67. [Google Scholar]
- Papageorgiou, E.I.; Iakovidis, D.K. Intuitionistic Fuzzy Cognitive Maps. IEEE Trans. Fuzzy Syst. 2013, 21, 342–354. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, Y.N.; Wang, H.K.; Chang, X.Q.; Zhao, M. Robust Fuzzy Dynamic Integrated Environmental Economic Dispatch for Multi-source System Considering the Double Uncertainty of Source-Load. High Volt. Eng. 2023, 44, 1–23. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, Y.; Li, T.; Ma, R.; Xu, K.; Xu, W. Evaluation of New Power System Based on Entropy Weight-TOPSIS Method. Math. Probl. Eng. 2022, 2022, 1–10. [Google Scholar] [CrossRef]
- Xiong, H.W.; Fan, W.; Niu, Y.Z.; Zeng, S.C.; Gong, H. Quality Evaluation Method of Power Cable Based on Fusion of Entropy Weight-analytic Hierarchy Process. High Volt. Appar. 2022, 58, 0185–0192. [Google Scholar]
- Fu, Z.Y.; Wang, T.; Kong, L.H.; Ma, H.; Xu, X.C. Power Consumption State Evaluation of Important Power Customers Based on AHP-TOPSIS Algorithm. Power Syst. Technol. 2022, 46, 4095–4101. [Google Scholar]
- Lu, H.; Zhao, Y.; Zhou, X.; Wei, Z. Selection of Agricultural Machinery Based on Improved CRITIC-Entropy Weight and GRA-TOPSIS Method. Processes 2022, 10, 266. [Google Scholar] [CrossRef]


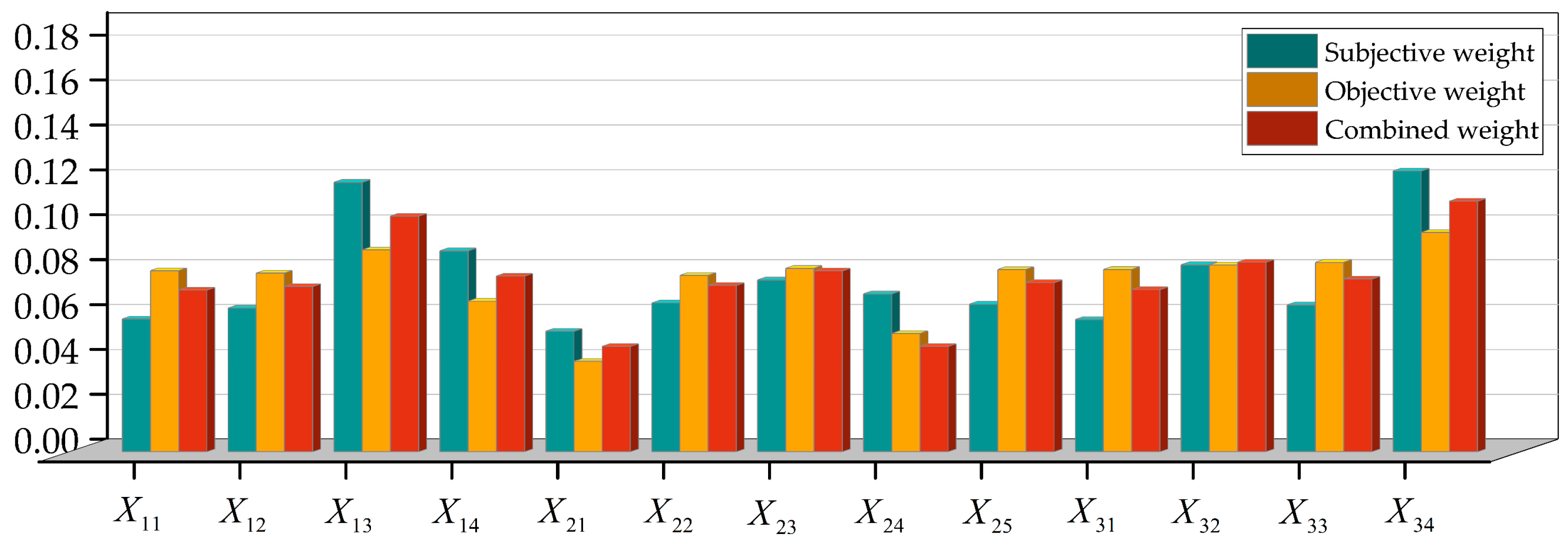

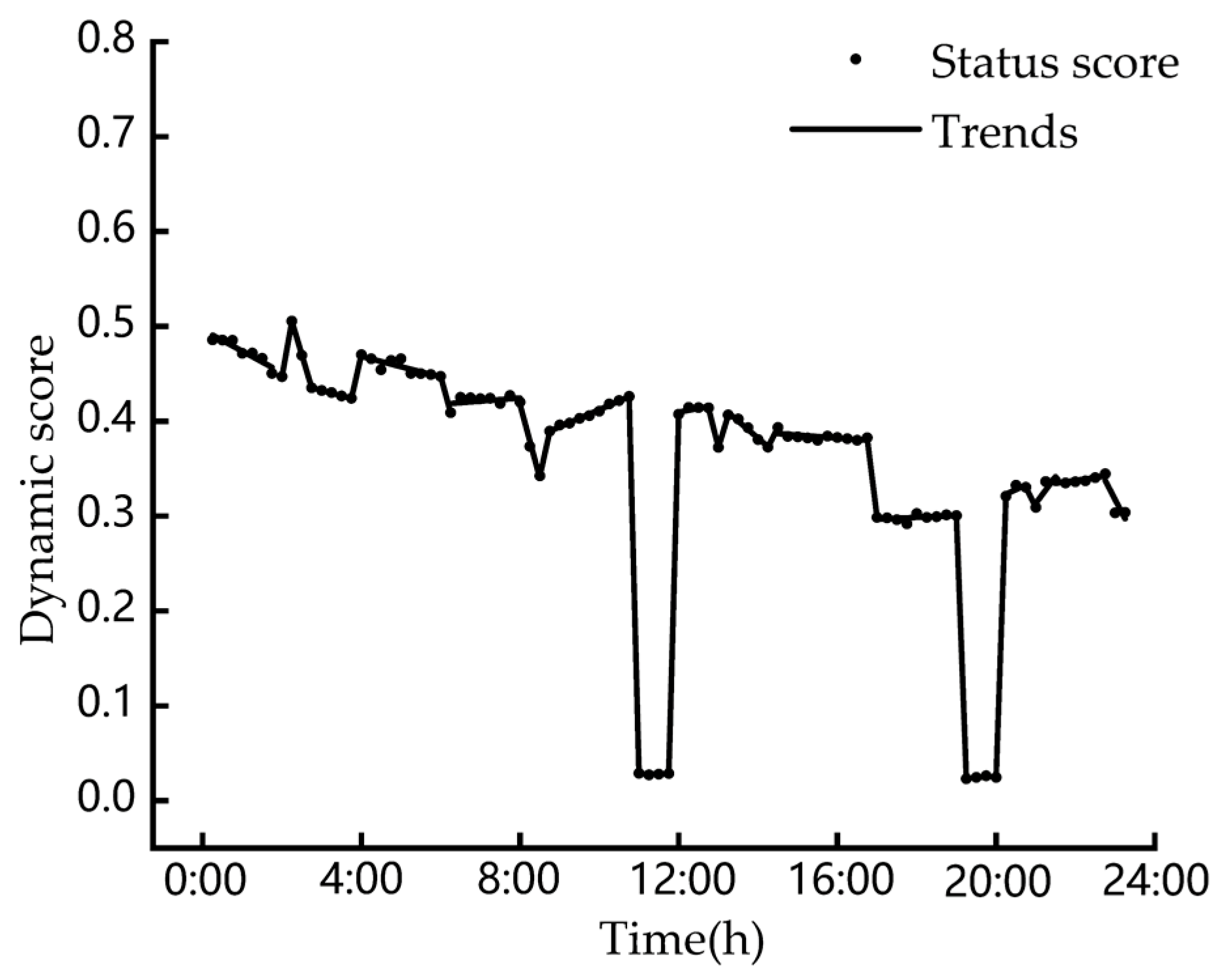
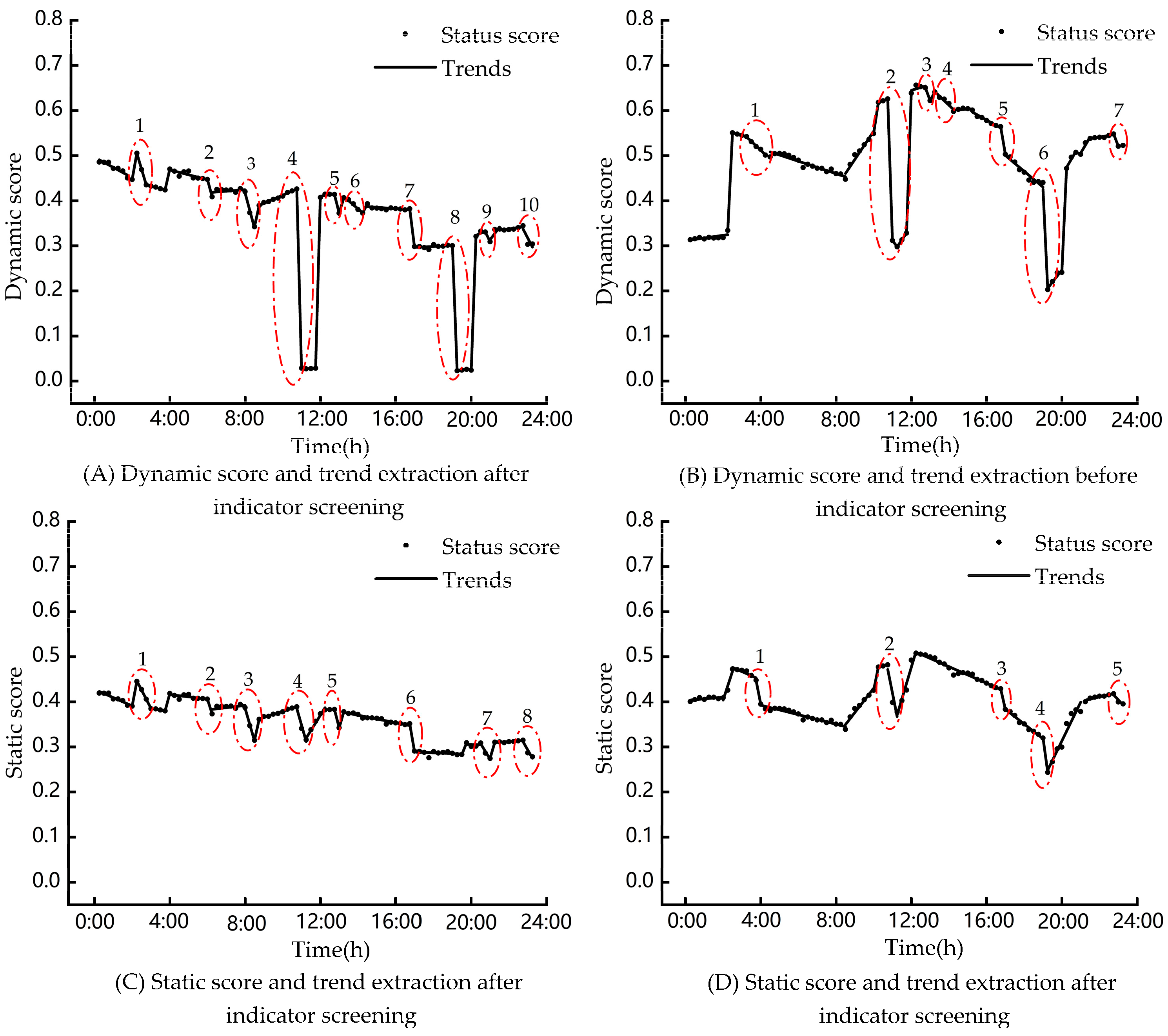
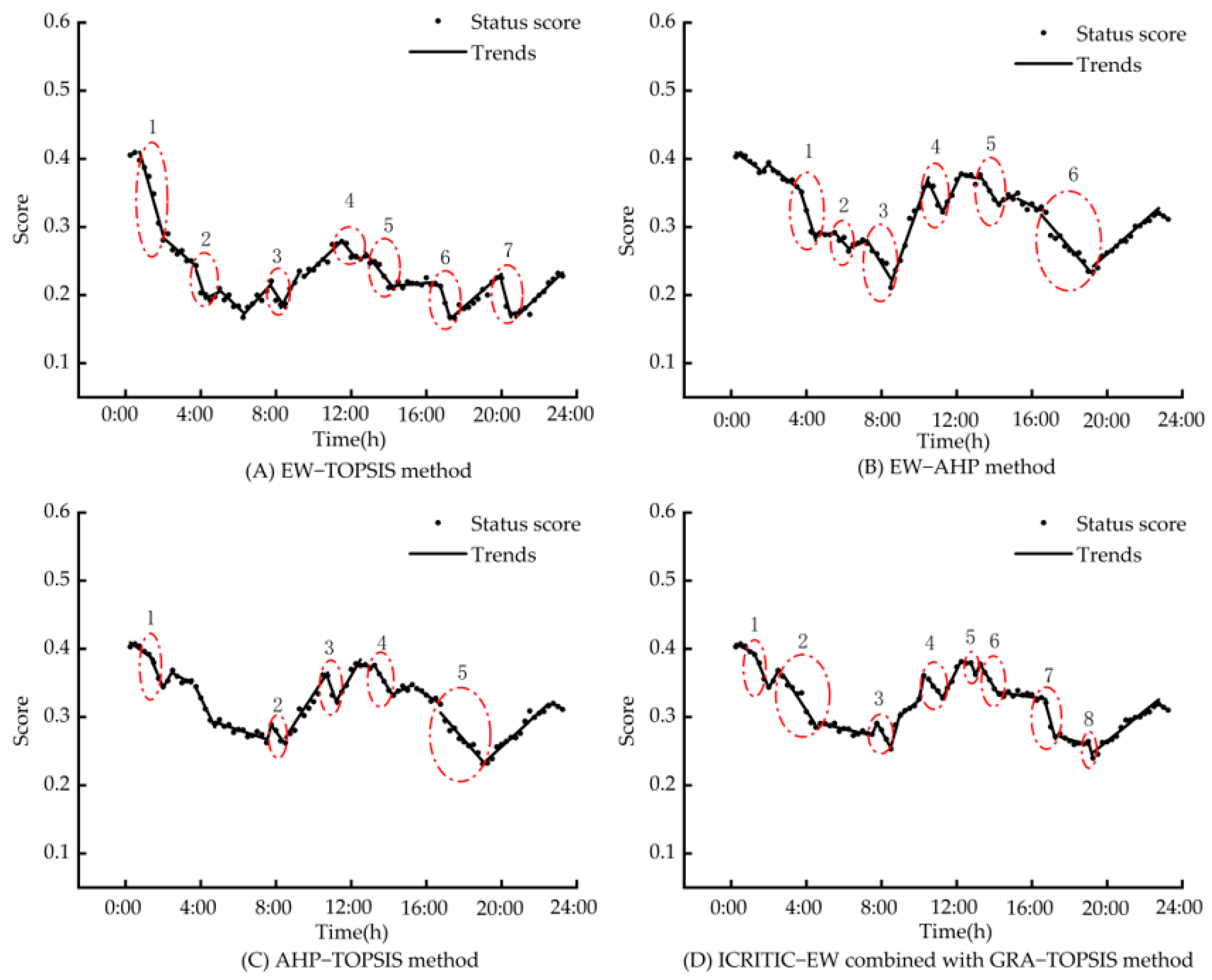

| Symbols | Meaning | Symbols | Meaning |
|---|---|---|---|
| KMO | Kaiser–Meyer–Olkin test statistics | renewable energy penetration | |
| MSA | Measure of Sampling Adequacy | active margin | |
| SA | Situation Awareness | static voltage stability margin | |
| static safety distance | initial decision matrix | ||
| average transformer load ratio | standardized decision matrix | ||
| average branch load ratio | correlation coefficient matrix | ||
| branch ratio | conflict coefficient | ||
| transformer specific ratio | objective indicator weight | ||
| short-circuit power flow over limit rate | belongs to with affiliation | ||
| the partial correlation coefficient | belongs to with non-affiliation | ||
| total harmonic distortion rate | belongs to with hesitation degrees | ||
| node voltage offset | intuitionistic fuzzy judgment matrix | ||
| frequency offset | product-type consistency judgment matrix | ||
| node voltage off-limit rate | subjective weights | ||
| the rate of power flow exceeding the limit | combined weight | ||
| the share of new energy generation | dynamic weighting | ||
| new energy abandonment rate | comprehensive score | ||
| share of incoming active power from the external grid | maximum branch load rate |
| Order | Evaluation Indexes | Order | Evaluation Indexes |
|---|---|---|---|
| Steady-state security distance | Node voltage off-limit rate | ||
| Average transformer load ratio | Rate of power flow exceeding the limit | ||
| Maximum branch load rate | Carbon dioxide emission reduction | ||
| Average branch load ratio | Share of new energy generation | ||
| Branch ratio | New energy abandonment rate | ||
| Transformer-specific ratio | Renewable energy penetration | ||
| Short-circuit power flow over limit rate | Share of external grid incoming active power | ||
| Total harmonic distortion rate | Active power margin | ||
| Node voltage offset | Static voltage stability margin | ||
| Frequency offset |
| Evaluation Indexes | Order | Allowable Fluctuation Range | Reference Standards |
|---|---|---|---|
| Total Voltage Distortion Rate | 0~8% | IEC 61000-2-2 [32] | |
| Nodal Voltage Offset | ±10% | EN 50160 [32] | |
| Frequency Shift | ±2% | IEC 61000-4-30 [33] |
| Number | Value | Maximum Indicator | Value | Results |
|---|---|---|---|---|
| 19 | 0.736 | 0.867 | Delete | |
| 18 | 0.689 | 0.829 | Delete | |
| 17 | 0.629 | 0.759 | Delete | |
| 16 | 0.359 | Stop |
| Indicators | … | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| - | 0.237 | 0.208 | 0.430 | … | 0.524 | 0.502 | 0.078 | 0.326 | 0.229 | |
| 0.237 | - | 0.135 | 0.917 1 | … | 0.631 | 0.619 | 0.349 | 0.395 | 0.344 | |
| … | … | … | … | … | … | … | … | … | … | … |
| 0.524 | 0.632 | 0.160 | 0.732 | … | - | 0.793 | 0.107 | 0.917 1 | 0.282 | |
| 0.503 | 0.619 | 0.165 | 0.717 | … | 0.793 | - | 0.157 | 0.916 1 | 0.301 | |
| … | … | … | … | … | … | … | … | … | … | … |
| 0.229 | 0.344 | 0.799 | 0.174 | … | 0.282 | 0.301 | 0.659 | 0.048 | - |
| Indicators | … | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| - | 0.766 | 0.070 | 0.307 | 0.425 | … | 0.078 | 0.374 | 0.803 | 0.185 | |
| 0.766 | - | 0.327 | 0.231 | 0.148 | … | 0.039 | 0.086 | 0.767 | 0.275 | |
| … | … | … | … | … | … | … | … | … | … | |
| 0.374 | 0.086 | 0.289 | 0.281 | 0.705 | … | 0.136 | - | 0.323 | 0.081 | |
| 0.803 | 0.768 | 0.058 | 0.075 | 0.437 | … | 0.108 | 0.323 | - | 0.229 | |
| 0.185 | 0.275 | 0.863 | 0.021 | 0.021 | … | 0.671 | 0.081 | 0.023 | - |
| Rule Layer | Index Layer | Index Attribute | |
|---|---|---|---|
| Stability | Average transformer load ratio | Small-type | |
| Maximum branch load rate | Small-type | ||
| Node voltage offset | Small-type | ||
| Frequency offset | Small-type | ||
| Safety | Total voltage distortion rate | Small-type | |
| branch ratio | Small-type | ||
| transformer ratio | Small-type | ||
| Node voltage crossing rate | Small-type | ||
| Rate of power flow exceeding the limit | Small-type | ||
| Adequacy | Share of external grid incoming active power | Small-type | |
| Share of new energy generation | Large-type | ||
| Static voltage stability margin | Large-type | ||
| Steady-state security distance | Large-type |
| Qualitative Evaluation Language (Indicator Compared with Indicator ) | Intuitive Blurred Numbers |
|---|---|
| Quite important | (0.90, 0.10, 0.00) |
| Very important | (0.80, 0.15, 0.05) |
| Obviously important | (0.70, 0.20, 0.10) |
| Slightly important | (0.60, 0.25, 0.15) |
| Equally important | (0.50, 0.30, 0.20) |
| Slightly unimportant | (0.40, 0.45, 0.15) |
| Obviously unimportant | (0.30, 0.60, 0.10) |
| Very unimportant | (0.20, 0.75, 0.05) |
| Quite unimportant | (0.10, 0.90, 0.00) |
| Time Period | Major Destabilizing Factors | Maximum Rate of Change (%) |
|---|---|---|
| 2:15~2:45 | Increases in external grid incoming active power | 4.71 |
| 6:00~6:30 | branch increase | 50 |
| 8:00~8:45 | branch circuit increase | 56.5 |
| 11:00~12:00 | Branch tide crosses the line | 100 |
| 12:45~13:15 | Static safety distance decreases | 29.3 |
| 13:15~13:30 | Static safety distance decreases | 3.4 |
| 16:45~17:15 | transformer increase | 75 |
| 19:00~20:00 | Branch tide crosses the line | 100 |
| 20:45~21:15 | Static safety distance decreases | 18.8 |
| 22:45~23:30 | transformer increase | 33.3 |
| Time Period | Trending Primitives | Time Period | Trending Primitives |
|---|---|---|---|
| 2:15~2:45 | C | 13:15~13:30 | C |
| 6:00~6:30 | C | 16:45~17:15 | C |
| 8:00~8:45 | C | 19:00~20:00 | C |
| 11:00~12:00 | C | 20:45~21:15 | C |
| 12:45~13:15 | C | 22:45~23:30 | C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Meng, Q.; Wu, J.; Wang, H. Research on New Energy Power System Stability Situation Awareness Based on Index Screening and Dynamic Evaluation. Processes 2023, 11, 1509. https://doi.org/10.3390/pr11051509
Meng Q, Wu J, Wang H. Research on New Energy Power System Stability Situation Awareness Based on Index Screening and Dynamic Evaluation. Processes. 2023; 11(5):1509. https://doi.org/10.3390/pr11051509
Chicago/Turabian StyleMeng, Qingyang, Jiahui Wu, and Haiyun Wang. 2023. "Research on New Energy Power System Stability Situation Awareness Based on Index Screening and Dynamic Evaluation" Processes 11, no. 5: 1509. https://doi.org/10.3390/pr11051509
APA StyleMeng, Q., Wu, J., & Wang, H. (2023). Research on New Energy Power System Stability Situation Awareness Based on Index Screening and Dynamic Evaluation. Processes, 11(5), 1509. https://doi.org/10.3390/pr11051509





