Fault Diagnosis of Bearings Using Wavelet Packet Energy Spectrum and SSA-DBN
Abstract
:1. Introduction
2. Theoretical Background
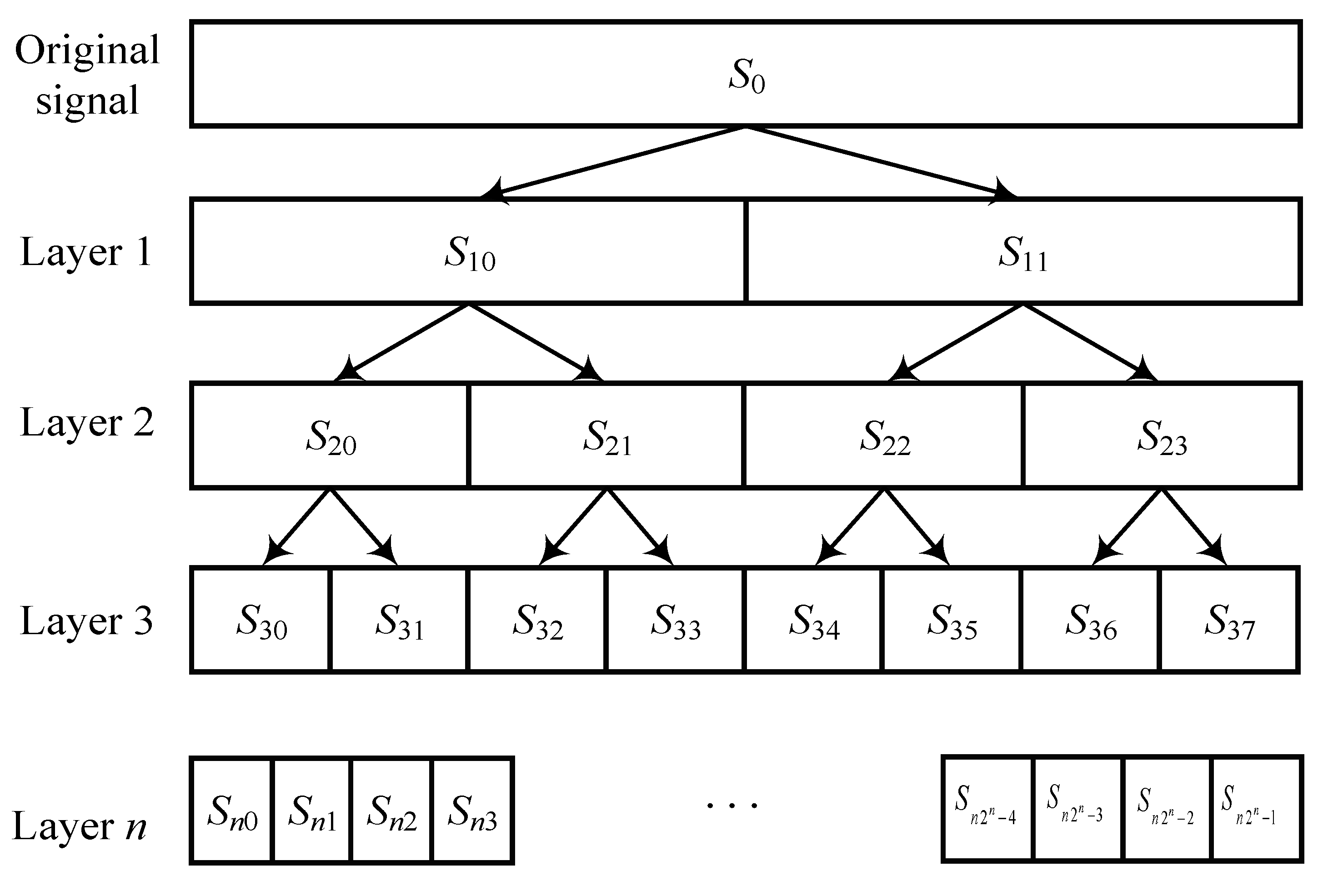
2.1. Wavelet Packet Energy Spectrum
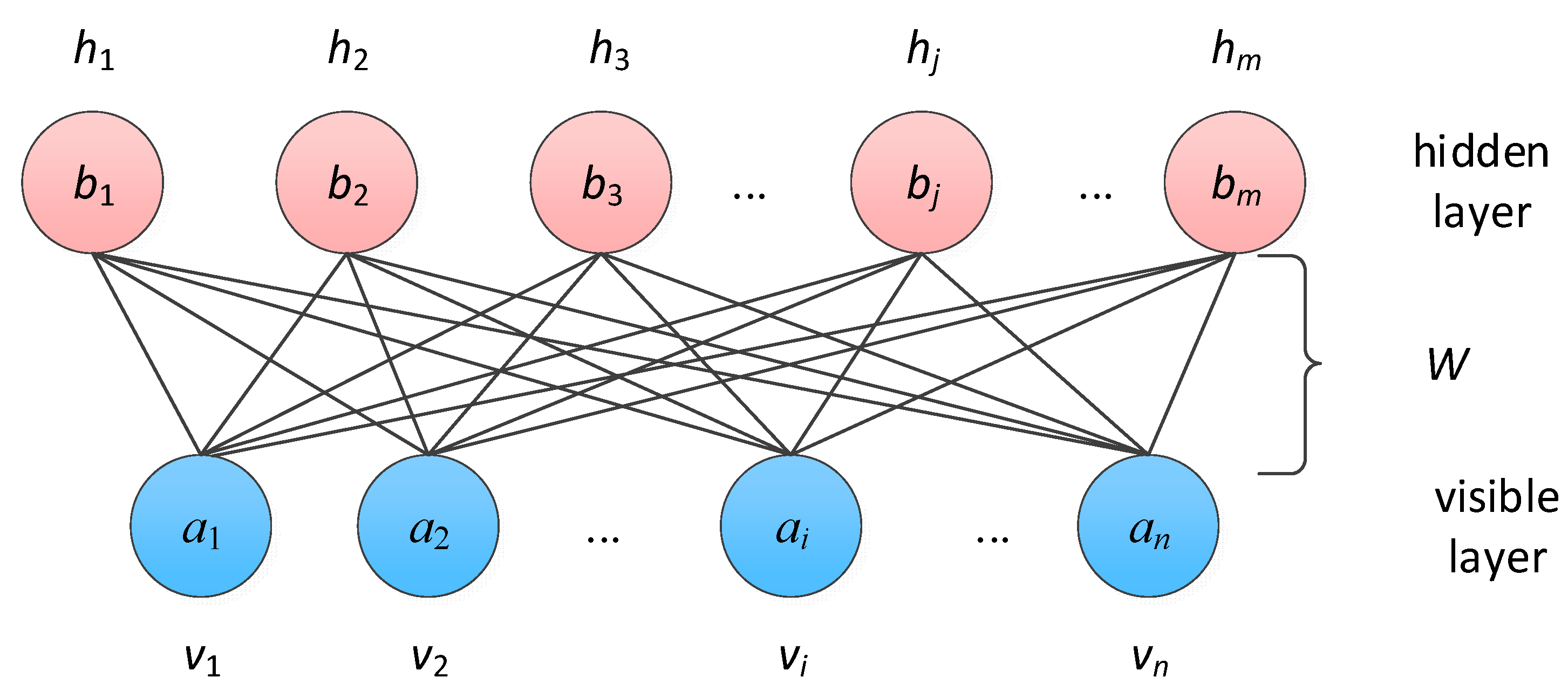
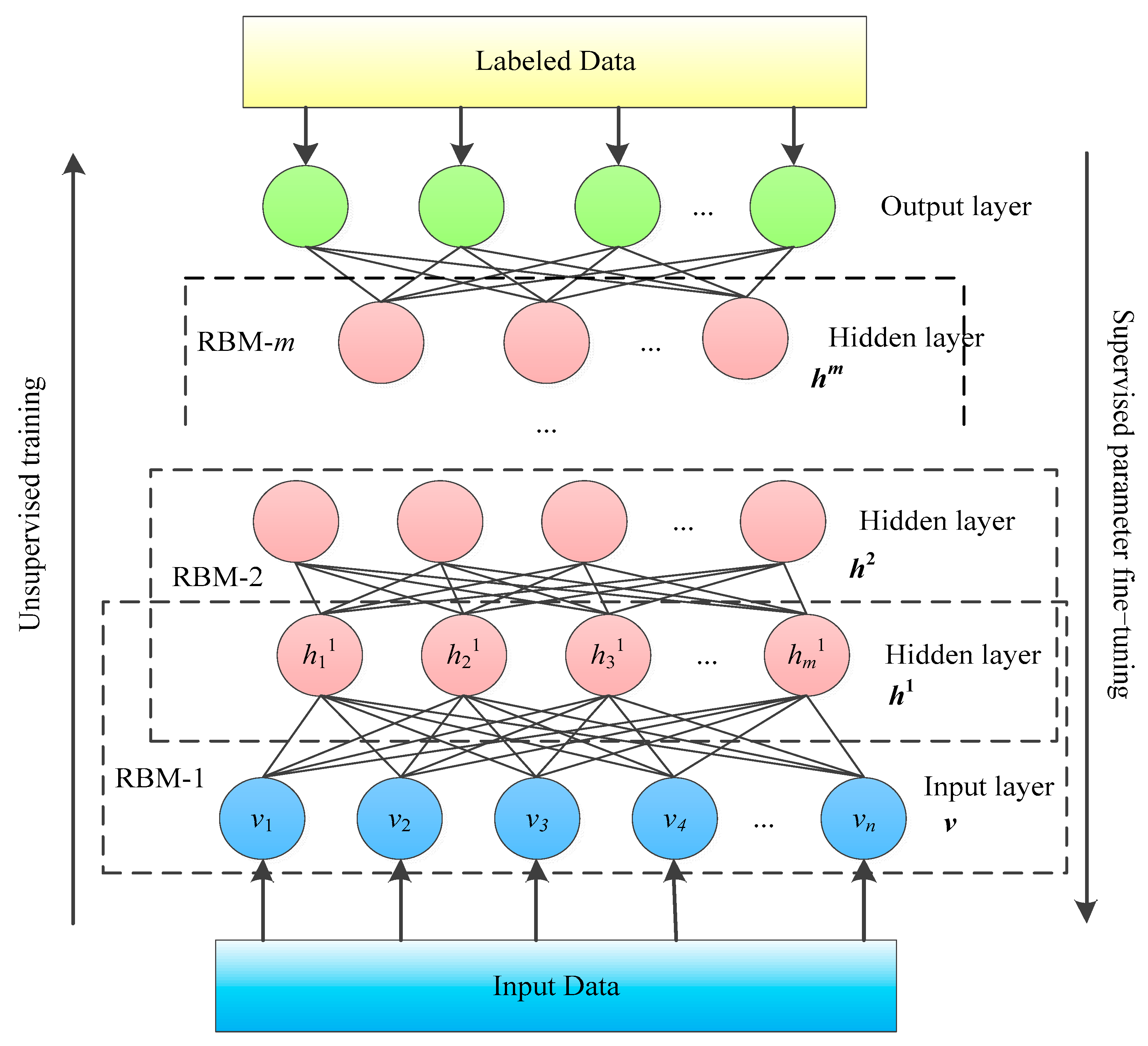
2.2. Deep Belief Networks
2.3. Sparrow Search Algorithm
- Explorers in sparrows generally have better fitness, are responsible for searching for food during the foraging process, and transmit the information of foraging direction and location to the followers.
- In the process of foraging, when individual sparrows encounter danger, they will sound an early warning signal. If it exceeds the pre-set safety threshold, explorers will take followers out of the area and find another safe area to continue foraging.
- The identity of explorers and followers in the sparrow population is not fixed. When a follower finds a better foraging place and food source, the individual will shift from follower to explorer, and will also have an equal amount of explorer-into-follower identity, because the calculation presupposes that the proportion of explorers and followers in the whole sparrow population is fixed.
- Since the explorer would arrive at the foraging site first to replenish his energy, the later followers would receive relatively little food. Therefore, the last follower has the worst fitness value, which prompts them to forage elsewhere, optimize their fitness, and increase the exploration of other unsearched areas.
- Followers, after receiving the information from the explorers, will choose to find the explorer with the most food and follow in their footsteps to forage or search around, because they believe that being beside the best explorer is more likely to result in them finding food. Some sparrows will monitor these explorers, and when the explorers find an area with food, they will participate in the competition for food resources.
- When attacked by outsiders, individuals on the edge of the foraging will constantly reposition themselves to the internal safety area. Individual sparrows in the internal safety zones will attempt to approach their peers in order to enhance their safety.
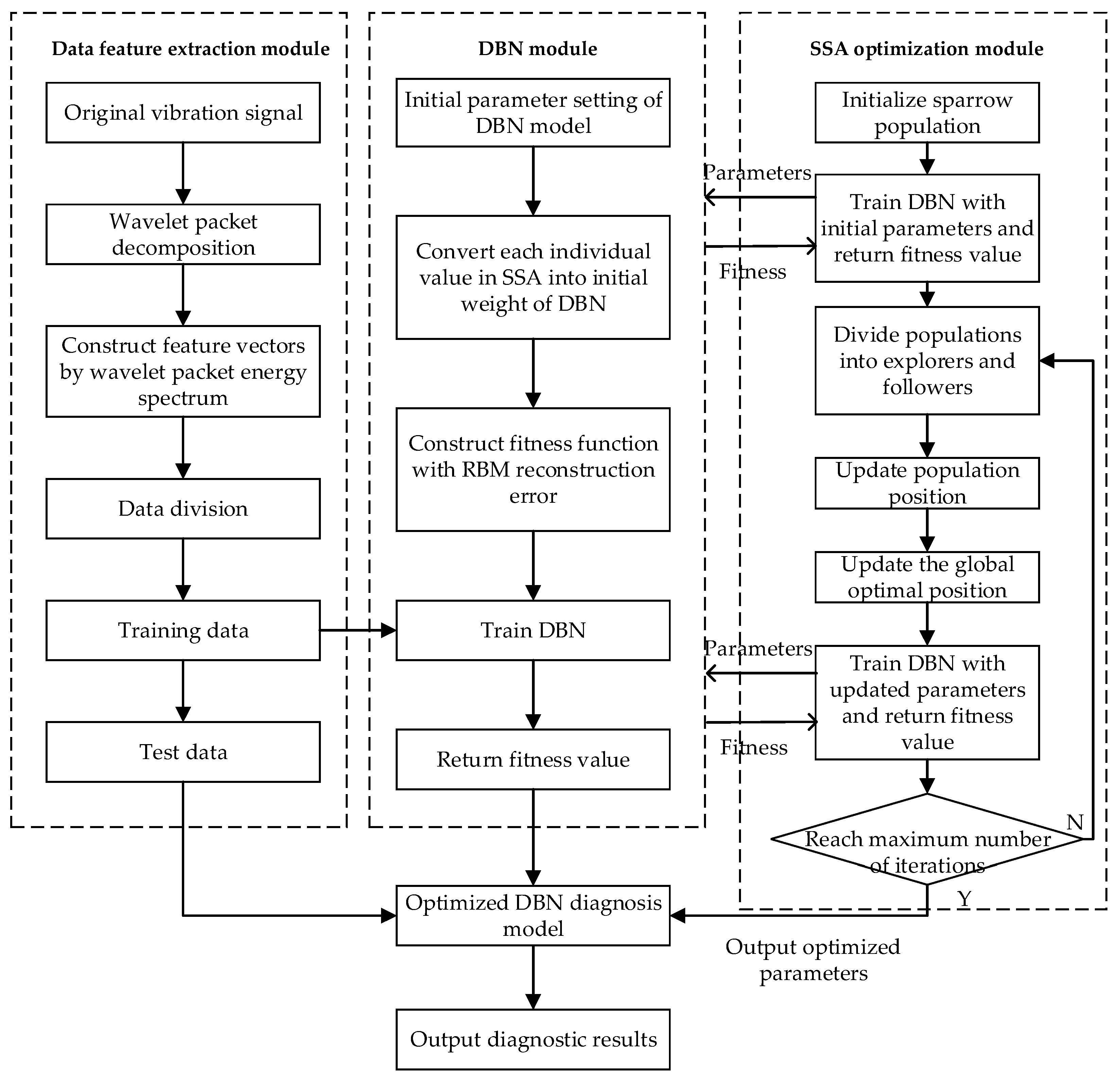
3. Proposed Methodologies
4. Experimentation
4.1. Experimental Environment
4.2. Experimental Dataset
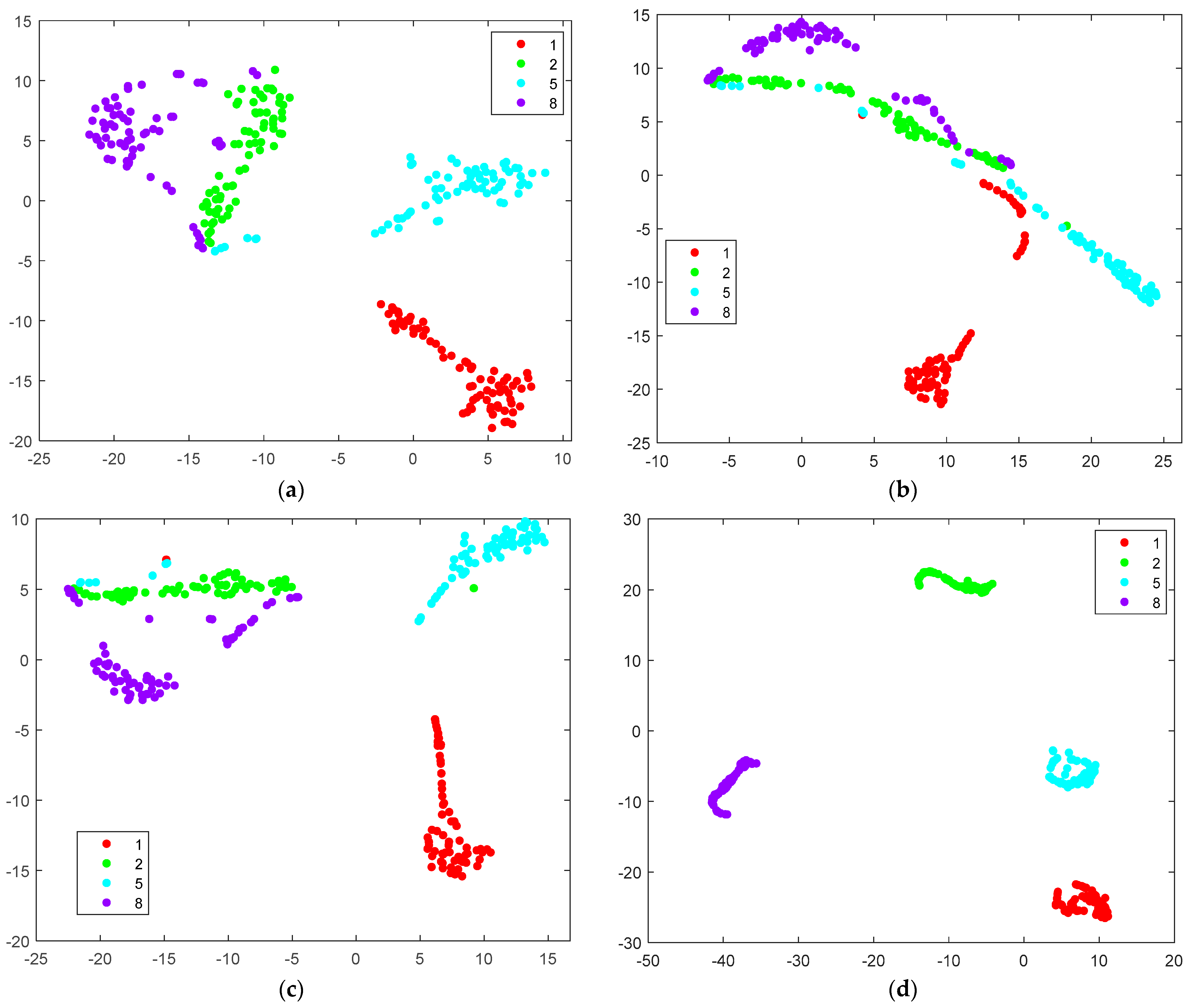
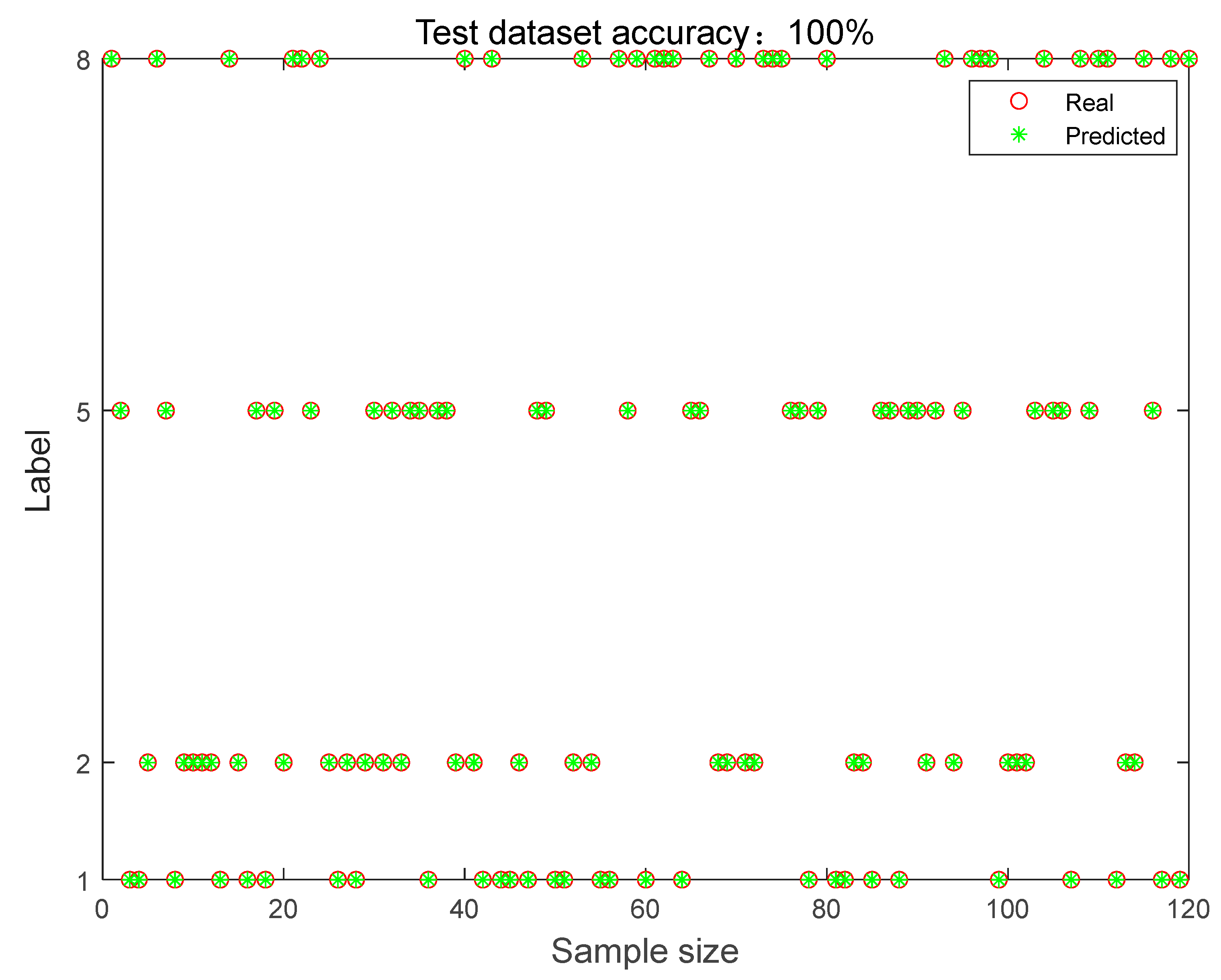
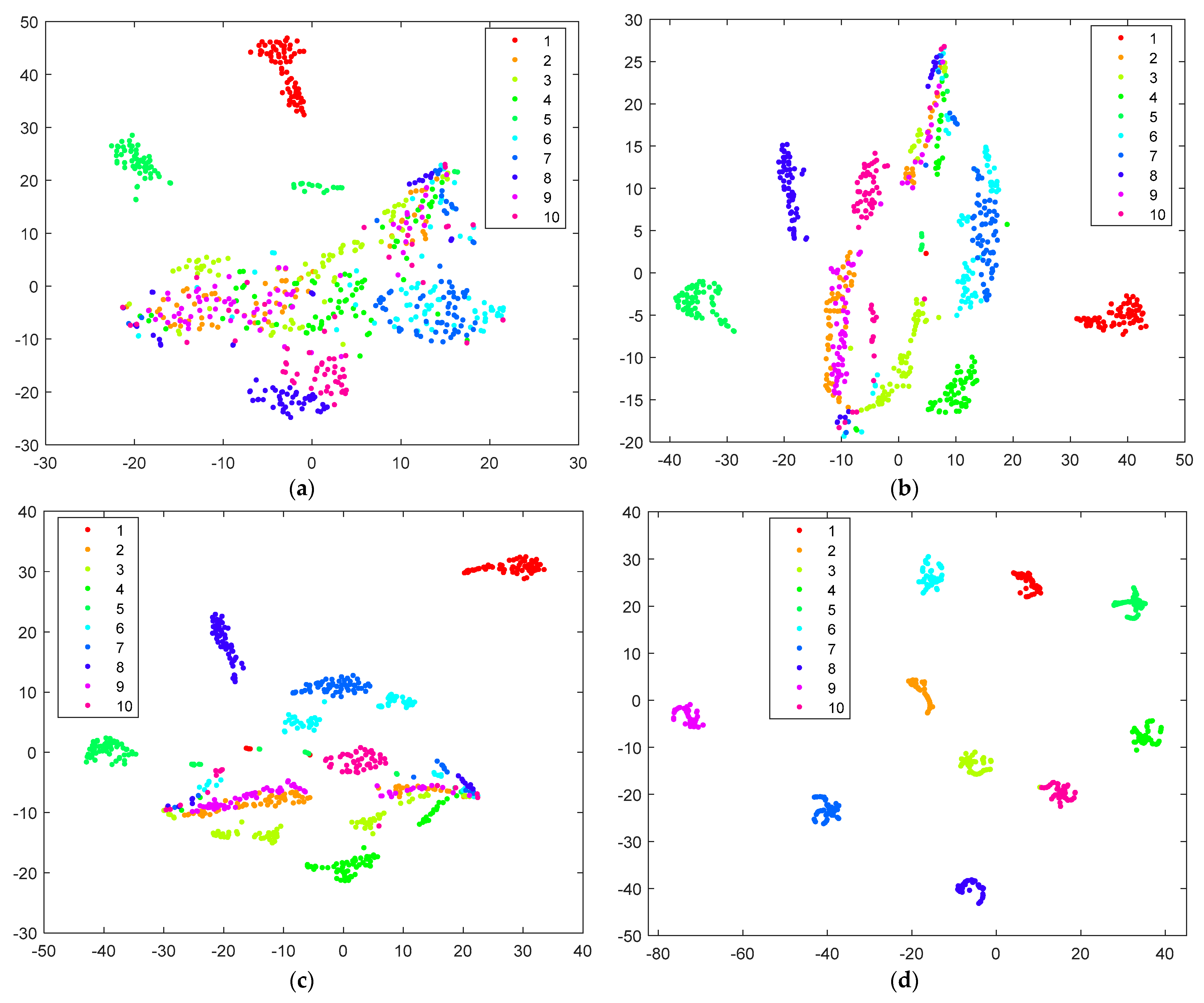
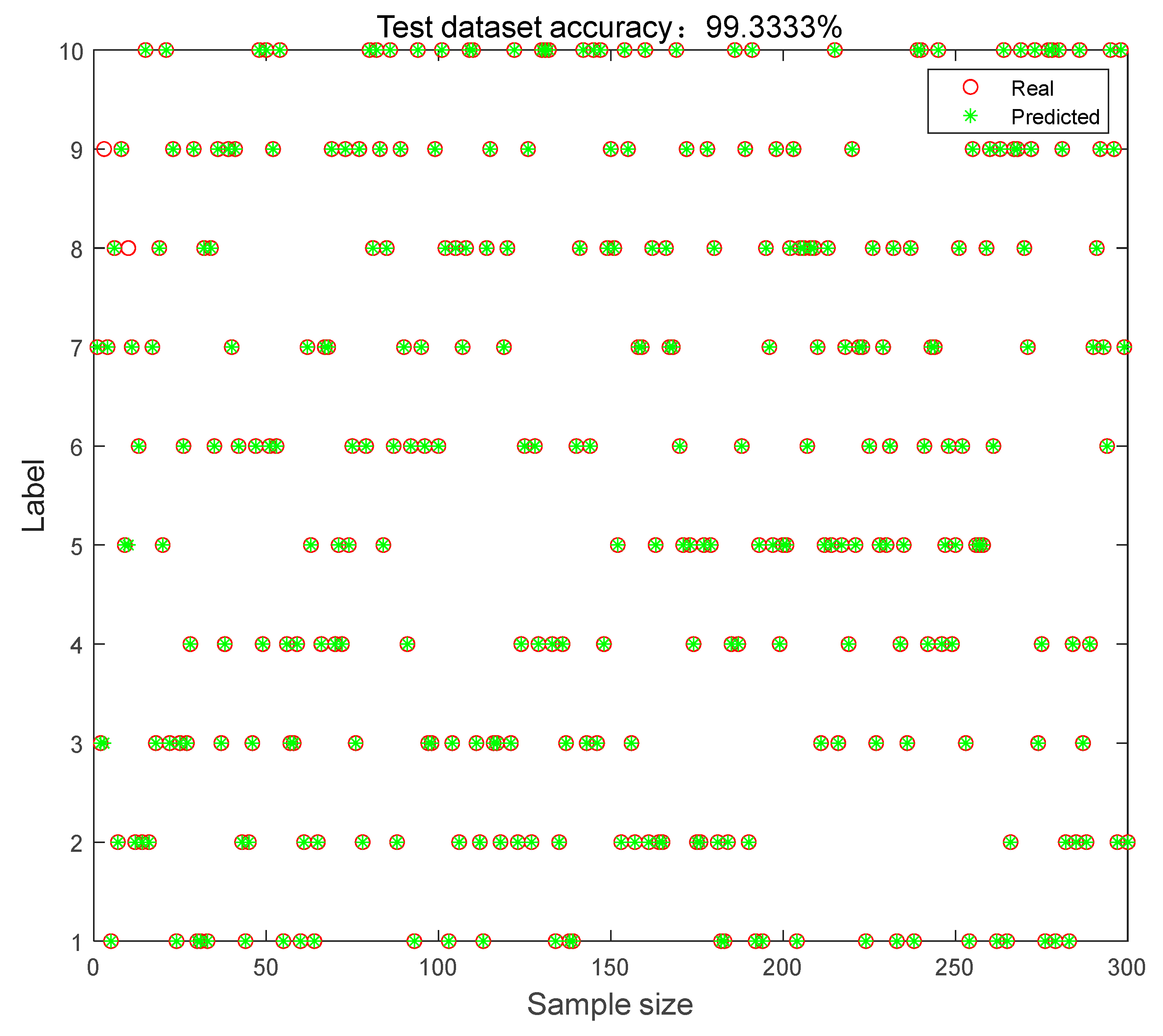
4.3. Results and Discussion
5. Conclusions, Limitations, and Future Research
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, H.; Jiang, B. A review of fault detection and diagnosis for the traction system in high-speed trains. IEEE Trans. Intell. Transp. Syst. 2019, 21, 450–465. [Google Scholar] [CrossRef]
- Sun, Q.; Xiong, J.; Zhang, Q. Research methods of the rotating machinery fault diagnosis. Mach. Tool Hydraul. 2018, 46, 133–139. [Google Scholar] [CrossRef]
- Rehman, N.; Afta, H. Multivariate variational mode decomposition. IEEE Trans. Signal Process. 2019, 67, 6039–6052. [Google Scholar] [CrossRef] [Green Version]
- Khalid, S.; Song, J.; Raouf, I.; Kim, H. Advances in Fault Detection and Diagnosis for Thermal Power Plants: A Review of Intelligent Techniques. Mathematics 2023, 11, 1767. [Google Scholar] [CrossRef]
- Han, T.; Liu, R.; Zhao, Z.; Kundu, P. Fault Diagnosis and Health Management of Power Machinery. Machines 2023, 11, 424. [Google Scholar] [CrossRef]
- Ding, X.; He, Q.; Luo, N. A fusion feature and its improvement based on locality preserving projections for rolling element bearing fault classification. J. Sound Vib. 2015, 335, 367–383. [Google Scholar] [CrossRef]
- Rostaghi, M.; Azami, H. Dispersion Entropy: A Measure for Time-Series Analysis. IEEE Signal Process. Lett. 2016, 23, 610–614. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; Zuo, M. Condition monitoring and fault diagnosis of planetary gearboxes: A review. Measurement 2014, 48, 292–305. [Google Scholar] [CrossRef]
- Lee, C.; Le, T.; Chang, C. Application of Hybrid Model between the Technique for Order of Preference by Similarity to Ideal Solution and Feature Extractions for Bearing Defect Classification. Mathematics 2023, 11, 1442. [Google Scholar] [CrossRef]
- Hoang, D.; Kang, H.; Kang, J. A motor current signal-based bearing fault diagnosis using deep learning and information fusion. IEEE Trans. Instrum. Meas. 2020, 69, 3325–3333. [Google Scholar] [CrossRef]
- Lian, Z.; Zhou, Z.; Zhang, X.; Feng, Z.; Han, X.; Hu, C. Fault Diagnosis for Complex Equipment Based on Belief Rule Base with Adaptive Nonlinear Membership Function. Entropy 2023, 25, 442. [Google Scholar] [CrossRef] [PubMed]
- Evgeny, A.; George, V.; Irina, S.; Alexander, P. An Overview of Vibration Analysis Techniques for the Fault Diagnostics of Rolling Bearings in Machinery. Shock Vib. 2022, 2022, 6136231. [Google Scholar] [CrossRef]
- Antonino, J.; Pons, J.; Lee, S. Advanced rotor fault diagnosis for medium-voltage induction motors via continuous transforms. IEEE Trans. Ind. Appl. 2016, 52, 4503–4509. [Google Scholar] [CrossRef] [Green Version]
- Chuan, L.; Oliveira, J.; Cerrada, M.; Cabrera, D.; Sánchez, R.; Zurita, G. A systematic review of fuzzy formalisms for bearing fault diagnosis. IEEE Trans. Fuzzy Syst. 2019, 27, 1362–1382. [Google Scholar] [CrossRef]
- Feng, Z.; Liang, M.; Chu, F. Recent advances in time-frequency analysis methods for machinery fault diagnosis:a review with application examples. Mech. Syst. Signal Process. 2013, 38, 165–205. [Google Scholar] [CrossRef]
- Attoui, I.; Fergani, N.; Boutasseta, N.; Oudjani, B.; Deliou, A. A new time-frequency method for identification and classification of ball bearing faults. J. Sound Vib. 2017, 397, 241–265. [Google Scholar] [CrossRef]
- Paulis, F.; Boudjefdjouf, H.; Bouchekara, H.; Orlandi, A.; Smail, M. Performance improvements of wire fault diagnosis approach based on time-domain reflectometry. IET Sci. Meas. Technol. 2017, 11, 538–544. [Google Scholar] [CrossRef]
- Han, W.; Wang, Z.; Shen, Y.; Xie, W. Robust fault estimation in the finite-frequency domain for multi-agent systems. Trans. Inst. Meas. Control 2019, 41, 3171–3181. [Google Scholar] [CrossRef]
- Karioja, K.; Lahdelma, S.; Litak, G.; Ambrozkiewicz, B. Extracting periodically repeating shocks in a gearbox from simultaneously occurring random vibration. In Proceedings of the 15th International Conference on Condition Monitoring and Machinery Failure Prevention Technologies, CM/MFPT, Nottingham, UK, 10–12 September 2018; pp. 456–464. [Google Scholar]
- Duan, Y.; Wang, C.; Chen, Y.; Liu, P. Improving the Accuracy of Fault Frequency by Means of Local Mean Decomposition and Ratio Correction Method for Rolling Bearing Failure. Appl. Sci. 2019, 9, 1888. [Google Scholar] [CrossRef] [Green Version]
- Burriel, J.; Puche, R.; Pineda, M. Short-Frequency Fourier Transform for Fault Diagnosis of Induction Machines Working in Transient Regime. IEEE Trans. Instrum. Meas. 2017, 66, 432–440. [Google Scholar] [CrossRef] [Green Version]
- Qin, Y.; Mao, Y.; Chen, H. M-band flexible wavelet transform and its application to the fault diagnosis of planetary gear transmission systems. Mech. Syst. Signal Process. 2019, 134, 106298. [Google Scholar] [CrossRef]
- Yan, B.; Wang, B.; Zhou, F.; Li, W.; Xu, B. Sparse feature extraction for fault diagnosis of rotating machinery based on sparse decomposition combined multiresolution generalized S transform. J. Low Freq. Noise Vib. Act. Control 2019, 38, 441–456. [Google Scholar] [CrossRef]
- Lv, Q.; Yu, X.; Ma, H.; Ye, J.; Wu, W.; Wang, X. Applications of Machine Learning to Reciprocating Compressor Fault Diagnosis: A Review. Processes 2021, 9, 909. [Google Scholar] [CrossRef]
- Fu, S.; Wu, Y.; Wang, R.; Mao, M. A Bearing Fault Diagnosis Method Based on Wavelet Denoising and Machine Learning. Appl. Sci. 2023, 13, 5936. [Google Scholar] [CrossRef]
- Yu, Y.; Gao, H.; Zhou, S.; Pan, Y.; Zhang, K.; Liu, P.; Yang, H.; Zhao, Z.; Madyira, D.M. Rotor Faults Diagnosis in PMSMs Based on Branch Current Analysis and Machine Learning. Actuators 2023, 12, 145. [Google Scholar] [CrossRef]
- Zhang, X.; Jiang, D.; Long, Q.; Han, T. Rotating machinery fault diagnosis for imbalanced data based on decision tree and fast clustering algorithm. J. Vibroeng. 2017, 19, 4247–4259. [Google Scholar] [CrossRef] [Green Version]
- Tang, G.; Pang, B.; Tian, T.; Zhou, C. Fault Diagnosis of Rolling Bearings Based on Improved Fast Spectral Correlation and Optimized Random Forest. Appl. Sci. 2018, 8, 1859. [Google Scholar] [CrossRef] [Green Version]
- Ren, L.; Yong, B. Wind Turbines Fault Classification Treatment Method. Symmetry 2022, 14, 688. [Google Scholar] [CrossRef]
- Qu, J.; Ma, B.; Ma, X.; Wang, M. Hybrid Fault Diagnosis Method based on Wavelet Packet Energy Spectrum and SSA-SVM. Int. J. Adv. Comput. Sci. Appl. (IJACSA) 2022, 13, 52–60. [Google Scholar] [CrossRef]
- Equbal, M.; Khan, S.; Islam, T. Transformer incipient fault diagnosis on the basis of energy-weighted DGA using an artificial neural network. Turk. J. Electr. Eng. Comput. Sci. 2018, 26, 77–88. [Google Scholar] [CrossRef]
- Duan, L.; Xie, M.; Wang, J.; Bai, T. Deep learning enabled intelligent fault diagnosis: Overview and applications. J. Intell. Fuzzy Syst. 2018, 35, 5771–5784. [Google Scholar] [CrossRef]
- Zhu, J.; Jiang, Q.; Shen, Y. Application of recurrent neural network to mechanical fault diagnosis: A review. J. Mech. Sci. Technol. 2022, 36, 527–542. [Google Scholar] [CrossRef]
- Tang, S.; Yuan, S.; Zhu, Y. Deep Learning-Based Intelligent Fault Diagnosis Methods Toward Rotating Machinery. IEEE Access 2020, 8, 9335–9346. [Google Scholar] [CrossRef]
- Jia, P.; Wang, C.; Zhou, F.; Hu, X. Trend Feature Consistency Guided Deep Learning Method for Minor Fault Diagnosis. Entropy 2023, 25, 242. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Li, J.; Wu, W.; Dong, F.; Wan, S. Multi-Fault Classification and Diagnosis of Rolling Bearing Based on Improved Convolution Neural Network. Entropy 2023, 25, 737. [Google Scholar] [CrossRef]
- Zhang, Q.; He, Q.; Qin, J.; Duan, J. Application of Fault Diagnosis Method Combining Finite Element Method and Transfer Learning for Insufficient Turbine Rotor Fault Samples. Entropy 2023, 25, 414. [Google Scholar] [CrossRef]
- Mansouri, M.; Dhibi, K.; Hajji, M.; Bouzara, K.; Nounou, H.; Nounou, M. Interval-Valued Reduced RNN for Fault Detection and Diagnosis for Wind Energy Conversion Systems. IEEE Sens. J. 2022, 22, 13581–13588. [Google Scholar] [CrossRef]
- Jiang, M.; Liang, Y.; Feng, X. Text classification based on deep belief network and softmax regression. Neural Comput. Applic. 2018, 29, 61–70. [Google Scholar] [CrossRef]
- Luo, H.; He, C.; Zhou, J.; Zhang, L. Rolling Bearing Sub-Health Recognition via Extreme Learning Machine Based on Deep Belief Network Optimized by Improved Fireworks. IEEE Access 2021, 9, 42013–42026. [Google Scholar] [CrossRef]
- Yang, E.; Wang, Y.; Wang, P.; Guan, Z.; Deng, W. An Intelligent Identification Approach Using VMD-CMDE and PSO-DBN for Bearing Faults. Electronics 2022, 11, 2582. [Google Scholar] [CrossRef]
- Smith, W.; Randall, R. Rolling element bearing diagnostics using the Case Western Reserve University data: A benchmark study. Mech. Syst. Signal Process 2015, 64–65, 100–113. [Google Scholar] [CrossRef]





| Item | Specification |
|---|---|
| Operating System | Windows 10 |
| CPU | Intel Core i7-10700K @ 3.80GHz |
| RAM | DDR4 2133MHz 64G |
| Matlab | R2020a |
| Status | Fault Depth/mm | Label | Single Type | Training Set Sample Size | Verification Set Sample Size |
|---|---|---|---|---|---|
| Normal state | -- | 1 | NOR | 70 | 30 |
| Inner ring failure | 0.1778 | 2 | IR007 | 70 | 30 |
| 0.3556 | 3 | IR014 | 70 | 30 | |
| 0.5334 | 4 | IR021 | 70 | 30 | |
| Outer ring failure | 0.1778 | 5 | OR007 | 70 | 30 |
| 0.3556 | 6 | OR014 | 70 | 30 | |
| 0.5334 | 7 | OR021 | 70 | 30 | |
| Rolling body failure | 0.1778 | 8 | BA007 | 70 | 30 |
| 0.3556 | 9 | BA014 | 70 | 30 | |
| 0.5334 | 10 | BA021 | 70 | 30 |
| Norm | SVM | ELM | GA-BP | DBN | WPES-SSA-DBN |
|---|---|---|---|---|---|
| Maximum | 95.83 | 97.5 | 99.17 | 99.17 | 100 |
| Minimum | 87.5 | 91.67 | 93.33 | 93.33 | 100 |
| Average | 93 | 94.5 | 96.67 | 96.4 | 100 |
| Standard Deviation | 0.028 | 0.017 | 0.015 | 0.018 | 0 |
| Norm | SVM | ELM | GA-BP | DBN | WPES-SSA-DBN |
|---|---|---|---|---|---|
| Maximum | 93.33 | 94.67 | 94.67 | 95.33 | 99.33 |
| Minimum | 86.67 | 86.67 | 92 | 90 | 96.67 |
| Average | 88.87 | 90.67 | 93.33 | 92.6 | 97.93 |
| Standard Deviation | 0.022 | 0.027 | 0.008 | 0.017 | 0.008 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qu, J.; Cheng, X.; Liang, P.; Zheng, L.; Ma, X. Fault Diagnosis of Bearings Using Wavelet Packet Energy Spectrum and SSA-DBN. Processes 2023, 11, 1875. https://doi.org/10.3390/pr11071875
Qu J, Cheng X, Liang P, Zheng L, Ma X. Fault Diagnosis of Bearings Using Wavelet Packet Energy Spectrum and SSA-DBN. Processes. 2023; 11(7):1875. https://doi.org/10.3390/pr11071875
Chicago/Turabian StyleQu, Jinglei, Xueli Cheng, Ping Liang, Lulu Zheng, and Xiaojie Ma. 2023. "Fault Diagnosis of Bearings Using Wavelet Packet Energy Spectrum and SSA-DBN" Processes 11, no. 7: 1875. https://doi.org/10.3390/pr11071875
APA StyleQu, J., Cheng, X., Liang, P., Zheng, L., & Ma, X. (2023). Fault Diagnosis of Bearings Using Wavelet Packet Energy Spectrum and SSA-DBN. Processes, 11(7), 1875. https://doi.org/10.3390/pr11071875






