CFD Investigation on the Performance of Cyclone Separators with Divergent or Convergent Insertion Pipes
Abstract
:1. Introduction
2. Model Description
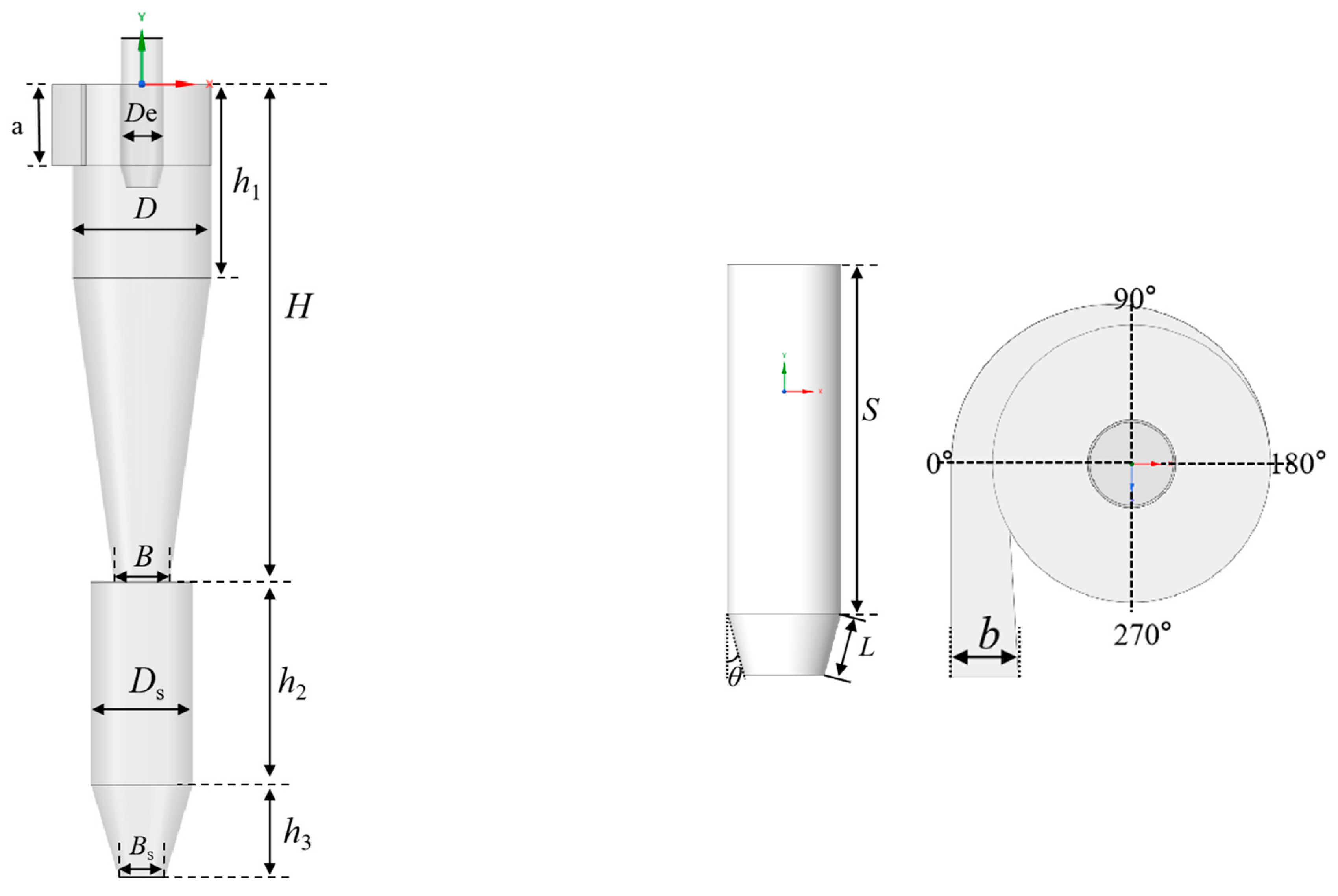
2.1. Geometrical Characteristics
2.2. Computational Fluid Dynamics Model
2.2.1. Reynolds Stress Model
2.2.2. Discrete Phase Model
2.3. Boundary Conditions
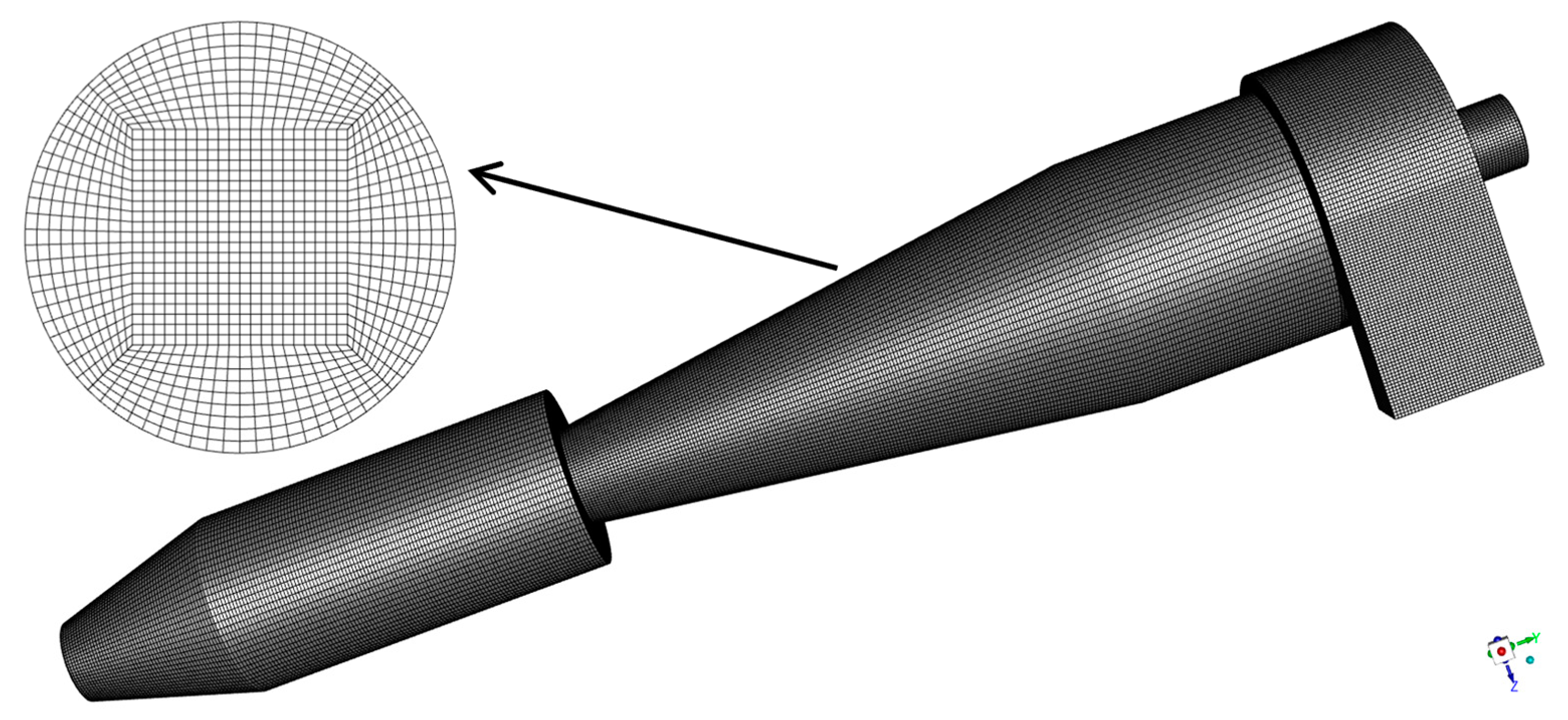
2.4. Grid Independence Analysis
2.5. Model Validation
3. Results and Discussion
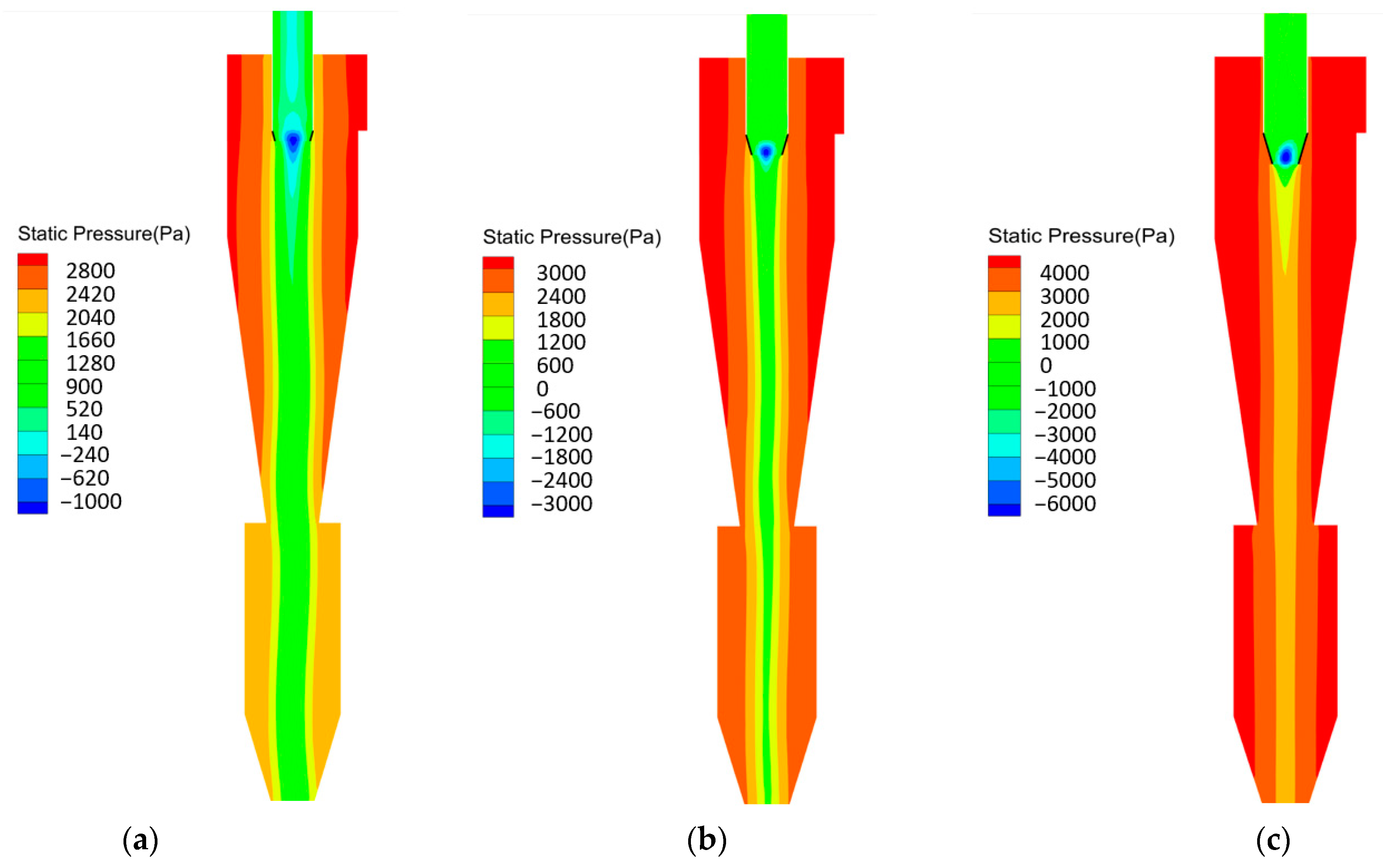
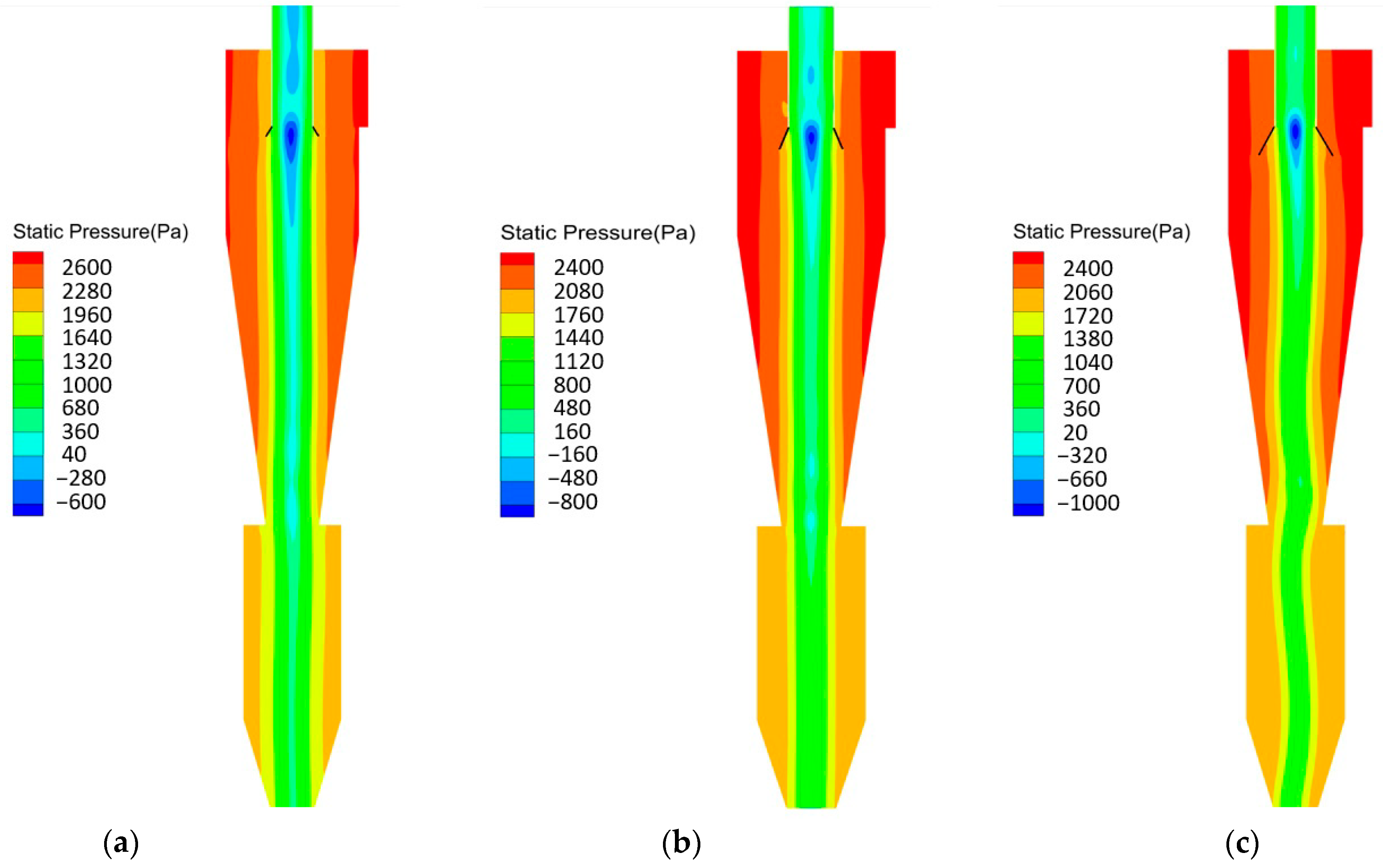
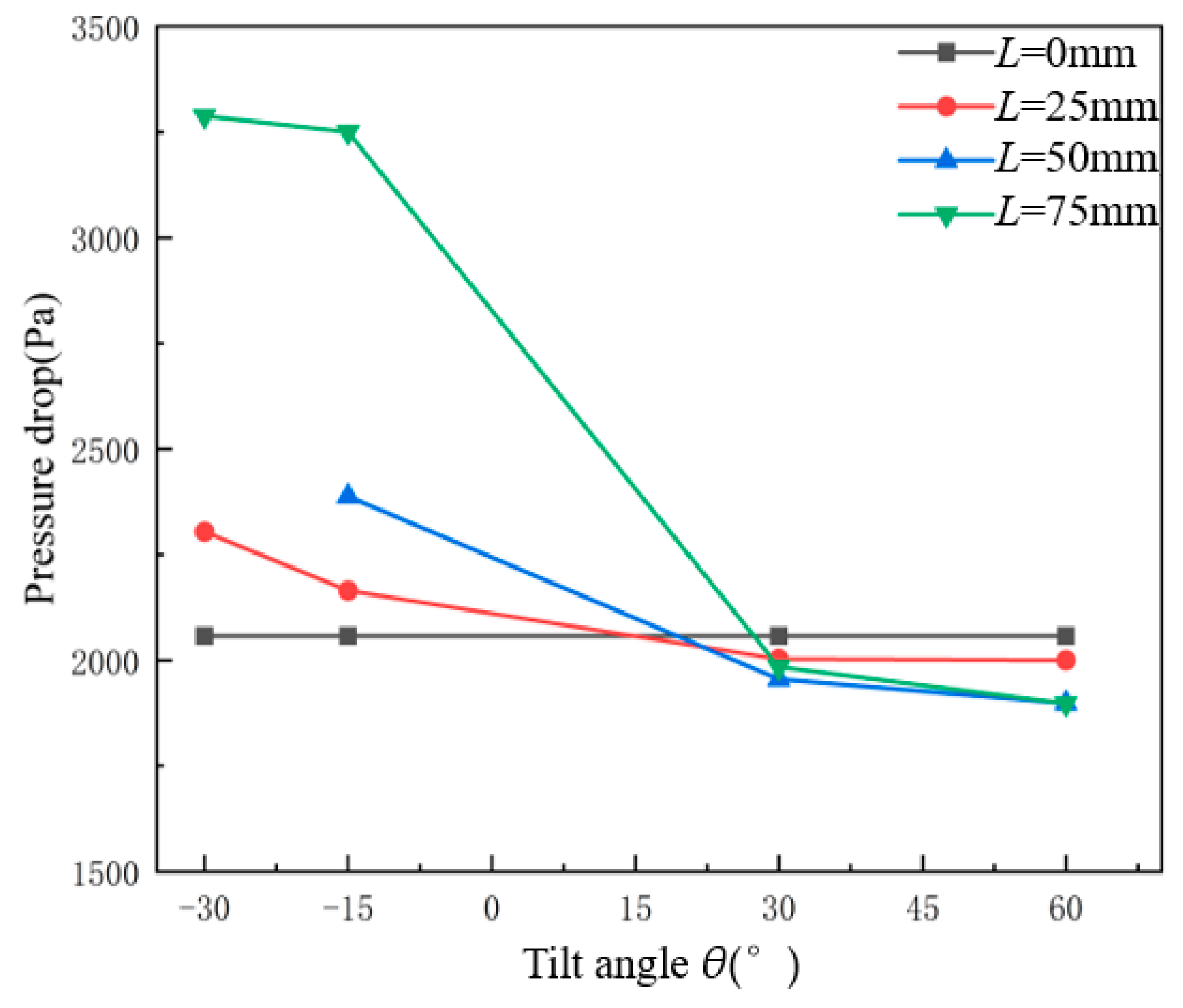
3.1. Pressure Drop Analysis
3.2. Axial Velocity
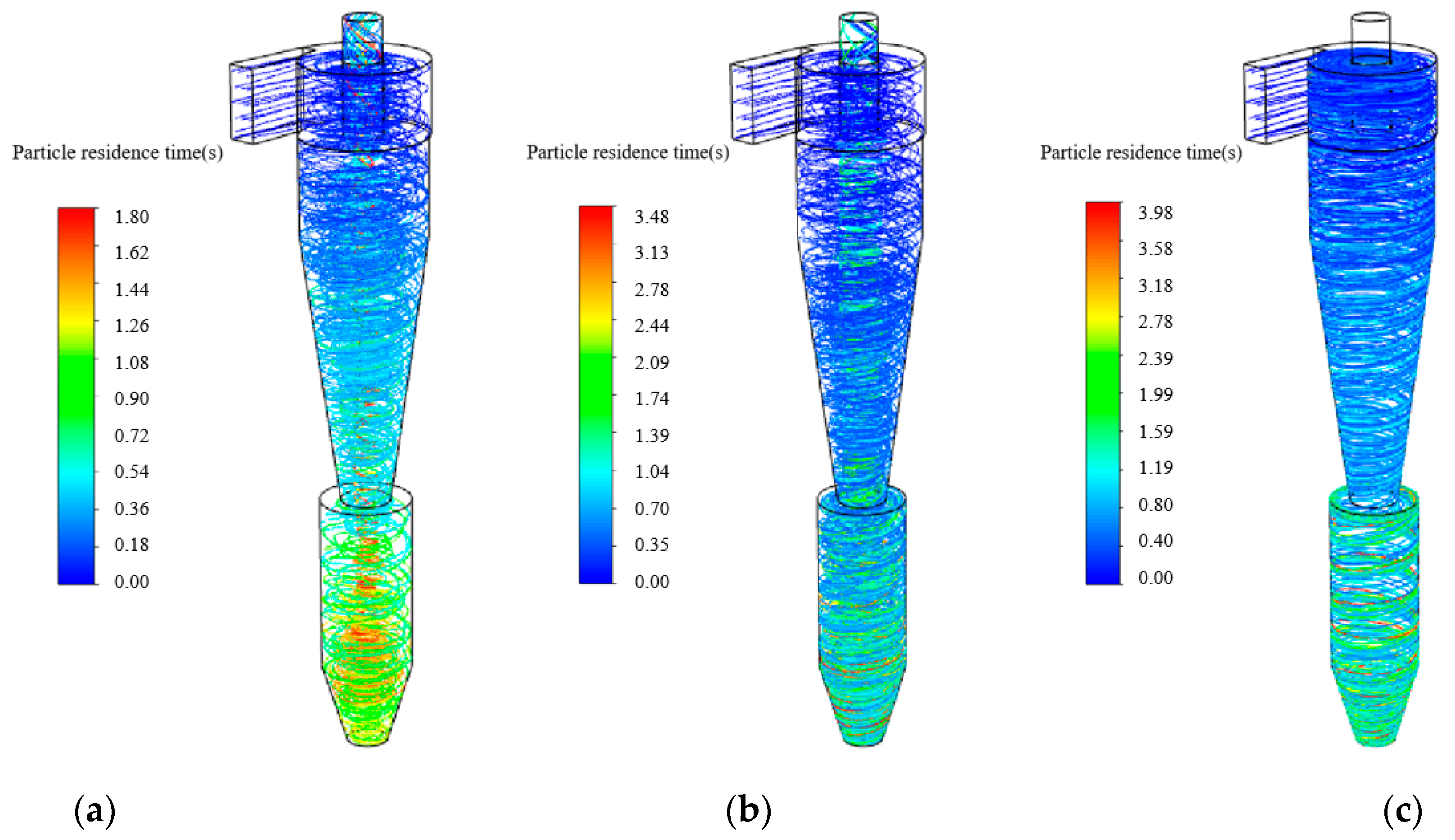
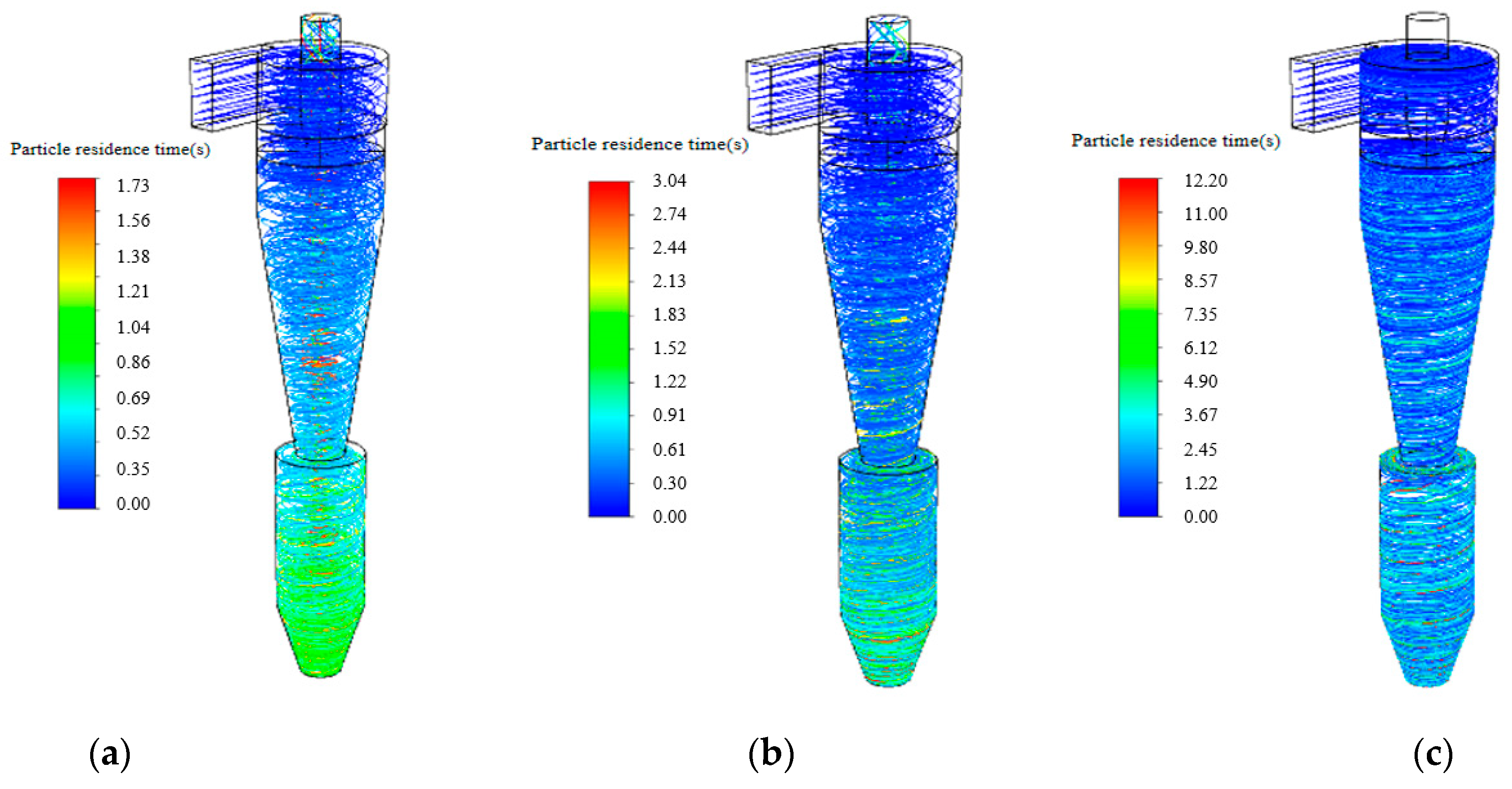
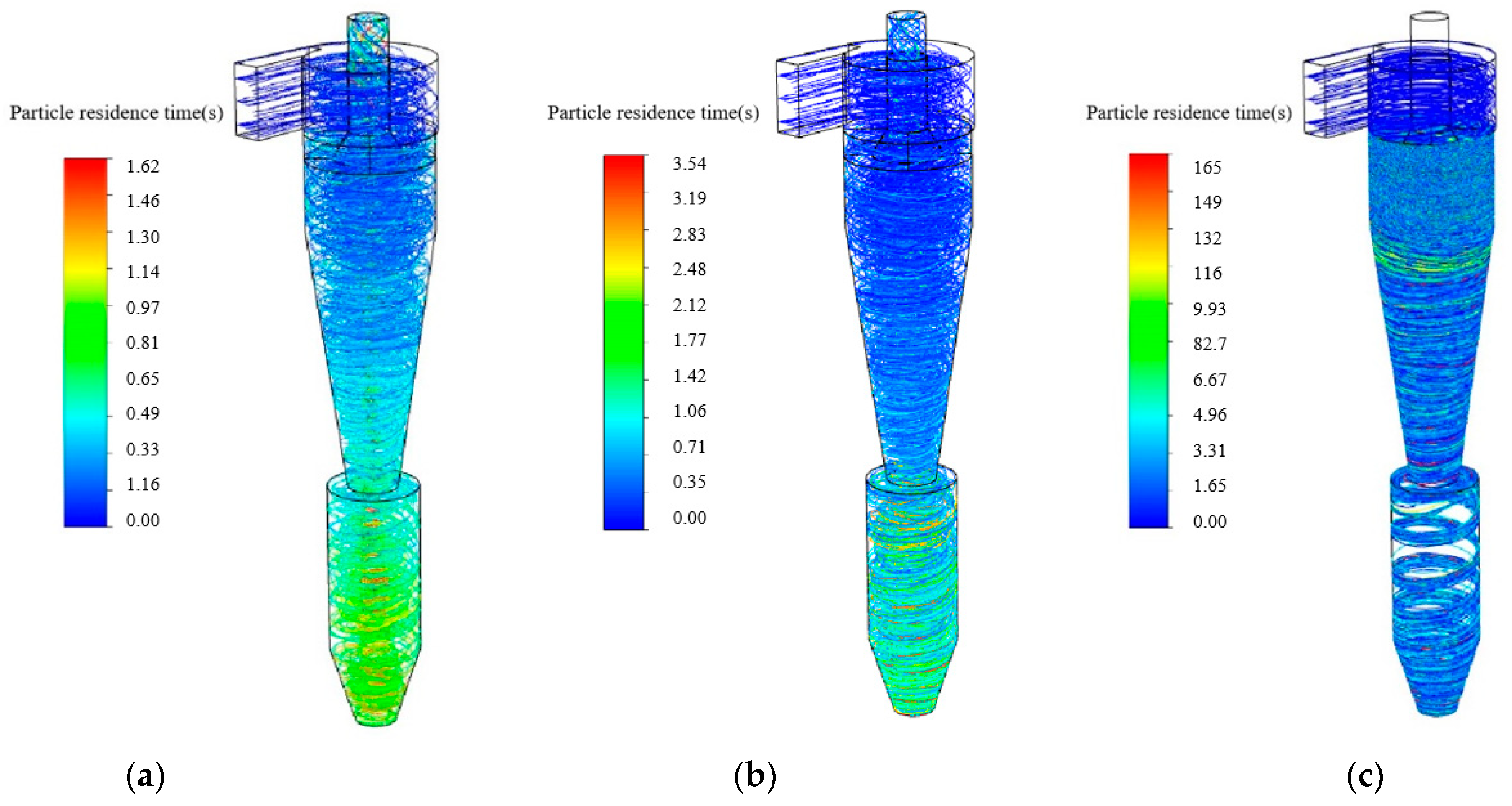
3.3. Particle Separation
4. Conclusions
- The insertion pipe can obviously affect the inside static pressure distribution inside. A longer insertion pipe length and larger tilt angle lead to wider central low-pressure areas and a smaller overall static pressure.
- The installed convergent insertion pipe increases the pressure loss, while the installed divergent insertion pipe augments the pressure loss. When L = 75 mm and θ = 60°, the pressure drop is reduced by 7.8%.
- With the insertion pipe installed, the maximum axial velocity is enhanced. A larger insertion pipe length contributes to the impact on the axial velocity distribution. For the divergent insertion pipes, the maximum central axial velocity increases with increasing tilt angles and then decreases.
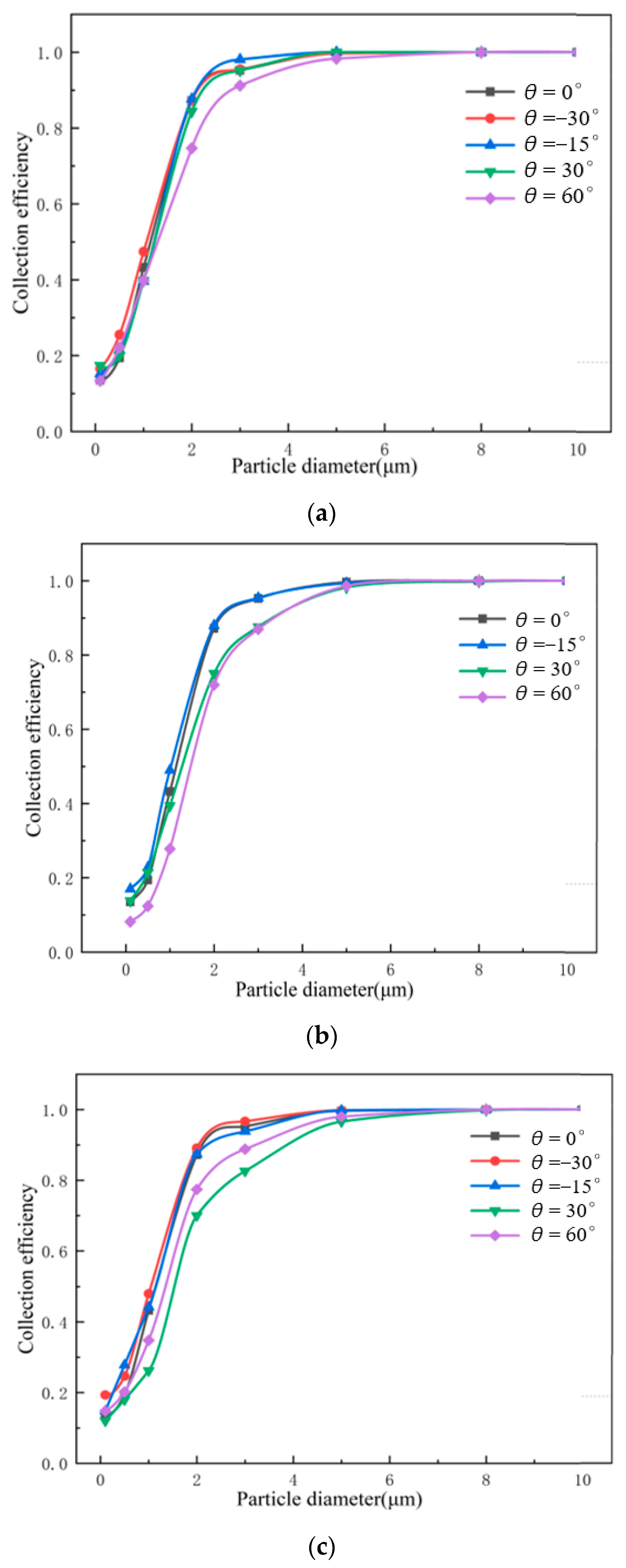
- For small particles dp ≤ 5 μm, a convergent insertion pipe of L = 75 mm and θ = −30° exhibits a better separation performance. When the particle diameter dp ≥ 5 μm, the divergent insertion pipes with larger angles and lengths can significantly decrease the pressure drop while guaranteeing satisfied collection efficiency.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| D | Cyclone diameter, mm |
| De | Vortex finder diameter, mm |
| a | Inlet height, mm |
| b | Inlet length, mm |
| h1 | Cylindrical body height, mm |
| h2 | Cylindrical height of expansion chamber, mm |
| h3 | Cone height of expansion chamber, mm |
| H | Cyclone height, mm |
| B | Cone-tip diameter, mm |
| Bs | Dipleg diameter, mm |
| Ds | Expansion chamber diameter, mm |
| L | Insertion pipe length, mm |
| θ | Insertion pipe angle, ° |
| Mean velocities, m/s | |
| ρ | Density, kg/m3 |
| Diffusive transport term | |
| Molecular viscous diffusion term | |
| Stress generation term | |
| Buoyancy generation term | |
| Pressure strain correlation term | |
| System rotation generation term | |
| Dissipative term | |
| k | Turbulent kinetic energy at a node near the wall, J/kg |
| y* | Fixed distance between node and wall, dimensionless |
| y | Distance of a point near the wall from the wall, m |
| Karman number, dimensionless | |
| Cμ, E | Stress constants |
| Average velocity of the fluid near the wall, m/s | |
| Shear stress at the wall, Pa | |
| Particle mass, kg | |
| F | Sum of the particle swaying forces acting inside the grid cell, N |
| Particle residence time, s | |
| Particle diameters, μm | |
| S | Flow cross-sectional area, m2 |
| C | Inlet wetted perimeter, m |
| μ | Inlet gas viscosity, Pa·s |
| Inlet turbulence intensity, % | |
| Inlet hydraulic diameter, m | |
| Subscripts | |
| g | gas |
| p | particle |
| i, j, k | (=1, 2, 3) components in the Cartesian coordinate system |
References
- Tang, Y.; Li, Z.; Wang, G.; He, Y. A novel approach for nature gas hydrate separation: Downhole spiral-cyclone coupled hydraulic in-situ separation. Chem. Eng. Res. Des. 2022, 188, 808–822. [Google Scholar] [CrossRef]
- Li, T.; Sun, Z.; Geng, K.; Sun, M.; Wang, Z. Numerical analysis of a novel cascading gas–liquid cyclone separator. Chem. Eng. Sci. 2023, 270, 118518. [Google Scholar] [CrossRef]
- Song, W.; Li, S.; Ouyang, Z. Operational performance characteristics of a novel fluidized bed with the internal separator for pulverized coal self-sustained preheating. Powder Technol. 2020, 361, 782–790. [Google Scholar] [CrossRef]
- Yang, H.; Wang, N.; Cao, Y.; Meng, X.; Yao, L. Effects of helical fins on the performance of a cyclone separator: A numerical study. Adv. Powder Technol. 2023, 34, 103929. [Google Scholar] [CrossRef]
- Feng, D.; Chang, X.; Zhang, X.; Li, S. The Research to Hydrocyclone Desander of Sand Removing Based on Crude Oil. Mech. Eng. Mater. 2012, 152, 1336–1341. [Google Scholar] [CrossRef]
- Zhang, L.; Fan, J.; Zhang, P.; Gao, F.; Chen, G.; Li, J. Effect of local erosion on the flow field and separation performance of the cyclone separator. Powder Technol. 2023, 413, 118007. [Google Scholar] [CrossRef]
- Zhu, L.; Wang, S.; Ru, Y.; Wang, J.; Yang, P.; Li, A.; Ma, Z.; Wang, Z. Numerical investigation on dynamic characteristics of flow field in cyclone separators with different dust hopper structures. Particuology 2023, 82, 134–145. [Google Scholar] [CrossRef]
- Wang, Q.Q.; Chen, J.Q.; Wang, C.S.; Ji, Y.P.; Shang, C.; Zhang, M.; Shi, Y.; Ding, G.D. Design and performance study of a two-stage inline gas-liquid cyclone separator with large range of inlet gas volume fraction. J. Pet. Sci. Eng. 2023, 220, 111218. [Google Scholar] [CrossRef]
- Jiao, J.; Liu, Z.; Zheng, Y. Evaluations and Modifications on Reynolds Stress Model in Cyclone Simulations. Chem. Eng. Technol. 2007, 30, 15–20. [Google Scholar] [CrossRef]
- Feng, D.; Huang, S.; Luo, L.; Ma, W. Prediction of liquid viscosity effect on flow field and performance in a solid-liquid hydrocyclone. Adv. Mater. Res. 2011, 318, 401–404. [Google Scholar] [CrossRef]
- Shukla, S.K.; Shukla, P.; Ghosh, P. Evaluation of numerical schemes using different simulation methods for the continuous phase modeling of cyclone separators. Adv. Powder Technol. 2011, 22, 209–219. [Google Scholar] [CrossRef]
- Feng, D.; Huang, S.; Luo, L.; Ma, W. CFD analysis of two-phase flow in a solid-liquid hydrocyclone. Appl. Mech. Mater. 2012, 130, 3640–3643. [Google Scholar] [CrossRef]
- Slack, M.D.; Prasad, R.O.; Bakker, A.; Boysan, F. Advances in Cyclone Modelling Using Unstructured Grids. Chem. Eng. Res. Des. 2000, 78, 1098–1104. [Google Scholar] [CrossRef]
- Brar, L.S.; Wasilewski, M. Investigating the effects of temperature on the performance of novel cyclone separators using large-eddy simulation. Powder Technol. 2023, 416, 118213. [Google Scholar] [CrossRef]
- Wei, Q.; Sun, G.; Gao, C. Numerical analysis of axial gas flow in cyclone separators with different vortex finder diameters and inlet dimensions. Powder Technol. 2020, 369, 321–333. [Google Scholar] [CrossRef]
- Griffiths, W.; Boysan, F. Computational fluid dynamics(CFD) and empirical modeling of the performance of a number of cyclone samplers. J. Aerosol Sci. 1996, 27, 281–304. [Google Scholar] [CrossRef]
- Le, D.K.; Guo, M.; Yoon, J.Y. A hybrid CFD—Deep Learning methodology to improve the accuracy of cut-off diameter prediction in coarse-grid simulations for cyclone separators. J. Aerosol Sci. 2023, 170, 106143. [Google Scholar] [CrossRef]
- Le, D.K.; Yoon, J.Y. A hybrid CFD—Deep learning methodology for improving the accuracy of pressure drop prediction in cyclone separators. Chem. Eng. Res. Des. 2023, 190, 296–311. [Google Scholar] [CrossRef]
- Gopalakrishnan, B.; Saravana Kumar, G.; Prakash, K.A. Parametric analysis and optimization of gas-particle flow through axial cyclone separator: A numerical study. Adv. Powder Technol. 2023, 34, 103959. [Google Scholar] [CrossRef]
- Guo, M.; Le, D.K.; Sun, X.; Yoon, J.Y. Multi-objective optimization of a novel vortex finder for performance improvement of cyclone separator. Powder Technol. 2022, 410, 117856. [Google Scholar] [CrossRef]
- Iozia, D.L.; Leith, D. The Logistic Function and Cyclone Fractional Efficiency. Aerosol Sci. Technol. 2007, 12, 598–606. [Google Scholar] [CrossRef] [Green Version]
- Iozia, D.L.; Leith, D. Effect of Cyclone Dimensions on Gas Flow Pattern and Collection Efficiency. Aerosol Sci. Technol. 1989, 10, 491–500. [Google Scholar] [CrossRef]
- Cortes, C.; Gil, A. Modeling the gas and particle flow inside cyclone separators. Prog. Energy Combust. Sci. 2007, 33, 409–452. [Google Scholar] [CrossRef]
- Elsayed, K.; Lacor, C. The effect of cyclone inlet dimensions on the flow pattern and performance. Appl. Math. Model. 2011, 35, 1952–1968. [Google Scholar] [CrossRef] [Green Version]
- Horvath, A.; Jordan, C.; Harasek, M. Influence of vortex-finder diameter on axial gas flow in simple cyclone. Chem. Prod. Process. Model. 2008, 3, 1–26. [Google Scholar] [CrossRef]
- Qian, F.P.; Zhang, M.Y. Effects of the Inlet Section Angle on the Flow Field of a Cyclone. Chem. Eng. Technol. 2007, 30, 1564–1570. [Google Scholar] [CrossRef]
- Tan, H.M.; Wang, J.J.; Jin, Y.H. The Investigation of Back-Mixing Particles near Dust Outlet in Cyclone Separator with Tangential Inlet. Adv. Mater. Res. 2011, 239–242, 2142–2148. [Google Scholar] [CrossRef]
- Liu, L.; Dou, H.-S.; Chen, X. Effect of particle diameter and injection position on the separation performance of cyclone separators. J. Comput. Multiph. Flows 2016, 8, 40–47. [Google Scholar] [CrossRef]
- Dehdarinejad, E.; Bayareh, M. Experimental and numerical investigation on the performance of a gas-solid cyclone with twisted baffles and roughened cone surface. Powder Technol. 2023, 420, 118401. [Google Scholar] [CrossRef]
- Dehdarinejad, E.; Bayareh, M.; Ashrafizaadeh, M. Impact of cone wall roughness on turbulence swirling flow in a cyclone separator. Chem. Pap. 2022, 76, 5579–5599. [Google Scholar] [CrossRef]
- Li, W.; Huang, Z.; Li, G. Improvement of the cyclone separator performance by the wedge-shaped roof: A multi-objective optimization study. Chem. Eng. Sci. 2023, 268, 118404. [Google Scholar] [CrossRef]
- Lee, J.W.; Yang, H.J.; Lee, D.Y. Effect of the cylinder shape of a long-coned cyclone on the stable flow-field establishment. Powder Technol. 2006, 165, 30–38. [Google Scholar] [CrossRef]
- Brar, L.S.; Sharma, R.P.; Elsayed, K. The effect of the cyclone length on the performance of Stairmand high-efficiency cyclone. Powder Technol. 2015, 286, 668–677. [Google Scholar] [CrossRef]
- Demir, S.; Karadeniz, A.; Aksel, M. Effects of cylindrical and conical heights on pressure and velocity fields in cyclones. Powder Technol. 2016, 295, 209–217. [Google Scholar] [CrossRef]
- Hamdy, O.; Bassily, M.A.; El-Batsh, H.M.; Mekhail, T.A. Numerical study of the effect of changing the cyclone cone length on the gas flow field. Appl. Math. Model. 2017, 46, 81–97. [Google Scholar] [CrossRef]
- Gimbun, J.; Chuah, T.G.; Choong, T.S.Y.; Fakhru’l-Razi, A. Prediction of the effects of cone tip diameter on the cyclone performance. J. Aerosol Sci. 2005, 36, 1056–1065. [Google Scholar] [CrossRef]
- Elsayed, K.; Lacor, C. Numerical modeling of the flow field and performance in cyclones of different cone-tip diameters. Comput. Fluids 2011, 51, 48–59. [Google Scholar] [CrossRef]
- Elsayed, K.; Lacor, C. The effect of the dust outlet geometry on the performance and hydrodynamics of gas cyclones. Comput. Fluids 2012, 68, 134–147. [Google Scholar] [CrossRef]
- Pandey, S.; Brar, L.S. On the performance of cyclone separators with different shapes of the conical section using CFD. Powder Technol. 2022, 407, 117629. [Google Scholar] [CrossRef]
- Parvaz, F.; Hosseini, S.H.; Ahmadi, G.; Elsayed, K. Impacts of the vortex finder eccentricity on the flow pattern and performance of a gas cyclone. Sep. Purif. Technol. 2017, 187, 1–13. [Google Scholar] [CrossRef]
- Guo, M.; Xue, H.; Pang, J.; Le, D.K.; Sun, X.; Yoon, J.Y. Numerical investigation on the swirling vortical characteristics of a Stairmand cyclone separator with slotted vortex finder. Powder Technol. 2023, 416, 118236. [Google Scholar] [CrossRef]
- El-Batsh, H.M. Improving cyclone performance by proper selection of the exit pipe. Appl. Math. Model. 2013, 37, 5286–5303. [Google Scholar] [CrossRef]
- Tan, F.; Karagoz, I.; Avci, A. Effects of Geometrical Parameters on the Pressure Drop for a Modified Cyclone Separator. Chem. Eng. Technol. 2016, 39, 576–581. [Google Scholar] [CrossRef]
- Hoekstra, A.J. Gas Flow Field and Collection Efficiency of Cyclone Separators; Technical University Delft: Delft, The Netherlands, 2000. [Google Scholar]
- Hugi, E.; Reh, L. Focus on solids strand formation improves separation performance of highly loaded circulating fluidized bed recycle cyclones. Chem. Eng. Process. 2000, 39, 263–273. [Google Scholar] [CrossRef]
- de Souza, F.J.; Salvo, R.d.V.; Martins, D.d.M. Effects of the gas outlet duct length and shape on the performance of cyclone separators. Sep. Purif. Technol. 2015, 142, 90–100. [Google Scholar] [CrossRef]
- Noé-Landry-Privace, M.B. Numerical Simulation of Dense Gas-Solid Separation in Cyclone Separators; Harbin Institute of Technology: Harbin, China, 2014. [Google Scholar]
- Singer, B.A. Modeling the Transition Region; NASA Report, the United States: Washington, DC, USA, 1993; NASA CR-4492.
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Methods Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Azadi, M.; Azadi, M.; Mohebbi, A. A CFD study of the effect of cyclone size on its performance parameters. J. Hazard. Mater. 2010, 182, 835–841. [Google Scholar] [CrossRef]





| Parameter | Value |
|---|---|
| Cyclone diameter, D (mm) | 300 |
| Length of the inlet, b (mm) | 73 |
| Height of the inlet, a (mm) | 176 |
| Parameter of the vortex finder | |
| S (mm) | 276 |
| De (mm) | 95 |
| L (mm) | 25 50 75 |
| θ (°) | −30 −15 30 60 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Feng, D.; Wang, J.; Hou, L.; Miao, E. CFD Investigation on the Performance of Cyclone Separators with Divergent or Convergent Insertion Pipes. Processes 2023, 11, 2061. https://doi.org/10.3390/pr11072061
Wang M, Feng D, Wang J, Hou L, Miao E. CFD Investigation on the Performance of Cyclone Separators with Divergent or Convergent Insertion Pipes. Processes. 2023; 11(7):2061. https://doi.org/10.3390/pr11072061
Chicago/Turabian StyleWang, Mengyang, Ding Feng, Jiangang Wang, Lingxia Hou, and Enming Miao. 2023. "CFD Investigation on the Performance of Cyclone Separators with Divergent or Convergent Insertion Pipes" Processes 11, no. 7: 2061. https://doi.org/10.3390/pr11072061
APA StyleWang, M., Feng, D., Wang, J., Hou, L., & Miao, E. (2023). CFD Investigation on the Performance of Cyclone Separators with Divergent or Convergent Insertion Pipes. Processes, 11(7), 2061. https://doi.org/10.3390/pr11072061






