Experimental and Simulation Analysis of Siloxane Mixtures Used in Organic Rankine Cycle with Thermal Stability Limits ^†

Abstract

The thermal stability of siloxanes has significant influence on the selection of working fluid and the performance of organic Rankine cycle systems. In this study, a thermal decomposition experimental apparatus was designed to measure the thermal stability of hexamethyldisiloxane (MM), octamethyltrisiloxane (MDM), and their mixtures; a reaction kinetics model based on first order reaction theory was built to analyze the thermal stability of siloxane mixture fluids in a long operation period. And the influence of the mass fraction and evaporation temperature on the net power and thermal efficiency of the system was analyzed under the constraints of thermal stability. The results showed that the thermal stability of MDM was worse than that of MM, and the mixture of MM and MDM had significant inhibition effects on the de-composition of pure fluids. The activation energy of decomposition reaction was 50.50 kJ/mol, and the pre-exponential factor was 5.80 × 10⁻³ s⁻¹. With the evaporation temperature limit, the net power and thermal efficiency were both lower than those without the evaporation temperature limit. Comparing the obvious decrease in the thermal efficiency, the change of the net power was limited. Siloxane mixtures emerged as a superior choice for ORC systems in the conditions of this paper. MM/MDM (0.6/0.4) improved the net power and heat efficiency of the system by 8.1% and 1.7%, respectively, comparing with that of the pure working fluids.

1. Introduction

The focus on industrial waste heat recovery and the utilization of renewable energy has been intensified as a potential solution to pressing energy and environmental challenges. Compared with other cycle forms such as the steam Rankine cycle, the organic Rankine cycle (ORC) uses organics as working fluids and can have good performance at 150 °C to 300 °C, so it is a potential heat utilization technology for industrial waste heat and renewable energy [1,2]. ORCs have been widely used in solar power, geothermal power, biomass power, and industrial waste heat recovery systems because of their high thermal efficiencies and easy realization. ORCs are applicable across a wide range of temperature intervals. The low- and medium-temperature heat sources, such as geothermal energy, have the main position in the installed capacity of commercial ORC systems in the world [3]. The ORC systems with high-temperature heat sources have attracted much interest because of their higher thermal efficiency [4,5,6,7].

For high-temperature ORCs, the selection of the working fluid is of paramount importance. At present, the most widely used working fluid mainly includes hydrofluorocarbons (HFCs), hydrocarbons (HCs), and siloxanes [8,9,10,11]. HFCs have good thermodynamic properties to be working fluids of ORCs. However, the high GWP value is a key factor restricting the application of some HFCs. HCs usually have lower GWP than HFCs, and they are suitable for a wide temperature range of heat sources. However, its flammability can lead to system safety issues. Siloxanes are esteemed as fitting working fluids due to their low toxicity, non-flammability, high critical temperatures, and notably superior thermal stability at high temperatures [12,13,14,15]. The frequently used siloxane working fluids include linear siloxane fluids such as hexamethyldisiloxane (MM) and octamethyltrisiloxane (MDM). Nami et al. [16] analyzed the performances of different working fluids in a cascade ORC system using gas turbine exhaust gas heat. The results showed that the siloxane working fluids had higher efficiencies when using a recuperator, and MM was the best option for the cascade configuration. Uusitalo et al. [17] compared the power output, the heat exchanger design, and the preliminary turbine design of different working fluids in a high temperature ORC system for the recovery of thermal energy from engine exhaust gas, which showed that the siloxane MDM was the most suitable fluid.

Some studies suggested that mixed working fluids could enhance the performance of ORC systems. Dong et al. [18] compared the performance of high-temperature ORCs with siloxane pure substances and mixtures as working fluids. The mixture MM/MDM with a ratio of 0.4/0.6 was regarded as the optimal working fluid, enabling the system thermal efficiency of up to 16.88%, representing relative increases of 9.4% and 5.96% compared to the use of pure MM and pure MDM as working fluid, respectively. Oyekale et al. [19] proposed that the mixture MM/MDM with a ratio of 0.8/0.2 and 0.9/0.1 could increase the net power by 1.4% and 2%, respectively.

Thermal stability of ORC working fluids is significant with high temperature heat sources, because organics can easily decompose at high temperatures, which can lead to serious problems for ORC systems. Studies have shown that the solid decomposition byproducts could obstruct tubes or enhance the thermal resistance of the heat exchange surface. More critically, the presence of potentially corrosive products could degrade system materials, consequently posing serious safety risks [11]. Previous studies have shed light on the thermal stability of MM and MDM. Erhart et al. [13] measured the working fluid decomposition of eight ORC power plants in Europe using MDM as working fluids. The result showed that thermal decomposition occurred in all plants at operating temperatures ranging from 290 to 315 °C and operating periods ranging from 38,500 to 90,000 h, and the decomposition ratio of the MDM samples was 5% to 34%. Dai et al. [14] measured the decomposition ratios of MM at varying pressures and temperatures. The result revealed that pressure had little effect on the MM decomposition, while the rise of temperature significantly increased the thermal decomposition ratio of MM. Preißinger along with Brüggemann [15] also measured the thermal stability of MM and suggested that MM was stable at 300 °C with annual decomposition ratio of less than 3.5%. Keulen et al. [20] measured the vapor pressure differences of MM and MDM at various temperatures, discerning appreciable decomposition phenomena at 240 °C and 260 °C, respectively. Rajabloo et al. [21] delved into the repercussions of thermal decomposition on the ORC system, considering the off-design conditions. The results emphasized that the fluid decomposition profoundly impacted cycle performance, particularly when the decomposed products were volatile.

However, the previous studies did not focus on the thermal stability of siloxane mixtures and the decomposition extents of siloxanes in long operation periods. In this work, the decomposition ratios of MDM and MM/MDM mixtures were measured. The reaction kinetics parameters were obtained, and a reaction kinetics model was built for siloxanes to predict the thermal stability of siloxane fluids in a long operation period (Section 2). Moreover, most previous studies for ORC system optimization using siloxane mixtures did not consider the thermal stability limits. Thus, a deeper exploration into the performance of ORCs within the confines of siloxane thermal stability is necessitated. In this work, we calculated the cycle performance incorporating thermal stability temperature limits and compared it with the theoretical performance devoid of such limits (Section 3). The novelty of this work includes the experimental results of siloxane mixture thermal stability, the thermal stability reaction kinetics model of siloxanes, and the system performance analysis with thermal stability limit.

2. System and Method

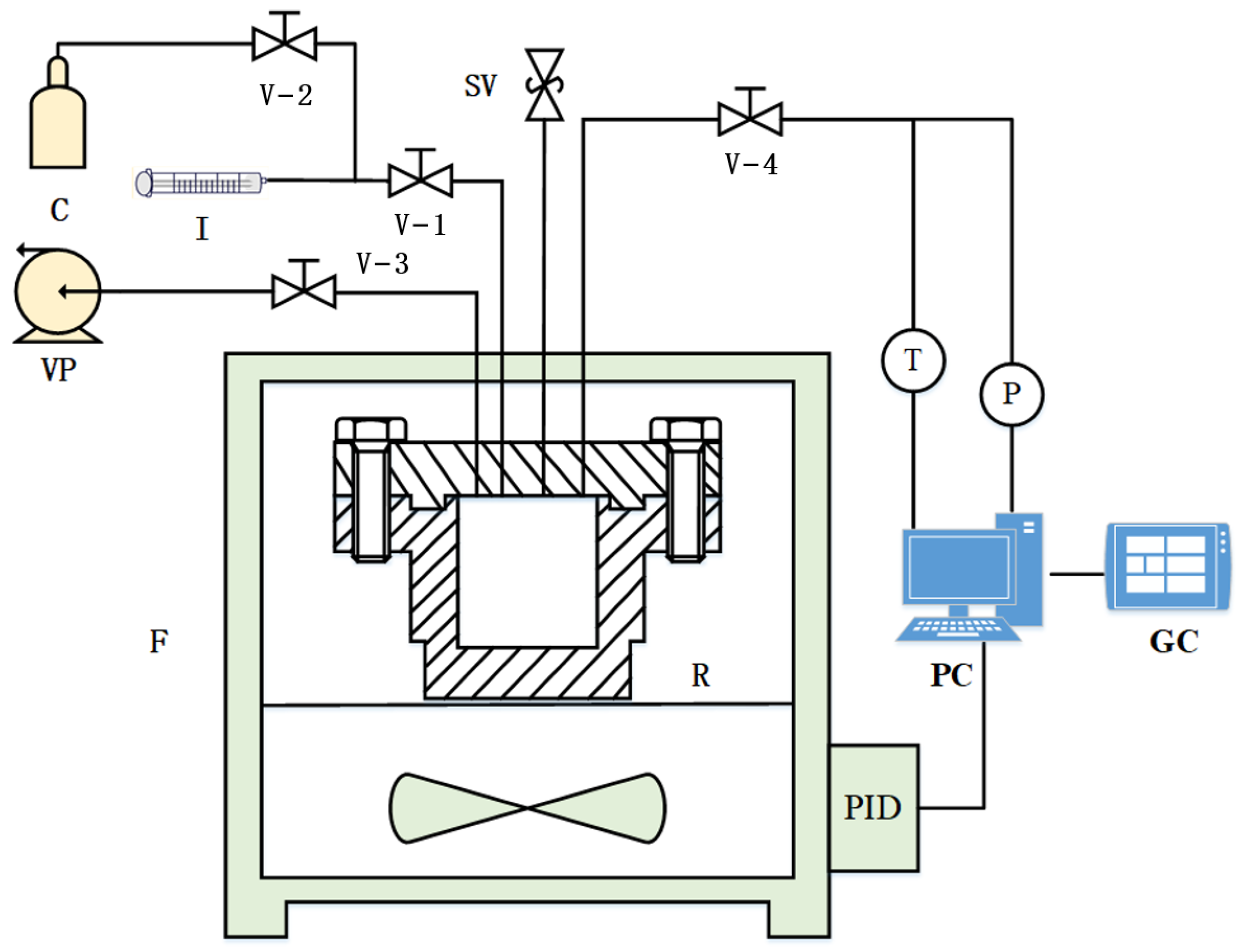
2.1. Experimental System and Method

The MM and MDM samples employed in this study were procured from commercial suppliers, with purities exceeding 99.2% and 97.5%, respectively. The respective fluid properties are comprehensively enumerated in

Table 1. Fluid properties of MM and MDM.

Siloxane	Molecular Formula	Tb/°C	Tc/°C	pc/MPa
MM	C6H18OSi2	100.25	245.60	1.94
MDM	C8H24O2Si3	152.51	290.94	1.42

.

The experimental system is shown in Figure 1. The high-temperature reactor was made from 316L stainless steel and had an internal volume of 25 mL, which had good corrosion resistance at high temperature [22,23,24]. Graphite washers and bolts provided a seal for the reactor. The reactor could withstand a maximum pressure of 20 MPa and a maximum temperature of 400 °C. Four reactors were positioned within a heating furnace to reduce the experimental errors. The control valves were used to facilitate the inflow and outflow of working fluids, while a safety valve was deployed to avert potential damage from excessive pressure. The furnace temperature was regulated via a thermocouple and a PID controller, ensuring stable thermal conditions. Before each experiment, the reactor was evacuated using a vacuum pump to negate the influence of air on decomposition.

The experimental pressure was predetermined to ensure that the working fluid remains in a gaseous state when heated in the reactor. The density of the working fluid under experimental conditions was calculated utilizing commercial software REFPROP 10.0 and was subsequently used to determine the requisite filling mass, which was equal to the product of the density and the reactor volume. The fluid was introduced at room temperature using a syringe, with an injection mass uncertainty of ±0.05 g. Upon completion of the filling procedure, all valves were sealed, and the reactors were placed within the heating furnace and heated to the predetermined temperature. Each experiment spanned a period of 24 h. After the heating phase, gaseous decomposition products were captured in gas bags, and their mass was determined by assessing the mass of the residual liquid sample. Both gaseous and liquid decomposition products were examined through gas chromatography (GC) and GC-mass spectrometry (MS). More than four repetitions were performed for each experimental condition, and the average results of these repetitions were deemed the final results to mitigate random errors. The standard deviation of the repeated experiment data was considered a rough estimate of the experimental uncertainty. The decomposition ratio was defined as Equation (1):

$$x_{\mathrm{A}}=\frac{C_{\mathrm{A},0}-C_{\mathrm{A},\mathrm{d}}}{C_{\mathrm{A},0}}\times 100\%$$

(1)

where x_A is the decomposition ratio of fluid A, and C_A,0 and C_A,d are the mass fraction of fluid A in the original sample and the decomposed sample, respectively.

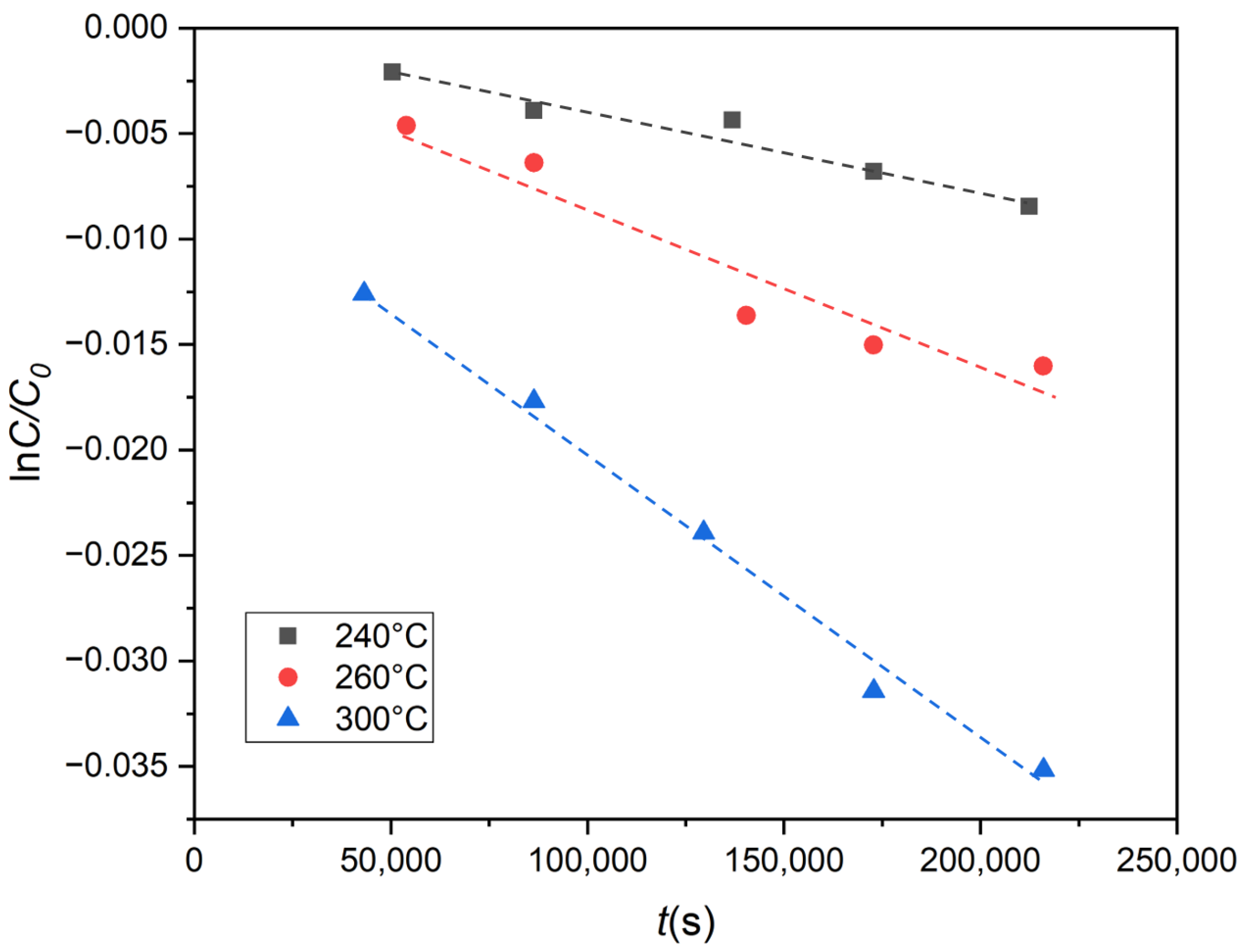
2.2. Reaction Kinetics Model

The thermal decomposition of the working fluid in ORC conditions is always considered as a first order reaction in previous studies [25]. The reaction rate of a first order reaction was defined as Equation (2):

$$\frac{d{C}_{\mathrm{A}}}{dt}=-k{C}_{\mathrm{A}}$$

(2)

where t is the time and k is the reaction rate constant which is only related to the reaction temperature. Equation (2) can also be written in the integral form as Equation (3):

$$-\ln \frac{C_{\mathrm{A}}}{C\mathrm{A},0}=-\ln (1-x\mathrm{A})=kt$$

(3)

Equation (3) shows that the reaction rate constant k can be calculated from lnC_A/C_A,0–t curves at a certain temperature. The Arrhenius Equation (Equation (4)) can be used to calculate the reaction ratio at different temperatures.

$$k=A{e}^{-E_{\mathrm{a}}/RT}$$

(4)

where A is the pre-exponential factor, E_a is the activation energy, R is the gas constant, and T is the temperature. The Arrhenius Equation also can be written in the form as Equation (5):

$$\ln k=-\frac{E\mathrm{a}}{R}\frac{1}{T}+\ln A$$

(5)

The pre-exponential factor A and the activation energy E_a can be assumed to be constants in most ORC experimental conditions. Thus, they can be calculated from the lnk-1/T curves at different temperatures. Then, the decomposition ratio at different temperatures for certain periods can be calculated by Equations (3) and (4).

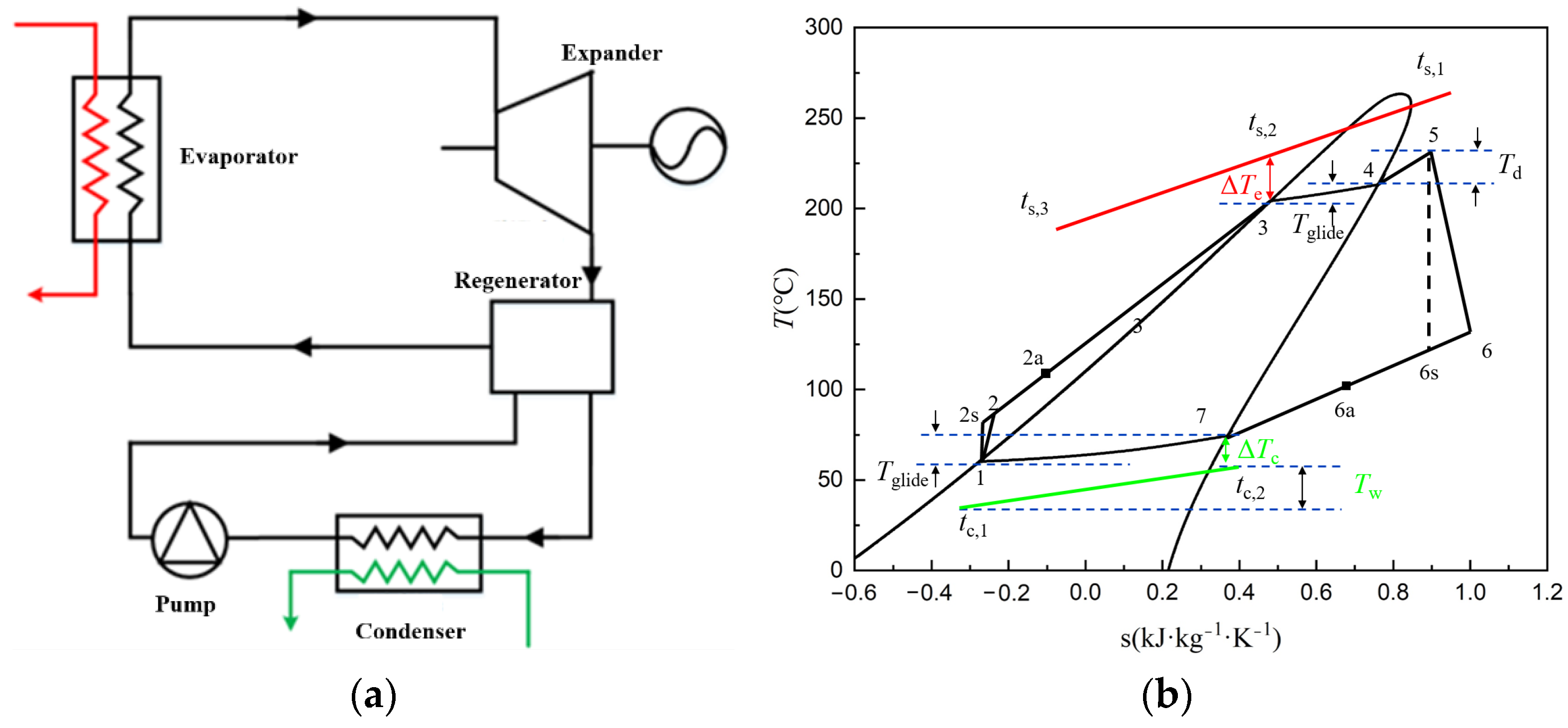
2.3. Simulation Method

With reference to the experimental results, it is necessary to establish a simulation model to analyze the influence of thermal stability limit on system performance [26,27,28,29,30,31,32]. Figure 2a depicts the schematic of the ORC system, while Figure 2b represents the temperature–entropy curve of the cycle when using a 0.6/0.4 MM/MDM mixture as the working fluid. The temperature profiles of these mixtures conform more effectively with the heat source and sink due to the temperature slides of mixtures. The thermodynamic parameters of the ORC system are detailed in

Table 2. Thermodynamic parameters of the ORC system.

Parameters	Unit	Value
Heat source (air) temperature	ts,1/°C	300
Heat source flow	$\dot{m}$/kg·s−1	1
Cold source (water) temperature	tc,1/°C	25
Evaporator pinch	ΔTe/°C	10
Condenser pinch	ΔTc/°C	5
Expander design isentropic efficiency	$\eta$t/%	85
Pump design isentropic efficiency	$\eta$/%	90

. The heat source of the cycle was constituted by hot air, featuring an inlet temperature of 300 °C and a mass flow rate of 1 kg/s. Meanwhile, cooling water, with an inlet temperature of 25 °C, served as the cold source. The evaporator and condenser pinches were 10 °C and 5 °C, respectively. The isentropic efficiencies of the pump and the expander stood at 0.9 and 0.85, correspondingly.

A simulation model of the ORC system was developed in MATLAB, leveraging the fluid property database from REFPROP Version 10.0. Prior to modeling, several assumptions were established:

• All components in the cycle operate under steady-state conditions;
• The heat exchangers incorporated into the cycle utilize a counter-flow configuration;
• Heat losses and pressure drops in the pipeline are disregarded.

In the case of the evaporator, various pinch points can determine distinct mass flows of the working fluids. If the evaporator pinch appears at the position illustrated in Figure 2, the mass flow of the working fluid can be calculated via the following equation:

$${\dot{m}}_{\mathrm{s}}\left(h_{s,1}-h_{s,2}\right)={\dot{m}}_{\mathrm{wf}}\left(h_5-h_3\right)$$

(6)

where ${\dot{m}}_{\mathrm{s}}$ and ${\dot{m}}_0$ denote the mass flow of heat source and working fluid, respectively. While the pinch point appears at the inlet of the evaporator, the mass flow of the working fluid can be calculated via the following equation:

$${\dot{m}}_{\mathrm{s}}\left(h_{s,1}-h_{s,3}\right)={\dot{m}}_{\mathrm{wf}}\left(h_5-h_{2\mathrm{a}}\right)$$

(7)

$$h_{2\mathrm{a}}=\alpha h_6+(1-\alpha )h_2$$

(8)

where h_2a is the enthalpy value of the working fluid at the outlet of the regenerator. The regenerative steam extraction rate α was set as 0.2. The net power W_net, and thermal efficiency η_th can be calculated via the following equation:

$$Q_{\mathrm{e}}={\dot{m}}_{\mathrm{wf}}\left(h_5-h_{2\mathrm{a}}\right)$$

(9)

$$Q_{\mathrm{c}}={\dot{m}}_{\mathrm{wf}}\left(h_{6\mathrm{a}}-h_1\right)$$

(10)

$$W_{\mathrm{net}}=W_{\mathrm{t}}-W_{\mathrm{p}}$$

(11)

$${\eta }_{\mathrm{th}}=\frac{W_{\mathrm{t}}-W_{\mathrm{p}}}{Q_{\mathrm{e}}}$$

(12)

where W_t and W_p are the expander output power and the power consumed by the pump, respectively, which can be calculated using Equations (13) and (14):

$$W_{\mathrm{t}}={\dot{m}}_{\mathrm{o}}\left(h_5-h_{6\mathrm{s}}\right){\eta }_{\mathrm{t}}={\dot{m}}_{\mathrm{o}}\left(h_5-h_6\right)$$

(13)

$$W_{\mathrm{p}}=\frac{{\dot{m}}_{\mathrm{wf}}\left(h_{2\mathrm{s}}-h_1\right)}{\eta }={\dot{m}}_{\mathrm{wf}}\left(h_2-h_1\right)$$

(14)

3. Results and Discussion

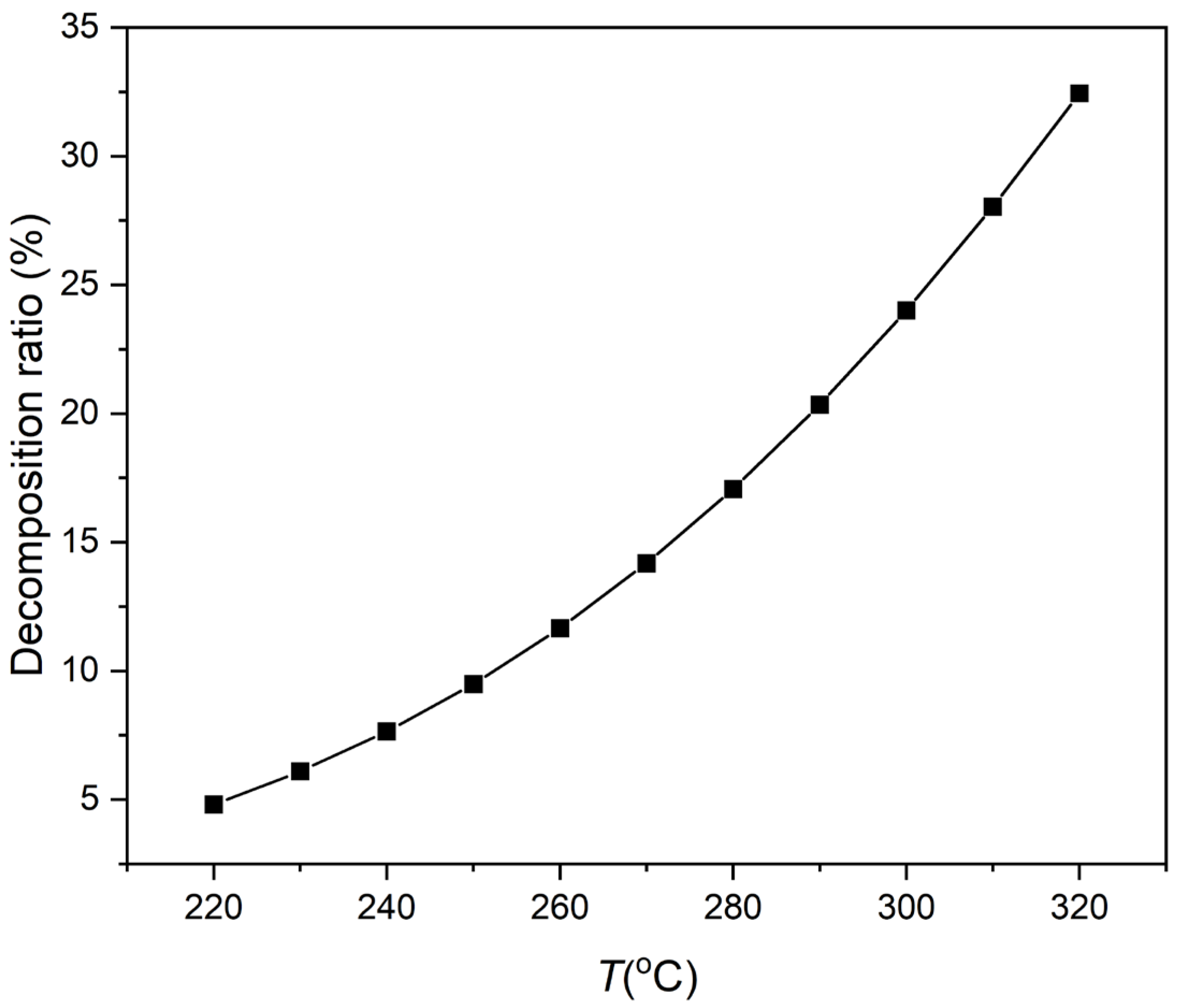
3.1. Experimental Results and Discussion

The decomposition ratios of MM [14] and MDM at different temperatures are shown in Figure 3. The results indicated a significant influence of temperature on MDM’s thermal decomposition. The decomposition ratio of MDM increased with the rise in heating temperature. Thermal decomposition occurred at 240 °C, recording an MDM decomposition ratio of 2.95%. As the temperature continued to increase, so did the decomposition ratio, reaching 6.64% at 320 °C. The decomposition ratios of MM at different temperatures in reference [14] were measured using the same experimental methodology as this study, so could be compared with the decomposition ratios of MDM directly. The results revealed that within the temperature range of 240 to 320 °C, the decomposition ratio of MM also increased with the rise in heating temperature, and the decomposition ratio of MM was 0.45% at 240 °C and 2.83% at 320 °C, which was significantly lower than MDM. Thus, MDM had worse thermal stability compared with MM.

The species and mass fractions of decomposition products (320 °C, 24 h) in a representative MDM sample are enumerated in

Table 3. Product detection results at 320 °C.

Product	Mass Fraction/%	Product	Mass Fraction/%
MDM	90.47	MM	5.82
MD2M	1.85	MD3M	0.57
MD4M	0.28	MD5M	0.20
D4	0.35	D5	0.14
QM4	0.23	Others	0.09

. The results revealed that the decomposition products of MDM were mainly linear siloxanes and small amounts of cyclic siloxanes. MM was the main product of MDM’s thermal decomposition, with a mass fraction of 5.82%, which is significantly higher than other products. It is worth noting that the main decomposition product of MM is MDM in previous experimental results [14]. So, there is the strong possibility that the decomposition of MM and MDM may be restrained in the MM/MDM mixtures compared to the pure working fluid.

An experiment of MM/MDM mixture at 280 °C was made to verify this guess. The mass ratio of MM/MDM was set as 0.73/0.27 to ensure that the partial pressures of MM and MDM were close to the experimental pressures in pure fluid tests. The decomposition ratio of MM/MDM mixture is shown in Figure 4. The decomposition ratio of MM/MDM mixture in theory in Figure 4 was calculated by the decomposition ratios of pure fluids and their mass ratios in the mixture. The results showed that the experimental decomposition ratio of MM/MDM mixture was significantly smaller than that in theory, even smaller than that of pure MM. Thus, the mixture of MM/MDM had big inhibiting effects on the decomposition of MM and MDM. The mixture working fluids of MM/MDM could not only improve the performance of the ORC system but also weaken the thermal decomposition of working fluids.

Reaction kinetics experiments for siloxanes were designed to predict the thermal stability of siloxane mixture fluids in a long operation period. MM was chosen as the test fluid because of its similar thermal stability with MM/MDM mixture to avoid the complicated experiments for different mixture ratios. The decomposition ratios of MM at 240 °C, 260 °C, and 300° C are shown in Figure 5. The results showed that the decomposition ratios rose over time at different temperatures and the temperature had big effects on the decomposition of MM. The decomposition ratio curves at 240 °C, 260 °C, and 300 °C were converted to the lnC/C₀–t curves shown in Figure 6 to calculate the reaction rate constants at different temperatures. The lnC/C₀–t curves were almost linear, which indicated that the decomposition of MM followed a first order reaction model. The reaction rate constants at 240 °C, 260 °C, and 300 °C are listed in

Table 4. Product detection results at 320 °C.

k (s−1)	T (K)			Ea (kJ/mol)	A (s−1)
	513.15	533.15	573.15
k	3.76 × 10−8	7.76 × 10−8	1.36 × 10−7	50.50	5.80 × 10−3

. Then, the pre-exponential factor A and the activation energy Ea can be calculated using Equation (5) as shown in Table 3.

The decomposition ratios after long system operation periods can be estimated using the reaction kinetics model. The service life of the ORC systems was set to be 20 years. The equivalent residence time at the highest temperatures in the loop was calculated referring to the flow times in a practical ORC loop example [33]. The decomposition ratios after 20 years at different highest temperatures are shown in Figure 7. The results showed that the long-term decomposition ratios increased by the increasing temperatures, and the increasing rate also increased by the increasing temperatures. When the highest temperature was higher than 300 °C, the long-term decomposition ratio after 20 years would be larger than 25%, which could lead to big effects on the efficiency and operation safety of the ORC systems. The long-term decomposition ratio after 20 years at 220 °C was smaller than 5% by the reaction kinetics model, which resulted in a limited loss of the ORC system performance referring to the previous studies [34]. Thus, 220 °C could be assumed as the maximum evaporation temperature for ORC systems utilizing MM and MDM mixtures as working fluids in this work. While this may not precisely coincide with the theoretical stable temperature for siloxanes, it provides a practical benchmark for the analysis of mixture working fluids in practical system studies.

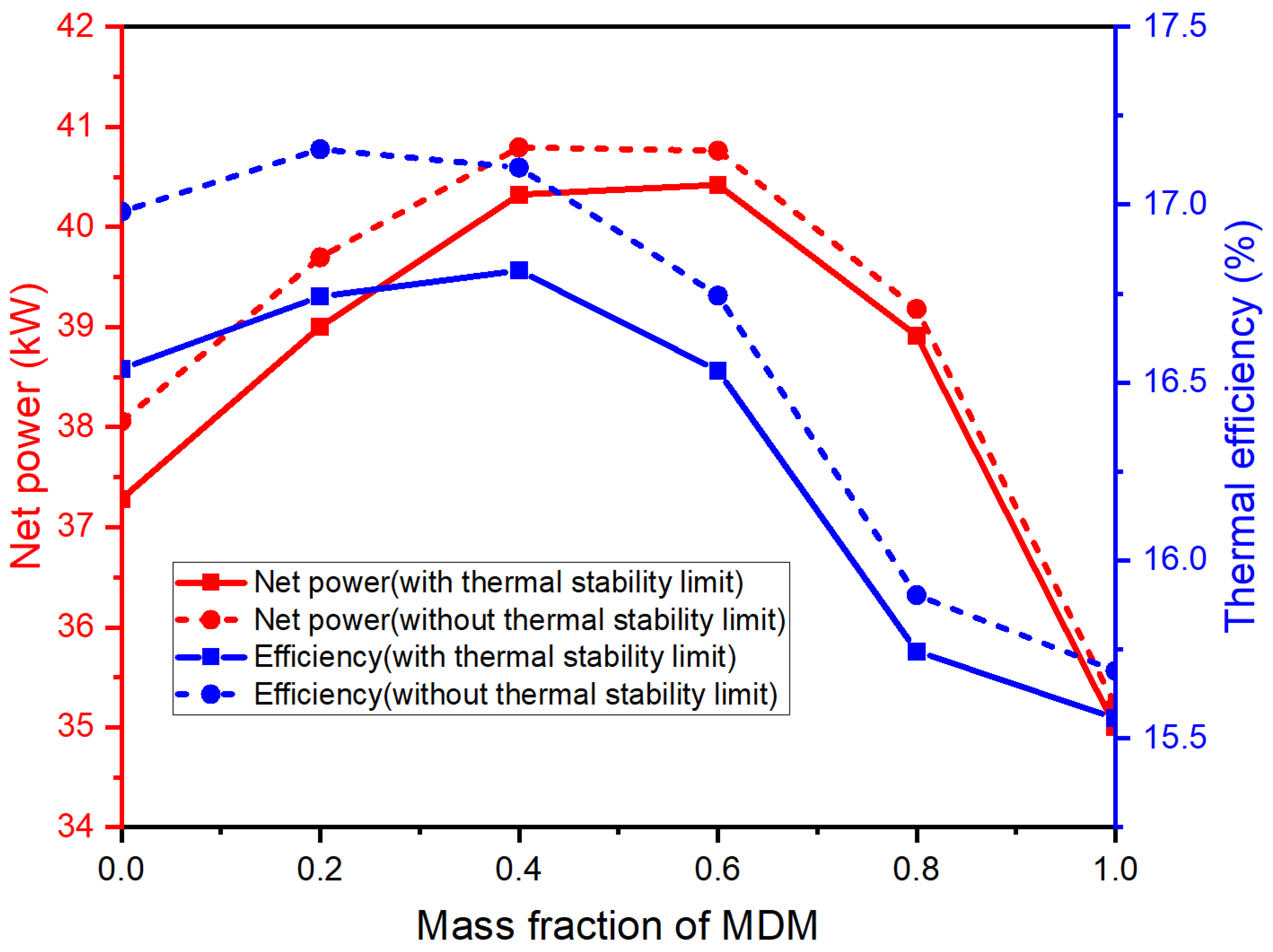
3.2. Simulation Results and Discussion

The thermal performance of mixtures and pure working fluid was compared, whereby the thermal efficiency and net power of the system were computed for various mixing ratios. Initially, the maximum net power of the ORC system and the thermal efficiency under this net power condition were evaluated without imposing an evaporation temperature limit. Subsequently, a cap of 220 °C was applied to the maximum evaporation temperature, after which similar computations were undertaken, calculating the maximum net power and corresponding thermal efficiency of the system within a specified evaporation temperature range.

The results, depicted in Figure 8, demonstrated that certain mixtures noticeably outperformed the pure working fluid in terms of net power and thermal efficiency. Moreover, it was also observed that both the net power and thermal efficiency underwent a decline when the evaporation temperature was limited to 220 °C. While the reduction in net power was relatively limited, a significant decrease was observed in the thermal efficiency. The maximum net power without thermal stability limit was 40.79 kW with the MDM mass fraction of 0.4. While considering the thermal stability limit, the maximum net power was 40.42 kW with the MDM mass fraction of 0.6. The relative decrease was 0.92%. The maximum thermal efficiency without thermal stability limit was 17.16% and occurred in the MDM mass fraction of 0.2, while that with thermal stability limit was 16.82% and occurred in the MDM mass fraction of 0.4 by a relative decrease of 1.98%.

The variations in net power and thermal efficiency with differing evaporation temperatures are depicted in Figure 9a,b, respectively. The results demonstrated that the net power of the system initially exhibited a minor increase before sharply declining with the rising evaporation temperature, regardless of the working fluid mixing ratio. This steep decline was attributed to the change in the evaporator’s pinch point, which resulted in a reduced heat transfer rate from the heat source to the working fluid. The maximum net power of the mixtures occurred within the evaporation temperature range of 220 °C to 250 °C, surpassing the evaporation temperature limit. However, the maximum net power of the mixtures, with the evaporation temperature limit, only decreased by 0.6–2.0% compared to the theoretical maximum values obtained without evaporation temperature constraints. Thus, the impact of thermal stability limitations on net power was found to be acceptable.

The thermal efficiency of the system exhibited a substantial increase with the rise in the evaporation temperature. And the increase rate of different mixed working medium is different. The thermal efficiency of MM pure working fluid was the most significant, while the efficiency of MDM pure working fluid was relatively gentle. However, for all working fluids, the decrease in thermal efficiency cannot be ignored when the evaporation temperature is limited to 220 °C. Thus, if thermal efficiency is the primary performance indicator, a higher evaporation temperature should be adopted to enhance the system’s efficiency. Conversely, if the net power output is viewed as the principal criterion for ORC system design, it can be considered that the evaporation temperature should be controlled lower than 220 °C, so as to improve the safety and stability of the system at the cost of small net power loss.

These results further suggested that the MM/MDM mixture with a ratio of 0.6/0.4 enhanced the net power and thermal efficiency by 8.1% and 1.7%, respectively. This composition could be regarded as a superior working fluid for these ORC systems.

4. Conclusions

In this study, a thermal decomposition experimental system was established, and the thermal stability of MM, MDM, and their mixtures was assessed. A reaction kinetics model was built to analyze the thermal stability of siloxane mixture fluids in a long operation period. Furthermore, the influence of the MM/MDM mass ratio and evaporation temperature on the system’s net power and thermal efficiency was analyzed. The major conclusions are summarized as follows:

(1)

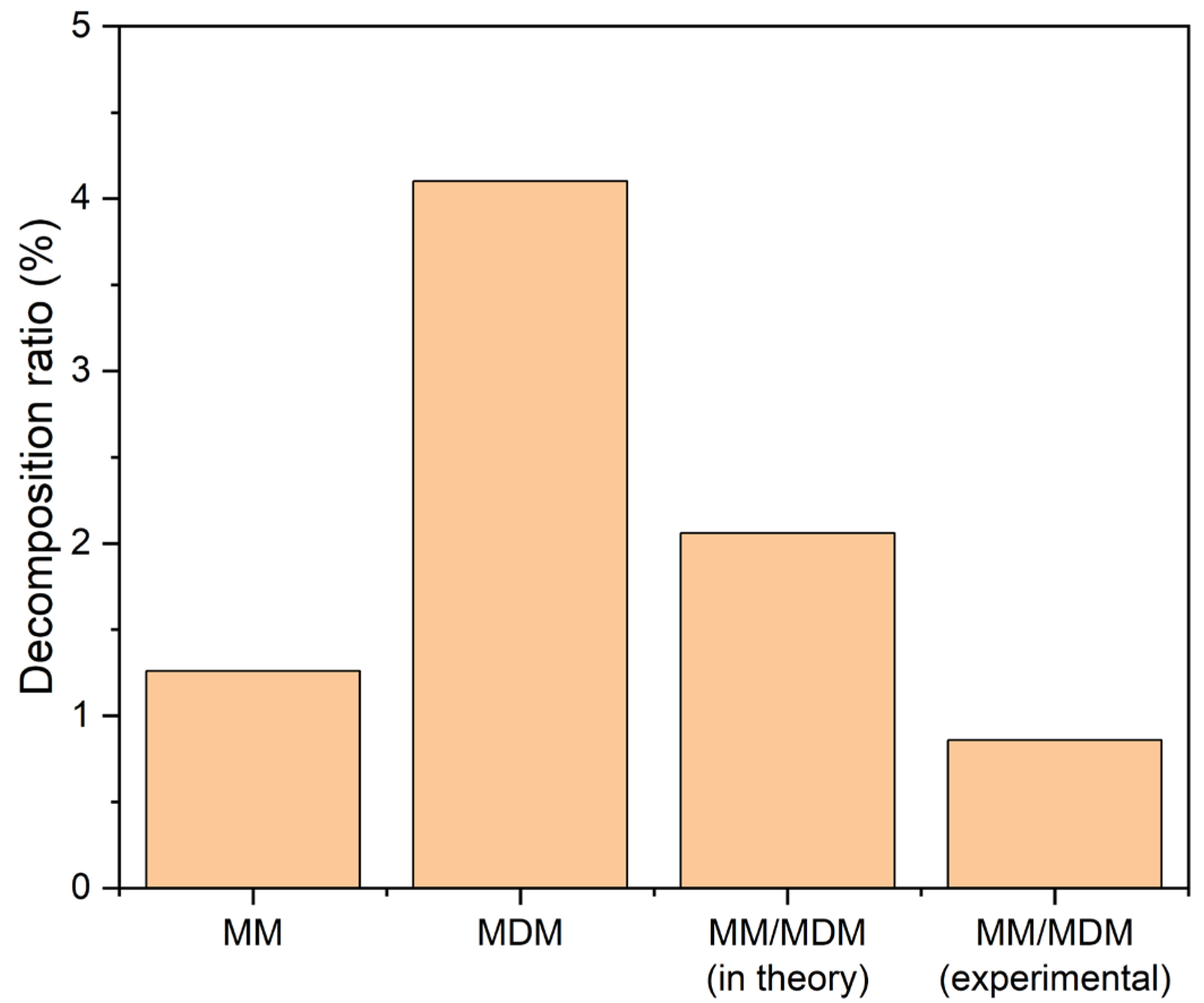
MDM demonstrated inferior thermal stability compared to MM within the temperature range of 240~320 °C. The MM/MDM mixture had a smaller decomposition ratio than pure MM or MDM. Using MM/MDM mixture as the working fluid of high-temperature ORCs is a good choice by the thermal stability.

(2)

MM decomposed by just about 5% at 220 °C after a long operation period of 20 years, resulting in a limited loss of the ORC system performance. A temperature of 220 °C can be considered as the limiting highest temperature for ORCs using MM, MDM, and their mixtures as working fluids.

(3)

Both the net power and the thermal efficiency of the system were diminished when an evaporation temperature limit was imposed. The impact of this temperature limit on the net power was relatively minor, while the decrease in thermal efficiency was more pronounced. Different design strategies considering the thermal stability limitation should be used with the different output parameter optimization objectives.

(4)

Certain siloxane mixtures demonstrated superior performance compared to pure fluid, given the system model and conditions outlined in this study. The MM/MDM (0.6/0.4) emerged as an optimal working fluid selection within the scope of this work.