Flow in a Taylor–Couette Reactor with Ribbed Rotors
Abstract
:1. Introduction
2. Methodology
2.1. Experimental Setup
2.2. PIV System
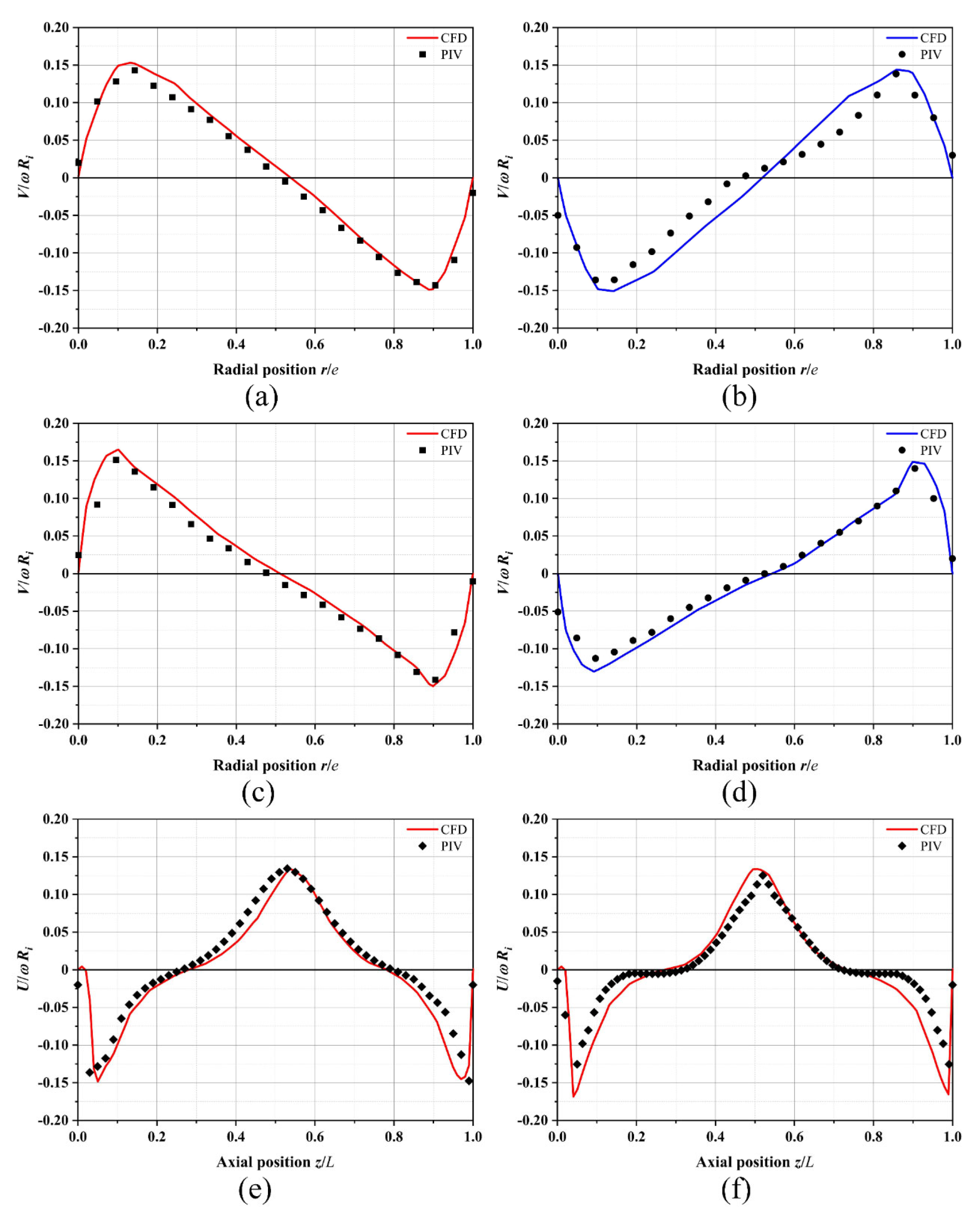
2.3. Numerical Method
3. Results and Discussion
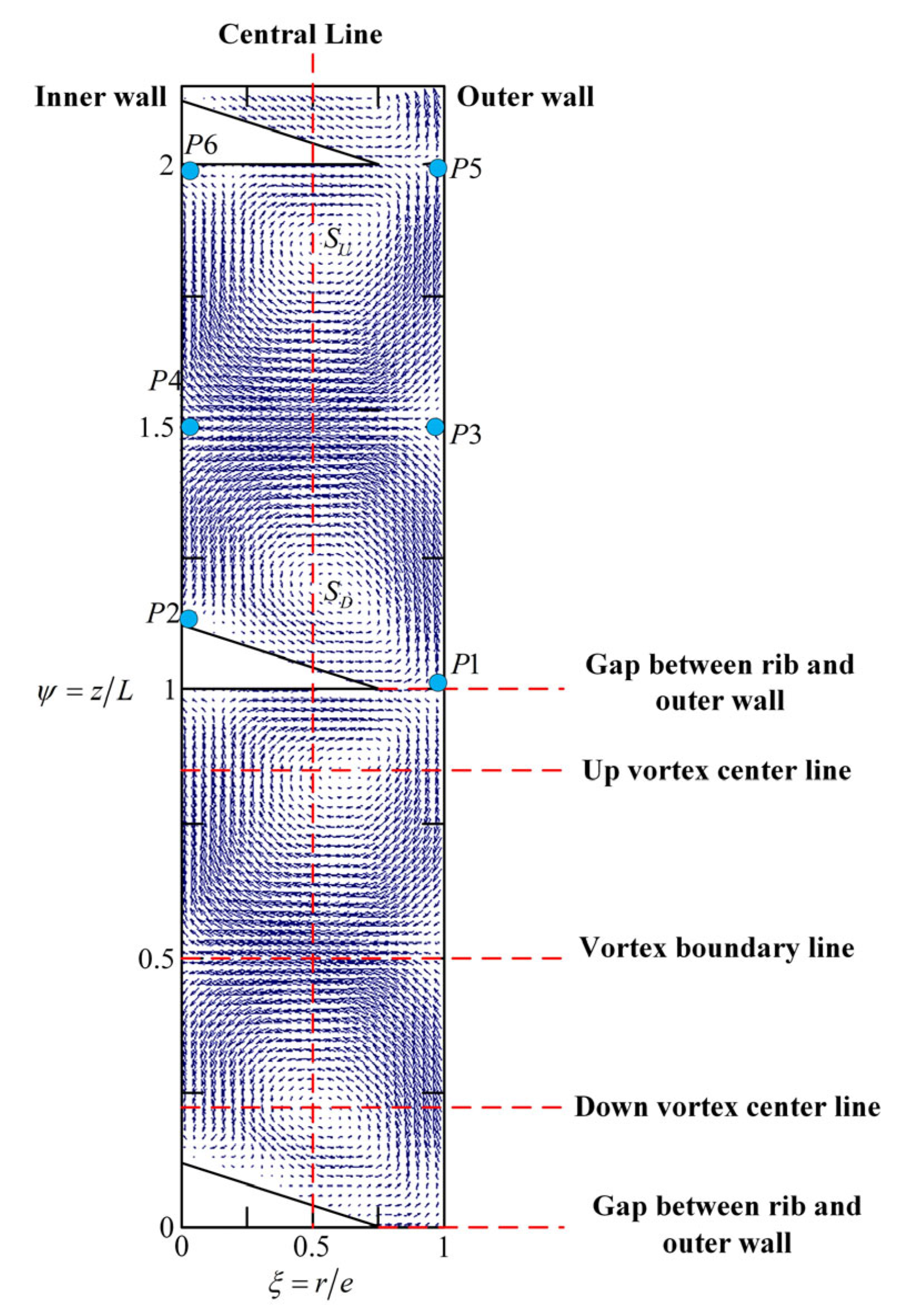
3.1. The Flow Structure in the Ribbed TCR
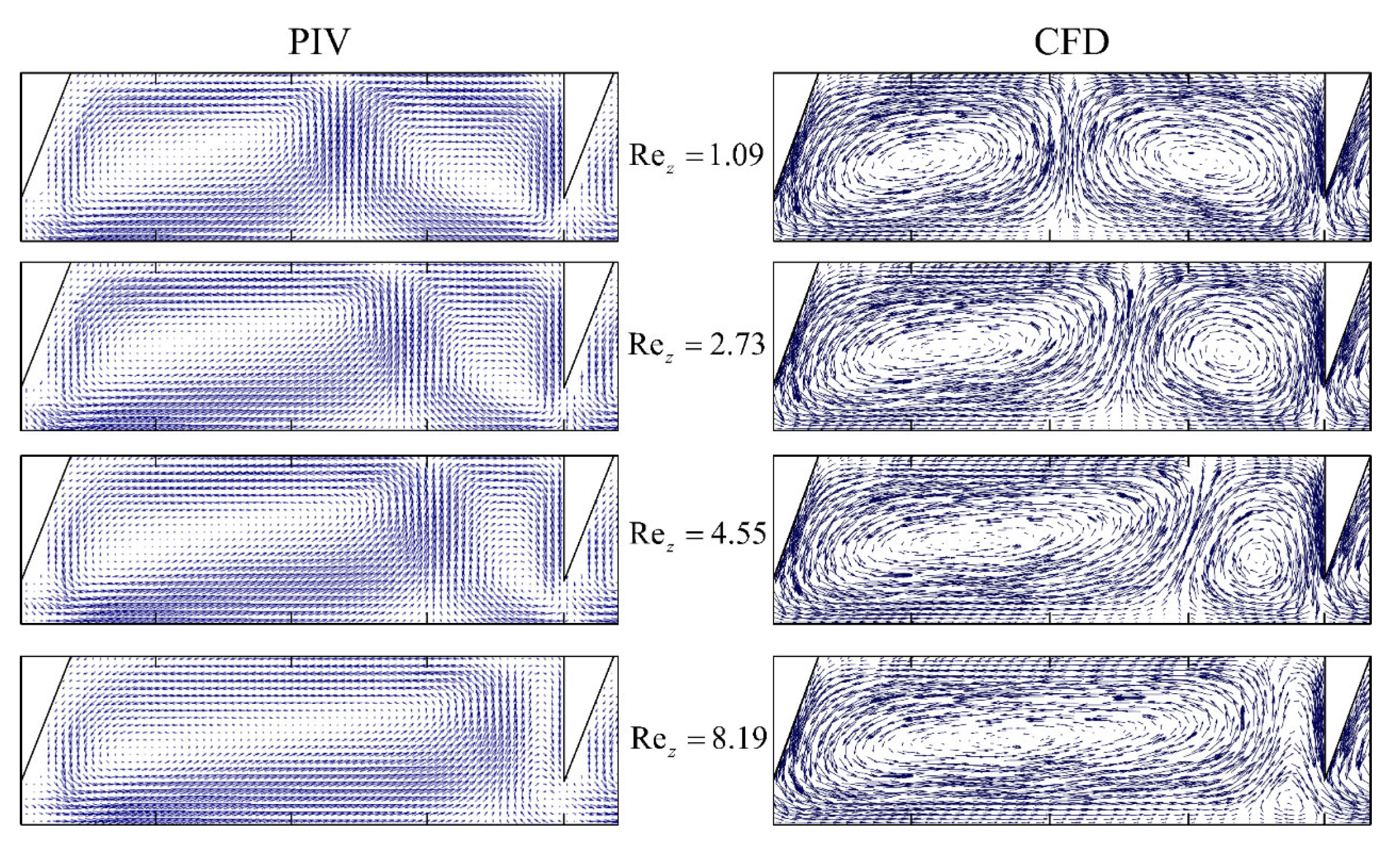
3.2. Vortex Structure without Axial Flow
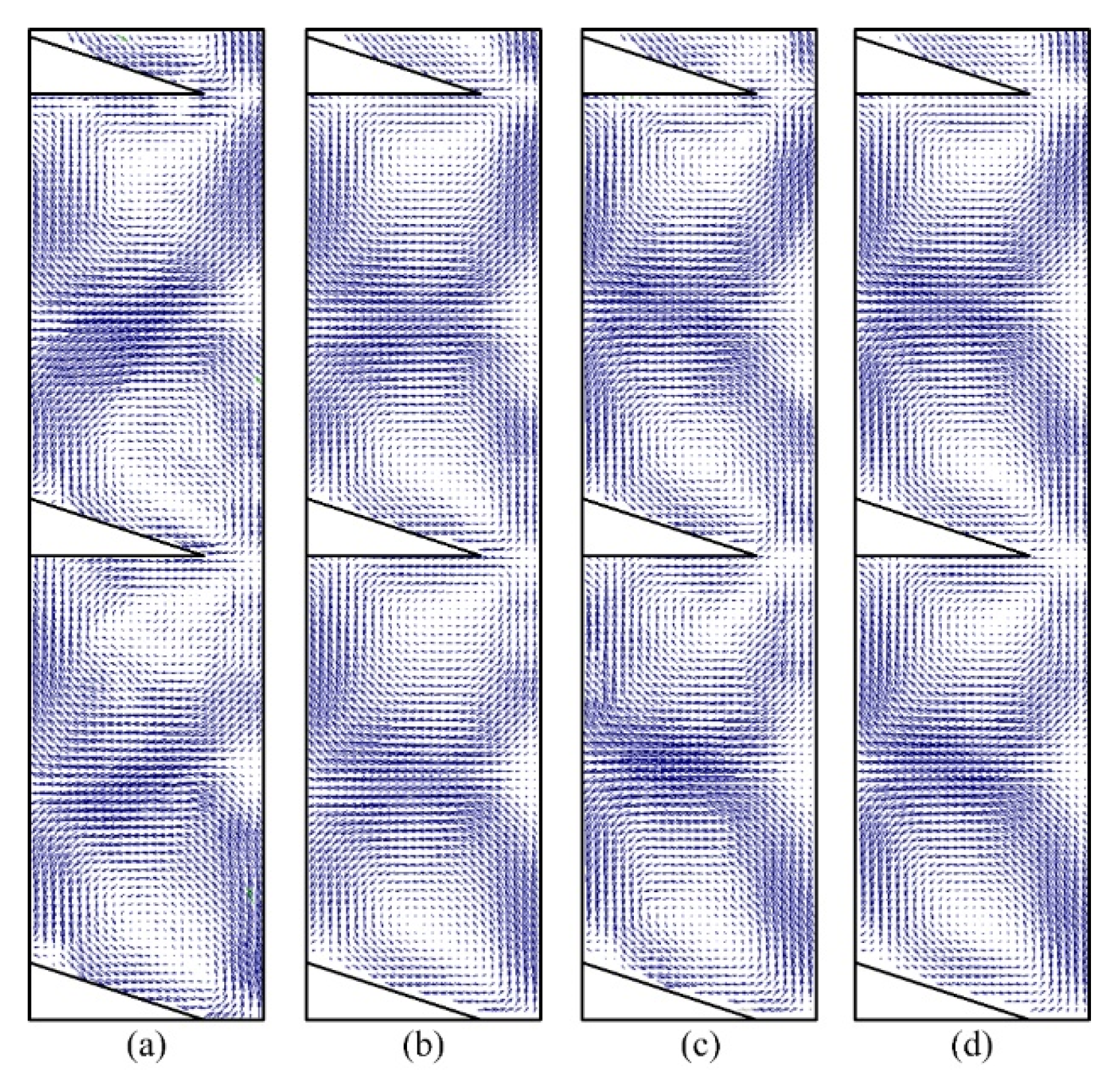
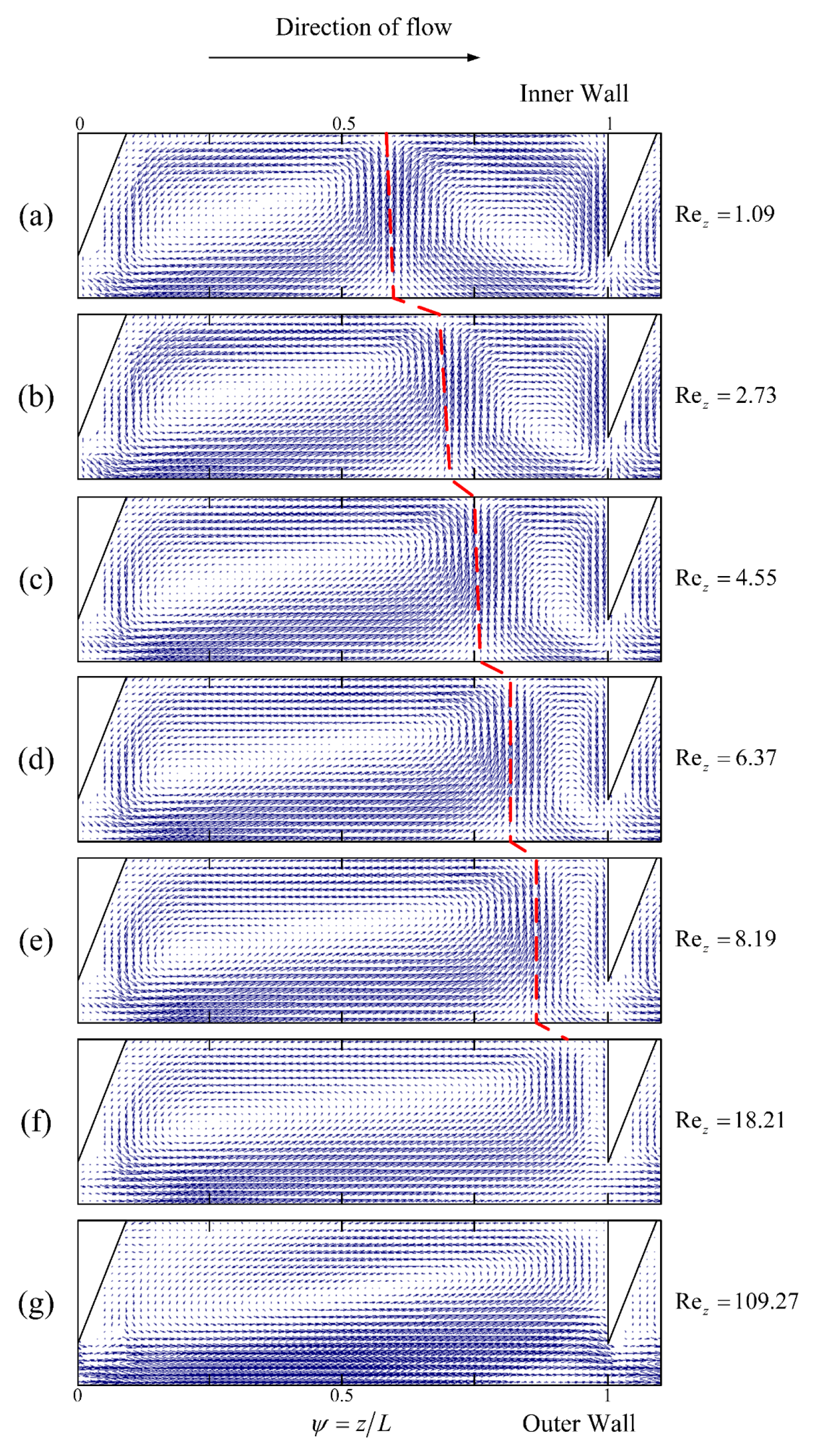
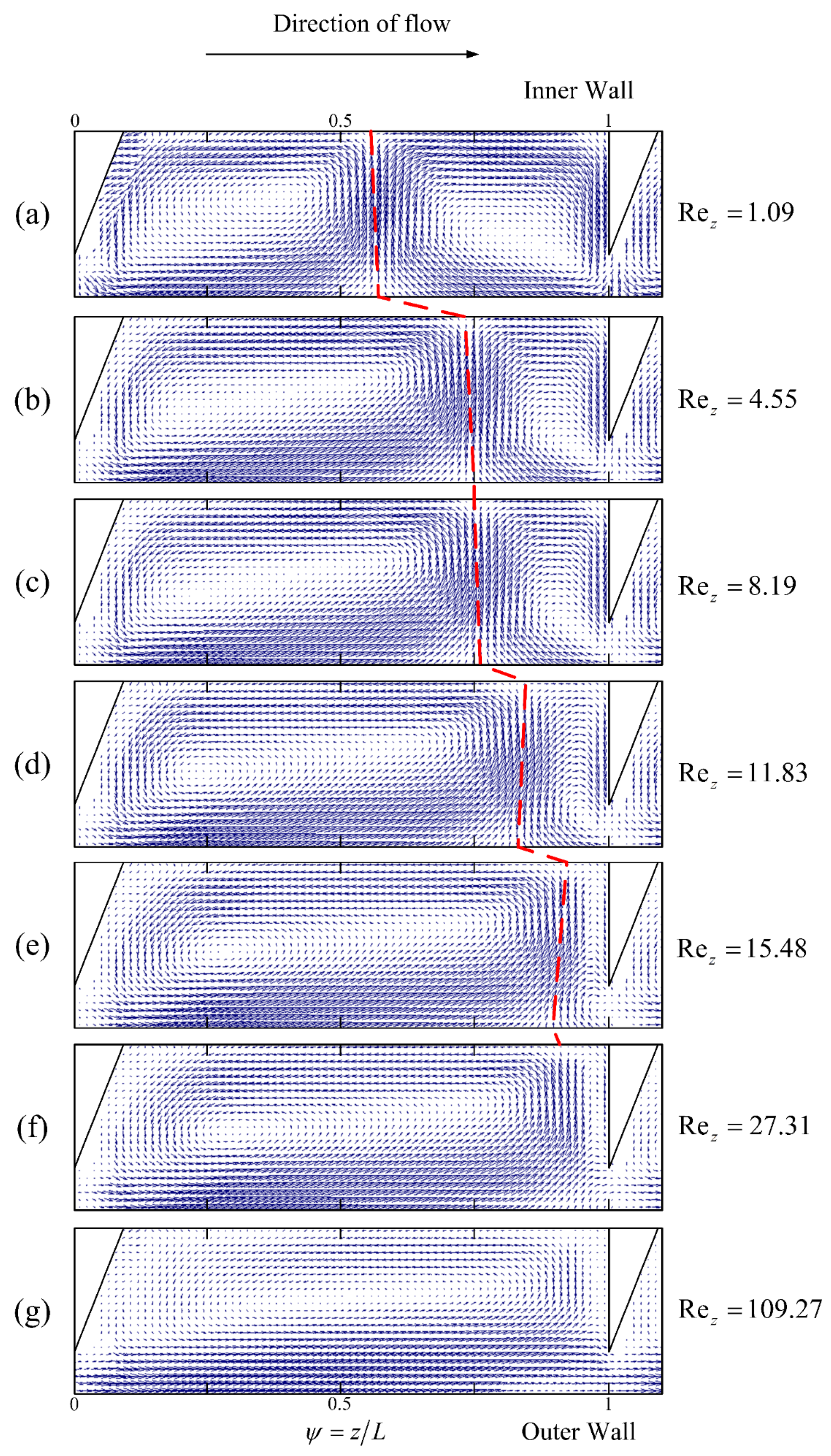
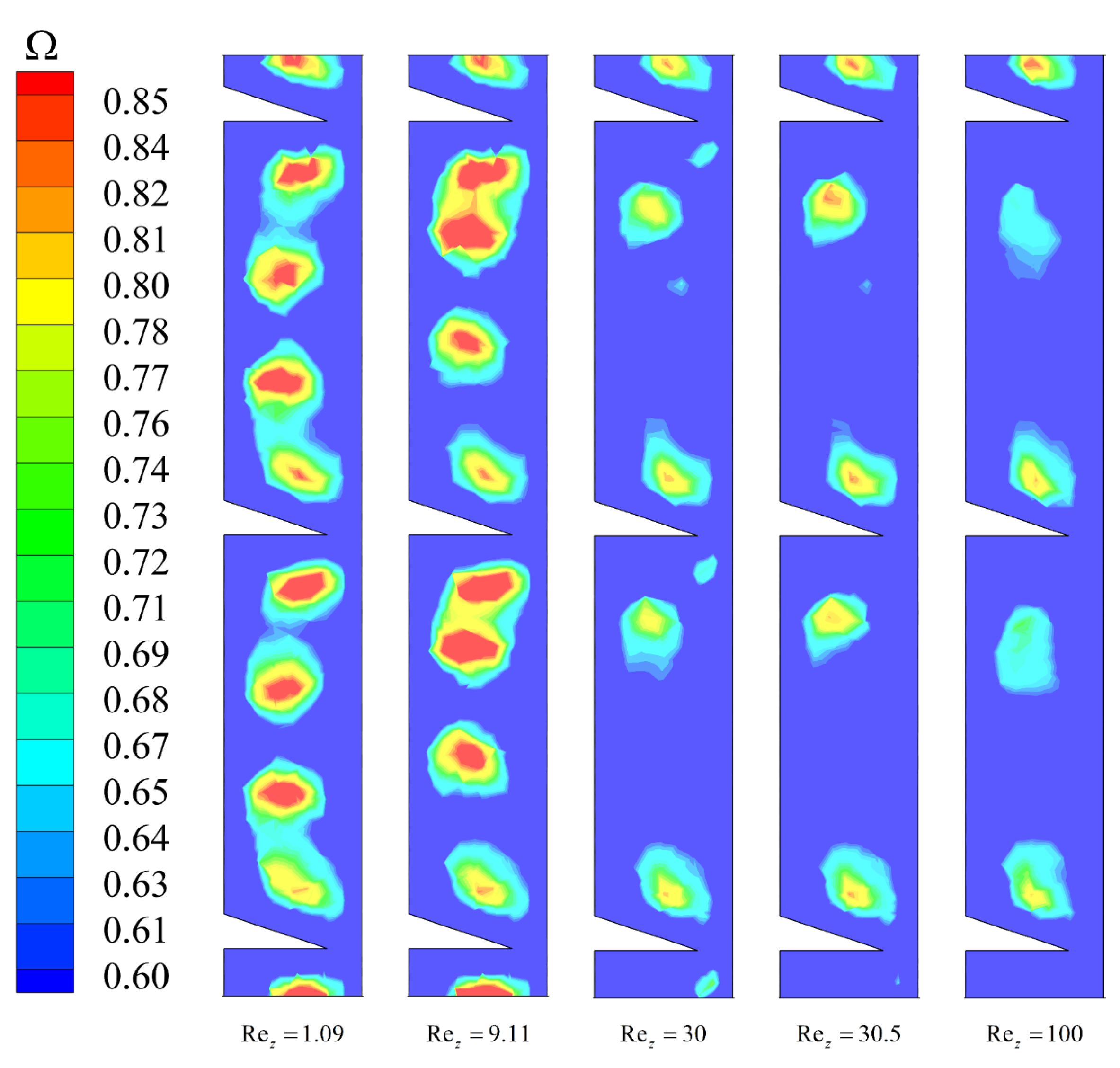
3.3. Vortex Structure with Axial Flow
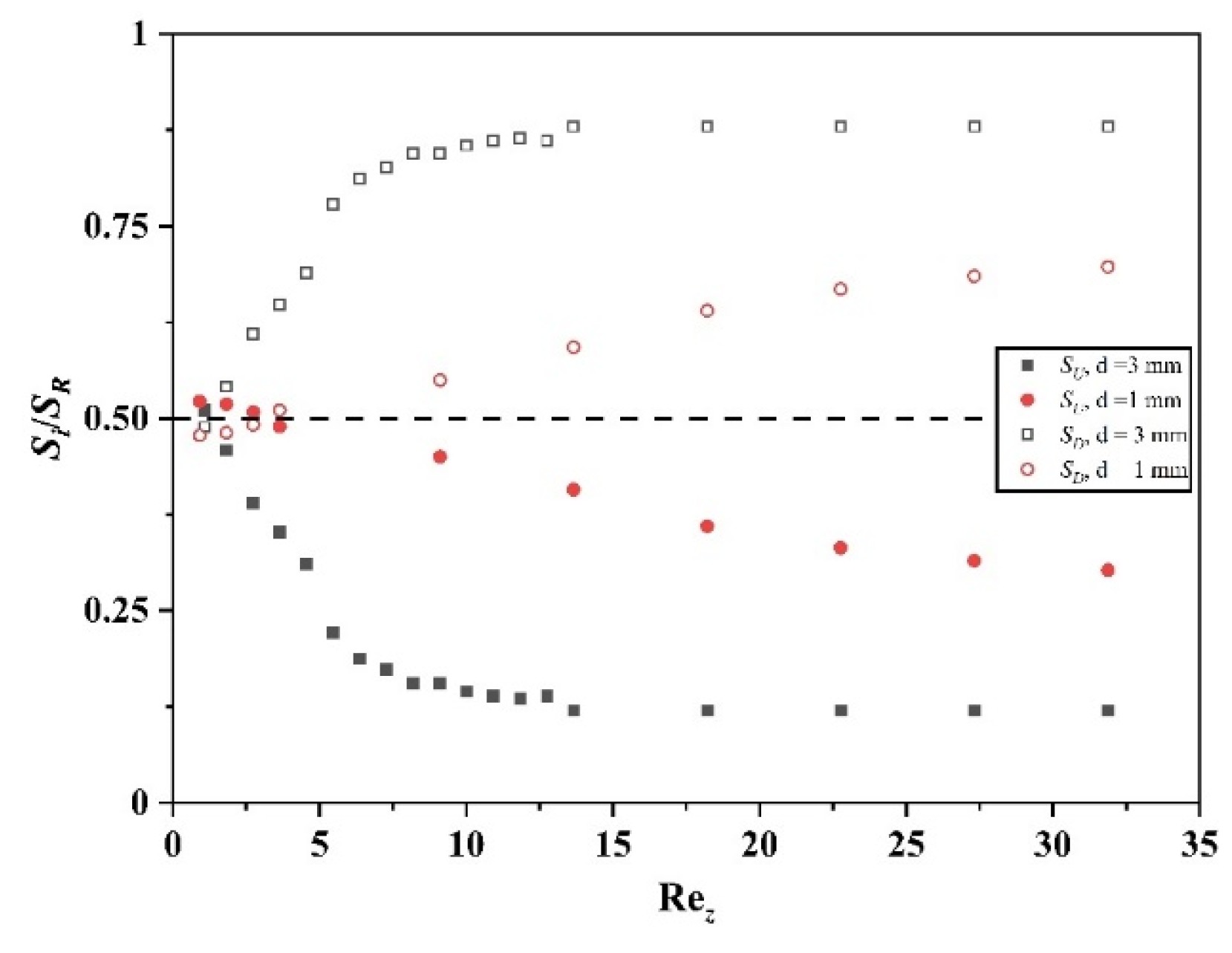
3.4. Critical Axial Reynolds Number for Flow Pattern Transformation
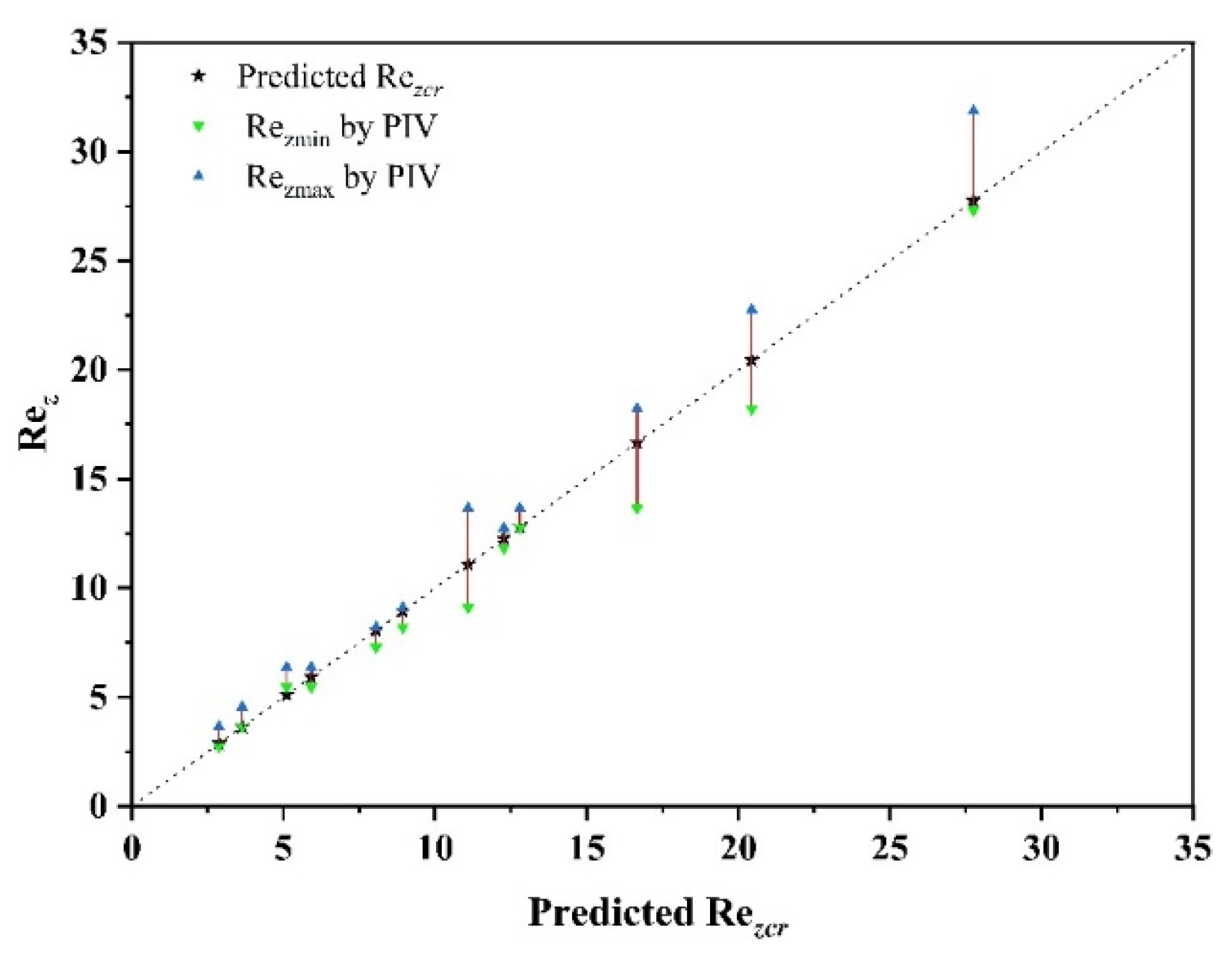
3.4.1. Validation of the CFD Results
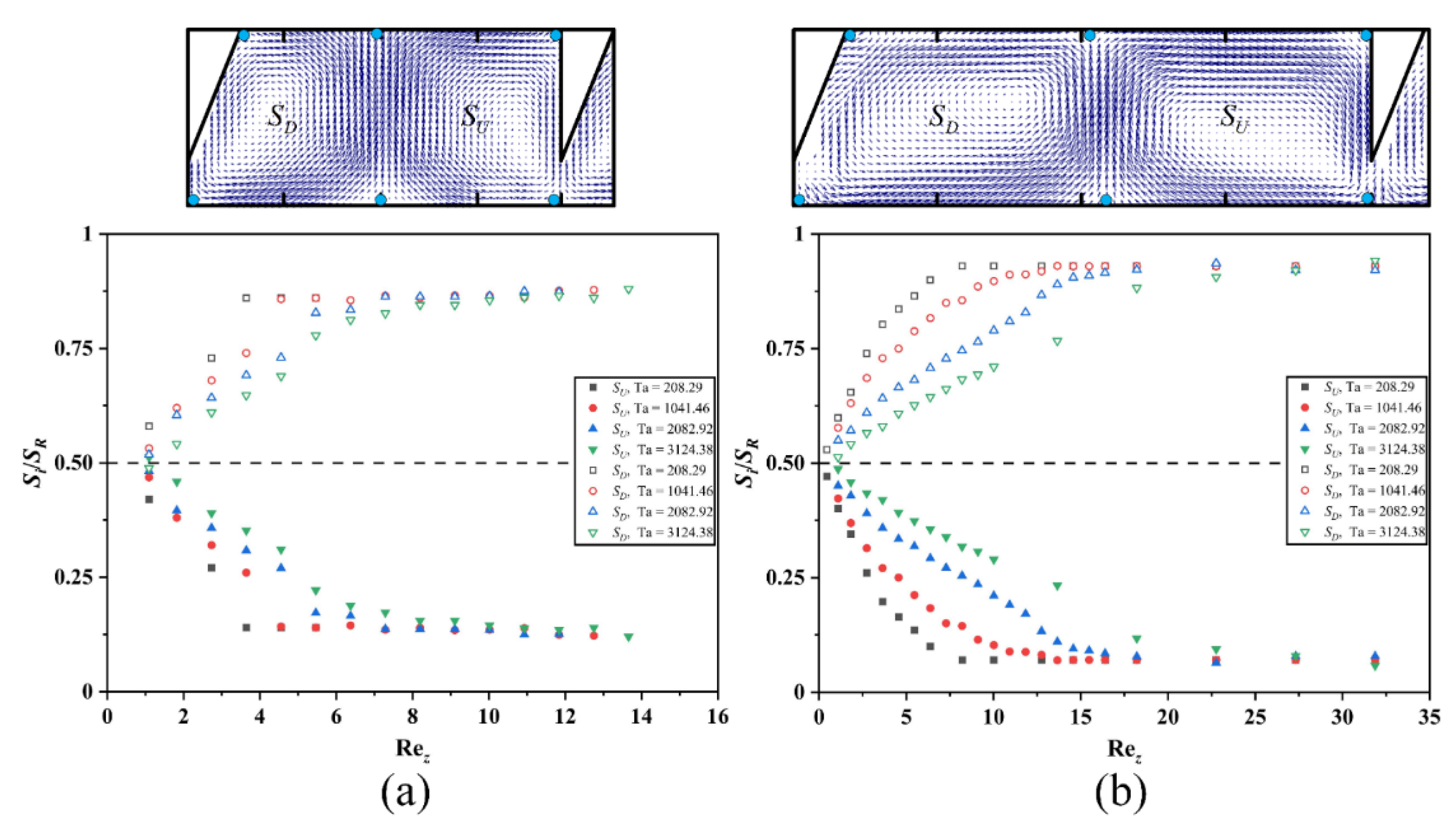
3.4.2. Vortex Identification Method
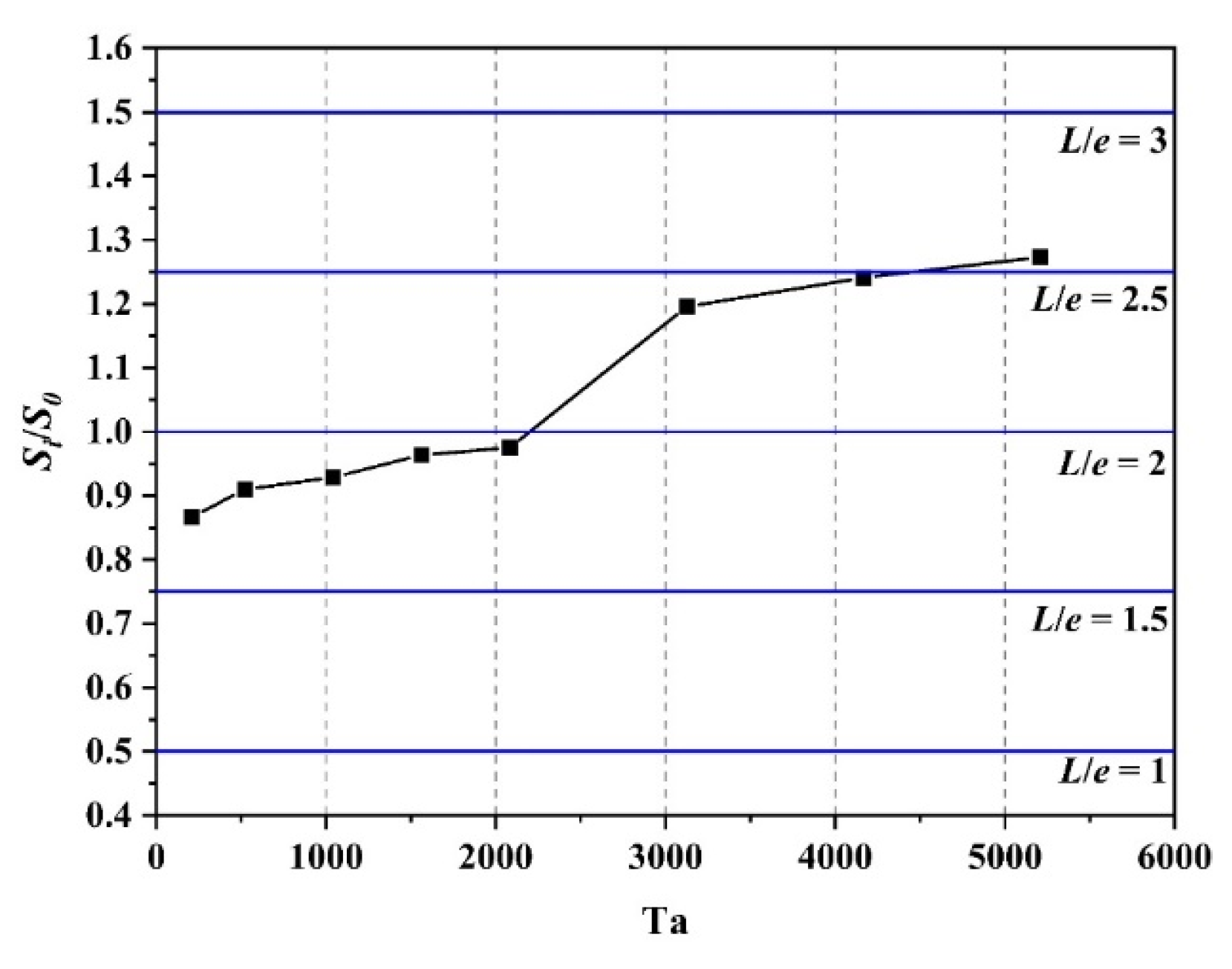
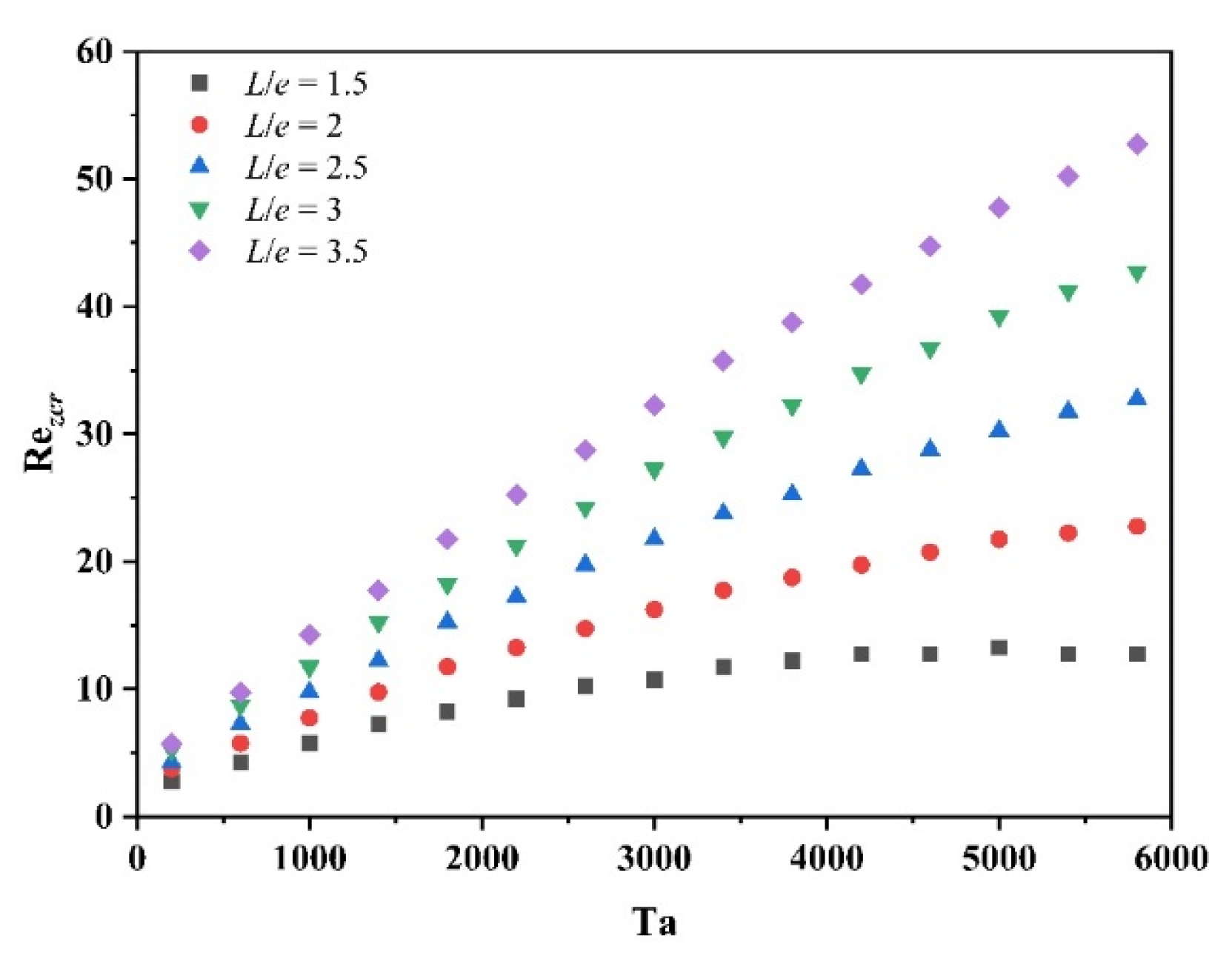
3.4.3. Estimation of the Critical Axial Reynolds Number
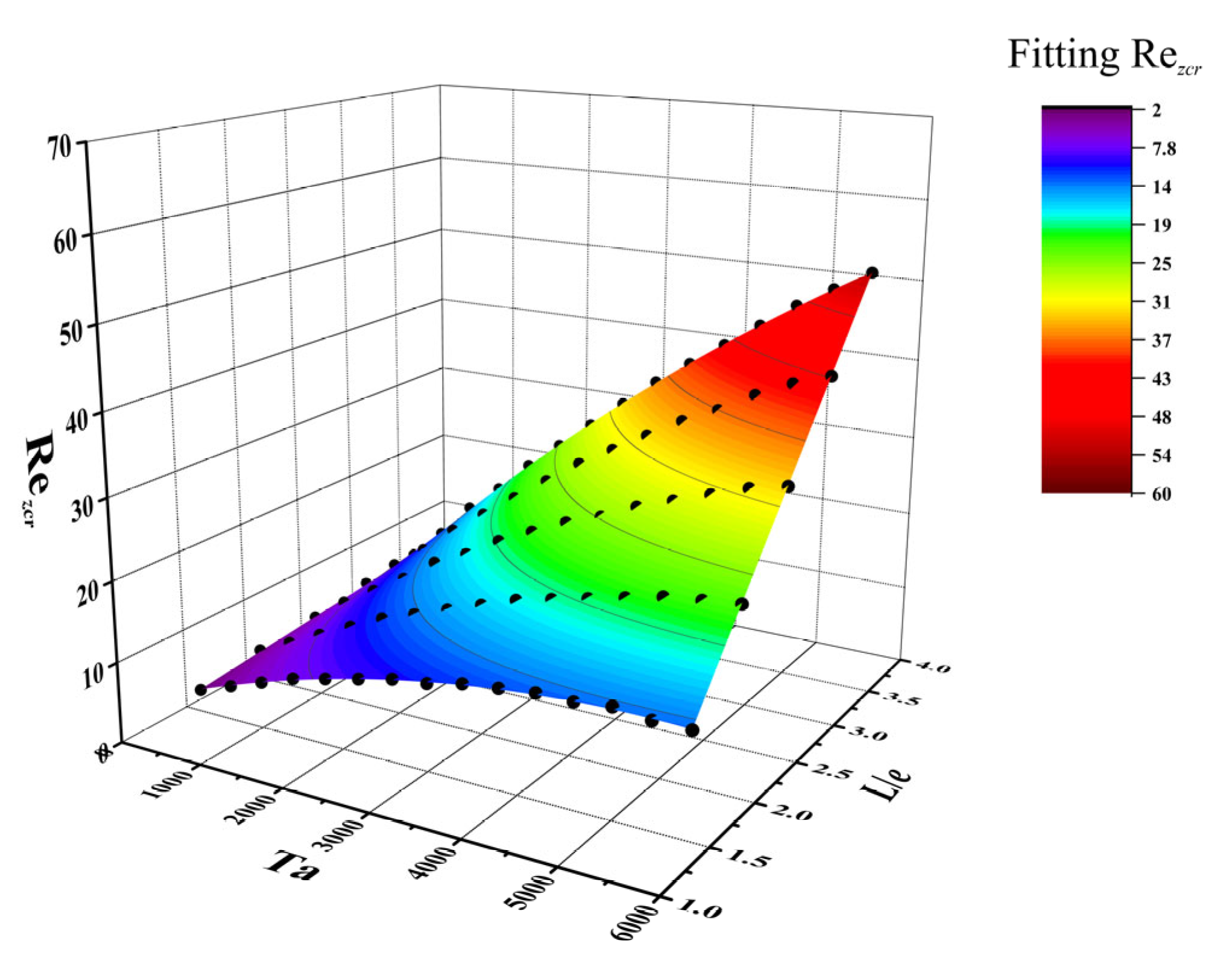
3.4.4. Critical Reynolds Number Correlation
4. Conclusions
- (1)
- The ribbed TCR enables control of the flow field structure while maintaining the symmetry of the flow field, due to the outer cylindrical surface provided by the ribs. Under certain conditions, a Taylor vortex pair can form between the ribs, with the down vortex rotating clockwise and the up vortex rotating counterclockwise. The area around the ribs is the outflow zone, and the area where the two vortices meet is the inflow zone.
- (2)
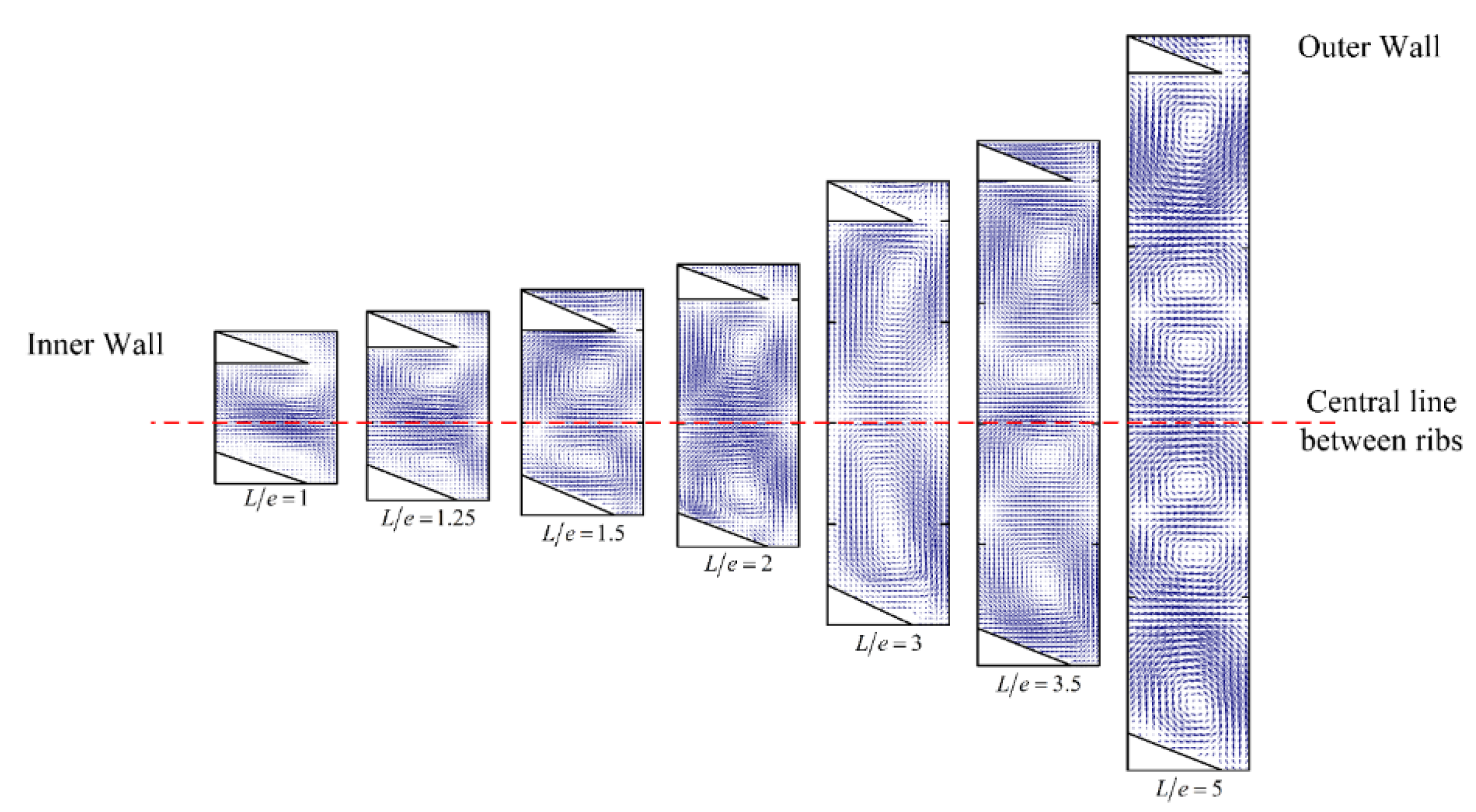
- We investigated the variations in the Taylor vortex structure with Ta within a ribbed TCR in the absence of axial flow. We found that the axial dimension of the Taylor vortex can be controlled by adjusting the rib spacing, which can be summarized into four different conditions according to the size of the rib spacing. When L/e is less than 1.5, the Taylor vortex that forms between the ribs is more sensitive to the wall effect of the ribs, and the up vortex is gradually compressed as the rotor speed increases. When L/e is between 1.5 and 3, a stable Taylor vortex pair can form between the ribs that are less susceptible to the boundary effect of the rib wall. When L/e is greater than 3 and less than 4, two pairs of Taylor vortices can form between the ribs, which can be converted into a pair by increasing the speed, while for L/e greater than 4, three pairs of Taylor vortices can be formed between the ribs, which can be converted into two pairs by increasing the Ta value.
- (3)
- The axial Reynolds number Rez greatly impacts the Taylor vortex structure within the ribbed TCR. As the axial Reynolds number increases, the up vortex appears to be compressed, and the down vortex appears to be stretched; when a specific critical value is reached, the double-vortex flow pattern between the ribs is transformed into a single vortex. The operating parameter Ta and the structural parameters (L, d) strongly influence the transition rate and the critical point. Larger critical axial Reynolds numbers (Rezcr) and lower transition rates are observed when a higher Ta value, larger rib spacing, and smaller rib widths are utilized.
- (4)
- By using the Ω method to identify the Taylor vortex within the TCR and setting 0.6 as the threshold for the flow pattern transition, we obtained a Rezcr value with greater accuracy via CFD methods for the various rib spacings and Ta values. We correlated Rezcr with Ta and L/e via binary polynomial fitting and found that Rezcr is strongly correlated with Ta and L/e. The empirical correlation equation that we have developed shows strong predictive power, which we validated with the experimental results of PIV.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| CFD | Computational fluid dynamics |
| d | Rib width, mm |
| e | Annular gap width, mm |
| h | Rib edge thickness, mm |
| l | Rotor length, mm |
| L | Rib spacing, mm |
| N | Number of regions |
| P | Point |
| R2 | Regression coefficient |
| Ri | Inner cylinder radius, mm |
| Ro | Outer cylinder radius, mm |
| Rez | Axial Reynolds number |
| Rezcr | The critical axial Reynolds number |
| RSM | Reynolds stress model |
| S | Area of the specific region, m2 |
| Ta | Taylor number |
| TCR | Taylor–Couette reactor |
| TCF | Taylor–Couette flow |
| uax | The axial flow velocity, m/s |
| V | Velocity, m/s |
| (r, z) | Dimensional coordinates |
| Greek | |
| turbulent kinetic energy dissipation rate, m2/s3 | |
| ϕ | Factor ϕ, characterizing the relationship between the local energy dissipation rate and the volume-averaged energy dissipation rate, which is introduced as a constant value |
| ω | Rotation speed of rotor, rad/s |
| ν | Kinematic viscosity, m2/s |
| ρ | The density of liquid, kg/m3 |
| (ψ, ξ) | Dimensionless coordinates |
References
- Jung, T.; Kim, W.S.; Choi, C.K. Effect of monovalent salts on morphology of calcium carbonate crystallized in couette–taylor reactor. Cryst. Res. Technol. J. Exp. Ind. Crystallogr. 2005, 40, 586–592. [Google Scholar] [CrossRef]
- Aljishi, M.F.; Ruo, A.; Park, J.H.; Nasser, B.; Kim, W.; Joo, Y.L. Effect of flow structure at the onset of instability on barium sulfate precipitation in taylor–couette crystallizers. J. Cryst. Growth 2013, 373, 20–31. [Google Scholar] [CrossRef]
- Hong, S.B.; Jeong, J.; Kang, H.G.; Seo, D.; Cha, Y.; Jeon, H.; Lee, G.Y.; Irshad, M.; Kim, D.H.; Hwang, S.Y. Fast and scalable hydrodynamic synthesis of mno2/defect-free graphene nanocomposites with high rate capability and long cycle life. ACS Appl. Mater. Interfaces 2018, 10, 35250–35259. [Google Scholar] [CrossRef]
- Lee, S.; Park, S. Enhanced dispersion and material properties of multi-walled carbon nanotube composites through turbulent taylor-couette flow. Compos. Part A Appl. Sci. Manuf. 2017, 95, 118–124. [Google Scholar] [CrossRef]
- Haut, B.; Amor, H.B.; Coulon, L.; Jacquet, A.; Halloin, V. Hydrodynamics and mass transfer in a couette–taylor bioreactor for the culture of animal cells. Chem. Eng. Sci. 2003, 58, 777–784. [Google Scholar] [CrossRef]
- Qiao, J.; Yan, W.; Teoh, J.H.; Tong, Y.W.; Wang, C. Experimental and computational studies of oxygen transport in a taylor-couette bioreactor. Chem. Eng. J. 2018, 334, 1954–1964. [Google Scholar] [CrossRef]
- Sorg, R.; Tanzeglock, T.; Soos, M.; Morbidelli, M.; Périlleux, A.; Solacroup, T.; Broly, H. Minimizing hydrodynamic stress in mammalian cell culture through the lobed taylor-couette bioreactor. Biotechnol. J. 2011, 6, 1504–1515. [Google Scholar] [CrossRef] [PubMed]
- Färber, T.; Riechert, O.; Zeiner, T.; Sadowski, G.; Behr, A.; Vorholt, A.J. Homogeneously catalyzed hydroamination in a taylor–couette reactor using a thermormorphic multicomponent solvent system. Chem. Eng. Res. Des. 2016, 112, 263–273. [Google Scholar] [CrossRef]
- Behr, A.; Vorholt, A.J.; Färber, T.; Behr, A.; Vorholt, A.J. Hydroamination and telomerisation of β-myrcene. In Homogeneous Catalysis with Renewables; Springer: Berlin/Heidelberg, Germany, 2017; pp. 177–189. [Google Scholar]
- Bernstein, G.J.; Grosvenor, D.E.; Lenc, J.F.; Levitz, N.M. Development and Performance of a High-Speed, Long-Rotor Centrifugal Contactor for Application to Reprocessing Lmfbr Fuels; Argonne National Laboratory: Argonne, ILL, USA, 1973. [Google Scholar]
- Haim, D.; Pismen, L.M. Performance of a photochemical reactor in the regime of taylor-grtler vortical flow. Chem. Eng. Sci. 1994, 49, 1119–1129. [Google Scholar] [CrossRef]
- Sczechowski, J.G.; Koval, C.A.; Noble, R.D. A taylor vortex reactor for heterogeneous photo-catalysis. Chem. Eng. Sci. 1995, 50, 3163–3173. [Google Scholar] [CrossRef]
- Sengupta, T.K.; Kabir, M.F.; Ray, A.K. A taylor vortex photocatalytic reactor for water purification. Ind. Eng. Chem. Res. 2001, 40, 5268–5281. [Google Scholar] [CrossRef]
- Forney, L.J.; Pierson, J.A. Optimum photolysis in taylor–couette flow. AICHE J. 2003, 49, 727–733. [Google Scholar] [CrossRef]
- Dutta, P.K.; Ray, A.K. Experimental investigation of taylor vortex photocatalytic reactor for water purification. Chem. Eng. Sci. 2004, 59, 5249–5259. [Google Scholar] [CrossRef]
- Lee, S.; Lueptow, R.M. Rotating reverse osmosis: A dynamic model for flux and rejection. J. Membr. Sci. 2001, 192, 129–143. [Google Scholar] [CrossRef]
- Forney, L.J.; Pierson, J.A.; Ye, Z. Juice irradiation with taylor-couette flow: UV inactivation of Escherichia coli. J. Food Prot. 2004, 67, 2410–2415. [Google Scholar] [CrossRef] [PubMed]
- Krintiras, G.A.; Diaz, J.G.; Van Der Goot, A.J.; Stankiewicz, A.I.; Stefanidis, G.D. On the use of the couette cell technology for large scale production of textured soy-based meat replacers. J. Food Eng. 2016, 169, 205–213. [Google Scholar] [CrossRef] [Green Version]
- Nemri, M.; Cazin, S.; Charton, S.; Climent, E. Experimental investigation of mixing and axial dispersion in taylor–couette flow patterns. Exp. Fluids 2014, 55, 1769. [Google Scholar] [CrossRef] [Green Version]
- Richter, O.; Hoffmann, H.; Kraushaar-Czarnetzki, B. Effect of the rotor shape on the mixing characteristics of a continuous flow taylor-vortex reactor. Chem. Eng. Sci. 2008, 63, 3504–3513. [Google Scholar] [CrossRef] [Green Version]
- Richter, O.; Menges, M.; Kraushaar-Czarnetzki, B. Investigation of mixing in a rotor shape modified taylor-vortex reactor by the means of a chemical test reaction. Chem. Eng. Sci. 2009, 64, 2384–2391. [Google Scholar] [CrossRef]
- Lueptow, R.M.; Docter, A.; Min, K. Stability of axial flow in an annulus with a rotating inner cylinder. Phys. Fluids A Fluid Dyn. 1992, 4, 2446–2455. [Google Scholar] [CrossRef] [Green Version]
- Wereley, S.T.; Lueptow, R.M. Velocity field for taylor–couette flow with an axial flow. Phys. Fluids 1999, 11, 3637–3649. [Google Scholar] [CrossRef] [Green Version]
- Hwang, J.; Yang, K. Numerical study of taylor–couette flow with an axial flow. Comput. Fluids 2004, 33, 97–118. [Google Scholar] [CrossRef]
- Deshmukh, S.S.; Joshi, J.B.; Koganti, S.B. Flow visualization and three-dimensional cfd simulation of the annular region of an annular centrifugal extractor. Ind. Eng. Chem. Res. 2008, 47, 3677–3686. [Google Scholar] [CrossRef]
- Deng, R.; Yohanes Arifin, D.; Ye Chyn, M.; Wang, C. Taylor vortex flow in presence of internal baffles. Chem. Eng. Sci. 2010, 65, 4598–4605. [Google Scholar] [CrossRef]
- Carlos Álvarez, M.; Vicente, W.; Solorio, F.; Mancilla, E.; Salinas, M.; Zenit, V.R. A study of the taylor-couette flow with finned surface rotation. J. Appl. Fluid Mech. 2019, 12, 1371–1382. [Google Scholar] [CrossRef]
- Maccioni, L.; Chernoray, V.G.; Bohnert, C.; Concli, F. Particle image velocimetry measurements inside a tapered roller bearing with an outer ring made of sapphire: Design and operation of an innovative test rig. Tribol. Int. 2022, 165, 107313. [Google Scholar] [CrossRef]
- Tang, J.; Wang, C.; Liu, F.; Yang, X.; Wang, R. A refractive index-and density-matched liquid–liquid system developed using a novel design of experiments. Processes 2023, 11, 1922. [Google Scholar] [CrossRef]
- Deshmukh, S.S.; Vedantam, S.; Joshi, J.B.; Koganti, S.B. Computational flow modeling and visualization in the annular region of annular centrifugal extractor. Ind. Eng. Chem. Res. 2007, 46, 8343–8354. [Google Scholar] [CrossRef]
- Sofia, H.; Sébastien, P. Turbulence modeling of torsional couette flows. Int. J. Rotating Mach. 2008, 2008, 635138. [Google Scholar]
- Tamhane, T.V.; Joshi, J.B.; Kamachi Mudali, U.; Natarajan, R.; Patil, R.N. Axial mixing in annular centrifugal extractors. Chem. Eng. J. 2012, 207–208, 462–472. [Google Scholar] [CrossRef]
- Liu, C.; Wang, Y.; Yang, Y.; Duan, Z. New omega vortex identification method. Sci. China Phys. Mech. Astron. 2016, 59, 684711. [Google Scholar] [CrossRef]
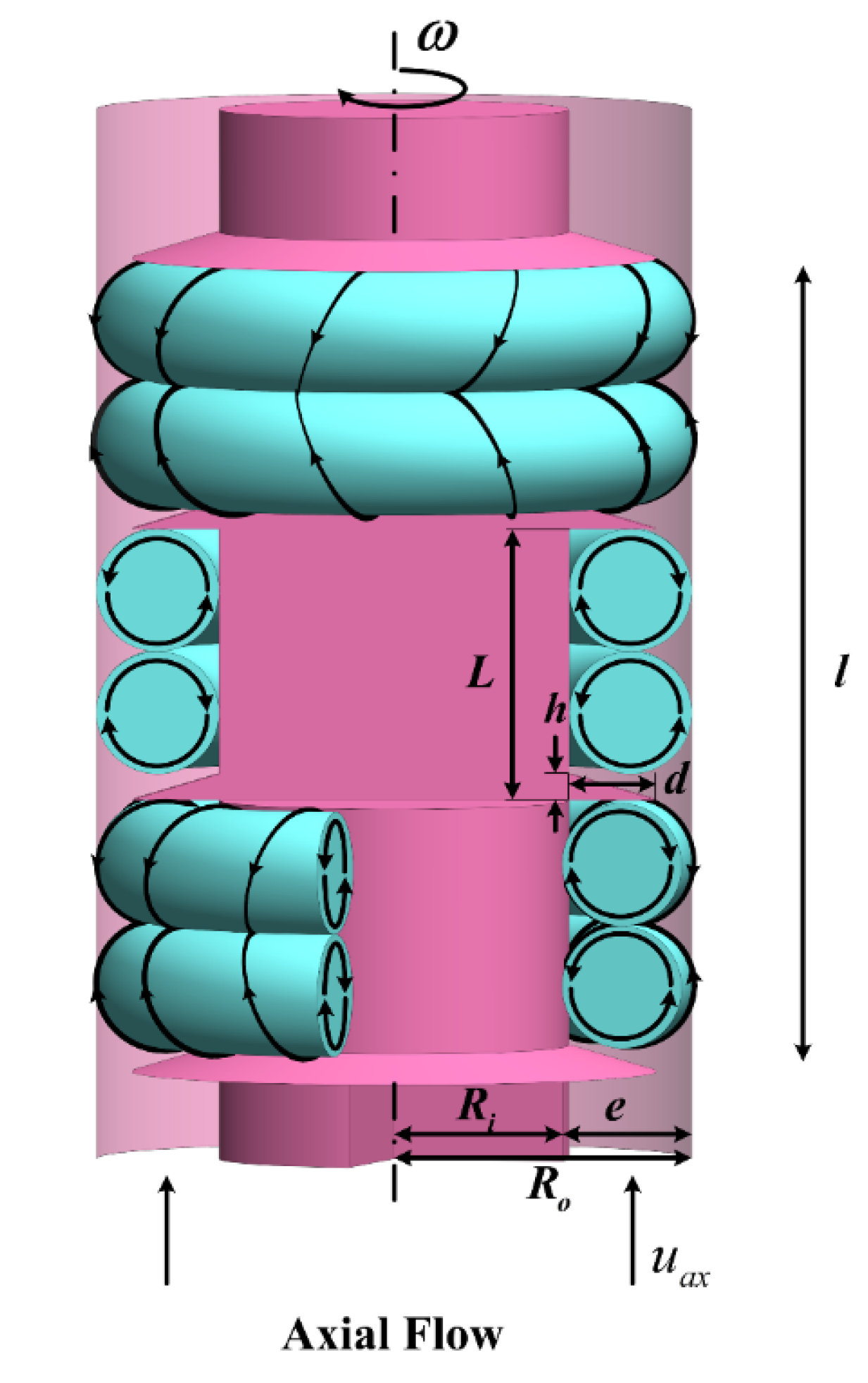




| Structural Parameters | Range |
|---|---|
| Inner cylinder radius (Ri), mm | 12.5 |
| Outer cylinder radius (Ro), mm | 16.5 |
| Annular gap width (e), mm | 4 |
| Rotor length (l), mm | 200 |
| Rib spacing (L), mm | 4–20 |
| Rib width (d), mm | 1–3 |
| Rib thickness (h), mm | 1 |
| Number of regions (N) | 10–50 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, J.; Wang, C.; Liu, F.; Yang, X.; Wang, R. Flow in a Taylor–Couette Reactor with Ribbed Rotors. Processes 2023, 11, 2162. https://doi.org/10.3390/pr11072162
Tang J, Wang C, Liu F, Yang X, Wang R. Flow in a Taylor–Couette Reactor with Ribbed Rotors. Processes. 2023; 11(7):2162. https://doi.org/10.3390/pr11072162
Chicago/Turabian StyleTang, Jianxin, Chenfeng Wang, Fei Liu, Xiaoxia Yang, and Rijie Wang. 2023. "Flow in a Taylor–Couette Reactor with Ribbed Rotors" Processes 11, no. 7: 2162. https://doi.org/10.3390/pr11072162
APA StyleTang, J., Wang, C., Liu, F., Yang, X., & Wang, R. (2023). Flow in a Taylor–Couette Reactor with Ribbed Rotors. Processes, 11(7), 2162. https://doi.org/10.3390/pr11072162






