Remaining Useful Life Prediction for Lithium-Ion Batteries Based on a Hybrid Deep Learning Model

Abstract

Lithium-ion batteries are widely utilized in various fields, including aerospace, new energy vehicles, energy storage systems, medical equipment, and security equipment, due to their high energy density, extended lifespan, and lightweight design. Precisely predicting the remaining useful life (RUL) of lithium batteries is crucial for ensuring the safe use of a device. In order to solve the problems of unstable prediction accuracy and difficultly modeling lithium-ion battery RUL with previous methods, this paper combines a channel attention (CA) mechanism and long short-term memory networks (LSTM) to propose a new hybrid CA-LSTM lithium-ion battery RUL prediction model. By incorporating a CA mechanism, the utilization of local features in situations where data are limited can be improved. Additionally, the CA mechanism can effectively mitigate the impact of battery capacity rebound on the model during lithium-ion battery charging and discharging cycles. In order to ensure the full validity of the experiments, this paper utilized the National Aeronautics and Space Administration (NASA) and the University of Maryland Center for Advanced Life Cycle Engineering (CALCE) lithium-ion battery datasets and different prediction starting points for model validation. The experimental results demonstrated that the hybrid CA-LSTM lithium-ion battery RUL prediction model proposed in this paper exhibited a strong predictive performance and was minimally influenced by the prediction starting point.

1. Introduction

Starting Point Research Institute (SPIR) data show that global shipments of lithium-ion batteries for energy storage reached 153.5 GWh in 2022, representing a significant increase of 117% year-on-year. Lithium-ion batteries for power storage accounted for 103.9 GWh, a remarkable increase of 185.4% year-on-year. It is projected that global shipments of lithium-ion batteries for power storage will continue to increase and reach 322.4 GWh by 2025 [1]. The growth of wind power and photovoltaic installations is driving the demand for energy storage batteries, resulting in a significant increase in the shipment of power storage. Additionally, the cost of energy storage is decreasing, and the economy of energy storage has been further enhanced. Therefore, the energy storage industry has huge potential for development in the future.

Lithium-ion batteries are regarded as one of the most promising clean energy sources, owing to their extended cycle life and excellent durability. They have many advantages regarding their energy density, weight, and power density. They are being used more and more widely in aerospace, new energy vehicles, the military, 5G smart era communication devices, and other related fields [2,3,4,5].

However, with the increase in the frequency of charging and discharging cycles of lithium-ion batteries, a series of irreversible chemical reactions take place. These reactions include lithium deposition, electrolyte decomposition, loss of active materials, and the formation of solid electrolyte intermediates. As a result, battery performance degrades and corrosion occurs in the anode, cathode, electrolyte, and diaphragm. Additionally, the charging and discharging process results in increased internal resistance, reduced charging and discharging efficiency, increased heating, and other phenomena. These factors significantly impact the reliability of the battery. These phenomena typically result in a decrease in the maximum capacity of a fully charged lithium-ion battery compared to its rated capacity. This decrease indicates a shortened battery life [6,7].

When a battery is fully charged, the maximum capacity of the battery will drop to 70–80% of the rated capacity, which is considered the end of the battery’s life [8]. There are many electrochemical and chemical reactions inside batteries. As these reactions occur, a large amount of heat and small molecule gas is generated, resulting in overheating and overpressurizing of the battery. Lithium-ion batteries as a power source are critical for ensuring the regular operation of a device and the realization of its system functions. When the RUL of the battery approaches its threshold, the safety performance of the battery will be significantly reduced and should be replaced in time. If the battery is not replaced in time, the consequences of its failure may bring catastrophic accidents or the failure of large tasks [9,10,11].

For example, Samsung Electronics Company smartphones have cost the company billions of dollars due to battery failures [12]. In January 2013, two consecutive accidents involving lithium-ion batteries in a Boeing B787-800 prompted Boeing to ground B787 aircraft and make improvements to address the battery defects. The B787 could return to flight after passing FAA airworthiness certification. However, in July 2013, the Boeing B787 was again involved in a lithium battery fire in London [13]. In 2019, there was an explosion and injury to five firefighters at a grid-side energy storage project in Arizona, U.S. The accident investigation report indicated that a battery failure caused the incident. On 16 April 2021, three people were killed and one injured in a fire and explosion at the Beijing Dahongmen Energy Storage Power Station. The accident investigation report indicated that the direct cause of the fire was an internal short-circuit fault in a lithium battery, which triggered a thermal runaway of the battery fire [14].

Prediction of lithium-ion batteries’ remaining useful life at regular intervals can detect the number of uses left in the batteries and better determine the health status of batteries. Thus, certain adjustments can be made to equipment using batteries, to make the equipment operate safely and steadily and avoid the recurrence of accidents. Therefore, it is of great significance to estimate the RUL of lithium-ion batteries quickly and accurately [15,16,17,18].

Currently, lithium-ion battery RUL prediction can be broadly classified into two main categories: model-based RUL methods and data-driven RUL methods [19].

The model-based approach involves analyzing the internal mechanisms of lithium-ion batteries and the degradation and failure mechanisms during their charging and discharging cycles. This analysis is based on the physical and chemical reactions within the batteries and is used to establish an RUL prediction model for lithium-ion batteries [20,21].

T.R. Ashwin et al. [22] presented a pseudo-two-dimensional (P2D) electrochemical lithium-ion battery model that can effectively forecast the capacity decay of batteries undergoing cyclic charging and discharging. This model considers the electrochemical reactions within the battery, provides a more precise estimation of battery performance over time, and conducts tests at voltages ranging from 4.0 V to 3.3 V. The research demonstrated that the chemical–electrical model successfully captured the critical electrochemical effects that occur within the battery during cyclic charging and discharging. Prasad et al. [23] presented a simplified electro-chemical model, which helped to establish the correlation between degradation mechanisms and cell parameters, to obtain the RUL of batteries. Virkar [24] proposed a degradation theory for active electrochemical devices based on linear nonequilibrium thermodynamics. This theory was used to develop a degradation model for lithium batteries and to accurately predict their RUL. Zhang et al. [25] proposed an unscented particle filter (UPF) that utilizes linear optimized combined resampling to enhance the accuracy of RUL prediction. This approach improved the accuracy of RUL prediction using a combination of UPF and linear optimization techniques. Guha et al. [26] presented a method for estimating lithium-ion batteries’ electrochemical impedance spectrum (EIS) using a fractional order equivalent circuit model (FOECM). This method involves calculating various parameters based on the battery’s input current and output terminal voltage, obtaining a regression model from the estimated EIS spectrum and using this regression model in a particle filtering framework to predict the RUL from the EIS data. Pham Luu Trung Duong et al. [27] presented a heuristic Kalman algorithm combined with particle filtering for battery RUL prediction. They compared this with a particle swarm optimization (PSO) particle filtering technique, to achieve high prediction accuracy. Walker et al. [28] proposed an untraced Kalman filter (UKF) with particle filter and nonlinear least squares techniques for RUL prediction and achieved high prediction accuracy. Li et al. [29] presented an RUL prediction method by introducing a robust UKF algorithm based on a double-Gaussian mixed (DGM) cost function. They combined this algorithm with a kernel adaptive filter (KAF)-based prediction model to achieve a more precise estimation of RUL. Fan et al. [30] presented a fusion of fault physics and particle filtering for predicting a lithium batteries’ RUL. The method involved creating a model framework that links the physical parameters of the battery to its degradation capacity. Experiments showed the method enabled precise forecasting of a lithium-ion batteries’ RUL.

A data-driven approach can directly tap into the degradation information of lithium-ion batteries, without analyzing the internal functional characteristics of the batteries. Degradation models for predicting the RUL of lithium-ion batteries are developed by analyzing the intrinsic laws of lithium-ion battery monitoring data and the evolution of health states [31,32,33].

Liu et al. [34] presented an approach for determining running batteries’ RUL using multi-Gaussian process regression (GPR) models with indirect health indicators (HI). This approach effectively addresses the issue of the unmeasurable capacity in running batteries. Chen et al. [35] presented a method that combines support vector regression (SVR) and error compensation (EC) to improve RUL prediction accuracy. This method involves using SVR for RUL prediction and optimizing the critical parameters of SVR using a genetic algorithm (GA). Jia et al. [36] presented a method for predicting the short-term state of health (SOH) of batteries using GPR. By establishing a mapping relationship between SOH and RUL, this method enables accurate prediction of RUL. Deng et al. [37] presented an empirical model of lithium batteries’ RUL. Their proposed model can simulate the aging process and local degradation of lithium batteries, unifying the exponential function for modeling the global and regional degradation processes, cleverly designing corresponding loops, and using a particle filter framework to estimate the model parameters, using measured data to predict the future capacity. Jiang et al. [38] proposed a multicore correlation vector machine (RVM) model to solve the problem of adaptive and early prediction of the RUL of lithium-ion batteries and combined it with a PSO algorithm to determine the kernel function and weight parameters. At the same time, a similarity criterion was used to screen offline data. The method was experimentally validated and achieved a high prediction accuracy. Wang et al. [39] proposed a gated recursive unit network based on adaptive sliding windows, to achieve prediction of lithium-ion batteries’ RUL through soft measurement methods and using the inherent storage unit and gate mechanism of a gated recursive unit (GRU). Liu et al. [40] presented an approach for predicting the RUL of batteries by combining a gradient boosting decision tree (GBDT) algorithm with a grid search (GS) approach. This approach optimized the parameters of the GBDT algorithm to improve the accuracy of RUL prediction. Ren et al. [41] presented an auto-encoder integrated with a deep neural network (DNN) to predict lithium-ion batteries’ RUL. Chen et al. [42] proposed a mixed model based on convolutional neural networks (CNN)-LSTM to select a health factor through gray correlation analysis and to achieve the prediction of RUL for lithium batteries. Liao et al. [43] presented a stochastic configuration network (SCN)-based method for predicting lithium-ion batteries’ RUL. This method utilizes the battery capacity as a direct health factor and battery discharge voltage as an indirect health factor to assign random parameters through inequality constraints. Additionally, the range of random parameters is adaptively selected to achieve accurate RUL prediction. Khumprom et al. [44] presented a DNN approach for SOH and RUL prediction of lithium batteries and validated it on battery datasets from NASA, achieving a good prediction accuracy.

Based on the analysis above, there are still challenges present regarding the current methods used for predicting the RUL of lithium batteries. First, a model-based approach necessitates a comprehensive understanding of the battery’s internal working principles. However, due to the complex nature of battery internals, significant prior knowledge is required, thus posing modeling challenges for model-based methods. Second, most data-driven methods only use a single model, whose prediction accuracy is often limited by the amount of data. When the data are limited, the model prediction capability is significantly challenged, thus affecting the accuracy and stability of RUL prediction.

To address the above challenges, and in order to improve the accuracy of RUL prediction and reduce the difficulty of modeling, this paper proposes a hybrid deep learning model for lithium battery RUL prediction. The main contributions of this paper are as follows:

(1) This paper proposes a hybrid model of LSTM based on CA mechanism for lithium battery RUL prediction and based on a data-driven approach;

(2) Introducing a channel attention mechanism can effectively alleviate the impact of the capacity rebound during the battery charge/discharge cycle on battery RUL prediction. Meanwhile, in the case of limited data, the channel attention mechanism can enhance the utilization of local features of the data, thus improving the model’s prediction accuracy;

(3) This paper focuses on exploring the effects of different data and different prediction starting points on model prediction. The experimental results show that the model in this paper had a higher prediction accuracy and robustness compared with traditional recurrent neural networks.

2. Model Building

2.1. LSTM

LSTM networks were initially introduced by Hochreiter and Schmidhuber in 1997, as a novel approach to addressing the challenges of recurrent neural networks [45]. This network builds on recurrent neural networks (RNN) with a long-time delay mechanism that can effectively capture the association between long sequences, thus serving to mitigate the gradient disappearance or gradient explosion phenomenon [46,47]. The LSTM uses stored information to learn long-term dependencies, which are saved, written, and read using three gates: input gate, forget gate, and output gate. The structure of the LSTM abstraction network is shown in Figure 1:

Figure 1. LSTM abstract network structure.

The input gate manages the information entering the network, the forget gate regulates the memory unit’s retention, and the output gate regulates the network’s output. Among them, the forgetting gate is the most important, deciding which memories in the network will be retained and which will be removed, giving the LSTM the function of long-term memory. There is always a capacity rebound process in the iterative process of lithium-ion batteries charge/discharge cycle. However, the forgetting gate can selectively forget these memories, thus making the capacity rebound process have less impact on the training of the model and improving the accuracy of prediction. The internal structure of a LSTM network is shown in Figure 2:

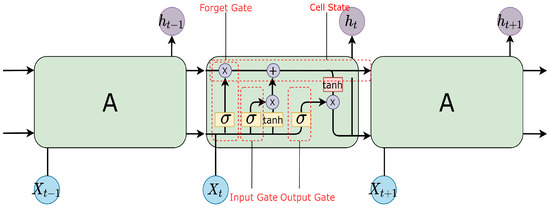
Figure 2. Diagram of the structure of LSTM.

The specific formula for the forget gate is

$$f_t=\sigma \left(w_f·\left[h_{t-1},x_t\right]+b_f\right)$$

(1)

In Equation (1), we first splice the current time step input $x_t$ with the previous time step output $h_{t-1}$ to obtain $\left[h_{t-1},x_t\right]$ and then transform it through the fully connected (FC) layer. Finally, we obtain the memory decay coefficient $f_t$ by activating the sigmoid function. The sigmoid activation function compresses the output to between 0 and 1, and is used to help regulate the values flowing through the network.

The specific formula for the input gate is

$$i_t=\sigma \left(w_i·\left[h_{t-1},x_t\right]+b_i\right)$$

(2)

$$\tilde{C}=tan\mathrm{h}\left(w_c·\left[h_{t-1},x_t\right]+b_c\right)$$

(3)

In Equation (2), in the same way as in Equation (1), after a series of transformations in the FC layer, we obtain the currently learned memory decay coefficient $i_t$, obtained by activating the sigmoid function. In Equation (3), we obtain the input for the current time step $x_t$ spliced with the previous time step output $h_{t-1}$ to obtain $\left[h_{t-1},x_t\right]$. Then the $\left[h_{t-1},x_t\right]$ is transformed using the FC layer. The current state learned memory $\tilde{C}$ is finally obtained using the $tan\mathrm{h}$ activation function.The $tan\mathrm{h}$ activation function compresses the output between −1 and 1, limiting the values flowing through the network.

The specific formula for the cell state update is

$$C_t=f_t·C_{t-1}+i_t·\tilde{C}$$

(4)

In Equation (4), we obtain the memory state $C_t$ at the current moment, obtained by multiplying the decay coefficient $f_t$ by the memory $C_{t-1}$ of the previous time step, plus the current memory decline coefficient $i_t$ by the currently learned memory $\tilde{C}$.

The specific equation for the output gate is

$$o_t=\sigma \left(w_o\left[h_{t-1},x_t\right]+b_o\right)$$

(5)

$$h_t=o_t·tan\mathrm{h}\left(C_t\right)$$

(6)

In Equation (5), after a series of transformations in the FC layer, we obtain the output gate coefficient $o_t$ obtained by the sigmoid function in the activation. In Equation (6), we obtain the output $h_t$ of a single cell of the LSTM network at the current moment, obtained from the cell state and the output gate coefficient at the current moment.

2.2. Attentional Mechanism

The attention mechanism (AM) has emerged as one of the most significant advancements in deep learning in recent years. Attention-based methods have gained popularity in academia and industry for their interpretability and effectiveness in recent years. Attentional mechanisms were initially inspired by the study of human vision. In the field of cognitive science, it is well-established that humans have a limited capacity for information processing, therefore selectively attending to some available information while disregarding the rest [48]. Incorporating an attention mechanism into a model makes it rapidly identify high-value information from a vast amount of data, enhances the significance of critical information, and reduces the impact of less important data [49,50].

This paper uses a channel attention(CA) mechanism squeeze-and-excitation block [51]. The CA mechanism can dynamically adjust the weights of the features by adaptively learning the importance of the feature channels and weighting the aggregation of features from different channels. Therefore, the CA mechanism can enable the model to pay more attention to important features and reduce the impact of redundant or unimportant features. In lithium battery RUL prediction, the CA mechanism can effectively mitigate the impact of capacity rebound on the model prediction during lithium-ion battery charging and discharging cycles and, at the same time, improve the utilization of features when data are limited. As shown in Figure 3:

Figure 3. Squeeze-and-Excitation Block.

The CA mechanism can be divided into three steps.

The first step is the squeeze operation, which extracts global spatial features from each channel, compresses the spatial information into channel descriptors, and generates statistics for each channel using global average pooling. The specific formula can be expressed as follows:

$$Z_c=F_{sq}\left(u_c\right)=\frac{1}{H\times W}\sum _{i=1}^H\sum _{j=1}^W{u}_c\left(i,j\right)$$

(7)

The second step is the excitation operation, which is to completely capture the dependencies for each channel. The specific formula can be expressed as follows:

$$s=F_{ex}\left(z,W\right)=\sigma \left(g\left(z,W\right)\right)=\sigma \left(W_2\delta \right(W_{1}z\left)\right)$$

(8)

The third step is the scale operation, which multiplies the weight coefficients learned from each channel with the original features to obtain the weighted features, giving the model a more vital recognition ability for each feature. The specific formula can be expressed as follows:

$${\tilde{x}}_c=F_{scale}\left(u_c,s_c\right)=s_c{u}_c$$

(9)

2.3. RUL Prediction Model with LSTM Based on a Channel Attention Mechanism

The structure of the RUL prediction hybrid model based on a channel attention mechanism LSTM in this paper is shown in Figure 4:

Figure 4. Model Structure Diagram.

The model mainly contains the channel attention mechanism, LSTM, and FC layer. Prediction of lithium-ion batteries’ RUL is separated into the following four main steps:

Step1: We first normalize the input lithium-ion battery data. Normalization is the process of scaling the data to a specific range, to maintain consistency across the dataset and help improve the model’s performance.

Step2: Channel attention first assigns corresponding weights to different channels and calculates the weights for each channel, enabling the model to focus on the channels that are more important for the prediction task. In this way, the model can automatically learn which channels are more critical for predicting the RUL of Li-ion batteries, thus improving the performance of the model.

Step3: We use the LSTM to process the data further. The data adjusted using channel attention have a more robust recognition capability, allowing the LSTM gating unit to process the data more efficiently and faster.

Step4: We use the FC layer to convert the output of the LSTM to the predicted value of the lithium-ion batteries’ RUL. The role of the FC layer is to map the hidden states of the LSTM to an actual value that represents the predicted remaining useful life.

3. Data Sources and Experimental Settings

3.1. Data Introduction

The experimental data utilized in this paper includes datasets of lithium-ion batteries from both the National Aeronautics and Space Administration (NASA) [52] and the University of Maryland Center for Advanced Life Cycle Engineering (CALCE) [53]. There is a significant difference in the average battery life between the two datasets. The NASA dataset contains four groups of 18650 $LiCo{O}_2$ batteries: B0005, B0006, B0007, and B0018. These batteries undergo a charging and discharging process that begins with a constant current (CC) of 1.5 A until the battery voltage reaches 4.2 V, followed by a constant voltage (CV) mode until the battery current drops to 0.02 A. The discharge process involves a continuous current of 2 A, until the voltages of the four batteries reach 2.7 V, 2.5 V, 2.2 V, and 2.5 V, respectively. The CALCE dataset contains four batteries: CS2_35, CS2_36, CS2_37, and CS2_38. These batteries are also charged at a constant current of 0.55 A, until the battery voltage reaches 4.2 V, followed by a CV mode, until the battery current drops below 0.05 A. The discharge process involves a CC of 0.55 A, until the voltage of the four batteries groups drops to 2.7 V. The specific parameters of the two groups of battery aging experiments are shown in Table 1.

Table 1. Battery aging experiment parameters.

Battery	Constant Current Charge (A)	Cut off Current of Constant Voltage Charge (A)	Constant Current Discharge (A)	Cut off Voltaget of Discharge (V)	Average Life (Cycle)
B0005	1.50	0.02	2.00	2.70	113
B0006	1.50	0.02	2.00	2.50
B0007	1.50	0.02	2.00	2.20
B0018	1.50	0.02	2.00	2.50
CS2_35	0.55	0.05	0.55	2.70	678
CS2_36	0.55	0.05	0.55	2.70
CS2_37	0.55	0.05	0.55	2.70
CS2_38	0.55	0.05	0.55	2.70

The charging and discharging cycle of a lithium-ion battery makes the maximum capacity of the battery a decreasing trend, and this decreasing trend has a good time continuity. In this paper, the capacity of lithium batteries is used as the health factor to build a model to predict lithium-ion batteries’ RUL.

SOH is an indicator of the health of the batteries, where the equation defines SOH:

$$SOH=\frac{R_i}{R_e}\times 100\%\left(i=1,2,3.....N\right)$$

(10)

where $R_i$ is the battery’s maximum capacity after the i th charge/discharge cycle, and $R_e$ is the battery’s rated capacity. When the battery’s maximum capacity drops to 70–80% of the rated capacity, it is considered end-of-life.The decreasing trend of the maximum capacity of the charge/discharge cycle for the two battery datasets is shown in Figure 5 and Figure 6:

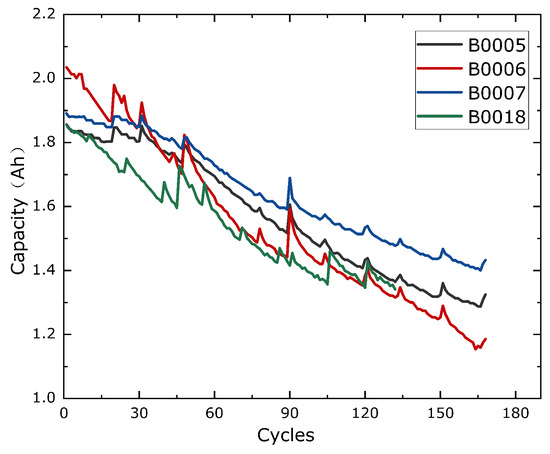
Figure 5. NASA battery datasets.

Figure 6. CALCE battery datasets.

3.2. Experiment Settings

In this paper, a hybrid LSTM model based on a channel attention mechanism (CA-LSTM) was trained and evaluated for validation, and the optimal parameters of the model were selected using a grid search. The NASA datasets used three sets of battery data, B0006, B0007, and B0018, as the training set and B0005 battery as the test set, which was recognized as the end of life, when the maximum capacity reduced to 1.39 Ah. The CALCE dataset used three sets of battery data, CS2_36, CS2_37, and CS2_38, as the training set and the CS2_35 battery as the test set, and the end-of-life was recognized when the maximum capacity reduced to 0.78 Ah.

The NASA data were validated with 35, 55, and 70 as the forecast starting points, and the CALCE data were validated with 200, 300, and 400 as the forecast starting points, respectively, to verify the robustness of the model.

To verify the validity and reliability of the prediction model proposed in this paper for lithium battery RUL, we used the M1, M2, M3, and M4 (as shown in Table 2) models to compare the results.

Table 2. Four models for battery RUL prediction.

Model	Description
M1	LSTM
M2	GRU
M3	RNN
M4	CA-LSTM

Among them, M1 uses a LSTM without channel attention, M2 uses GRU, M3 uses RNN, and M4 uses LSTM with channel attention; M1, M2, and M3 are classical recurrent neural networks, which are widely used for RUL prediction.

Experiments were conducted to evaluate the model using training data fitting to achieve the prediction of battery capacity decay and validated using both NASA and CALCE datasets.

The input and output of the model can be represented as D:

$$D=\left\{\underset{Input}{\underbrace{\stackrel{Windowsize\left(T\right)}{\overbrace{x_1{x}_2{x}_3{x}_4{x}_5...x_T}}}}\underset{output}{\underbrace{x_{T+1}}}{x}_{T+2}.........\right\}$$

(11)

The experiment used a sliding window to partition the data. The window slides in steps of 1 toward the data sequence and is input to the network in a batch manner, and the size of each batch of data input to the network is controlled by the window size (T), where the data length is L. The inputs and outputs are shown in Figure 7:

Figure 7. Window sliding to divide the data.

3.3. Evaluation Criteria

In order to fully validate the experiment, the following three evaluation criteria were used as indicators of RUL prediction performance in this experiment:

$\left(1\right)$ Mean absolute error (MAE), the lower the value, the better the prediction performance. Its expression is as follows:

$$MAE=\frac{1}{t}{\displaystyle \sum _{i=1}^t}\left|x_i-\overline{x_i}\right|$$

(12)

$\left(2\right)$ Root mean square error (RMSE), the lower the value, the better the prediction performance. Its expression is as follows:

$$RMSE=\sqrt{\frac{1}{t}\sum _{i=1}^t{\left(x_i-\overline{x_i}\right)}^2}$$

(13)

$\left(3\right)$ Prediction error (PError), which is used to evaluate the RUL prediction error. Its expression is as follows:

$$PError=\frac{\left|RUL-\overline{RUL}\right|}{RUL}$$

(14)

where t is the data size, $x_i$ is the actual value, $\overline{x_i}$ is the predicted value, $RUL$ is the true remaining life value, and $\overline{RUL}$ is the predicted remaining life value. The experiments were performed in five iterations, and the average value of each index was obtained.

4. Experiment Results and Analysis

4.1. Battery Life Prediction

As shown in Figure 8 and Figure 9, the four models obtained different results on the NASA and CALCE datasets, with the NASA data starting at cycle 55 and the CALCE data starting at cycle 300 for prediction. The results for the NASA datasets showed that the M1, M2, and M3 models were unable to determine the rate of lithium battery capacity decline at the beginning of the prediction and showed a significant decline, indicating a poor fit with the original data, but with the fit reversing as the capacity continued to decline. The M4 model (the model proposed in this paper) could capture the battery capacity ramp-up and reduce the impact of capacity ramp-up on the prediction, thus achieving better results.

Figure 8. Prediction starting at cycle 55 for NASA data.

Figure 9. Prediction starting at cycle 300 for CALCE data.

Meanwhile, with the CALCE datasets, the M3 model significantly differed from the initial prediction, due to the battery capacity rebound. At the same time, the M2 and M1 models also showed different degrees of variation, and the M1 model showed a year-on-year increase in deviation as the cycle time increased. The M4 model was significantly better optimized than the first three models and could better fit the battery capacity drop curve and achieved better results in predicting the end of battery life.

It can be seen that the M1, M2, and M3 models showed more significant deviations for batteries with a higher number of cycles, thus biasing the end-of-life judgments. On the other hand, the M4 model showed better prediction accuracy for both batteries with a low number of cycles and those with a high number of cycles.

Table 3 shows the evaluation criteria for the prediction results of the four models. It can be seen that the M1, M2, and M3 models performed differently on different datasets, but the M4 model performed well on the different datasets and achieved better prediction results.

Table 3. Comparison of the four models on the two datasets.

DataSet	Prediction Starting Point	Model	RMSE	MAE	PError
NASA	55	M1	0.0275	0.0218	0.0471
		M2	0.0333	0.0253	0.0580
		M3	0.0416	0.0328	0.0471
		M4	0.0213	0.0145	0.0109
CALCE	300	M1	0.0576	0.0491	0.0769
		M2	0.0439	0.0363	0.0333
		M3	0.1140	0.0896	0.1620
		M4	0.0355	0.0288	0.0118

4.2. Different Starting Points for Prediction

To comprehensively validate the effectiveness of the model (M4) proposed in this paper, prediction experiments were conducted using two different prediction starting points (35, 70) on the NASA datasets and with two different prediction starting points (200, 400) on the CALCE datasets. The experimental results were compared with the M1, M2, and M3 models.

Figure 10 shows the prediction comparison plots for the NASA datasets, with the 35th cycle and 70th cycle as the prediction starting point, respectively. Figure 11 shows the prediction comparison plots for the CALCE datasets, with the 200th cycle and 400th cycle as the prediction starting point, respectively. These figures clearly demonstrate that the prediction results of the model varied significantly depending on the prediction starting point.

Figure 10. Comparison of the four models with different prediction starting points for NASA data.

Figure 11. Comparison of the four models with different prediction starting points for CALCE data.

Table 4 shows the evaluation criteria table for the prediction results of the four models on the NASA datasets starting at the 35th cycle and 70th cycle, and the CALCE datasets starting at the 200th cycle and 400th cycle. On both the NASA datasets and CALCE datasets, the M1, M2, and M3 models had different degrees of prediction errors. A larger prediction error occurred on the CALCE datasets with a longer data series.

Table 4. Comparison of four models with different prediction starting points on two datasets.

DataSet	Prediction Starting Point	Model	RMSE	MAE	PError
NASA	35	M1	0.0324	0.0261	0.0927
		M2	0.0372	0.0281	0.0421
		M3	0.0308	0.0239	0.0506
		M4	0.0251	0.0179	0.0084
	70	M1	0.0245	0.0200	0.0602
		M2	0.0379	0.0307	0.0694
		M3	0.0286	0.0237	0.0972
		M4	0.0178	0.0132	0.0139
CALCE	200	M1	0.0579	0.0442	0.0565
		M2	0.0727	0.0635	0.1182
		M3	0.0593	0.0514	0.0879
		M4	0.0379	0.0313	0.0245
	400	M1	0.0502	0.0429	0.0893
		M2	0.0478	0.0356	0.0315
		M3	0.0506	0.0382	0.0452
		M4	0.0401	0.0309	0.0231

However, the proposed model (M4) showed a better prediction accuracy with different datasets and different prediction starting points, which means that the prediction accuracy of the proposed model was not significantly affected by the change of the prediction starting point.

Figure 12 and Figure 13 show the RUL prediction results of the four models on the NASA and CALCE datasets, respectively. It can be concluded that the model (M4) proposed in this paper exhibited better prediction accuracy with stronger robustness, both for batteries with more cycle counts and with fewer cycle counts, at different prediction starting points.

Figure 12. Comparison of the prediction results of the four model RUL forecasts for NASA data.

Figure 13. Comparison of the prediction results of the four model RUL forecasts for CALCE data.

5. Conclusions

To improve the accuracy of RUL prediction for lithium-ion batteries and reduce the difficulty of model building, this paper proposed a hybrid model with LSTM based on a channel attention mechanism, to achieve prediction of the RUL of lithium batteries. First, we extracted the lithium-ion batteries’ data for normalization, then created channels using channel attention and calculated the weights of each channel. Channel attention automatically learns which channel data are more critical for predicting the lithium-ion batteries’ RUL and assigns higher weights accordingly. Finally, the data were further processed using LSTM, and prediction of RUL was achieved using a fully connected layer. Introducing a channel attention mechanism can improve the utilization of the local features of data when data are limited, and can effectively mitigate the impact of the battery capacity re-rise phenomenon on the model when the lithium-ion battery charge/discharge cycle occurs. The experimental results showed that, compared with other classical recurrent neural networks, the model proposed in this paper had a higher prediction accuracy and offered better performance in terms of RMSE, MASE, and PError evaluation metrics when validated on NASA datasets and CALCE datasets. To verify the effectiveness of the model proposed in this paper more comprehensively, we set different prediction starting points. After verification, the prediction performance of the model presented in this paper was stable and less influenced by different prediction starting points.

In future studies, we will consider introducing additional parameters for capacity fluctuations of lithium-ion batteries and incorporate additional health factors. Furthermore, we aim to examine a broader spectrum of battery types and external factors, such as the influence of different temperatures on RUL.