Experimental Study and Mathematical Modeling under Various Hot-Air Drying Conditions of Thin Layer Olive Pomaces
Abstract
:1. Introduction
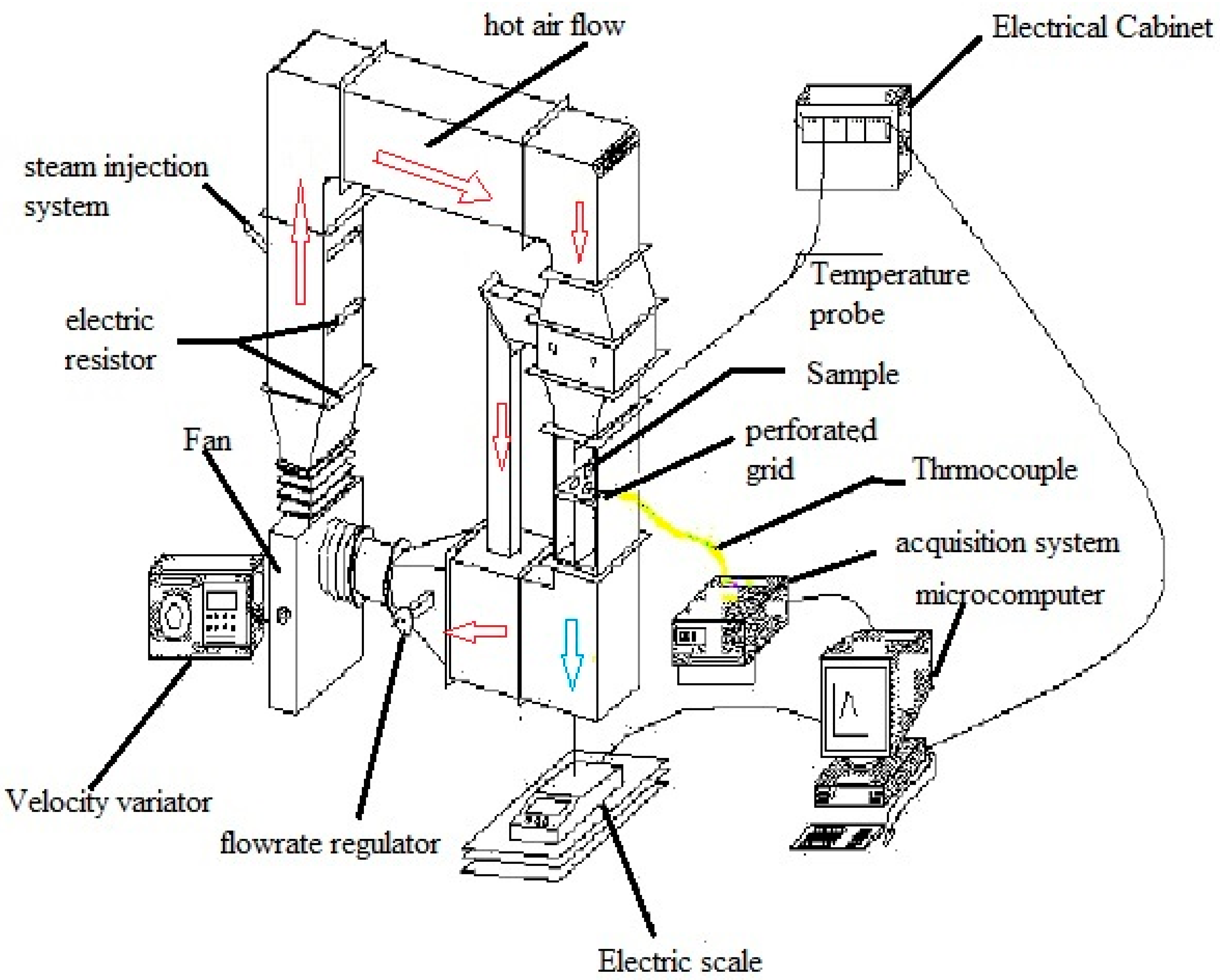
2. Materials and Methods
2.1. Experiment
2.1.1. Drying Models
2.1.2. The Effective Diffusivity (Deff) and the Activation Energy (Ea)
3. Results and Interpretations
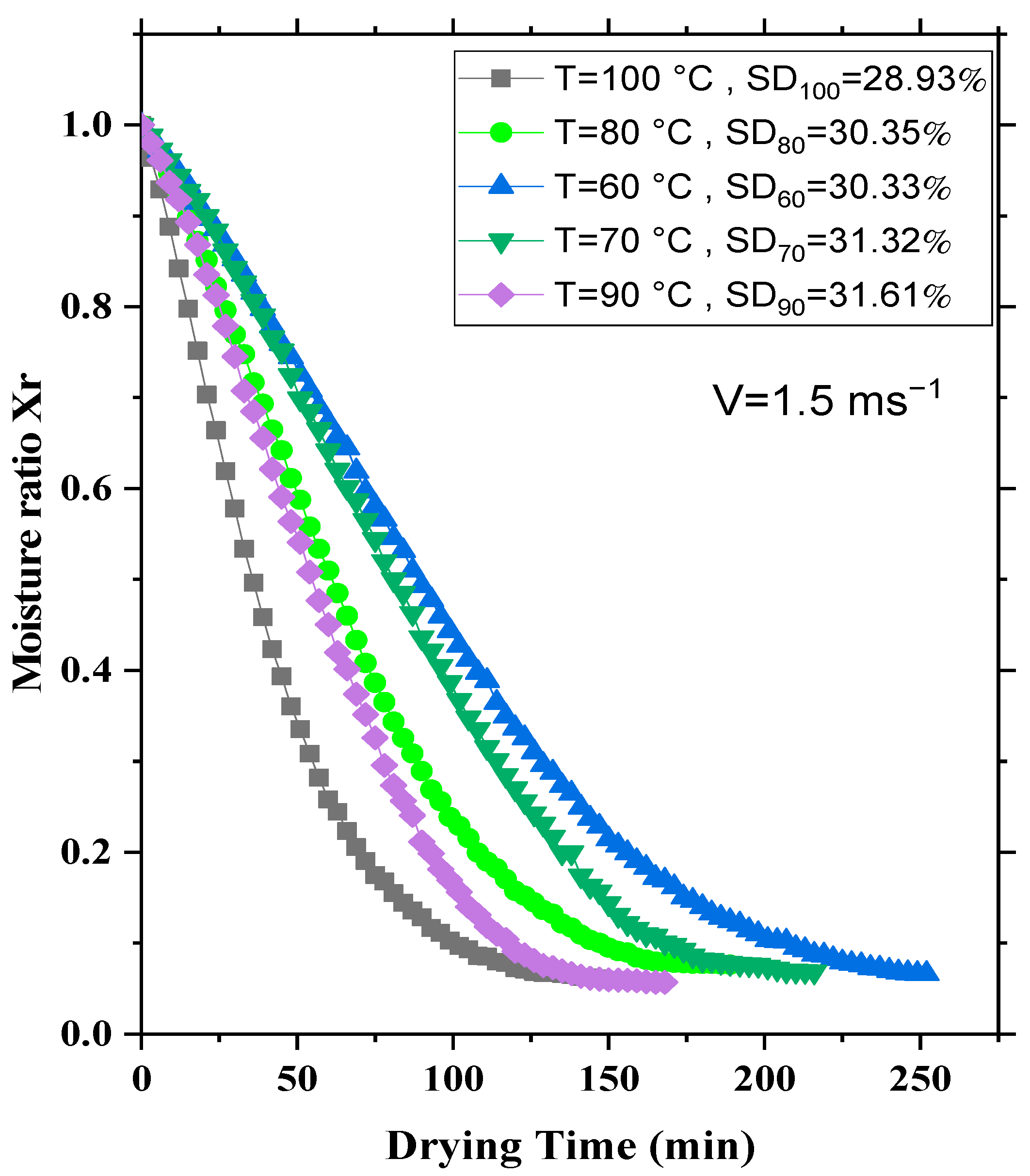
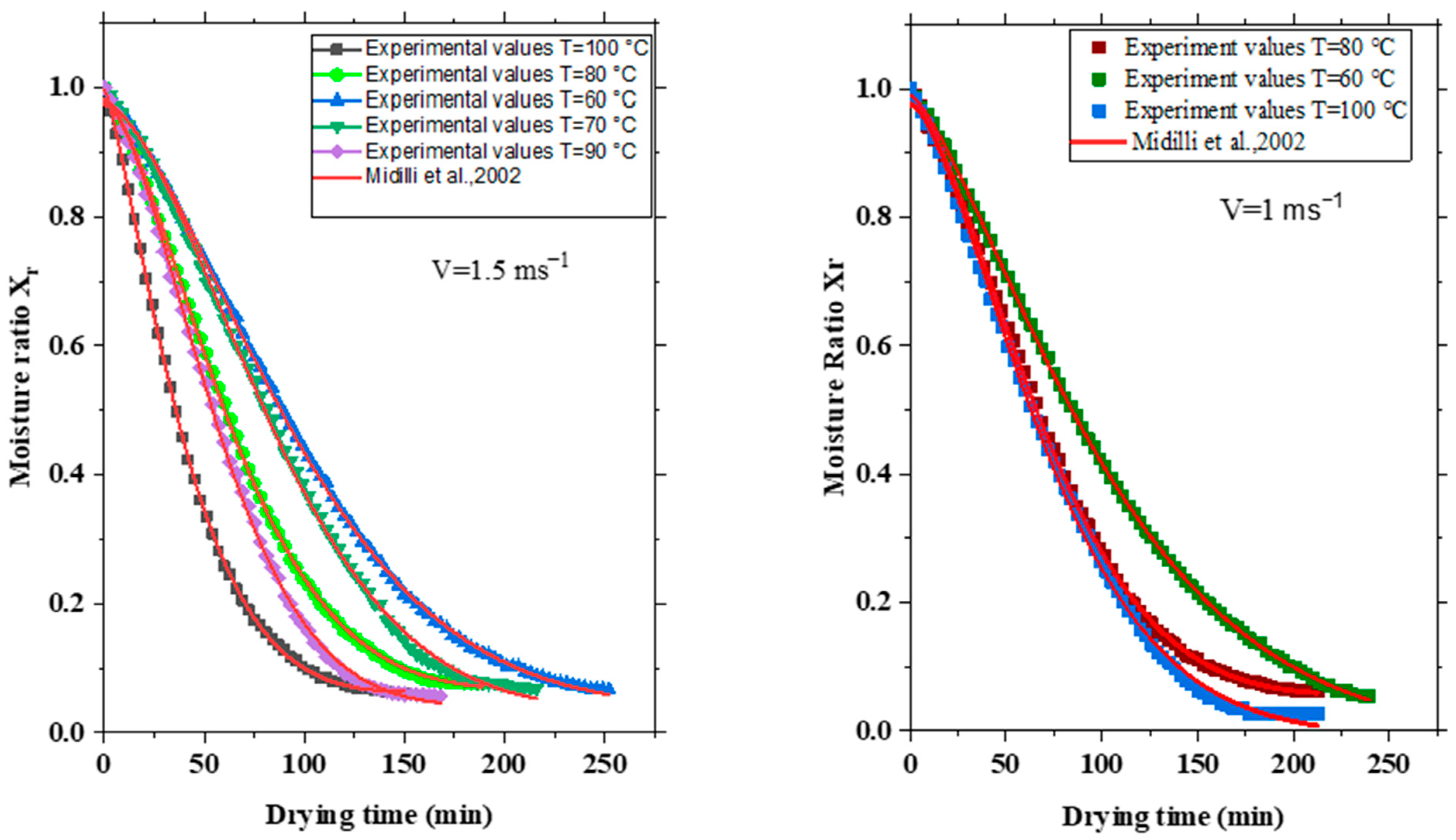
3.1. Influence of the Temperature of the Drying Air
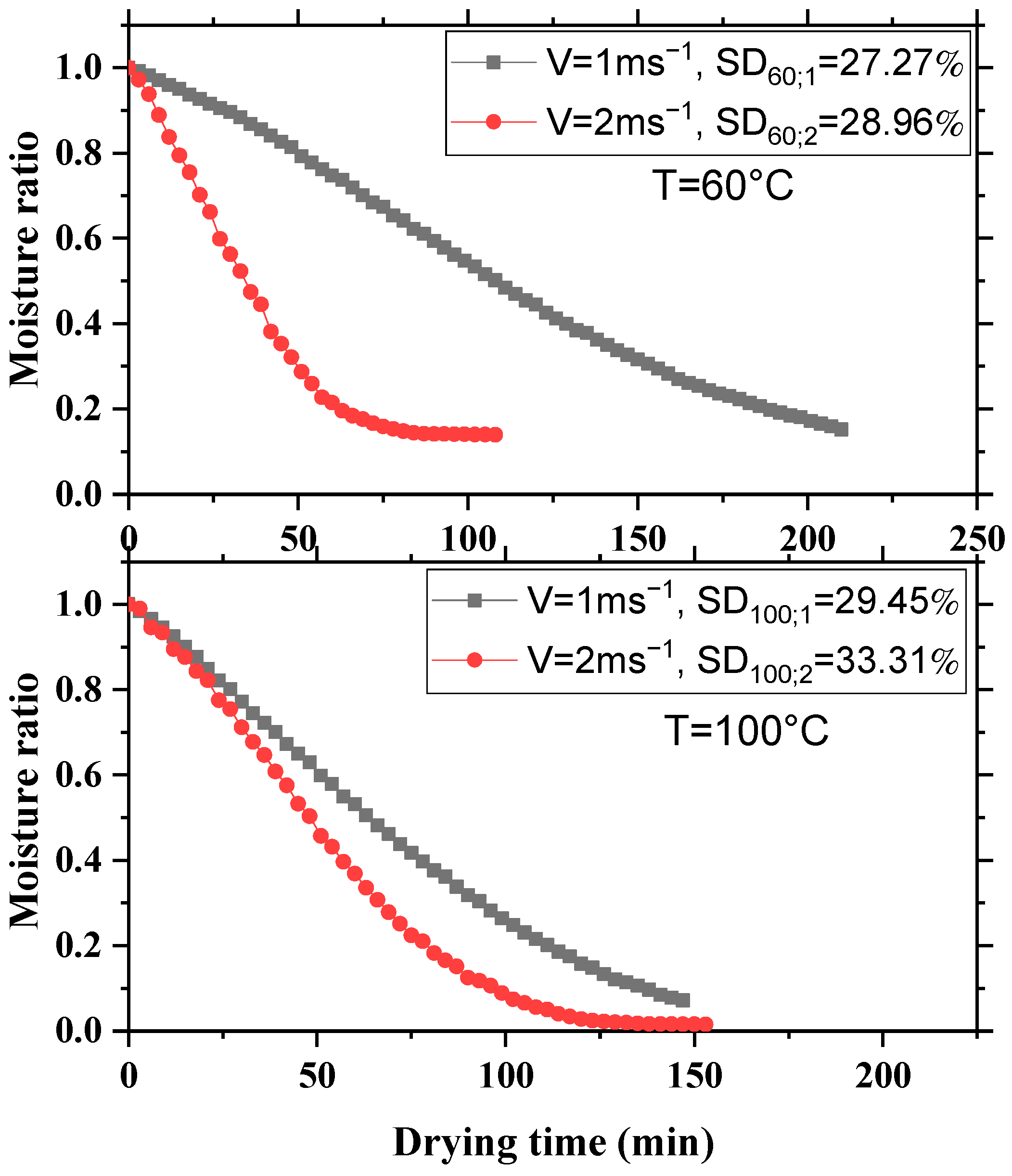
3.2. Impact of the Velocity of the Drying Air
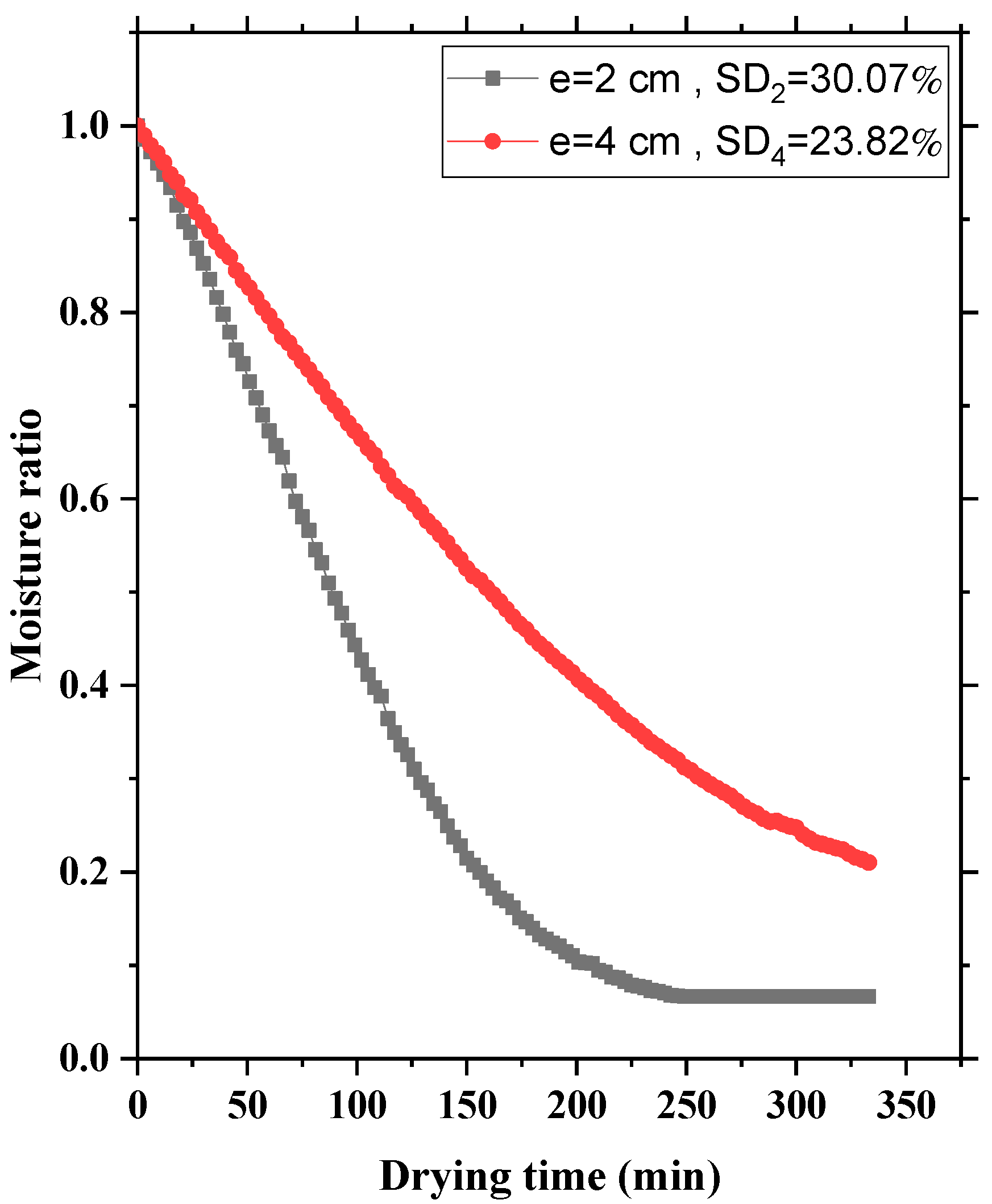
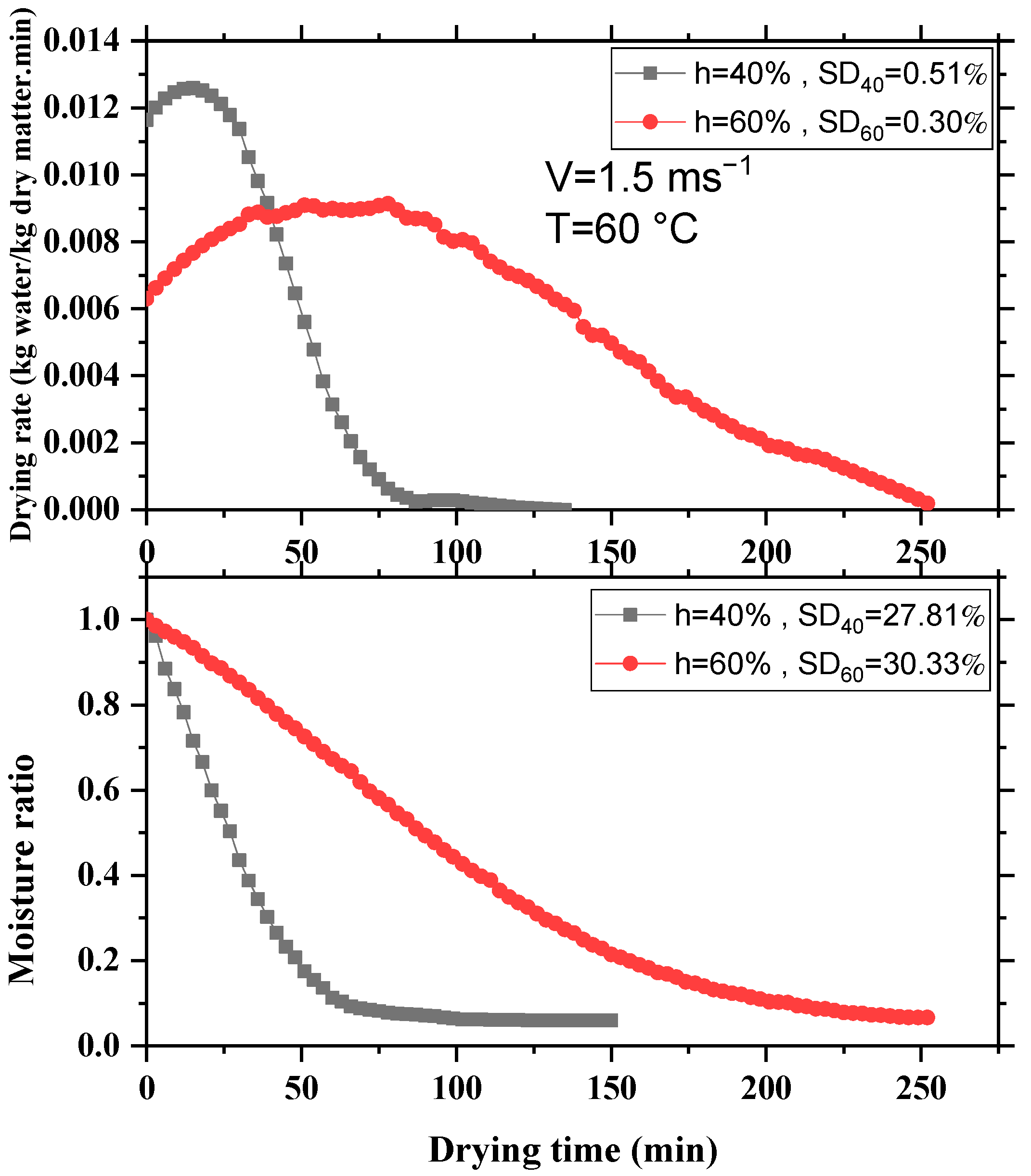
3.3. Influence of Layer Thickness
3.4. Influence of Initial Moisture
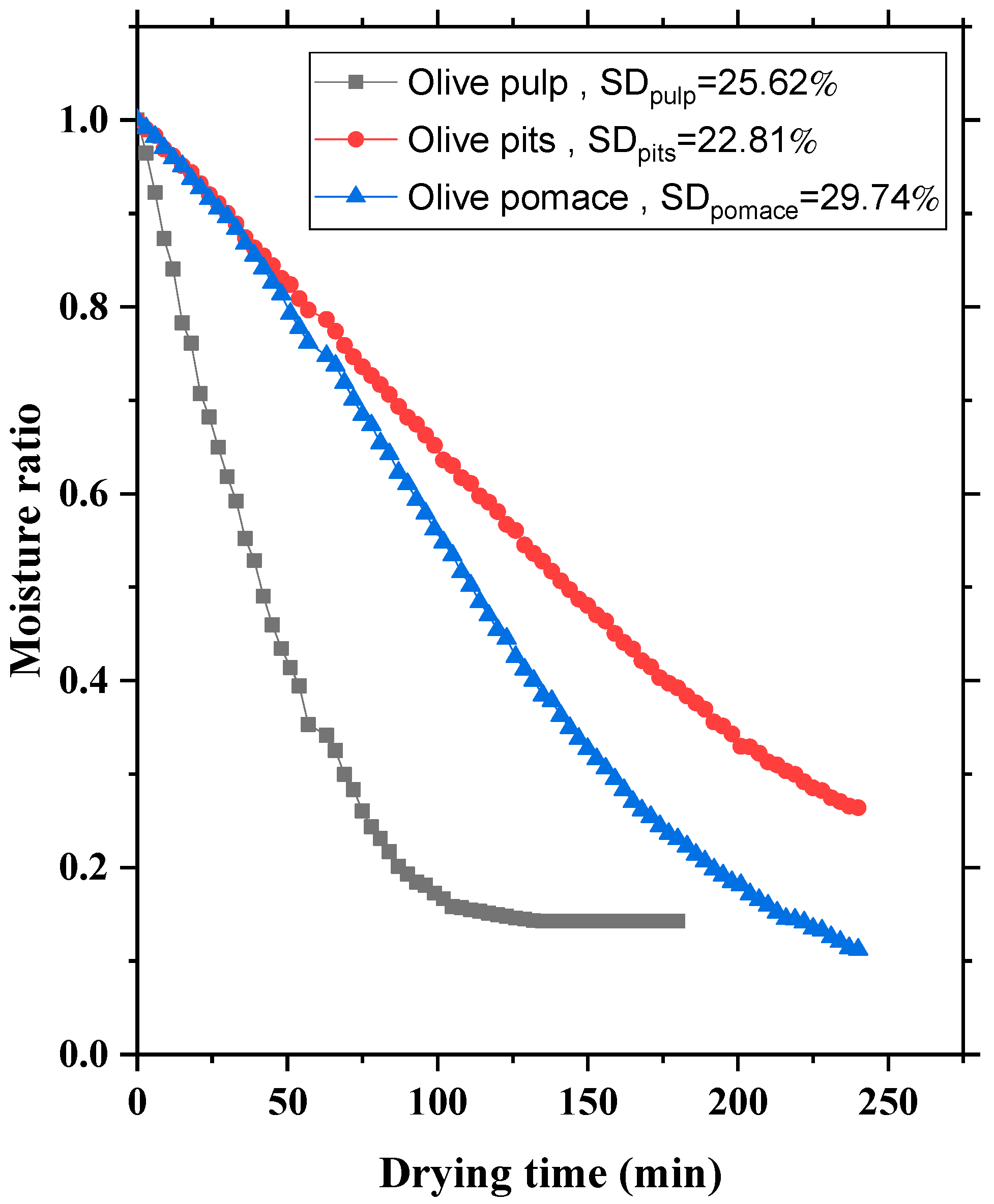
3.5. Influence of Olive Pomace Composition
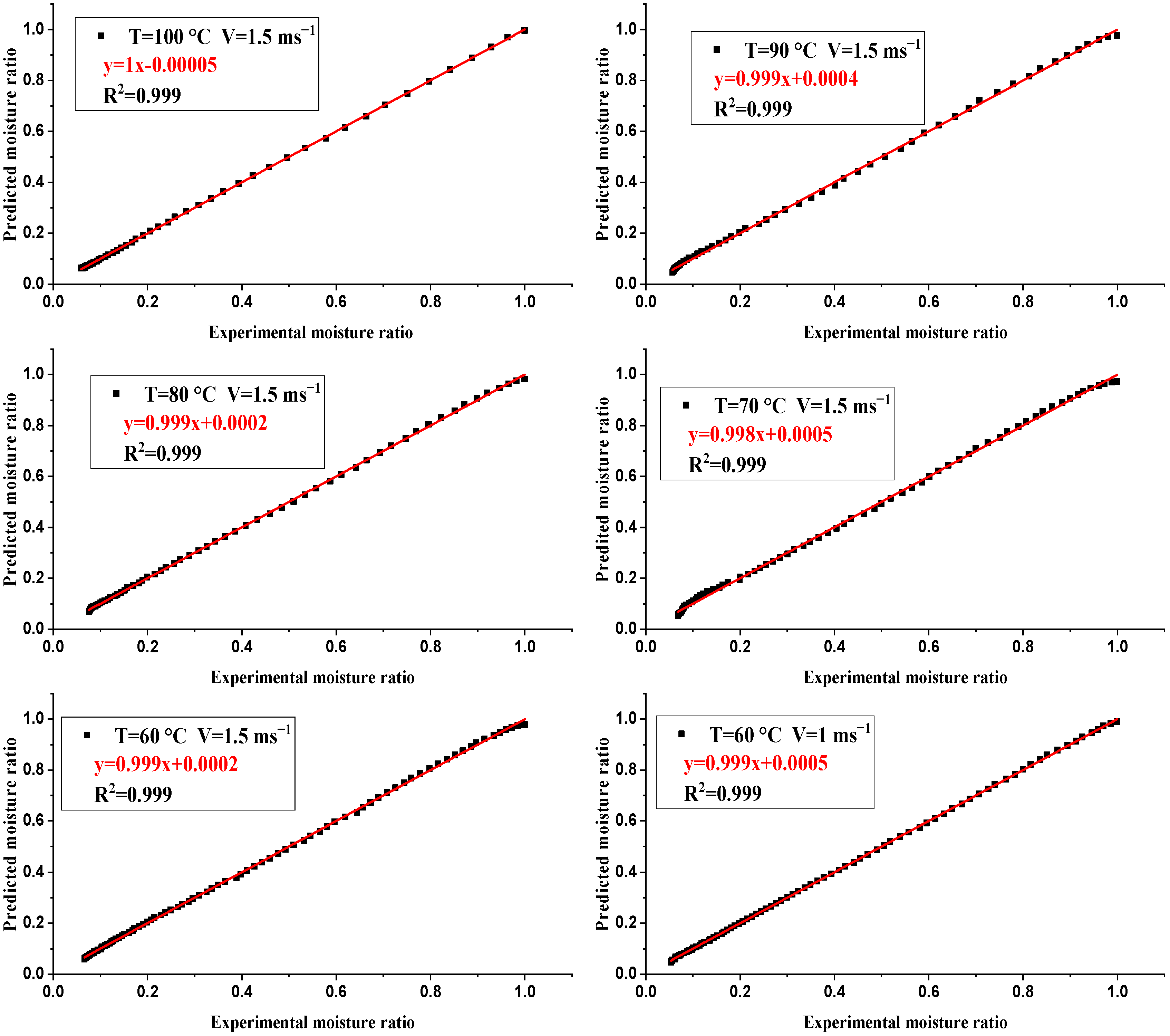
4. Drying Modeling
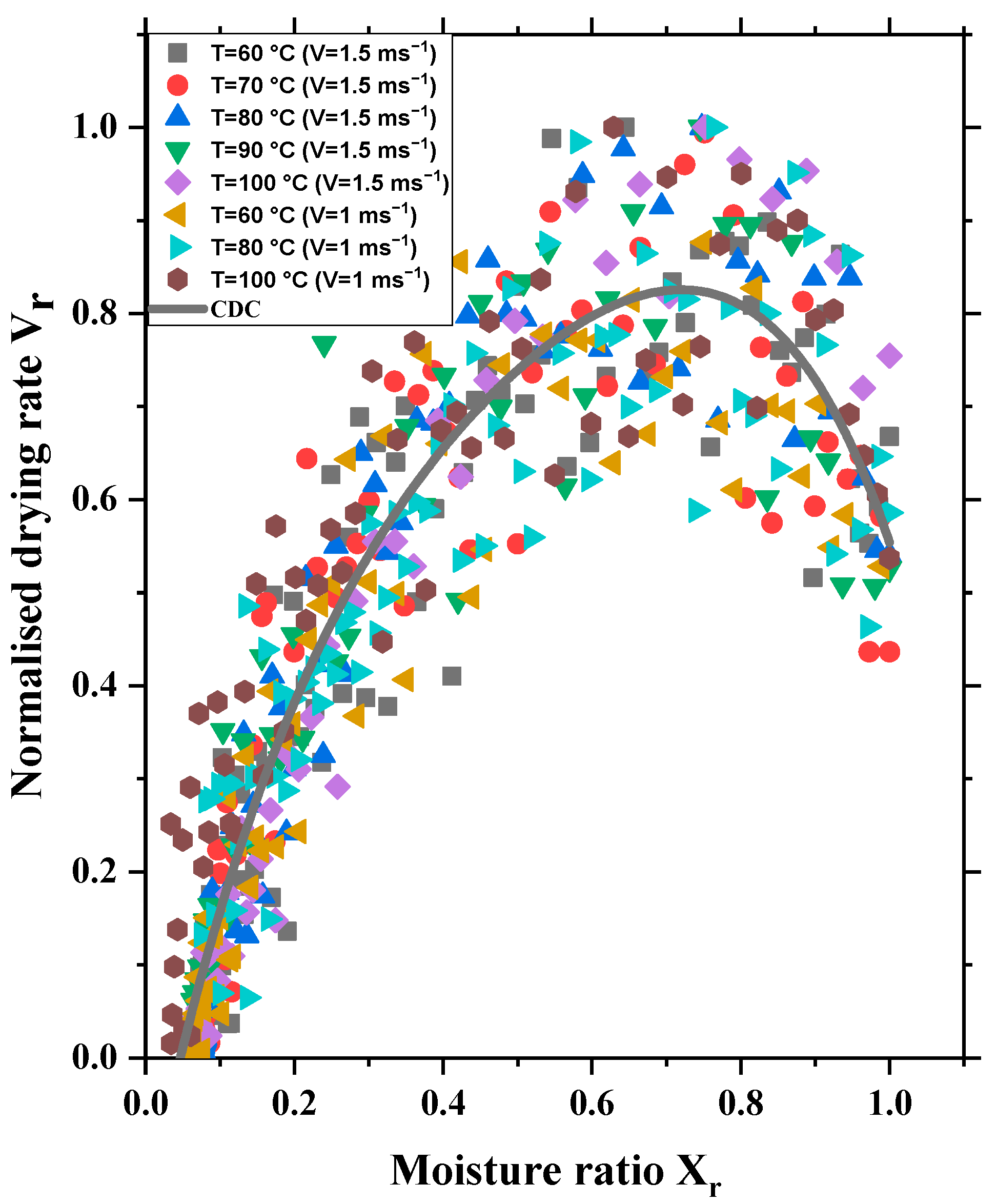
5. Characteristic Drying Curve
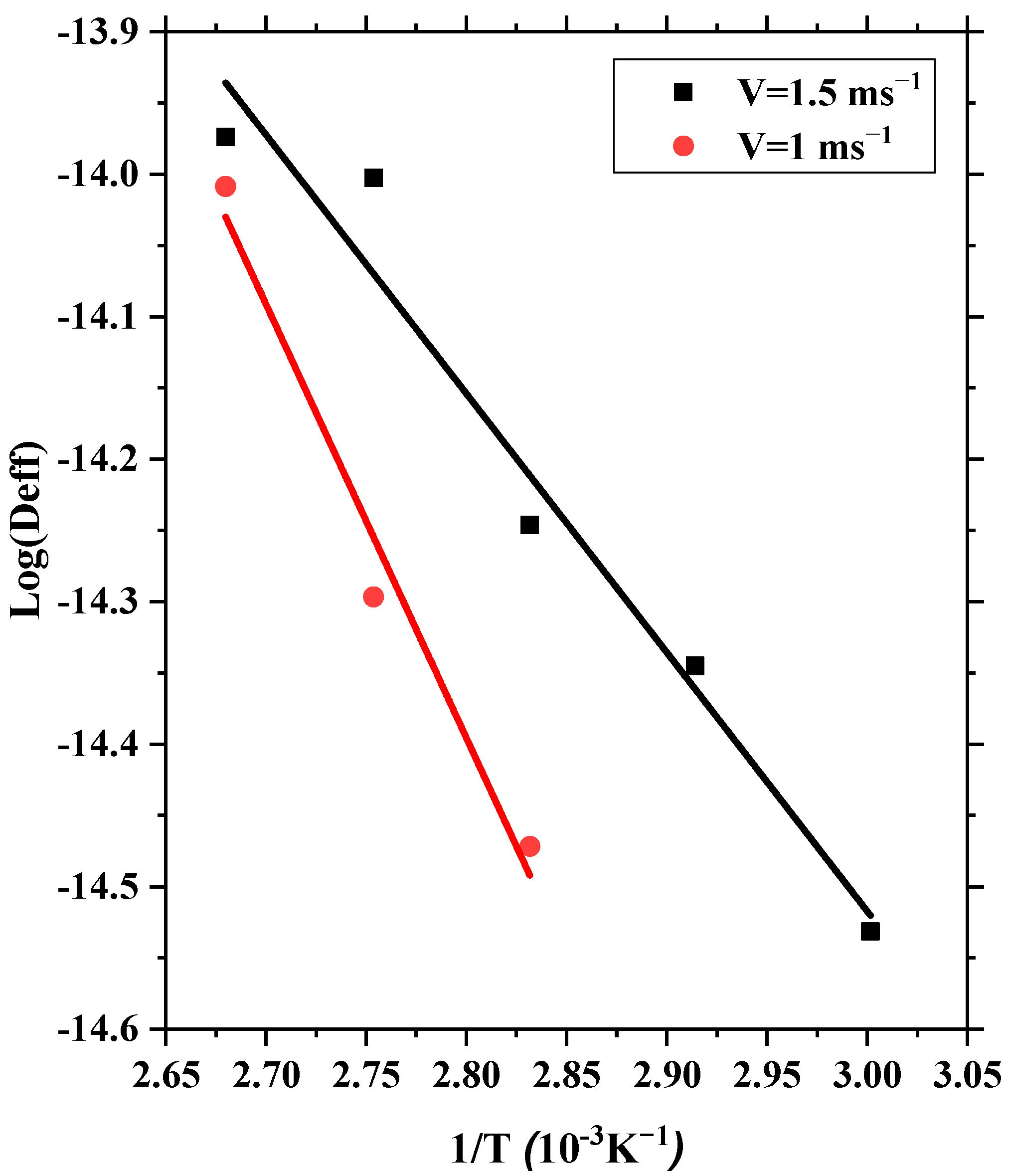
6. Effective Diffusivity and Energy Activation
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IPCC. Contributing of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Synthesis Report; IPCC: Geneva, Switzerland, 2014; Available online: https://www.ipcc.ch/pdf/assessmentreport/ar5/syr/SYR_AR5_FINAL_full.pdf (accessed on 1 April 2020).
- ANGED. Strategic Options for the Promotion of Value of Organic Waste VDO Tunisia; ANGED: Tunis, Tunisia, 2009. [Google Scholar]
- World Bioenergy Association. Statistics, Global Bioenergy; World Bioenergy Association: Stockholm, Sweden, 2020. [Google Scholar]
- Mami, M.A.; Lajili, M.; Echekki, T. CFD Multiphase Combustion Modelling of Oleic by-Products Pellets in a Counter-Current Fixed Bed Combustor. Comptes Rendus Chim. 2022, 25, 113–127. [Google Scholar] [CrossRef]
- Doymaz, I.; Gorel, O.; Akgun, N. Drying Characteristics of the Solid By-Product of Olive Oil Extraction. Biosyst. Eng. 2004, 88, 213–219. [Google Scholar] [CrossRef]
- Vitali Čepo, D.; Radić, K.; Jurmanović, S.; Jug, M.; Grdić Rajković, M.; Pedisić, S.; Moslavac, T.; Albahari, P. Valorization of Olive Pomace-Based Nutraceuticals As Antioxidants in Chemical, Food, and Biological Models. Molecules 2018, 23, 2070. [Google Scholar] [CrossRef]
- Ungureanu, G.; Pătrăuţanu, O.A.; Volf, I. A Bio-Based Carbon Rich Material for Efficient Remediation of Environmental Hazardous. Comptes Rendus Chim. 2022, 25, 153–163. [Google Scholar] [CrossRef]
- Alburquerque, J. Agrochemical Characterisation of “alperujo”, a Solid by-Product of the Two-Phase Centrifugation Method for Olive Oil Extraction. Bioresour. Technol. 2004, 91, 195–200. [Google Scholar] [CrossRef]
- Roig, A.; Cayuela, M.; Sánchez-Monedero, M. An Overview on Olive Mill Wastes and Their Valorisation Methods. Waste Manag. 2006, 26, 960–969. [Google Scholar] [CrossRef]
- Vossen, P. Olive Oil: History, Production, and Characteristics of the World. HortScience 2007, 42, 1093–1100. [Google Scholar] [CrossRef]
- Zomorodian, A.; Kavoosi, Z.; Momenzadeh, L. Determination of EMC Isotherms and Appropriate Mathematical Models for Canola. Food Bioprod. Process. 2011, 89, 407–413. [Google Scholar] [CrossRef]
- Rabha, D.; Muthukumar, P.; Somayaji, C. Experimental Investigation of Thin Layer Drying Kinetics of Ghost Chilli Pepper (Capsicum Chinense Jacq.) Dried in a Forced Convection Solar Tunnel Dryer. Renew. Energy 2017, 105, 583–589. [Google Scholar] [CrossRef]
- Abderrahman, M.; Abdelaziz, B.; Abdelkader, O. Thermal Performances and Kinetics Analyses of Greenhouse Hybrid Drying of Two-Phase Olive Pomace: Effect of Thin Layer Thickness. Renew. Energy 2022, 199, 407–418. [Google Scholar] [CrossRef]
- Han, R.; Zhou, A.; Zhang, N.; Li, Z. A Review of Kinetic Studies on Evaporative Dehydration of Lignite. Fuel 2022, 329, 125445. [Google Scholar] [CrossRef]
- Krokida, M.K.; Maroulis, Z.B.; Kremalis, C. Process Design of Rotary Dryers for Olive Cake. Dry. Technol. 2002, 20, 771–788. [Google Scholar] [CrossRef]
- Koukouch, A.; Idlimam, A.; Asbik, M.; Sarh, B.; Izrar, B.; Bah, A.; Ansari, O. Thermophysical Characterization and Mathematical Modeling of Convective Solar Drying of Raw Olive Pomace. Energy Convers. Manag. 2015, 99, 221–230. [Google Scholar] [CrossRef]
- Ertekin, C.; Yaldiz, O. Drying of Eggplant and Selection of a Suitable Thin Layer Drying Model. J. Food Eng. 2004, 63, 349–359. [Google Scholar] [CrossRef]
- Midilli, A.; Kucuk, H.; Yapar, Z. A New Model for Single-Layer Drying. Dry. Technol. 2002, 20, 1503–1513. [Google Scholar] [CrossRef]
- O’Callaghan, J.; Menzies, D.; Bailey, P. Digital Simulation of Agricultural Drier Performance. J. Agric. Eng. Res. 1971, 16, 223–244. [Google Scholar] [CrossRef]
- Guo, X.-H.; Xia, C.-Y.; Tan, Y.-R.; Chen, L.; Ming, J. Mathematical Modeling and Effect of Various Hot-Air Drying on Mushroom (Lentinus Edodes). J. Integr. Agric. 2014, 13, 207–216. [Google Scholar] [CrossRef]
- Raffalli, J. Community-Based Outbreaks of Tuberculosis. Arch. Intern. Med. 1996, 156, 1053–1060. [Google Scholar] [CrossRef] [PubMed]
- Aghbashlo, M.; Kianmehr, M.H.; Khani, S.; Ghasemi, M. Mathematical modeling of carrot thin-layer drying using new model. Int. Agrophysics 2009, 23, 313–317. [Google Scholar]
- Bruce, D. Exposed-Layer Barley Drying: Three Models Fitted to New Data up to 150 °C. J. Agric. Eng. Res. 1985, 32, 337–348. [Google Scholar] [CrossRef]
- Diamante, L.M.; Munro, P.A. Mathematical Modelling of Hot Air Drying of Sweet Potato Slices. Int. J. Food Sci. Technol. 2007, 26, 99–109. [Google Scholar] [CrossRef]
- Srikiatden, J.; Roberts, J.S. Moisture Transfer in Solid Food Materials: A Review of Mechanisms, Models, and Measurements. Int. J. Food Prop. 2007, 10, 739–777. [Google Scholar] [CrossRef]
- Fick, A. Ueber Diffusion. Ann. Der Phys. Und Chem. 1855, 170, 59–86. [Google Scholar] [CrossRef]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1975. [Google Scholar]
- Içier, F.; Baysal, T.; Taştan, Ö.; Özkan, G. Microwave Drying of Black Olive Slices: Effects on Total Phenolic Contents and Colour. Gıda 2014, 39, 323–330. [Google Scholar] [CrossRef]
- Zhao, H.; Li, Y.; Song, Q.; Wang, X.; Shu, X. Drying, Re-Adsorption Characteristics, and Combustion Kinetics of Xilingol Lignite in Different Atmospheres. Fuel 2017, 210, 592–604. [Google Scholar] [CrossRef]
- Li, L.; Jiang, X.; Qin, X.; Yan, K.; Chen, J.; Feng, T.; Wang, F.; Song, Z.; Zhao, X. Experimental Study and Energy Analysis on Microwave-Assisted Lignite Drying. Dry. Technol. 2019, 37, 962–975. [Google Scholar] [CrossRef]
- Freire, F.; Figueiredo, A.; Ferrão, P. PH—Postharvest Technology. J. Agric. Eng. Res. 2001, 78, 397–406. [Google Scholar] [CrossRef]
- Putra, R.N.; Ajiwiguna, T.A. Influence of Air Temperature and Velocity for Drying Process. Procedia Eng. 2017, 170, 516–519. [Google Scholar] [CrossRef]
- Gómez-de la Cruz, F.J.; Casanova-Peláez, P.J.; López-García, R.; Cruz-Peragón, F. Review of the Drying Kinetics of Olive Oil Mill Wastes: Biomass Recovery. BioResources 2015, 10, 6055–6080. [Google Scholar] [CrossRef]
- Toscano, P.; Cutini, M.; Di Giacinto, L.; Di Serio, M.G.; Bisaglia, C. Development of a Lab-Scale Prototype for Validating an Innovative Pitting Method of Oil Olives. AgriEngineering 2021, 3, 622–632. [Google Scholar] [CrossRef]
- Sadi, T.; Meziane, S. Mathematical modelling, moisture diffusion and specific energy consumption of thin layer microwave drying of olive pomace. Int. Food Res. J. 2015, 22, 494–501. [Google Scholar]
- Koukouch, A.; Idlimam, A.; Asbik, M.; Sarh, B.; Izrar, B.; Bostyn, S.; Bah, A.; Ansari, O.; Zegaoui, O.; Amine, A. Experimental Determination of the Effective Moisture Diffusivity and Activation Energy During Convective Solar Drying of Olive Pomace Waste. Renew. Energy 2017, 101, 565–574. [Google Scholar] [CrossRef]
- Baysan, U.; Koç, M.; Güngör, A.; Ertekin, F.K. Investigation of Drying Conditions to Valorize 2-Phase Olive Pomace in Further Processing. Dry. Technol. 2020, 40, 65–76. [Google Scholar] [CrossRef]
- Akpinar, E.K. Determination of Suitable Thin Layer Drying Curve Model for Some Vegetables and Fruits. J. Food Eng. 2006, 73, 75–84. [Google Scholar] [CrossRef]
- Amiri Chayjan, R.; Amiri Parian, J.; Esna-Ashari, M. Modeling of Moisture Diffusivity, Activation Energy and Specific Energy Consumption of High Moisture Corn in a Fixed and Fluidized Bed Convective Dryer. Span. J. Agric. Res. 2011, 9, 28–40. [Google Scholar] [CrossRef]
- Sitorus, A.; Putra, S.A.; Cebro, I.S.; Bulan, R. Modelling Drying Kinetics of Paddy in Swirling Fluidized Bed Dryer. Case Stud. Therm. Eng. 2021, 28, 101572. [Google Scholar] [CrossRef]
- Meziane, S. Drying Kinetics of Olive Pomace in a Fluidized Bed Dryer. Energy Convers. Manag. 2011, 52, 1644–1649. [Google Scholar] [CrossRef]
- Göğüş, F.; Maskan, M. Air Drying Characteristics of Solid Waste (pomace) of Olive Oil Processing. J. Food Eng. 2006, 72, 378–382. [Google Scholar] [CrossRef]
- Kingsly, R.P.; Goyal, R.K.; Manikantan, M.R.; Ilyas, S.M. Effects of Pretreatments and Drying Air Temperature on Drying Behaviour of Peach Slice. Int. J. Food Sci. Technol. 2007, 42, 65–69. [Google Scholar] [CrossRef]
- Van Meel, D. Adiabatic Convection Batch Drying With Recirculation of Air. Chem. Eng. Sci. 1958, 9, 36–44. [Google Scholar] [CrossRef]
- Ait Mohamed, L.; Ethmane Kane, C.; Kouhila, M.; Jamali, A.; Mahrouz, M.; Kechaou, N. Thin Layer Modelling of Gelidium Sesquipedale Solar Drying Process. Energy Convers. Manag. 2008, 49, 940–946. [Google Scholar] [CrossRef]
- Touil, A.; Chemkhi, S.; Zagrouba, F. Modelling of the Drying Kinetics of Opuntia Ficus Indica Fruits and Cladodes. Int. J. Food Eng. 2010, 6, 11. [Google Scholar] [CrossRef]
- Doymaz, İ. Effect of Pre-Treatments Using Potassium Metabisulphide and Alkaline Ethyl Oleate on the Drying Kinetics of Apricots. Biosyst. Eng. 2004, 89, 281–287. [Google Scholar] [CrossRef]
- Lahsasni, S.; Kouhila, M.; Mahrouz, M.; Idlimam, A.; Jamali, A. Thin Layer Convective Solar Drying and Mathematical Modeling of Prickly Pear Peel (Opuntia Ficus Indica). Energy 2004, 29, 211–224. [Google Scholar] [CrossRef]
- Aghbashlo, M.; Kianmehr, M.H.; Arabhosseini, A.; Nazghelichi, T. Modelling the Carrot Thin-Layer Drying in a Semi-Industrial Continuous Band Dryer. Czech J. Food Sci. 2011, 29, 528–538. [Google Scholar] [CrossRef]
- Meziane, S.; Mesbahi, N. Determination of Moisture Diffusivity and Activation Energy in Thin Layer Drying of Olive Pomace. Int. J. Food Eng. 2012, 8, 34. [Google Scholar] [CrossRef]


| Model Name | Model Expression | References |
|---|---|---|
| Midilli et al. | [18] | |
| Newton | [19] | |
| Wang and Singh | [20] | |
| Henderson and Pabis | [21] | |
| Aghabashlo model | [22] | |
| Yagcioglu et al. | [23] | |
| Simplified.Fick’s. diffusion | [24] |
| Model | Temperature (°C) | ||
|---|---|---|---|
| Midilli et al. [18] | 60 | 0.999 | 0.31 × 10−4 |
| 70 | 0.999 | 0.91 × 10−4 | |
| 80 | 0.999 | 0.26 × 10−4 | |
| 90 | 0.999 | 0.64 × 10−4 | |
| 100 | 0.999 | 0.07 × 10−4 | |
| Newton [19] | 60 | 0.963 | 33.90 × 10−4 |
| 70 | 0.947 | 51.81 × 10−4 | |
| 80 | 0.969 | 28.00 × 10−4 | |
| 90 | 0.957 | 42.80 × 10−4 | |
| 100 | 0.988 | 9.34 × 10−4 | |
| Wang and Singh [20] | 60 | 0.992 | 6.58 × 10−4 |
| 70 | 0.987 | 12.40 × 10−4 | |
| 80 | 0.992 | 6.63 × 10−4 | |
| 90 | 0.989 | 10.30 × 10−4 | |
| 100 | 0.994 | 4.85 × 10−4 | |
| Henderson and Pabis [21] | 60 | 0.980 | 18.30 × 10−4 |
| 70 | 0.969 | 29.80 × 10−4 | |
| 80 | 0.984 | 14.40 × 10−4 | |
| 90 | 0.975 | 24.20 × 10−4 | |
| 100 | 0.994 | 4.81 × 10−4 | |
| Aghabashlo model [22] | 60 | 0.994 | 4.80 × 10−4 |
| 70 | 0.993 | 6.44 × 10−4 | |
| 80 | 0.991 | 7.74 × 10−4 | |
| 90 | 0.992 | 7.52 × 10−4 | |
| 100 | 0.992 | 6.18 × 10−4 | |
| Yagcioglu et al. [23] | 60 | 0.992 | 6.99 × 10−4 |
| 70 | 0.989 | 10.90 × 10−4 | |
| 80 | 0.990 | 8.93 × 10−4 | |
| 90 | 0.988 | 12.40 × 10−4 | |
| 100 | 0.994 | 4.87 × 10−4 | |
| Simplified.Fick’s.diffusion [24] | 60 | 0.980 | 18.30 × 10−4 |
| 70 | 0.970 | 29.80 × 10−4 | |
| 80 | 0.984 | 14.40 × 10−4 | |
| 90 | 0.976 | 24.20 × 10−4 | |
| 100 | 0.994 | 4.81 × 10−4 |
| V (ms−1) | T (°C) | a | k | b | n |
|---|---|---|---|---|---|
| 1 | 60 | 0.9890 | 1.45 × 10−3 | −40.60 × 10−4 | 1.3847 |
| 80 | 0.9758 | 0.99 × 10−3 | 2.13 × 10−4 | 1.5637 | |
| 100 | 0.9781 | 1.30 × 10−3 | −39.60 × 10−4 | 1.5054 | |
| 1.5 | 60 | 0.9775 | 0.73 × 10−3 | 1.11 × 10−4 | 1.5292 |
| 70 | 0.9735 | 0.46 × 10−3 | 1.17 × 10−4 | 1.6642 | |
| 80 | 0.9814 | 1.35 × 10−3 | 2.78 × 10−4 | 1.5284 | |
| 90 | 0.9760 | 1.07 × 10−3 | 2.02 × 10−4 | 1.6231 | |
| 100 | 0.9962 | 6.69 × 10−3 | 3.61 × 10−4 | 1.3074 |
| Drying Air Velocity (ms−1) | T (°C) | ||
|---|---|---|---|
| 1 | 100 | 8.24 | 0.958 |
| 80 | 6.18 | 0.988 | |
| 60 | 5.18 | 0.982 | |
| 1.5 | 100 | 8.53 | 0.979 |
| 90 | 8.29 | 0.980 | |
| 80 | 6.50 | 0.987 | |
| 70 | 5.88 | 0.977 | |
| 60 | 4.88 | 0.989 | |
| 2 | 100 | 11.01 | 0.949 |
| 80 | 7.81 | 0.975 |
| Air Drying Velocity (ms−1) | |||
|---|---|---|---|
| 1 | 25.3 | −28.15 × 10−4 | 0.951 |
| 1.5 | 15.1 | −115.20 × 10−4 | 0.954 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nsibi, C.; Lajili, M. Experimental Study and Mathematical Modeling under Various Hot-Air Drying Conditions of Thin Layer Olive Pomaces. Processes 2023, 11, 2513. https://doi.org/10.3390/pr11092513
Nsibi C, Lajili M. Experimental Study and Mathematical Modeling under Various Hot-Air Drying Conditions of Thin Layer Olive Pomaces. Processes. 2023; 11(9):2513. https://doi.org/10.3390/pr11092513
Chicago/Turabian StyleNsibi, Chafaa, and Marzouk Lajili. 2023. "Experimental Study and Mathematical Modeling under Various Hot-Air Drying Conditions of Thin Layer Olive Pomaces" Processes 11, no. 9: 2513. https://doi.org/10.3390/pr11092513
APA StyleNsibi, C., & Lajili, M. (2023). Experimental Study and Mathematical Modeling under Various Hot-Air Drying Conditions of Thin Layer Olive Pomaces. Processes, 11(9), 2513. https://doi.org/10.3390/pr11092513








