Active Steering Controller for Driven Independently Rotating Wheelset Vehicles Based on Deep Reinforcement Learning
Abstract
:1. Introduction
2. DIRW Vehicle Dynamics Model
3. Controller Design Based on Ape-X DDPG Algorithm
3.1. Basic DRL Theory
3.2. DDPG Algorithm
3.3. Introduction of Prioritized Experience Replay
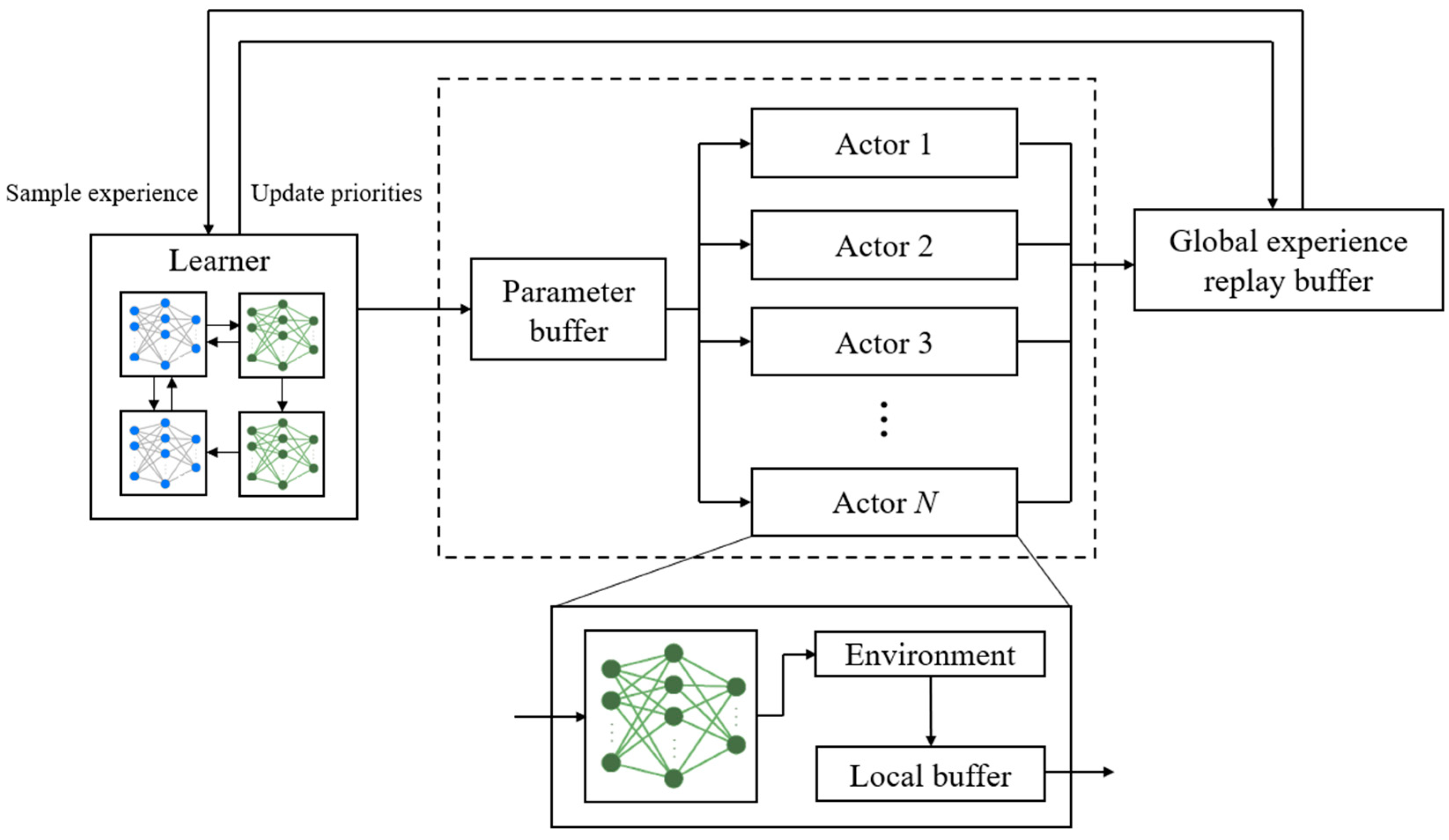
3.4. Structure of Ape-X DDPG Algorithm
| Algorithm 1: Pseudocode of the Actor |
| Input: Initial state s0 from the environment; policy network parameters θμ from the Learner’s parameter buffer; local buffer size Dm; maximum interaction timesteps T |
| Output: Updated experience tuples and priorities to shared experience replay buffer D |
| 01: Initialize local buffer Dl and shared experience replay buffer D. |
| 02: Initialize state s0. |
| 03: for t = 1 to T do |
| 04: Calculate action at−1 = μ(st−1; θμ). |
| 05: Obtain reward rt, next state st, and discount factor γt based on action at−1. |
| 06: Add experience tuple (st−1, at−1, rt, γt) to local buffer Dl. |
| 07: if the size of Dl reaches Dm then |
| 08: Retrieve experience tuples from Dl, denoted as τl. |
| 09: Calculate the priority p for each experience tuple in τl. |
| 10: Add τl and corresponding priorities p to D. |
| 11: end if |
| 12: Periodically fetch the latest network parameters θμ from the Learner. |
| 13: end for |
| 14: end procedure |
| Algorithm 2: Pseudocode of the Learner |
| Input: Maximum interaction timesteps T; initial value network parameters θQ; initial policy network parameters θμ; initial shared experience replay buffer D |
| Output: Updated network parameters θQ and θμ |
| 01: Initialize value network parameters θQ and policy network parameters θμ. |
| 02: Send θQ and θμ to the parameter buffer shared with Actors. |
| 03: for t = 1 to T do |
| 04: Sample training samples I and IS weights wi from D using PER sampling. |
| 05: Compute the loss function L according to Equation (21) based on I, θQ and θμ. |
| 06: Update the value network parameters θQ using L. |
| 07: Compute the policy network gradient according to Equation (22) and update θμ. |
| 08: Recalculate priorities p for sample I based on the TD error yi for each training sample. |
| 09: Update the priorities of samples in D with the newly computed priorities p. |
| 10: if the size of D reaches maximum capacity then |
| 11: Remove the experiences with the lowest priorities from D. |
| 12: end if |
| 13: end for |
| 14: end procedure |
3.5. DRL-Based Controller Design
3.5.1. Definition of State Space
3.5.2. Definition of Action Space
3.5.3. Control Objectives and Reward Function
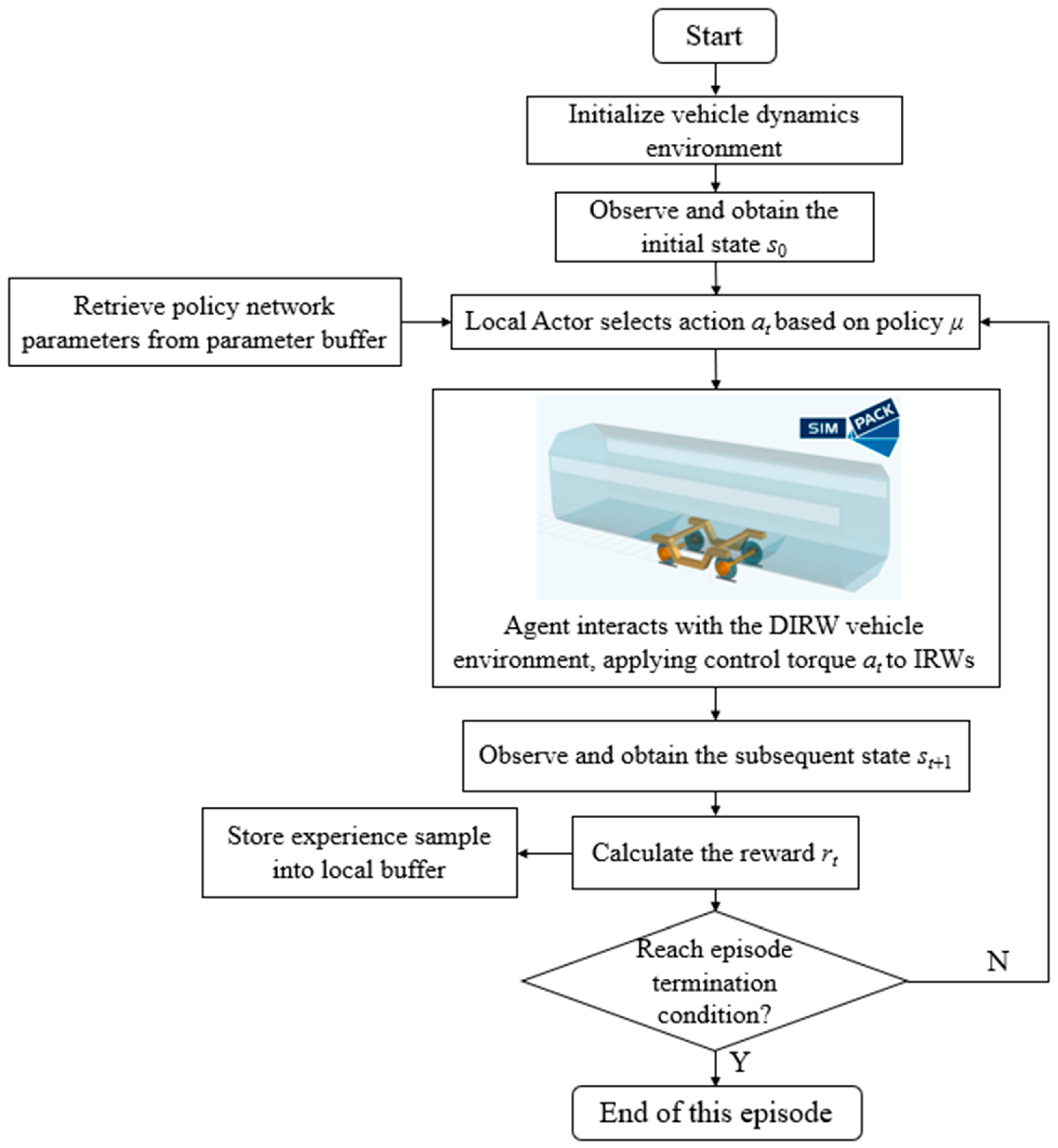
3.5.4. DRL Interaction and Training Process
- (a)
- The training episode reaches the maximum timestep T.
- (b)
- The lateral displacement of the IRWs reaches the maximum wheel–rail clearance.
- (c)
- The control torque output from the policy network exceeds the maximum limit.
- (d)
- Under the effect of the active steering controller, the lateral acceleration of the vehicle body exceeds the threshold.
4. Training and Simulation Results
4.1. Training Environment
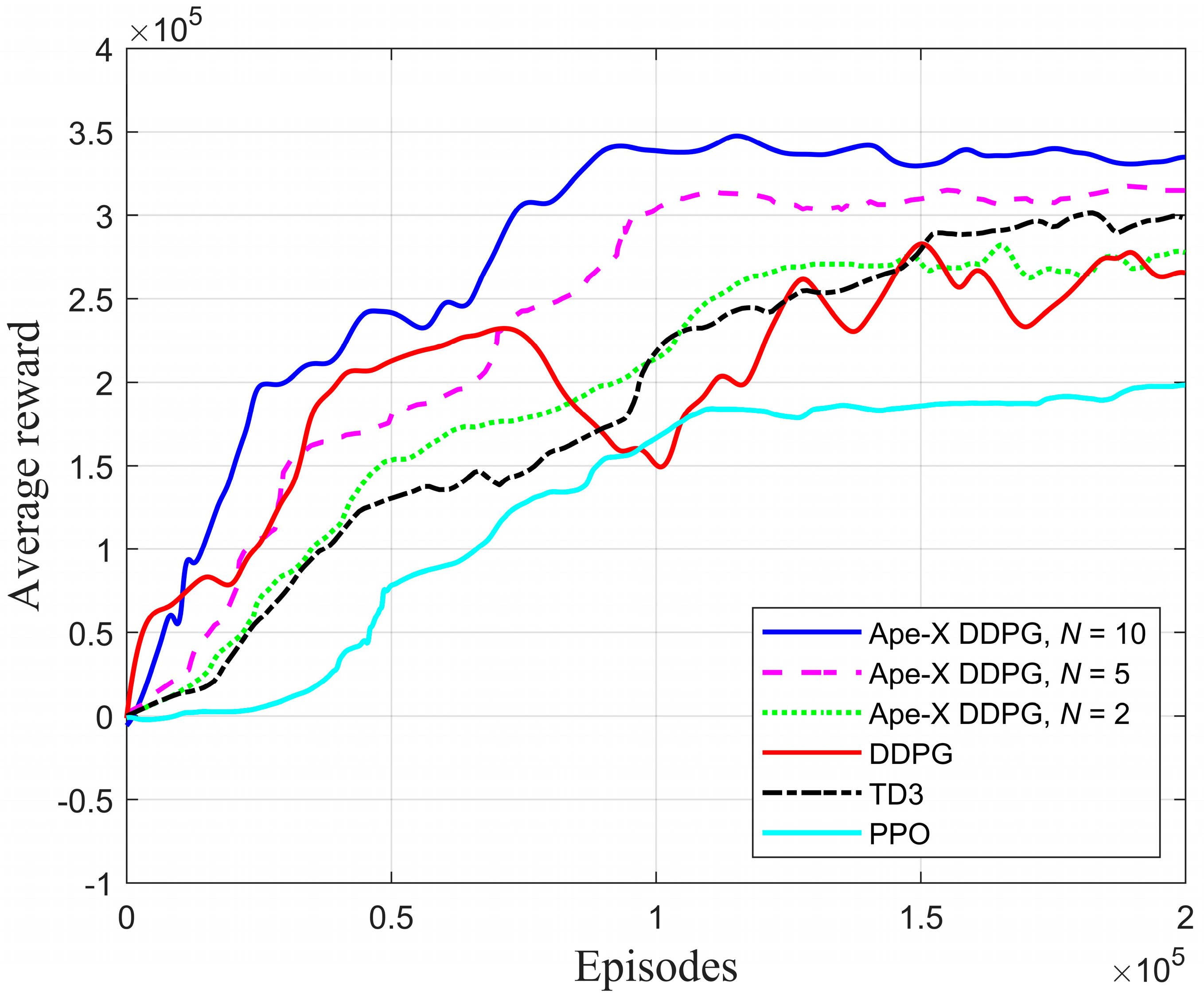
4.2. Training Comparison of DRL
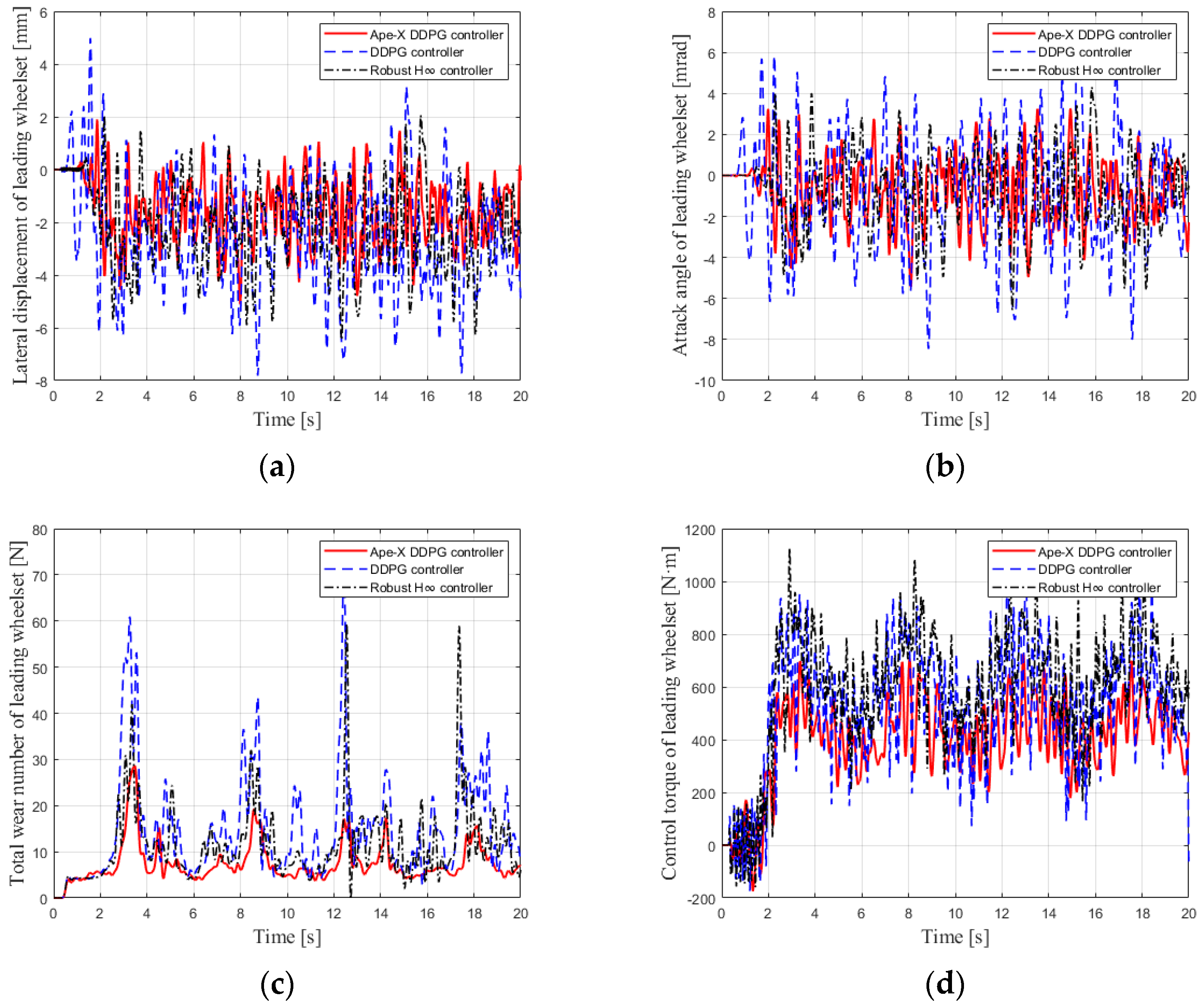
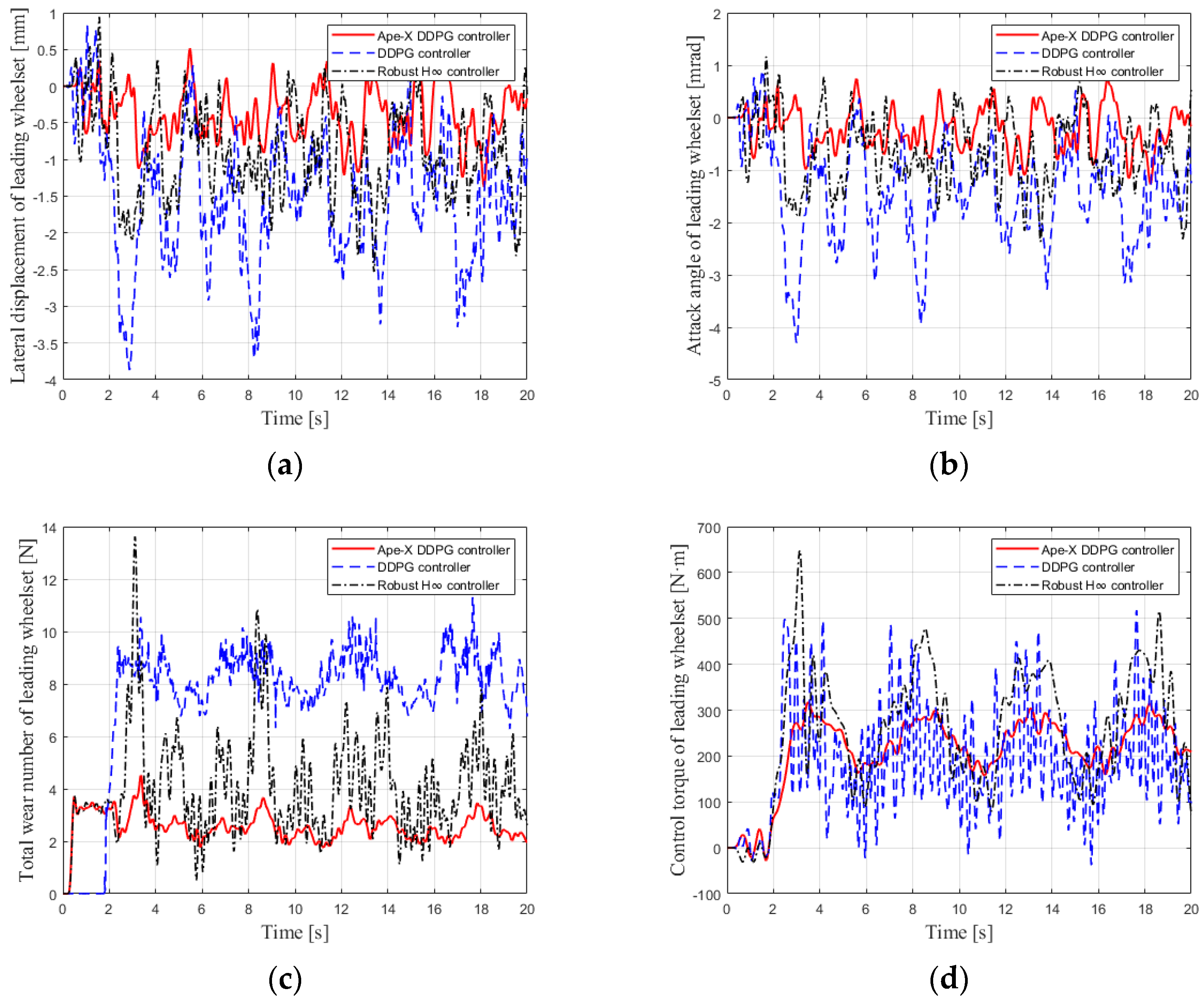
4.3. Comparative Analysis of Control Effects between Model-Based and Data-Based Algorithms
- (1)
- Case 1: Operation on a straight track at 120 km/h.
- (2)
- Case 2: Operation on a curved track with Rc = 70 m at 30 km/h.
- (3)
- Case 3: Operation on a curved track with Rc = 250 m at 80 km/h.
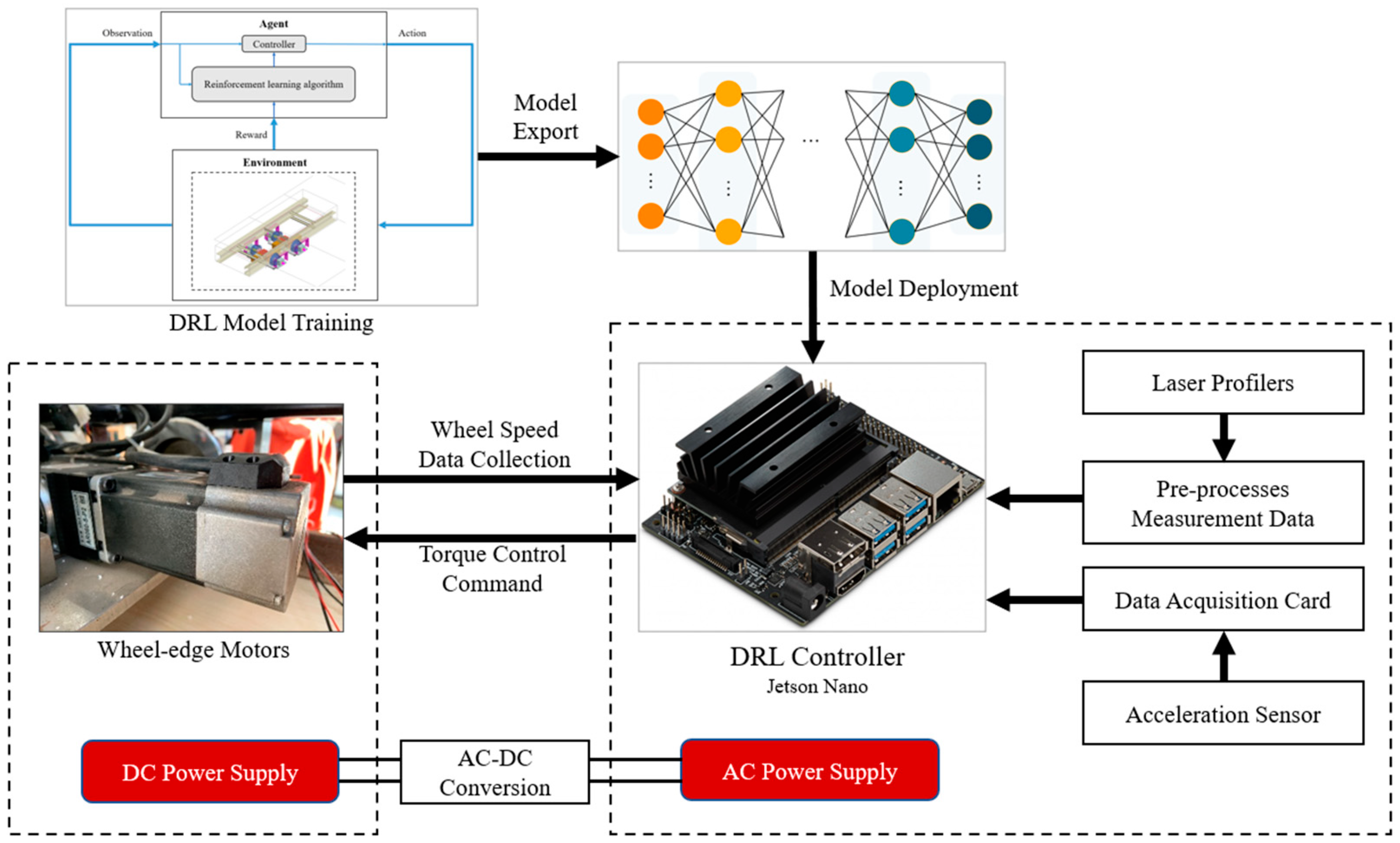
5. Scale Model Experiments
5.1. Scale DIRW Vehicle
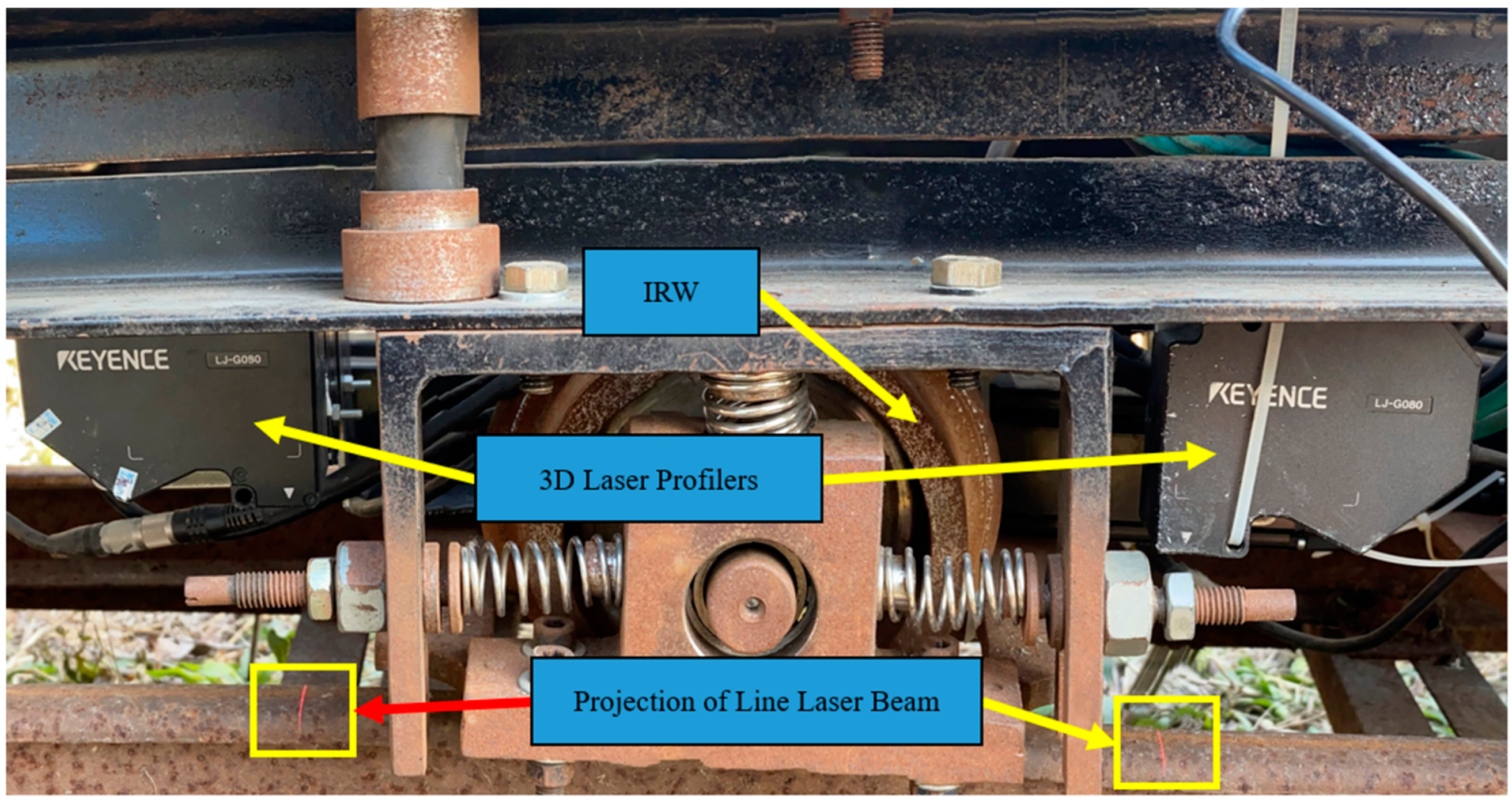
5.2. Acquisition of Sensor Signals
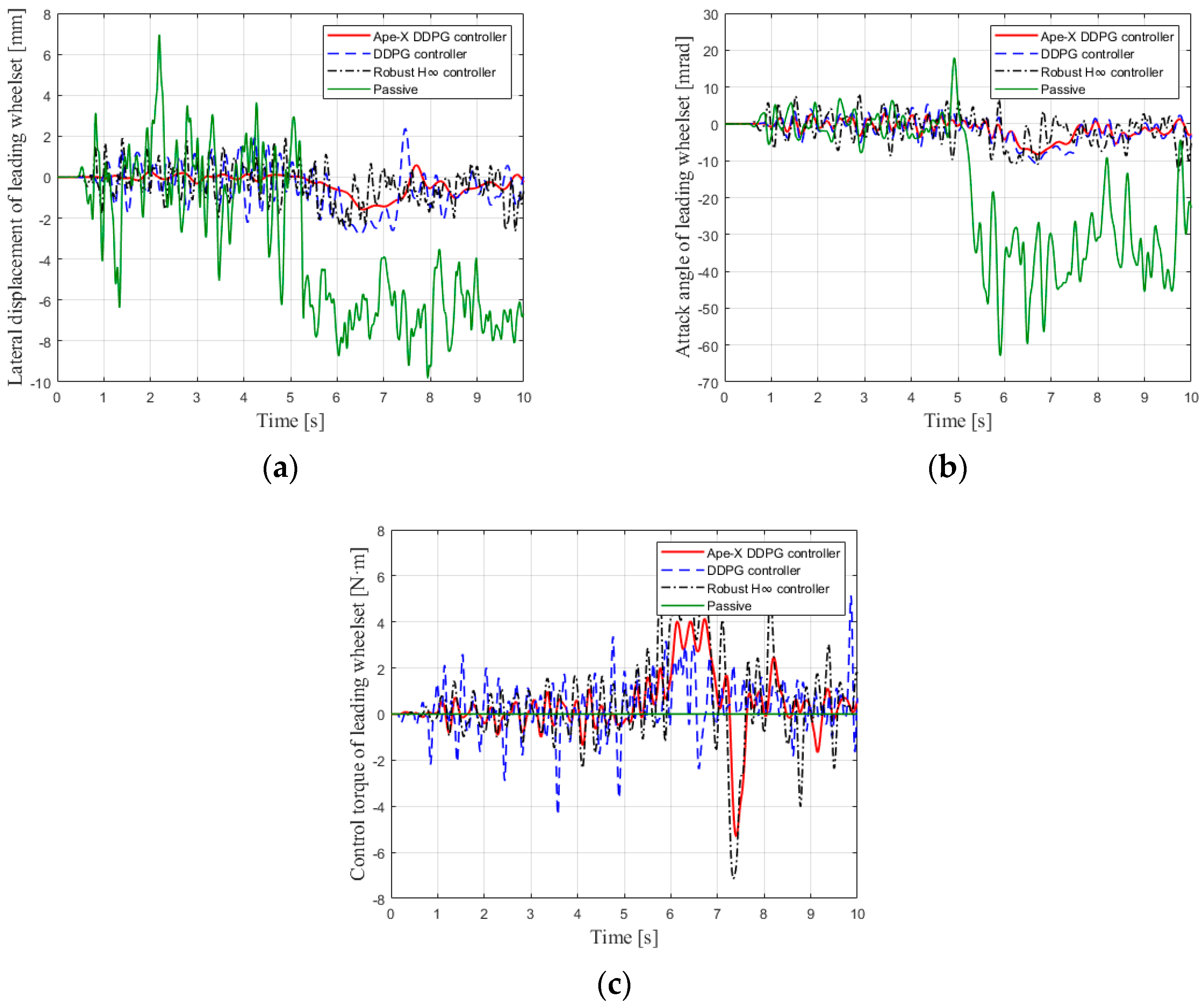
5.3. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Dynamic Parameters | Value | Unit |
|---|---|---|
| Wheel base | 2.0 | m |
| Lateral length of primary suspension | 1.08 | m |
| Longitudinal length of primary suspension | 0.39 | m |
| Lateral length of secondary suspension | 1.80 | m |
| Longitudinal length of secondary suspension | 0.50 | m |
| Mass of carbody | 9000 | kg |
| Pitch moment of inertia of carbody | 80,000 | kg·m2 |
| Yaw moment of inertia of carbody | 80,000 | kg·m2 |
| Roll moment of inertia of carbody | 10,000 | kg·m2 |
| Mass of bogie | 1600 | kg |
| Pitch moment of inertia of bogie | 900 | kg·m2 |
| Yaw moment of inertia of bogie | 1300 | kg·m2 |
| Roll moment of inertia of bogie | 1500 | kg·m2 |
| Mass of IRW | 1250 | kg |
| Pitch moment of inertia per wheel | 30 | kg·m2 |
| Yaw moment of inertia of IRW | 600 | kg·m2 |
| Primary longitudinal stiffness per axle box | 600 | kN·m−1 |
| Primary lateral stiffness per axle box | 8000 | kN·m−1 |
| Primary vertical stiffness per axle box | 15,000 | kN·m−1 |
| Primary longitudinal damping per axle box | 100 | kN·m·s−1 |
| Primary lateral damping per axle box | 500 | kN·m·s−1 |
| Primary vertical damping per axle box | 800 | kN·m·s−1 |
| Secondary longitudinal stiffness per side | 200 | kN·m−1 |
| Secondary lateral stiffness per side | 200 | kN·m−1 |
| Secondary vertical stiffness per side | 600 | kN·m−1 |
| Secondary longitudinal damping side | 50 | kN·m·s−1 |
| Secondary lateral damping per side | 50 | kN·m·s−1 |
| Secondary vertical damping per side | 50 | kN·m·s−1 |
References
- Fu, B.; Giossi, R.L.; Persson, R.; Stichel, S.; Bruni, S.; Goodall, R. Active suspension in railway vehicles: A literature survey. Railw. Eng. Sci. 2020, 28, 3–35. [Google Scholar] [CrossRef]
- Goodall, R.; Mei, T.X. Mechatronic strategies for controlling railway wheelsets with independently rotating wheels. In Proceedings of the 2001 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Proceedings (Cat. No.01TH8556), Como, Italy, 8–12 July 2001; Volume 1, pp. 225–230. [Google Scholar]
- Oh, Y.J.; Liu, H.-C.; Cho, S.; Won, J.H.; Lee, H.; Lee, J. Design, modeling, and analysis of a railway traction motor with independently rotating wheelsets. IEEE Trans. Magn. 2018, 54, 8205305. [Google Scholar] [CrossRef]
- Pérez, J.; Busturia, J.M.; Mei, T.X.; Vinolas, J. Combined active steering and traction for mechatronic bogie vehicles with independently rotating wheels. Annu. Rev. Control 2004, 28, 207–217. [Google Scholar] [CrossRef]
- Mei, T.X.; Li, H.; Goodall, R.M.; Wickens, A.H. Dynamics and control assessment of rail vehicles using permanent magnet wheel motors. Veh. Syst. Dyn. 2002, 37 (Suppl. 1), 326–337. [Google Scholar] [CrossRef]
- Chudzikiewicz, A.; Gerlici, J.; Sowinska, M.; Sowinska, M.; Stelmach AWawrzyński, W. Modeling and simulation of a control system of wheels of wheelset. Arch. Transp. 2020, 55, 73–83. [Google Scholar] [CrossRef]
- Ji, Y.; Ren, L.; Zhou, J. Boundary conditions of active steering control of independent rotating wheelset based on hub motor and wheel rotating speed difference feedback. Veh. Syst. Dyn. 2018, 56, 1883–1898. [Google Scholar] [CrossRef]
- Mei, T.X.; Qu, K.W.; Li, H. Control of wheel motors for the provision of traction and steering of railway vehicles. IET Power Electron. 2014, 7, 2279–2287. [Google Scholar] [CrossRef]
- Heckmann, A.; Schwarz, C.; Keck, A.; Bünte, T. Nonlinear observer design for guidance and traction of railway vehicles. In Advances in Dynamics of Vehicles on Roads and Tracks: Proceedings of the 26th Symposium of the International Association of Vehicle System Dynamics, IAVSD 2019, Gothenburg, Sweden, 12–16 August 2019; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar]
- Ahn, H.; Lee, H.; Go, S.; Cho, Y.; Lee, J. Control of the lateral displacement restoring force of IRWs for sharp curved driving. J. Electr. Eng. Technol. 2016, 11, 1042–1048. [Google Scholar] [CrossRef]
- Liu, X.; Goodall, R.; Iwnicki, S. Active control of independently-rotating wheels with gyroscopes and tachometers–simple solutions for perfect curving and high stability performance. Veh. Syst. Dyn. 2021, 59, 1719–1734. [Google Scholar] [CrossRef]
- Kurzeck, B.; Heckmann, A.; Wesseler, C.; Rapp, M. Mechatronic track guidance on disturbed track: The trade-off between actuator performance and wheel wear. Veh. Syst. Dyn. 2014, 52 (Suppl. 1), 109–124. [Google Scholar] [CrossRef]
- Grether, G. Dynamics of a running gear with IRWs on curved tracks for a robust control development. PAMM 2017, 17, 797–798. [Google Scholar] [CrossRef]
- Lu, Z.; Yang, Z.; Huang, Q.; Wang, X. Robust active guidance control using the µ-synthesis method for a tramcar with independently rotating wheelsets. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2019, 233, 33–48. [Google Scholar] [CrossRef]
- Yang, Z.; Lu, Z.; Sun, X.; Zou, J.; Wan, H.; Yang, M.; Zhang, H. Robust LPV-H∞ control for active steering of tram with independently rotating wheels. Adv. Mech. Eng. 2022, 14, 16878132221130574. [Google Scholar] [CrossRef]
- Lu, Z.; Sun, X.; Yang, J. Integrated active control of independently rotating wheels on rail vehicles via observers. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit 2017, 231, 295–305. [Google Scholar] [CrossRef]
- Wei, J.; Lu, Z.; Yang, Z.; He, Y.; Wang, X. Data-Driven Robust Control for Railway Driven Independently Rotating Wheelsets Using Deep Deterministic Policy Gradient. In Proceedings of the IAVSD International Symposium on Dynamics of Vehicles on Roads and Tracks, Saint Petersburg, Russia, 17–19 August 2021; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar]
- Ramos-Fernández, J.C.; López-Morales, V.; Márquez-Vera, M.A.; Pérez JM, X.; Suarez-Cansino, J. Neuro-fuzzy modelling and stable PD controller for angular position in steering systems. Int. J. Automot. Technol. 2021, 22, 1495–1503. [Google Scholar] [CrossRef]
- Mei, T.X.; Goodall, R.M. Robust control for independently rotating wheelsets on a railway vehicle using practical sensors. IEEE Trans. Control. Syst. Technol. 2001, 9, 599–607. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; MIT Press: Cambridge, MA, USA, 2018; p. 342. [Google Scholar]
- Deng, H.; Zhao, Y.; Nguyen, A.T.; Huang, C. Fault-tolerant predictive control with deep-reinforcement-learning-based torque distribution for four in-wheel motor drive electric vehicles. IEEE/ASME Trans. Mechatron. 2023, 28, 668–680. [Google Scholar] [CrossRef]
- Wei, H.; Zhao, W.; Ai, Q.; Zhang, Y.; Huang, T. Deep reinforcement learning based active safety control for distributed drive electric vehicles. IET Intell. Transp. Syst. 2022, 16, 813–824. [Google Scholar] [CrossRef]
- Albarella, N.; Lui, D.G.; Petrillo, A.; Santini, S. A Hybrid Deep Reinforcement Learning and Optimal Control Architecture for Autonomous Highway Driving. Energies 2023, 16, 3490. [Google Scholar] [CrossRef]
- Cheng, Y.; Hu, X.; Chen, K.; Yu, X.; Luo, Y. Online longitudinal trajectory planning for connected and autonomous vehicles in mixed traffic flow with deep reinforcement learning approach. J. Intell. Transp. Syst. 2023, 27, 396–410. [Google Scholar] [CrossRef]
- Wang, H.; Han, Z.; Liu, Z.; Wu, Y. Deep reinforcement learning based active pantograph control strategy in high-speed railway. IEEE Trans. Veh. Technol. 2022, 72, 227–238. [Google Scholar] [CrossRef]
- Zhu, F.; Yang, Z.; Lin, F.; Xin, Y. Decentralized cooperative control of multiple energy storage systems in urban railway based on multiagent deep reinforcement learning. IEEE Trans. Power Electron. 2020, 35, 9368–9379. [Google Scholar] [CrossRef]
- Sresakoolchai, J.; Kaewunruen, S. Railway infrastructure maintenance efficiency improvement using deep reinforcement learning integrated with digital twin based on track geometry and component defects. Sci. Rep. 2023, 13, 2439. [Google Scholar] [CrossRef]
- Farazi, N.P.; Zou, B.; Ahamed, T.; Barua, L. Deep reinforcement learning in transportation research: A review. Transp. Res. Interdiscip. Perspect. 2021, 11, 100425. [Google Scholar]
- Lee, M.F.R.; Yusuf, S.H. Mobile robot navigation using deep reinforcement learning. Processes 2022, 10, 2748. [Google Scholar] [CrossRef]
- Moriya, N.; Shigemune, H.; Sawada, H. A robotic wheel locally transforming its diameters and the reinforcement learning for robust locomotion. Int. J. Mechatron. Autom. 2022, 9, 22–31. [Google Scholar] [CrossRef]
- Li, Y. Deep reinforcement learning: An overview. arXiv 2017, arXiv:1701.07274. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2015, arXiv:1509.02971. [Google Scholar]
- Moritz, P.; Nishihara, R.; Wang, S.; Tumanov, A.; Liaw, R.; Liang, E.; Elibol, M.; Yang, Z.; Paul, W.; Jordan, M.I.; et al. Ray: A distributed framework for emerging AI applications. In Proceedings of the 13th USENIX Symposium on Operating Systems Design and Implementation (OSDI 18), Carlsbad, CA, USA, 8–10 October 2018. [Google Scholar]
- Liang, E.; Liaw, R.; Nishihara, R.; Moritz, P.; Fox, R.; Goldberg, K.; Gonzalez, J.; Jordan, M.; Stoica, I. RLlib: Abstractions for distributed reinforcement learning. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L.; et al. Pytorch: An imperative style, high-performance deep learning library. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; Volume 32. [Google Scholar]
- Kingma, D.P.; Jimmy, B. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018. [Google Scholar]
- Skogestad, S.; Postlethwaite, I. Multivariable feedback control: Analysis and design. In Multivariable Feedback Control: Analysis and Design, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]







| Track 1 | Track 2 | Track 3 | Track 4 | Track 5 | |
|---|---|---|---|---|---|
| Track Type | Straight line | Straight line | Curve line | Curve line | Curve line |
| Curve Radius (m) | — | — | 70 | 250 | 600 |
| Speed (km/h) | 80 | 120 | 30 | 80 | 100 |
| Cant (mm) | — | — | 0 | 150 | 80 |
| Track Irregularities | AAR5 | AAR5 | AAR5 | AAR5 | AAR5 |
| Parameter | Value | Description |
|---|---|---|
| LRμ | 10−4 | Learning rate of the policy network μ |
| LRQ | 10−3 | Learning rate of the value network Q |
| γ | 0.99 | Temporal discount rate |
| τ | 10−4 | Soft update rate |
| batchsize | 512 | Batch size for training |
| |D| | 106 | Storage limit for the public sample pool |
| α | 0.8 | Exponent for priority sampling |
| β | 0.3 | IS hyperparameter |
| Dm | 104 | Storage limit for the local sample pool |
| N | 10 | Number of Actors |
| σOU | 0.2 | Standard deviation of OU disturbance noise |
| Tmax | 1200 N·m | Maximum output control torque |
| ymax | 9.2 mm | Maximum lateral clearance between wheel and rail |
| η11 | 1 | Reward coefficient for the lateral displacement of the front IRW |
| η12 | 0.5 | Reward coefficient for the yaw angle of the front IRW |
| η21 | 0.2 | Reward coefficient for the lateral displacement of the rear IRW |
| η22 | 0.1 | Reward coefficient for the yaw angle of the rear IRW |
| η13 | 5 | Reward coefficient for the steering torque of the front IRW |
| η23 | 2 | Reward coefficient for the steering torque of the rear IRW |
| amax | 2.5 m·s−2 | Lateral acceleration limit |
| rp | 100 | Penalty for exceeding lateral acceleration limit |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.; Wei, J.; Wang, Z. Active Steering Controller for Driven Independently Rotating Wheelset Vehicles Based on Deep Reinforcement Learning. Processes 2023, 11, 2677. https://doi.org/10.3390/pr11092677
Lu Z, Wei J, Wang Z. Active Steering Controller for Driven Independently Rotating Wheelset Vehicles Based on Deep Reinforcement Learning. Processes. 2023; 11(9):2677. https://doi.org/10.3390/pr11092677
Chicago/Turabian StyleLu, Zhenggang, Juyao Wei, and Zehan Wang. 2023. "Active Steering Controller for Driven Independently Rotating Wheelset Vehicles Based on Deep Reinforcement Learning" Processes 11, no. 9: 2677. https://doi.org/10.3390/pr11092677
APA StyleLu, Z., Wei, J., & Wang, Z. (2023). Active Steering Controller for Driven Independently Rotating Wheelset Vehicles Based on Deep Reinforcement Learning. Processes, 11(9), 2677. https://doi.org/10.3390/pr11092677







