Automated Shape and Process Parameter Optimization for Scaling Up Geometrically Non-Similar Bioreactors
Abstract
:1. Introduction
2. Materials and Methods
2.1. Computational Fluid Dynamics
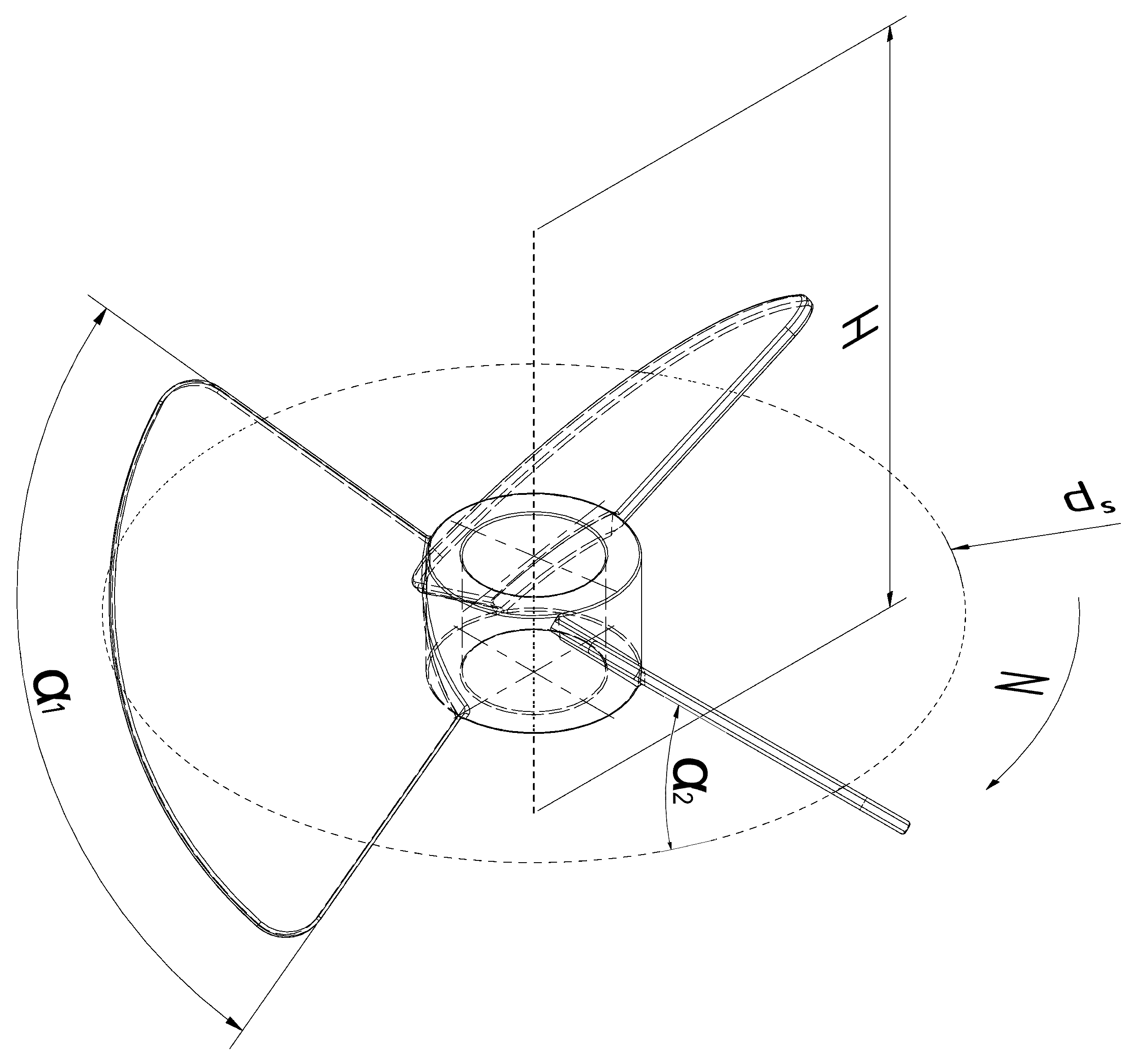
2.2. Optimization Process
| Parameter | Minimum | Maximum |
|---|---|---|
| Stirrer speed N | 50 rpm | 500 rpm |
| Stirrer height H | 0.10 m | 0.45 m |
| Stirrer diameter | 50 mm | 170 mm |
| Blade angle | 20 | 120 |
| Pitch angle | 90 |
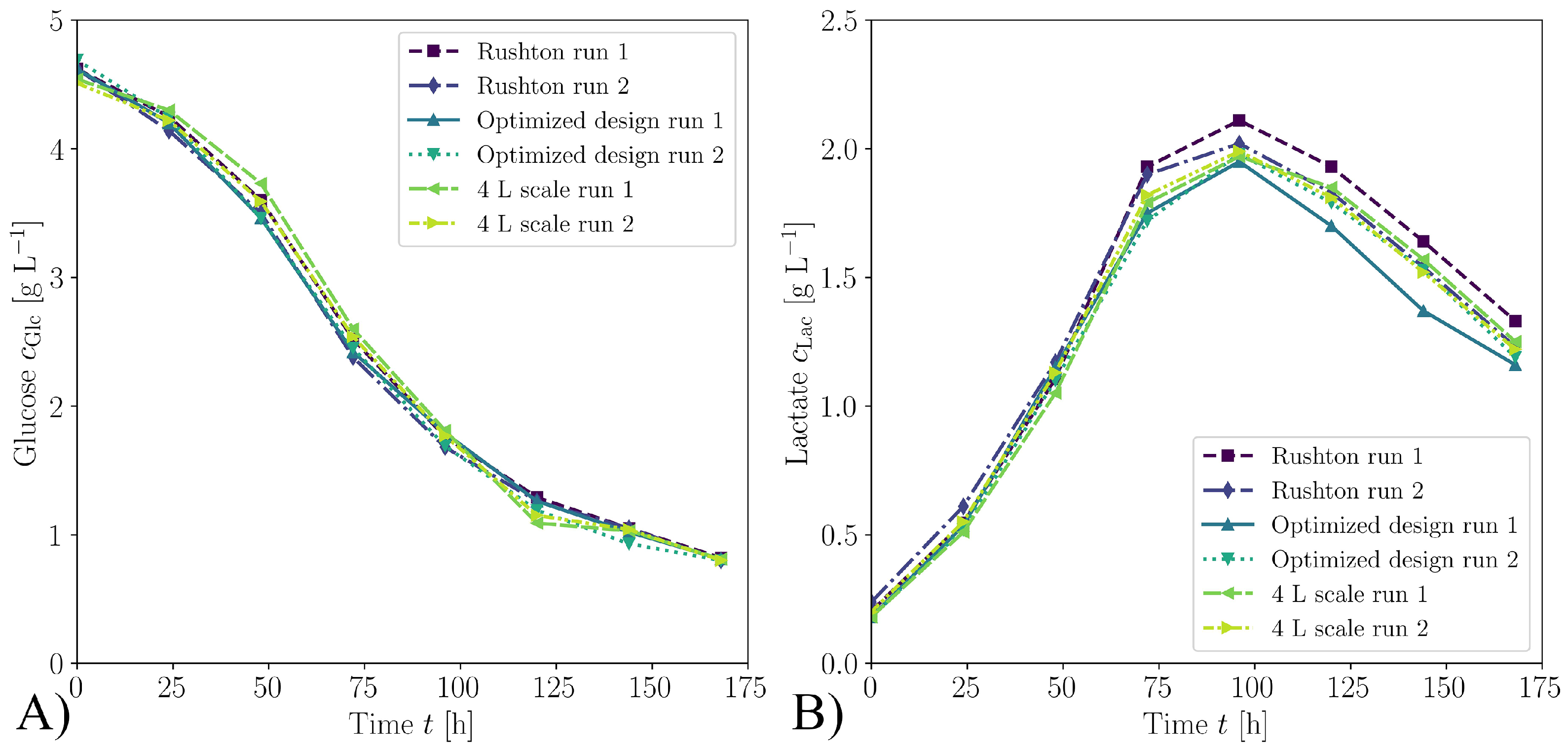
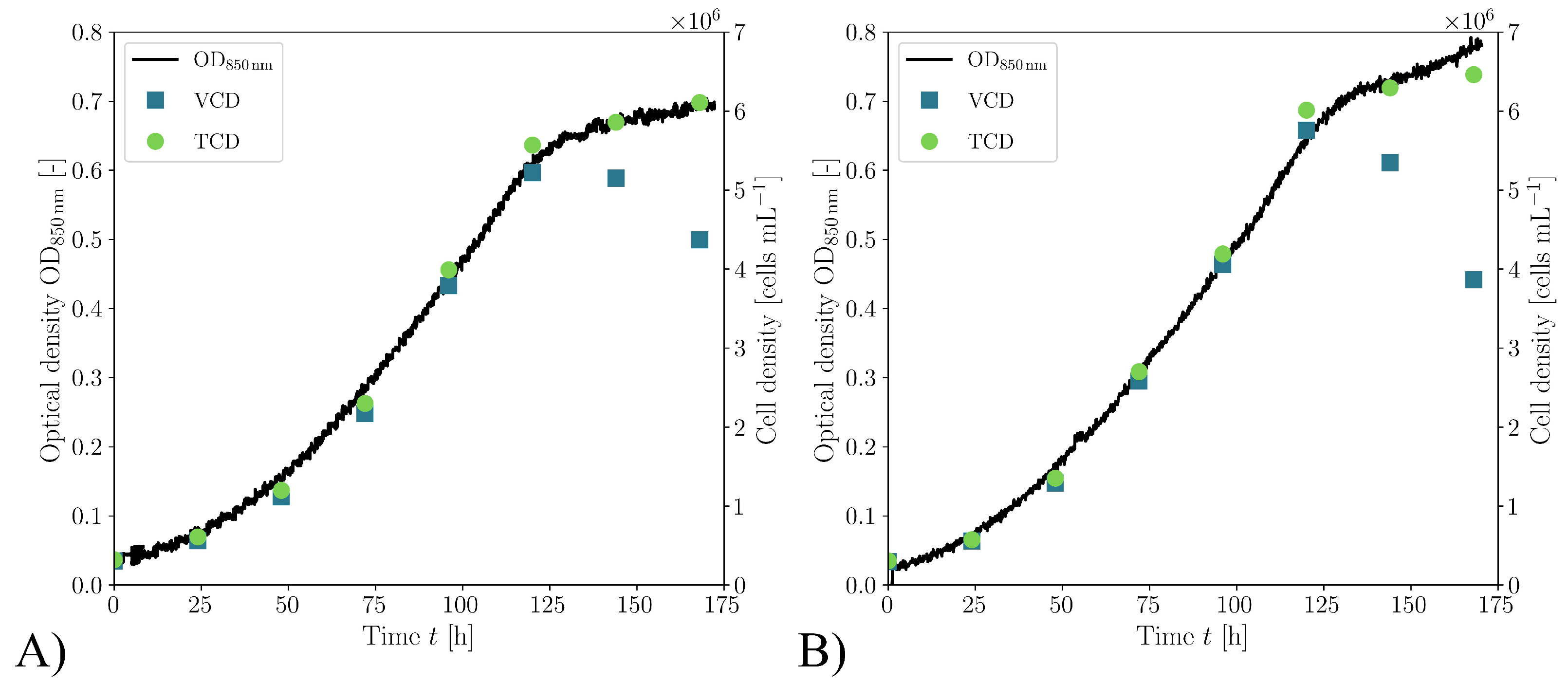
2.3. Cultivations for Biological Evaluation
3. Results and Discussion
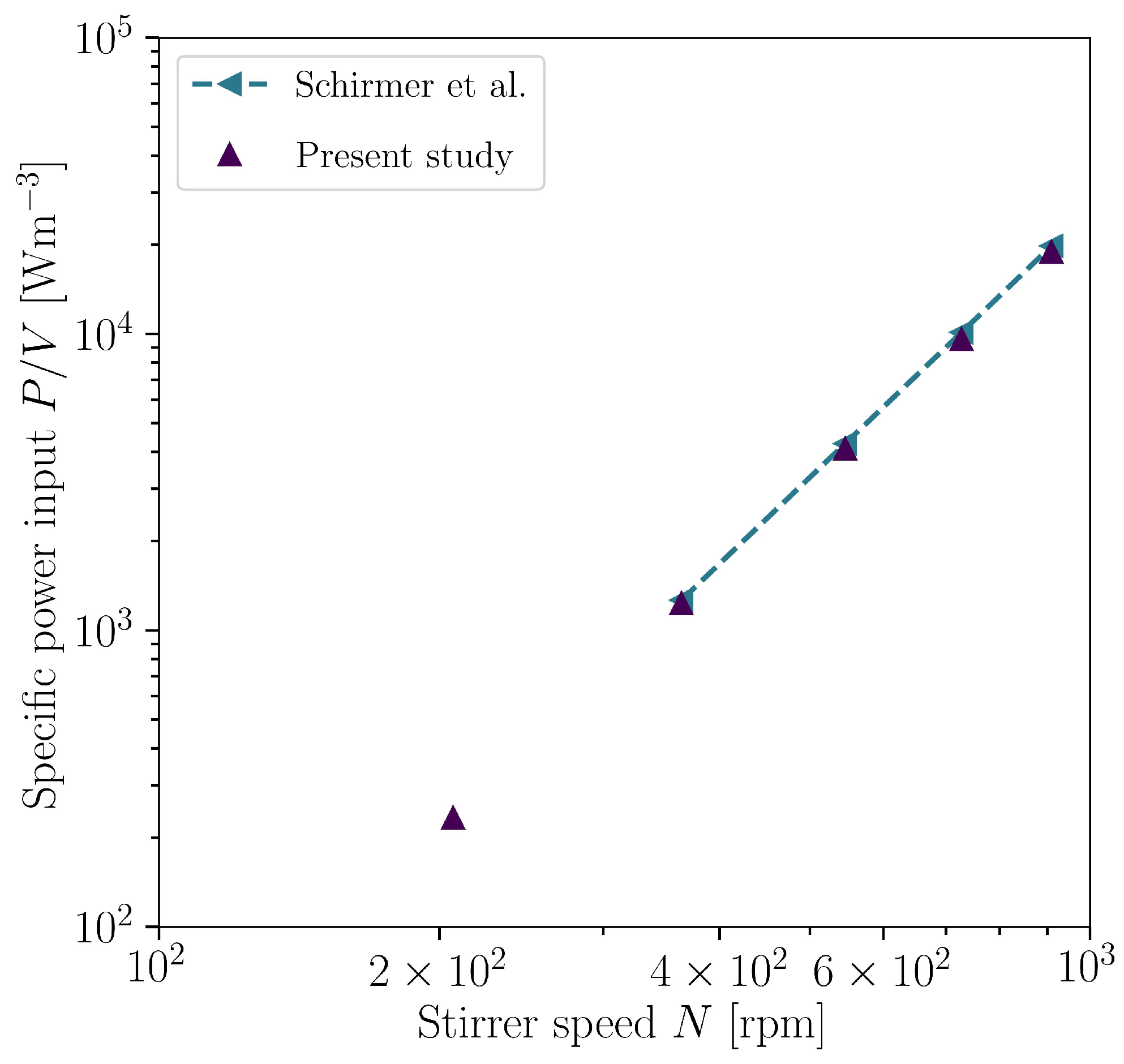
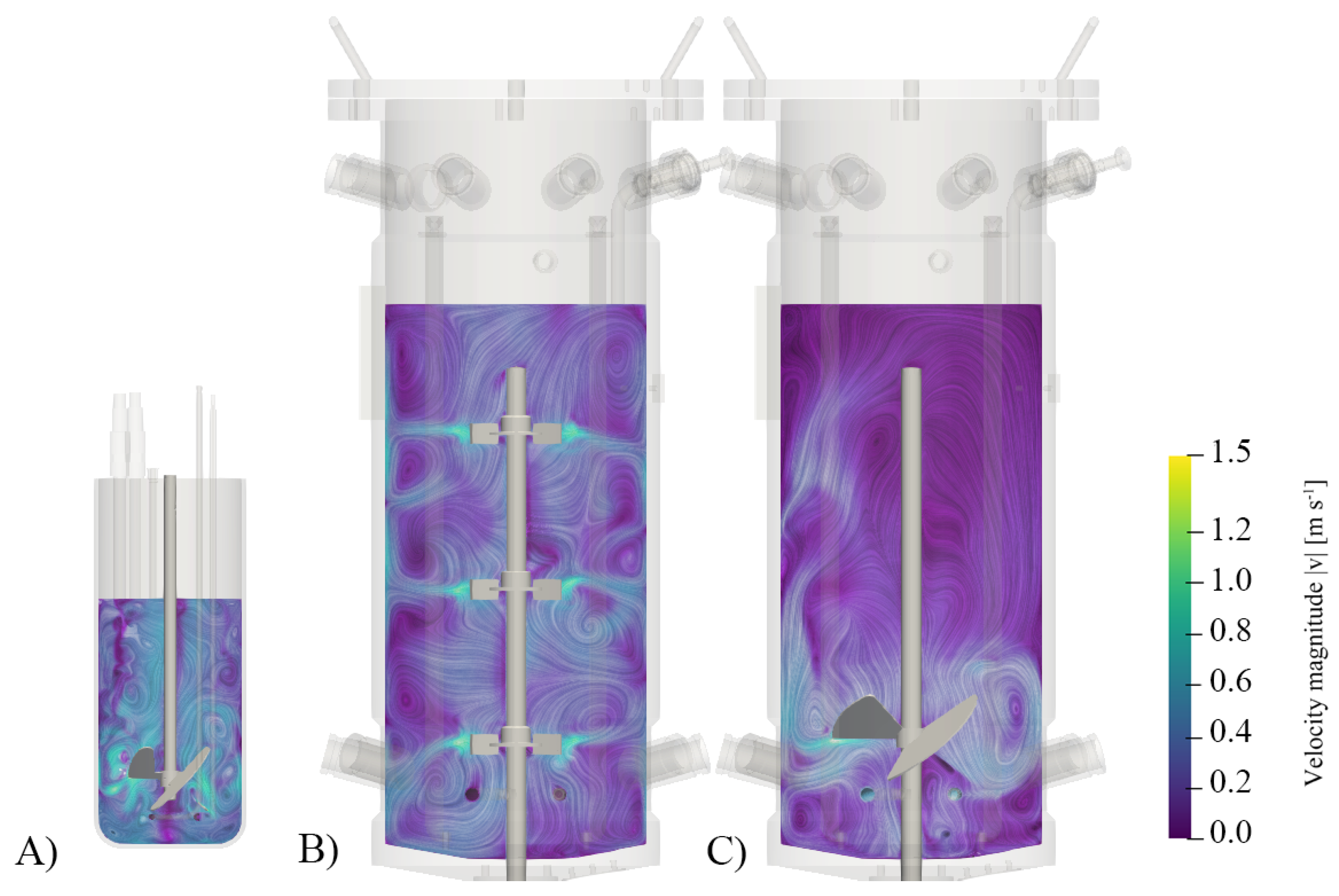
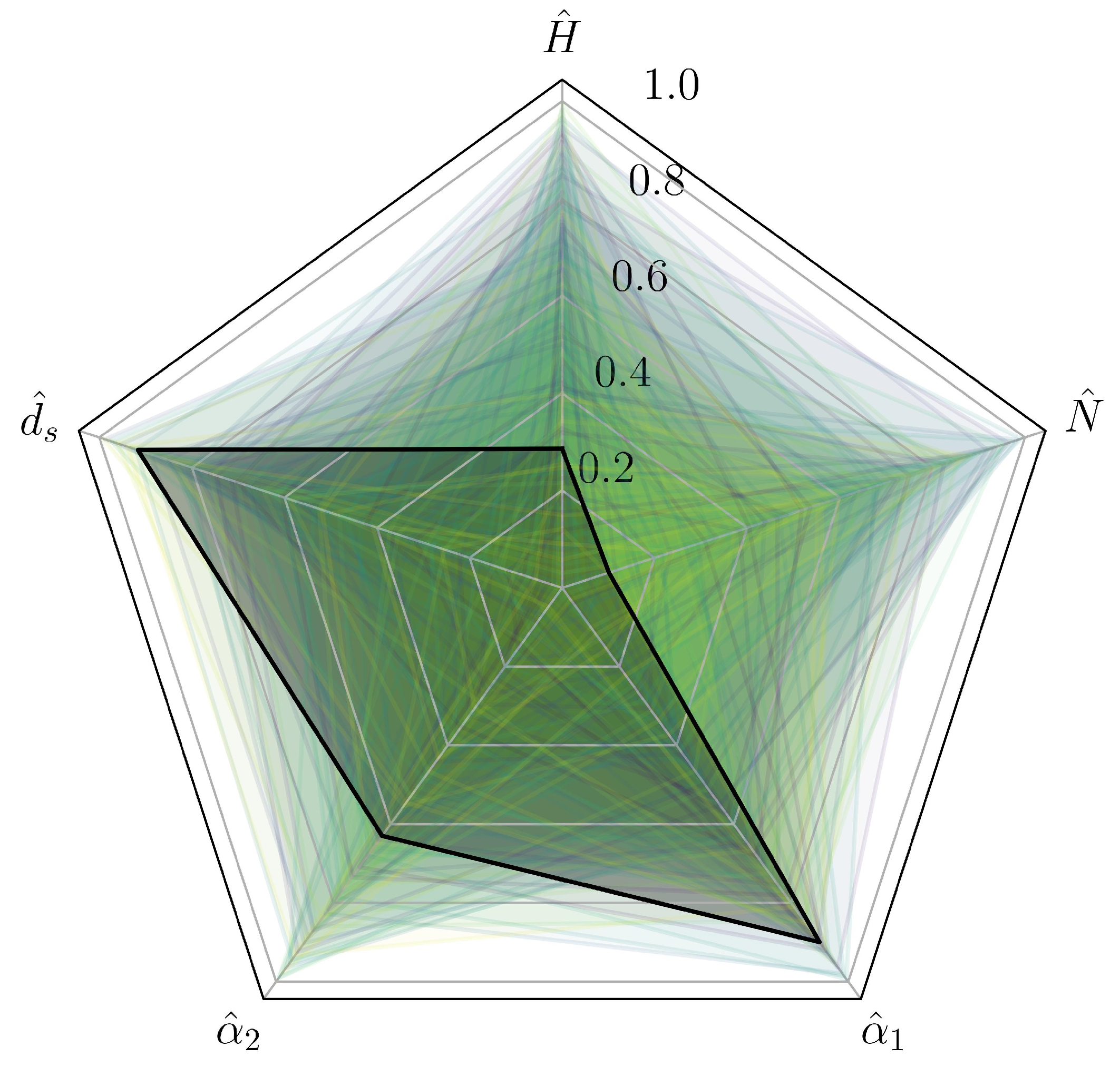
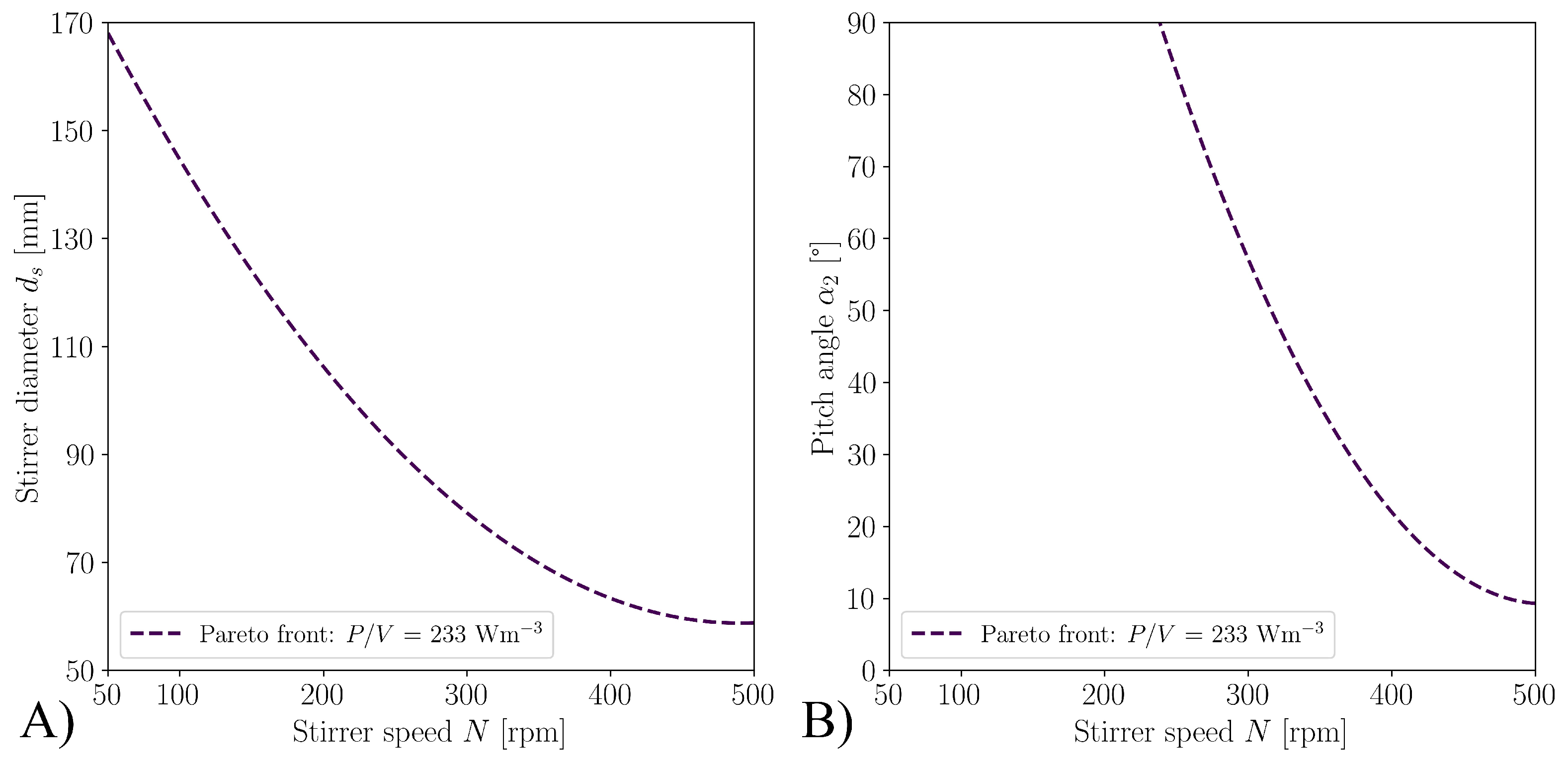
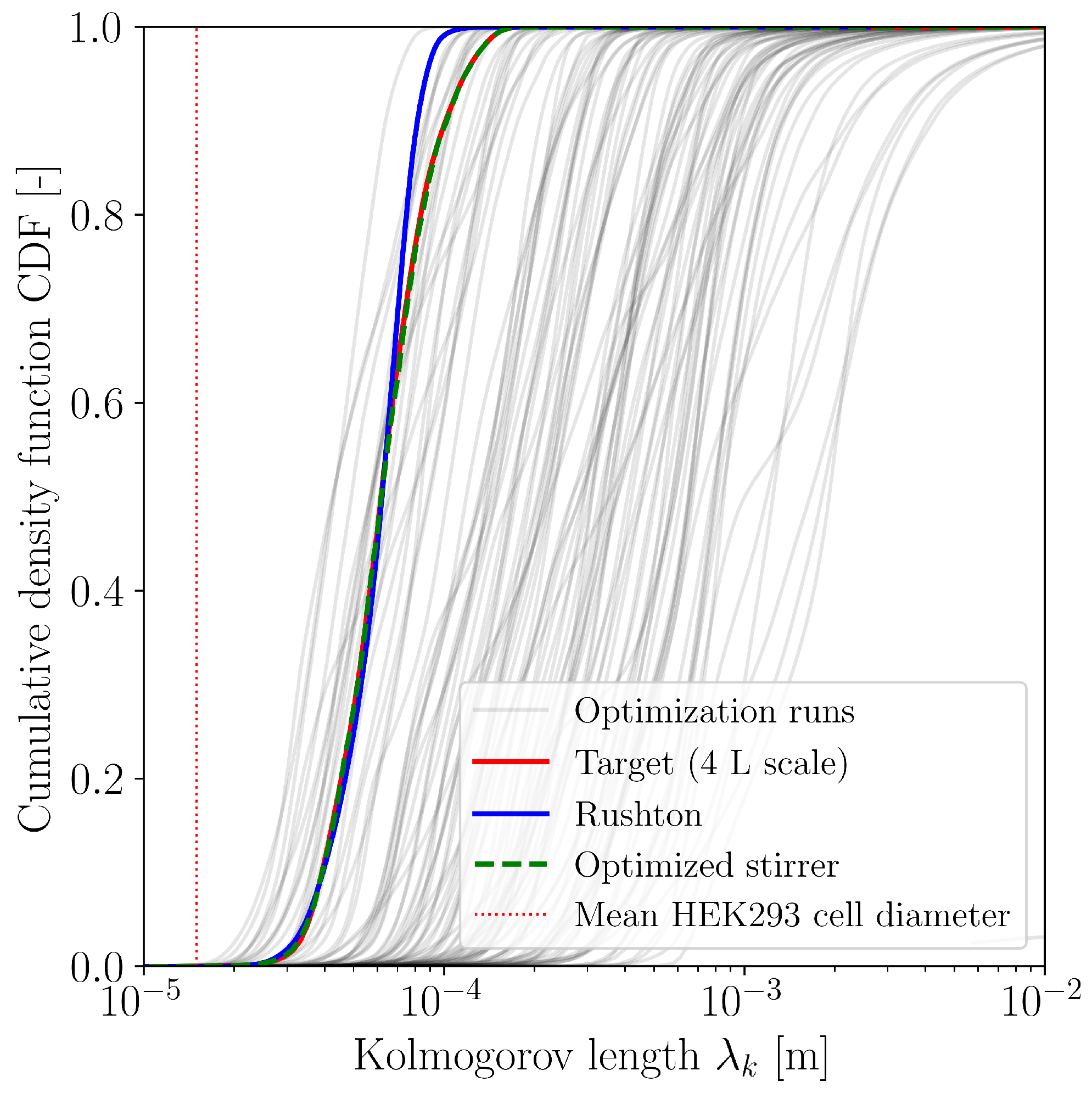
3.1. Optimization with CFD
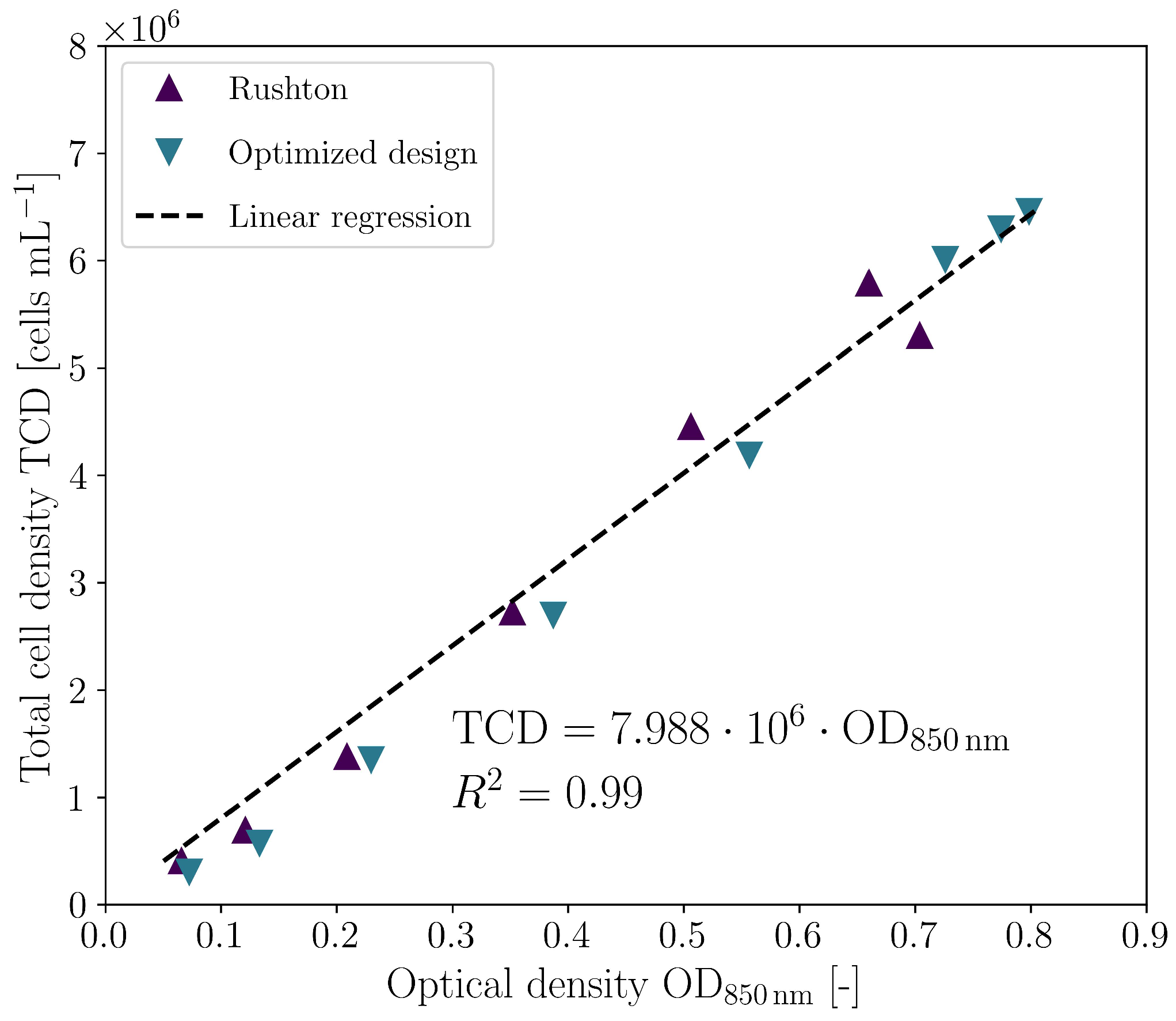
3.2. Biological Verification
4. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| API | Application Programming Interface |
| CDF | Cumulative Distribution Function |
| CFD | Computational Fluid Dynamics |
| CHO | Chinese Hamster Ovary |
| DACE | Design and Analysis of Computer Experiments |
| DAKOTA | Design Analysis Kit for Optimisation and Terascale Applications |
| FDA | Food and Drug Administration |
| HEK | Human Embryonic Kidney |
| HPC | High Performance Computing |
| KS | Kolmogorov–Smirnov |
| LHS | Latin Hypercube Sampling |
| MRF | Multiple Reference Frame |
| NIR | Near-Infrared |
| PA | Polyamide |
| PIV | Particle Image Velocimetry |
| PLIC | Piece-wise Linear Interface Calculation |
| RANS | Reynolds-Averaged Navier–Stokes |
| SBO | Surrogate-Based Optimization |
| SIMPLE | Semi-Implicit Method for Pressure-Linked Equations |
| SLS | Selective Laser Sinter |
| SST | Shear Stress Transport |
| USP | United States Pharmacopeia |
Nomenclature
| Latin symbols | ||
| Model constant | [-] | |
| Concentration of CO in the shaking incubator | [%] | |
| Glucose concentration | [g L−1] | |
| Lactate concentration | [g L−1] | |
| D | Test statistic of the Kolmogorov–Smirnov test | [-] |
| Shaking amplitude | [mm] | |
| Stirrer diameter | [mm] | |
| DO | Dissolved oxygen concentration | [%] |
| EDCF | Energy Dissipation Circulation Function | [W m−3 s−1] |
| Cumulative distribution | [-] | |
| Geometric function | [-] | |
| Safety factor | [-] | |
| GCI | Grid convergence index | [%] |
| H | Stirrer height | [m] |
| Null hypothesis | [-] | |
| k | Turbulent kinetic energy | [m2 s−2] |
| Volumetric oxygen mass transfer coefficient | [h−1] | |
| M | Moment/Torque | [N m] |
| N | Shaking/Stirring speed | [rpm] |
| Number of mesh cells | [-] | |
| OD | Optical density at 850 | [-] |
| P | Power | [W] |
| p | Free parameter of the geometric distribution | [-] |
| Observed order of accuracy | [-] | |
| Pressure | [Pa] | |
| Specific power input | [W m−3] | |
| r | Mesh refinement factor | [-] |
| Coefficient of determination | [-] | |
| Re | Reynolds number | [-] |
| Relative humidity | [%] | |
| Reynolds stress tensor | [N m−2] | |
| T | Temperature | [K] |
| t | Time | [s] |
| Circulation time | [s] | |
| TCD | Total cell density | [cells mL−1] |
| V | Volume | [m3] |
| Impeller swept volume | [m3] | |
| Velocity | [m s−1] | |
| Superficial gas velocity | [m s−1] | |
| Tip speed | [m s−1] | |
| VCD | Viable cell density | [cells mL−1] |
| VCD | Maximum viable cell density | [cells mL−1] |
| Greek symbols | ||
| Blade angle | [∘] | |
| Pitch angle | [∘] | |
| Energy dissipation rate | [m2 s−3] | |
| Volume-averaged energy dissipation rate | [m2 s−3] | |
| Maximum energy dissipation rate | [m2 s−3] | |
| Relative error | [%] | |
| Mixing time | [s] | |
| Kolmogorov length scale | [m] | |
| Volume-averaged Kolmogorov length scale | [m] | |
| Kinematic viscosity | [m2 s−1] | |
| Effective viscosity | [m2 s−1] | |
| Turbulent eddy viscosity | [m2 s−1] | |
| Density | [kg m−3] | |
| Hydrodynamic heterogeneity | [-] | |
| Specific dissipation rate | [s−1] | |
Appendix A

| Mesh | Number of Cells [-] | Min. Cell Volume [m3] | Max. Cell Volume [m3] | Max. Skewness [-] | [W m−3] |
|---|---|---|---|---|---|
| M1 | |||||
| M2 | |||||
| M3 | |||||
| M4 |
| Parameter | Minifors 2 | D-DCU Reference | D-DCU Optimized |
|---|---|---|---|
| V | 4 L | 30 L | 30 L |
| Stirrer type | 3-blade segment | 3x Rushton | 3-blade segment |
| 85 mm | 105 mm | 160 mm | |
| N | 275 rpm | 213 rpm | 67 rpm |
| 233 W m−3 | 233 W m−3 | 233 W m−3 | |
| Same as in the Minifors 2 | – | No | Yes |
| DO set point | 40% | 40% | 40% |
| pH set point |

References
- Walsh, G.; Walsh, E. Biopharmaceutical benchmarks 2022. Nat. Biotechnol. 2022, 40, 1722–1760. [Google Scholar] [CrossRef]
- Oosterhuis, N.M.; Junne, S. Design, Applications, and Development of Single-Use Bioreactors. In Bioreactors, 1st ed.; Mandenius, C.F., Ed.; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2016; pp. 261–294. [Google Scholar] [CrossRef]
- Shanley, A. Scaling Up Novel Therapies. Biopharm Int. 2018, 31, 14–16. [Google Scholar]
- Kaiser, S.C.; Löffelholz, C.; Werner, S.; Eibl, D. CFD for Characterizing Standard and Single-use Stirred Cell Culture Bioreactors. In Computational Fluid Dynamics Technologies and Applications; Minin, I.V., Minin, O.V., Eds.; IntechOpen: London, UK, 2011. [Google Scholar] [CrossRef]
- Böhm, L.; Hohl, L.; Bliatsiou, C.; Kraume, M. Multiphase Stirred Tank Bioreactors—New Geometrical Concepts and Scale-up Approaches. Chem. Ing. Tech. 2019, 91, 1724–1746. [Google Scholar] [CrossRef]
- Xing, Z.; Kenty, B.M.; Li, Z.J.; Lee, S.S. Scale-up analysis for a CHO cell culture process in large-scale bioreactors. Biotechnol. Bioeng. 2009, 103, 733–746. [Google Scholar] [CrossRef] [PubMed]
- Karimi Alavijeh, M.; Baker, I.; Lee, Y.Y.; Gras, S.L. Digitally enabled approaches for the scale up of mammalian cell bioreactors. Digit. Chem. Eng. 2022, 4, 100040. [Google Scholar] [CrossRef]
- Neubauer, P.; Junne, S. Scale-Up and Scale-Down Methodologies for Bioreactors. In Bioreactors; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2016; pp. 323–354. [Google Scholar] [CrossRef]
- Platas Barradas, O.; Jandt, U.; Minh Phan, L.D.; Villanueva, M.E.; Schaletzky, M.; Rath, A.; Freund, S.; Reichl, U.; Skerhutt, E.; Scholz, S.; et al. Evaluation of criteria for bioreactor comparison and operation standardization for mammalian cell culture. Eng. Life Sci. 2012, 12, 518–528. [Google Scholar] [CrossRef]
- Löffelholz, C.; Kaiser, S.C.; Kraume, M.; Eibl, R.; Eibl, D. Dynamic Single-Use Bioreactors Used in Modern Liter- and m3-Scale Biotechnological Processes: Engineering Characteristics and Scaling Up. In Disposable Bioreactors II; Eibl, D., Eibl, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 1–44. [Google Scholar] [CrossRef]
- Junker, B.H. Scale-up methodologies for Escherichia coli and yeast fermentation processes. J. Biosci. Bioeng. 2004, 97, 347–364. [Google Scholar] [CrossRef] [PubMed]
- McConville, F.X.; Kessler, S.B. Scale-Up of Mixing Processes: A Primer. In Chemical Engineering in the Pharmaceutical Industry; Wiley: Hoboken, NJ, USA, 2010; pp. 249–267. [Google Scholar] [CrossRef]
- Baert, J.; Delepierre, A.; Telek, S.; Fickers, P.; Toye, D.; Delamotte, A.; Lara, A.R.; Jaén, K.E.; Gosset, G.; Jensen, P.R.; et al. Microbial population heterogeneity versus bioreactor heterogeneity: Evaluation of Redox Sensor Green as an exogenous metabolic biosensor. Eng. Life Sci. 2016, 16, 643–651. [Google Scholar] [CrossRef]
- Haringa, C. An analysis of organism lifelines in an industrial bioreactor using Lattice-Boltzmann CFD. Eng. Life Sci. 2022, 23, e2100159. [Google Scholar] [CrossRef]
- Villiger, T.K.; Neunstoecklin, B.; Karst, D.J.; Lucas, E.; Stettler, M.; Broly, H.; Morbidelli, M.; Soos, M. Experimental and CFD physical characterization of animal cell bioreactors: From micro- to production scale. Biochem. Eng. J. 2018, 131, 84–94. [Google Scholar] [CrossRef]
- Li, C.; Teng, X.; Peng, H.; Yi, X.; Zhuang, Y.; Zhang, S.; Xia, J. Novel scale-up strategy based on three-dimensional shear space for animal cell culture. Chem. Eng. Sci. 2020, 212, 115329. [Google Scholar] [CrossRef]
- Jüsten, P.; Paul, G.C.; Nienow, A.W.; Thomas, C.R. Dependence of mycelial morphology on impeller type and agitation intensity. Biotechnol. Bioeng. 1996, 52, 672–684. [Google Scholar] [CrossRef]
- Esperança, M.N.; Buffo, M.M.; Mendes, C.E.; Rodriguez, G.Y.; Béttega, R.; Badino, A.C.; Cerri, M.O. Linking maximal shear rate and energy dissipation/circulation function in airlift bioreactors. Biochem. Eng. J. 2022, 178, 108308. [Google Scholar] [CrossRef]
- Bauer, I.; Dreher, T.; Eibl, D.; Glöckler, R.; Husemann, U.; John, G.T.; Kaiser, S.C.; Kampeis, P.; Kauling, J.; Kleebank, S.; et al. Recommendations for Process Engineering Characterisation of Single-Use Bioreactors and Mixing Systems by Using Experimental Methods, 2nd ed.; Gesellschaft für Chemische Technik und Biotechnologie e.V.: Frankfurt am Main, Germany, 2020. [Google Scholar]
- Seidel, S.; Schirmer, C.; Maschke, R.W.; Rossi, L.; Eibl, R.; Eibl, D. Computational Fluid Dynamics for Advanced Characterisation of Bioreactors Used in the Biopharmaceutical Industry: Part I: Literature Review. In Computational Fluid Dynamics-Recent Advances, New Perspectives and Applications; IntechOpen: London, UK, 2023. [Google Scholar] [CrossRef]
- Nienow, A.W.; Hewitt, C.J.; Heathman, T.R.; Glyn, V.A.; Fonte, G.N.; Hanga, M.P.; Coopman, K.; Rafiq, Q.A. Agitation conditions for the culture and detachment of hMSCs from microcarriers in multiple bioreactor platforms. Biochem. Eng. J. 2016, 108, 24–29. [Google Scholar] [CrossRef]
- Zhou, G.; Kresta, S.M. Impact of tank geometry on the maximum turbulence energy dissipation rate for impellers. AIChE J. 1996, 42, 2476–2490. [Google Scholar] [CrossRef]
- Seidel, S.; Maschke, R.W.; Kraume, M.; Eibl-Schindler, R.; Eibl, D. CFD Modelling of a wave-mixed bioreactor with complex geometry and two degrees of freedom motion. Front. Chem. Eng. 2022, 4, 1021416. [Google Scholar] [CrossRef]
- Freiberger, F.; Budde, J.; Ateş, E.; Schlüter, M.; Pörtner, R.; Möller, J. New Insights from Locally Resolved Hydrodynamics in Stirred Cell Culture Reactors. Processes 2022, 10, 107. [Google Scholar] [CrossRef]
- Johnson, C.; Natarajan, V.; Antoniou, C. Verification of energy dissipation rate scalability in pilot and production scale bioreactors using computational fluid dynamics. Biotechnol. Prog. 2014, 30, 760–764. [Google Scholar] [CrossRef]
- Seidel, S.; Maschke, R.W.; Mozaffari, F.; Eibl, R.; Eibl, D. Improvement of HEK293 cell growth by adapting hydrodynamic stress and predicting cell aggregate size distribution. Bioengineering 2023, 10, 478. [Google Scholar] [CrossRef]
- Nienow, A.W. Reactor Engineering in Large Scale Animal Cell Culture. Cytotechnology 2006, 50, 9–33. [Google Scholar] [CrossRef]
- Nienow, A.W.; Scott, W.H.; Hewitt, C.J.; Thomas, C.R.; Lewis, G.; Amanullah, A.; Kiss, R.; Meier, S.J. Scale-down studies for assessing the impact of different stress parameters on growth and product quality during animal cell culture. Chem. Eng. Res. Des. 2013, 91, 2265–2274. [Google Scholar] [CrossRef]
- Wang, K.; Han, Z.H.; Zhang, K.S.; Song, W.P. An efficient geometric constraint handling method for surrogate-based aerodynamic shape optimization. Eng. Appl. Comput. Fluid Mech. 2023, 17, e2153173. [Google Scholar] [CrossRef]
- Yu, Y.; Lyu, Z.; Xu, Z.; Martins, J.R. On the influence of optimization algorithm and initial design on wing aerodynamic shape optimization. Aerosp. Sci. Technol. 2018, 75, 183–199. [Google Scholar] [CrossRef]
- Hoang Quan, N.N.; Lam, P.V.; Long, L.V. Wind Turbine Blade Design Optimization using OpenFOAM and DAKOTA software. Transp. Res. Procedia 2021, 56, 71–78. [Google Scholar] [CrossRef]
- Cruz, L.E.B.; Carmo, B.S. Wind farm layout optimization based on CFD simulations. J. Braz. Soc. Mech. Sci. Eng. 2020, 42, 433. [Google Scholar] [CrossRef]
- Guerrero, J.; Mantelli, L.; Naqvi, S.B. Cloud-Based CAD Parametrization for Design Space Exploration and Design Optimization in Numerical Simulations. Fluids 2020, 5, 36. [Google Scholar] [CrossRef]
- De Donno, R.; Ghidoni, A.; Noventa, G.; Rebay, S. Shape optimization of the ERCOFTAC centrifugal pump impeller using open-source software. Optim. Eng. 2019, 20, 929–953. [Google Scholar] [CrossRef]
- Thakkar, S.; Vala, H.; Patel, V.K.; Patel, R. Performance improvement of the sanitary centrifugal pump through an integrated approach based on response surface methodology, multi-objective optimization and CFD. J. Braz. Soc. Mech. Sci. Eng. 2021, 43, 24. [Google Scholar] [CrossRef]
- Benchikh Le Hocine, A.E.; Poncet, S.; Fellouah, H. CFD modeling and optimization by metamodels of a squirrel cage fan using OpenFoam and Dakota: Ventilation applications. Build. Environ. 2021, 205, 108145. [Google Scholar] [CrossRef]
- Hoseini, S.; Najafi, G.; Ghobadian, B.; Akbarzadeh, A. Impeller shape-optimization of stirred-tank reactor: CFD and fluid structure interaction analyses. Chem. Eng. J. 2021, 413, 127497. [Google Scholar] [CrossRef]
- Wu, M.; Jurtz, N.; Walle, A.; Kraume, M. Evaluation and application of efficient CFD-based methods for the multi-objective optimization of stirred tanks. Chem. Eng. Sci. 2022, 263, 118109. [Google Scholar] [CrossRef]
- Jossen, V.; Kaiser, S.C.; Schirmaier, C.; Herrmann, J.; Tappe, A.; Eibl, D.; Siehoff, A.; van den Bos, C.; Eibl, R. Modification and qualification of a stirred single-use bioreactor for the improved expansion of human mesenchymal stem cells at benchtop scale. Pharm. Bioprocess. 2014, 2, 311–322. [Google Scholar] [CrossRef]
- Siddappaji, K.; Turner, M.G. An Advanced Multifidelity Multidisciplinary Design Analysis Optimization Toolkit for General Turbomachinery. Processes 2022, 10, 1845. [Google Scholar] [CrossRef]
- Chen, F.; Zhu, G.; Wang, X.; Yao, B.; Guo, W.; Xu, T.; Peng, M.; Cheng, D. Optimization of the impeller of sand-ejecting fire extinguisher based on CFD-DEM simulations and Kriging model. Adv. Powder Technol. 2023, 34, 103898. [Google Scholar] [CrossRef]
- Afzal, A.; Kim, K.Y.; Seo, J.w. Effects of Latin hypercube sampling on surrogate modeling and optimization. Int. J. Fluid Mach. Syst. 2017, 10, 240–253. [Google Scholar] [CrossRef]
- Daymo, E.; Tonkovich, A.L.; Hettel, M.; Guerrero, J. Accelerating reactor development with accessible simulation and automated optimization tools. Chem. Eng. Process. Process Intensif. 2019, 142, 107582. [Google Scholar] [CrossRef]
- Kamath, C. Intelligent sampling for surrogate modeling, hyperparameter optimization, and data analysis. Mach. Learn. Appl. 2022, 9, 100373. [Google Scholar] [CrossRef]
- Lin, Y.C.; Boone, M.; Meuris, L.; Lemmens, I.; Van Roy, N.; Soete, A.; Reumers, J.; Moisse, M.; Plaisance, S.; Drmanac, R.; et al. Genome dynamics of the human embryonic kidney 293 lineage in response to cell biology manipulations. Nat. Commun. 2014, 5, 4767. [Google Scholar] [CrossRef]
- Hacker, D.L.; Durrer, L.; Quinche, S. CHO and HEK293 Cultivation and Transfection in Single-Use Orbitally Shaken Bioreactors. In Recombinant Protein Expression in Mammalian Cells. Methods in Molecular Biology, 1st ed.; Hacker, D.L., Ed.; Humana Press: New York, NY, USA, 2018; pp. 123–131. [Google Scholar] [CrossRef]
- Shaw, G.; Morse, S.; Ararat, M.; Graham, F.L. Preferential transformation of human neuronal cells by human adenoviruses and the origin of HEK 293 cells. FASEB J. Off. Publ. Fed. Am. Soc. Exp. Biol. 2002, 16, 869–871. [Google Scholar] [CrossRef]
- Ghani, K.; Garnier, A.; Coelho, H.; Transfiguracion, J.; Trudel, P.; Kamen, A. Retroviral vector production using suspension-adapted 293GPG cells in a 3 L acoustic filter-based perfusion bioreactor. Biotechnol. Bioeng. 2006, 95, 653–660. [Google Scholar] [CrossRef]
- Ansorge, S.; Lanthier, S.; Transfiguracion, J.; Henry, O.; Kamen, A. Monitoring lentiviral vector production kinetics using online permittivity measurements. Biochem. Eng. J. 2011, 54, 16–25. [Google Scholar] [CrossRef]
- Le Ru, A.; Jacob, D.; Transfiguracion, J.; Ansorge, S.; Henry, O.; Kamen, A.A. Scalable production of influenza virus in HEK-293 cells for efficient vaccine manufacturing. Vaccine 2010, 28, 3661–3671. [Google Scholar] [CrossRef]
- Tan, E.; Chin, C.S.H.; Lim, Z.F.S.; Ng, S.K. HEK293 Cell Line as a Platform to Produce Recombinant Proteins and Viral Vectors. Front. Bioeng. Biotechnol. 2021, 9, 796991. [Google Scholar] [CrossRef] [PubMed]
- Malm, M.; Saghaleyni, R.; Lundqvist, M.; Giudici, M.; Chotteau, V.; Field, R.; Varley, P.G.; Hatton, D.; Grassi, L.; Svensson, T.; et al. Evolution from adherent to suspension: Systems biology of HEK293 cell line development. Sci. Rep. 2020, 10, 18996. [Google Scholar] [CrossRef]
- Henry, O.; Durocher, Y. Enhanced glycoprotein production in HEK-293 cells expressing pyruvate carboxylase. Metab. Eng. 2011, 13, 499–507. [Google Scholar] [CrossRef] [PubMed]
- Jang, M.; Pete, E.S.; Bruheim, P. The impact of serum-free culture on HEK293 cells: From the establishment of suspension and adherent serum-free adaptation cultures to the investigation of growth and metabolic profiles. Front. Bioeng. Biotechnol. 2022, 10, 964397. [Google Scholar] [CrossRef]
- Liste-Calleja, L.; Lecina, M.; Cairó, J.J. HEK293 cell culture media study towards bioprocess optimization: Animal derived component free and animal derived component containing platforms. J. Biosci. Bioeng. 2014, 117, 471–477. [Google Scholar] [CrossRef]
- Fuge, G. New Approaches for Characterizing and Monitoring Mammalian Cell Cycle and Specific Growth Rate in Production Cell Lines. Ph.D. Thesis, Technische Universität Hamburg, Hamburg, Germany, 2018. [Google Scholar] [CrossRef]
- Maschke, R.W.; Pretzner, B.; John, G.T.; Herwig, C.; Eibl, D. Improved Time Resolved KPI and Strain Characterization of Multiple Hosts in Shake Flasks Using Advanced Online Analytics and Data Science. Bioengineering 2022, 9, 339. [Google Scholar] [CrossRef]
- Liu, X.M.; Liu, H.; Wu, B.C.; Li, S.C.; Ye, L.L.; Wang, Q.W.; Huang, P.T.; Chen, Z.L. Suspended aggregates as an immobilization mode for high-density perfusion culture of HEK 293 cells in a stirred tank bioreactor. Appl. Microbiol. Biotechnol. 2006, 72, 1144–1151. [Google Scholar] [CrossRef]
- Liu, H.; Liu, X.M.; Li, S.C.; Wu, B.C.; Ye, L.L.; Wang, Q.W.; Chen, Z.L. A high-yield and scaleable adenovirus vector production process based on high density perfusion culture of HEK 293 cells as suspended aggregates. J. Biosci. Bioeng. 2009, 107, 524–529. [Google Scholar] [CrossRef]
- Faust, C.; Beil, C.; Dittrich, W.; Rao, E.; Langer, T. Impact of lipopolysaccharides on cultivation and recombinant protein expression in human embryonal kidney (HEK-293) cells. Eng. Life Sci. 2021, 21, 778–785. [Google Scholar] [CrossRef]
- Decaria, P. Growth and Scale-Up of HEK293F Derivatives in HyPerforma DynaDrive Single-Use Bioreactors. Available online: https://assets.thermofisher.com/TFS-Assets/BPD/Application-Notes/hek293f-derivatives-dynadrive-sub-application-note.pdf (accessed on 10 August 2023).
- Liu, H.; Liu, X.; Wu, B.; YE, L.; Ni, X.; Wang, Q.; Chen, Z. Effects of Hydrodynamics on Aggregates Formation, Growth and Metabolism of HEK 293 Cells in Suspension Culture. Chin. J. Biotechnol. 2006, 22, 101–106. [Google Scholar] [CrossRef]
- Patel, S.; Fong, E.; George, H. Considerations for Bioreactor Process Development and Scale-Up for Transient Transfection-Based Lentivirus Production in Suspension. Available online: https://www.emdmillipore.com/Web-US-Site/en_CA/-/USD/ShowDocument-Pronet?id=202008.048 (accessed on 10 August 2023).
- Arena, T.A.; Chou, B.; Harms, P.D.; Wong, A.W. An anti-apoptotic HEK293 cell line provides a robust and high titer platform for transient protein expression in bioreactors. mAbs 2019, 11, 977–986. [Google Scholar] [CrossRef] [PubMed]
- Schirmer, C.; Blaschczok, K.; Husemann, U.; Leupold, M.; Zahnow, C.; Rupprecht, J.; Glöckler, R.; Greller, G.; Pörtner, R.; Eibl, R.; et al. Standardized Qualification of Stirred Bioreactors for Microbial Biopharmaceutical Production Processes. Chem. Ing. Tech. 2017, 89, 1766–1772. [Google Scholar] [CrossRef]
- Menter, F. Zonal Two Equation k-ω Turbulence Models For Aerodynamic Flows. In Proceedings of the 23rd Fluid Dynamics, Plasmadynamics, and Lasers Conference, Reston, VA, USA, 6–9 July 1993. [Google Scholar] [CrossRef]
- Götz, S.; Sperling, R.; Liepe, F.; Jembere, S. Numerical determination of the three-dimensional velocity distribution in a baffled pitched blade impeller stirred vessel. Chem. Eng. Technol. 1997, 20, 596–605. [Google Scholar] [CrossRef]
- Jaworski, Z.; Wyszynski, M.L.; Moore, I.P.T.; Nienow, A.W. Sliding mesh computational fluid dynamics—A predictive tool in stirred tank design. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 1997, 211, 149–156. [Google Scholar] [CrossRef]
- Stephan, P.; Kabelac, S.; Kind, M.; Mewes, D.; Schaber, K.; Wetzel, T. (Eds.) VDI-Wärmeatlas; Springer Reference Technik; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar] [CrossRef]
- Seidel, S.; Eibl, D. Influence of Interfacial Force Models and Population Balance Models on the kLa Value in Stirred Bioreactors. Processes 2021, 9, 1185. [Google Scholar] [CrossRef]
- Ahrens, J.; Geveci, B.; Law, C. ParaView: An End-User Tool for Large Data Visualization, Visualization Handbook; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Ramírez-Durán, V.J.; Berges, I.; Illarramendi, A. Towards the implementation of Industry 4.0: A methodology-based approach oriented to the customer life cycle. Comput. Ind. 2021, 126, 103403. [Google Scholar] [CrossRef]
- Berger, V.W.; Zhou, Y. Kolmogorov–Smirnov Test: Overview. In Wiley StatsRef: Statistics Reference Online; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar] [CrossRef]
- Sullivan, C.; Kaszynski, A. PyVista: 3D plotting and mesh analysis through a streamlined interface for the Visualization Toolkit (VTK). J. Open Source Softw. 2019, 4, 1450. [Google Scholar] [CrossRef]
- Cates, S.; Ciccarone, V.C.; Gruber, D.F.; Hawley-Nelson, P. Novel Attached Cell Lines. WO2004085620A2, 7 October 2004. [Google Scholar]
- EOS GmbH. PA 2200 Regulatory Information; Technical Report; EOS GmbH: München, Germany, 2013. [Google Scholar]
- Baker, N.; Kelly, G.; O’Sullivan, P.D. A grid convergence index study of mesh style effect on the accuracy of the numerical results for an indoor airflow profile. Int. J. Vent. 2020, 19, 300–314. [Google Scholar] [CrossRef]
- Ramírez, L.A.; Pérez, E.L.; García Díaz, C.; Camacho Luengas, D.A.; Ratkovich, N.; Reyes, L.H. CFD and Experimental Characterization of a Bioreactor: Analysis via Power Curve, Flow Patterns and kLa. Processes 2020, 8, 878. [Google Scholar] [CrossRef]
- Pappalardo, F.; Moscatello, A.; Ledda, G.; Uggenti, A.C.; Gerboni, R.; Carpignano, A.; Di Maio, F.; Mereu, R.; Zio, E. Quantification of Uncertainty in CFD Simulation of Accidental Gas Release for O & G Quantitative Risk Assessment. Energies 2021, 14, 8117. [Google Scholar] [CrossRef]
- Roache, P.J. Perspective: A Method for Uniform Reporting of Grid Refinement Studies. J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Weiser, S.; Tiso, T.; Willing, K.; Bardl, B.; Eichhorn, L.; Blank, L.M.; Regestein, L. Foam-free production of the rhamnolipid precursor 3-(3-hydroxyalkanoyloxy) alkanoic acid (HAA) by Pseudomonas putida. Discov. Chem. Eng. 2022, 2, 8. [Google Scholar] [CrossRef]
- Noppiboon, S.; Lapanusorn, N.; Ekkpongpaisit, P.; Slack, S.; Frank, S.; Hocharoen, L. A Simple and Cost-Efficient Platform for a Novel Porcine Circovirus Type 2d (PCV2d) Vaccine Manufacturing. Vaccines 2023, 11, 169. [Google Scholar] [CrossRef] [PubMed]
- Zlokarnik, M. Stirring; Wiley: Hoboken, NJ, USA, 2001. [Google Scholar] [CrossRef]
- Navid, A.; Khalilarya, S.; Abbasi, M. Diesel engine optimization with multi-objective performance characteristics by non-evolutionary Nelder-Mead algorithm: Sobol sequence and Latin hypercube sampling methods comparison in DoE process. Fuel 2018, 228, 349–367. [Google Scholar] [CrossRef]
- Dhamotharan, V.; Jadhav, P.D.; Ramu, P.; Prakash, A.K. Optimal design of savonius wind turbines using ensemble of surrogates and CFD analysis. Struct. Multidiscip. Optim. 2018, 58, 2711–2726. [Google Scholar] [CrossRef]
- Akram, M.T.; Kim, M.H. CFD Analysis and Shape Optimization of Airfoils Using Class Shape Transformation and Genetic Algorithm—Part I. Appl. Sci. 2021, 11, 3791. [Google Scholar] [CrossRef]
- Espinosa Sarmiento, A.L.; Ramirez Camacho, R.G.; de Oliveira, W.; Gutiérrez Velásquez, E.I.; Murthi, M.; Diaz Gautier, N.J. Design and off-design performance improvement of a radial-inflow turbine for ORC applications using metamodels and genetic algorithm optimization. Appl. Therm. Eng. 2021, 183, 116197. [Google Scholar] [CrossRef]
- Morita, Y.; Rezaeiravesh, S.; Tabatabaei, N.; Vinuesa, R.; Fukagata, K.; Schlatter, P. Applying Bayesian optimization with Gaussian process regression to computational fluid dynamics problems. J. Comput. Phys. 2022, 449, 110788. [Google Scholar] [CrossRef]
- Diessner, M.; O’Connor, J.; Wynn, A.; Laizet, S.; Guan, Y.; Wilson, K.; Whalley, R.D. Investigating Bayesian optimization for expensive-to-evaluate black box functions: Application in fluid dynamics. Front. Appl. Math. Stat. 2022, 8, 1076296. [Google Scholar] [CrossRef]
- Peng, K.; Koubaa, M.; Bals, O.; Vorobiev, E. Effect of Pulsed Electric Fields on the Growth and Acidification Kinetics of Lactobacillus delbrueckii Subsp. bulgaricus. Foods 2020, 9, 1146. [Google Scholar] [CrossRef] [PubMed]
- Jensch, C.; Knierim, L.; Tegtmeier, M.; Strube, J. Development of a General PAT Strategy for Online Monitoring of Complex Mixtures—On the Example of Natural Product Extracts from Bearberry Leaf (Arctostaphylos uva-ursi). Processes 2021, 9, 2129. [Google Scholar] [CrossRef]
- Zhuang, S.; Renault, N.; Archer, I. A brief review on recent development of multidisciplinary engineering in fermentation of Saccharomyces cerevisiae. J. Biotechnol. 2021, 339, 32–41. [Google Scholar] [CrossRef]
- Sandadi, S.; Pedersen, H.; Bowers, J.S.; Rendeiro, D. A comprehensive comparison of mixing, mass transfer, Chinese hamster ovary cell growth, and antibody production using Rushton turbine and marine impellers. Bioprocess Biosyst. Eng. 2011, 34, 819–832. [Google Scholar] [CrossRef] [PubMed]


| Case | Mesh | r | GCI [%] | |||
|---|---|---|---|---|---|---|
| Case 1 | M1-M2 | 1.08 | 2.46 | 2.24 | 1.13 | |
| M2-M3 | 1.13 | 1.63 | ||||
| Case 2 | M2-M3 | 1.13 | 2.04 | 2.01 | 1.04 | |
| M3-M4 | 1.17 | 1.52 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Seidel, S.; Mozaffari, F.; Maschke, R.W.; Kraume, M.; Eibl-Schindler, R.; Eibl, D. Automated Shape and Process Parameter Optimization for Scaling Up Geometrically Non-Similar Bioreactors. Processes 2023, 11, 2703. https://doi.org/10.3390/pr11092703
Seidel S, Mozaffari F, Maschke RW, Kraume M, Eibl-Schindler R, Eibl D. Automated Shape and Process Parameter Optimization for Scaling Up Geometrically Non-Similar Bioreactors. Processes. 2023; 11(9):2703. https://doi.org/10.3390/pr11092703
Chicago/Turabian StyleSeidel, Stefan, Fruhar Mozaffari, Rüdiger W. Maschke, Matthias Kraume, Regine Eibl-Schindler, and Dieter Eibl. 2023. "Automated Shape and Process Parameter Optimization for Scaling Up Geometrically Non-Similar Bioreactors" Processes 11, no. 9: 2703. https://doi.org/10.3390/pr11092703
APA StyleSeidel, S., Mozaffari, F., Maschke, R. W., Kraume, M., Eibl-Schindler, R., & Eibl, D. (2023). Automated Shape and Process Parameter Optimization for Scaling Up Geometrically Non-Similar Bioreactors. Processes, 11(9), 2703. https://doi.org/10.3390/pr11092703








