Simulation Analysis of the Influence of Amplitude on Deformation and Fracture Characteristics of Hard Rock under Ultrasonic Vibration Load
Abstract
:1. Introduction
2. Numerical Simulation of Rock Breaking by Ultrasonic Vibration
2.1. Establishment of the Particle Flow Model
2.2. Mesoscopic Energy Theory of Rock
3. Results
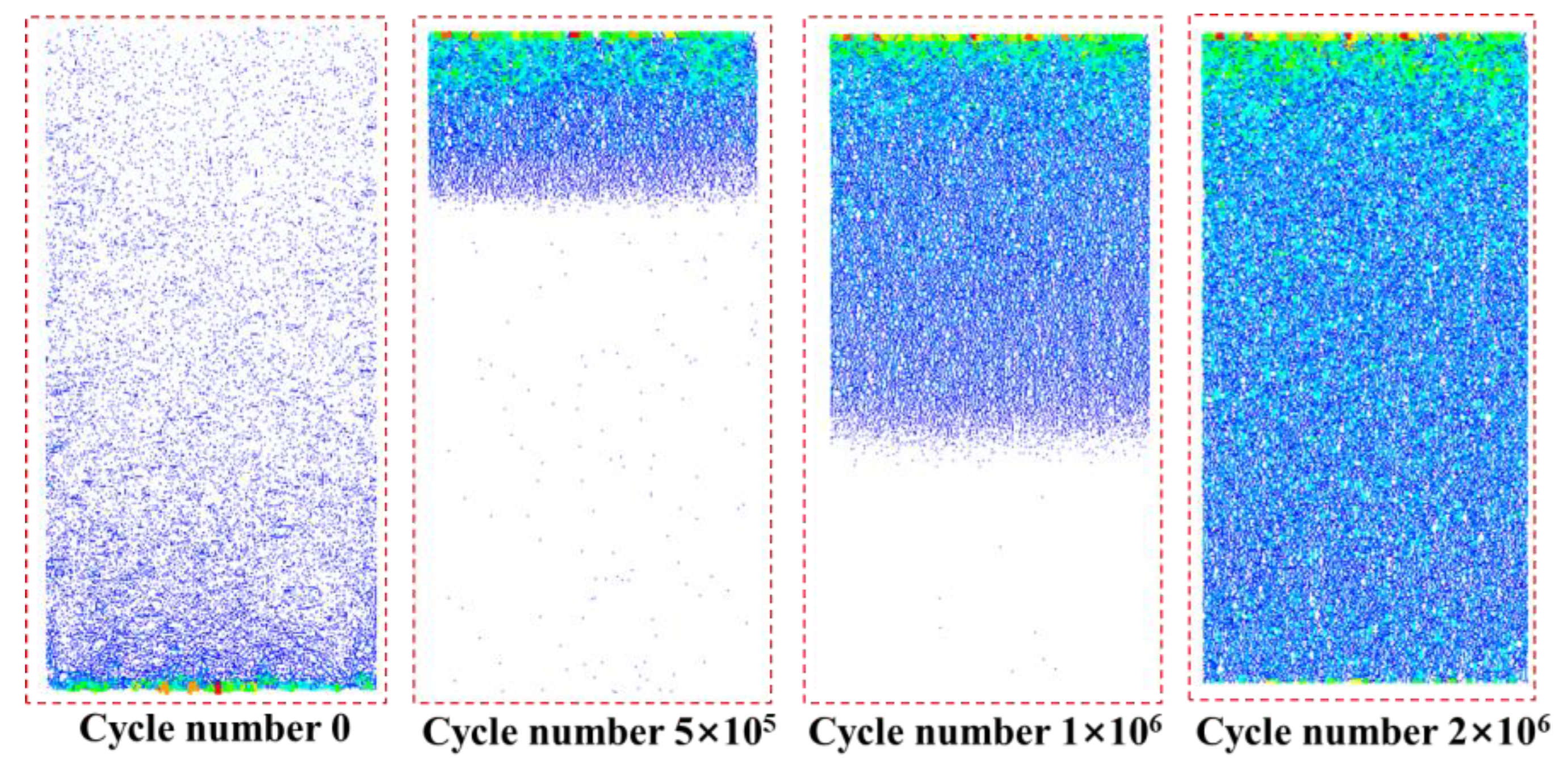
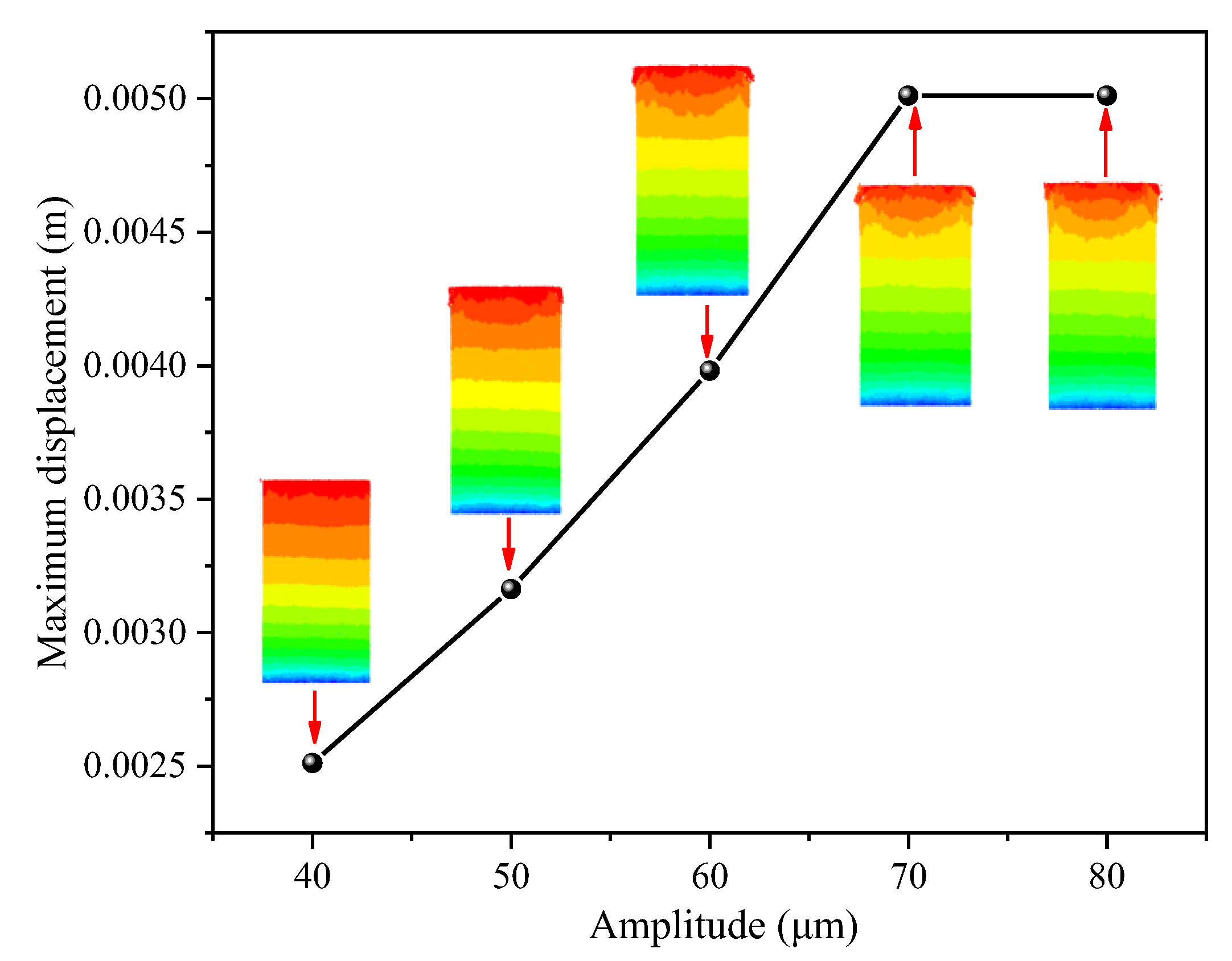
3.1. Deformation and Displacement Characteristics of Hard Rock under Ultrasonic Vibration Load
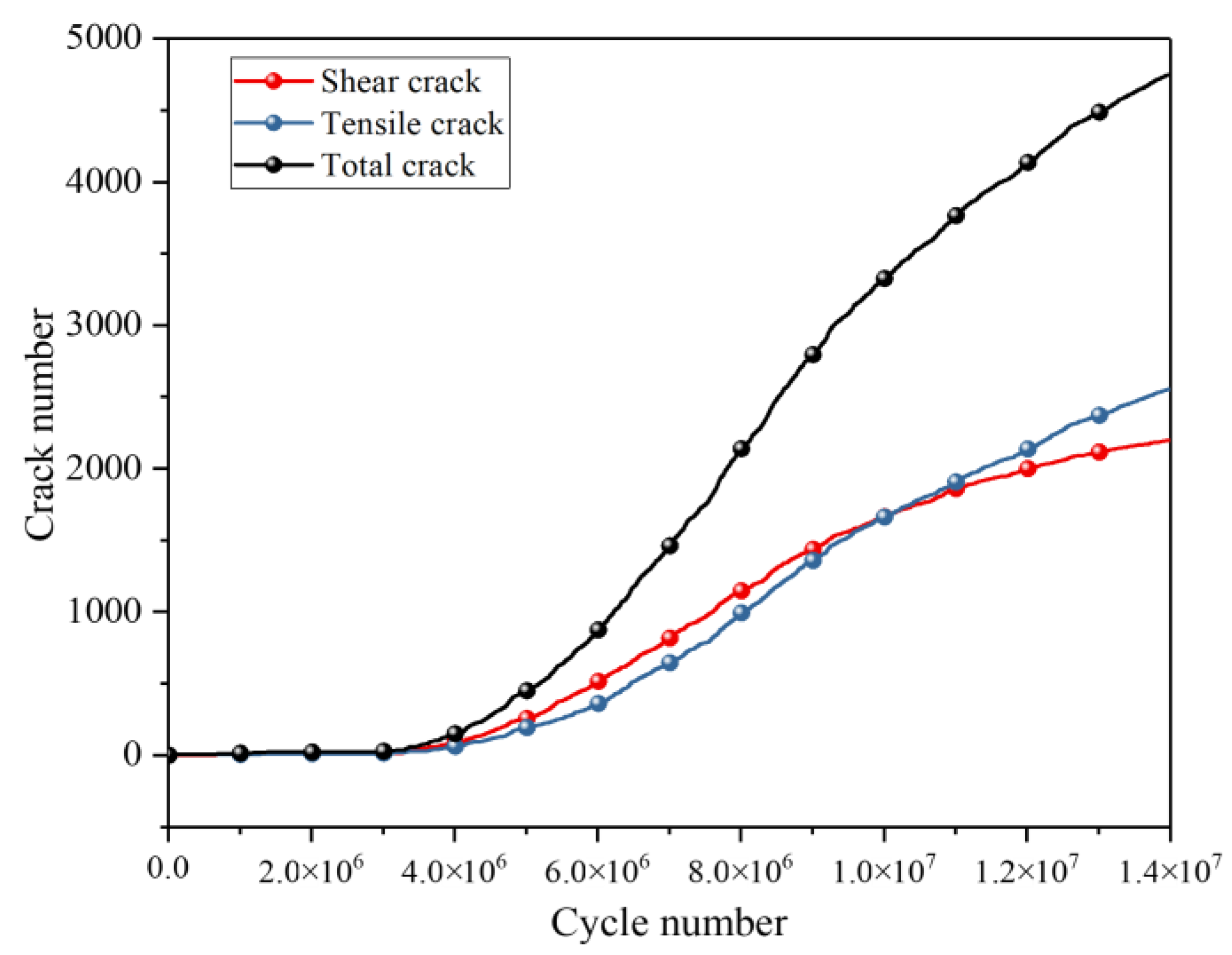
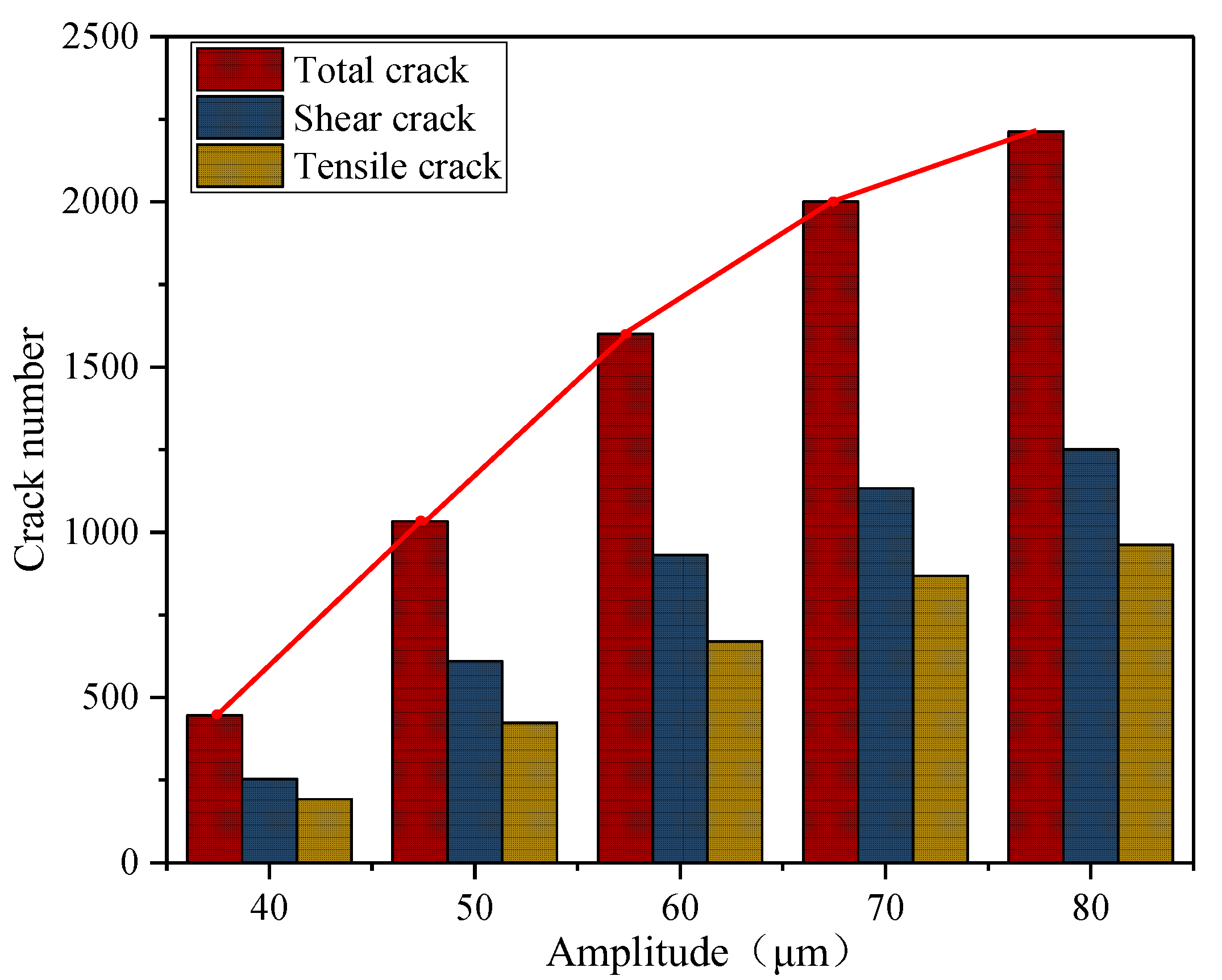
3.2. Characteristics of Rock Fracture under Ultrasonic Vibration Load
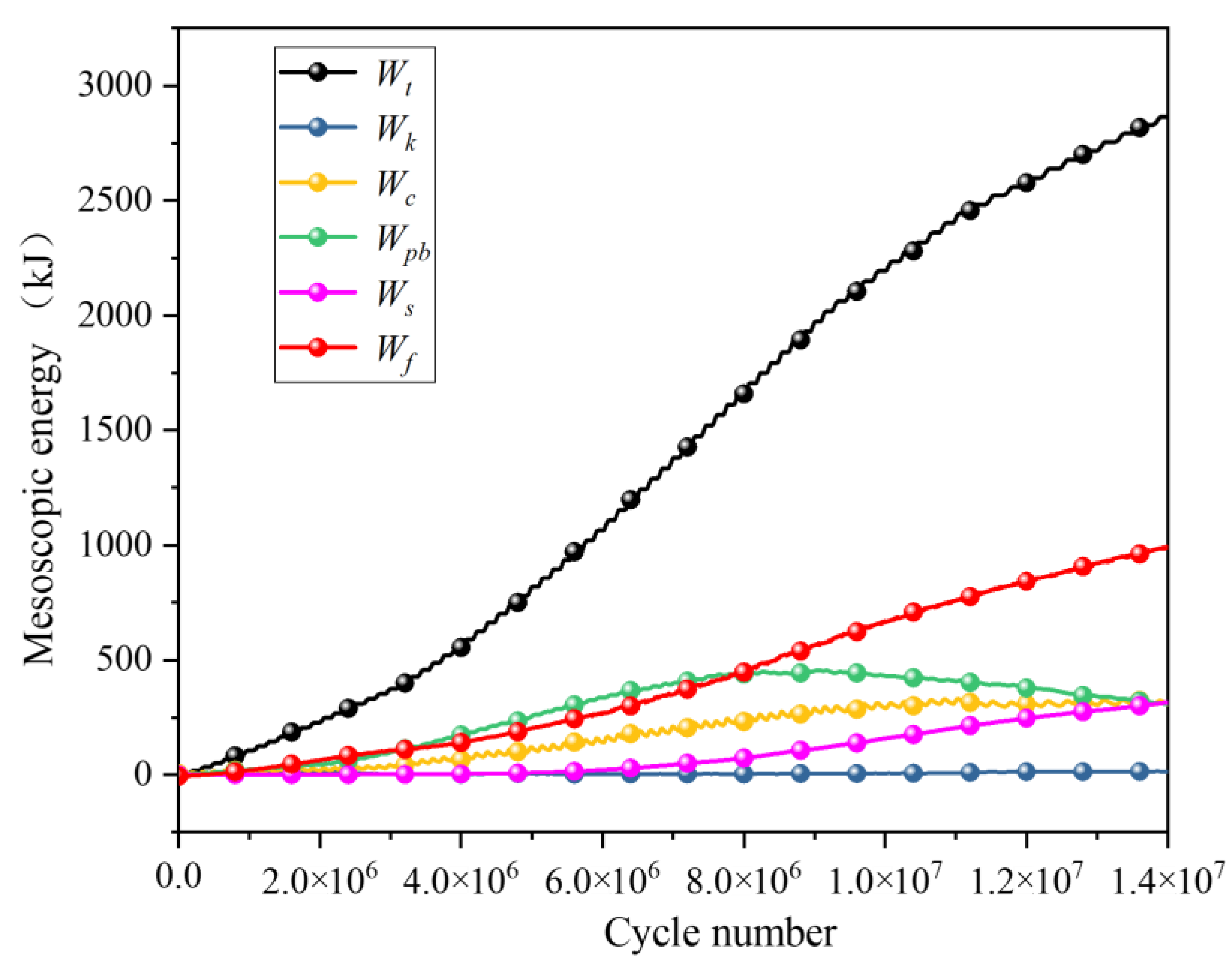
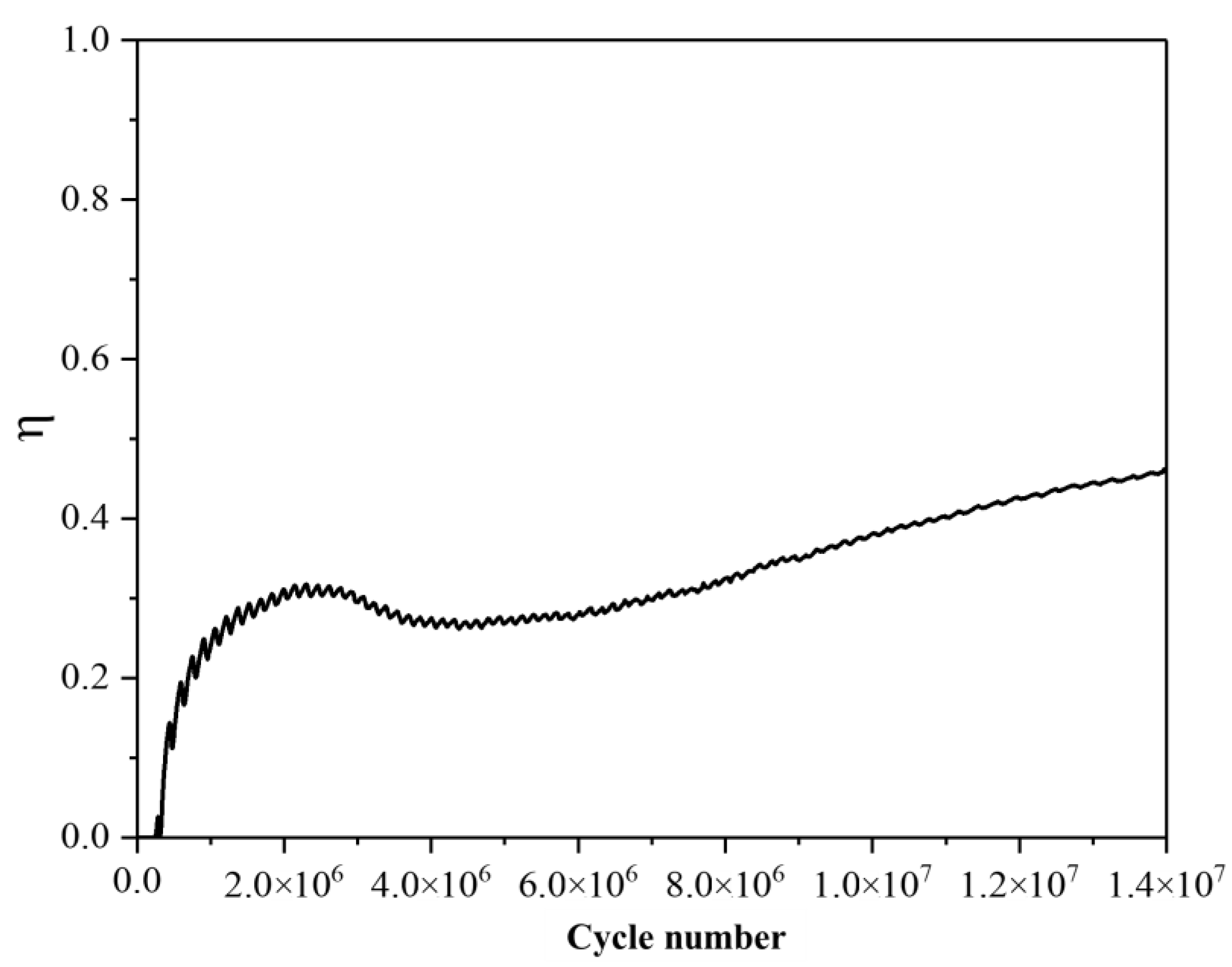
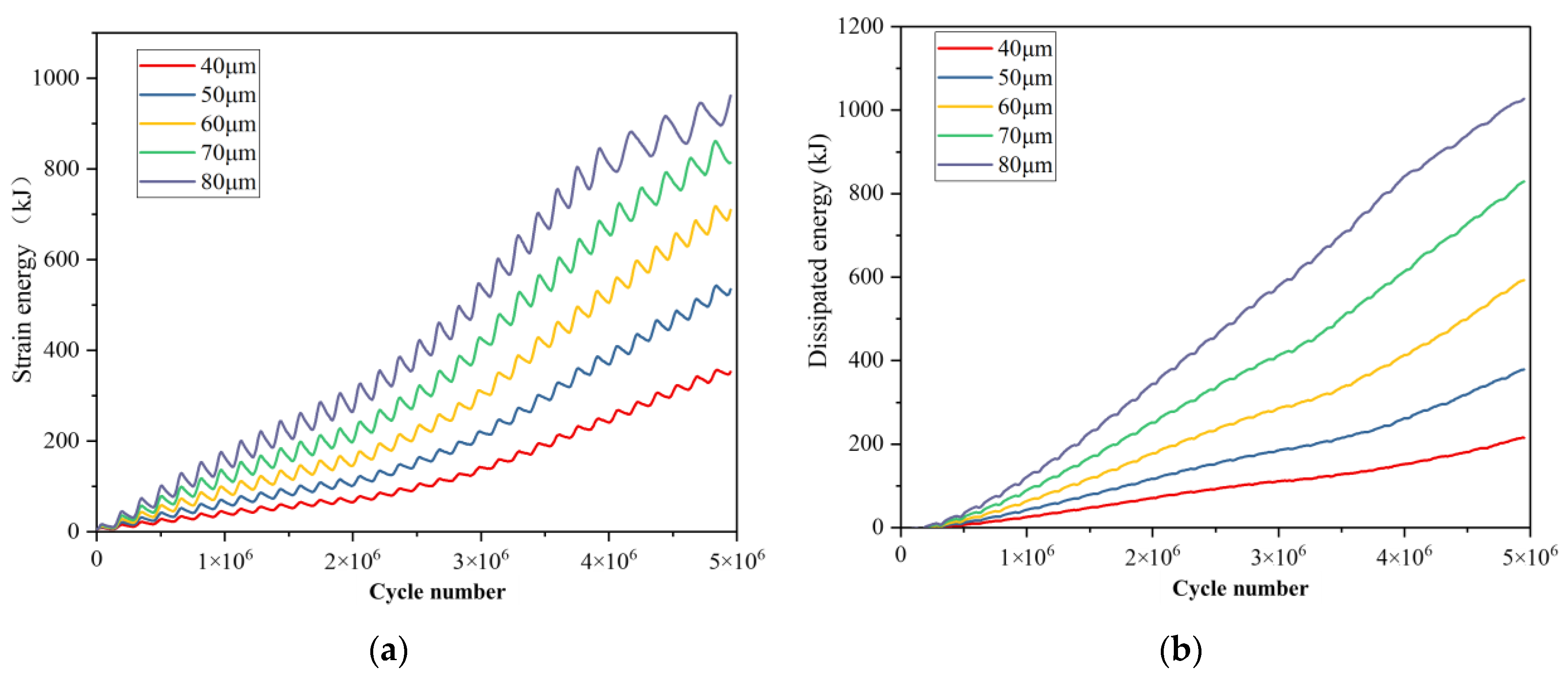
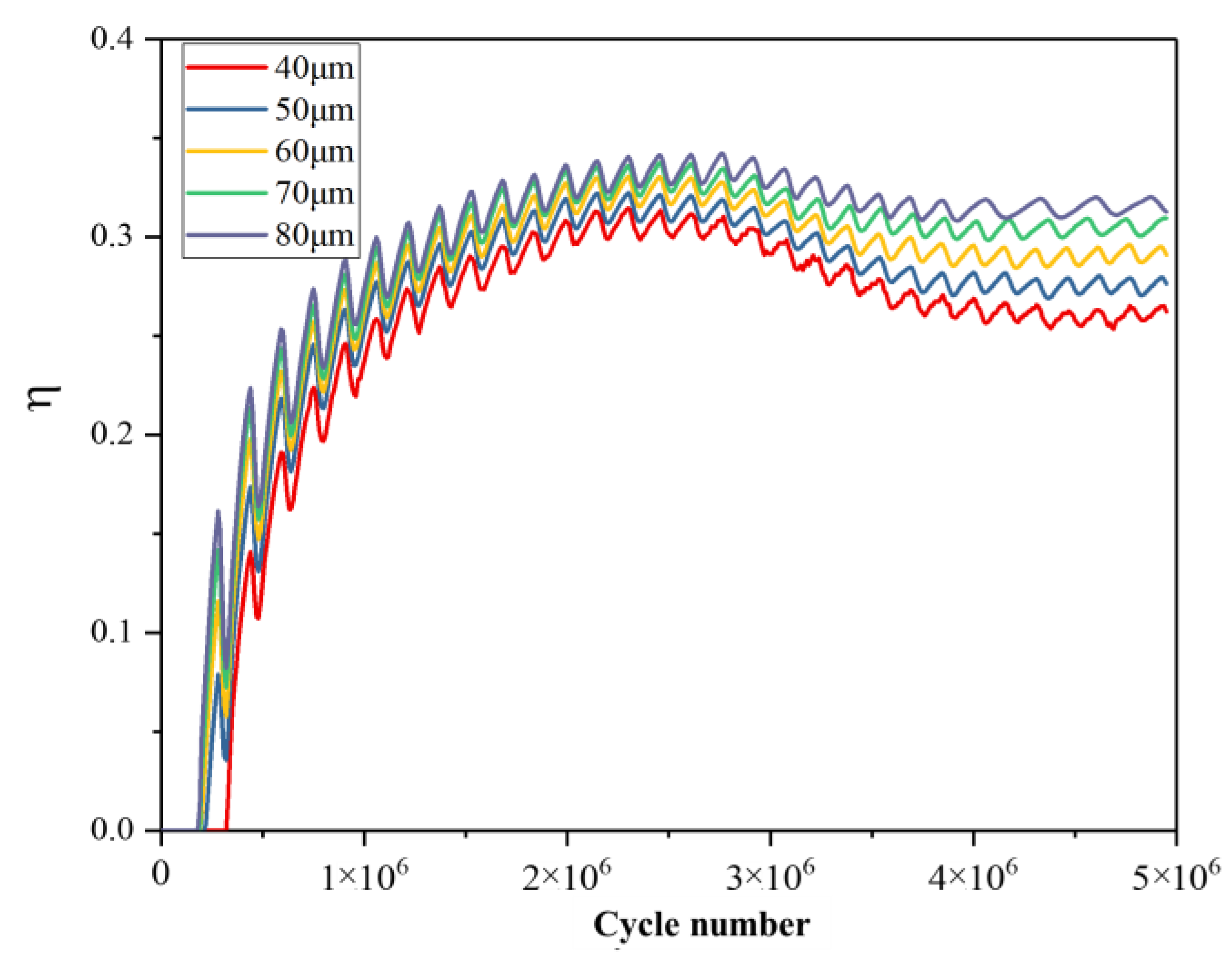
3.3. Energy Evolution of Rock under Ultrasonic Vibration Load
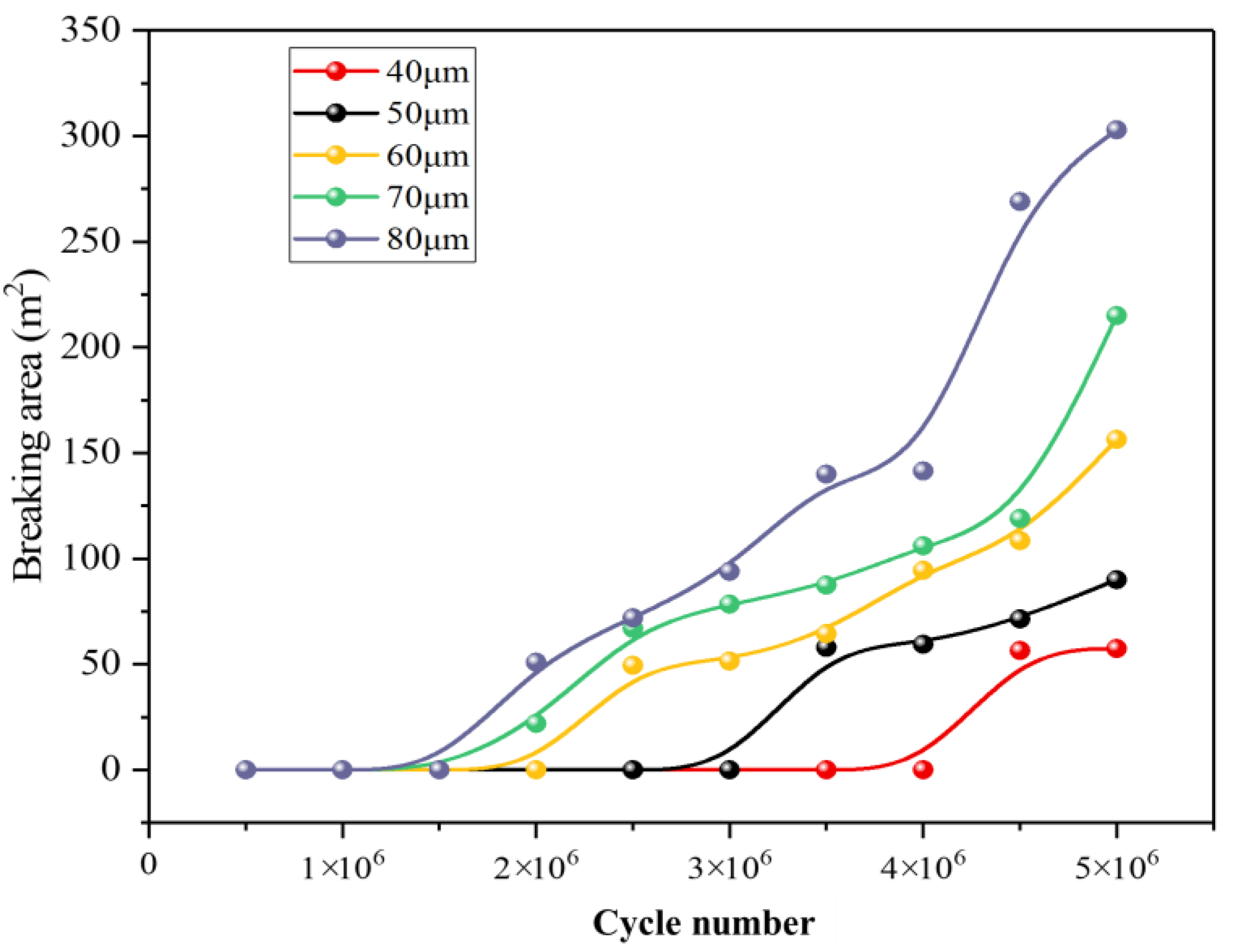
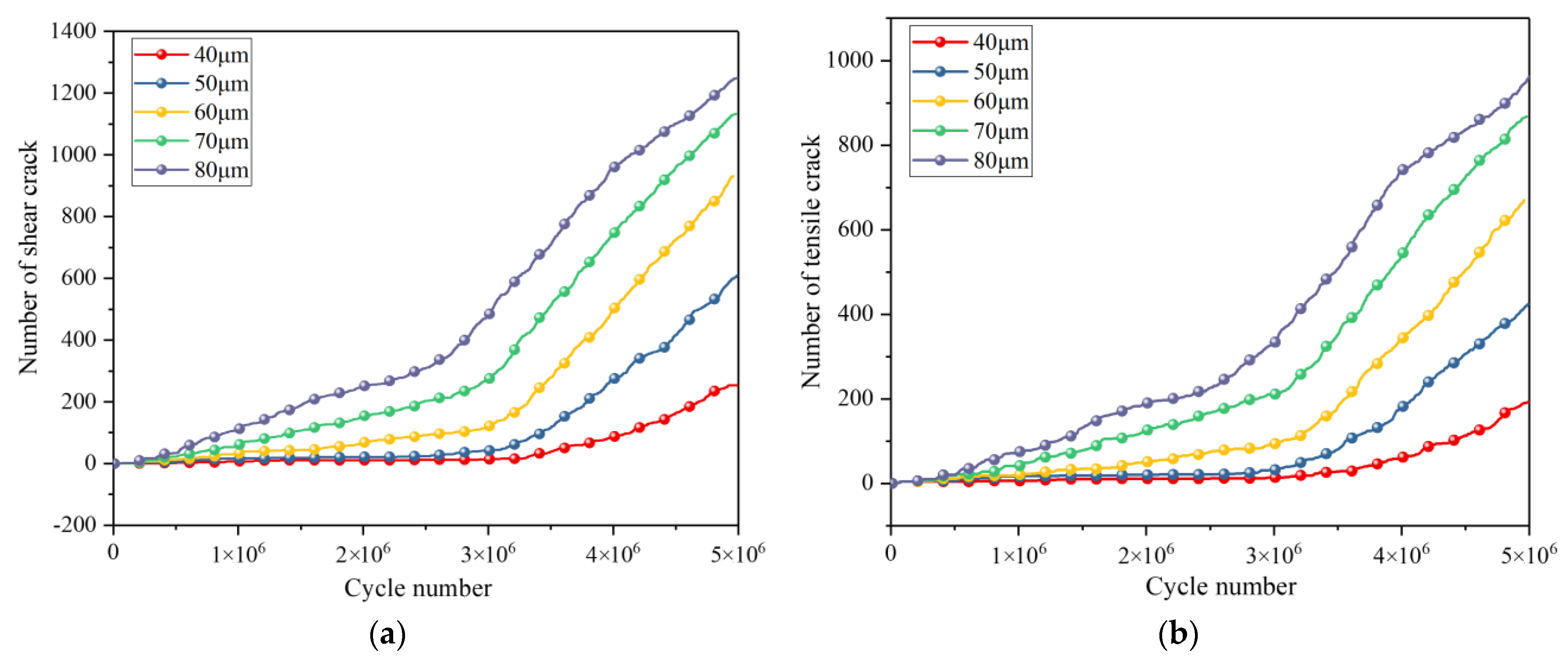
3.4. Effect of Amplitude on Rock Fracture
4. Conclusions
- (1)
- Ultrasonic vibration excitation leads to a maximum deformation of 5.0199 × 10−3 m in the rock, causing initial cracks at the load surface that propagate towards both edges and experience maximum shear stress. Continuous vibration further induces shear failure within the region experiencing maximum shear stress, resulting in crack propagation downwards and along both boundaries, ultimately leading to an X-shaped fracture surface in the rock.
- (2)
- Under ultrasonic vibration load, a compressive stress-dominated stress concentration zone forms beneath the load surface and extends downwards. The degree of stress concentration decreases with increasing distance from the excitation surface. Internal kinetic energy generated within the rock is minimal; instead, primary sources of energy include particle strain energy, parallel bond strain energy, frictional energy, and plastic deformation energy. The curve representing energy dissipation coefficient exhibits an initial increase followed by a decrease before eventually increasing again.
- (3)
- The deformation, fracture, and energy evolution characteristics of the rock under the five different amplitudes are compared and analyzed. The results demonstrate that while amplitude variations do not affect the maximum displacement value of the rock, they do accelerate its deformation rate. As the maximum displacement within the rock reaches its limit deformation value, increasing the amplitude expands the range of maximum deformation. Moreover, there exists a proportional relationship between amplitude changes and rock fragmentation, crack propagation, as well as energy dissipation coefficient. Increasing the amplitude contributes to enhancing rock breaking efficiency. Under an equal number of cycle steps (5,000,000 cycles), when increasing from 40 μm to 80 μm in amplitude, fracture volume, crack count, and energy dissipation coefficient increase by 429.67%, 494.44%, and 19.272% respectively.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chang, Z.; Sherrit, S.; Bao, X.; Bar-Cohen, Y. Design and analysis of ultrasonic horn for USDC (ultrasonic/sonic driller/corer). Smart Struct. Mater. 2004 Ind. Commer. Appl. Smart Struct. Technol. 2004, 5388, 320–326. [Google Scholar]
- Bar-Cohen, Y.; Bao, Z.; Chang, Z.; Sherrit, S. An ultrasonic sampler and sensor platform for in-situ astrobiological exploration. Smart Struct. Mater. 2003 Smart Struct. Integr. Syst. 2003, 5056, 457–465. [Google Scholar]
- Bagde, M.N.; Petros, V. Fatigue properties of intact sandstone samples subjected to dynamic uniaxial cyclical loading. Int. J. Rock Mech. Min. Sci. 2005, 42, 237–250. [Google Scholar] [CrossRef]
- Wiercigroch, M.; Wojewoda, J.; Krivtsov, A.M. Dynamics of ultrasonic percussive drilling of hard rocks. J. Sound Vib. 2005, 280, 739–757. [Google Scholar] [CrossRef]
- Wang, H.; Li, J. Mechanical Behavior Evolution and Damage Characterization of Coal under Different Cyclic Engineering Loading. Geofluids 2020, 2020, 8812188. [Google Scholar] [CrossRef]
- Liu, B.; Zhao, Y.; Hua, X.; Ling, C.; Wang, X. Failure characteristic and acoustic emission spatio-temporal evolution of coal under different cyclic loading rates. Energy Sci. Eng. 2023, 11, 2039–2051. [Google Scholar] [CrossRef]
- Geranmayeh Vaneghi, R.; Ferdosi, B.; Okoth, A.; Kuek, B. Strength degradation of sandstone and granodiorite under uniaxial cyclic loading. J. Rock Mech. Geotech. Eng. 2018, 10, 117–126. [Google Scholar] [CrossRef]
- Erarslan, N.; Alehossein, H.; Williams, D.J. Tensile Fracture Strength of Brisbane Tuff by Static and Cyclic Loading Tests. Rock Mech. Rock Eng. 2013, 47, 1135–1151. [Google Scholar] [CrossRef]
- Liu, J.; Qin, G.; Cao, J.; Zhai, M. Analysis Deformation Failure Characteristics and the Energy Evolution of Varying Lithologies under Cyclic Loading. Geofluids 2022, 2022, 7984910. [Google Scholar] [CrossRef]
- Fan, L.; Qiu, B.; Cao, J.; Du, X. A Real-Time Visual Investigation on Microscopic Progressive Fatigue Deterioration of Granite Under Cyclic Loading. Rock Mech. Rock Eng. 2023, 56, 5133–5147. [Google Scholar] [CrossRef]
- Erarslan, N.; Williams, D. The damage mechanism of rock fatigue and its relationship to the fracture toughness of rocks. Int. J. Rock Mech. Min. Sci. 2012, 56, 15–26. [Google Scholar] [CrossRef]
- Li, W.; Yan, T.; Li, S.; Zhang, X. Rock fragmentation mechanisms and an experimental study of drilling tools during high-frequency harmonic vibration. Pet. Sci. 2013, 10, 205–211. [Google Scholar] [CrossRef]
- Li, S.; Tian, S.; Li, W.; Ling, X.; Kapitaniak, M.; Vaziri, V. Numerical study on the elastic deformation and the stress field of brittle rocks under harmonic dynamic load. Energies 2020, 13, 851. [Google Scholar] [CrossRef]
- Yin, S.; Zhao, D.; Zhai, G. Investigation into the characteristics of rock damage caused by ultrasonic vibration. Int. J. Rock Mech. Min. Sci. 2016, 84, 159–164. [Google Scholar] [CrossRef]
- Zhou, Y.; Tang, Q.; Zhang, S.; Zhao, D. The Mechanical Properties of Granite under Ultrasonic Vibration. Adv. Civ. Eng. 2019, 2019, 9649165. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X.; Wang, J.; Yang, Z. Mechanical characteristics and pore evolution of red sandstone under ultrasonic high-frequency vibration excitation. AIP Adv. 2021, 11, 055202. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, X.; Wang, J.; Yang, Z. Research on Fracture Characteristics and Energy Dissipation of Hard Rock under the Excitation of Ultrasonic Vibration. Geofluids 2022, 2022, 8351316. [Google Scholar] [CrossRef]
- Wang, Y.; Cui, F. Energy evolution mechanism in process of Sandstone failure and energy strength criterion. J. Appl. Geophys. 2018, 154, 21–28. [Google Scholar] [CrossRef]
- Yang, S.; Tian, W.; Huang, Y.; Ranjith, P.; Ju, Y. An Experimental and Numerical Study on Cracking Behavior of Brittle Sandstone Containing Two Non-coplanar Fissures Under Uniaxial Compression. Rock Mech. Rock Eng. 2016, 49, 1497–1515. [Google Scholar] [CrossRef]
- Li, X.; Li, H.; Liu, Y.; Zhou, Q.; Xia, X. Numerical simulation of rock fragmentation mechanisms subject to wedge penetration for TBMs. Tunn. Undergr. Space Technol. 2016, 53, 96–108. [Google Scholar] [CrossRef]


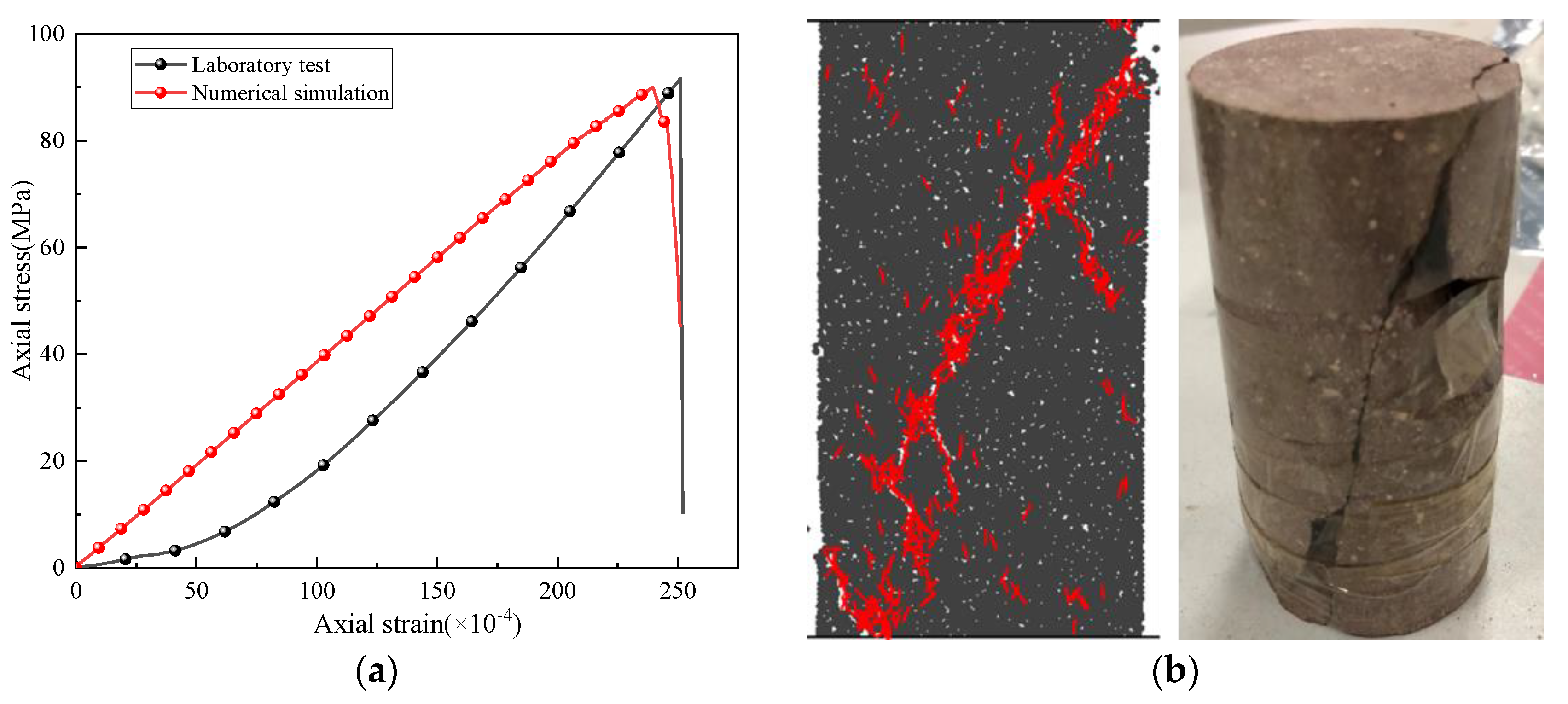




| Particle density/(kg/m3) | Particle stiffness ratio | parallel bond modulus/(GPa) |
| 2700 | 1.5 | 4.5 |
| Particle contact modulus (GPa) | Friction coefficient | parallel bond stiffness ratio |
| 4.8 | 0.5 | 2.5 |
| Tangential bond strength (MPa) | Normal bond strength (MPa) | parallel bond radius factor |
| 45 | 37 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Wang, X.; Niu, Z.; Dai, J. Simulation Analysis of the Influence of Amplitude on Deformation and Fracture Characteristics of Hard Rock under Ultrasonic Vibration Load. Processes 2024, 12, 74. https://doi.org/10.3390/pr12010074
Zhang L, Wang X, Niu Z, Dai J. Simulation Analysis of the Influence of Amplitude on Deformation and Fracture Characteristics of Hard Rock under Ultrasonic Vibration Load. Processes. 2024; 12(1):74. https://doi.org/10.3390/pr12010074
Chicago/Turabian StyleZhang, Lei, Xufeng Wang, Zhijun Niu, and Jianbo Dai. 2024. "Simulation Analysis of the Influence of Amplitude on Deformation and Fracture Characteristics of Hard Rock under Ultrasonic Vibration Load" Processes 12, no. 1: 74. https://doi.org/10.3390/pr12010074








