Multi-Type Energy Storage Collaborative Planning in Power System Based on Stochastic Optimization Method
Abstract
:1. Introduction
- A MESS planning framework, including short-term ESS (battery energy storage) and long-term ESS (hydrogen energy storage) is proposed in this paper to address the risk of a mismatch between supply and demand on multiple time scales.
- The proposed planning framework of MESS is modeled as a two-stage stochastic MILP model based on typical scenarios. This allows the MESS planning results to adapt to the uncertainty of RES.
- The progressive hedging (PH) algorithm is used to solve the proposed model. Results demonstrate that the PH algorithm can boost computational efficiency under more scenarios.
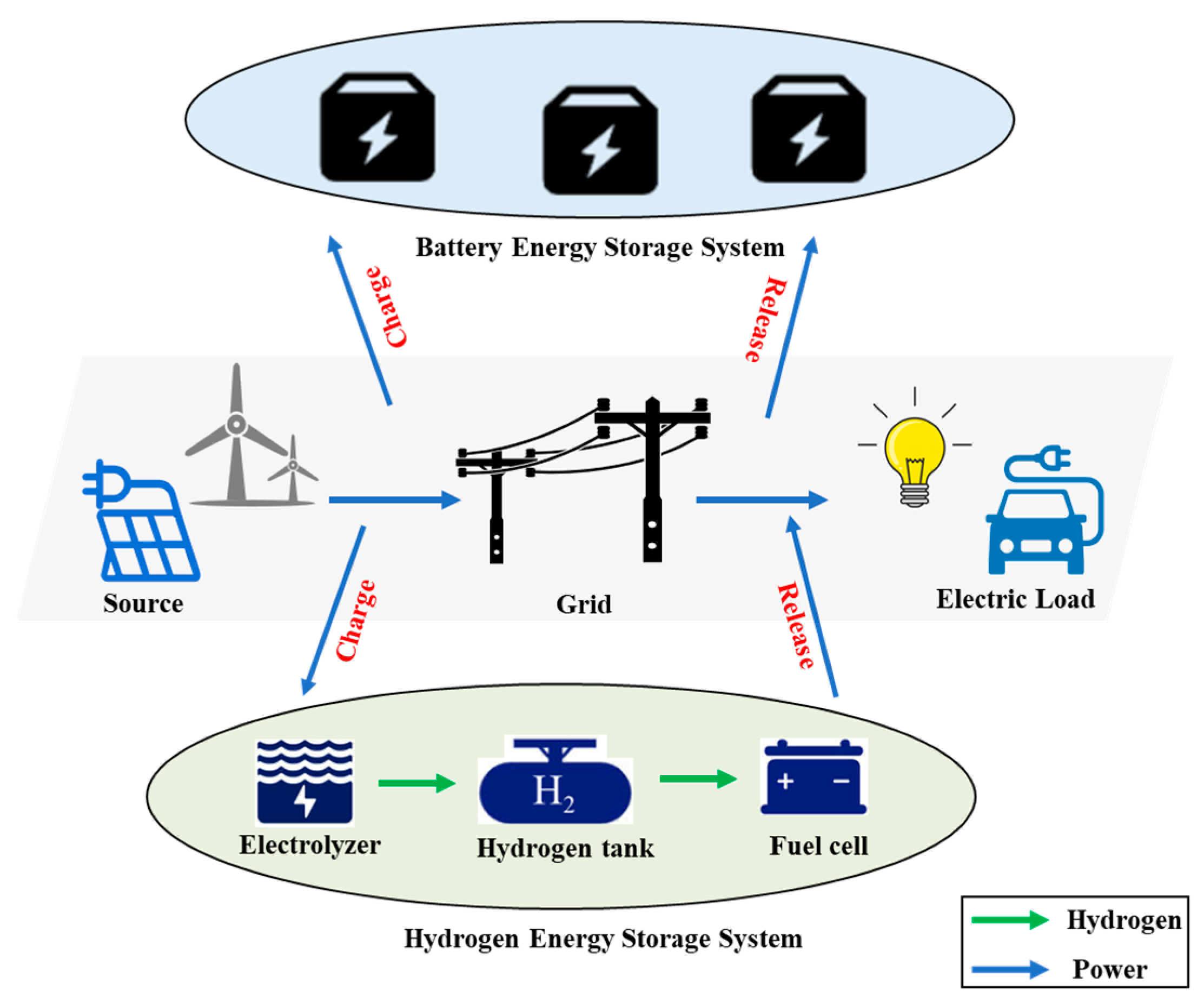
2. Multi-Type Energy Storage Collaborative Optimization Planning Framework
3. Collaborative Optimization Planning Model
3.1. ESS Investment and Planning Constraints
3.2. Short-Term ESS Operation Constraints
3.3. Long-Term ESS Operation Constraints
3.4. Generators Operation Constraints
3.5. Power System Operation Constraints
4. Solution Algorithm
| Algorithm 1. Progressive Hedging (PH) Algorithm. |
| Step 1 Initialization: Step 2 Iteration update: Step 3 Update multiplier and decomposition: Step 4 Termination: Else go to Step 2 and continue |
5. Case Study
5.1. Test System Introduction
5.2. MESS Planning Results
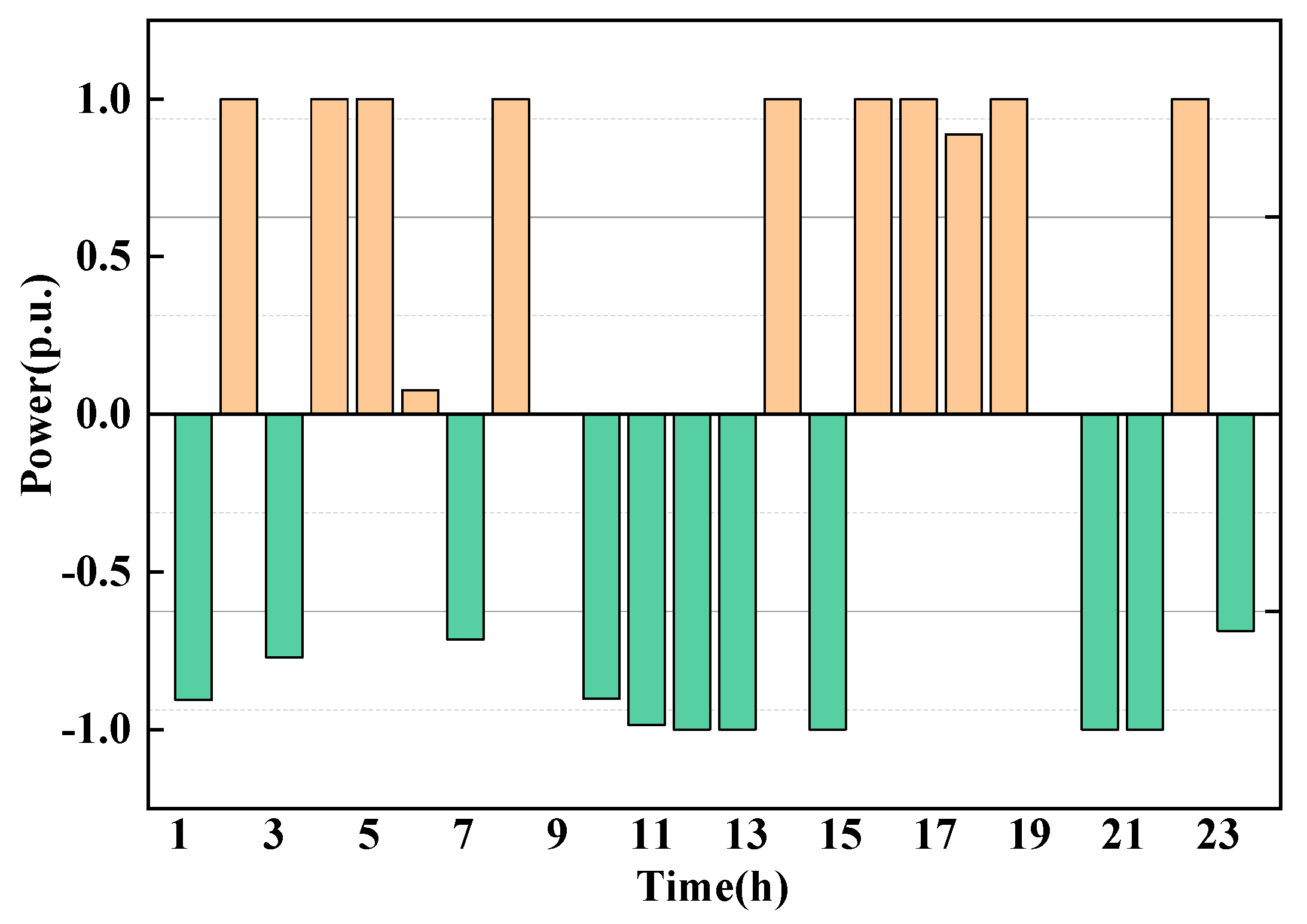
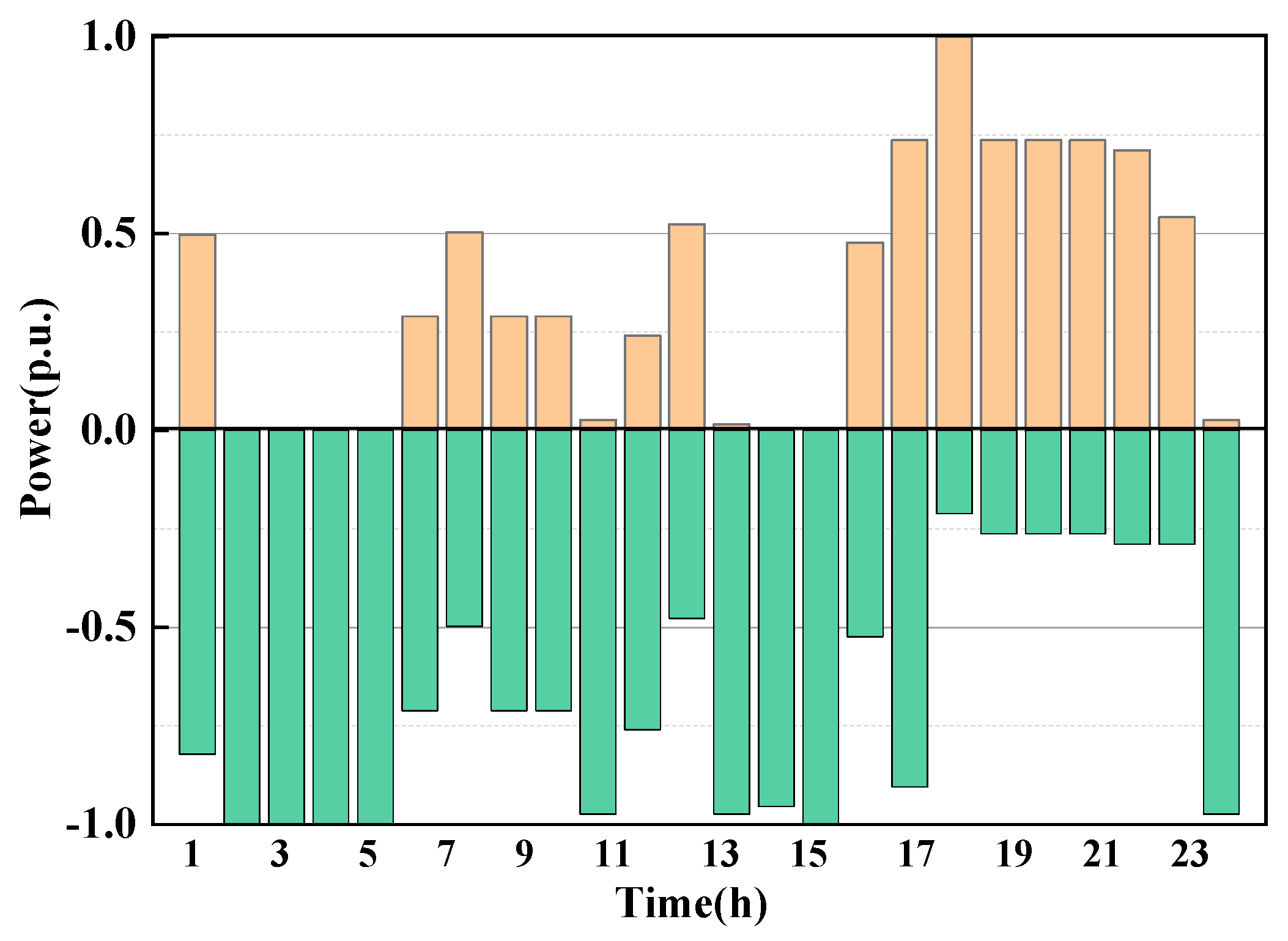
5.3. MESS Operation Strategy Results
5.4. Proposed Model and Algorithm Efficiency
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Agency IRE. World Energy Transitions Outlook: 1.5 °C Pathway. 2021. Available online: https://www.irena.org/Energy-Transition/Outlook (accessed on 24 July 2024).
- EPRI Head: Duck Curve Now Looks like a Canyon. 2023. Available online: https://www.powermag.com/epri-head-duck-curve-now-looks-like-a-canyon/ (accessed on 24 July 2024).
- Petkov, I.; Gabrielli, P. Power-to-hydrogen as seasonal energy storage: An uncertainty analysis for optimal design of low-carbon multi-energy systems. Appl. Energy 2020, 274, 115197. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, Z.; Yang, M.; Jia, D.; Pei, W.; Xu, B. Overview of energy storage in renewable energy power fluctuation mitigation. CSEE J. Power Energy Syst. 2020, 6, 160–173. [Google Scholar]
- Revinova, S.; Lazanyuk, I.; Gabrielyan, B.; Shahinyan, T.; Hakobyan, Y. Hydrogen in Energy Transition: The Problem of Economic Efficiency, Environmental Safety, and Technological Readiness of Transportation and Storage. Resources 2024, 13, 92. [Google Scholar] [CrossRef]
- Agency IEA. Electricity Market Report 2023—Analysis. 2023. Available online: https://iea.blob.core.windows.net/assets/255e9cba-da84-4681-8c1f-458ca1a3d9ca/ElectricityMarketReport2023.pdf. (accessed on 24 July 2024).
- Wang, C.; Zhang, X.; Xia, Y.; Xiong, H.; Guo, C.; Wang, L.; Wang, Y. A two-stage robust optimal configuration model of generation-side cloud energy storage system based on cooperative game. IET Gener. Transm. Distrib. 2022, 17, 1723–1733. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, X.; Duan, N.; Pengjiang, G.; Jinli, L.; Wenzhuo, W.; Ying, W. The Synergistic and Optimal Configuration of Energy Storage and Renewable Energy Based on the Equal Area Principle. Power Syst. Technol. 2023, 47, 4131–4142. (In Chinese) [Google Scholar]
- Zhu, X.; Shan, Y. Multi-stage distributionally robust planning of energy storage capacity considering flexibility. Electr. Power Autom. Equip. 2023, 43, 152–159+167. (In Chinese) [Google Scholar]
- Tang, S.; Li, G.; Wang, Z.; Yang, Y.; Lu, Q.; Xie, P.; Chen, Y. A Distributionally Robust Energy Storage Planning Model for Wind Integrated Power System Based on Scenario Probability. In Proceedings of the 2023 International Conference on Power Energy Systems and Applications (ICoPESA), Nanjing, China, 20–22 June 2023; pp. 554–560. [Google Scholar]
- Fu, P.; Pudjianto, D.; Zhang, X.; Strbac, G. Integration of Hydrogen into Multi-Energy Systems Optimisation. Energies 2020, 13, 1606. [Google Scholar] [CrossRef]
- Luo, W.; Wu, J.; Cai, J.; Mao, Y.; Chen, S. Capacity Allocation Optimization Framework for Hydrogen Integrated Energy System Considering Hydrogen Trading and Long-Term Hydrogen Storage. IEEE Access 2023, 11, 15772–15787. [Google Scholar]
- Li, J.; Li, G.; Ma, S.; Liang, Z.; Li, Y.; Zeng, W. Modeling and Simulation of Hydrogen Energy Storage System for Power-to-gas and Gas-to-power Systems. J. Mod. Power Syst. Clean Energy 2021, 11, 885–895. [Google Scholar] [CrossRef]
- Xiong, Y.; Chen, L.; Zheng, T.; Si, Y.; Mei, S. Electricity-Heat-Hydrogen Modeling of Hydrogen Storage System Considering Off-Design Characteristics. IEEE Access 2021, 9, 156768–156777. [Google Scholar] [CrossRef]
- Lu, Q.; Zhang, X.; Yang, Y.; Hu, Q.; Wu, G.; Huang, Y.; Liu, Y.; Li, G. Multi-Time-Scale Energy Storage Optimization Configuration for Power Balance in Distribution Systems. Electronics 2024, 13, 1379. [Google Scholar] [CrossRef]
- Du, E.; Jiang, H.; Xiao, J.; Hou, J.; Zhang, N.; Kang, C. Preliminary analysis of long-term storage requirement in enabling high renewable energy penetration: A case of East Asia. IET Renew. Power Gener. 2021, 15, 1255–1269. [Google Scholar] [CrossRef]
- Jiang, S.; Wen, S.; Zhu, M.; Huang, Y.; Ye, H. Scenario-Transformation-Based Optimal Sizing of Hybrid Hydrogen-Battery Storage for Multi-Timescale Islanded Microgrids. IEEE Trans. Sustain. Energy 2023, 14, 1784–1795. [Google Scholar] [CrossRef]
- Wu, X.; Cao, B.; Liu, B.; Wang, X. A Planning Model of Standalone Hydrogen-Based Carbon-Free Microgrid through Convex Relaxation. IEEE Trans. Smart Grid 2023, 14, 2668–2680. [Google Scholar] [CrossRef]
- Wang, J.; Deng, H.; Qi, X. Cost-based site and capacity optimization of multi-energy storage system in the regional integrated energy networks. Energy 2022, 261, 125240. [Google Scholar] [CrossRef]
- Gao, M.; Han, Z.; Zhao, B.; Li, P.; Wu, D.; Li, P. Optimal planning method of multi-energy storage systems based on the power response analysis in the integrated energy system. J. Energy Storage 2023, 73, 109015. [Google Scholar] [CrossRef]
- Luo, Y.; Tian, P.; Yan, X.; Xiao, X.; Ci, S.; Zhou, Q.; Yang, Y. Energy Storage Dynamic Configuration of Active Distribution Networks—Joint Planning of Grid Structures. Processes 2024, 12, 79. [Google Scholar] [CrossRef]
- Alharthi, Y.Z. An Analysis of Hybrid Renewable Energy-Based Hydrogen Production and Power Supply for Off-Grid Systems. Processes 2024, 12, 1201. [Google Scholar] [CrossRef]
- Yan, C.; Geng, X.; Bie, Z.; Xie, L. Two-stage robust energy storage planning with probabilistic guarantees: A data-driven approach. Appl. Energy 2022, 313, 118623. [Google Scholar] [CrossRef]
- Pan, G.; Gu, W.; Lu, Y.; Qiu, H.; Lu, S.; Yao, S. Optimal Planning for Electricity-Hydrogen Integrated Energy System Considering Power to Hydrogen and Heat and Seasonal Storage. IEEE Trans. Sustain. Energy 2020, 11, 2662–2676. [Google Scholar] [CrossRef]
- Chen, Y.; Hu, Q.; Lin, X.; Lu, Q.; Zhu, Y.; Li, G. Energy Storage Stochastic Optimization Planning Considering Dynamic Frequency Constraints. In Proceedings of the 2023 2nd Asia Power and Electrical Technology Conference (APET), Shanghai, China, 28–30 December 2023; pp. 828–833. [Google Scholar]
- Watson, J.-P.; Woodruff, D.L. Progressive hedging innovations for a class of stochastic mixed-integer resource allocation problems. Comput. Manag. Sci. 2010, 8, 355–370. [Google Scholar] [CrossRef]
- Shapiro, A.; Dentcheva, D.; Ruszczynski, A. Lectures on Stochastic Programming: Modeling and Theory; SIAM: Philadelphia, PA, USA, 2014. [Google Scholar]
- Popela, P.; Novotný, J.; Roupec, J.; Hrabec, D.; Olstad, A. Two-stage Stochastic Programming for Engineering Problems. Eng. Mech. 2014, 21, 335–353. [Google Scholar]
- Illinois. IEEE 39-Bus System [EB/OL]. Available online: https://icseg.iti.illinois.edu/ieee-39-bus-system (accessed on 2 November 2023).
- Hu, Q.; Li, G.; Sun, S.; Bie, Z. Incorporating catastrophe insurance in power distribution systems investment and planning for resilience enhancement. Int. J. Electr. Power Energy Syst. 2024, 155, 109438. [Google Scholar] [CrossRef]
- Lu, J.; Li, X. Annual Benefit Analysis of Integrating the Seasonal Hydrogen Storage into the Renewable Power Grids. In Proceedings of the 2023 IEEE Power & Energy Society General Meeting (PESGM), Orlando, FL, USA, 16–20 July 2023; pp. 1–5. [Google Scholar]
- Zhang, Z.; Guo, Z.; Zhou, M.; Wu, Z.; Yuan, B.; Chen, Y.; Li, G. Equalizing multi-temporal scale adequacy for low carbon power systems by co-planning short-term and seasonal energy storage. J. Energy Storage 2024, 84, 111518. [Google Scholar] [CrossRef]
- Chen, C.; Xing, J.; Li, Q.; Liu, S.; Ma, J.; Chen, J.; Han, L.; Qiu, W.; Lin, Z.; Yang, L. Wasserstein distance-based distributionally robust optimal scheduling in rural microgrid considering the coordinated interaction among source-grid-load-storage. Energy Rep. 2021, 7, 60–66. [Google Scholar] [CrossRef]
- Teng, M.; Chen, C.; Zhao, Y.; Zhong, J.; Geng, J.; Lv, J.; Bie, Z. Distribution Robust Optimal Day-ahead Dispatch Method for Power Systems with Uncertain Wind Power Access Considering Deep Peak Regulation of Coal-fired Units and Energy Storage. Power Syst. Technol. 2024, 48, 3122–3132. (In Chinese) [Google Scholar]



| Node | Power (MW) | Capacity (MWh) |
|---|---|---|
| 15 | 86.03 | 172.06 |
| 17 | 94.8 | 189.6 |
| 20 | 13.83 | 27.66 |
| 32 | 37.87 | 75.74 |
| Total | 232.53 | 465.06 |
| Node | Power (MW) | Capacity (t H2) |
|---|---|---|
| 30 | 100 | 2400 |
| 34 | 10.15 | 243.6 |
| 36 | 167.54 | 4020.96 |
| Total | 277.69 | 6664.56 |
| Model | Short-Term ESS Planning Result | Long-Term ESS Planning Result | Solving Time |
|---|---|---|---|
| SO | 232.53 MW/465.06 MWh | 277.69 MW/6664.56 t H2 | 126 s |
| RO | 326.59 MW/692.38 MWh | 344.36 MW/8635.19 t H2 | 682 s |
| DRO | 248.51 MW/513.09 MWh | 288.96 MW/7069.87 t H2 | 2153 s |
| Scenarios Number | PH Algorithm | Directly Solving by Gurobi |
|---|---|---|
| 4 | 126 s | 86 s |
| 8 | 194 s | 161 s |
| 16 | 452 s | 450 s |
| 64 | 1634 s | 2608 s |
| 128 | 4259 s | N/A |
| Scenarios Number | IEEE 39-Bus System | IEEE 300-Bus System |
|---|---|---|
| 4 | 126 s | 232 s |
| 8 | 194 s | 361 s |
| 16 | 452 s | 708 s |
| 64 | 1634 s | 2793 s |
| 128 | 4259 s | 7693 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Lu, Q.; Yu, Z.; Wang, W.; Hu, Q. Multi-Type Energy Storage Collaborative Planning in Power System Based on Stochastic Optimization Method. Processes 2024, 12, 2079. https://doi.org/10.3390/pr12102079
Yang Y, Lu Q, Yu Z, Wang W, Hu Q. Multi-Type Energy Storage Collaborative Planning in Power System Based on Stochastic Optimization Method. Processes. 2024; 12(10):2079. https://doi.org/10.3390/pr12102079
Chicago/Turabian StyleYang, Yinguo, Qiuyu Lu, Zhenfan Yu, Weihua Wang, and Qianwen Hu. 2024. "Multi-Type Energy Storage Collaborative Planning in Power System Based on Stochastic Optimization Method" Processes 12, no. 10: 2079. https://doi.org/10.3390/pr12102079
APA StyleYang, Y., Lu, Q., Yu, Z., Wang, W., & Hu, Q. (2024). Multi-Type Energy Storage Collaborative Planning in Power System Based on Stochastic Optimization Method. Processes, 12(10), 2079. https://doi.org/10.3390/pr12102079






