Geometric Evaluation of an Oscillating Water Column Wave Energy Converter Device Using Representative Regular Waves of the Sea State Found in Tramandaí, Brazil
Abstract
1. Introduction
2. Mathematical and Numerical Modeling
Generation of Representative Regular Waves
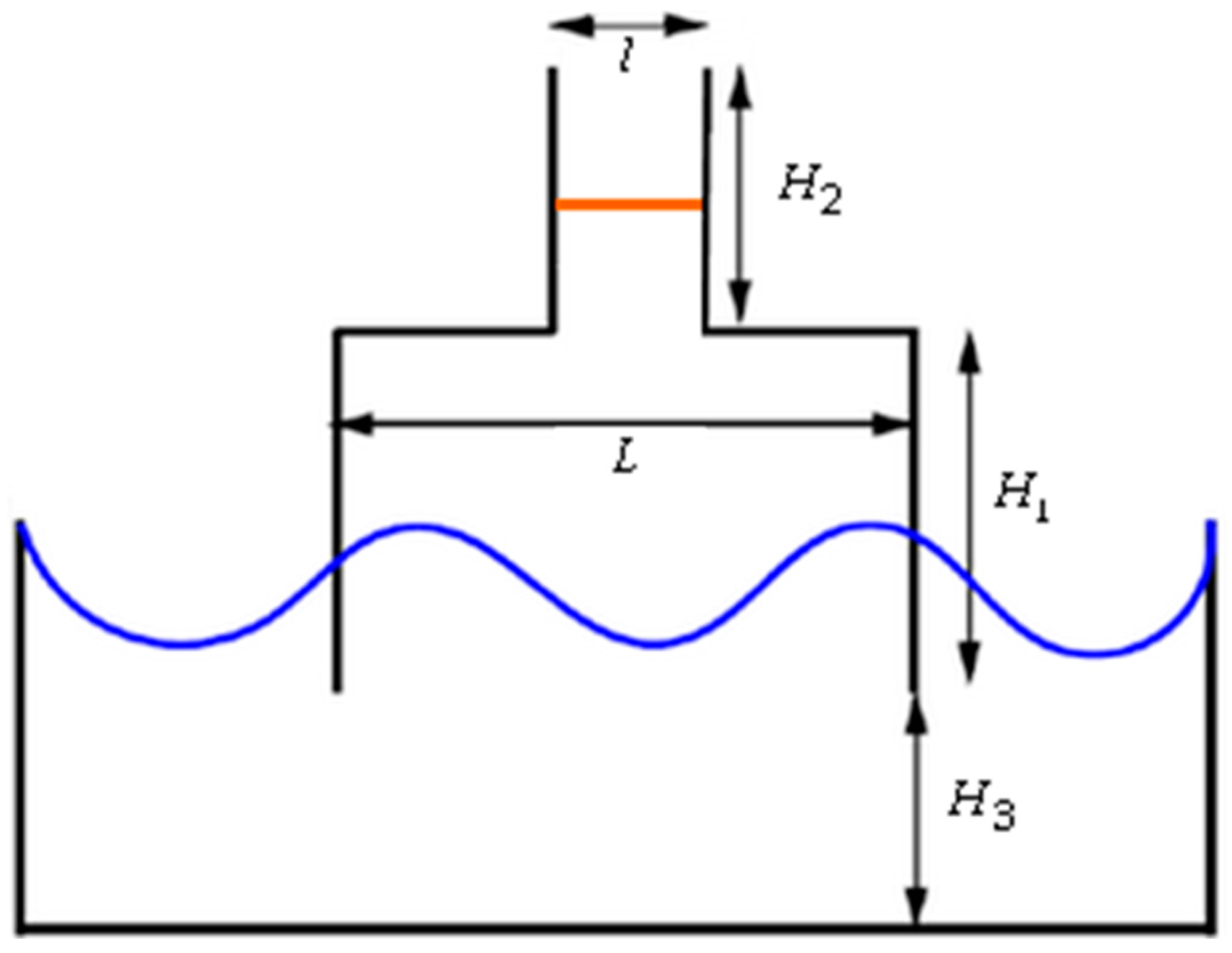
3. Constructal Design Applied to the Oscillating Water Column Device
- The performance indicator: the available hydropneumatic power, which must be maximized;
- Geometric constraints: the area of the hydropneumatic chamber () and the total area of the wave channel ();
- Degrees of freedom: the ratio between the height and length of the hydropneumatic chamber of the OWC device ( (see Figure 1).
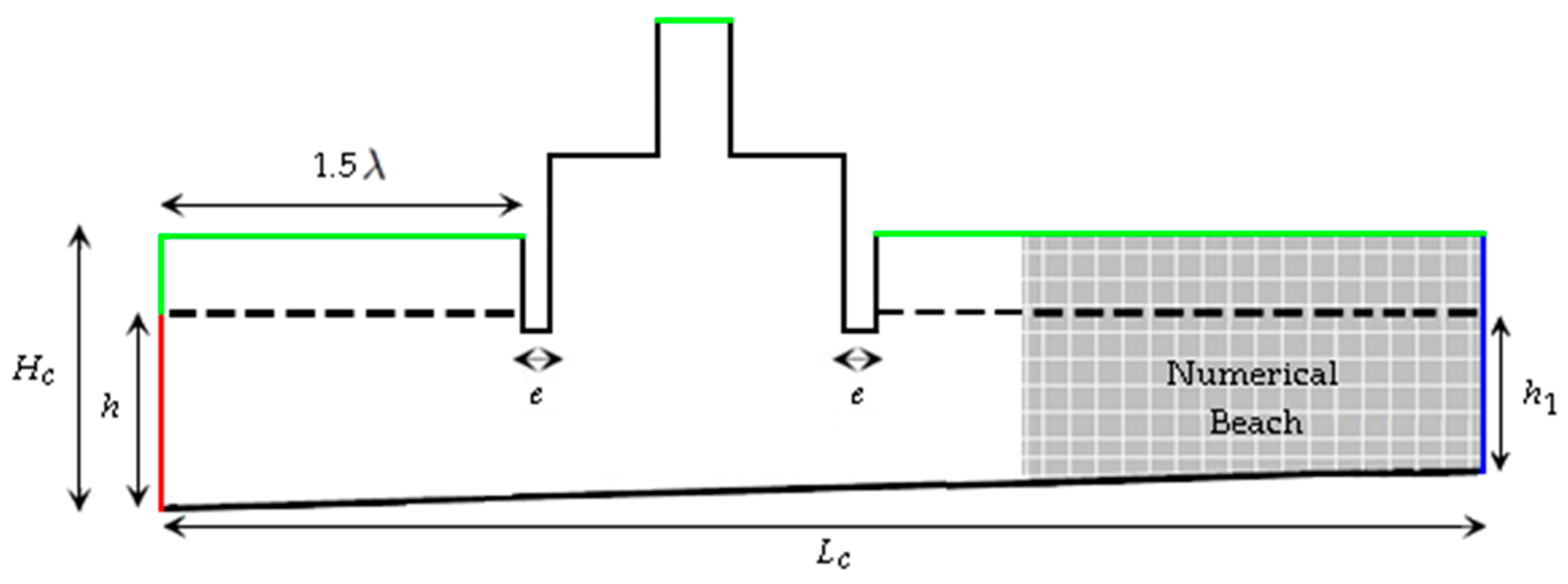
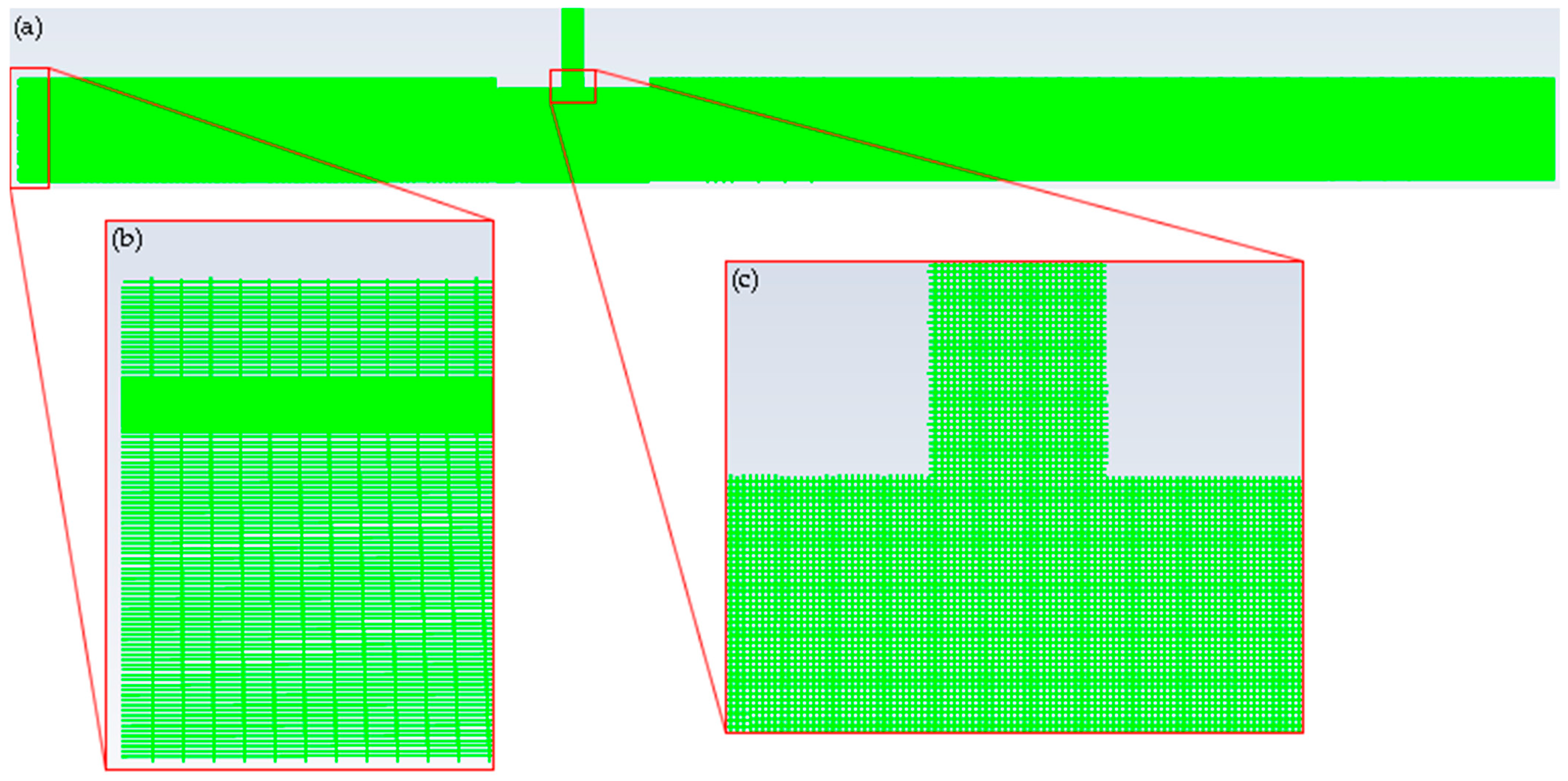
4. Computational Domain
5. Results and Discussions
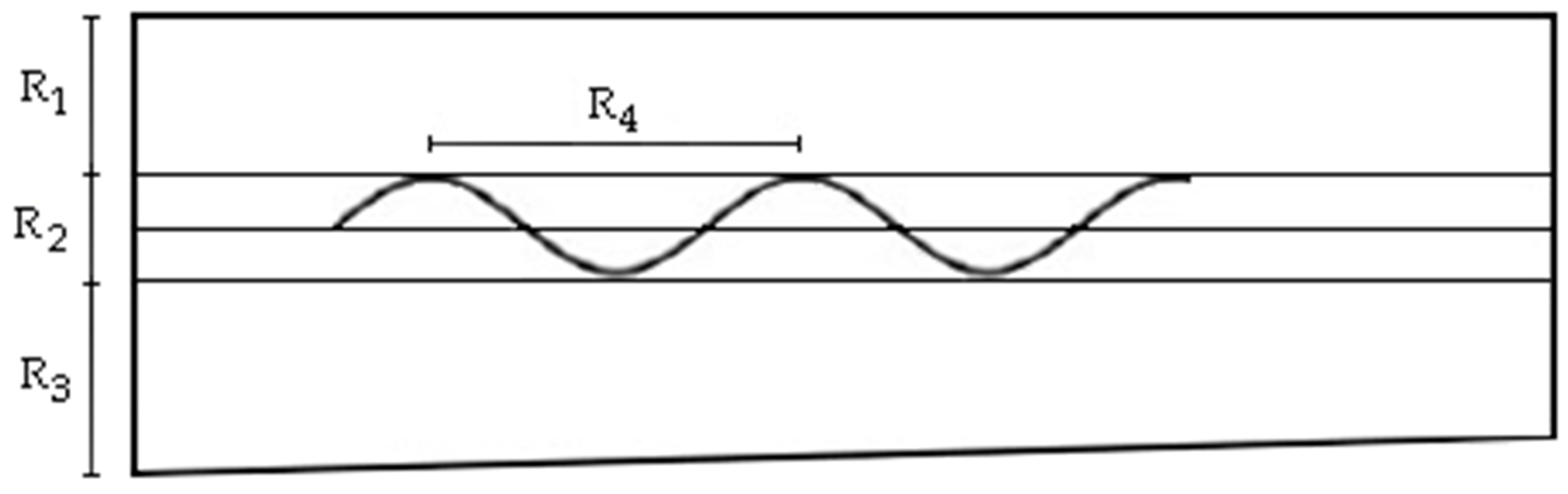
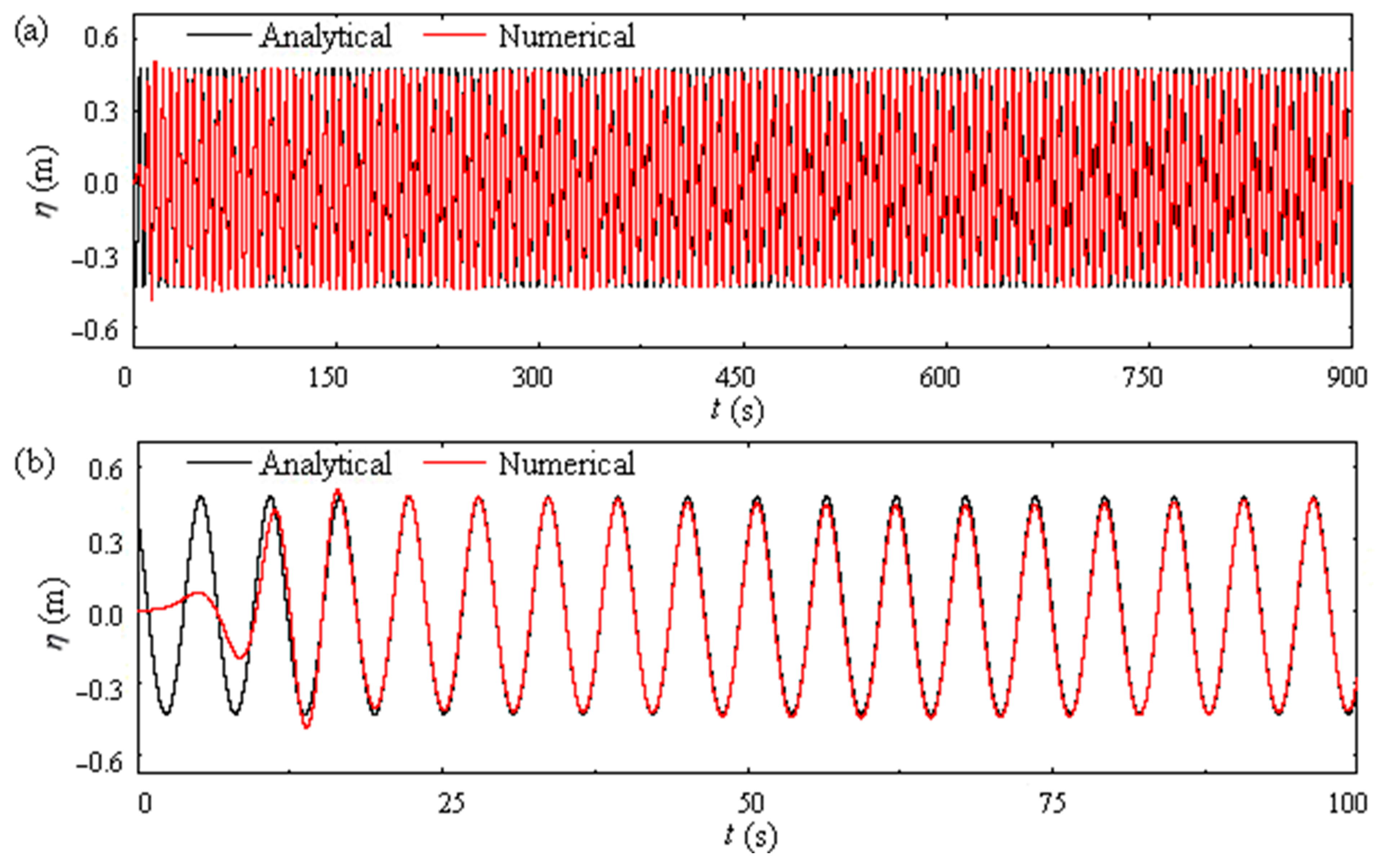
5.1. Numerical Model Verification
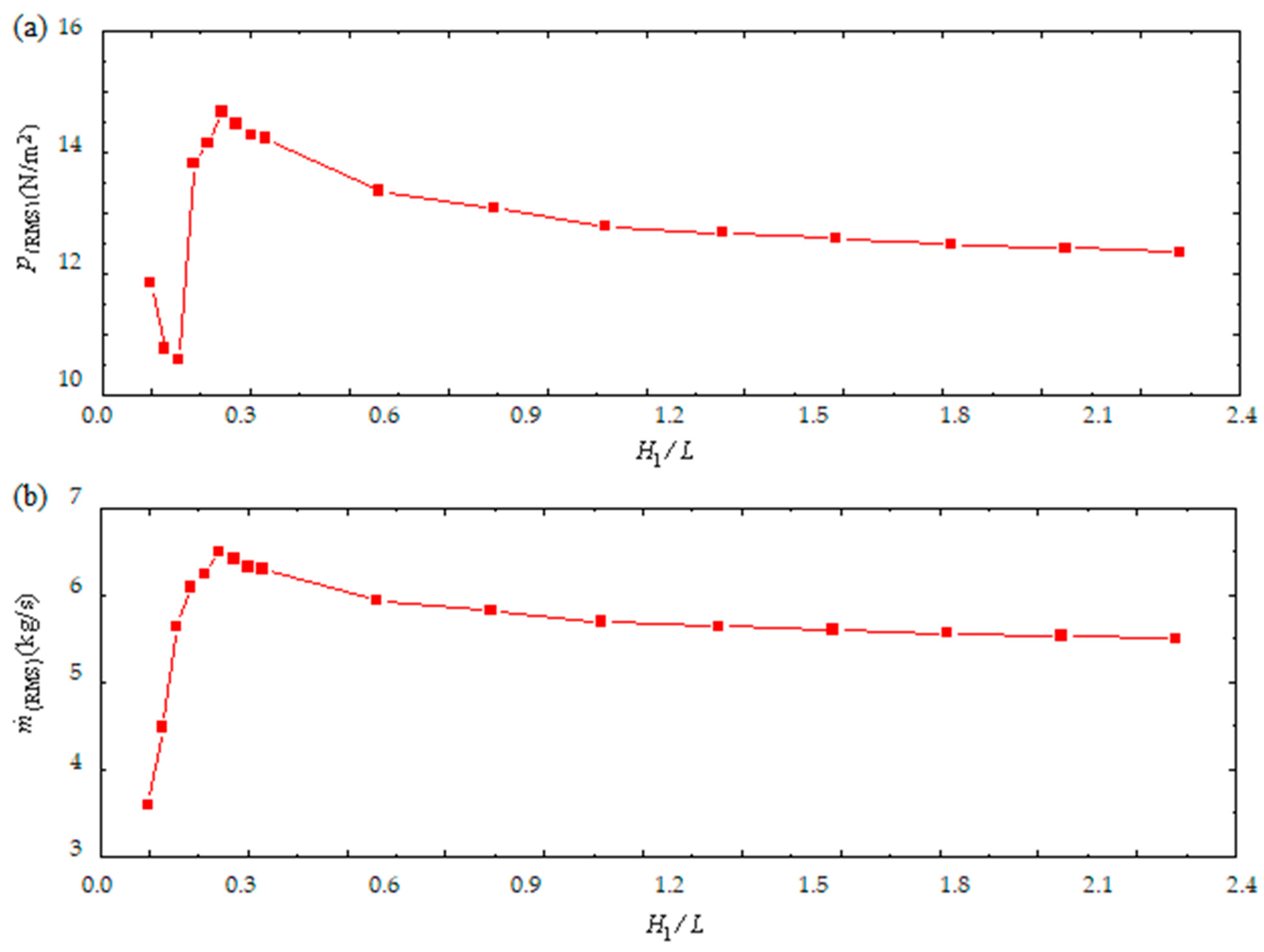
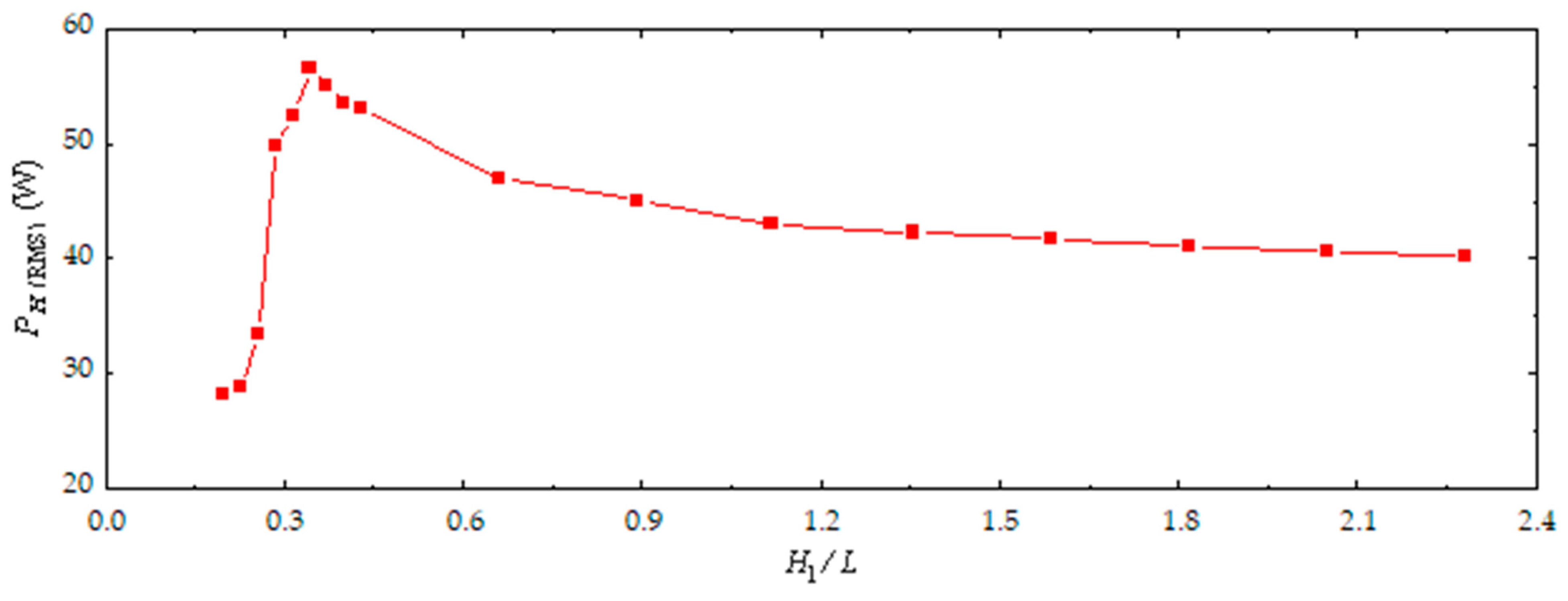
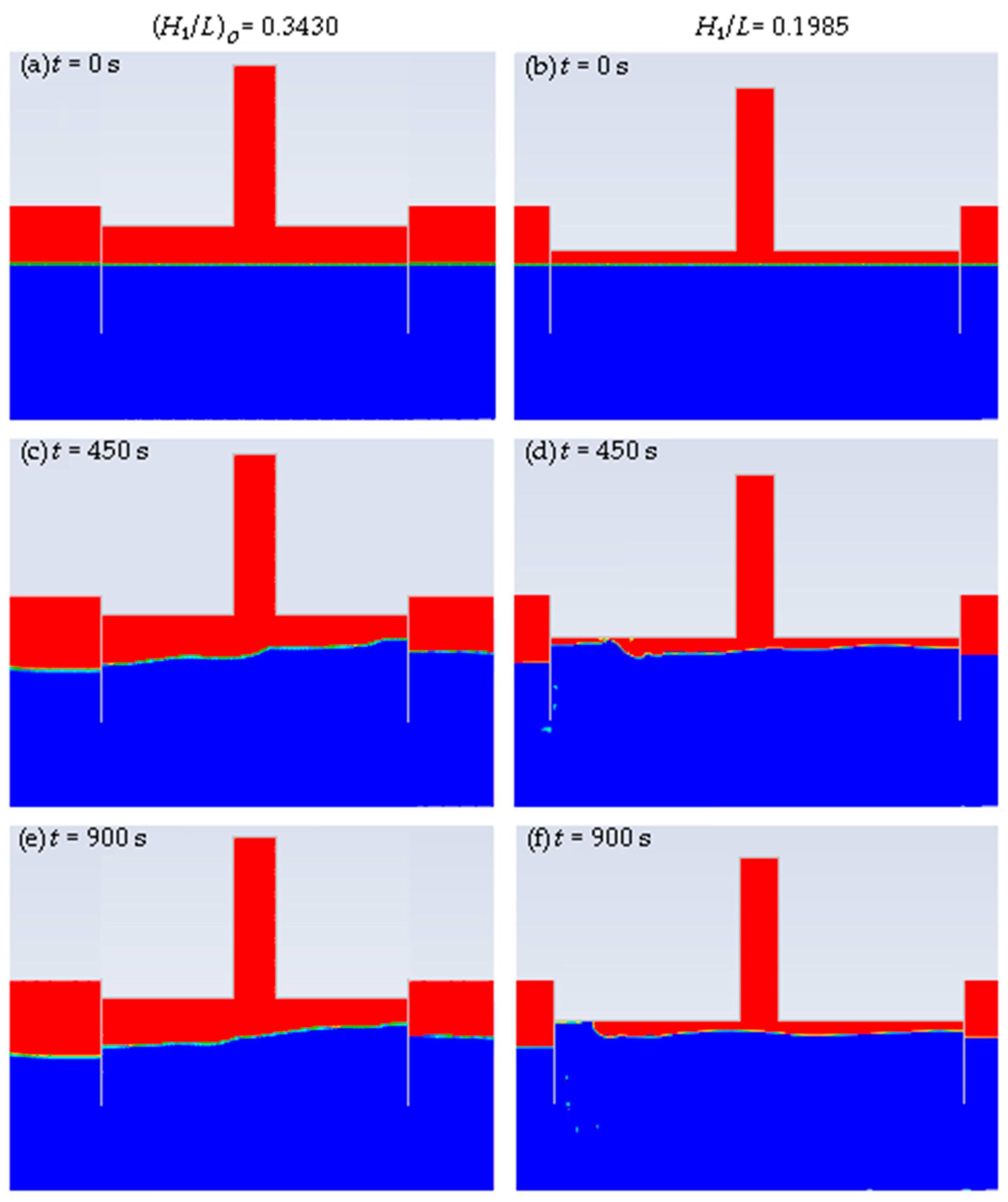
5.2. Geometric Evaluation of the Oscillating Water Column Device
5.3. Comparison with Results Found by Mocellin et al. [22]
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| channel area [m2] | |
| turbine duct area [m2] | |
| hydropneumatics chamber area [m2] | |
| linear damping coefficient [s−1] | |
| quadratic damping coefficient [m−1] | |
| relative differences [%] | |
| difference relative to the waves considered [%] | |
| espessura nas laterais do dispositivo OWC [m] | |
| gravity acceleration vector [m/s2] | |
| depth [m] | |
| height of the hydropneumatics chamber [m] | |
| height of the turbine duct [m] | |
| device submersion depth [m] | |
| wave channel height [m] | |
| significant height of the realistic sea state [m] | |
| final depth of the wave channel [m] | |
| wave number [m−1] | |
| l | length of the turbine duct [m] |
| length of the hydropneumatics chamber [m] | |
| wave channel length [m] | |
| mass flow rate of the air [kg/s] | |
| mean mass flow rate of the air [kg/s] | |
| N | total number of data [-] |
| numerical value [m] | |
| static pressure [pa] | |
| mean static pressure [pa] | |
| reference value [m] | |
| hydropneumatics power available [w] | |
| mean hydropneumatics power available [w] | |
| numerical beach sink term [-] | |
| mean period of the realistic sea state [s] | |
| T | wave period [s] |
| t | time [s] |
| horizontal velocity component [m/s] | |
| V | velocity along the z direction [m/s] |
| velocity vector [m/s] | |
| mesh elements [m] | |
| time step [s] | |
| horizontal coordinate axis [m] | |
| start position of the numerical beach [m] | |
| ending position of the numerical beach [m] | |
| X | quantity analyzed by the RMS metric [-] |
| vertical velocity component [m/s] | |
| vertical coordinate axis [m] | |
| vertical position of the channel bottom [m] | |
| vertical positions of the free surface [m] | |
| volume fraction [-] | |
| free surface elevation [m] | |
| wave length [m] | |
| fluid density [kg/m3] | |
| angular frequency [hz] | |
| stress deformation tensor [n/m2] | |
| dimensionless area fraction [-] |
References
- Sayed, E.T.; Olabi, A.G.; Alami, A.H.; Radwan, A.; Mdallal, A.; Rezk, A.; Abdelkareem, M.A. Renewable Energy and Energy Storage Systems. Energies 2023, 16, 1415. [Google Scholar] [CrossRef]
- Moreira, J.R.S.; Hernandez Neto, A.; Amaral, A.C.D.; Leite, B.M.; Pacheco, C.R.D.F.; Sowmy, D.S.; Parente, V. Energias Renováveis, Geração Distribuída e Eficiência Energética; LTC: Rio de Janeiro, Brazil, 2019. (In Portuguese) [Google Scholar]
- Falcão, A.F.D.O. Wave energy utilization: A review of the technologies. Renew. Sustain. Energy Rev. 2010, 14, 899–918. [Google Scholar] [CrossRef]
- Bejan, A. Shape and Structure, from Engineering to Nature; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Bejan, A.; Lorente, S. Constructal Theory of generation of configuration in nature and engineering. J. Appl. Phys. 2006, 100, 5. [Google Scholar] [CrossRef]
- Bejan, A.; Lorente, S. Design with Constructal Theory; Wiley: New Jersey, NJ, USA, 2008. [Google Scholar]
- Portillo, J.C.C.; Collins, K.M.; Gomes, R.P.F.; Henriques, J.C.C.; Gato, L.M.C.; Howey, B.D.; Hann, M.R.; Greaves, D.M.; Falcão, A.F.O. Wave energy converter physical model design and testing: The case of floating oscillating-water-columns. Appl. Energy 2020, 278, 115638. [Google Scholar] [CrossRef]
- Zabihi, M.; Mazaheri, S.; Namin, M.M.; Mazyak, A.R. Irregular wave interaction with an offshore OWC wave energy converter. Ocean Eng. 2021, 222, 108619. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, C.; Kim, K.; Li, M. Experimental study on the overall performance of a model OWC system under the free-spinning mode in irregular waves. Energy 2022, 250, 123779. [Google Scholar] [CrossRef]
- Pecher, A.; Kofoed, J.P. Handbook of Ocean Wave Energy; Springer Open: Cham, Switzerland, 2017. [Google Scholar]
- Rosa-Santos, P.; Taveira-Pinto, F.; Clemente, D.; Cabral, T.; Fiorentin, F.; Belga, F.; Morais, T. Experimental Study of a Hybrid Wave Energy Converter Integrated in a Harbor Breakwater. J. Mar. Sci. Eng. 2019, 7, 33. [Google Scholar] [CrossRef]
- Cabral, T.; Clemente, D.; Rosa-Santos, P.; Taveira-Pinto, F.; Morais, T.; Belga, F.; Cestaro, H. Performance Assessment of a Hybrid Wave Energy Converter Integrated into a Harbor Breakwater. Energies 2020, 13, 236. [Google Scholar] [CrossRef]
- Calheiros-Cabral, T.; Clemente, D.; Rosa-Santos, P.; Taveira-Pinto, F.; Ramos, V.; Morais, T.; Cestaro, H. Evaluation of the annual electricity production of a hybrid breakwater-integrated wave energy converter. Energy 2020, 213, 118845. [Google Scholar] [CrossRef]
- Clemente, D.; Calheiros-Cabral, T.; Rosa-Santos, P.; Taveira-Pinto, F. Hydraulic and Structural Assessment of a Rubble-Mound Breakwater with a Hybrid Wave Energy Converter. J. Mar. Sci. Eng. 2021, 9, 922. [Google Scholar] [CrossRef]
- Simonetti, I.; Esposito, A.; Cappietti, L. Experimental Proof-of-Concept of a Hybrid Wave Energy Converter Based on Oscillating Water Column and Overtopping Mechanisms. Energies 2022, 15, 8065. [Google Scholar] [CrossRef]
- Fenu, B.; Bonfanti, M.; Bardazzi, A.; Pilloton, C.; Lucarelli, A.; Mattiazzo, G. Experimental investigation of a Multi-OWC wind turbine floating platform. Ocean Eng. 2023, 281, 114619. [Google Scholar] [CrossRef]
- Hayati, M.; Nikseresht, A.H.; Haghighi, A.T. Sequential optimization of the geometrical parameters of an OWC device based on the specific wave characteristics. Renew. Energy 2020, 161, 386–394. [Google Scholar] [CrossRef]
- Bloss, V.; Cardozo, C.F.; Zinani, F.S.F.; Rocha, L.A.O. Evaluation of 3-D Computational Model of Oscillating Water Column Converter with Constructal Design with Three Degrees of Freedom and Limited Chimney Height. Defect Diffus. Forum 2021, 407, 128–137. [Google Scholar] [CrossRef]
- Chen, J.; Wen, H.; Wang, Y.; Wang, G. A correlation study of optimal chamber width with the relative front wall draught of onshore OWC device. Energy 2021, 225, 120307. [Google Scholar] [CrossRef]
- López, I.; Carballo, R.; Fouz, D.M.; Iglesias, G. Design Selection and Geometry in OWC Wave Energy Converters for Performance. Energies 2021, 14, 1707. [Google Scholar] [CrossRef]
- Mia, M.R.; Zhao, M.; Wu, H.; Munir, A. Numerical investigation of offshore oscillating water column devices. Renew. Energy 2022, 191, 380–393. [Google Scholar] [CrossRef]
- Mocellin, A.P.G.; Maciel, R.P.; Oleinik, P.H.; dos Santos, E.D.; Rocha, L.A.O.; Ziebell, J.S.; Isoldi, L.A.; Machado, B.N. Geometrical Analysis of an Oscillating Water Column Converter Device Considering Realistic Irregular Wave Generation with Bathymetry. J. Exp. Theor. Anal. 2023, 1, 24–43. [Google Scholar] [CrossRef]
- De Lima, Y.T.B.; Isoldi, L.A.; dos Santos, E.D.; Machado, B.N.; Gomes, M.d.N.; Biserni, C.; Rocha, L.A.O. Study of the Geometry of an Oscillating Water Column Device with Five Chambers Coupled under Regular Waves through the Constructal Design Method. Fluids 2024, 9, 86. [Google Scholar] [CrossRef]
- Koutrouveli, T.I.; Di Lauro, E.; das Neves, L.; Calheiros-Cabral, T.; Rosa-Santos, P.; Taveira-Pinto, F. Proof of concept of a breakwater-integrated hybrid wave energy converter using a composite modelling approach. J. Mar. Sci. Eng. 2021, 9, 226. [Google Scholar] [CrossRef]
- Wan, C.; Yang, C.; Bai, X.; Bi, C.; Chen, H.; Li, M.; Jin, Y.; Zhao, L. Numerical investigation on the hydrodynamics of a hybrid OWC wave energy converter combining a floating buoy. Ocean Eng. 2023, 281, 114818. [Google Scholar] [CrossRef]
- Yang, C.; Wan, C.; Bai, X.; Xu, T.; Zhao, L.; Chen, H.; Lars, J.; Baldock, T.E. Numerical investigation on the hydrodynamic and conversion performance of a dual cylindrical OWC integrated into a caisson-type breakwater. Ocean Eng. 2024, 305, 117991. [Google Scholar] [CrossRef]
- Zheng, S.; Antonini, A.; Zhang, Y.; Miles, J.; Greaves, D.; Zhu, G.; Iglesias, G. Hydrodynamic performance of a multi-oscillating water column (OWC) platform. Appl. Ocean Res. 2020, 99, 102168. [Google Scholar] [CrossRef]
- Liu, Z.; Xu, C.; Shi, H.; Qu, N. Wave-flume tests of a model-scaled OWC chamber-turbine system under irregular wave conditions. Appl. Ocean Res. 2020, 99, 102141. [Google Scholar] [CrossRef]
- Moretti, G.; Malara, G.; Scialò, A.; Daniele, L.; Romolo, A.; Vertechy, R.; Fontana, M.; Arena, F. Modelling and field testing of a breakwater-integrated U-OWC wave energy converter with dielectric elastomer generator. Renew. Energy 2020, 146, 628–642. [Google Scholar] [CrossRef]
- Singh, U.; Abdussamie, N.; Hore, J. Hydrodynamic performance of a floating offshore OWC wave energy converter: An experimental study. Renew. Sustain. Energy Rev. 2020, 117, 109501. [Google Scholar] [CrossRef]
- Zhou, Y.; Ning, D.; Shi, W.; Johanning, L.; Liang, D. Hydrodynamic investigation on an OWC wave energy converter integrated into an offshore wind turbine monopile. Coast. Eng. 2020, 162, 103731. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, L.; Li, M.; Johanning, L. Experimental investigation on the hydrodynamic performance of a multi-chamber OWC-breakwater. Renew. Sustain. Energy Rev. 2021, 150, 111512. [Google Scholar] [CrossRef]
- Yu, T.; Guo, Q.; Shi, H.; Li, T.; Meng, X.; He, S.; Li, P. Experimental investigation of a novel OWC wave energy converter. Ocean Eng. 2022, 257, 111567. [Google Scholar] [CrossRef]
- Çelik, A. An experimental investigation into the effects of front wall geometry on OWC performance for various levels of applied power take off dampings. Ocean Eng. 2022, 248, 110761. [Google Scholar] [CrossRef]
- Zhou, Y.; Ning, D.; Chen, L.; Mayon, R.; Zhang, C. Experimental investigation on an OWC wave energy converter integrated into a floating offshore wind turbine. Energy Convers. Manag. 2023, 276, 116546. [Google Scholar] [CrossRef]
- Kim, J.-S.; Nam, B.W.; Kim, K.-H.; Park, S.; Shin, S.H.; Hong, K. A Numerical Study on Hydrodynamic Performance of an Inclined OWC Wave Energy Converter with Nonlinear Turbine–Chamber Interaction based on 3D Potential Flow. J. Mar. Sci. Eng. 2020, 8, 176. [Google Scholar] [CrossRef]
- Han, M.M.; Wang, C.M. Coupled analytical-numerical approach for determining hydrodynamic responses of breakwater with multiple OWCs. Mar. Struct. 2021, 80, 103097. [Google Scholar] [CrossRef]
- Kim, J.-S.; Kim, K.-H.; Park, J.; Park, S.; Shin, S.H. A Numerical Study on Hydrodynamic Energy Conversions of OWC-WEC with the Linear Decomposition Method under Irregular Waves. Energies 2021, 14, 1522. [Google Scholar] [CrossRef]
- Pols, A.; Gubesch, E.; Abdussamie, N.; Penesis, I.; Chin, C. Mooring Analysis of a Floating OWC Wave Energy Converter. J. Mar. Sci. Eng. 2021, 9, 228. [Google Scholar] [CrossRef]
- Cong, P.; Teng, B.; Liu, Y.; Ning, D. A numerical approach for hydrodynamic performance evaluation of multi-degree-of-freedom floating oscillating water column (OWC) devices. J. Fluids Struct. 2022, 114, 103730. [Google Scholar] [CrossRef]
- Gang, A.; Guo, B.; Hu, Z.; Hu, R. Performance analysis of a coast–OWC wave energy converter integrated system. App. Energy 2022, 311, 118605. [Google Scholar] [CrossRef]
- Qu, M.; Yu, D.; Xu, Z.; Gao, Z. The effect of the elliptical front wall on energy conversion performance of the offshore OWC chamber: A numerical study. Energy 2022, 255, 124428. [Google Scholar] [CrossRef]
- Cannata, G.; Simone, M.; Gallerano, F. Numerical Investigation into the Performance of an OWC Device under Regular and Irregular Waves. J. Mar. Sci. Eng. 2023, 11, 735. [Google Scholar] [CrossRef]
- Maciel, R.P.; Oleinik, P.H.; Dos Santos, E.D.; Rocha, L.A.O.; Machado, B.N.; Gomes, M.d.N.; Isoldi, L.A. Constructal Design Applied to an Oscillating Water Column Wave Energy Converter Device under Realistic Sea State Conditions. J. Mar. Sci. Eng. 2023, 11, 2174. [Google Scholar] [CrossRef]
- Naik, N.; Gayathri, R.; Behera, H.; Tsai, C.C. Wave power extraction by a dual OWC chambers over an undulated bottom. Renew. Energy 2023, 216, 119026. [Google Scholar] [CrossRef]
- Qu, M.; Yu, D.; Li, Y.; Gao, Z. Effect of relative chamber width on energy conversion and mechanical characteristics of the offshore OWC device: A numerical study. Energy 2023, 275, 127372. [Google Scholar] [CrossRef]
- ANSYS. ANSYS Fluent Theory Guide, Release 20.2; ANSYS Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Maliska, C.R. Tranferência de Calor e Mecânica dos Fluidos Computacional; LTC—Livros Técnicos e Científicos: Rio de Janeiro, Brazil, 2004. (In Portuguese) [Google Scholar]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary Layer Theory, 7th ed.; McGraw-Hill: New York, NY, USA, 1979. [Google Scholar]
- Versteeg, H.K.; Malalasekera, W. An Introduction to Computational Fluid Dynamics—The Finite Volume Method; Pearson Education Limited: London, UK, 2007. [Google Scholar]
- Park, J.C.; Kim, M.H.; Miyata, H.; Chun, H.H. Fully nonlinear numerical wave tank (NWT) simulations and wave run-up prediction around 3-D structures. Ocean Eng. 2003, 30, 1969–1996. [Google Scholar] [CrossRef]
- Foyhirun, C.; Kositgittiwong, D.; Ekkawatpanit, C. Wave Energy Potential and Simulation on the Andaman Sea Coast of Thailand. Sustainability 2020, 12, 3657. [Google Scholar] [CrossRef]
- Lisboa, R.C.; Teixeira, P.R.; Didier, E. Regular and Irregular wave propagation analysis in a flume with numerical beach using a Navier-stokes based model. Defect Diffus. Forum 2017, 372, 81–90. [Google Scholar] [CrossRef]
- Gomes, M.N.; Lorenzini, G.; Rocha, L.A.O.; Dos Santos, E.D.; Isoldi, L.A. Constructal Design Applied to the Geometric Evaluation of an Oscillating Water Column Wave Energy Converter Considering Different Real Scale Wave Periods. J. Eng. Thermophys. 2018, 27, 173–190. [Google Scholar] [CrossRef]
- Issa, R.I. Solution of the implicitly discretized fluid flow equations by operator-splitting. J. Comput. Phys. 1986, 62, 40–65. [Google Scholar] [CrossRef]
- Patankar, S.V. Numerical Heat Transfer and Fluid Flow; McGraw Hill: New York, NY, USA, 1980. [Google Scholar]
- Holthuijsen, L.H. Waves in Oceanic and Coastal Waters; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Oleinik, P.H. O programa Spec2Wave. Manual do usuário. Versão 1.2.1. 2022. Available online: https://gist.github.com/PhelypeOleinik/6dc87900dbde73ad33575b9d333e1f35 (accessed on 20 January 2024). (In Portuguese).
- Awk, T. TOMAWAC User Manual; Version 7.2. 7.2.3; The Telemac-Mascaret Consortium; TELEMAC: Chambéry, France, 2017. [Google Scholar]
- Dean, R.G.; Dalrymple, R.A. Water Wave Mechanics for Engineers and Scientists; World Scientific Publishing Company: Singapore, 1991. [Google Scholar]
- Chakrabarti, S.K. Handbook of Offshore Engineering; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar]
- Dos Santos, E.D.; Isoldi, L.A.; Gomes, M.D.N.; Rocha, L.A. The constructal design applied to renewable energy systems. In Sustainable Energy Technologies; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Dizadji, N.; Sajadian, S.E. Modeling and optimization of the chamber of OWC system. Energy 2011, 36, 2360–2366. [Google Scholar] [CrossRef]
- Gomes, M.D.N.; Nascimento, C.D.D.; Bonafini, B.L.; Santos, E.D.D.; Isoldi, L.A.; Rocha, L.A.O. Two-dimensional geometric optimization of an oscillating water column converter in laboratory scale. Thermal Eng. 2012, 11, 30–36. [Google Scholar] [CrossRef]
- Cardoso, S.D.; Marques, W.C.; Kirinus, E.d.P.; Stringari, C.E. Levantamento batimétrico usando cartas náuticas. In 13ª Mostra da Produção Universitária; Federal University of Rio Grande: Rio Grande, Brazil, 2014. (In Portuguese) [Google Scholar]
- Mavriplis, D.J. Unstructured Grid Techniques. Annual Rev. Fluid Mec. 1997, 29, 473–514. [Google Scholar] [CrossRef]
- Gomes M das, N.; Isoldi, L.A.; Santos, E.D.; Rocha, L.A.O. Análise de Malhas para Geração Numérica de Ondas em Tanques. In Proceedings of the VII Congresso Nacional de Engenharia Mecânica, São Luiz, MA, USA, 1–10 July 2012. (In Portuguese). [Google Scholar]
- Barros, A.S.; Fragassa, C.; Paiva, M.d.S.; Rocha, L.A.O.; Machado, B.N.; Isoldi, L.A.; Gomes, M.d.N.; dos Santos, E.D. Numerical Study and Geometrical Investigation of an Onshore Overtopping Device Wave Energy Converter with a Seabed Coupled Structure. J. Mar. Sci. Eng. 2023, 11, 412. [Google Scholar] [CrossRef]
- Thum, G.Ü.; Maciel, R.P.; Oleinik, P.H.; Rocha, L.A.O.; dos Santos, E.D.; Seibt, F.M.; Machado, B.N.; Isoldi, L.A. Numerical Analysis of the Submerged Horizontal Plate Device Subjected to Representative Regular and Realistic Irregular Waves of a Sea State. Fluids 2024, 9, 188. [Google Scholar] [CrossRef]
- Barreiro, T.G. Estudo da Interação de uma onda Monocromática com um Conversor de Energia. Master’s Thesis, Universidade de Nova Lisboa, Lisbon, Portugal, 2009. (In Portuguese). [Google Scholar]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)? Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Maciel, R.P.; Fragassa, C.; Machado, B.N.; Rocha, L.A.O.; dos Santos, E.D.; Gomes, M.N.; Isoldi, L.A. Verification and Validation of a Methodology to Numerically Generate Waves Using Transient Discrete Data as Prescribed Velocity Boundary Condition. J. Mar. Sci. Eng. 2021, 9, 896. [Google Scholar] [CrossRef]



| Parameters | Numerical Inputs | |
|---|---|---|
| Solver | Pressure Based | |
| Pressure–Velocity Coupling | PISO | |
| Spatial Discretization | Gradient Evaluation | Green Gauss Cell Based |
| Pressure | PRESTO | |
| Momentum | First Order Upwind | |
| Volume Fraction | Geo-Reconstruct | |
| Temporal Differencing Scheme | First Order Implicit | |
| Under-Relaxation Factors | Pressure | 0.3 |
| Momentum | 0.7 | |
| Residual | Continuity | 10−3 |
| x Velocity | ||
| z Velocity | ||
| Regime Flow | Laminar |
| Characteristic | Nomenclature | Magnitude |
|---|---|---|
| Height | (m) | 0.90 |
| Length | λ (m) | 45.91 |
| Period | (s) | 5.70 |
| Depth | h (m) | 10.98 |
| (m) | (m) | |
|---|---|---|
| 0.1985 | 5.65 | 28.46 |
| 0.2274 | 6.04 | 26.59 |
| 0.2563 | 6.42 | 25.04 |
| 0.2852 | 6.77 | 23.74 |
| 0.3141 | 7.10 | 22.62 |
| 0.3430 | 7.42 | 21.65 |
| 0.3719 | 7.73 | 20.79 |
| 0.4008 | 8.02 | 20.03 |
| 0.4297 | 8.31 | 19.34 |
| 0.6608 | 10.31 | 15.16 |
| 0.8920 | 11.98 | 13.43 |
| 1.1167 | 13.40 | 12.00 |
| 1.3543 | 14.76 | 10.90 |
| 1.5854 | 15.97 | 10.07 |
| 1.8166 | 17.09 | 9.41 |
| 2.0478 | 18.15 | 8.86 |
| 2.2789 | 19.14 | 8.40 |
| (%) | ||
|---|---|---|
| 0.1985 | 28.19 | - |
| 0.2274 | 28.71 | +1.81 |
| 0.2563 | 33.38 | +13.99 |
| 0.2852 | 49.79 | +32.95 |
| 0.3141 | 52.41 | +5.26 |
| 0.3430 | 56.66 | +7.50 |
| 0.3719 | 55.07 | −2.88 |
| 0.4008 | 53.57 | −2.80 |
| 0.4297 | 53.15 | −0.78 |
| 0.6608 | 46.95 | −11.66 |
| 0.8920 | 45.09 | −3.96 |
| 1.1167 | 43.06 | −4.50 |
| 1.3543 | 42.26 | −1.87 |
| 1.5854 | 41.70 | −1.31 |
| 1.8166 | 41.04 | −1.59 |
| 2.0478 | 40.64 | −0.98 |
| 2.2789 | 40.19 | −1.09 |
| —Mocellin et al. [22] | —Present Study | (%) | |
|---|---|---|---|
| 0.1985 | 25.44 | 28.19 | +10.80 |
| 0.4297 | 19.86 | 53.15 | +167.67 |
| 0.6608 | 17.65 | 46.95 | +166.06 |
| 0.8920 | 16.07 | 45.09 | +180.61 |
| 1.1167 | 14.88 | 43.06 | +189.38 |
| 1.3543 | 13.94 | 42.26 | +203.20 |
| 1.5854 | 13.10 | 41.70 | +218.42 |
| 1.8166 | 12.39 | 41.04 | +231.30 |
| 2.0478 | 11.73 | 40.64 | +246.40 |
| 2.2789 | 11.15 | 40.19 | +260.65 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mocellin, A.P.G.; Paiva, M.d.S.; dos Santos, E.D.; Rocha, L.A.O.; Isoldi, L.A.; Ziebell, J.S.; Machado, B.N. Geometric Evaluation of an Oscillating Water Column Wave Energy Converter Device Using Representative Regular Waves of the Sea State Found in Tramandaí, Brazil. Processes 2024, 12, 2352. https://doi.org/10.3390/pr12112352
Mocellin APG, Paiva MdS, dos Santos ED, Rocha LAO, Isoldi LA, Ziebell JS, Machado BN. Geometric Evaluation of an Oscillating Water Column Wave Energy Converter Device Using Representative Regular Waves of the Sea State Found in Tramandaí, Brazil. Processes. 2024; 12(11):2352. https://doi.org/10.3390/pr12112352
Chicago/Turabian StyleMocellin, Ana Paula Giussani, Maycon da Silveira Paiva, Elizaldo Domingues dos Santos, Luiz Alberto Oliveira Rocha, Liércio André Isoldi, Juliana Sartori Ziebell, and Bianca Neves Machado. 2024. "Geometric Evaluation of an Oscillating Water Column Wave Energy Converter Device Using Representative Regular Waves of the Sea State Found in Tramandaí, Brazil" Processes 12, no. 11: 2352. https://doi.org/10.3390/pr12112352
APA StyleMocellin, A. P. G., Paiva, M. d. S., dos Santos, E. D., Rocha, L. A. O., Isoldi, L. A., Ziebell, J. S., & Machado, B. N. (2024). Geometric Evaluation of an Oscillating Water Column Wave Energy Converter Device Using Representative Regular Waves of the Sea State Found in Tramandaí, Brazil. Processes, 12(11), 2352. https://doi.org/10.3390/pr12112352











