Study on the Vertical Propagation Behavior of Hydraulic Fractures in Thin Interbedded Tight Sandstone
Abstract
1. Introduction
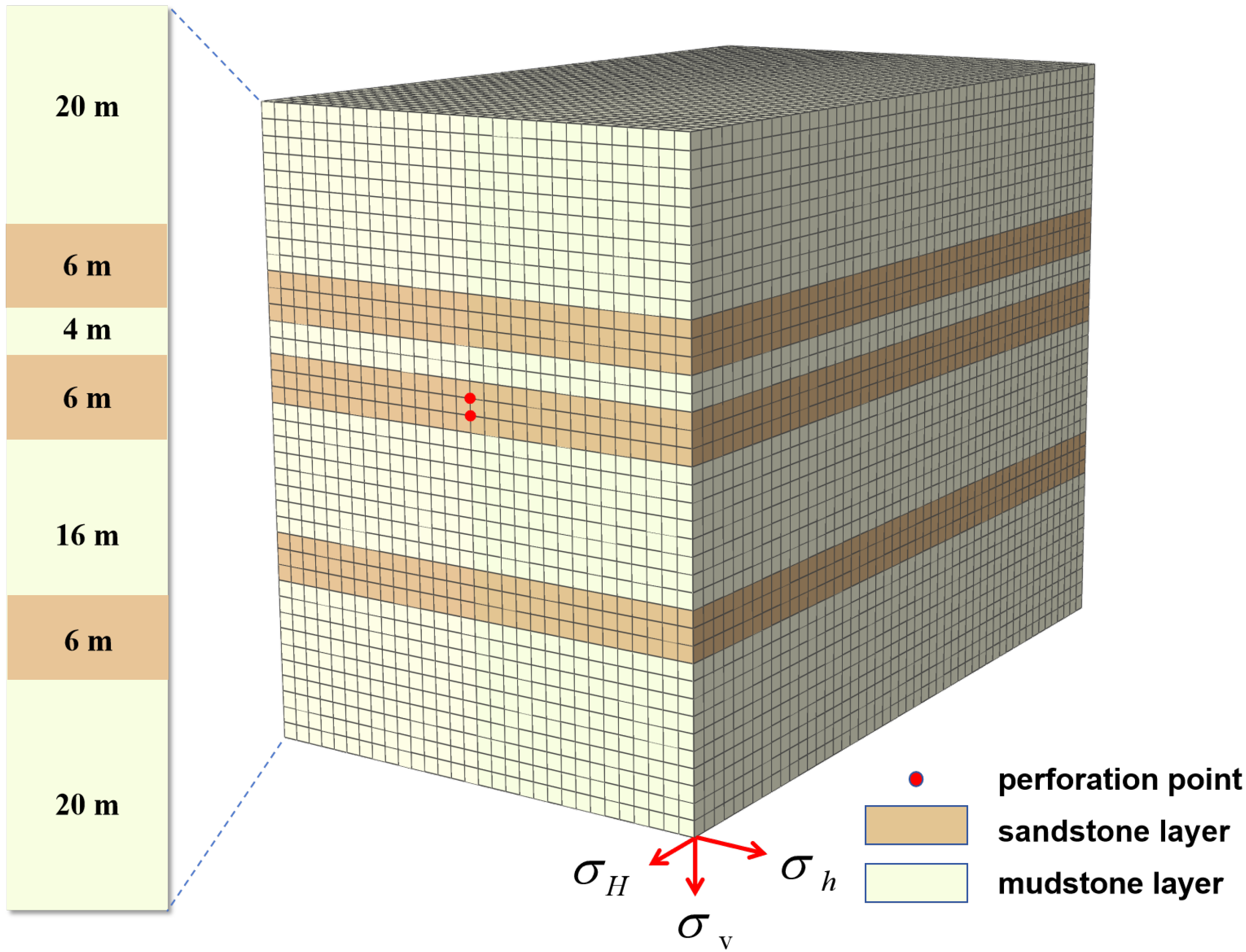
2. Overview of the Study Area
3. Method
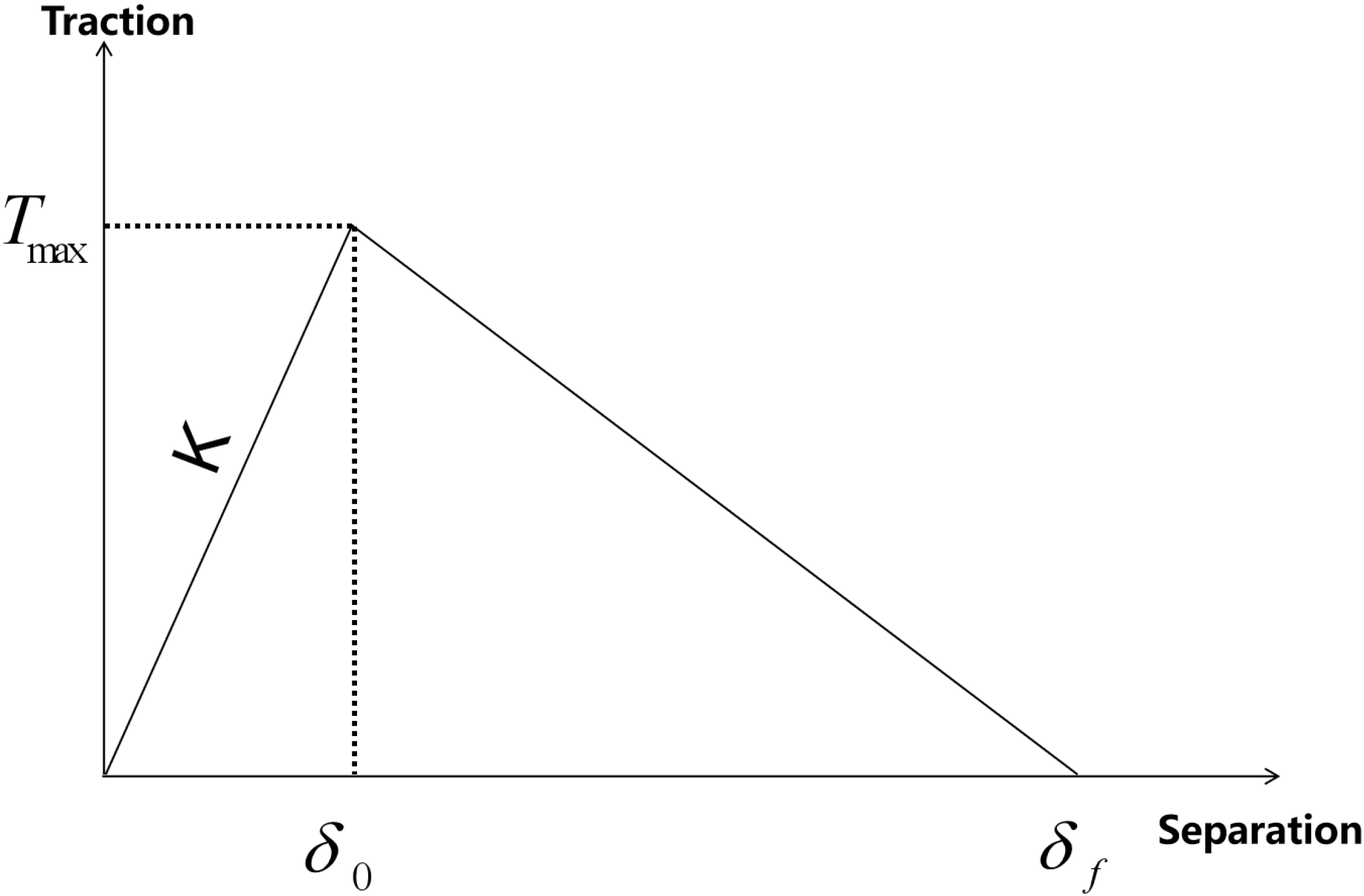
3.1. Cohesive Zone Model
3.1.1. Cohesive Element
- represents the initial thickness of the cohesive element;
- represents the displacement in the normal direction;
- and represent the displacements in the two directions perpendicular to the normal.
3.1.2. The Criterion for Crack Initiation and Propagation
- represents the normal stress;
- and represent the shear stresses in two directions;
- 〈〉 indicates that no damage occurs under tensile or compressive stress;
- the superscript denotes the critical values.
- represents the actual normal stress;
- D is the damage factor;
- is the undamaged normal stress, which characterizes the overall failure extent of the cohesive element;
- and represent the shear stresses in two directions;
- and are the undamaged shear stresses in the two directions.
- and represent the initial and final damage displacements,
- represents the maximum displacement.
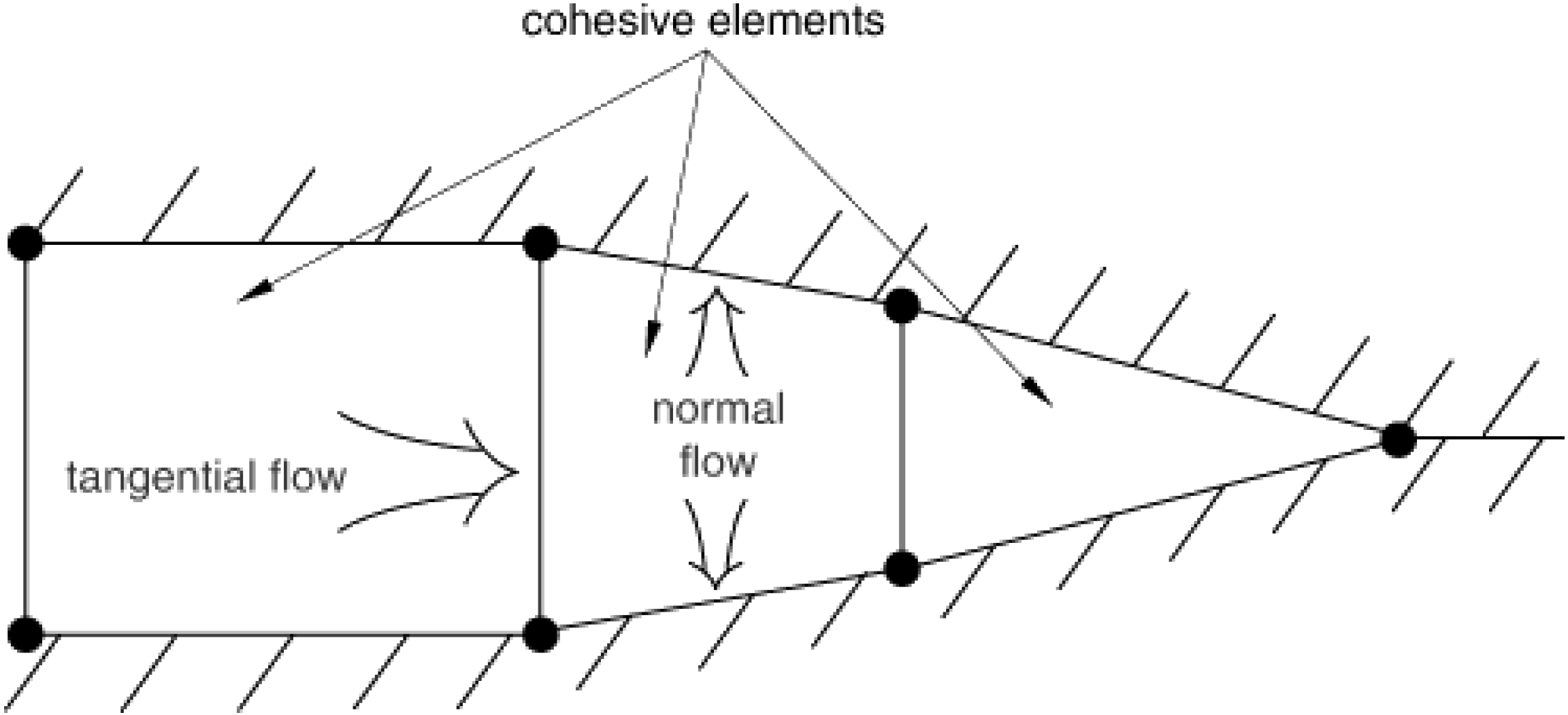
3.1.3. The Fluid Flow Equation Within Fractures
- q represents the tangential flow rate;
- d is the fracture width;
- is the viscosity of the fracturing fluid;
- is the fluid pressure gradient.
- and represent the flow rates at the upper and lower surfaces, respectively;
- and are the leakage coefficients at the upper and lower surfaces, respectively;
- is the fluid pressure within the hydraulic fracture;
- and are the pore pressures at the upper and lower surfaces, respectively.
3.2. Numerical Model
4. Result and Discussion
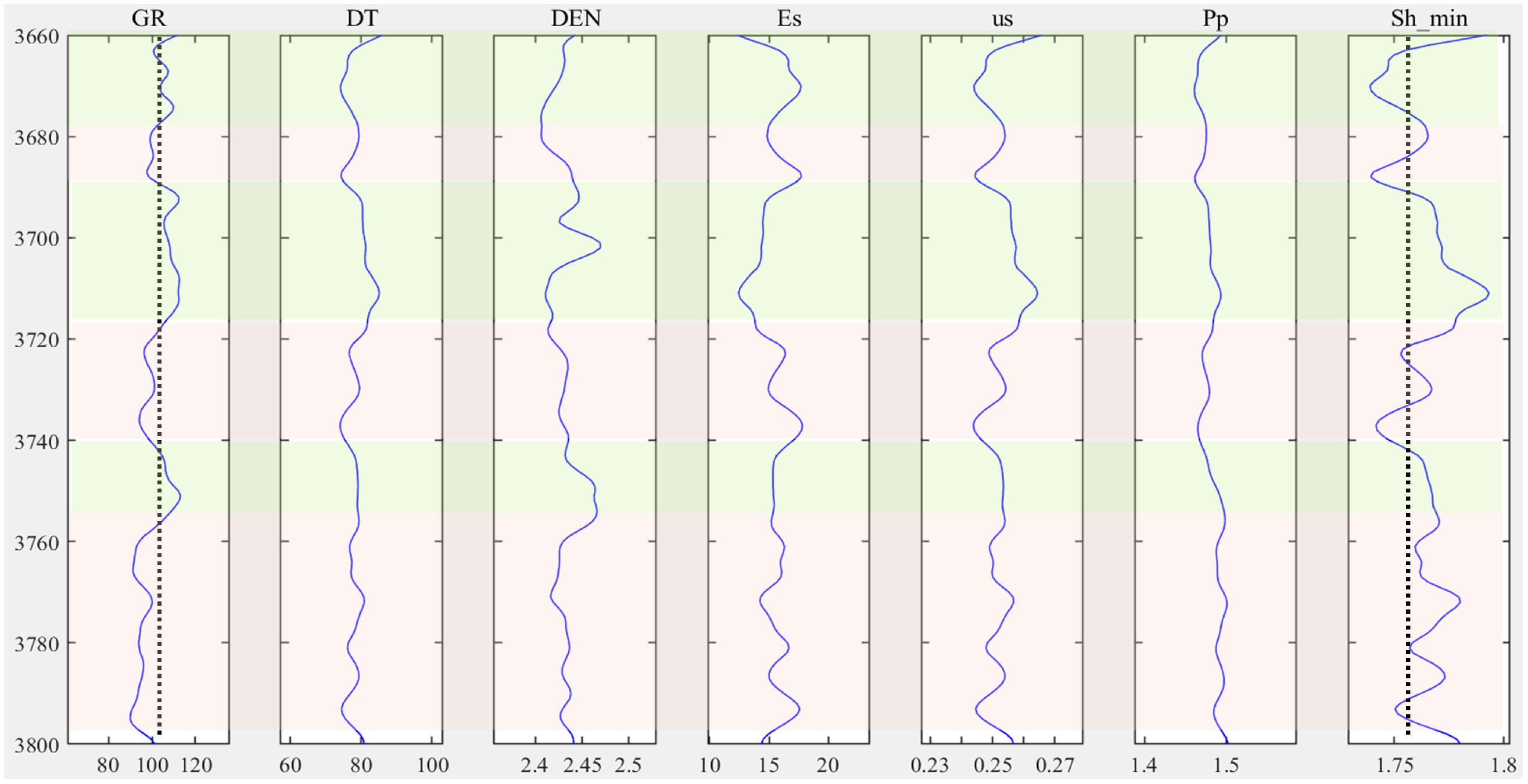
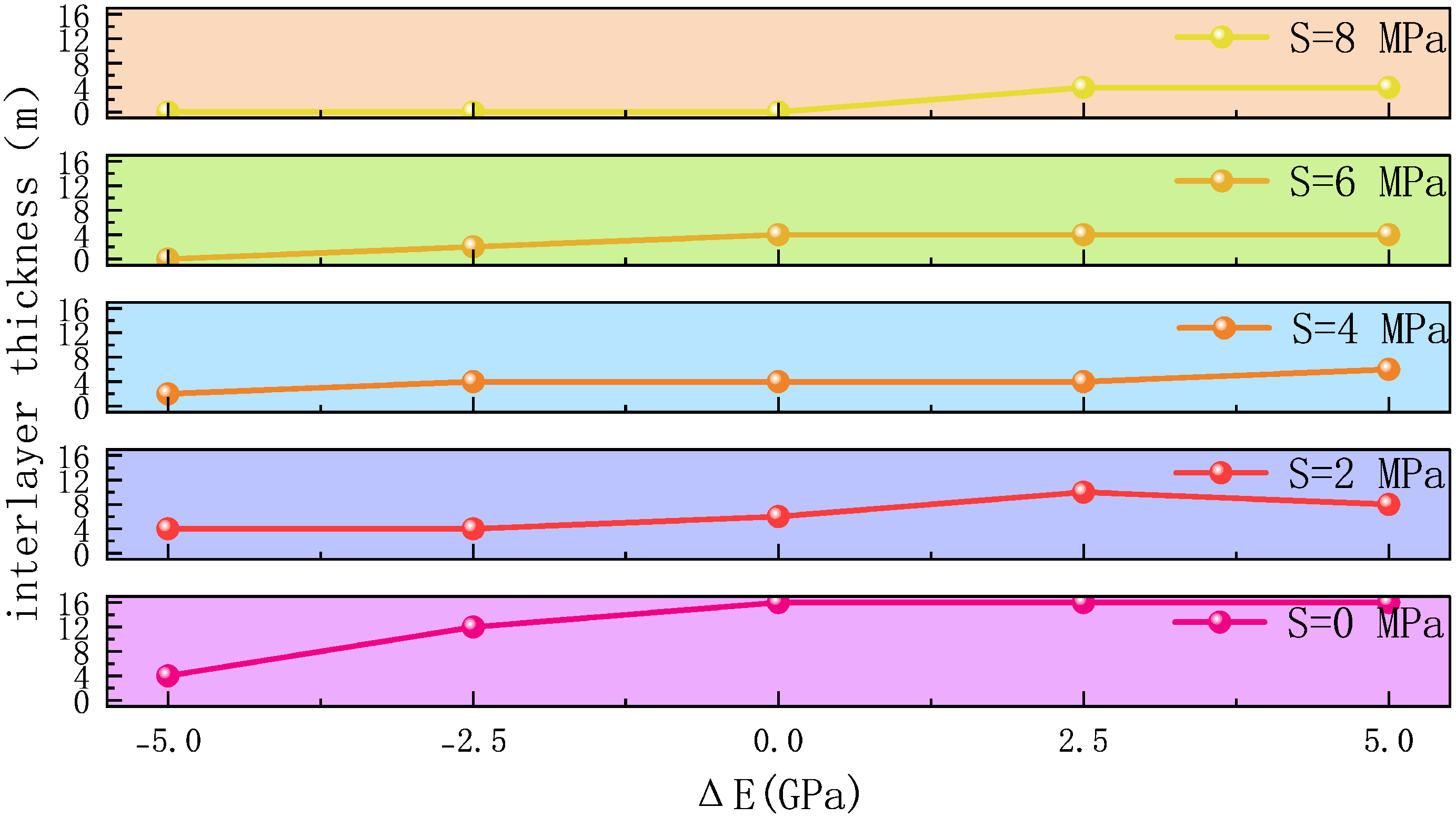
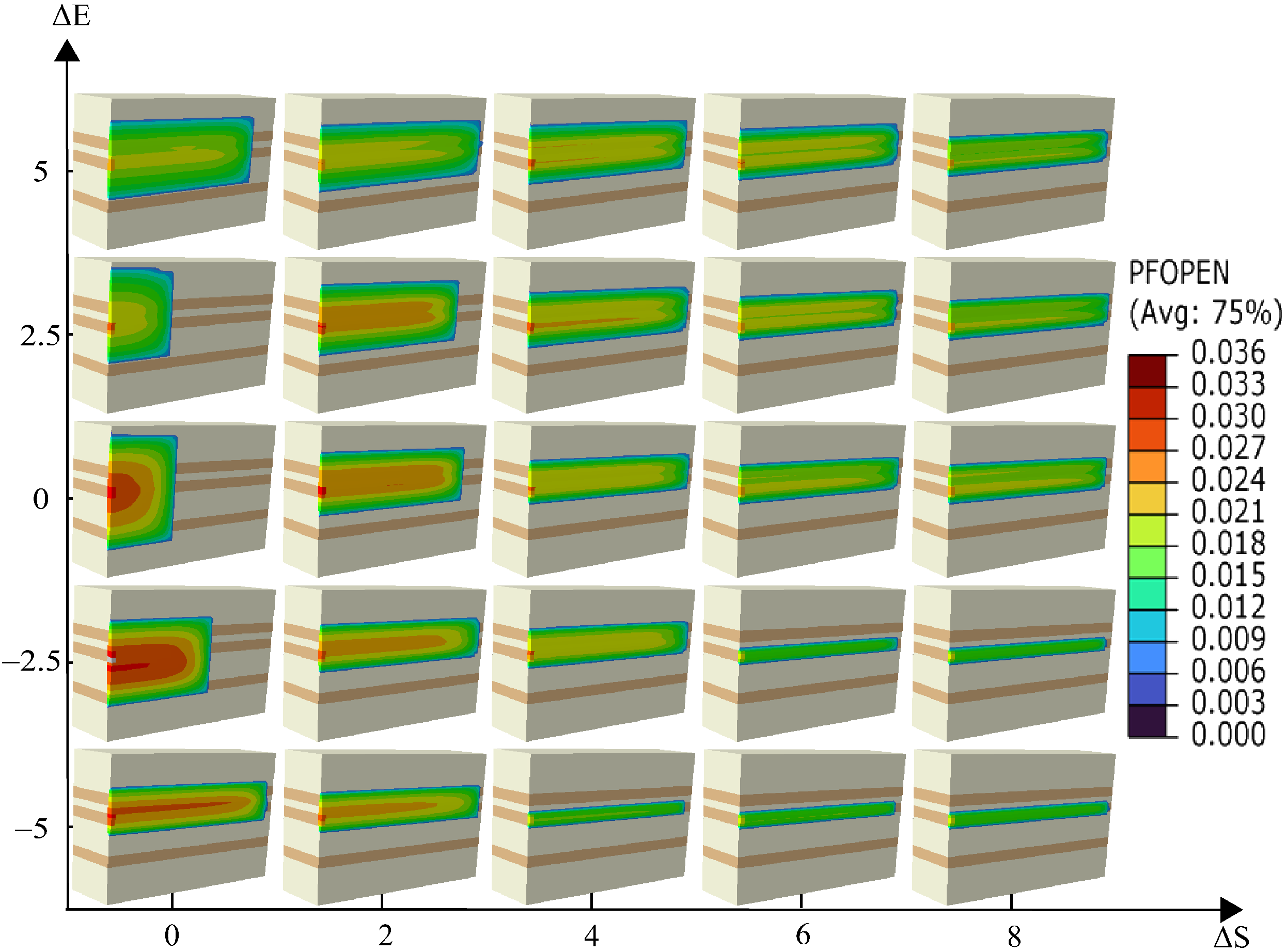
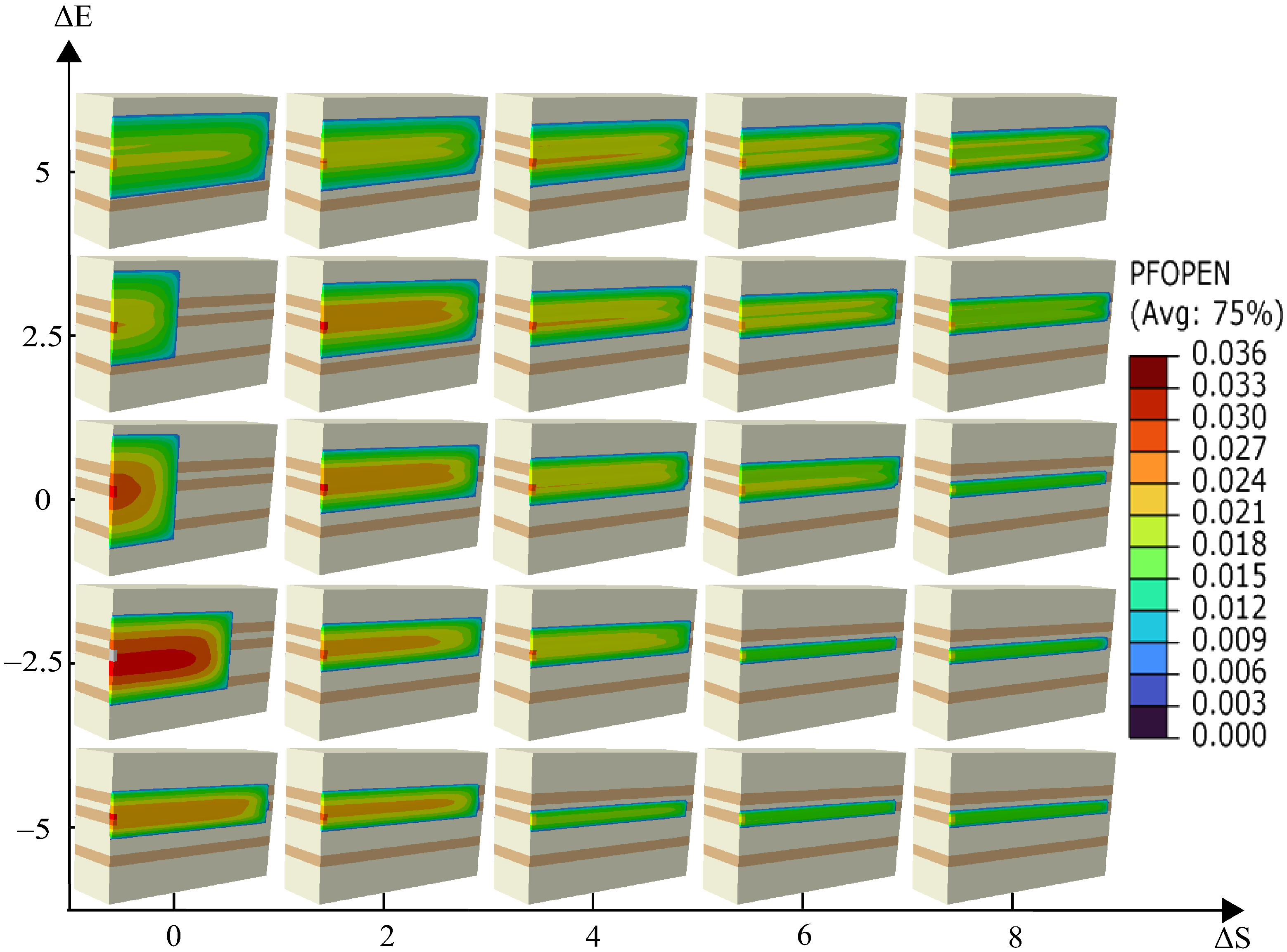
4.1. Interlayer Stress Contrast
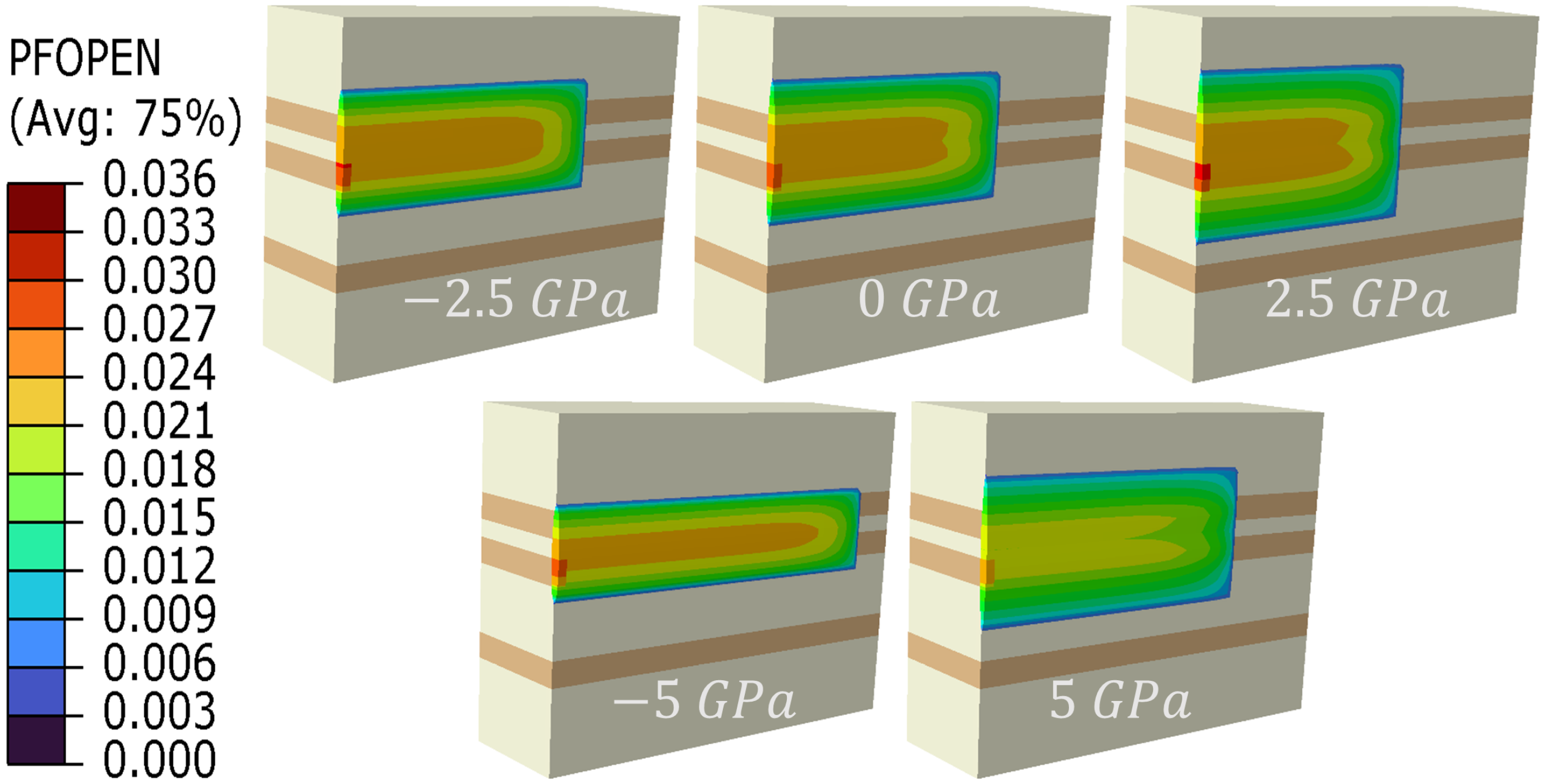
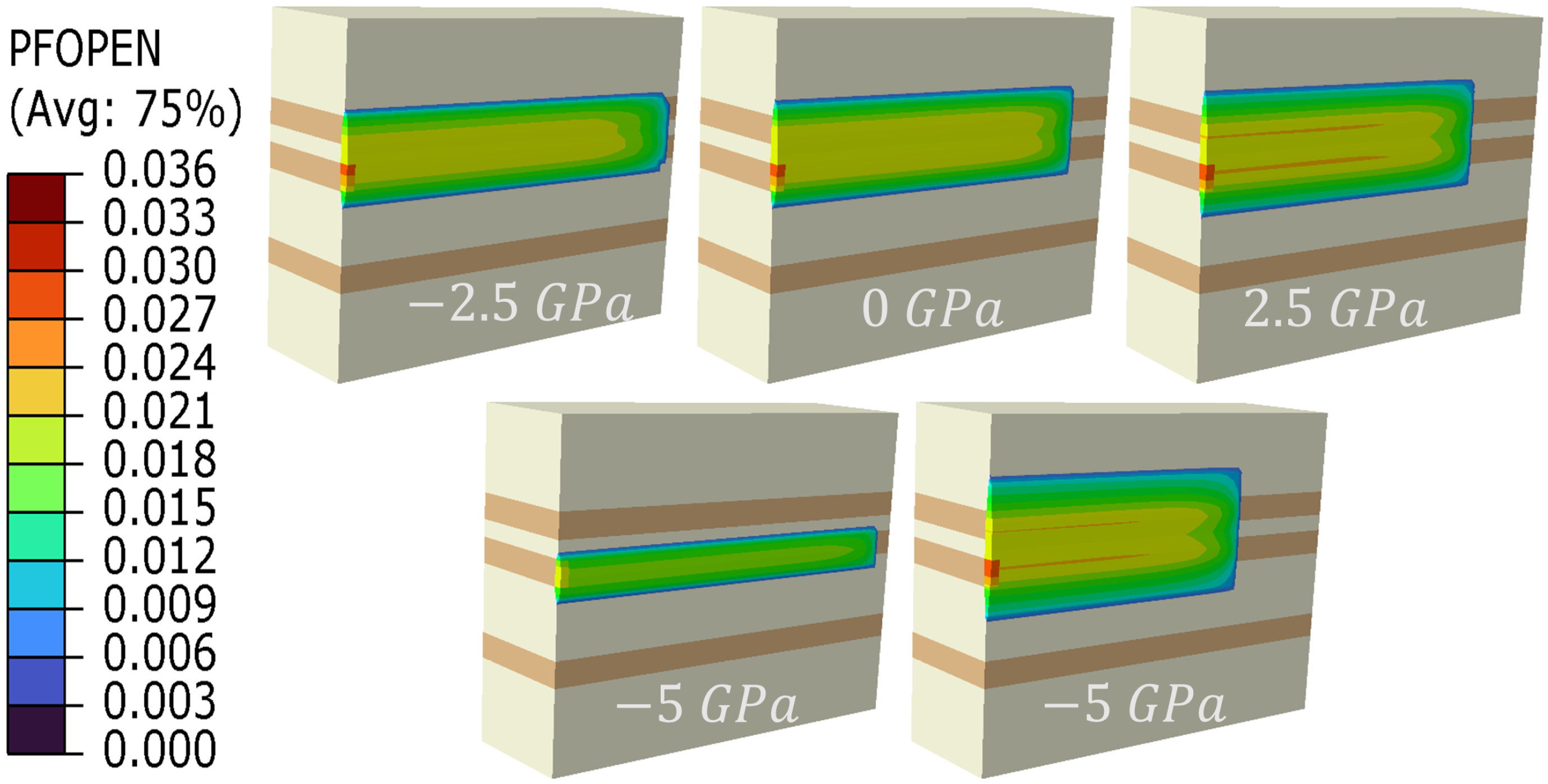
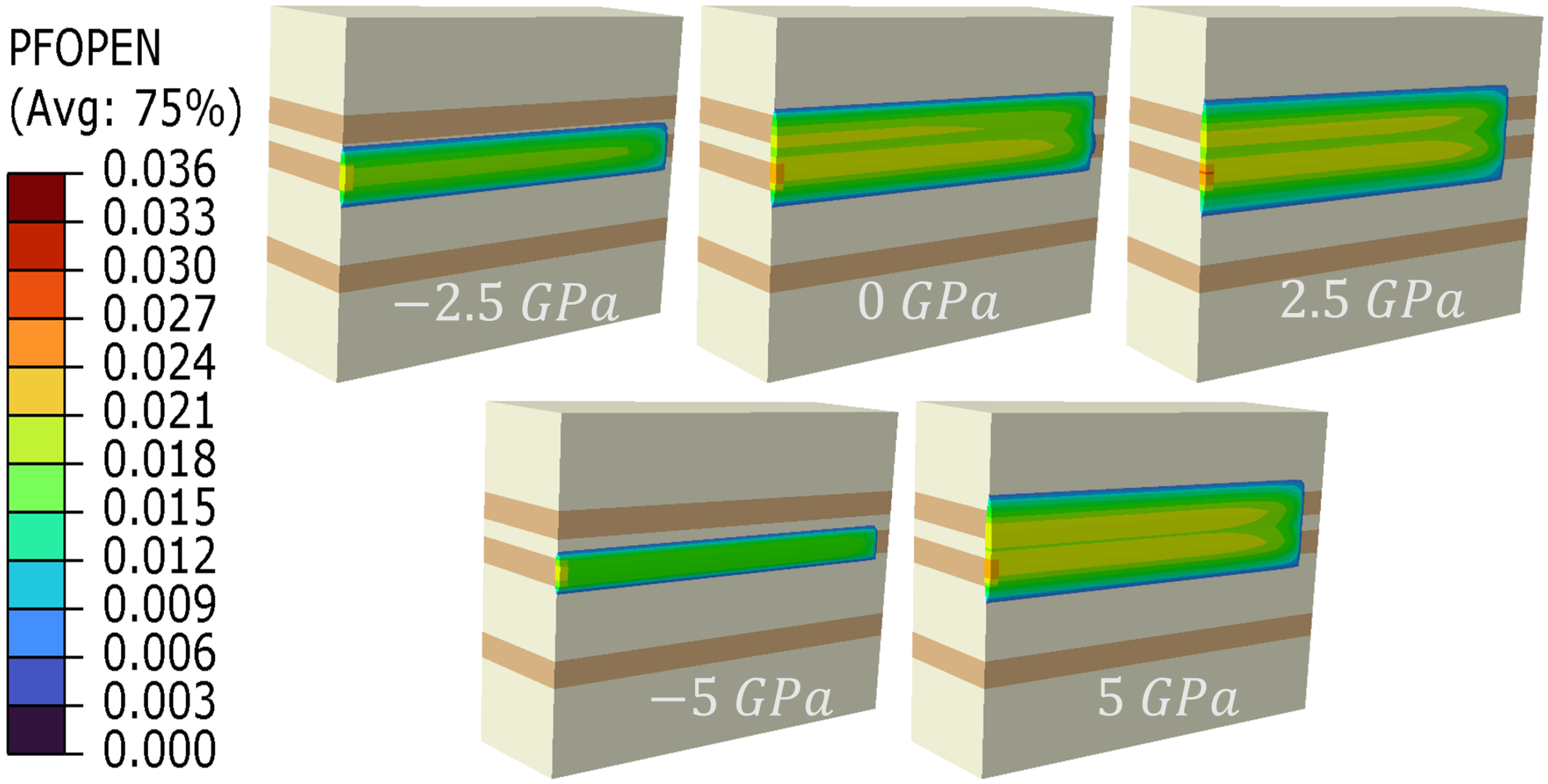
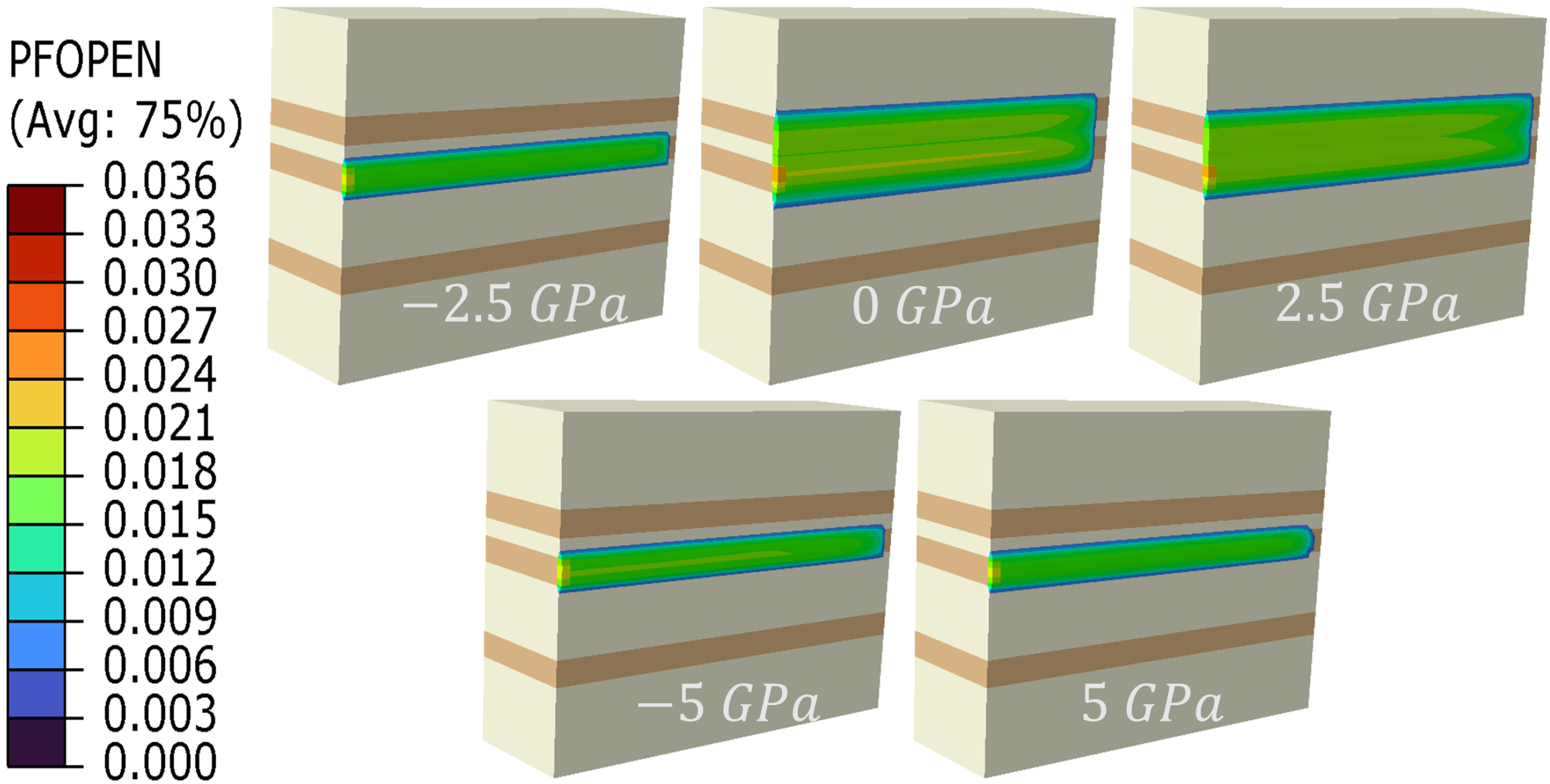
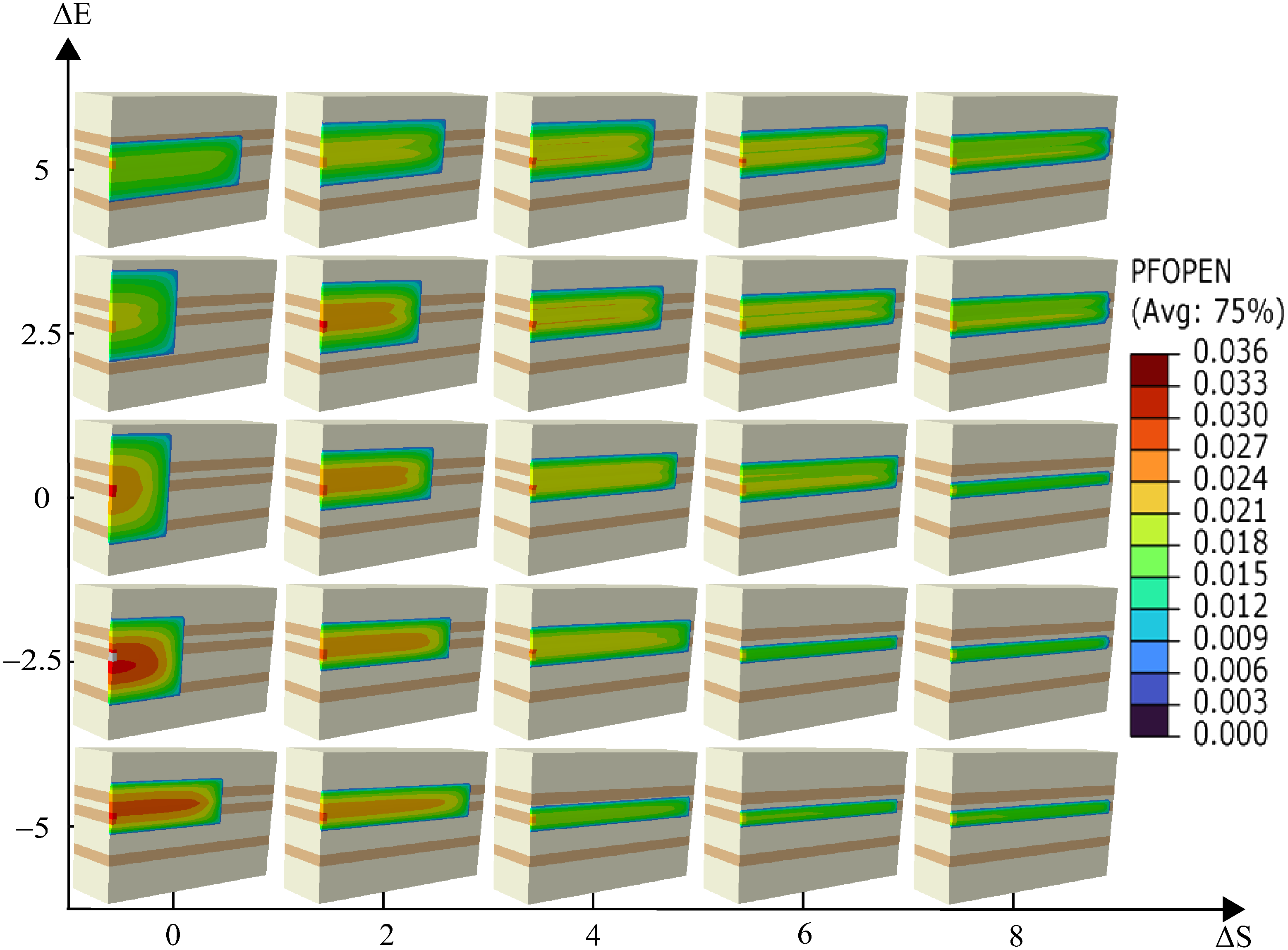
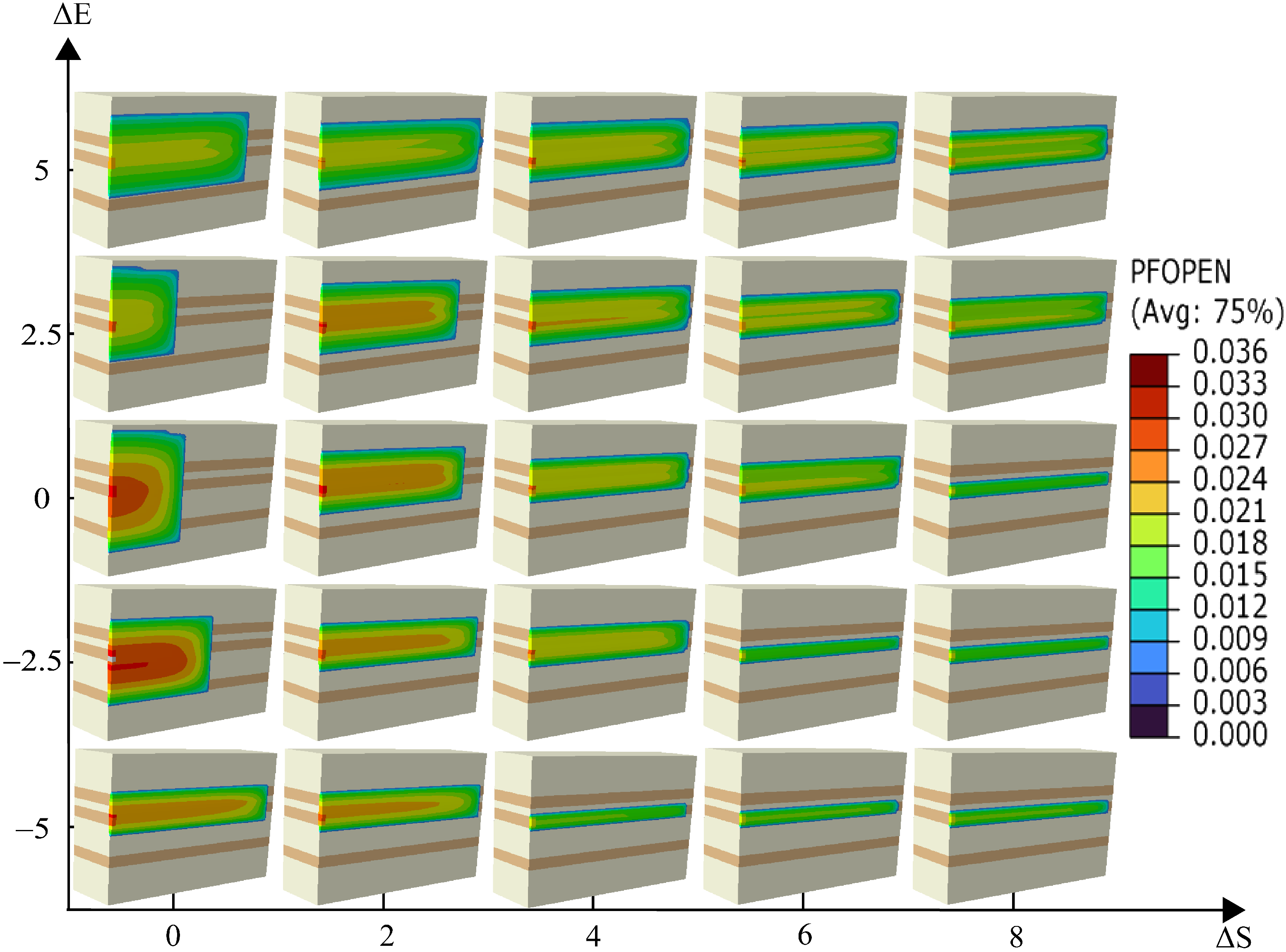
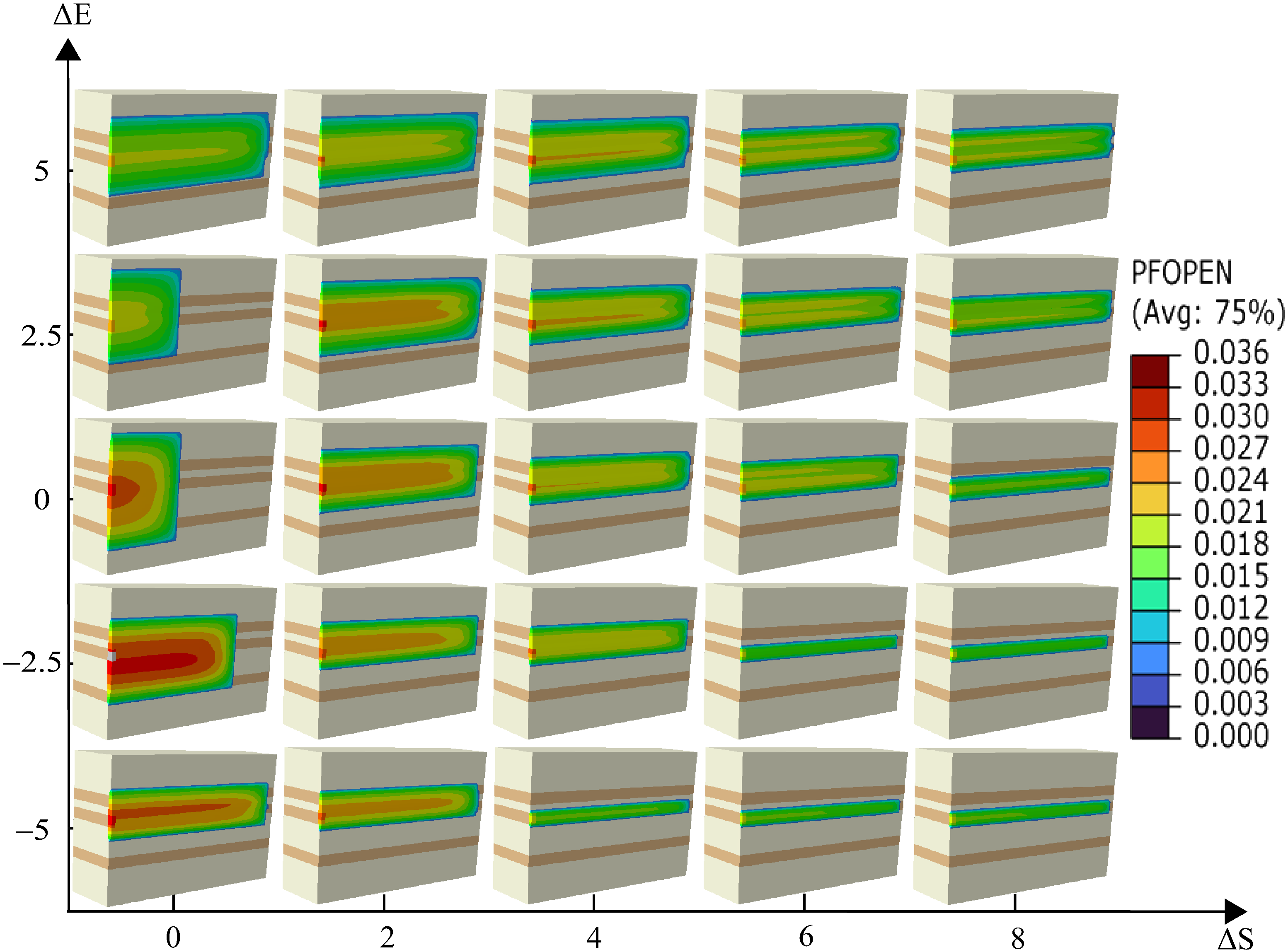
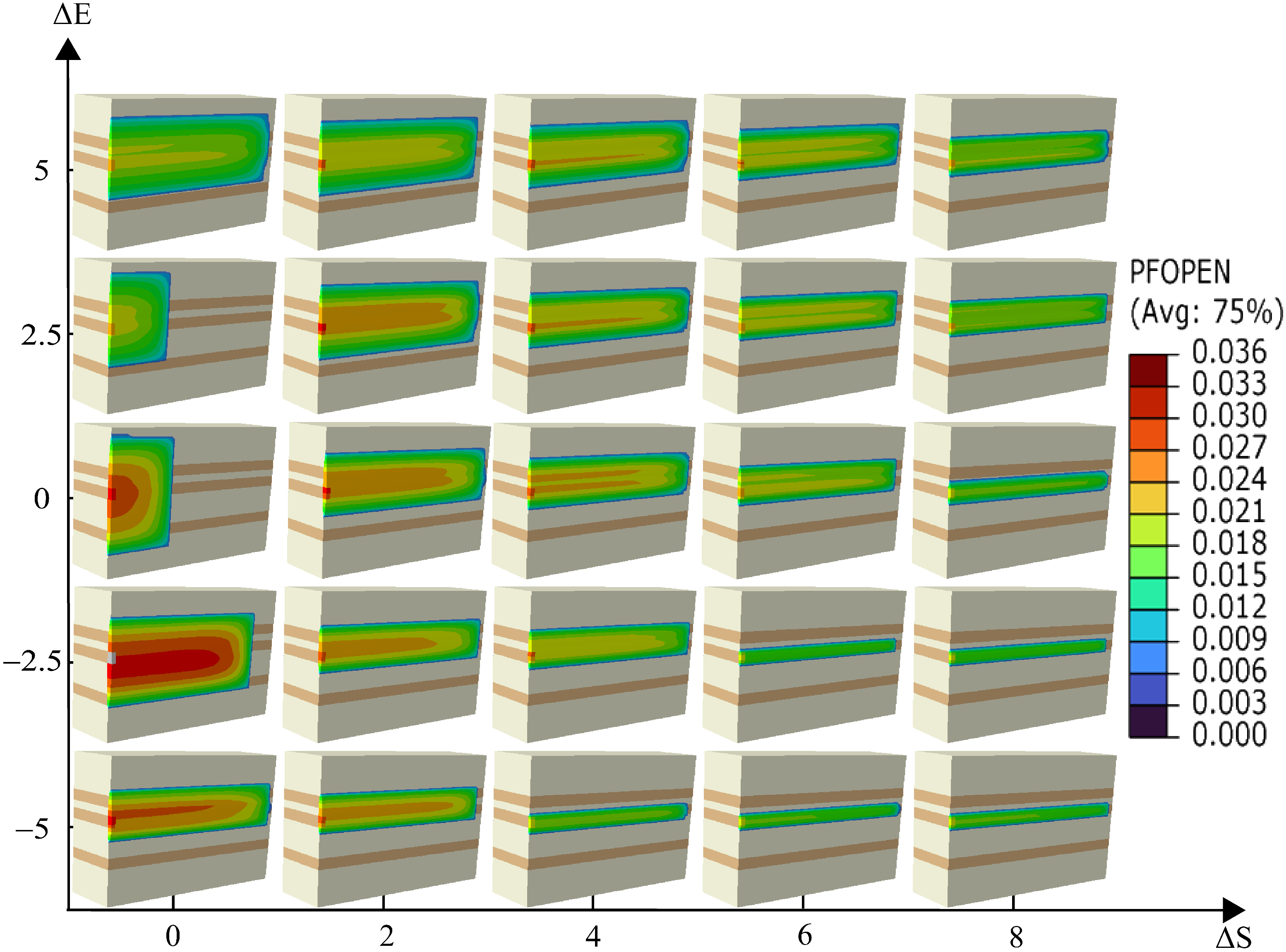
4.2. Interlayer Elastic Modulus Contrast
- Elastic Modulus Contrast = 0 GPa: The fracture propagates uniformly, extending equally in both upward and downward directions.
- Elastic Modulus Contrast = 2.5 GPa: The fracture penetrates the upper reservoir layer completely but does not extend into the lower reservoir.
- Elastic Modulus Contrast = 5 GPa: The fracture reaches both the upper and lower reservoir layers but does not fully penetrate either layer; propagation occurs predominantly along the fracture length.
- Elastic Modulus Contrast = −2.5 GPa: The fracture penetrates the upper reservoir layer but does not reach the lower layer.
- Elastic Modulus Contrast = −5 GPa: The fracture minimally penetrates the upper reservoir layer and does not continue upward, primarily extending along its length.

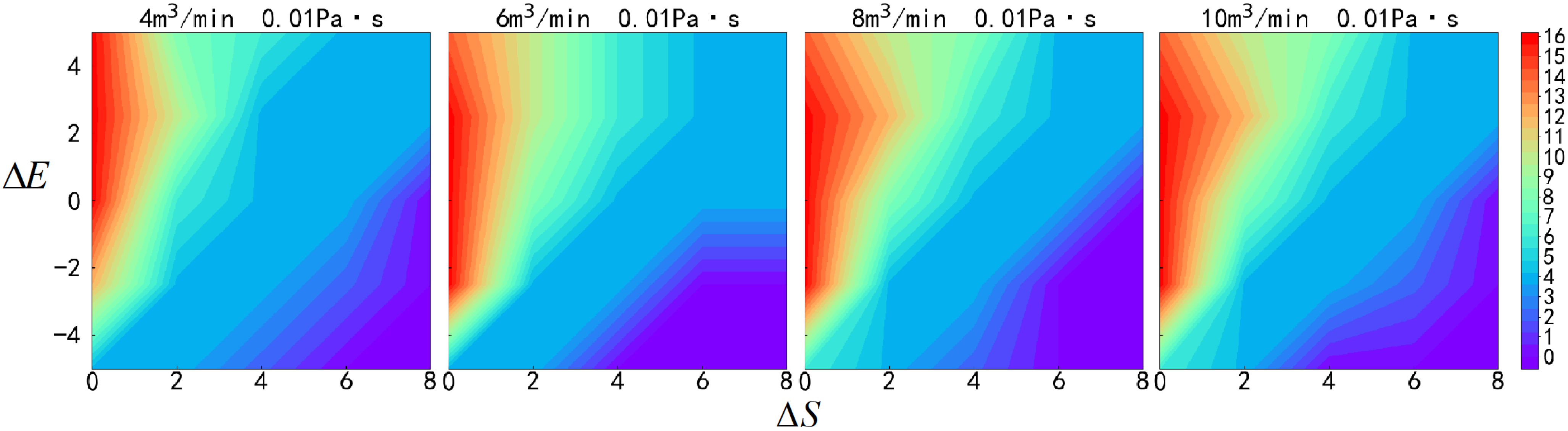
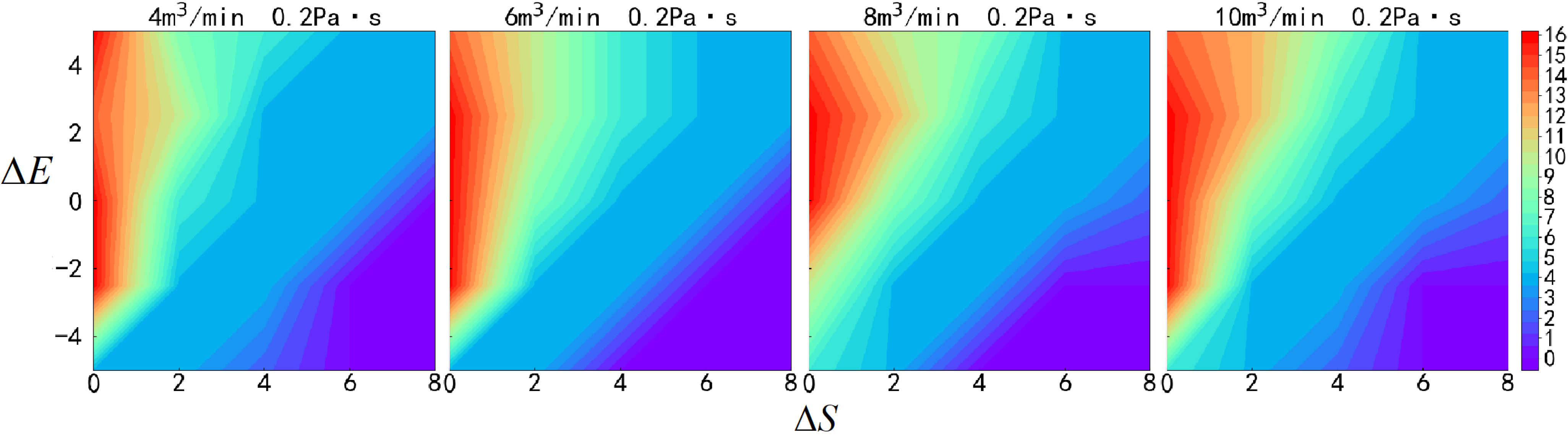
4.3. Pumping Rate Variation
4.4. Fracturing Fluid Viscosity Variation
5. Conclusions
- Interlayer stress contrast is the most critical factor influencing fracture propagation. When the stress differential reaches 8 MPa, fractures are entirely confined within the reservoir, which can be strategically used in field operations to prevent connecting with water-bearing zones.
- Elastic modulus contrast between reservoir and barrier layers significantly affects fracture propagation. Barrier layers with a higher elastic modulus are more susceptible to fracture penetration, while those with a lower modulus tend to inhibit vertical fracture growth.
- Pumping rate and fracturing fluid viscosity have minimal impact on the fracture propagation pattern and do not significantly improve fracture penetration. These operational parameters should be optimized alongside geological factors to achieve effective reservoir stimulation.
- When the interlayer stress contrast is low, multi-layer reservoir fracturing can result in substantial fracture connectivity. However, when stress contrasts exist, even after perforation, the reservoir with lower stress may still fail to develop fractures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Roche, V.; Van Der Baan, M.; Preisig, G. A Study of 3D Modeling of Hydraulic Fracturing and Stress Perturbations during Fluid Injection. J. Pet. Sci. Eng. 2018, 170, 829–843. [Google Scholar] [CrossRef]
- Heng, S.; Liu, X.; Li, X.; Zhang, X.; Yang, C. Experimental and Numerical Study on the Non-Planar Propagation of Hydraulic Fractures in Shale. J. Pet. Sci. Eng. 2019, 179, 410–426. [Google Scholar] [CrossRef]
- Wu, S.; Li, T.; Ge, H.; Wang, X.; Li, N.; Zou, Y. Shear-Tensile Fractures in Hydraulic Fracturing Network of Layered Shale. J. Pet. Sci. Eng. 2019, 183, 106428. [Google Scholar] [CrossRef]
- Yang, Y.; Li, X.; Yang, X.; Li, X. Influence of reservoirs/interlayers thickness on hydraulic fracture propagation laws in low-permeability layered rocks. J. Pet. Sci. Eng. 2022, 219, 111081. [Google Scholar] [CrossRef]
- Yang, F.; Mei, W.; Li, L.; Sun, Z.; An, Q.; Yang, Q.; Lu, M.; Yang, R. Propagation of hydraulic fractures in thin interbedded tight sandstones. Coal Geol. Explor. 2023, 51, 61–71. [Google Scholar]
- Jia, A.; Wei, Y.; Guo, Z.; Wang, G.; Meng, D.; Huang, S. Development status and prospect of tight sandstone gas in China. Nat. Gas Ind. 2022, 42, 83–92. [Google Scholar] [CrossRef]
- Du, J.; Zhu, G.; Li, Y.; Wu, P.; Gao, J.; Zhu, Y. Exploration and development challenges and technological countermeasures for tight sandstone gas reservoirs in Ordos basin margin: A case study of Linxing—Shenfu Gas Field. Nat. Gas Ind. 2022, 42, 114–124. [Google Scholar]
- Li, A. Study of Influence Factors for Horizontal Well Layer-Penetration Fracturing in Thin Interbed Tight Sand Reservoirs. J. Jianghan Pet. Univ. Staff. Work. 2020, 33, 10–13. [Google Scholar]
- Yang, L. Numerical Simulation of Hydraulic Fracturing in Tight Sand Reservoirs. Ph.D. Thesis, China University of Petroleum, Beijing, China, 2019. [Google Scholar]
- Wu, R.; Deng, J.; Mao, S.; Yu, B.; Liu, W.; Li, Y. Numerical Modeling of Hydraulic Fracture Containment of Tight Sandstone Gas Reservoir. In Proceedings of the 51st U.S. Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 25–28 June 2017; p. ARMA–2017–0050. [Google Scholar]
- Wu, R.; Deng, J.; Yu, B.; Liu, W.; Li, Y.; Li, M.; Peng, C. Numerical modeling of hydraulic fracture containment of tight gas reservoir in Shihezi Formation, Linxing Block. J. China Coal Soc. 2017, 42, 2393–2401. [Google Scholar] [CrossRef]
- Pu, C.; Chen, Q.; Wu, F.; He, Y.; Sun, W. Staged Fracturing Pattern and Parameter Optimization of Horizontal Wells in Tight Sandstone Oil Reservoir. Pet. Drill. Tech. 2014, 42, 73–79. [Google Scholar]
- Guo, X.; Zhu, H.; Zhao, P.; Jiang, H.; Wu, G.; Tao, L.; Liu, C.; Chen, S.; Chen, J. Numerical Simulation on Cross-Layer Propagation of Hydraulic Fracture in Sand–Mud Interbedded Layers: Taking the Shahejie Formation in BZ 25–1 Offshore Oilfield as an Example. Rock Mech. Rock Eng. 2024, 1–21. [Google Scholar] [CrossRef]
- Wang, Y. Study on the Rules of Fracture Initiation and Propagation in Longitudinal Multilayer Hydraulic Fracturing. Master’s Thesis, China University of Petroleum, Beijing, China, 2021. [Google Scholar]
- Taleghani, A.D.; Gonzalez, M.; Shojaei, A. Overview of Numerical Models for Interactions between Hydraulic Fractures and Natural Fractures: Challenges and Limitations. Comput. Geotech. 2016, 71, 361–368. [Google Scholar] [CrossRef]
- Adachi, J.I.; Detournay, E.; Peirce, A.P. Analysis of the Classical Pseudo-3D Model for Hydraulic Fracture with Equilibrium Height Growth across Stress Barriers. Int. J. Rock Mech. Min. Sci. 2010, 47, 625–639. [Google Scholar] [CrossRef]
- Fisher, K.; Warpinski, N. Hydraulic-Fracture-Height Growth: Real Data. SPE Prod. Oper. 2012, 27, 8–19. [Google Scholar] [CrossRef]
- Chen, Z.; Jeffrey, R.G.; Zhang, X.; Kear, J. Finite-Element Simulation of a Hydraulic Fracture Interacting with a Natural Fracture. SPE J. 2017, 22, 219–234. [Google Scholar] [CrossRef]
- Gonzalez-Chavez, M.; Taleghani, A.D.; Olson, J.E. A Cohesive Model for Modeling Hydraulic Fractures in Naturally Fractured Formations. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 3–5 February 2015. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, X.; Guo, J.; Xu, Y.; Chen, L.; Yuan, S.; Wang, Y.; Huang, J. Stress Field Interference of Hydraulic Fractures in Layered Formation. Geomech. Eng. 2015, 9, 645–667. [Google Scholar] [CrossRef]
- Gutierrez, R.E.; Sanchez, E.C.M.; Roehl, D.; Romanel, C. Numerical Modeling of Fracture Containment in Multi-Layered Formations Using a Cohesive Zone Model. In Proceedings of the VII Simpósio Brasileiro de Mecânica Das Rochas, Belo Horizonte, Brazil, 19–22 October 2016. [Google Scholar] [CrossRef]
- Guo, J.; Luo, B.; Lu, C.; Lai, J.; Ren, J. Numerical Investigation of Hydraulic Fracture Propagation in a Layered Reservoir Using the Cohesive Zone Method. Eng. Fract. Mech. 2017, 186, 195–207. [Google Scholar] [CrossRef]
- Lyu, Z.; Pan, L.; Hao, L.; Zou, N.; Zou, Z. Numerical Simulation of Factors Influencing Hydraulic Fracture Propagation in Sandstone-Mudstone Interbedded Reservoirs. Xinjiang Pet. Geol. 2023, 44, 729–738. [Google Scholar]
- Tan, P.; Chen, Z.-W.; Huang, L.-K.; Zhao, Q.; Shao, S.-R. Evaluation of the Combined Influence of Geological Layer Property and In-Situ Stresses on Fracture Height Growth for Layered Formations. Pet. Sci. 2024, S1995822624001985. [Google Scholar] [CrossRef]
- Chitrala, Y.; Moreno, C.; Sondergeld, C.; Rai, C. An Experimental Investigation into Hydraulic Fracture Propagation under Different Applied Stresses in Tight Sands Using Acoustic Emissions. J. Pet. Sci. Eng. 2013, 108, 151–161. [Google Scholar] [CrossRef]
- Zhang, Y.; Okere, C.J.; Su, G. Effect of Loading Rates on Accurate In-Situ Stress Determination in Different Lithologies via Kaiser Effect. Arab. J. Geosci. 2021, 14, 1304. [Google Scholar] [CrossRef]
- Zhang, J.; Yu, Q.; Li, Y.; Pan, Z.; Liu, B. Hydraulic Fracture Vertical Propagation Mechanism in Interlayered Brittle Shale Formations: An Experimental Investigation. Rock Mech. Rock Eng. 2023, 56, 199–220. [Google Scholar] [CrossRef]
- Liu, S.; Valkó, P.P. An Improved Equilibrium-Height Model for Predicting Hydraulic Fracture Height Migration in Multi-Layer Formations. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 3–5 February 2015; p. D012S012R001. [Google Scholar] [CrossRef]
- Ju, Y.; Liu, P.; Chen, J.; Yang, Y.; Ranjith, P.G. CDEM-based Analysis of the 3D Initiation and Propagation of Hydrofracturing Cracks in Heterogeneous Glutenites. J. Nat. Gas Sci. Eng. 2016, 35, 614–623. [Google Scholar] [CrossRef]
- Zhang, B.; Guo, T.; Chen, M.; Wang, J.; Cao, J.; Wang, H.; Qu, Z. Effect of Bedding Planes and Property Contrast between Layers on the Propagation Mechanism of Hydraulic Fracture Height in Shale Reservoirs. Comput. Geotech. 2024, 175, 106715. [Google Scholar] [CrossRef]
- Zou, Y.; Ma, X.; Zhang, S.; Zhou, T.; Li, H. Numerical Investigation into the Influence of Bedding Plane on Hydraulic Fracture Network Propagation in Shale Formations. Rock Mech. Rock Eng. 2016, 49, 3597–3614. [Google Scholar] [CrossRef]
- Gao, Q.; Cheng, Y.; Yan, C. A 3D Numerical Model for Investigation of Hydraulic Fracture Configuration in Multilayered Tight Sandstone Gas Reservoirs. J. Pet. Explor. Prod. Technol. 2018, 8, 1413–1424. [Google Scholar] [CrossRef]
- Li, H.; Jiang, Z.; Shu, J.; Fan, Y.; Du, T. Numerical simulation of layer-crossing propagation behavior of hydraulic fractures at coal-rock interface. Coal Geol. Explor. 2020, 48, 106–113. [Google Scholar]
- Wang, Y.; Hou, B.; Wang, D.; Jia, Z. Features of Fracture Height Propagation in Cross-Layer Fracturing of Shale Oil Reservoirs. Pet. Explor. Dev. 2021, 48, 469–479. [Google Scholar] [CrossRef]
- Liao, S.; Hu, J.; Zhang, Y. Mechanism of Hydraulic Fracture Vertical Propagation in Deep Shale Formation Based on Elastic–Plastic Model. Eng. Fract. Mech. 2024, 295, 109806. [Google Scholar] [CrossRef]
- Zhang, S.; Liao, S.; Li, S.; Hu, J. Influence of Engineering Parameters on Fracture Vertical Propagation in Deep Shale Reservoir: A Numerical Study Based on FEM. ACS Omega 2024, 9, 4635–4646. [Google Scholar] [CrossRef]
- Tan, P.; Jin, Y.; Xiong, Z.; Mian, C.; Hou, B. Effect of Interface Property on Hydraulic Fracture Vertical Propagation Behavior in Layered Formation Based on Discrete Element Modeling. J. Geophys. Eng. 2018, 15, 1542–1550. [Google Scholar] [CrossRef]
- Huang, L.; Dontsov, E.; Fu, H.; Lei, Y.; Weng, D.; Zhang, F. Hydraulic Fracture Height Growth in Layered Rocks: Perspective from DEM Simulation of Different Propagation Regimes. Int. J. Solids Struct. 2022, 238, 111395. [Google Scholar] [CrossRef]
- Tan, P.; Jin, Y.; Han, K.; Hou, B.; Chen, M.; Guo, X.; Gao, J. Analysis of Hydraulic Fracture Initiation and Vertical Propagation Behavior in Laminated Shale Formation. Fuel 2017, 206, 482–493. [Google Scholar] [CrossRef]
- Gao, J.; Hou, B.; Tan, P.; Guo, X.; Chang, Z. Propagation Mechanism of Hydraulic Fracture in Sand Coal Interbedding. J. China Coal Soc. 2017, 42, 430–435. [Google Scholar] [CrossRef]
- Ouchi, H.; Foster, J.T.; Sharma, M.M. Effect of Reservoir Heterogeneity on the Vertical Migration of Hydraulic Fractures. J. Pet. Sci. Eng. 2017, 151, 384–408. [Google Scholar] [CrossRef]
- Xing, P.; Yoshioka, K.; Adachi, J.; El-Fayoumi, A.; Bunger, A.P. Laboratory Measurement of Tip and Global Behavior for Zero-Toughness Hydraulic Fractures with Circular and Blade-Shaped (PKN) Geometry. J. Mech. Phys. Solids 2017, 104, 172–186. [Google Scholar] [CrossRef]
- Xing, P.; Yoshioka, K.; Adachi, J.; El-Fayoumi, A.; Damjanac, B.; Bunger, A.P. Lattice Simulation of Laboratory Hydraulic Fracture Containment in Layered Reservoirs. Comput. Geotech. 2018, 100, 62–75. [Google Scholar] [CrossRef]
- Huang, B.; Liu, J. Fully Three-Dimensional Propagation Model of Horizontal Borehole Hydraulic Fractures in Strata under the Effect of Bedding Planes. Energy Explor. Exploit. 2018, 36, 1189–1209. [Google Scholar] [CrossRef]
- Cao, S.; Li, X.; Zhou, Z.; Wang, Y.; Ding, H. Investigation of Hydraulic Fracturing Crack Propagation Behavior in Multi-Layered Coal Seams. Appl. Sci. 2020, 10, 1153. [Google Scholar] [CrossRef]
- Cui, Z.; Hou, B.; Fu, S.; L, J. Fractures cross-layer propagation characteristics of integrated fracturing in shale oil tight reservoir. Fault-Block Oil Gas Field 2022, 29, 111–117. [Google Scholar]
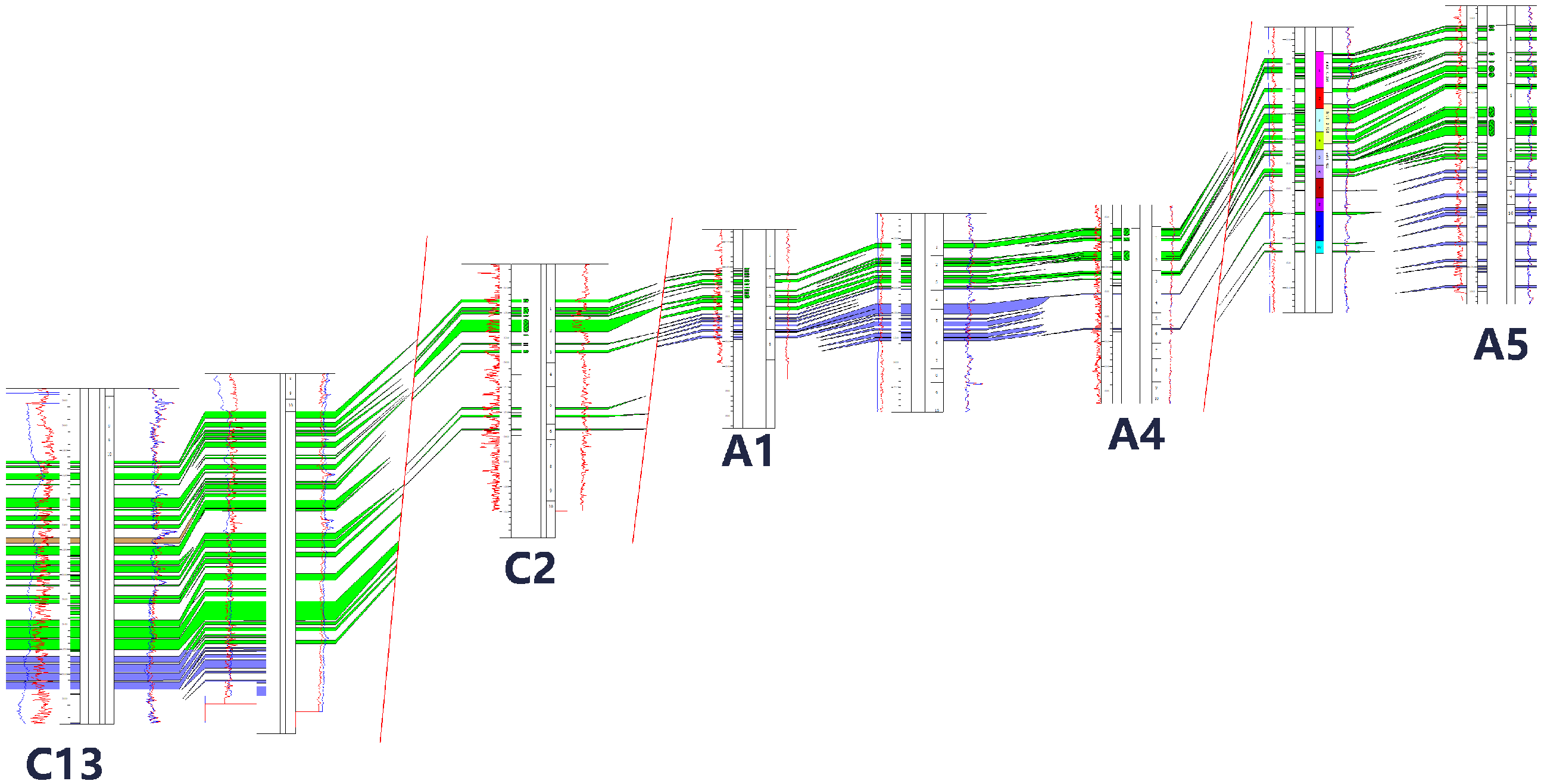



| Well Name | Designed Fracture Half-Length (m) | Created Fracture Half-Length Interpretation (m) | Dynamic Interpreted Fracture Half- Length (m) | Fracture Half- Length Ratio (Dynamic/Created) |
|---|---|---|---|---|
| A20 | 109 | 81 | 80 | 0.99 |
| A22 | 79.7 | 90 | 53 | 0.59 |
| C25 | 105 | 73 | 68 | 0.43 |
| C37H | 120 | 160 | 40 | 0.25 |
| C38H | 123 | 155 | 58 | 0.37 |
| A4 | 80 | 78 | 13 | 0.16 |
| Parameter | Value |
|---|---|
| Sandstone Layer Elastic Modulus (GPa) | 15 |
| Mudstone Layer Elastic Modulus (GPa) | 15 |
| Poisson’s Ratio of Sandstone Layer | 0.25 |
| Poisson’s Ratio of Mudstone Layer | 0.3 |
| Tensile Strength (MPa) | 3 |
| Fracture Energy (J) | 4000 |
| Maximum Horizontal Stress in Mudstone Layer (MPa) | 70 |
| Minimum Horizontal Stress in Mudstone Layer (MPa) | 62 |
| Overburden Pressure in Mudstone Layer (MPa) | 80 |
| Maximum Horizontal Stress in Sandstone Layer (MPa) | 70 |
| Minimum Horizontal Stress in Sandstone Layer (MPa) | 62 |
| Overburden Pressure in Sandstone Layer (MPa) | 80 |
| Fracturing Fluid Viscosity (Pa·s) | 0.01 |
| Pumping Rate (m3·min−1) | 2 |
| Operating Condition Parameters | Range of Variation |
|---|---|
| Interlayer stress contrast (MPa) | 0~8 |
| Interlayer elastic modulus contrast (GPa) | −5~5 |
| Pumping Rate (m³/min) | 4~10 |
| Fracturing Fluid Viscosity (Pa·s) | 0.01~0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, L.; Zhang, A.; Wu, G.; Chen, Z.; Liu, W.; Wang, J. Study on the Vertical Propagation Behavior of Hydraulic Fractures in Thin Interbedded Tight Sandstone. Processes 2024, 12, 2375. https://doi.org/10.3390/pr12112375
Zhao L, Zhang A, Wu G, Chen Z, Liu W, Wang J. Study on the Vertical Propagation Behavior of Hydraulic Fractures in Thin Interbedded Tight Sandstone. Processes. 2024; 12(11):2375. https://doi.org/10.3390/pr12112375
Chicago/Turabian StyleZhao, Liangliang, Anshun Zhang, Guangai Wu, Zhengrong Chen, Wei Liu, and Jinghe Wang. 2024. "Study on the Vertical Propagation Behavior of Hydraulic Fractures in Thin Interbedded Tight Sandstone" Processes 12, no. 11: 2375. https://doi.org/10.3390/pr12112375
APA StyleZhao, L., Zhang, A., Wu, G., Chen, Z., Liu, W., & Wang, J. (2024). Study on the Vertical Propagation Behavior of Hydraulic Fractures in Thin Interbedded Tight Sandstone. Processes, 12(11), 2375. https://doi.org/10.3390/pr12112375






