Integrated Hybrid Modelling and Surrogate Model-Based Operation Optimization of Fluid Catalytic Cracking Process
Abstract
:1. Introduction
- Proposed a unified framework for multi-source data collection, modeling, and optimization by integrating mechanistic model data with actual plant data;
- Constructed a multi-task learning prediction model to balance the patterns contained in different datasets, enhancing prediction accuracy and generalization ability;
- Formulated a non-linear programming (NLP) optimization model embedded with a data-driven surrogate model to improve gasoline yield in the FCC process.
2. Materials and Methods
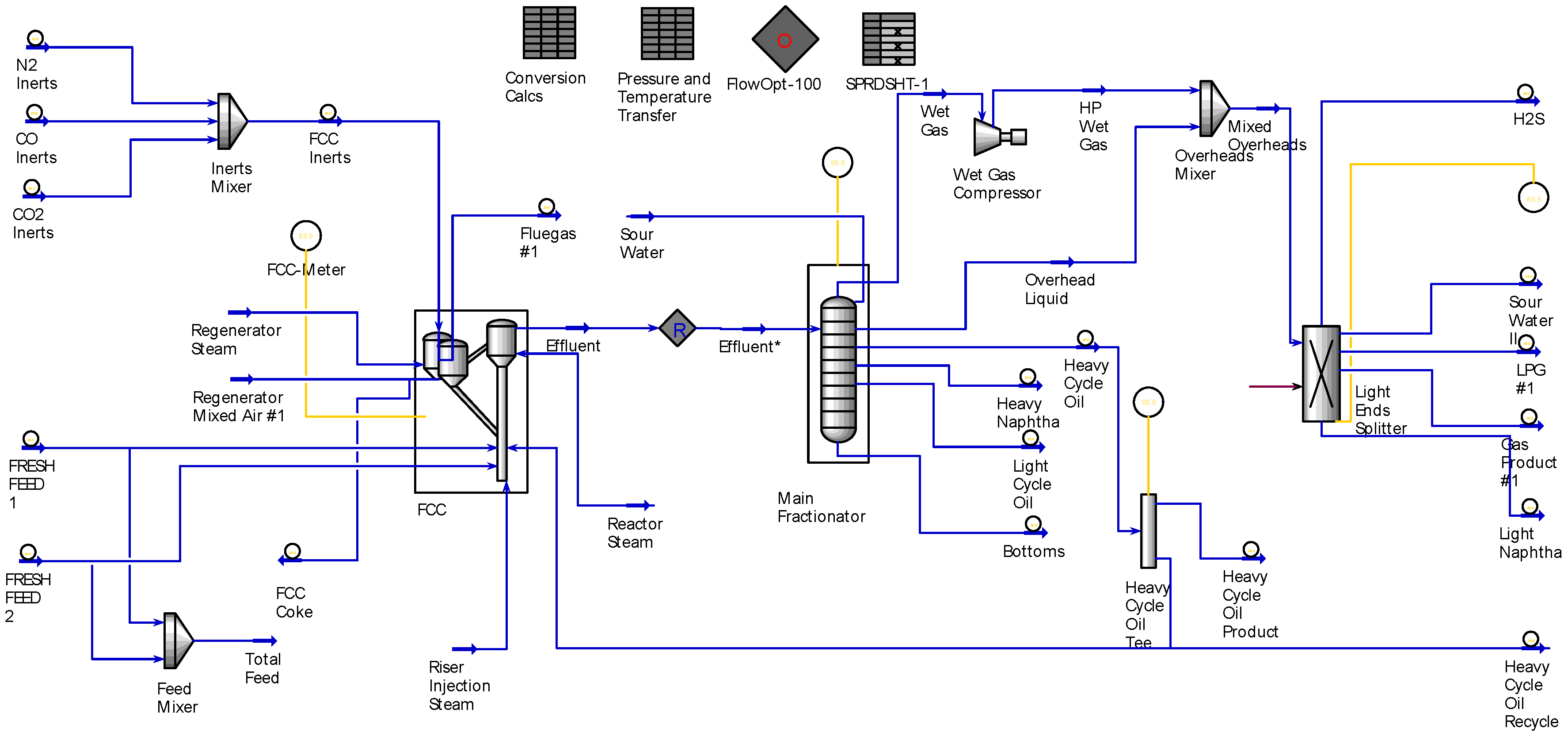
2.1. Hybrid Data Collection
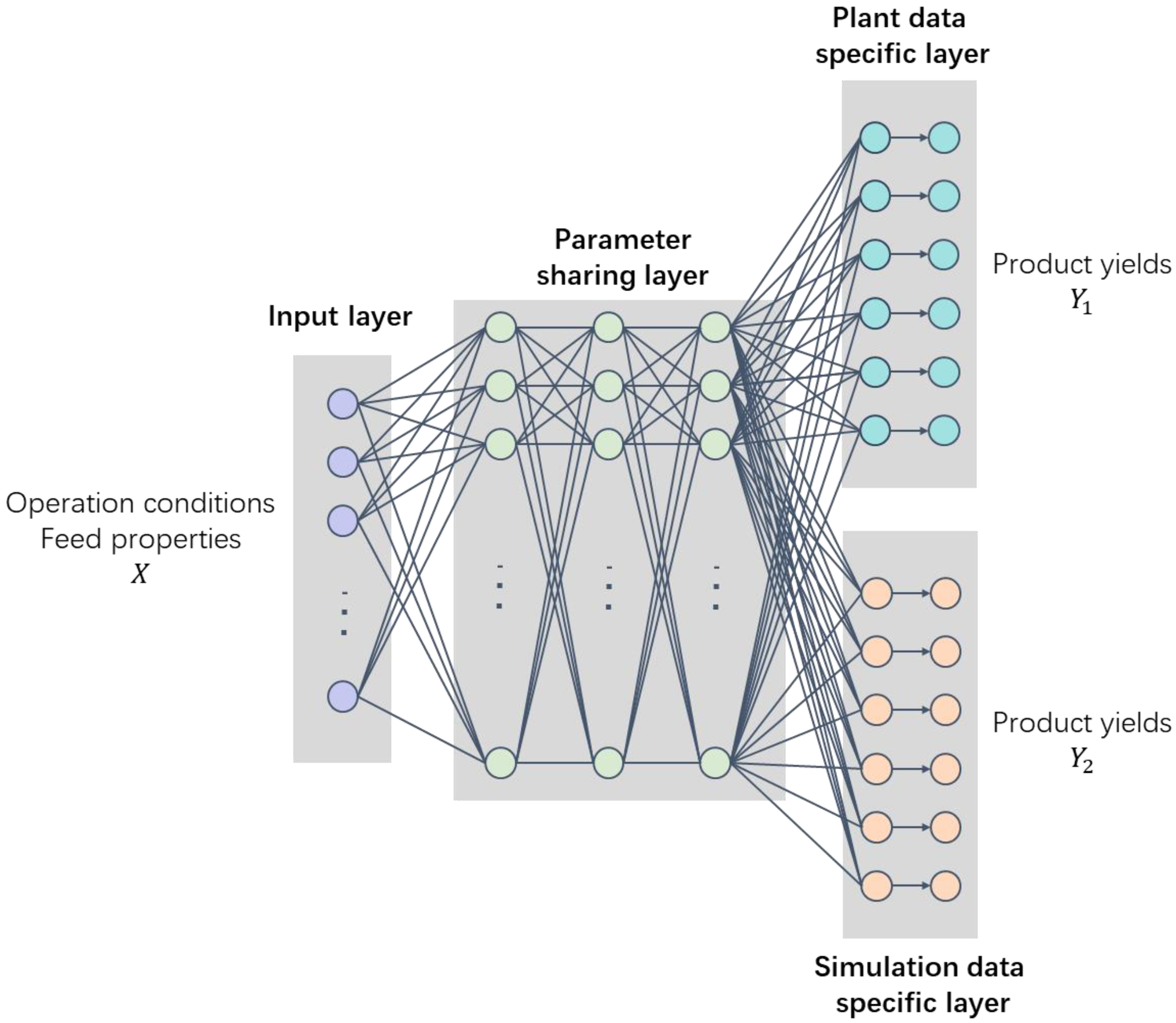
2.2. Multi-Task Learning Prediction Model
2.3. Surrogate Model-Based Optimization Model
3. Results
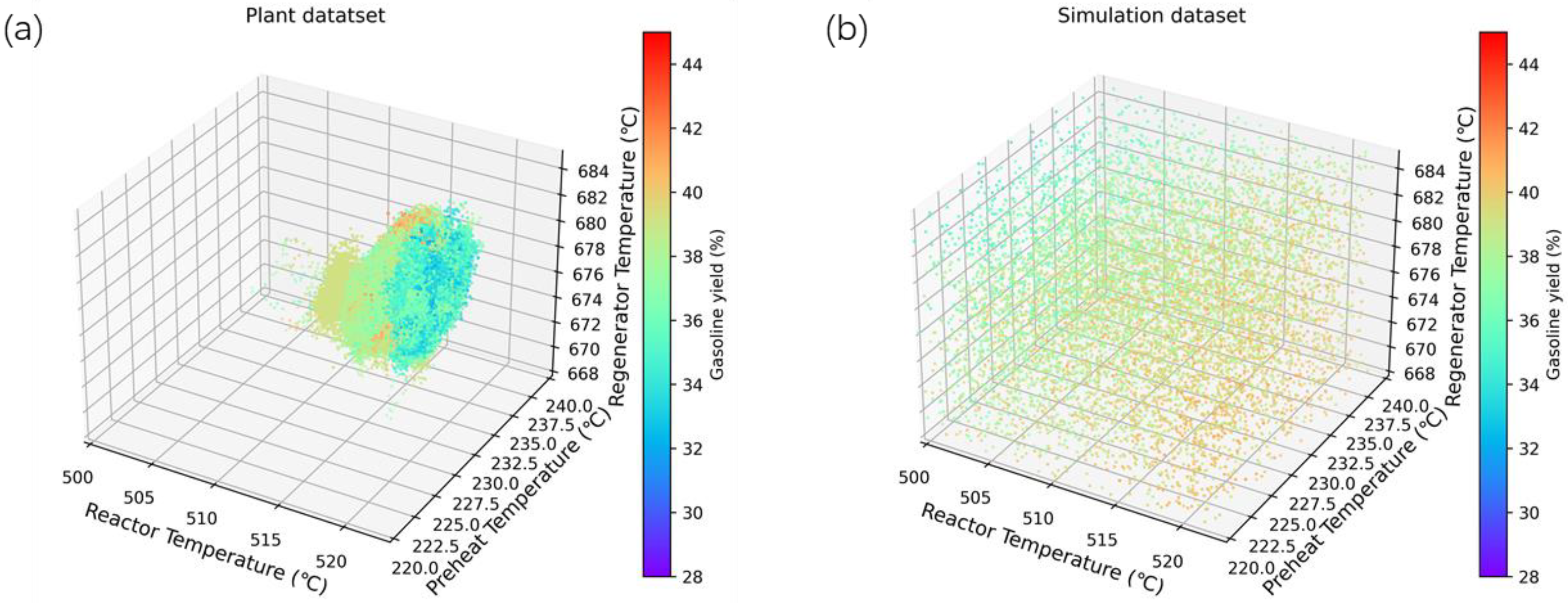
3.1. Plant and Simulation Dataset Distribution
3.2. Baseline Pure Data-Driven Model Prediction Results
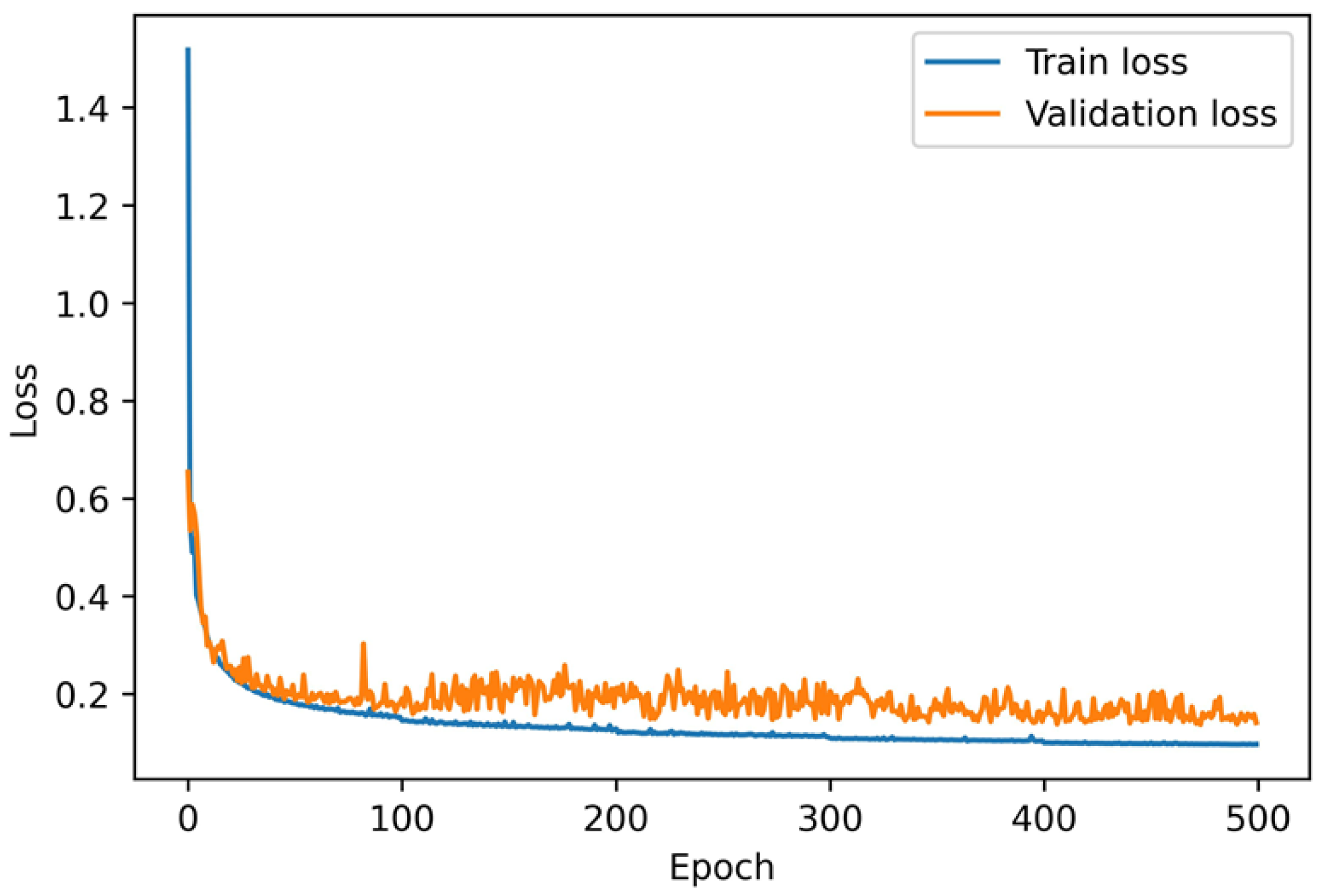
3.3. Multi-Task Model Prediction Results
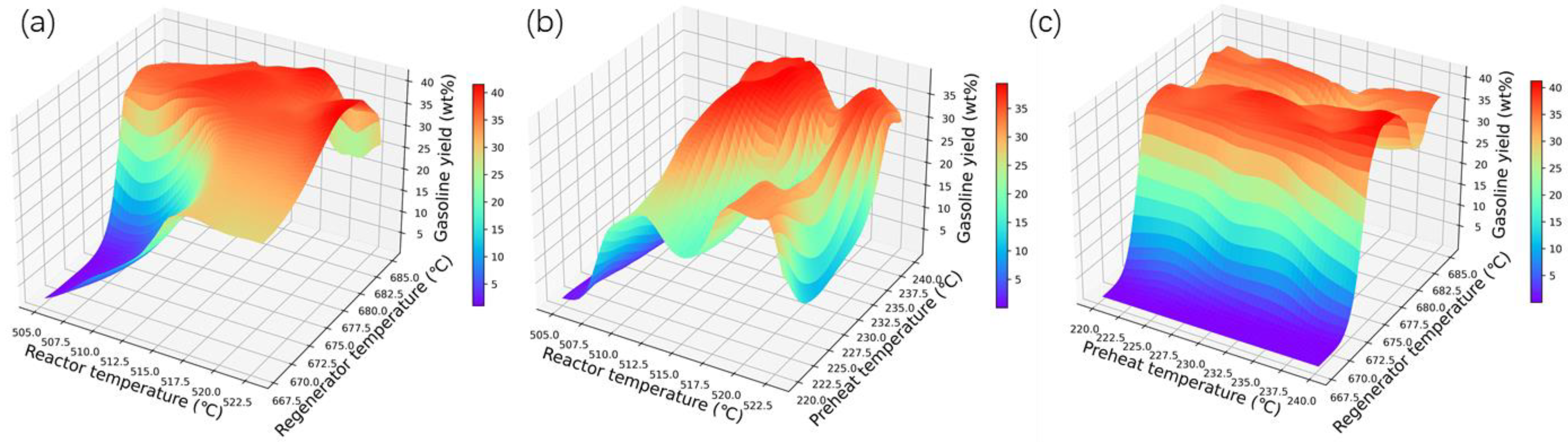
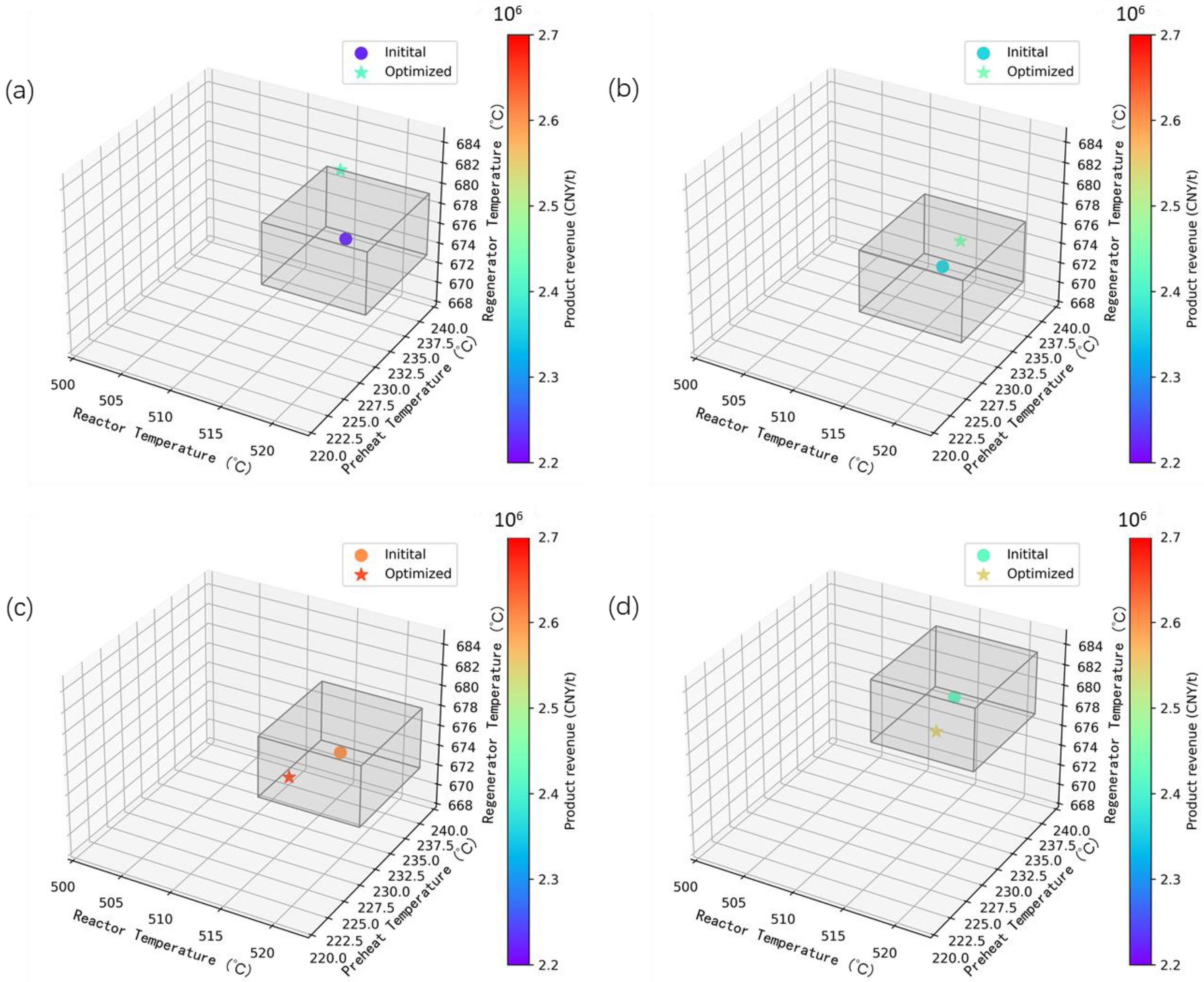
3.4. Optimization Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pinheiro, C.I.C.; Fernandes, J.L.; Domingues, L.; Chambel, A.J.S.; Graça, I.; Oliveira, N.M.C.; Cerqueira, H.S.; Ribeiro, F.R. Fluid Catalytic Cracking (FCC) Process Modeling, Simulation, and Control. Ind. Eng. Chem. Res. 2011, 51, 1–29. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, Y.; He, L.; Jia, C.Q.; Yao, Q.; Sun, M.; Ma, X. Anti-deactivation of zeolite catalysts for residue fluid catalytic cracking. Appl. Catal. A Gen. 2023, 657, 119159. [Google Scholar] [CrossRef]
- Palos, R.; Gutiérrez, A.; Fernández, M.L.; Azkoiti, M.J.; Bilbao, J.; Arandes, J.M. Converting the Surplus of Low-Quality Naphtha into More Valuable Products by Feeding It to a Fluid Catalytic Cracking Unit. Ind. Eng. Chem. Res. 2020, 59, 16868–16875. [Google Scholar] [CrossRef]
- Gholami, Z.; Gholami, F.; Tišler, Z.; Tomas, M.; Vakili, M. A Review on Production of Light Olefins via Fluid Catalytic Cracking. Energies 2021, 14, 1089. [Google Scholar] [CrossRef]
- Chen, Q.; Ding, J.; Chai, T.; Pan, Q. Evolutionary Optimization Under Uncertainty: The Strategies to Handle Varied Constraints for Fluid Catalytic Cracking Operation. IEEE Trans. Cybern. 2020, 52, 2249–2262. [Google Scholar] [CrossRef] [PubMed]
- Sildir, H.; Arkun, Y.; Canan, U.; Celebi, S.; Karani, U.; Er, I. Dynamic modeling and optimization of an industrial fluid catalytic cracker. J. Process Control 2015, 31, 30–44. [Google Scholar] [CrossRef]
- Lopes, G.; Rosa, L.; Mori, M.; Nunhez, J.; Martignoni, W. Three-dimensional modeling of fluid catalytic cracking industrial riser flow and reactions. Comput. Chem. Eng. 2011, 35, 2159–2168. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, M.; Zhao, L.; Liu, S.; Gao, J.; Xu, C.; Ma, M.; Meng, Q. Modeling, simulation, and optimization for producing ultra-low sulfur and high-octane number gasoline by separation and conversion of fluid catalytic cracking naphtha. Fuel 2021, 299, 120740. [Google Scholar] [CrossRef]
- Long, J.; Mao, M.S.; Zhao, G.Y. Model Optimization for an Industrial Fluid Catalytic Cracking Riser-regenerator Unit by Differential Evolution Algorithm. Pet. Sci. Technol. 2015, 33, 1380–1387. [Google Scholar] [CrossRef]
- He, G.; Zhou, C.; Luo, T.; Zhou, L.; Dai, Y.; Dang, Y.; Ji, X. Online Optimization of Fluid Catalytic Cracking Process via a Hybrid Model Based on Simplified Structure-Oriented Lumping and Case-Based Reasoning. Ind. Eng. Chem. Res. 2021, 60, 412–424. [Google Scholar] [CrossRef]
- Zhao, X.; Sun, S. Lumped Kinetic Modeling Method for Fluid Catalytic Cracking. Chem. Eng. Technol. 2020, 43, 2493–2500. [Google Scholar] [CrossRef]
- Weekman, V.W.; Nace, D.M. Kinetics of catalytic cracking selectivity in fixed, moving, and fluid bed reactors. AIChE J. 1970, 16, 397–404. [Google Scholar] [CrossRef]
- Weekman, V.W. Model of Catalytic Cracking Conversion in Fixed, Moving, and Fluid-Bed Reactors. Ind. Eng. Chem. Process Des. Dev. 1968, 7, 90–95. [Google Scholar] [CrossRef]
- Arbel, A.; Huang, Z.; Rinard, I.H.; Shinnar, R.; Sapre, A.V. Dynamic and Control of Fluidized Catalytic Crackers. 1. Modeling of the Current Generation of FCC’s. Ind. Eng. Chem. Res. 1995, 34, 1228–1243. [Google Scholar] [CrossRef]
- Ebrahimi, A.A.; Mousavi, H.; Bayesteh, H.; Towfighi, J. Nine-lumped kinetic model for VGO catalytic cracking; using catalyst deactivation. Fuel 2018, 231, 118–125. [Google Scholar] [CrossRef]
- Yang, B.; Zhou, X.; Chen, C.; Yuan, J.; Wang, L. Molecule Simulation for the Secondary Reactions of Fluid Catalytic Cracking Gasoline by the Method of Structure Oriented Lumping Combined with Monte Carlo. Ind. Eng. Chem. Res. 2008, 47, 4648–4657. [Google Scholar] [CrossRef]
- John, Y.M.; Mustafa, M.A.; Patel, R.; Mujtaba, I.M. Parameter estimation of a six-lump kinetic model of an industrial fluid catalytic cracking unit. Fuel 2019, 235, 1436–1454. [Google Scholar] [CrossRef]
- Lee, J.H.; Kang, S.; Kim, Y.; Park, S. New Approach for Kinetic Modeling of Catalytic Cracking of Paraffinic Naphtha. Ind. Eng. Chem. Res. 2011, 50, 4264–4279. [Google Scholar] [CrossRef]
- Yang, S.; Wang, N. A P systems based hybrid optimization algorithm for parameter estimation of FCCU reactor–regenerator model. Chem. Eng. J. 2012, 211–212, 508–518. [Google Scholar] [CrossRef]
- Du, Y.; Sun, L.; Berrouk, A.S.; Zhang, C.; Chen, X.; Fang, D.; Ren, W. Novel Integrated Reactor-Regenerator Model for the Fluidized Catalytic Cracking Unit Based on an Equivalent Reactor Network. Energy Fuels 2019, 33, 7265–7275. [Google Scholar] [CrossRef]
- Palos, R.; Rodríguez, E.; Gutiérrez, A.; Bilbao, J.; Arandes, J.M. Kinetic modeling for the catalytic cracking of tires pyrolysis oil. Fuel 2022, 309, 122055. [Google Scholar] [CrossRef]
- Nazarova, G.; Ivashkina, E.; Ivanchina, E.; Oreshina, A.; Vymyatnin, E. A predictive model of catalytic cracking: Feedstock-induced changes in gasoline and gas composition. Fuel Process. Technol. 2021, 217, 106720. [Google Scholar] [CrossRef]
- Qin, X.; Ye, L.; Liu, J.; Xu, Y.; Murad, A.; Ying, Q.; Shen, H.; Wang, X.; Hou, L.; Pu, X.; et al. A molecular-level coupling model of fluid catalytic cracking and hydrotreating processes to improve gasoline quality. Chem. Eng. J. 2023, 451, 138778. [Google Scholar] [CrossRef]
- Chen, Z.; Feng, S.; Zhang, L.; Wang, G.; Shi, Q.; Xu, Z.; Zhao, S.; Xu, C. Molecular-level kinetic modeling of heavy oil fluid catalytic cracking process based on hybrid structural unit and bond-electron matrix. AIChE J. 2021, 67, e17027. [Google Scholar] [CrossRef]
- Chen, C.; Zhou, L.; Ji, X.; He, G.; Dai, Y.; Dang, Y. Adaptive Modeling Strategy Integrating Feature Selection and Random Forest for Fluid Catalytic Cracking Processes. Ind. Eng. Chem. Res. 2020, 59, 11265–11274. [Google Scholar] [CrossRef]
- Long, J.; Li, T.; Yang, M.-L.; Hu, G.; Zhong, W. Hybrid Strategy Integrating Variable Selection and a Neural Network for Fluid Catalytic Cracking Modeling. Ind. Eng. Chem. Res. 2019, 58, 247–258. [Google Scholar] [CrossRef]
- Tian, W.; Wang, S.; Sun, S.; Li, C.; Lin, Y. Intelligent prediction and early warning of abnormal conditions for fluid catalytic cracking process. Chem. Eng. Res. Des. 2022, 181, 304–320. [Google Scholar] [CrossRef]
- Yang, F.; Dai, C.; Tang, J.; Xuan, J.; Cao, J. A hybrid deep learning and mechanistic kinetics model for the prediction of fluid catalytic cracking performance. Chem. Eng. Res. Des. 2020, 155, 202–210. [Google Scholar] [CrossRef]
- Li, X.; Zhang, L.; Sun, Y.; Jiang, B.; Zhang, R.; Li, X.; Yang, N. Investigation on steam injection condition in refining vacuum furnace. Chem. Eng. Sci. 2015, 135, 509–516. [Google Scholar] [CrossRef]
- Loh, W.-L. On Latin hypercube sampling. Ann. Stat. 1996, 24, 2058–2080. [Google Scholar] [CrossRef]
- Andrei, N. Continuous Nonlinear Optimization for Engineering Applications in Gams Technology; Springer Science+Business Media: New York, NY, USA, 2017. [Google Scholar]






| Notation | Variable | Unit | Notation | Variable | Unit |
|---|---|---|---|---|---|
| x1 | Reactor temperature | °C | y1 | Dry gas yield | wt% |
| x2 | Regenerator temperature | °C | y2 | Liquefied gas yield | wt% |
| x3 | Feed preheat temperature | °C | y3 | Gasoline yield | wt% |
| x4 | Feed flowrate | t/h | y4 | Diesel yield | wt% |
| x5 | Reflux flowrate | t/h | y5 | Slurry oil yield | wt% |
| x6 | Catalyst tank level | t | y6 | Residue yield | wt% |
| x7 | Fractionation tower cold reflux flow | t/h | |||
| x8 | Light cycle oil extraction temperature | °C | |||
| x9 | Fractionation tower bottom temperature | °C | |||
| x10 | Supplemental absorbent flow rate | t/h | |||
| x11 | Desorption tower top gas volume | Nm3/h | |||
| x12 | Desorption tower top temperature | °C | |||
| x13 | Mixed feedstock density (20 °C) | kg/cm3 | |||
| x14 | Mixed feedstock carbon residue content | wt% |
| Variable | Unit | Lower Bound | Upper Bound |
|---|---|---|---|
| Reactor temperature | °C | 505 | 528 |
| Regenerator temperature | °C | 668 | 685 |
| Feed preheat temperature | °C | 220 | 240 |
| Yield (wt%) | Plant Dataset | Simulation Dataset | ||
|---|---|---|---|---|
| MSE | MAPE | MSE | MAPE | |
| Dry gas | 0.0029 | 1.15% | 6.3814 | 72.11% |
| LNG | 0.0337 | 0.82% | 173.6118 | 78.71% |
| Gasoline | 0.2757 | 1.08% | 1073.6084 | 78.17% |
| Diesel | 0.1372 | 1.02% | 383.3285 | 78.65% |
| Slurry | 0.0139 | 1.37% | 128.6065 | 85.34% |
| Residual | 0.3712 | 4.90% | 5413.0770 | 715.72% |
| Yield (wt%) | Plant Dataset | Simulation Dataset | ||
|---|---|---|---|---|
| MSE | MAPE | MSE | MAPE | |
| Dry gas | 0.0032 | 1.20% | 0.0002 | 0.31% |
| LNG | 0.0311 | 0.78% | 0.0028 | 0.27% |
| Gasoline | 0.2695 | 1.05% | 0.0020 | 0.09% |
| Diesel | 0.1297 | 0.98% | 0.0015 | 0.13% |
| Slurry | 0.0148 | 1.45% | 0.0055 | 0.47% |
| Residual | 0.3621 | 4.84% | 0.0019 | 0.36% |
| Before Optimization | After Optimization | Relative Change | |
|---|---|---|---|
| Average LNG yield | 16.97 wt% | 17.07 wt% | +0.59% |
| Average gasoline yield | 37.06 wt% | 38.64 wt% | +4.26% |
| Average diesel yield | 26.36 wt% | 27.41 wt% | +3.98% |
| Average product revenue | 2,413,730 CNY/h | 2,502,356 CNY/h | +3.67% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, H.; Zhao, Q.; Wang, R.; Xu, W.; Qiu, T. Integrated Hybrid Modelling and Surrogate Model-Based Operation Optimization of Fluid Catalytic Cracking Process. Processes 2024, 12, 2474. https://doi.org/10.3390/pr12112474
Li H, Zhao Q, Wang R, Xu W, Qiu T. Integrated Hybrid Modelling and Surrogate Model-Based Operation Optimization of Fluid Catalytic Cracking Process. Processes. 2024; 12(11):2474. https://doi.org/10.3390/pr12112474
Chicago/Turabian StyleLi, Haoran, Qiming Zhao, Ruqiang Wang, Wenle Xu, and Tong Qiu. 2024. "Integrated Hybrid Modelling and Surrogate Model-Based Operation Optimization of Fluid Catalytic Cracking Process" Processes 12, no. 11: 2474. https://doi.org/10.3390/pr12112474
APA StyleLi, H., Zhao, Q., Wang, R., Xu, W., & Qiu, T. (2024). Integrated Hybrid Modelling and Surrogate Model-Based Operation Optimization of Fluid Catalytic Cracking Process. Processes, 12(11), 2474. https://doi.org/10.3390/pr12112474






