Feasibility Study of Material Deformation and Similarity of Spatial Characteristics of Standard Coal Rocks
Abstract
:1. Introduction
2. Principles and Methods of Similar Experiments
2.1. Similarity Principle
- (1)
- First theorem of similarity [26]
- (2)
- Second Theorem of Similarity [27]
- (3)
- The Third Theorem of Similarity
2.2. Similarity Conditions and Similarity Ratios of Models
- —geometric similarity ratio;
- —density of rock sample prototypes;
- —density of rock sample models;
- —length of rock sample prototype;
- —length of rock sample model.
- —stress similarity ratio;
- —similar ratio of modulus of elasticity;
- —similarity ratio of capacity to weight;
- —tolerance of rock sample prototypes;
- —tolerance of the rock sample model;
- —modulus of elasticity of prototype rock samples;
- —modulus of elasticity of rock sample model;
- —stress in rock sample prototypes;
- —stresses in rock sample models;
- —Poisson’s ratio similarity ratio.
- —similarity ratio of capacity to weight;
- —tolerance of rock sample prototypes;
- —tolerance of the rock sample model.
- —stress similarity ratio;
- —stress in rock sample prototypes;
- —stresses in rock sample models;
- —similarity ratio of capacity to weight;
- —geometric similarity ratio.
- —similar ratio of modulus of elasticity;
- —modulus of elasticity of prototype rock samples;
- —modulus of elasticity of rock sample model.
- —similar ratio of gravitational acceleration;
- —similar ratio of unloading time;
- —gravitational acceleration of rock sample prototypes;
- —gravitational acceleration of the rock sample model;
- —prototype unloading time for rock samples;
- —unloading time of the rock sample model.
- —similar ratio of unloading time;
- —prototype unloading time for rock samples;
- —unloading time of the rock sample model;
- —geometric similarity ratio.
2.3. Determination of Physical and Mechanical Parameters of Coal Rock Samples
3. Experimental Study of Orthogonal Matching of Similar Materials
3.1. Selection of Similar Materials
3.2. Orthogonal Test Protocol
3.3. Similar Material Production Method and Experimental System
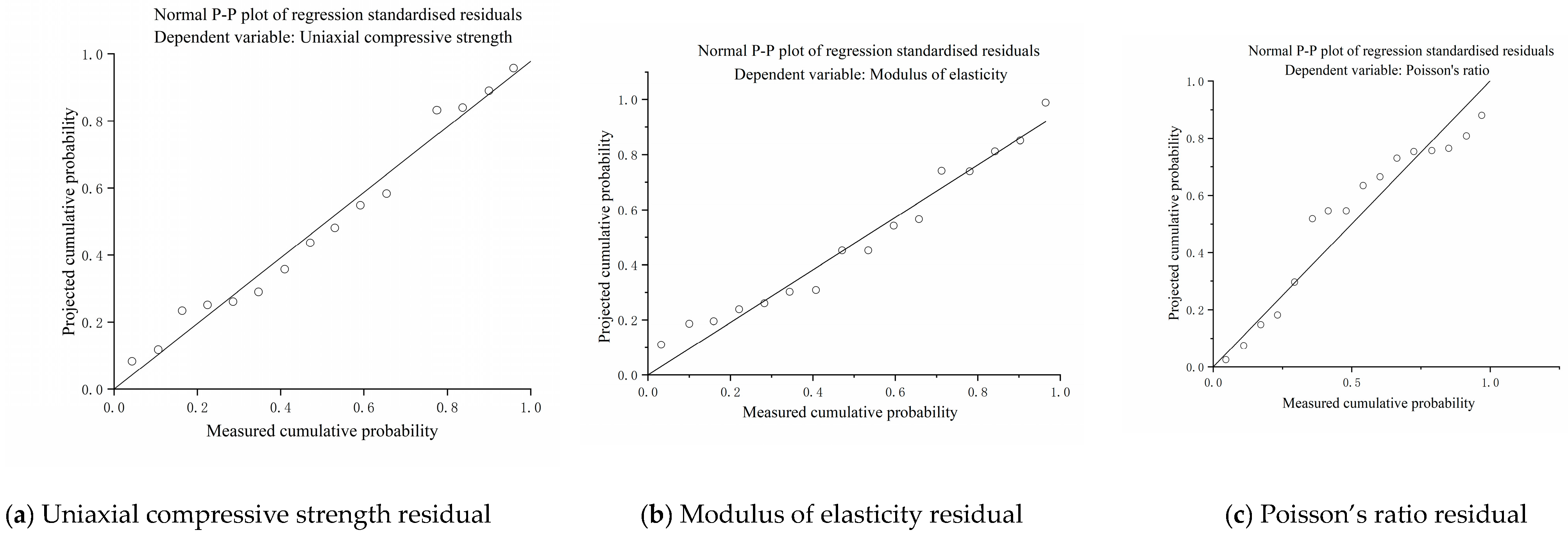
3.4. Analysis of Experimental Results
- (1)
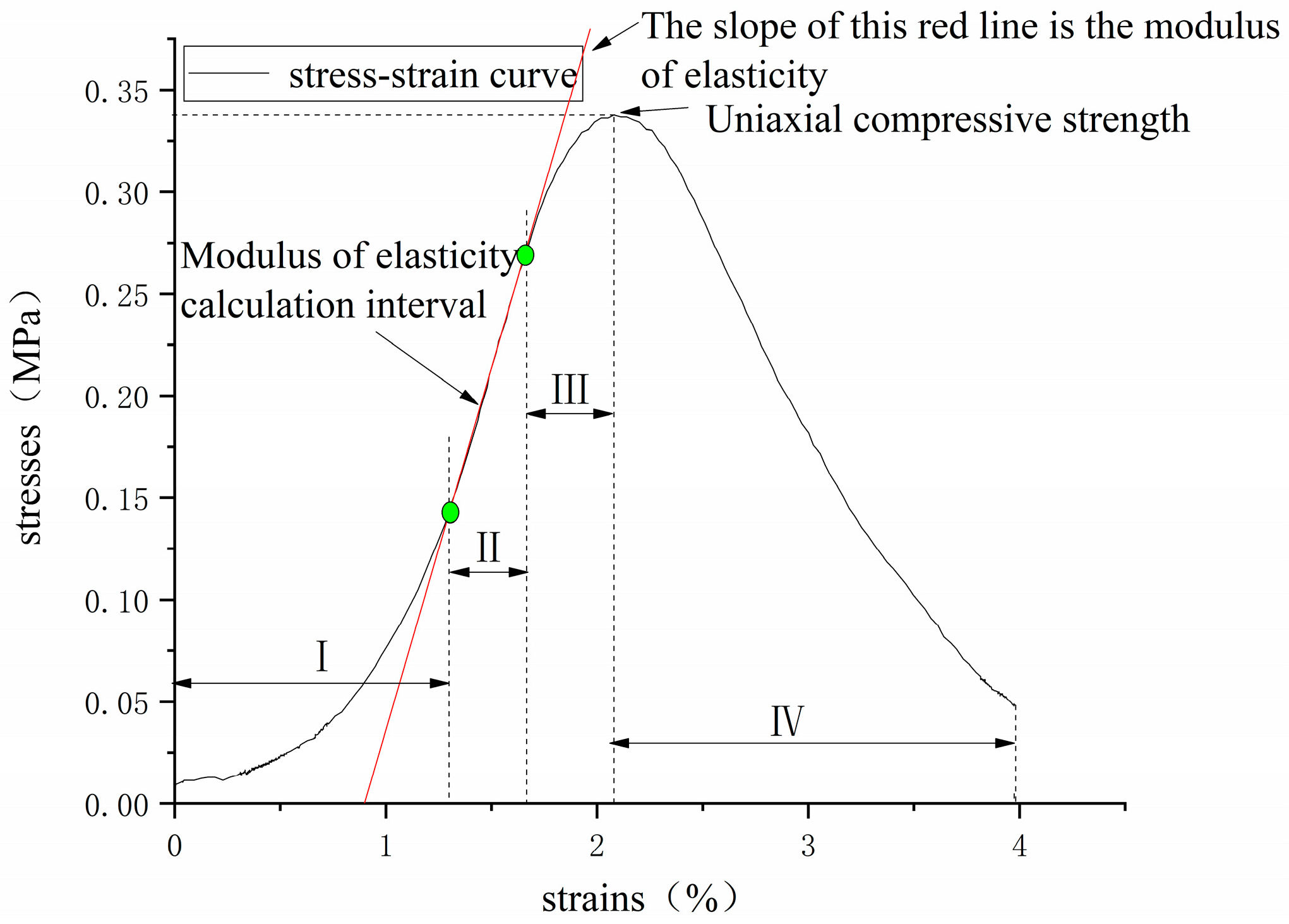
- Calculation and analysis of stress–strain curves.
- —modulus of elasticity;
- —stress at the corresponding points 1,2 in the figure;
- —strain at the corresponding points 1,2 in the figure.
- (2)
- Calculation of the Poisson’s ratio of the similar material proportion specimens.
- —Poisson’s ratio;
- —strain at the corresponding points 1,2 in the figure;
- —strain at the corresponding points 3,4 in the figure.
- (3)
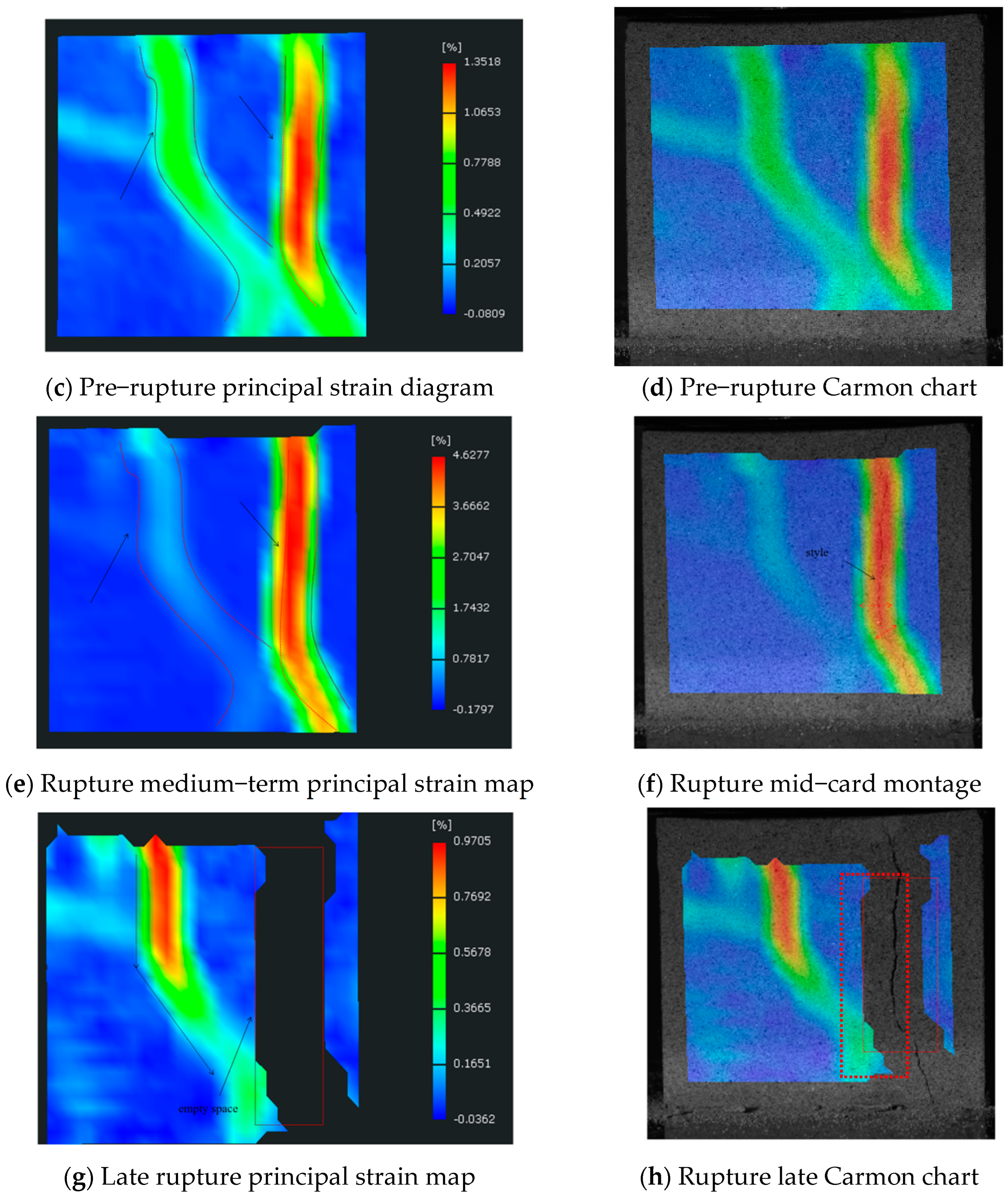
- Rupture analysis of specimens with similar material ratios.
- (4)
- Sensitivity analysis of factors.
- (5)
- Multivariate linear regression analysis.
- —implicit variable;
- —independent variable;
- —correlation ratio coefficient.
- —vector of characteristic indicators;
- —proportionality matrix for similar ratios;
- —correlation ratio coefficient;
- —sand-to-cement ratio;
- —carbon-to-paste ratio;
- —moisture content;
- —uniaxial compressive strength;
- —modulus of elasticity;
- —Poisson’s ratio.
- —vector of characteristic indicators;
- —proportionality matrix for similar ratios;
- —correlation coefficient.
- —sand-to-cement ratio
- —carbon-to-paste ratio
- —moisture content
- —uniaxial compressive strength
- —modulus of elasticity
- —Poisson’s ratio
- —sand-to-cement ratio;
- —carbon-to-paste ratio;
- —moisture content;
- —uniaxial compressive strength;
- —modulus of elasticity;
- —Poisson’s ratio.
4. Feasibility Analysis of Similar Analog Materials for Acoustic Emission and Digital Scattering Studies
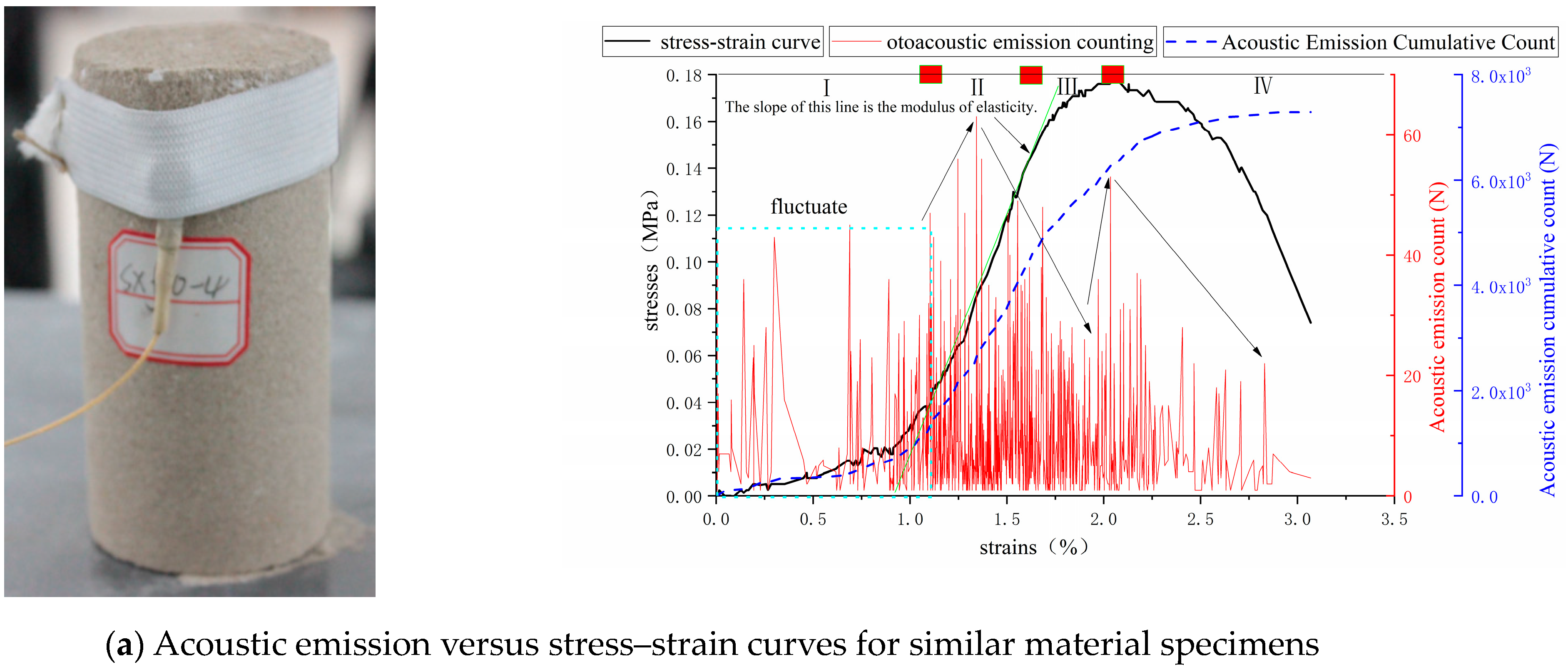
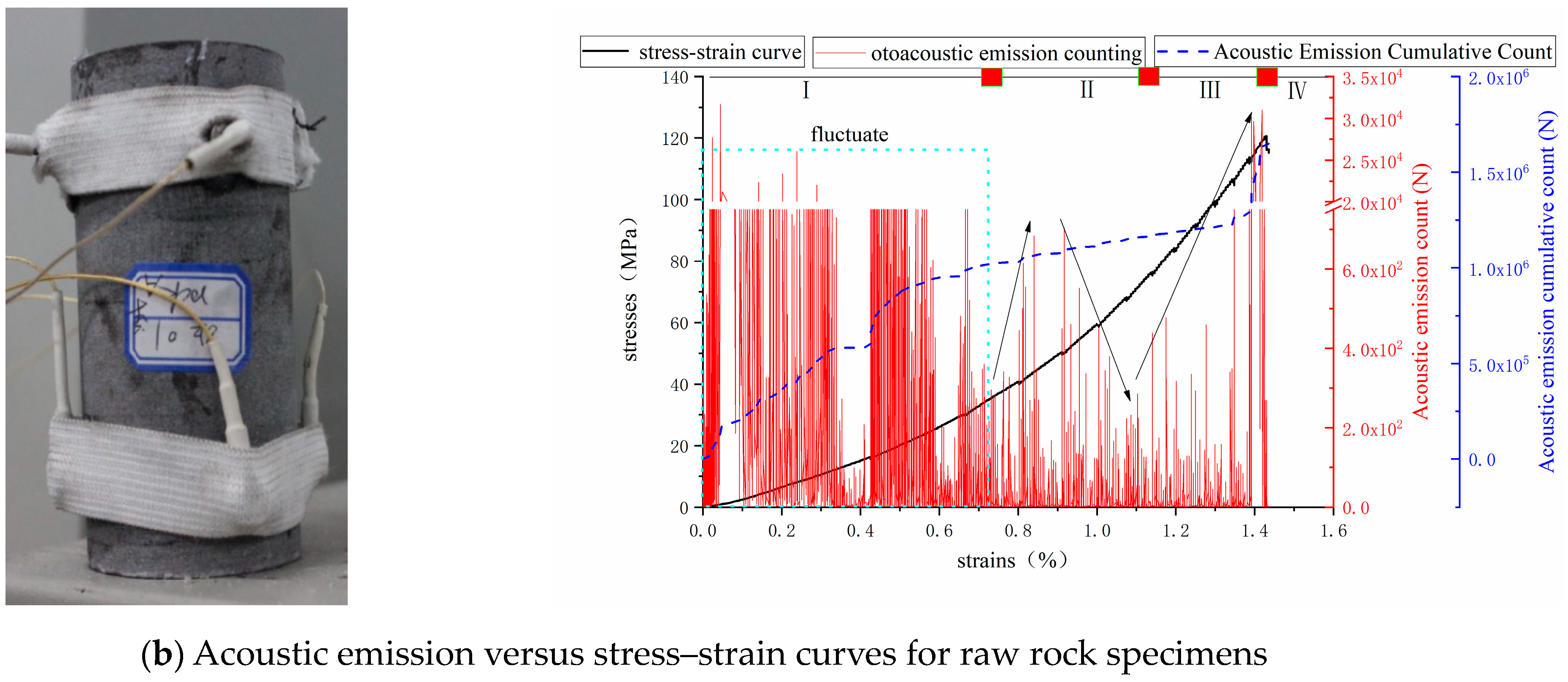
4.1. Feasibility Analysis of Similar Analog Materials for Acoustic Emission Studies
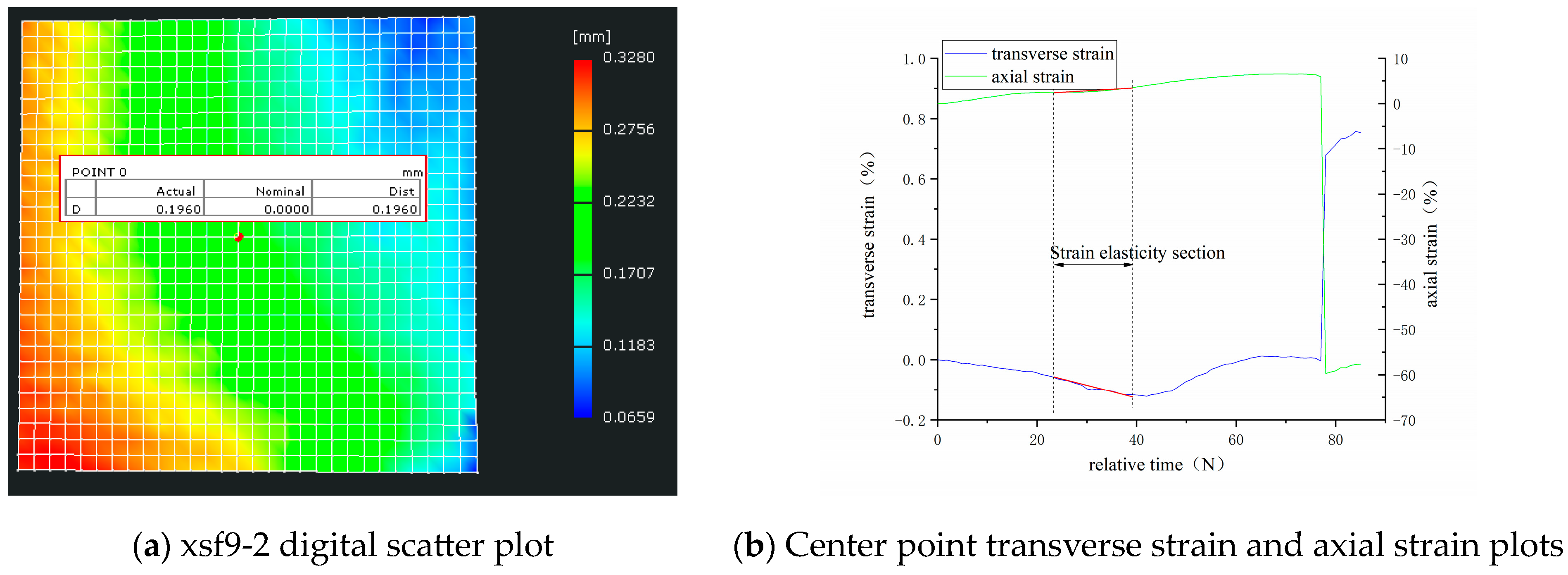
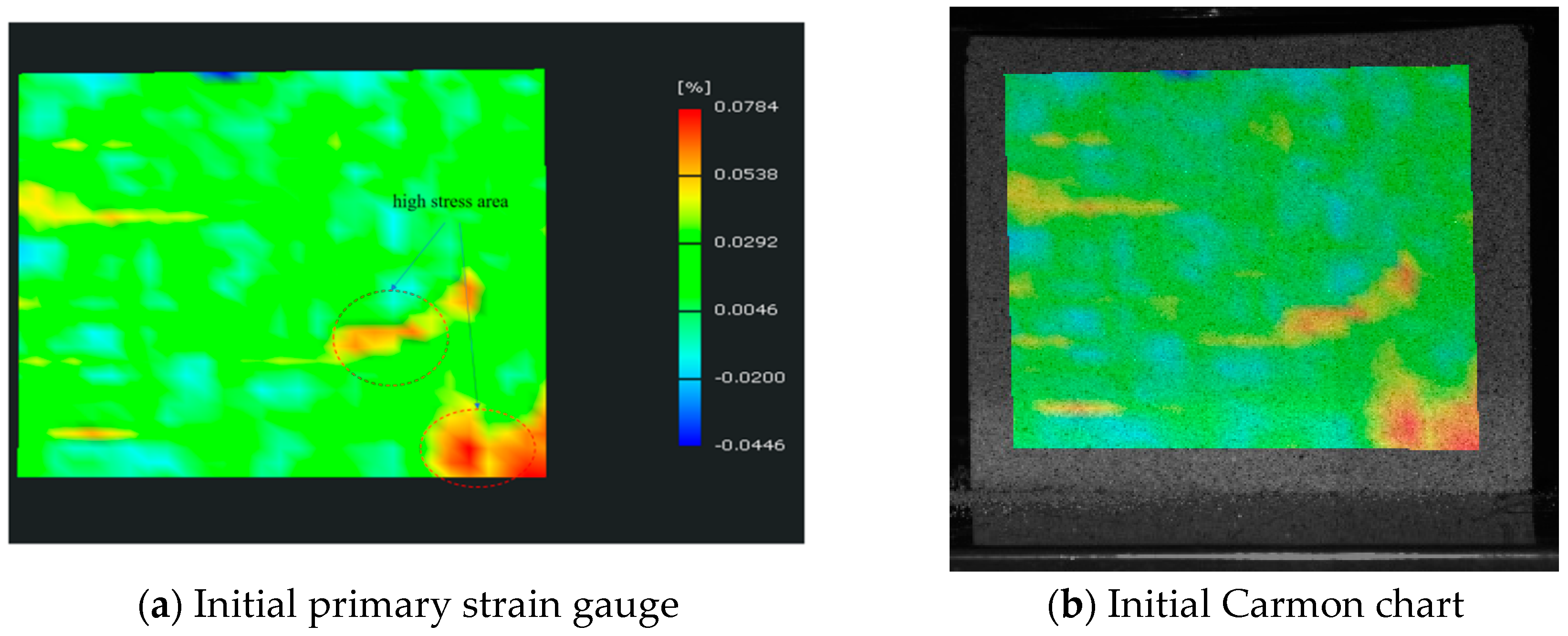
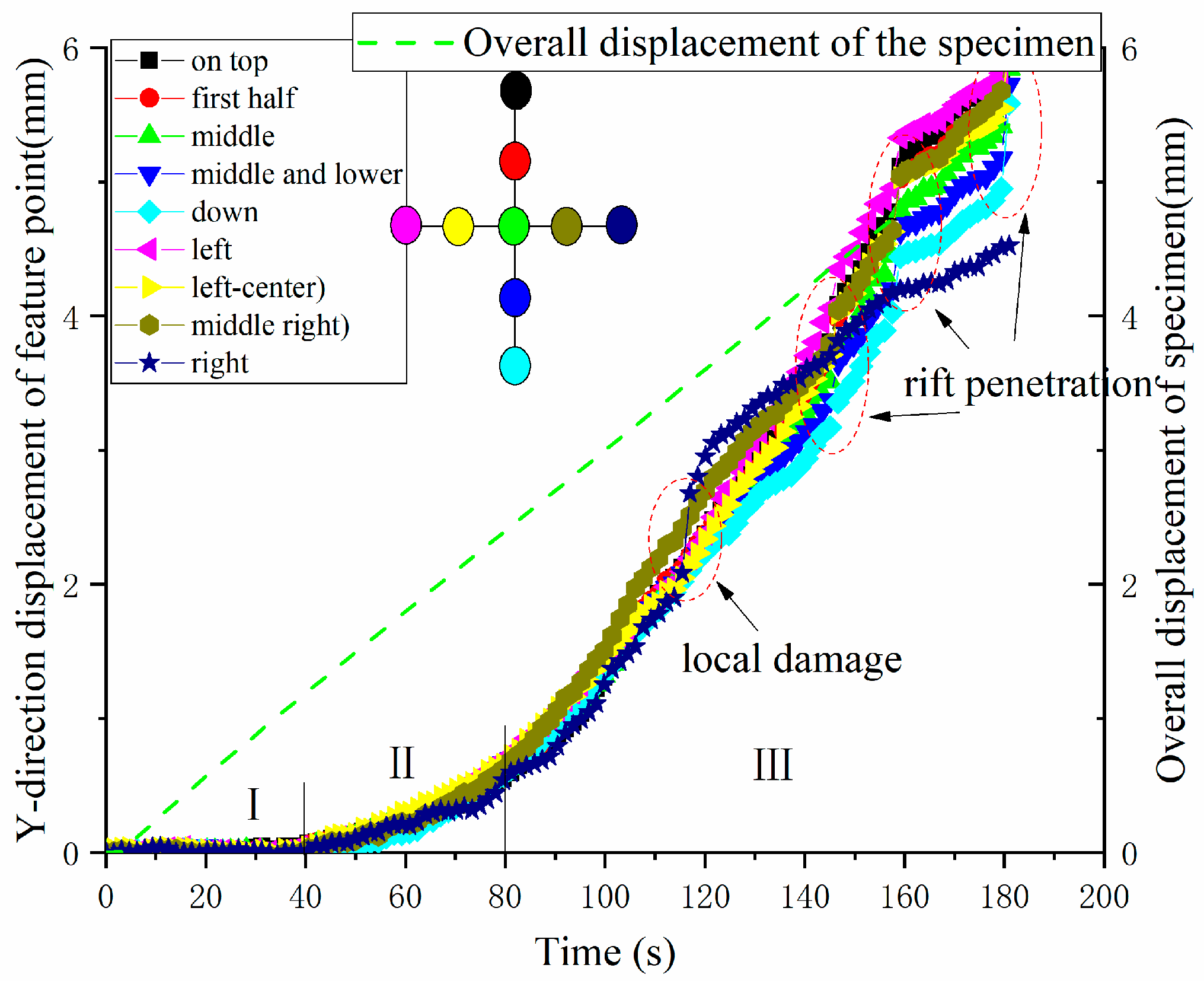
4.2. Feasibility Analysis of Similar Analog Materials for Digital Scattering Studies
- —gray scale value of a single pixel in the pre-deformation sub-area;
- —average value of individual pixels in the subarea before deformation;
- —gray scale value of a single pixel within the deformed sub-area;
- —average value of individual pixels in the subregion after deformation;
- —displacement in x-direction before and after deformation;
- —displacement in y-direction before and after deformation.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yang, Y.; Hu, F. Research on deformation and damage law of similar model based on digital scattering technology. Min. Technol. 2020, 20, 146–148+152. [Google Scholar]
- Yang, Y. Study and Application of Digital Speckle Technique in Physical Similar Simulation Experiment of Protective Layer Mining. Master’s Thesis, Chongqing University, Chongqing, China, 2017. [Google Scholar]
- Chen, Z.; Zhang, Y.; Zhou, J. Experimental study of deep tunnel surrounding rock rockburst proneness with similarity material simulating method based on digital speckle correlation technique. Geotechnics 2011, 32 (Suppl. S1), 141–148. [Google Scholar]
- Dong, J.; Yang, S.; Li, B.; Hu, Y. Experimental study on the tensile strength of rock-like materials containing two pre-existing coplanar flissures. Eng. Mech. 2020, 37, 188–201. [Google Scholar]
- Zhou, Z.L.; Wang, H.Q.; Cai, X.; Zang, H.Z.; Chen, L.; Liu, F. Bearing characteristics and fatigue damage mechanism of multi-pillar system subjected to different cyclic loads. J. Cent. South Univ. Sci. Technol. Min. Metall. 2020, 27, 542–553. [Google Scholar] [CrossRef]
- Li, B.; Yang, S.; Tian, W. Experimental study on mechanical behavior of brazilian disk with two filled and unfilled fissures. J. Appl. Basic Eng. Sci. 2019, 27, 628–645. [Google Scholar]
- Wang, Z.; Sun, Y.; Zhang, S.; Song, W.; Wang, Y. Study on failure evolution of in-seam boreholes under cycle constant vertical loadings. J. Rock Mech. Eng. 2020, 39, 262–271. [Google Scholar]
- Du, X. Experimental Study on the Effect of Loading Rate and Ratio on the Failure Characteristics of Similar Materials. Master’s Thesis, Xi’an University of Science and Technology, Xi’an, China, 2019. [Google Scholar]
- Yu, Y. Research on the Mechanical Properties of Rock-like Materials under the Loading and Unloading Conditions. Master’s Thesis, Kunming University of Science and Technology, Kunming, China, 2018. [Google Scholar]
- Li, S.; Cheng, X.; Liu, C.; Cheng, C.; Yang, M. Damage characteristics and space-time evolution law of rock similar material under uniaxial compression. J. Coal 2017, 42 (Suppl. S1), 104–111. [Google Scholar]
- Liu, X.; Ye, Y.; Wang, Q.; Zhang, H.; Liu, Y.; Liu, Y. Mechanical properties of similar material specimens of composite rock masses with different strengths under uniaxial compression. Geotechnics 2017, 38 (Suppl. S2), 183–190. [Google Scholar]
- Wang, H.W.; Zhou, H.W.; Zuo, J.P.; Wang, Z.G.; Xie, H.P. Application of optical measurement method in strata movement smiulation expermient. J. Coal 2006, 31, 278–281. [Google Scholar]
- Liu, X.J.; Song, S.L.; Fan, D.Y.; Fan, W.C. Experimental study on deformation and failure evolution of surrounding rock for deep super-large section chamber group. J. Min. Saf. Eng. 2020, 37, 40–49. [Google Scholar]
- Lu, X.F.; Pan, Y.S.; Li, Z.H.; Dai, S.H. Similarity-simulation tests for failure law of a rock burst roadway under shock wave. Vib. Shock 2011, 30, 212–215+235. [Google Scholar]
- Bi, D. Application of Digital Scatter Correlation Method in Similar Simulation of Underground Engineering. Master’s Thesis, Shandong University of Science and Technology, Qingdao, China, 2017. [Google Scholar]
- Wang, Z.G.; Zhou, H.W.; Xie, H.P.; Zuo, J.P.; Wang, H.W. Experimental study of the rule of overlying strata movement and breakage in deep mining. Exp. Mech. 2008, 23, 503–510. [Google Scholar]
- Shi, F.; Wang, H.; Shu, C. Similar simulation study on the influence of seam angle change ondeformation law of overburden strata in coal seam mining. J. Chongqing Univ. 2018, 41, 36–45. [Google Scholar]
- Wei, G. Similarity experiment of rock fracture evolution after covering layer exploitation in hongling coal mine. J. Liaoning Univ. Eng. Technol. 2012, 31, 185–188. [Google Scholar]
- Pan, Y.; Lu, X.; Li, Z.; Dai, S. Experimental study of dynamic failure process of roadway under high velocity impact loading. Geotech. Mech. 2011, 32, 1281–1286. [Google Scholar]
- Wang, L.; Yan, J.; Ma, L.; Feng, H.E. Experimental study of deformation and failure forslopes with weak planes under earthouake effect. J. Eng. Geol. 2012, 20, 471–477. [Google Scholar]
- Li, T.; Zhong, Y.; Pan, H.; Chen, G. Failure Characteristics Analysis on Physical Model of Rock Burst in High In-situ Stress Tunnel. J. Undergr. Space Eng. 2019, 15, 1639–1645. [Google Scholar]
- Zhao, C.; Liu, J.; Lyu, C.; Chen, W.; Li, X.; Li, Z. Experimental study on mechanical properties, permeability and energy characteristics of limestone from through-coal seam (TCS) tunnel. Eng. Geol. 2022, 303, 106673. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, J.; Lyu, C.; Xu, H.; Lin, H. Study on the shear-slip process and characteristics of fracture in shale. Eng. Geol. 2023, 319, 107097. [Google Scholar] [CrossRef]
- Gu, H.; Lai, X.; Tao, M.; Cao, W.; Yang, Z. The role of porosity in the dynamic disturbance resistance of water-saturated coal. Int. J. Rock Mech. Min. Sci. 2023, 166, 105388. [Google Scholar] [CrossRef]
- Zhang, Q. Similar Test and Numerical Simulation of Coal Seam Mining in Tarangaole Mining Area. Master’s Thesis, Jilin University, Changchun, China, 2019. [Google Scholar]
- Li, B. Study on Induced Mechanism of Roadway Floor Rock Burst under Super-Thick Conglomerate Stratum. Ph.D. Thesis, Henan University of Science and Technology, Luoyang, China, 2014. [Google Scholar]
- Tan, Y.; Wu, S.; Ning, J.; Zang, C.; Yin, Z.; Gu, S. Mining Pressure and Strata Control; Coal Industry Press: Beijing, China, 2008. [Google Scholar]
- Xiao, J. Selection of Similar Materials for Model Test & Research on Similar Material Proportioning Test. Master’s Thesis, Beijing Jiaotong University, Beijing, China, 2013. [Google Scholar]
- Gu, D. Similar Materials and Similar Models; China University of Mining and Technology Press: Xuzhou, China, 1995. [Google Scholar]
- Shi, X.; Liu, B.; Xiao, J. A method for determining the ratio of similar materials with cement and plaster as bonding agents. Geotechnics 2015, 36, 1357–1362. [Google Scholar]
- Cai, M. Rock Mechanics and Engineering, 2nd ed.; Science Press: Beijing, China, 2013. [Google Scholar]
- Zhu, H.; Xie, M. Orthogonal test route for determining similar material ratios. J. Wuhan Inst. Water Conserv. Electr. Power 1990, 23, 103–109. [Google Scholar]







| Coal Rock | Density (g·cm−3) | Tensile Strength (MPa) | Compressive Strength (MPa) | Modulus of Elasticity (GPa) | Poisson’s Ratio |
|---|---|---|---|---|---|
| pulverized sandstone | 2.69 | 6.36 | 148.02 | 24.83 | 0.14 |
| fine sandstone | 2.58 | 4.28 | 122.90 | 17.27 | 0.18 |
| medium sandstone | 2.44 | 2.94 | 109.53 | 11.04 | 0.20 |
| coarse sandstone | 2.35 | 1.23 | 79.43 | 6.81 | 0.22 |
| coal | 1.34 | 0.84 | 7.80 | 1.81 | 0.32 |
| Considerations | Sand-to-Cement Ratio (A) | Carbon Paste Ratio (B) | Water Content (C) | Note | |
|---|---|---|---|---|---|
| Level | |||||
| 1 | 7:1 | 4:6 | 1/8 | In order to ensure compactness, the full load of the jack (10 MPa, 5 min) was used | |
| 2 | 8:1 | 5:5 | 1/9 | ||
| 3 | 9:1 | 6:4 | 1/10 | ||
| 4 | 10:1 | 7:3 | 1/11 | ||
| Column Number | Sand (kg) | Calcium Carbonate (kg) | Gypsum (kg) | Water Weight (kg) | Note |
|---|---|---|---|---|---|
| 1 | 1.82 | 0.11 | 0.16 | 0.19 | |
| 2 | 1.82 | 0.13 | 0.13 | 0.26 | |
| 3 | 1.82 | 0.16 | 0.11 | 0.23 | |
| 4 | 1.82 | 0.18 | 0.08 | 0.21 | |
| 5 | 1.86 | 0.11 | 0.16 | 0.26 | |
| 6 | 1.86 | 0.13 | 0.13 | 0.23 | |
| 7 | 1.86 | 0.16 | 0.11 | 0.21 | |
| 8 | 1.86 | 0.18 | 0.08 | 0.19 | |
| 9 | 1.88 | 0.11 | 0.16 | 0.23 | |
| 10 | 1.88 | 0.13 | 0.13 | 0.21 | |
| 11 | 1.88 | 0.16 | 0.11 | 0.19 | |
| 12 | 1.88 | 0.18 | 0.08 | 0.26 | |
| 13 | 1.90 | 0.11 | 0.16 | 0.21 | |
| 14 | 1.90 | 0.13 | 0.13 | 0.19 | |
| 15 | 1.90 | 0.16 | 0.11 | 0.26 | |
| 16 | 1.90 | 0.18 | 0.08 | 0.23 |
| Test Number | A | B | C | Uniaxial Compressive Strength (MPa) | Modulus of Elasticity (MPa) | Poisson’s Ratio |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 4 | 0.459 | 0.059 | 0.272 |
| 2 | 1 | 2 | 1 | 0.365 | 0.043 | 0.269 |
| 3 | 1 | 3 | 2 | 0.327 | 0.036 | 0.243 |
| 4 | 1 | 4 | 3 | 0.251 | 0.032 | 0.275 |
| 5 | 2 | 1 | 1 | 0.374 | 0.038 | 0.284 |
| 6 | 2 | 2 | 2 | 0.317 | 0.032 | 0.272 |
| 7 | 2 | 3 | 3 | 0.286 | 0.029 | 0.258 |
| 8 | 2 | 4 | 4 | 0.210 | 0.026 | 0.222 |
| 9 | 3 | 1 | 2 | 0.326 | 0.035 | 0.261 |
| 10 | 3 | 2 | 3 | 0.289 | 0.032 | 0.246 |
| 11 | 3 | 3 | 4 | 0.200 | 0.026 | 0.256 |
| 12 | 3 | 4 | 1 | 0.212 | 0.020 | 0.203 |
| 13 | 4 | 1 | 3 | 0.299 | 0.022 | 0.248 |
| 14 | 4 | 2 | 4 | 0.206 | 0.027 | 0.207 |
| 15 | 4 | 3 | 1 | 0.188 | 0.033 | 0.219 |
| 16 | 4 | 4 | 2 | 0.176 | 0.021 | 0.245 |
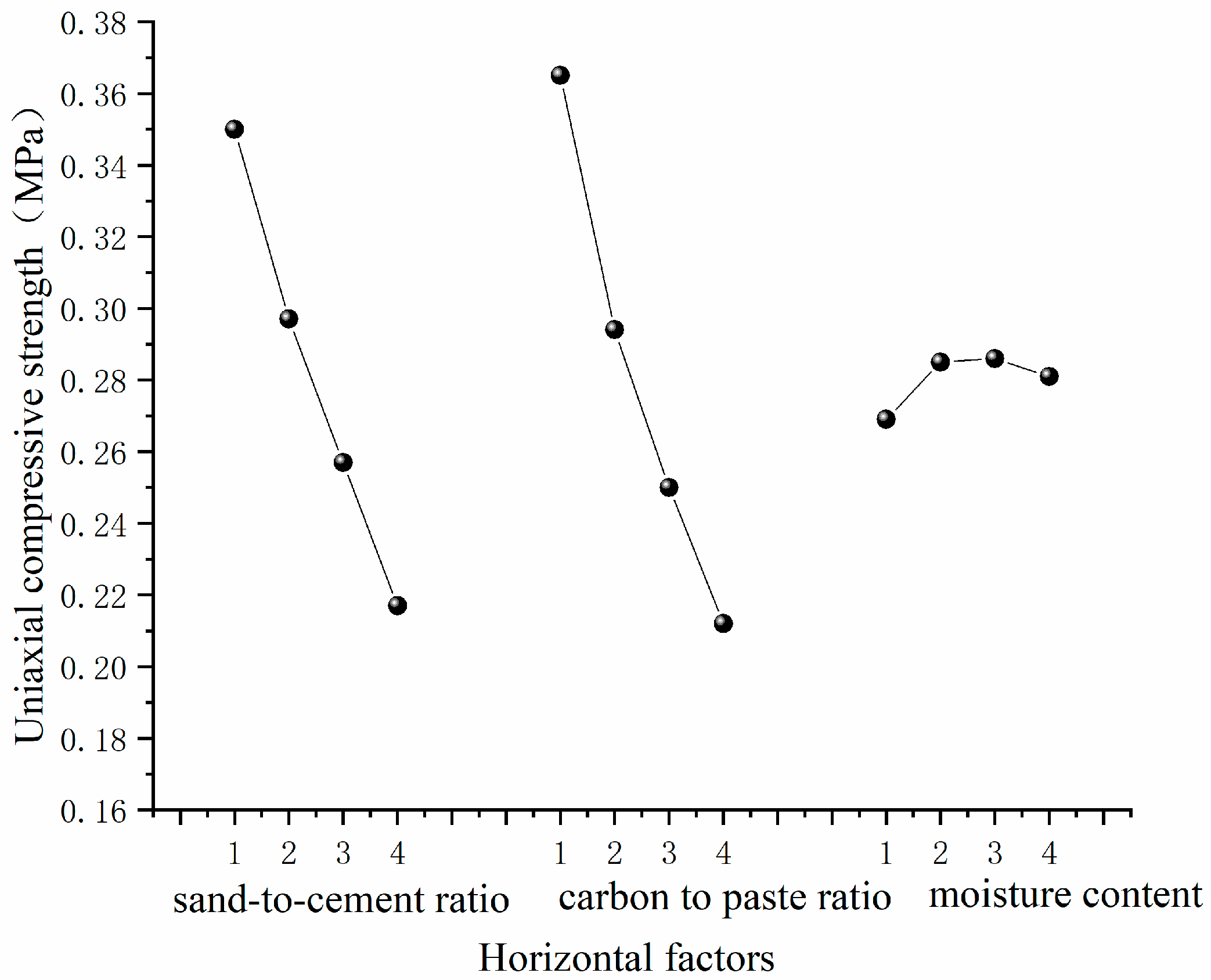
| K1 | 1.402 | 1.458 | 1.076 | compressive strength | ||
| K2 | 1.187 | 1.177 | 1.138 | |||
| K3 | 1.027 | 1.001 | 1.145 | |||
| K4 | 0.868 | 0.848 | 1.125 | |||
| k1 | 0.350 | 0.365 | 0.269 | |||
| k2 | 0.297 | 0.294 | 0.285 | |||
| k3 | 0.257 | 0.250 | 0.286 | |||
| k4 | 0.217 | 0.212 | 0.281 | |||
| Polar deviation R | 0.133 | 0.152 | 0.017 | |||
| order of priority | B > A > C | |||||
| excellent level | A4 | B4 | C1 | |||
| superior combination | B4A4C1 | |||||
| K1 | 0.170 | 0.154 | 0.138 | modulus of elasticity | ||
| K2 | 0.125 | 0.134 | 0.134 | |||
| K3 | 0.113 | 0.124 | 0.124 | |||
| K4 | 0.103 | 0.099 | 0.115 | |||
| k1 | 0.043 | 0.039 | 0.035 | |||
| k2 | 0.031 | 0.034 | 0.034 | |||
| k3 | 0.028 | 0.031 | 0.031 | |||
| k4 | 0.026 | 0.025 | 0.029 | |||
| Polar deviation R | 0.017 | 0.014 | 0.006 | |||
| order of priority | A > B > C | |||||
| excellent level | A4 | B4 | C4 | |||
| superior combination | A4B4C4 | |||||
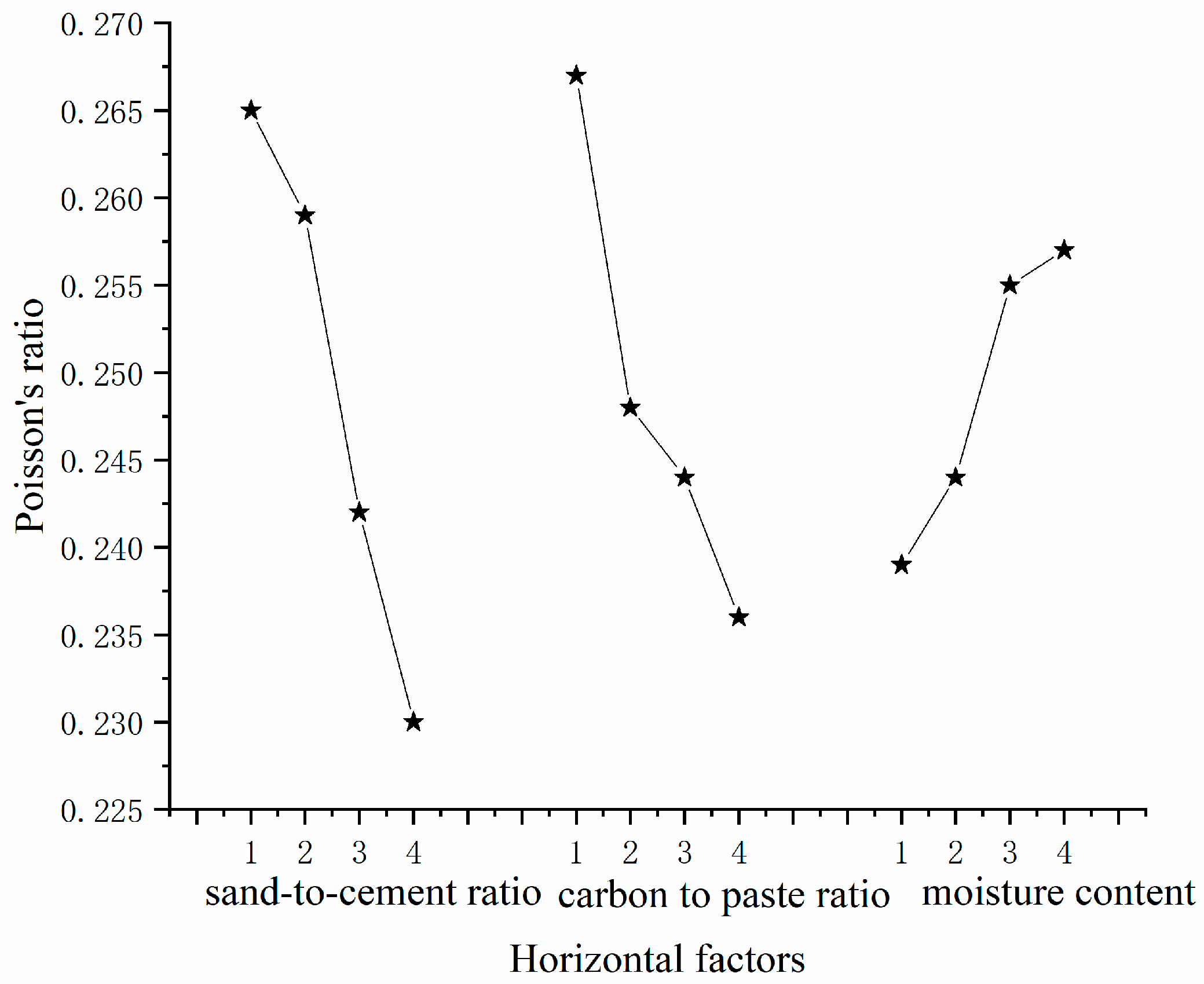
| K1 | 1.059 | 1.066 | 0.958 | Poisson’s ratio | ||
| K2 | 1.035 | 0.993 | 0.976 | |||
| K3 | 0.967 | 0.976 | 1.021 | |||
| K4 | 0.920 | 0.946 | 1.027 | |||
| k1 | 0.265 | 0.267 | 0.239 | |||
| k2 | 0.259 | 0.248 | 0.244 | |||
| k3 | 0.242 | 0.244 | 0.255 | |||
| k4 | 0.230 | 0.236 | 0.257 | |||
| Polar deviation R | 0.035 | 0.030 | 0.017 | |||
| order of priority | A > B > C | |||||
| excellent level | A4 | B4 | C1 | |||
| superior combination | A4B4C1 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, G.; Wang, D.; Zan, Y.; Wang, S.; Zhang, Q. Feasibility Study of Material Deformation and Similarity of Spatial Characteristics of Standard Coal Rocks. Processes 2024, 12, 454. https://doi.org/10.3390/pr12030454
Liu G, Wang D, Zan Y, Wang S, Zhang Q. Feasibility Study of Material Deformation and Similarity of Spatial Characteristics of Standard Coal Rocks. Processes. 2024; 12(3):454. https://doi.org/10.3390/pr12030454
Chicago/Turabian StyleLiu, Gang, Dongwei Wang, Yonglong Zan, Shengxuan Wang, and Qiqi Zhang. 2024. "Feasibility Study of Material Deformation and Similarity of Spatial Characteristics of Standard Coal Rocks" Processes 12, no. 3: 454. https://doi.org/10.3390/pr12030454
APA StyleLiu, G., Wang, D., Zan, Y., Wang, S., & Zhang, Q. (2024). Feasibility Study of Material Deformation and Similarity of Spatial Characteristics of Standard Coal Rocks. Processes, 12(3), 454. https://doi.org/10.3390/pr12030454






