Study of a Novel Method to Weaken the Backmixing in a Multi-Inlet Vortex Mixer
Abstract
:1. Introduction
2. MIVM Domain and Numerical Method
2.1. Simulation Domain
2.2. Materials and Operating Conditions
2.3. Numerical Models
3. Results and Discussion
3.1. Simulation Validation
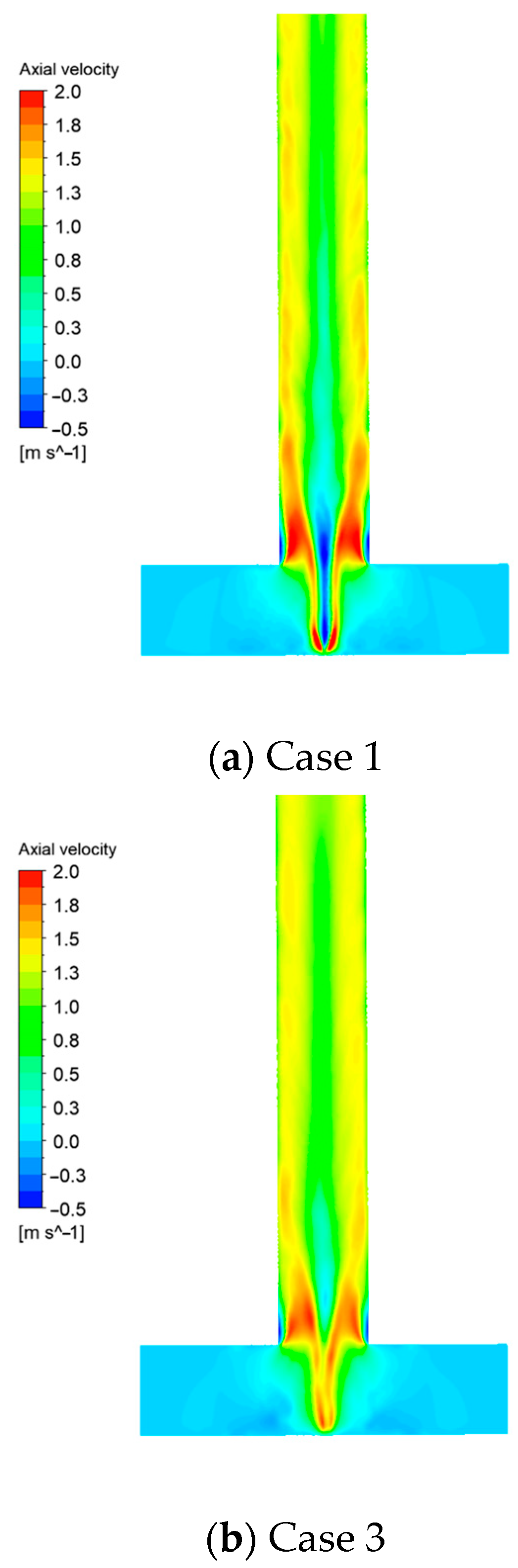
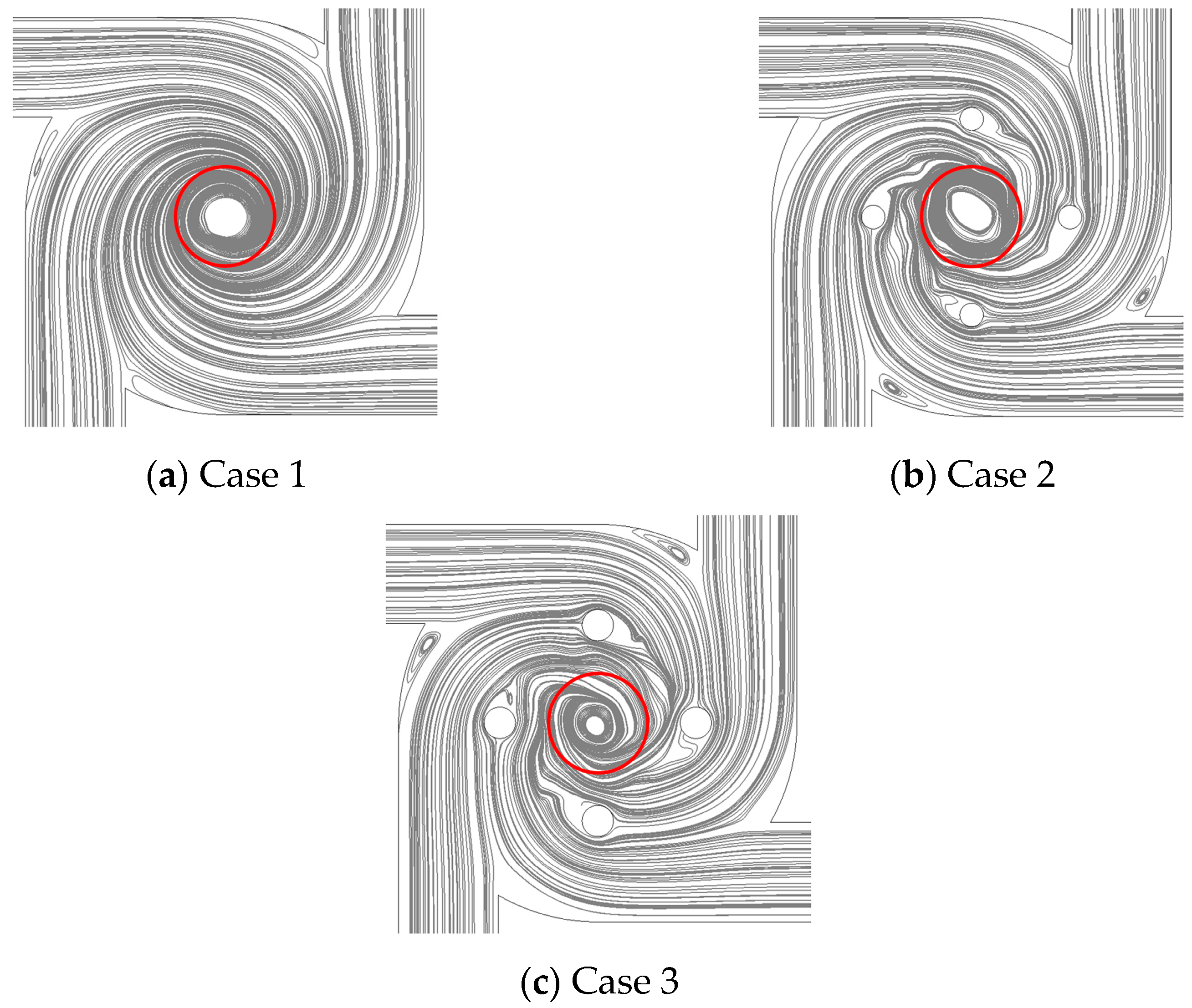
3.2. Residence Time of Fluid
- (1)
- There were multiple peaks appearing earlier than the average residence time, indicating that there may have been multiple short-circuit flows.
- (2)
- After the appearance of the maximum concentration on the RTD curve, the descending curve was not smooth, which showed that there may have been backflow.
- (3)
- There was an obvious tailing on the curve, which indicated the existence of backmixing in the mixer.
- (1)
- The peak of the RTD curve appeared later and was closer to the average residence time.
- (2)
- The RTD curve ascended and descended more rapidly near the peak.
- (3)
- On RTD curve, the multi-peak phenomenon was almost eliminated.
3.3. Tanks-in-Series Model
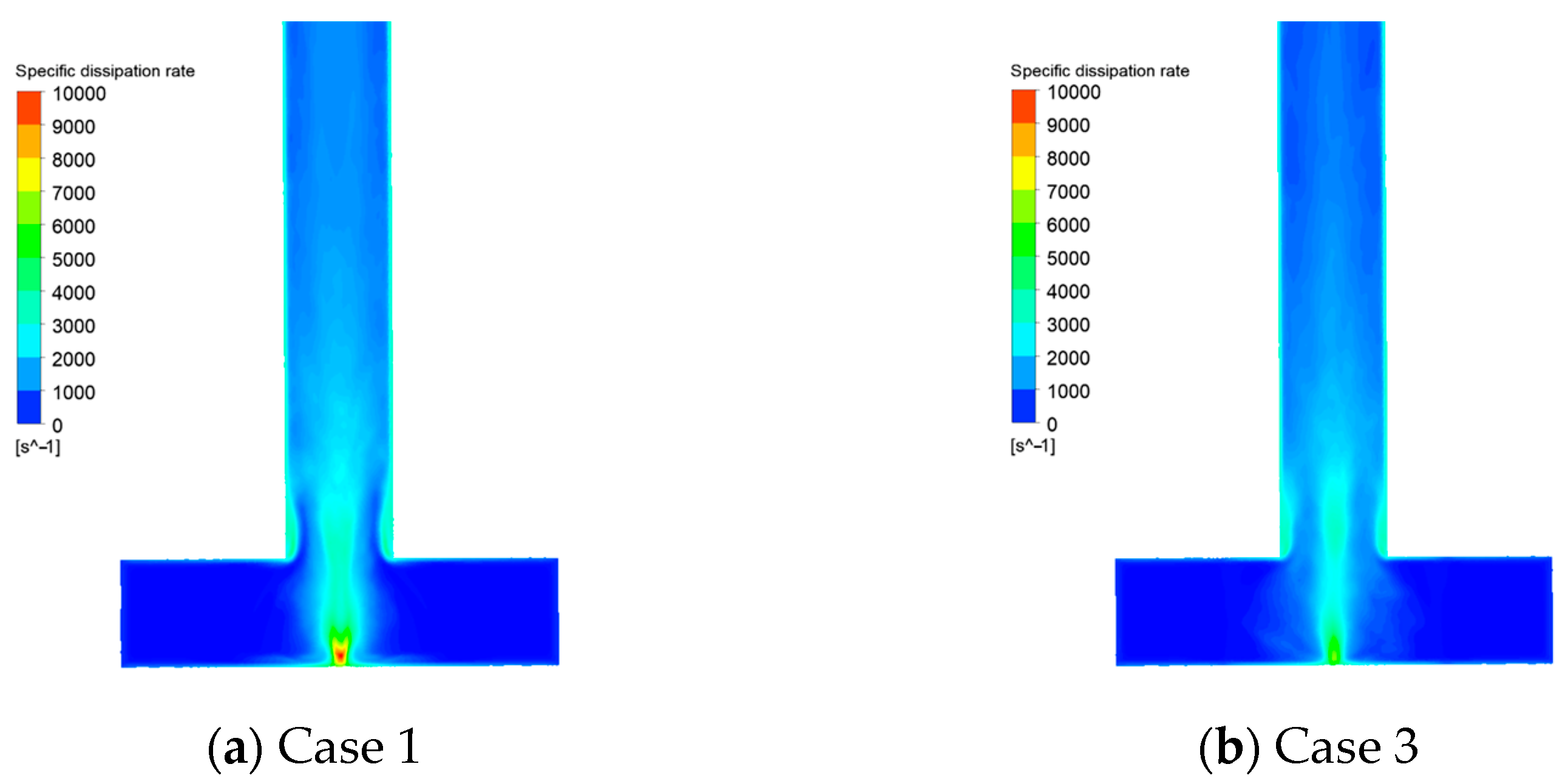
3.4. Turbulent Energy Dissipation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature | |
| k | Turbulent kinetic energy, m2·s−2 |
| ω | Specific energy dissipation rate, s−1 |
| Win | Width of the inlet, mm |
| Lin | Length of the inlet, mm |
| Dout | Diameter of the outlet pipe, mm |
| Lin | Length of the outlet pipe, mm |
| Hmix | Height of the mixing chamber, mm |
| Dmix | Diameter of the mixing chamber, mm |
| Re | Reynolds number |
| N | Number of columns |
| ΔL | Axis distance between the center of column and center of mixer, mm |
| φ | Diameter of the column, mm |
| θ | Angle of rotation around the center, ° |
| μt | Turbulent eddy viscosity, kg·m−1·s−1 |
| Pk | Generating term of the turbulent kinetic energy, kg·m−1·s−3 |
| ρ | Fluid density, kg·m−3 |
| U | Fluid velocity, m·s−1 |
| μ | Fluid viscosity, kg·m−1·s−1 |
| hmax | Maximum edge length of the grid, mm |
| l | Length scale of the turbulent model, mm |
| S | Magnitude of the strain rate tensor, s−1 |
| Ω | Magnitude of the vorticity tensor, s−1 |
| dw | Distance from the grid to the nearest wall, mm |
| V | Volume of the cell, mm3 |
| vz | Axial velocity, m·s−1 |
| vt | Tangential velocity, m·s−1 |
| Q | Q criterion, s−2 |
| uij | ∂ui/∂xj, s−1 |
| uji | ∂uj/∂xi, s−1 |
| Abbreviations | |
| FNP | Flash nanoprecipitation |
| CIJ | Confined impinging jet |
| MIVM | Multi-inlet vortex mixer |
| CFD | Computational fluid dynamics |
| PIV | Particle image velocimetry |
| PLIF | Planar laser-induced fluorescence |
| SDES | Shielded detached eddy simulation |
| SST | Shear-stress transport |
| RANS | Reynolds-averaged Navier–Stokes |
| LES | Large-eddy simulation |
| DDES | Delayed detached eddy simulation |
| DES | Detached eddy simulation |
| RTD | Residence time distribution |
| COV | Coefficient of variation |
References
- Zhao, Y.B.; Qiu, Z.M.; Huang, J.Y. Preparation and analysis of Fe3O4 magnetic nanoparticles used as targeted-drug carriers. Chin. J. Chem. Eng. 2008, 16, 451–455. [Google Scholar] [CrossRef]
- Wicki, A.; Witzigmann, D.; Balasubramanian, V.; Huwyler, J. Nanomedicine in cancer therapy: Challenges, opportunities, and clinical applications. J. Control. Release 2015, 200, 138–157. [Google Scholar] [CrossRef] [PubMed]
- Xiao, S.Y.; Tang, Y.F.; Lv, Z.; Lin, Y.M.; Chen, L. Nanomedicine—Advantages for their use in rheumatoid arthritis theranostics. J. Control. Release 2019, 316, 302–316. [Google Scholar] [CrossRef]
- Wilson, B.; Geetha, K.M. Neurotherapeutic applications of nanomedicine for treating Alzheimer’s disease. J. Control. Release 2020, 325, 25–37. [Google Scholar] [CrossRef]
- Huo, M.F.; Wang, L.Y.; Chen, Y.; Shi, J.L. Nanomaterials/microorganism-integrated microbiotic nanomedicine. Nano Today 2020, 32, 100854. [Google Scholar] [CrossRef]
- Johnson, B.K.; Prud’homme, R.K. Flash nanoprecipitation of organic actives and block copolymers using a confined impinging jets mixer. Aust. J. Chem. 2003, 56, 1021–1024. [Google Scholar] [CrossRef]
- Valente, I.; Stella, B.; Marchisio, D.L.; Dosio, F.; Barresi, A.A. Production of PEGylated nanocapsules through solvent displacement in confined impinging jet mixers. J. Pharm. Sci. 2012, 101, 2490–2501. [Google Scholar] [CrossRef]
- Tao, J.S.; Chow, S.F.; Zheng, Y. Application of flash nanoprecipitation to fabricate poorly water-soluble drug nanoparticles. Acta Pharm. Sin. B 2019, 9, 4–18. [Google Scholar] [CrossRef] [PubMed]
- Shi, L.; Shan, J.N.; Ju, Y.G.; Aikens, P.; Prud’homme, R.K. Nanoparticles as delivery vehicles for sunscreen agents. Colloids Surf. A Physicochem. Eng. Asp. 2012, 396, 122–129. [Google Scholar] [CrossRef]
- Liu, Y.; Olsen, M.G.; Fox, R.O. Turbulence in a microscale planar confined impinging-jets reactor. Lab Chip 2009, 9, 1110–1118. [Google Scholar] [CrossRef]
- Liu, Y.; Cheng, C.Y.; Liu, Y.; Prud’homme, R.K.; Fox, R.O. Mixing in a multi-inlet vortex mixer (MIVM) for flash nano-precipitation. Chem. Eng. Sci. 2008, 63, 2829–2842. [Google Scholar] [CrossRef]
- D’Addio, S.M.; Prud’homme, R.K. Controlling drug nanoparticle formation by rapid precipitation. Adv. Drug Deliv. Rev. 2011, 63, 417–426. [Google Scholar] [CrossRef]
- Akbulut, M.; Ginart, P.; Gindy, M.E.; Theriault, C.; Chin, K.H.; Soboyejo, W.; Prud’homme, R.K. Generic method of preparing multifunctional fluorescent nanoparticles using flash nanoprecipitation. Adv. Funct. Mater. 2009, 19, 718–725. [Google Scholar] [CrossRef]
- Kumar, V.; Adamson, D.H.; Prud’homme, R.K. Fluorescent polymeric nanoparticles: Aggregation and phase behavior of pyrene and amphotericin B molecules in nanoparticle cores. Small 2010, 6, 2907–2914. [Google Scholar] [CrossRef] [PubMed]
- Shen, H.; Hong, S.; Prud’homme, R.K.; Liu, Y. Self-assembling process of flash nanoprecipitation in a multi-inlet vortex mixer to produce drug-loaded polymeric nanoparticles. J. Nanoparticle Res. 2011, 13, 4109–4120. [Google Scholar] [CrossRef]
- Liu, Z.P.; Hill, J.C.; Fox, R.O.; Olsen, M.G. Investigation of turbulent mixing in a macro-scale multi-inlet vortex nanoprecipitation reactor by stereoscopic-PIV. In Proceedings of the ASME 2014 4th Joint US-European Fluids Engineering Division Summer Meeting, Chicago, IL, USA, 11–15 July 2014. [Google Scholar]
- Liu, Z.P.; Ramezani, M.; Fox, R.O.; Hill, J.C.; Olsen, M.G. Flow characteristics in a scaled-up multi-inlet vortex nanoprecipitation reactor. Ind. Eng. Chem. Res. 2015, 54, 4512–4525. [Google Scholar] [CrossRef]
- Liu, Z.P.; Passalacqua, A.; Olsen, M.G.; Fox, R.O.; Hill, J.C. Dynamic delayed detached eddy simulation of a multi-inlet vortex reactor. AIChE J. 2016, 62, 2570–2578. [Google Scholar] [CrossRef]
- Liu, Z.P.; Hitimana, E.; Olsen, M.G.; Hill, J.C.; Fox, R.O. Turbulent mixing in the confined swirling flow of a multi-inlet vortex reactor. AIChE J. 2017, 63, 2409–2419. [Google Scholar] [CrossRef]
- Cheng, J.C.; Olsen, M.G.; Fox, R.O. A microscale multi-inlet vortex nanoprecipitation reactor: Turbulence measurement and simulation. Appl. Phys. Lett. 2009, 94, 204104. [Google Scholar] [CrossRef]
- Leon, M.A.; Nijhuis, T.A.; Schaaf, J.V.D.; Schouten, J.C. Residence time distribution and reaction rate in the horizontal rotating foam stirrer reactor. Chem. Eng. Sci. 2014, 117, 8–17. [Google Scholar] [CrossRef]
- Bhutto, R.A.; Bhutto, N.H.; Iqbal, S.; Manoharadas, S.; Yi, J.; Fan, Y.T. Polyelectrolyte nanocomplex from sodium caseinate and chitosan as potential vehicles for oil encapsulation by flash nanoprecipitation. Food Hydrocolloid 2024, 150, 109666. [Google Scholar] [CrossRef]
- Lass, H.U.; Mohrholz, V.; Knoll, M.; Prandke, H. Enhanced mixing downstream of a pile in an estuarine flow. J. Mar. Syst. 2008, 74, 505–527. [Google Scholar] [CrossRef]
- Dundi, T.M.; Raju, V.R.K.; Chandramohan, V.P. Characterization of mixing in an optimized designed T–T mixer with cylindrical elements. Chin. J. Chem. Eng. 2019, 27, 2337–2351. [Google Scholar] [CrossRef]
- Li, L.; Xu, W.X.; Tan, Y.F.; Yang, Y.S.; Yang, J.G.; Tan, D.P. Fluid-induced vibration evolution mechanism of multiphase free sink vortex and the multi-source vibration sensing method. Mech. Syst. Signal Process. 2023, 189, 110058. [Google Scholar] [CrossRef]
- Blevins, R.D.; Scanlan, R.H. Flow-induced vibration. J. Mech. Des. N. Y. 1977, 44, 802. [Google Scholar] [CrossRef]
- Travin, A.; Shur, M.; Strelets, M.; Spalart, P. Detached-eddy simulations past a circular cylinder. Flow Turbul. Combust. 1999, 63, 293–313. [Google Scholar] [CrossRef]
- Zhao, W.W.; Wan, D.C.; Sun, R. Detached-eddy simulation of flows over a circular cylinder at high Reynolds number. In Proceedings of the 26th International Ocean and Polar Engineering Conference, Rhodes, Greece, 26 June–1 July 2016. [Google Scholar]
- ANSYS Inc. ANSYS Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2017. [Google Scholar]
- Gritskevich, M.S.; Garbaruk, A.V.; Schutze, J.; Menter, F.R. Development of DDES and IDDES formulations for the k-ω shear stress transport model. Flow Turbul. Combust. 2012, 88, 431–449. [Google Scholar] [CrossRef]
- Jeong, J.; Hussain, F. On the identification of a vortex. J. Fluid Mech. 1995, 285, 69–94. [Google Scholar] [CrossRef]
- Kuhnen, J.; Song, B.F.; Scarselli, D.; Budanur, N.B.; Riedl, M.; Willis, A.P.; Avila, M.; Hof, B. Destabilizing turbulence in pipe flow. Nat. Phys. 2018, 14, 386–390. [Google Scholar] [CrossRef]
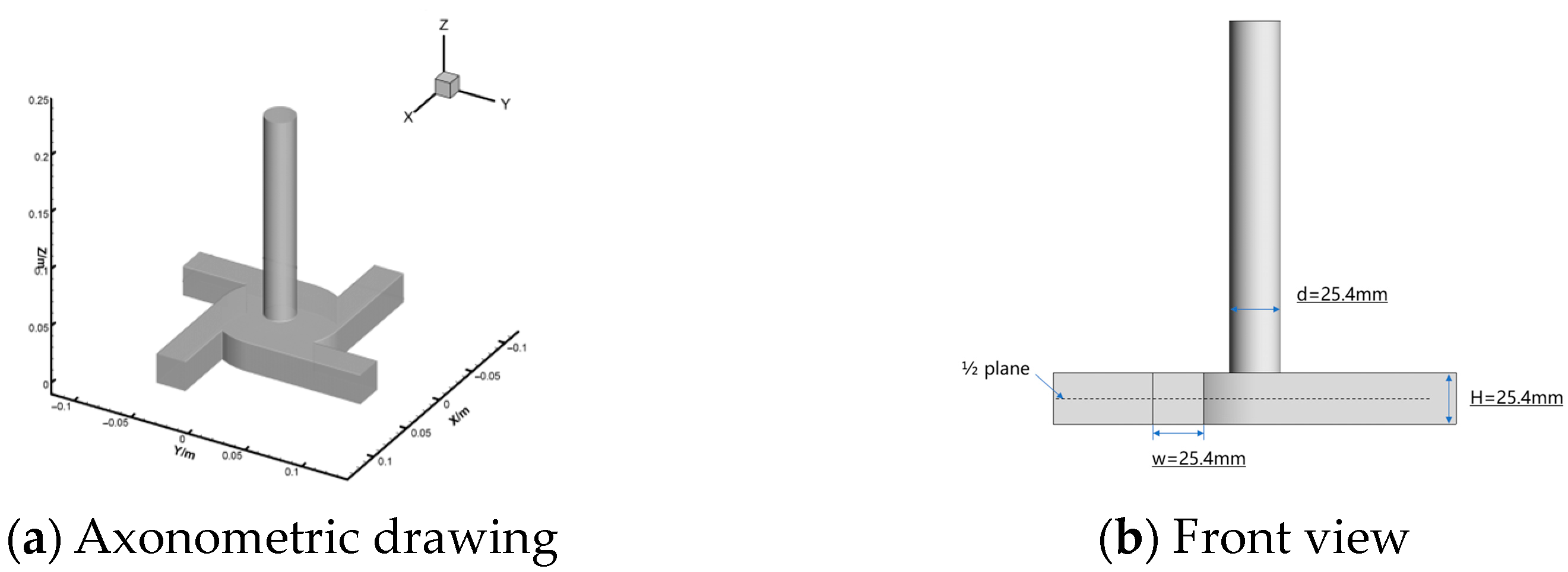

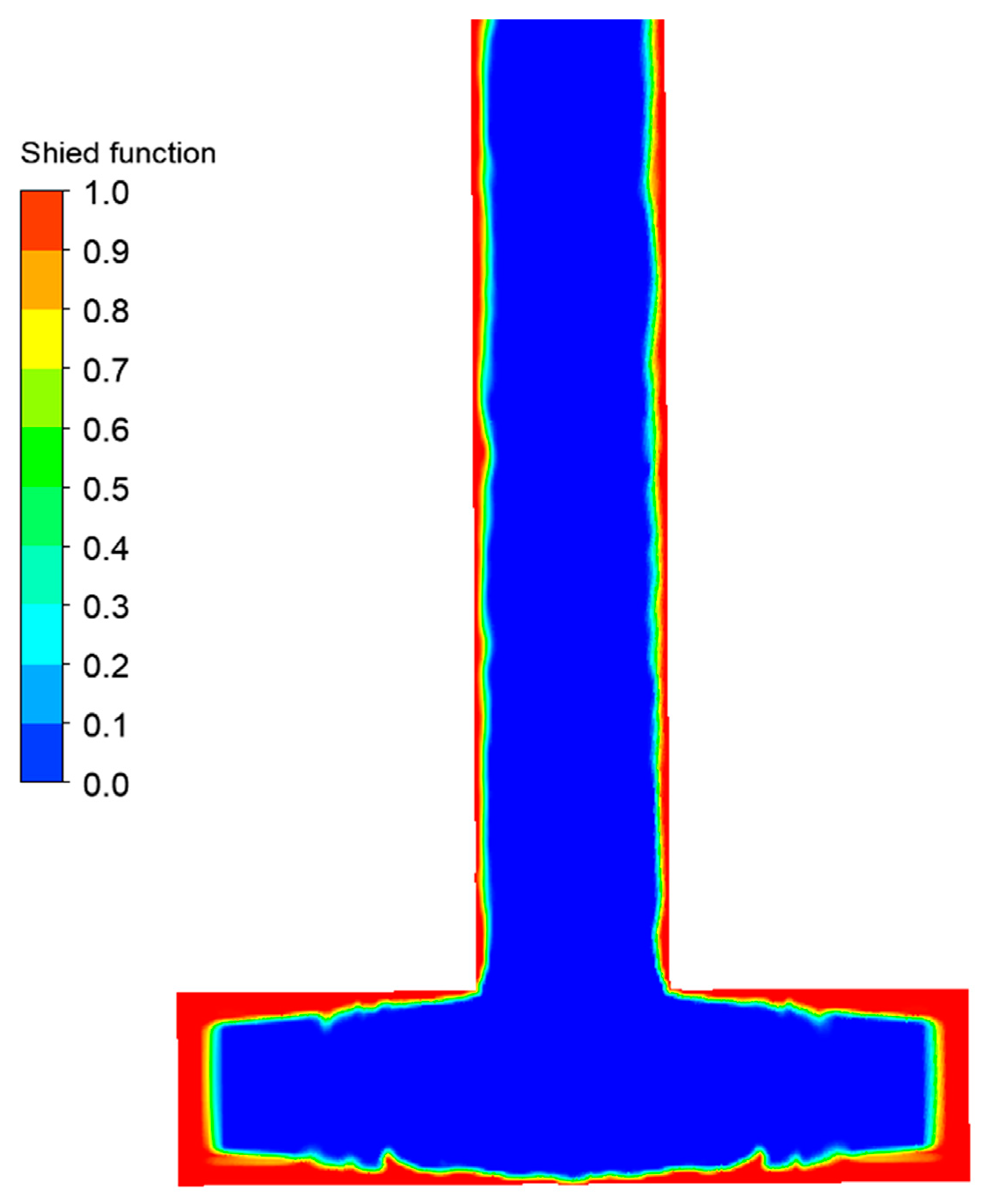
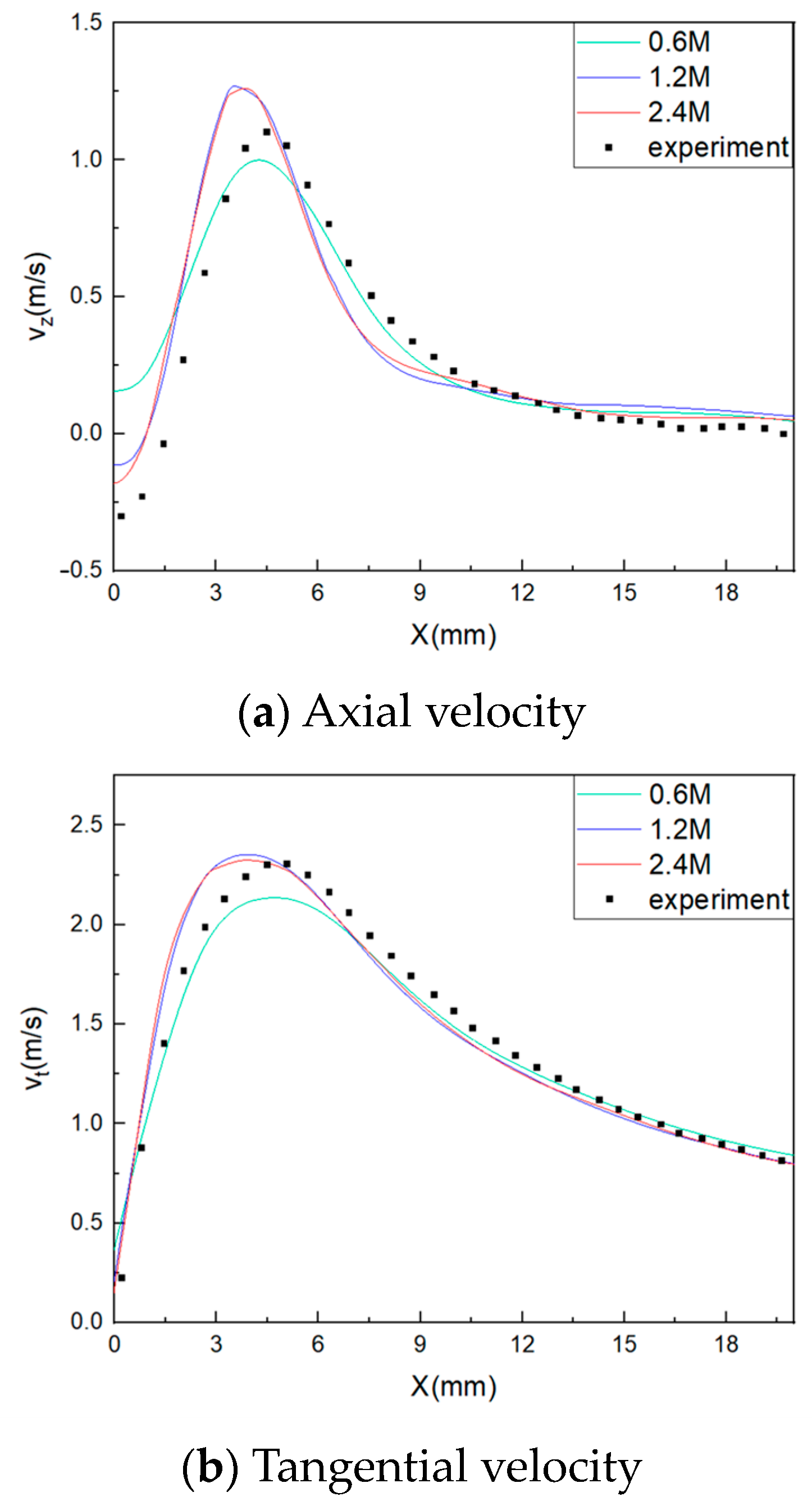
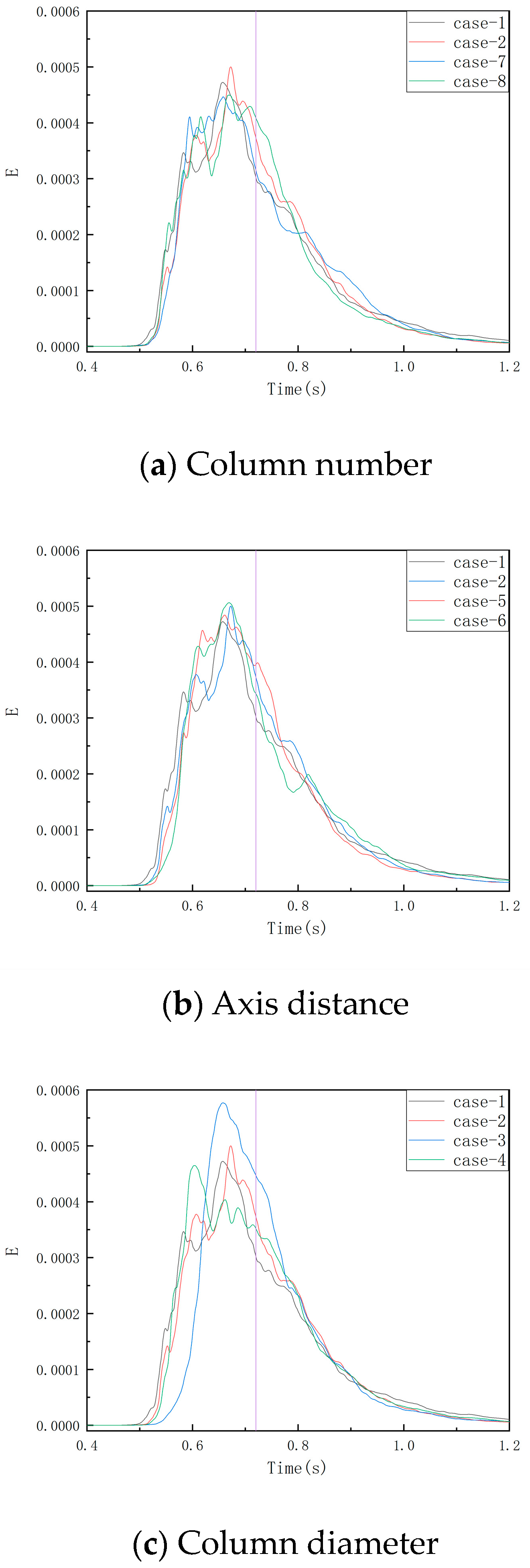




| Material | Density (kg/m3) | Viscosity (kg/m-s) |
|---|---|---|
| Water | 998.2 | 0.0009556 |
| Case No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Column number, N | / | 4 | 4 | 4 | 4 | 4 | 3 | 5 | 4 | 4 |
| Axis distance (mm), ΔL | / | 3 | 4 | 2 | 3 | 3 | 3 | 3 | 3 | 3 |
| Column diameter (mm), φ | / | 25 | 25 | 25 | 17 | 33 | 25 | 25 | 25 | 25 |
| Rotation angle (°), θ | / | / | / | / | / | / | / | / | 30 | 60 |
| Case No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Number of peaks | 4 | 5 | 1 | 4 | 6 | 4 | 6 | 6 | 6 | 4 |
| Case No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| Average residence time (s) | 0.722 | 0.722 | 0.732 | 0.720 | 0.717 | 0.728 | 0.726 | 0.716 | 0.712 | 0.719 |
| Variance | 0.0163 | 0.0134 | 0.0108 | 0.0143 | 0.0123 | 0.0149 | 0.0149 | 0.0135 | 0.0153 | 0.0141 |
| Dimensionless variance | 0.0313 | 0.0256 | 0.0202 | 0.0276 | 0.0238 | 0.0282 | 0.0283 | 0.0264 | 0.0302 | 0.0273 |
| Equivalent number of mixers | 31.9 | 39.0 | 49.6 | 36.3 | 41.9 | 35.5 | 35.3 | 37.8 | 33.1 | 36.6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Peng, H.; Li, Z.; Cai, Z.; Gao, Z. Study of a Novel Method to Weaken the Backmixing in a Multi-Inlet Vortex Mixer. Processes 2024, 12, 476. https://doi.org/10.3390/pr12030476
Peng H, Li Z, Cai Z, Gao Z. Study of a Novel Method to Weaken the Backmixing in a Multi-Inlet Vortex Mixer. Processes. 2024; 12(3):476. https://doi.org/10.3390/pr12030476
Chicago/Turabian StylePeng, Han, Zhipeng Li, Ziqi Cai, and Zhengming Gao. 2024. "Study of a Novel Method to Weaken the Backmixing in a Multi-Inlet Vortex Mixer" Processes 12, no. 3: 476. https://doi.org/10.3390/pr12030476
APA StylePeng, H., Li, Z., Cai, Z., & Gao, Z. (2024). Study of a Novel Method to Weaken the Backmixing in a Multi-Inlet Vortex Mixer. Processes, 12(3), 476. https://doi.org/10.3390/pr12030476






