A New Multi-Objective Optimization Strategy for Improved C3MR Liquefaction Process
Abstract
:1. Introduction
2. Process Design and Models
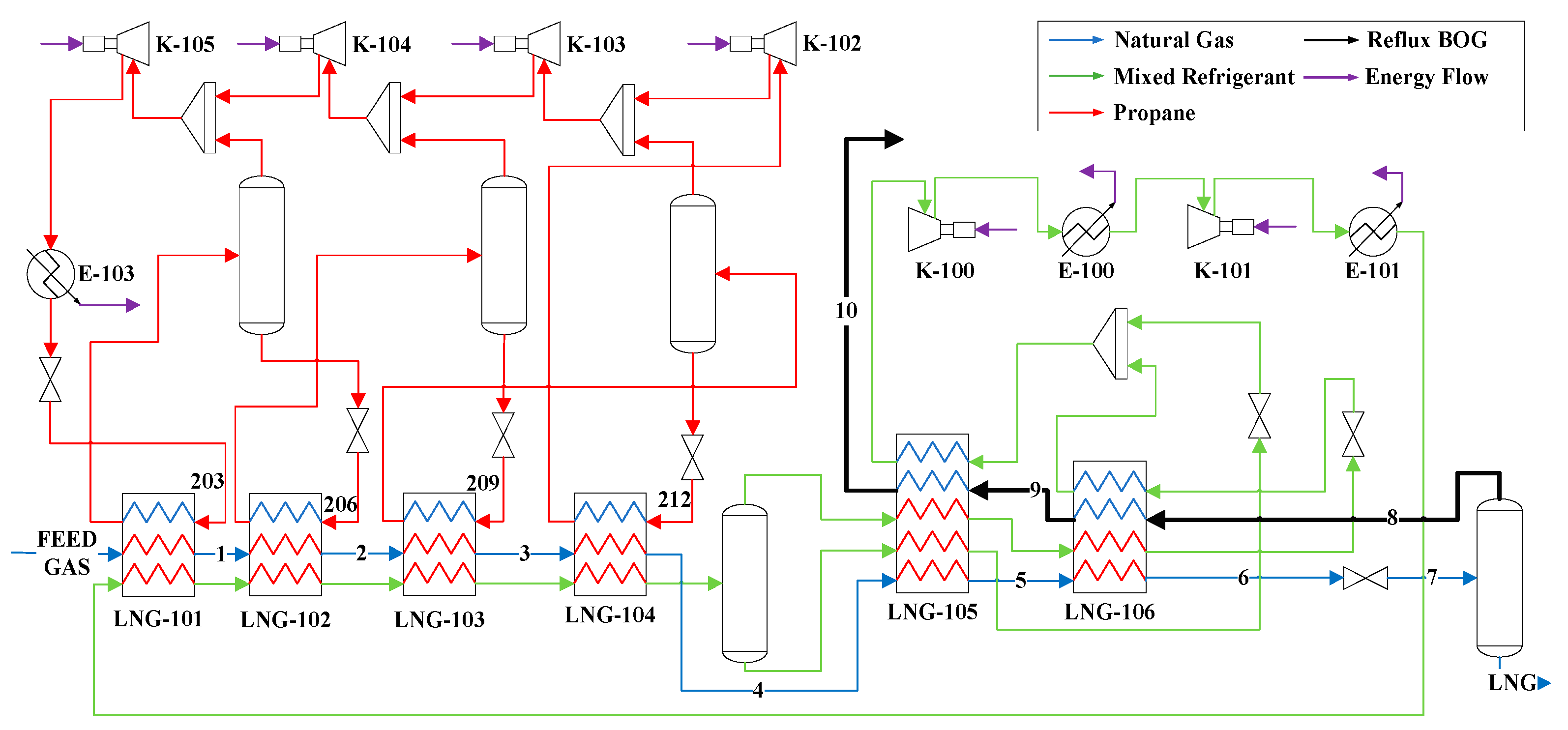
2.1. Process Description
2.2. Given Parameters
2.3. Thermodynamic Model
2.3.1. Phase Equilibrium Equations
2.3.2. Exergy Analytical Model
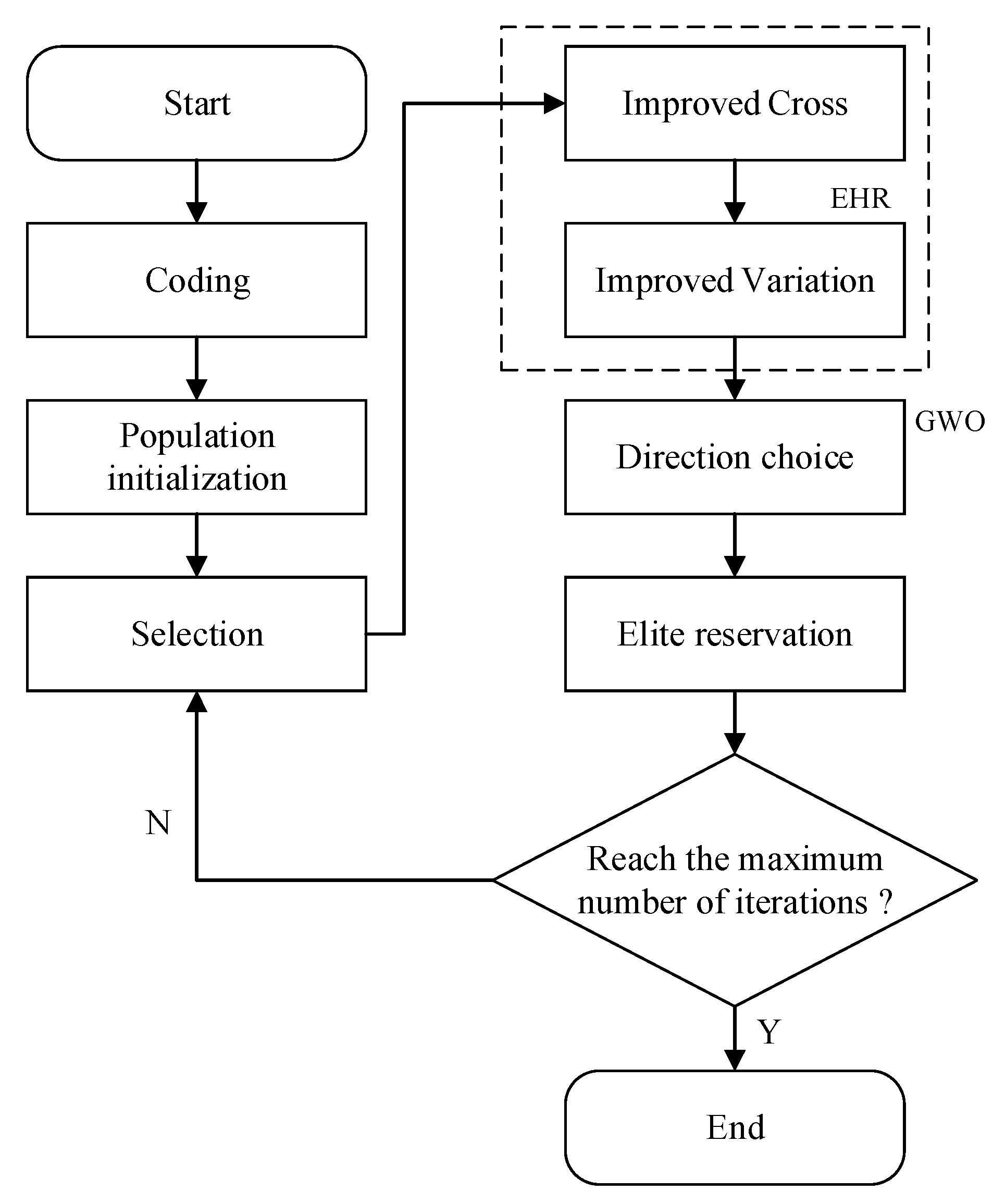
3. Improvement of GA
3.1. Improved GA Based on EHR
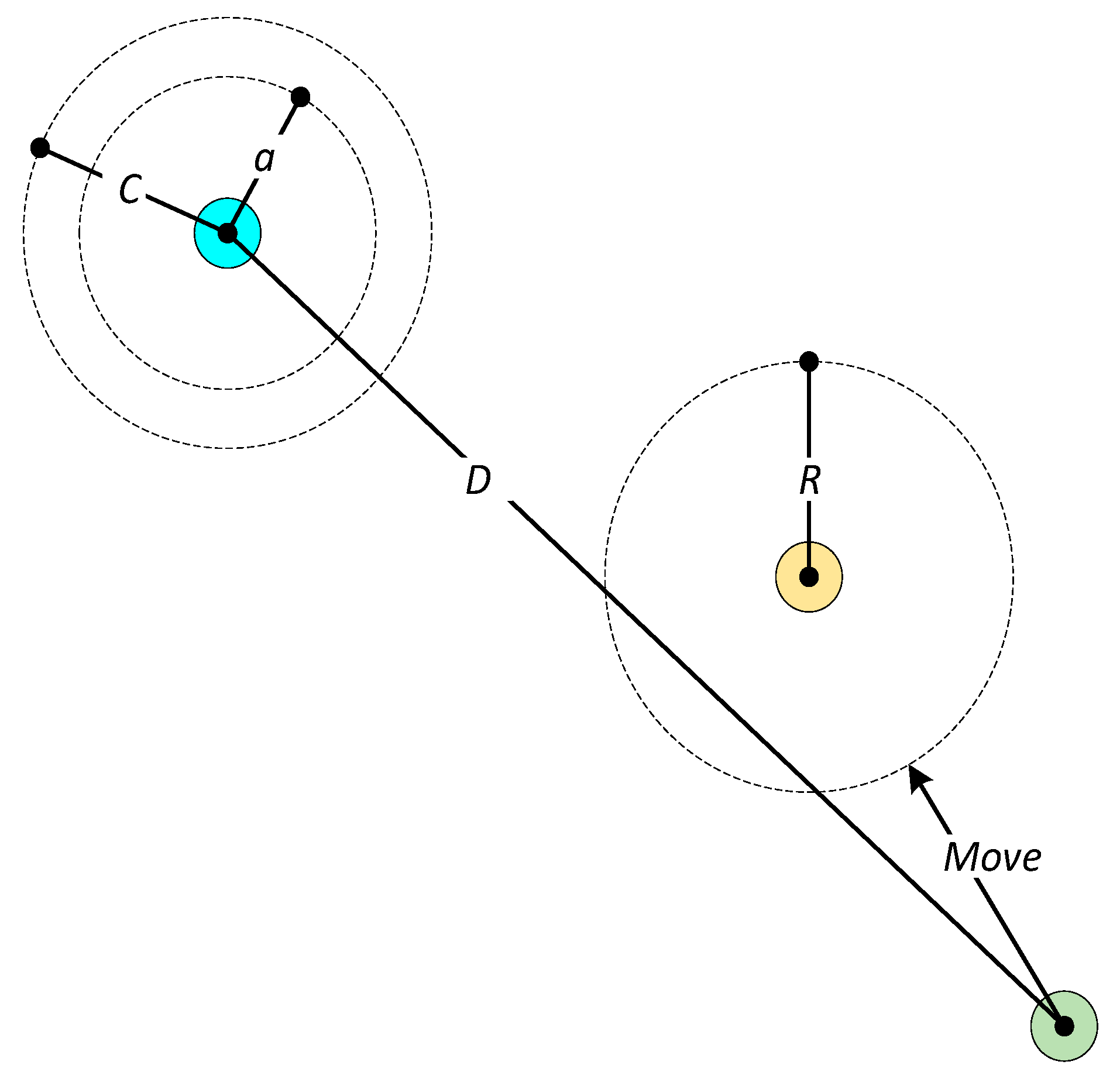
3.2. EHR-GA Combined with GWO
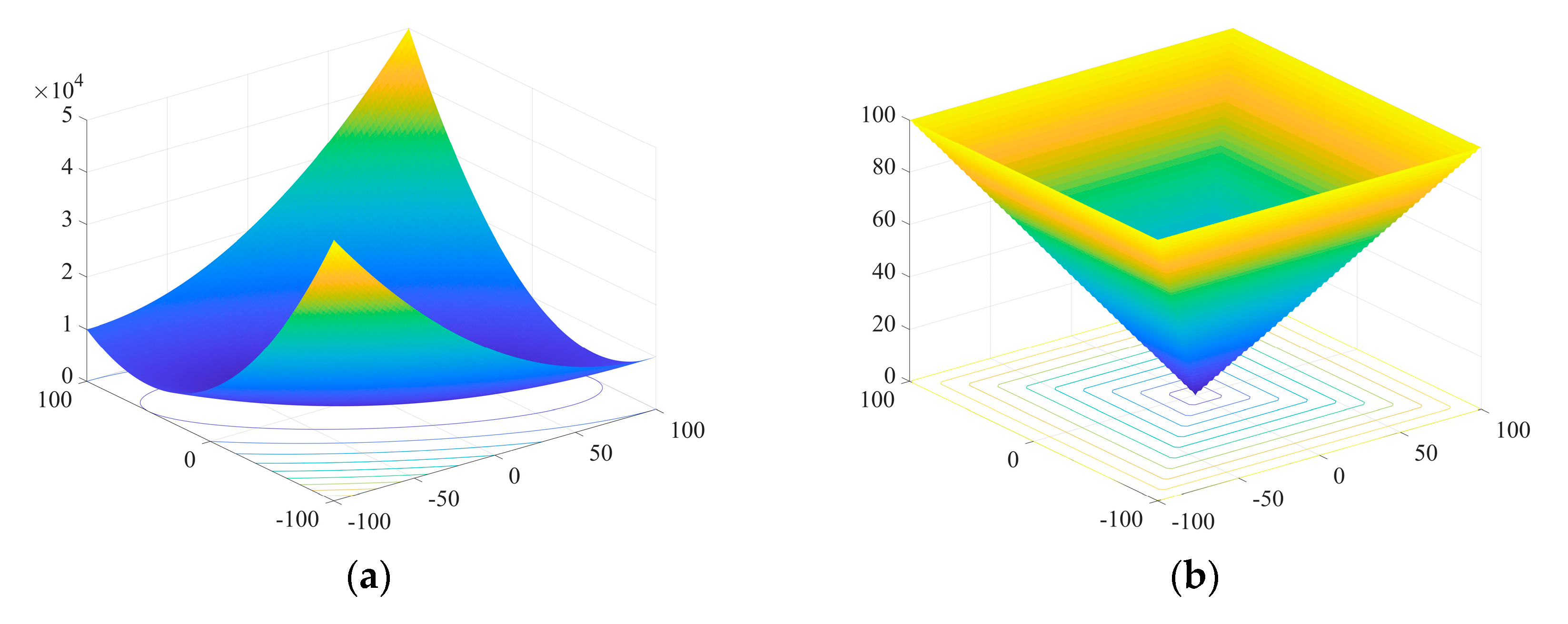
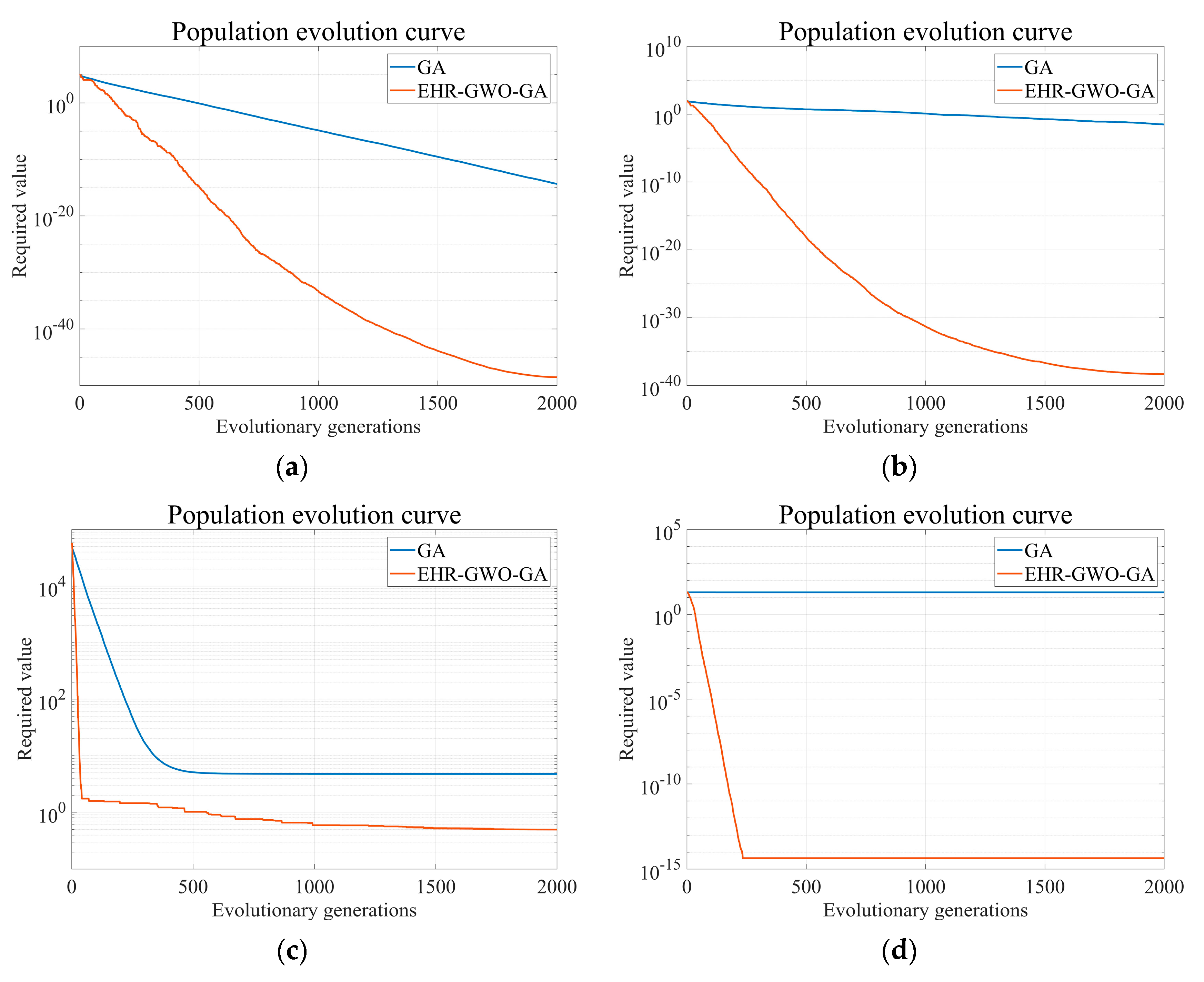
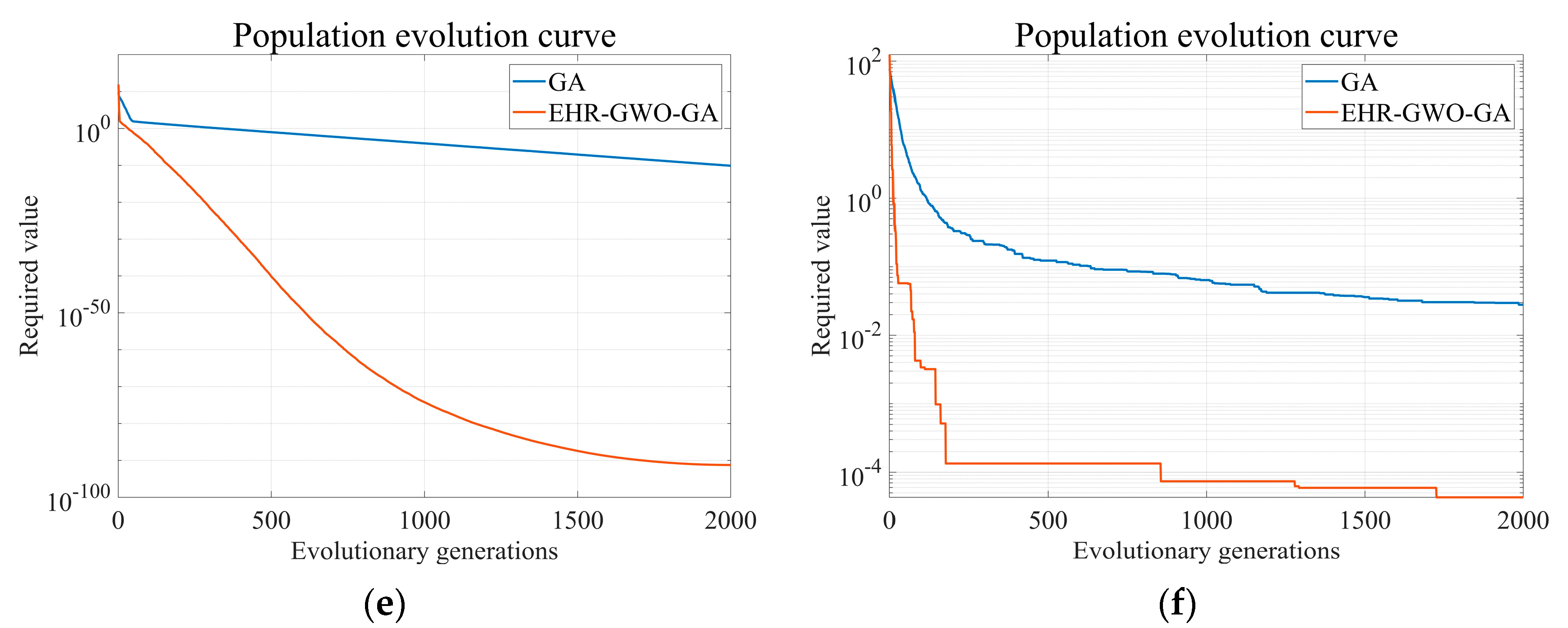
3.3. Performance Testing
4. Process Optimization
- (1)
- The isentropic efficiency was kept constant at 75%;
- (2)
- The valve inlet/outlet stream must be liquid;
- (3)
- Compressor inlet/outlet streams should be vapor;
- (4)
- The minimum temperature difference must not exceed 2 °C [40].
5. Results and Discussions
5.1. System Description
5.2. Optimal Results
5.2.1. Key Node Parameters
5.2.2. Heat Transfer
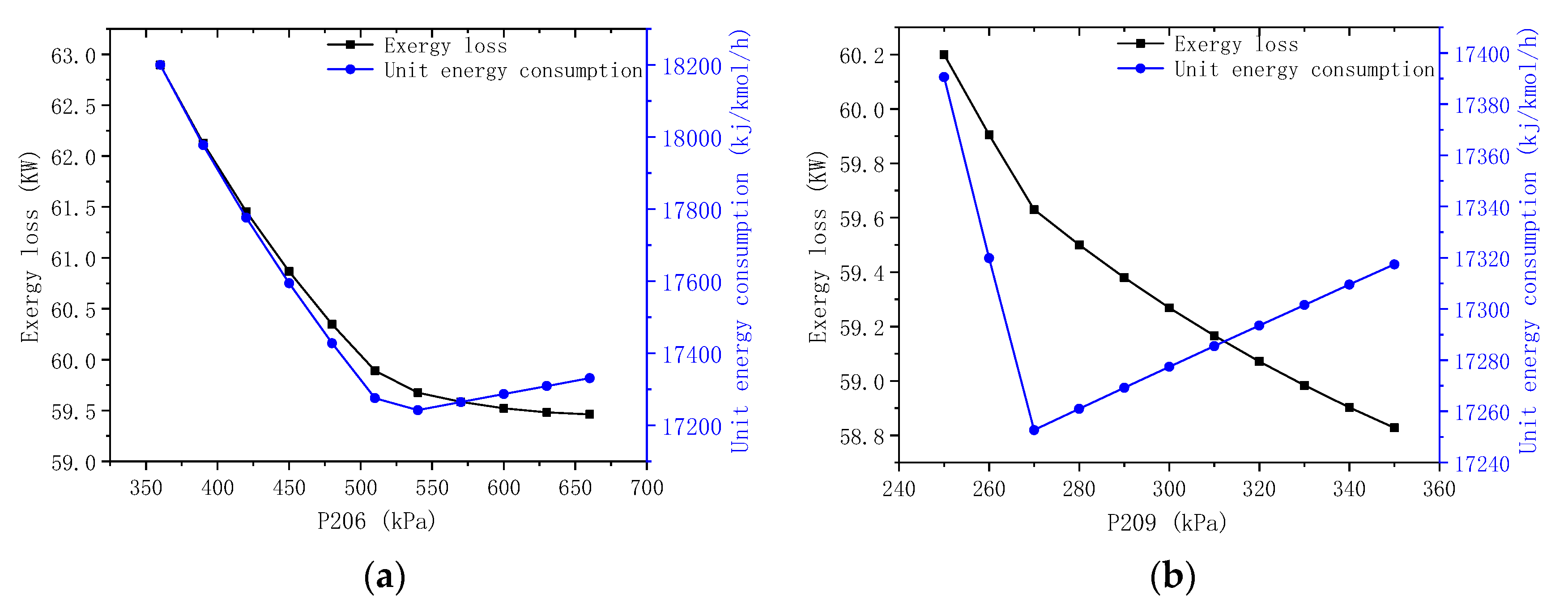
5.3. Sensitivity Analysis
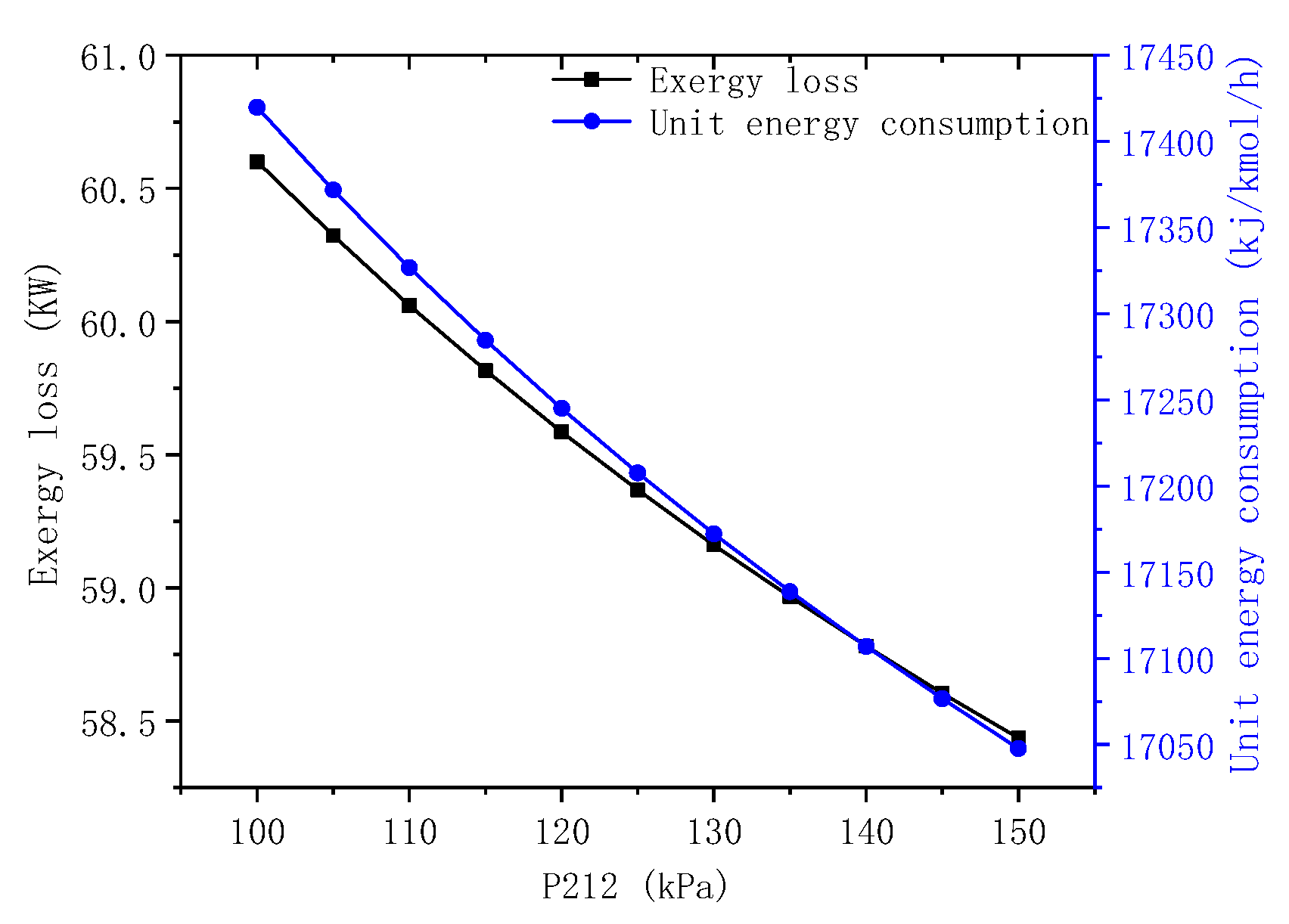
5.3.1. Effect of the Pressure Level
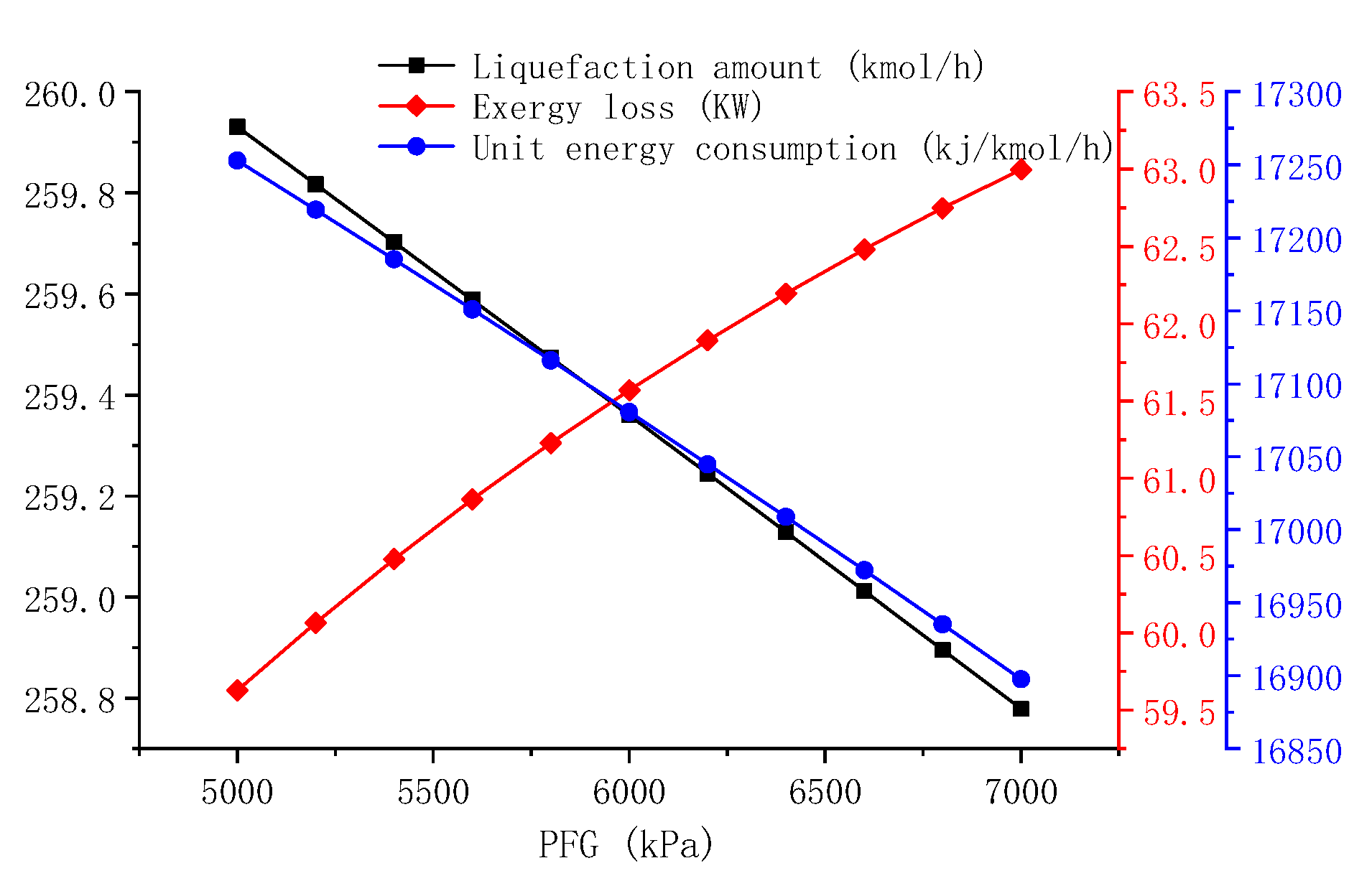
5.3.2. Effect of Feed Gas Parameters
5.3.3. Effect of the Mass Flow Rate of the C3MR Cycle
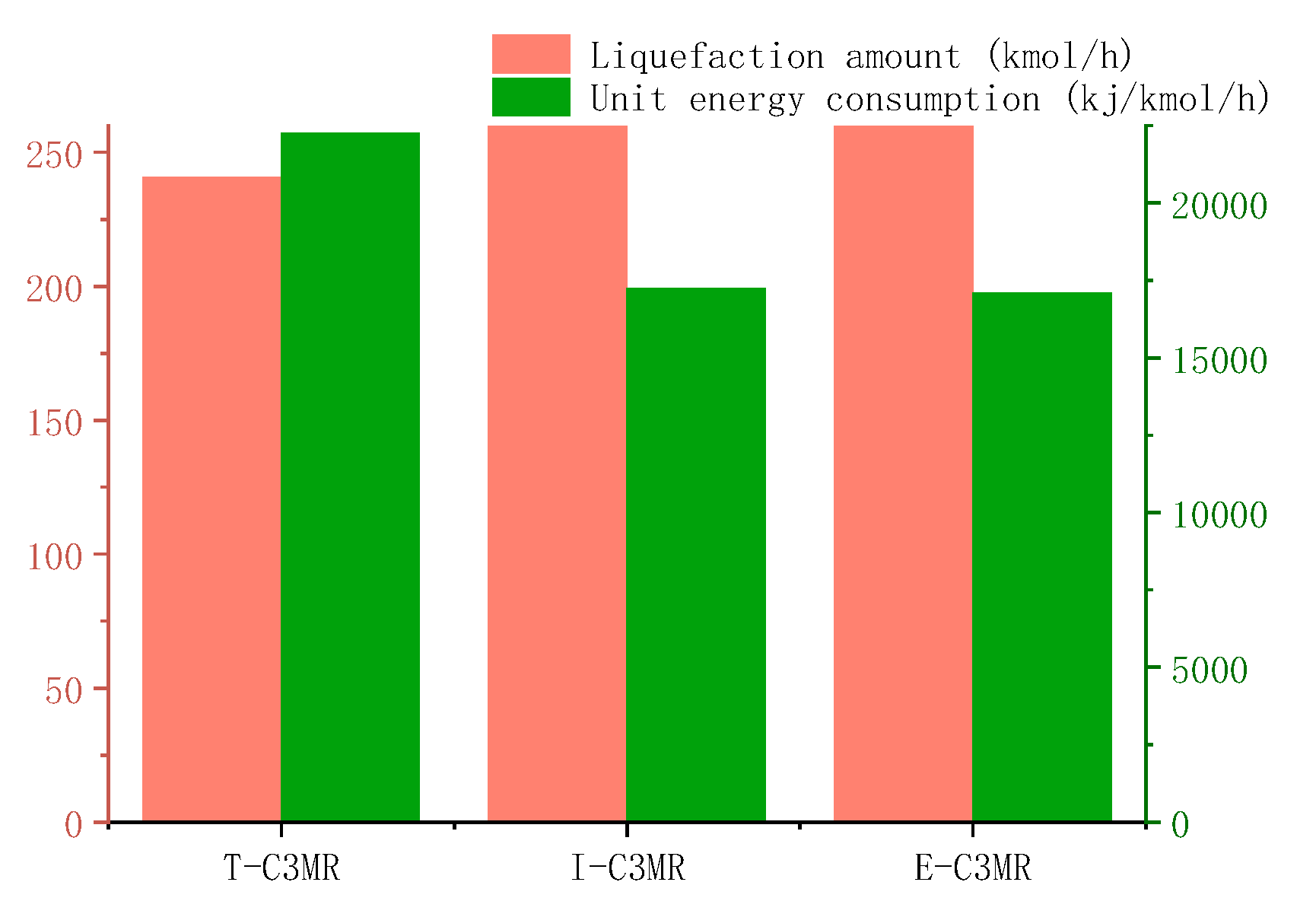
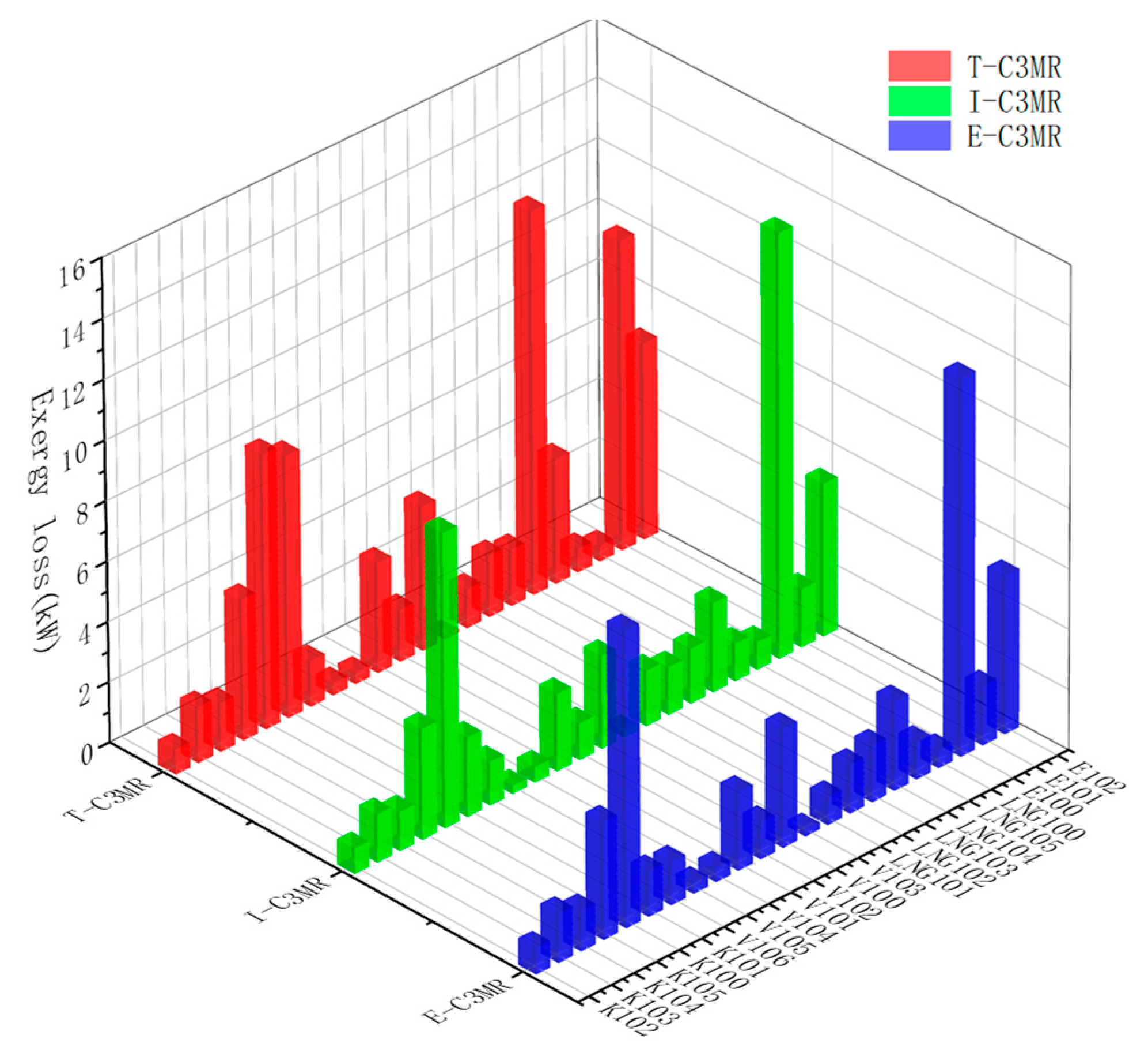
5.4. Comparative Analysis
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Son, H.; Austbø, B.; Gundersen, T.; Hwang, J.; Lim, Y. Techno-economic versus energy optimization of natural gas liquefaction processes with different heat exchanger technologies. Energy 2022, 245, 123232. [Google Scholar] [CrossRef]
- Qyyum, M.A.; Yasin, M.; Nawaz, A.; He, T.; Ali, W.; Haider, J.; Qadeer, K.; Nizami, A.-S.; Moustakas, K.; Lee, M. Single-solution-based vortex search strategy for optimal design of offshore and onshore natural gas liquefaction processes. Energies 2020, 13, 1732. [Google Scholar] [CrossRef]
- Furda, P.; Variny, M.; Labovska, Z. Towards time-effective optimization: Enviro-economic study of the C3MR LNG process. Energy Convers. Manag. 2022, 260, 115602. [Google Scholar] [CrossRef]
- Wang, Z.; Han, F.; Ji, Y.; Li, W. Combined Analysis of Parameter Sensitivity and Exergy for Natural Gas Liquefaction in Cryogenic Fuel Production Process. Processes 2020, 8, 561. [Google Scholar] [CrossRef]
- Lee, I.; Moon, I. Total cost optimization of a single mixed refrigerant process based on equipment cost and life expectancy. Ind. Eng. Chem. Res. 2016, 55, 10336–10343. [Google Scholar] [CrossRef]
- Lee, I.; Moon, I. Economic optimization of dual mixed refrigerant liquefied natural gas plant considering natural gas extraction rate. Ind. Eng. Chem. Res. 2017, 56, 2804–2814. [Google Scholar] [CrossRef]
- Lee, I.; Moon, I. Strategies for process and size selection of natural gas liquefaction processes: Specific profit portfolio approach by economic based optimization. Ind. Eng. Chem. Res. 2017, 57, 5845–5857. [Google Scholar] [CrossRef]
- Jin, C.; Son, H.; Lim, Y. Optimization and economic analysis of liquefaction processes for offshore units. Appl. Therm. Eng. 2019, 163, 114334. [Google Scholar] [CrossRef]
- He, T.; Lin, W. Energy saving and production increase of mixed refrigerant natural gas liquefaction plants by taking advantage of natural cold sources in winter. J. Clean. Prod. 2021, 299, 126884. [Google Scholar] [CrossRef]
- Park, J.; Mun, H.; Kim, J.; Lee, I. Advanced natural gas liquefaction process on LNG supply chain with liquid air: From design to thermodynamic and techno-economic analyses. Energy Convers. Manag. 2022, 252, 115107. [Google Scholar] [CrossRef]
- Hajji, A.; Chahartaghi, M.; Kahani, M. Thermodynamic analysis of natural gas liquefaction process with propane pre-cooled mixed refrigerant process (C3MR). Cryogenics 2019, 103, 102978. [Google Scholar] [CrossRef]
- Ghorbani, B.; Shirmohammadi, R.; Mehrpooya, M.; Hamedi, M.H. Structural, operational and economic optimization of cryogenic natural gas plant using NSGAII two-objective genetic algorithm. Energy 2018, 159, 410–428. [Google Scholar] [CrossRef]
- Rao, H.N.; Nair, S.K.; Karimi, I.A. Operational optimization of processes with multistream heat exchangers using data-driven predictive modeling. Ind. Eng. Chem. Res. 2019, 58, 5838–5850. [Google Scholar] [CrossRef]
- Wang, X.; Li, M.; Cai, L.; Li, Y. Propane and iso-butane pre-cooled mixed refrigerant liquefaction process for small-scale skid-mounted natural gas liquefaction. Appl. Energy 2020, 275, 115333. [Google Scholar] [CrossRef]
- Primabudi, E.; Morosuk, T.; Tsatsaronis, G. Multi-objective optimization of propane pre-cooled mixed refrigerant (C3MR) LNG process. Energy 2019, 185, 492–504. [Google Scholar] [CrossRef]
- Sabbagh, O.; Fanaei, M.A.; Arjomand, A. Optimal design of a novel NGL/LNG integrated scheme: Economic and exergetic evaluation. J. Therm. Anal. Calorim. 2021, 145, 851–866. [Google Scholar] [CrossRef]
- Ali, W.; Khan, M.S.; Qyyum, M.A.; Lee, M. Surrogate-assisted modeling and optimization of a natural-gas liquefaction plant. Comput. Chem. Eng. 2018, 118, 132–142. [Google Scholar] [CrossRef]
- Sabbagh, O.; Fanaei, M.A.; Arjomand, A.; Ahmadi, M.H. Multi-objective optimization assessment of a new integrated scheme for co-production of natural gas liquids and liquefied natural gas. Sustain. Energy Technol. Assess. 2021, 47, 101493. [Google Scholar] [CrossRef]
- Geng, J.; Sun, H. A novel integrated hydrogen and natural gas liquefaction process utilizing a modified double mixed refrigerant process pre-cooling system. Appl. Therm. Eng. 2023, 224, 120085. [Google Scholar] [CrossRef]
- Jin, C.; Yuan, Y.; Son, H.; Lim, Y. Novel propane-free mixed refrigerant integrated with nitrogen expansion natural gas liquefaction process for offshore units. Energy 2022, 238, 121765. [Google Scholar] [CrossRef]
- Li, S.; Zhao, Z.; Chen, Z.; Zeng, W.; Gong, H. Optimization and analysis of thermodynamic performance of boil-off gas reliquefication system with multiple refrigerant combinations. Sustain. Energy Technol. Assess. 2021, 47, 101408. [Google Scholar] [CrossRef]
- Awad, P.; Kimura, N.; Inoue, G.; Tsuge, Y. Energetic Minimization of Liquefied Natural Gas Single Nitrogen Expander Process Using Real Coded Genetic Algorithm. J. Chem. Eng. Jpn. 2019, 52, 130–137. [Google Scholar] [CrossRef]
- He, T.; Lin, W. Energy saving research of natural gas liquefaction plant based on waste heat utilization of gas turbine exhaust. Energy Convers. Manag. 2020, 225, 113468. [Google Scholar] [CrossRef]
- Park, J.; You, F.; Mun, H.; Lee, I. Liquefied natural gas supply chain using liquid air as a cold carrier: Novel method for energy recovery. Energy Convers. Manag. 2020, 227, 113611. [Google Scholar] [CrossRef]
- Nadimi-Shahraki, M.H.; Taghian, S.; Mirjalili, S. An improved grey wolf optimizer for solving engineering problems. Expert Syst. Appl. 2020, 166, 113917. [Google Scholar] [CrossRef]
- Sankaranarayanan, S.; Swaminathan, G.; Sivakumaran, N.; Radhakrishnan, T.K. A novel hybridized grey wolf optimzation for a cost optimal design of water distribution network. In Proceedings of the 2017 Computing Conference, London, UK, 18–20 July 2017. [Google Scholar] [CrossRef]
- Asaithambi, S.; Rajappa, M.; Ravi, L. Optimization and control of CMOS analog integrated circuits for cyber-physical systems using hybrid grey wolf optimization algorithm. J. Intell. Fuzzy Syst. 2019, 36, 4235–4245. [Google Scholar] [CrossRef]
- Mjahed, S.; Bouzaachane, K.; Taher Azar, A.; El Hadaj, S.; Raghay, S. Hybridization of fuzzy and hard semi-supervised clustering algorithms tuned with ant lion optimizer applied to higgs boson search. Comput. Model. Eng. Sci. 2020, 125, 459–494. [Google Scholar] [CrossRef]
- Khan, A.R.; Khan, S.; Harouni, M.; Abbasi, R.; Iqbal, S.; Mehmood, Z. Brain tumor segmentation using k-means clustering and deep learning with synthetic data augmentation for classification. Microsc. Res. Tech. 2021, 84, 1389–1399. [Google Scholar] [CrossRef]
- Khan, Z.; Koubaa, A.; Fang, S.; Lee, M.Y.; Muhammad, K. A connectivity-based clustering scheme for intelligent vehicles. Appl. Sci. 2021, 11, 2413. [Google Scholar] [CrossRef]
- Chrz, V. Cryogenic Mixed Refrigerant Processes. Int. J. Refrig. 2010, 33, 648–649. [Google Scholar] [CrossRef]
- Peng, D.Y.; Robinson, D.B. A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Mansour, E.; Desouky, S.; Batanoni, M.; Mahmoud, M.; Farag, A.; El-Dars, F. Modification proposed for SRK equation of state. Oil Gas J. 2012, 110, 78–91. [Google Scholar]
- Guo, H.; Tang, Q.; Gong, M.; Cheng, K. Optimization of a novel liquefaction process based on Joule–Thomson cycle utilizing high-pressure natural gas exergy by genetic algorithm. Energy 2018, 151, 696–706. [Google Scholar] [CrossRef]
- Zakaria, N.F.; Zulkifley, M.A.; Mustafa, M.M. Genetic algorithm. In Encyclopedic Reference of Genomics and Proteomics in Molecular Medicine; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Farhy, L.S. Modeling of oscillations in endocrine networks with feedback. In Methods in Enzymology; Academic Press: Cambridge, MA, USA, 2004; Volume 384, pp. 54–81. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey wolf optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Abualigah, L.; Diabat, A.; Mirjalili, S.; Elaziz, M.A.; Gandomi, A.H. The arithmetic optimization algorithm. Comput. Methods Appl. Mech. Eng. 2021, 376, 113609. [Google Scholar] [CrossRef]
- Popov, D.; Fikiin, K.; Stankov, B.; Alvarez, G.; Youbi-Idrissi, M.; Damas, A.; Evans, J.; Brown, T. Cryogenic heat exchangers for process cooling and renewable energy storage: A review. Appl. Therm. Eng. 2019, 153, 275–290. [Google Scholar] [CrossRef]
- Aspen Technology, Inc. Aspen and Hysys Software. 2020. Available online: www.aspentech.com (accessed on 18 January 2024).
- Bartolome, P.S.; Gerven, T.V. A comparative study on Aspen Hysys interconnection methodologies. Comput. Chem. Eng. 2022, 162, 107785. [Google Scholar] [CrossRef]
- Wensheng, C. Natural Gas Liquefaction Process for Small-scale LNG Project. In Proceedings of the 2012 International Conference on Computer Distributed Control and Intelligent Environmental Monitoring, Zhangjiajie, China, 5–6 March 2012. [Google Scholar] [CrossRef]
- Yuan, Z.; Cui, M.; Xie, Y.; Li, C. Design and analysis of a small-scale natural gas liquefaction process adopting single nitrogen expansion with carbon dioxide pre-cooling. Appl. Therm. Eng. 2014, 64, 139–146. [Google Scholar] [CrossRef]







| Parameter | Value | |
|---|---|---|
| Feed natural gas pressure | 6500 kPa | |
| Feed natural gas temperature | 25 °C | |
| Feed natural gas mass flow rate | 5000 kg/h | |
| Feed natural gas mole fraction composition | CH4 | 0.8748 |
| C2H6 | 0.0550 | |
| C3H8 | 0.0212 | |
| i-C4H10 | 0.0089 | |
| N2 | 0.0401 | |
| C3 mass flow rate | 17,000 kg/h | |
| MR mass flow rate | 10,000 kg/h | |
| MR mole fraction composition | CH4 | 0.42 |
| C2H6 | 0.3 | |
| C3H8 | 0.21 | |
| N2 | 0.07 | |
| LNG storage pressure | 110 kPa | |
| Pressure drops of heat exchangers and water coolers | 20 kPa | |
| Ambient temperature | 25 °C | |
| Insulation efficiency of the compressor | 75% | |
| The lowest approaching temperature of the heat exchanger | 2 °C | |
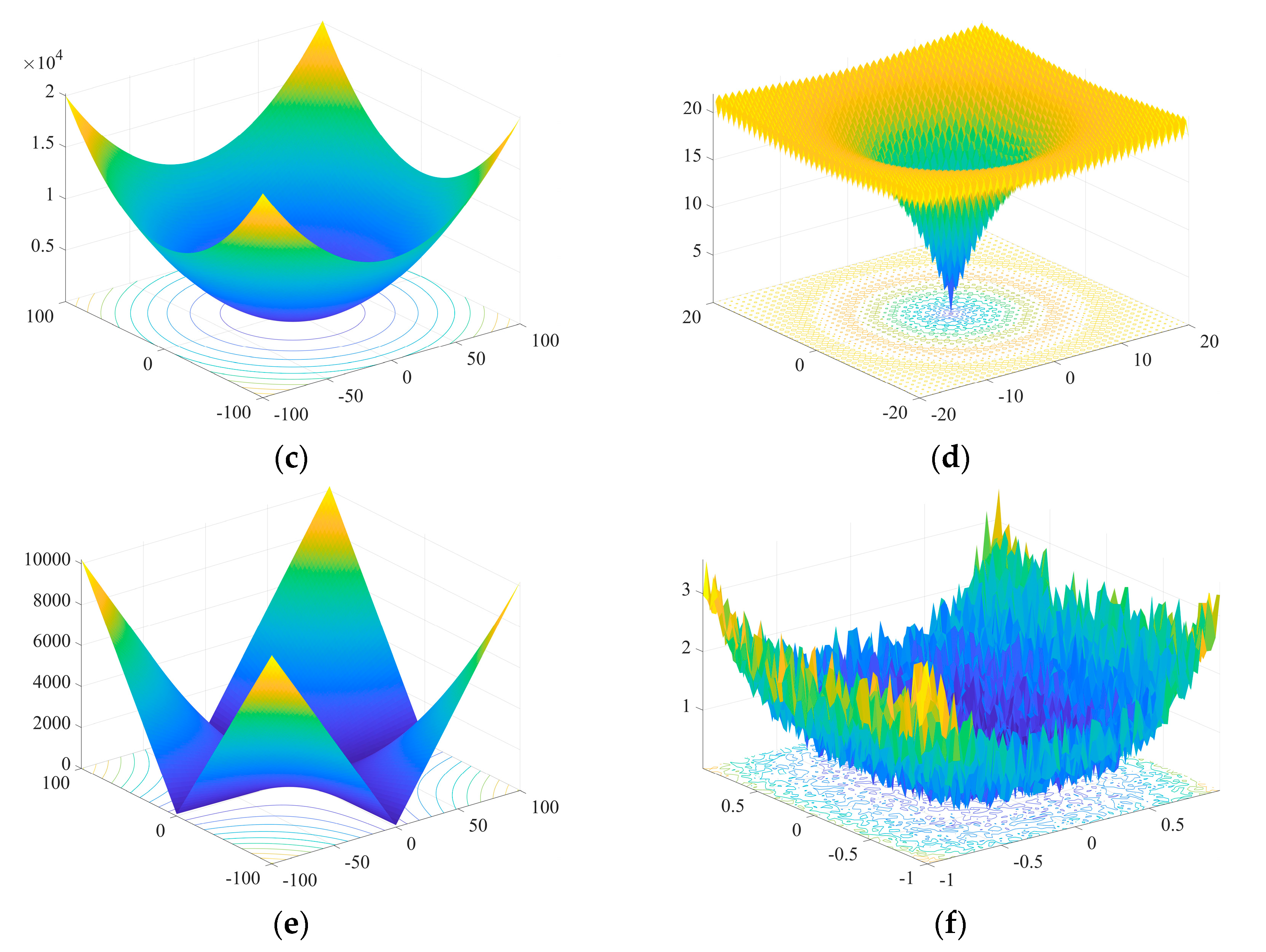
| Test Function | n | Hunting Zone | Optimal |
|---|---|---|---|
| 30 | [–100, 100] | 0 | |
| 30 | [–100, 100] | 0 | |
| 30 | [–100, 100] | 0 | |
| 30 | [–20, 20] | 0 | |
| 30 | [–100, 100] | 0 | |
| 30 | [–1.28, 1.28] | 0 |
| Variable | Lower Bound | Upper Bound | Initialization Value |
|---|---|---|---|
| Main-Pressure Level (kPa) | 590 | 1000 | 800 |
| High-pressure level (kPa) | 370 | 650 | 520 |
| Medium-pressure level (kPa) | 250 | 350 | 270 |
| Low-pressure level (kPa) | 100 | 150 | 130 |
| C3 Mass flow rate (kg/h) | 15,000 | 20,000 | 17,000 |
| MR Mass flow rate (kg/h) | 7000 | 13,000 | 10,000 |
| Input pressure (kPa) | 5000 | 7000 | 6500 |
| Input temperature (°C) | 10 | 35 | 25 |
| Key Parameter | E-C3MR |
|---|---|
| Input pressure (kPa) | 6440 |
| Input temperature (°C) | 19 |
| Main-Pressure Level (kPa) | 790 |
| High-pressure level (kPa) | 533 |
| Medium-pressure level (kPa) | 270 |
| Low-pressure level (kPa) | 120 |
| C3 Mass flow rate (kg/h) | 16,300 |
| MR Mass flow rate (kg/h) | 7020 |
| W100 (kW) | 710.74 |
| W101 (kW) | 151.02 |
| W102 (kW) | 35.90 |
| W103 (kW) | 71.94 |
| W104 (kW) | 62.13 |
| W105 (kW) | 198.03 |
| Liquefaction amount (kmol/h) | 259.91 |
| Unit energy consumption (kJ/kmol) | 17,086.29 |
| Exergy loss (kW) | 58.55 |
| Types of Equipment | Value of the Exergy Loss (kW) | Percentage (%) |
|---|---|---|
| Compactors | 19.133 | 32.7 |
| Water coolers | 19.778 | 33.8 |
| Heat exchangers | 9.304 | 15.8 |
| Valve | 10.338 | 17.7 |
| Process Parameters | T-C3MR | N2/CH4 | Pressure Exergy | MEW/MRC | N2/CO2 | E-C3MR | |
|---|---|---|---|---|---|---|---|
| Liquefaction rate(%) | 87 | 90 | 36 | 90 | 77 | 94 | |
| Unit energy consumption(kJ/kmol) | 22,248 | 63,648 | 972 | 29,340 | 35,640 | 17,086 | |
| Number of key equipment | Compressor | 6 | 2 | 5 | 2 | 4 | 6 |
| Expander | 0 | 1 | 0 | 0 | 1 | 0 | |
| Heat exchanger | 6 | 3 | 5 | 3 | 3 | 6 | |
| Separator | 4 | 2 | 1 | 4 | 2 | 4 | |
| Valve | 7 | 2 | 5 | 4 | 2 | 7 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, F.; Pan, L.; Pang, Y.; Chen, J.; Shi, F.; Liang, Y. A New Multi-Objective Optimization Strategy for Improved C3MR Liquefaction Process. Processes 2024, 12, 542. https://doi.org/10.3390/pr12030542
Cui F, Pan L, Pang Y, Chen J, Shi F, Liang Y. A New Multi-Objective Optimization Strategy for Improved C3MR Liquefaction Process. Processes. 2024; 12(3):542. https://doi.org/10.3390/pr12030542
Chicago/Turabian StyleCui, Fenghe, Lei Pan, Yi Pang, Jianwei Chen, Fan Shi, and Yin Liang. 2024. "A New Multi-Objective Optimization Strategy for Improved C3MR Liquefaction Process" Processes 12, no. 3: 542. https://doi.org/10.3390/pr12030542
APA StyleCui, F., Pan, L., Pang, Y., Chen, J., Shi, F., & Liang, Y. (2024). A New Multi-Objective Optimization Strategy for Improved C3MR Liquefaction Process. Processes, 12(3), 542. https://doi.org/10.3390/pr12030542





