An Experimental Study on Nodular Iron Machined Surfaces Utilizing a Capable 2D Finite Element Model for Precise Surface Roughness Estimation
Abstract
1. Introduction
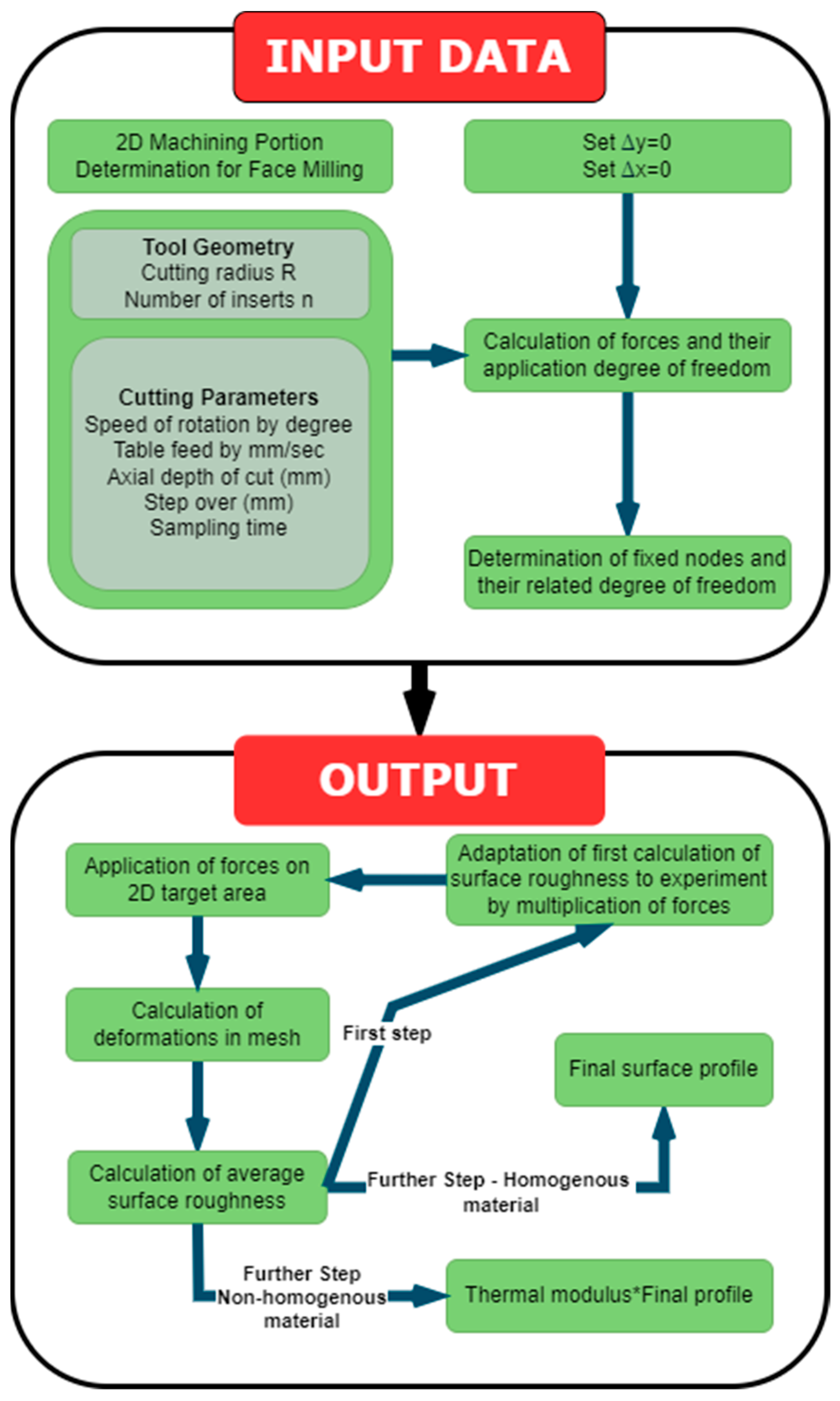
2. Materials and Methods
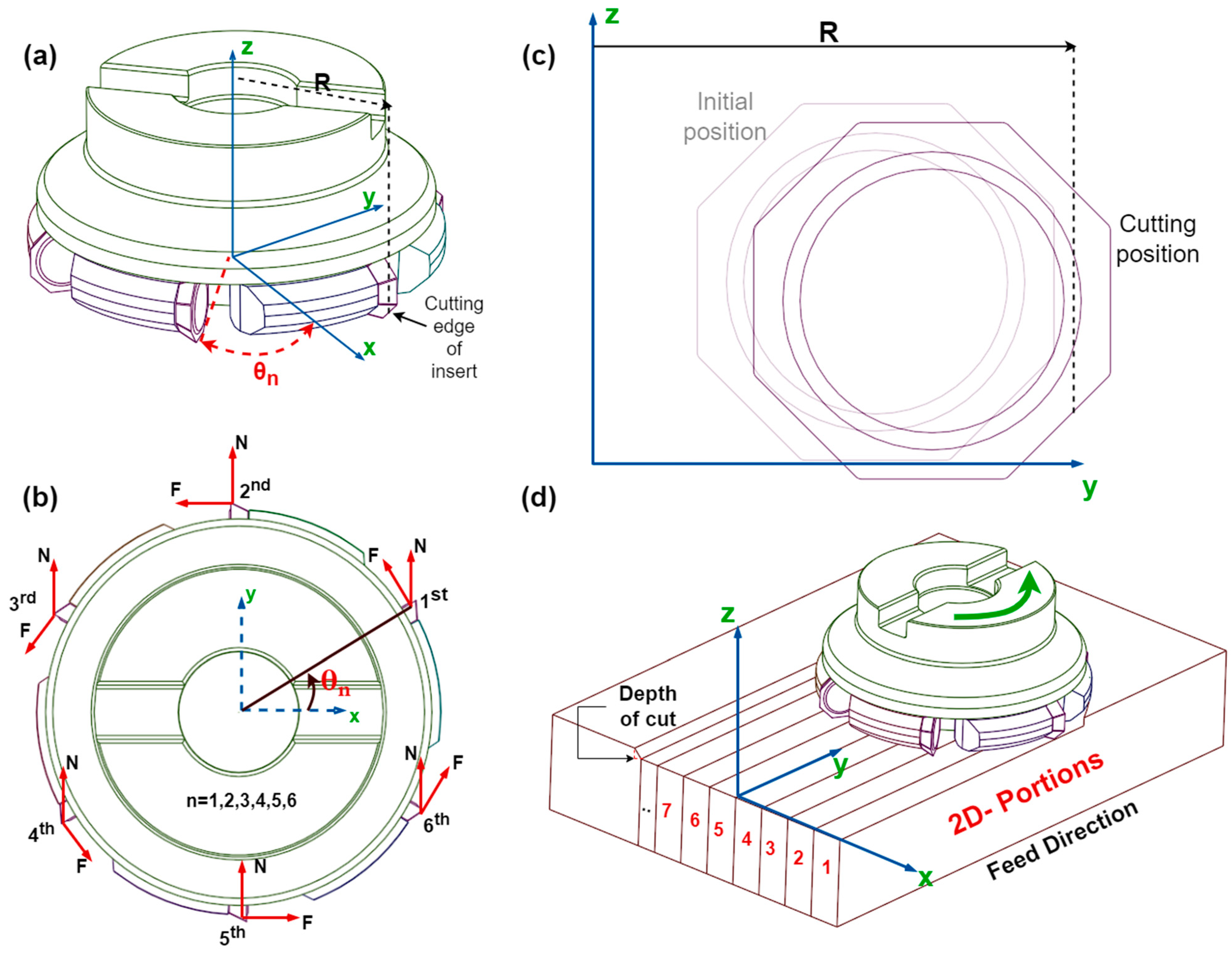
2.1. Explanation of the Force Matrix Algorithm
2.1.1. 1st–24th Rows of the Algorithm
2.1.2. 25th to 41st Rows of the Algorithm
2.1.3. 42nd to 53rd Rows of the Algorithm
2.1.4. 54th to 66th Rows of the Algorithm
2.1.5. 67th to 69th Rows of the Algorithm

2.2. Method Validation
2.2.1. First Application
2.2.2. Second Application
2.2.3. Third Application
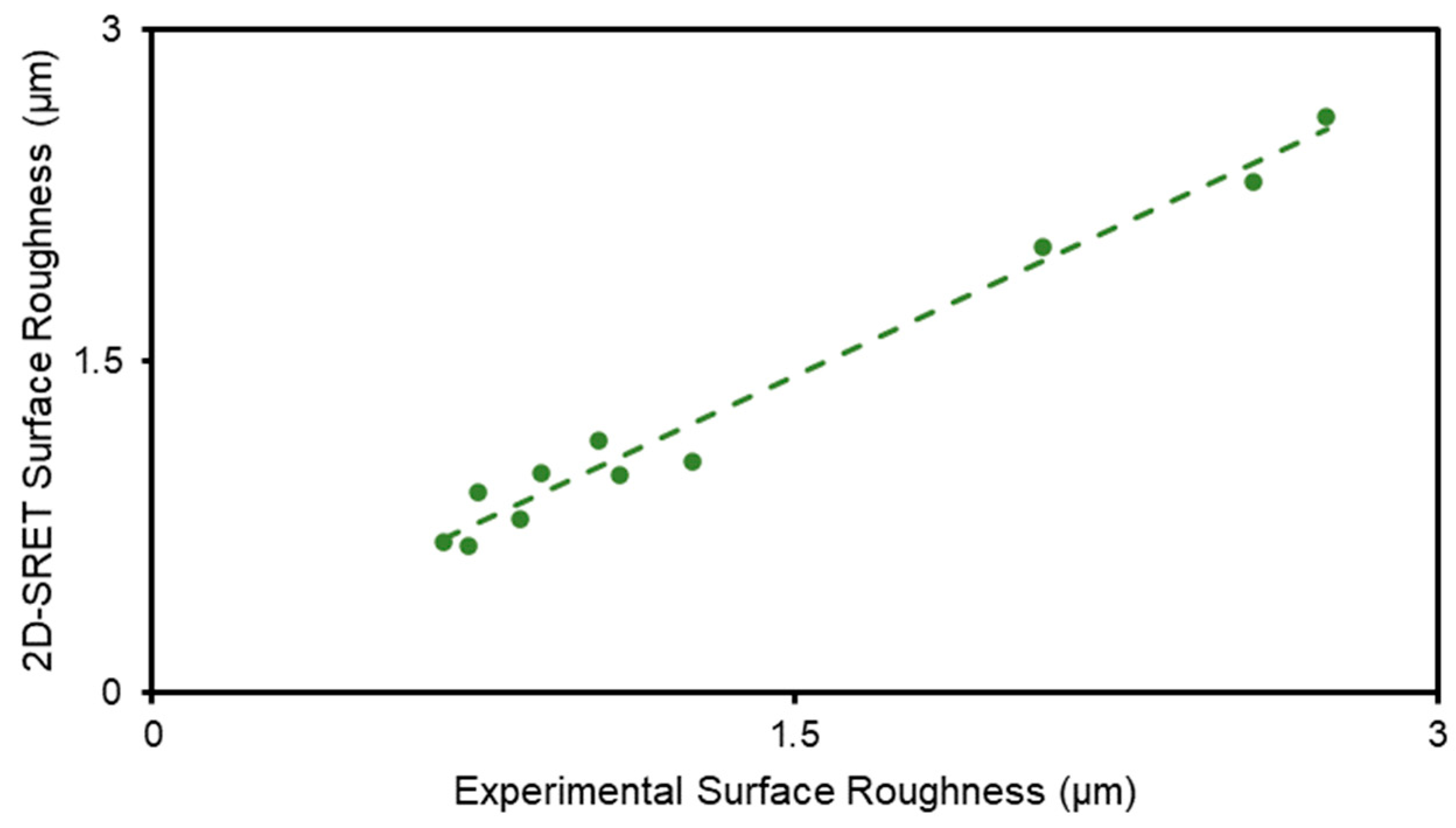
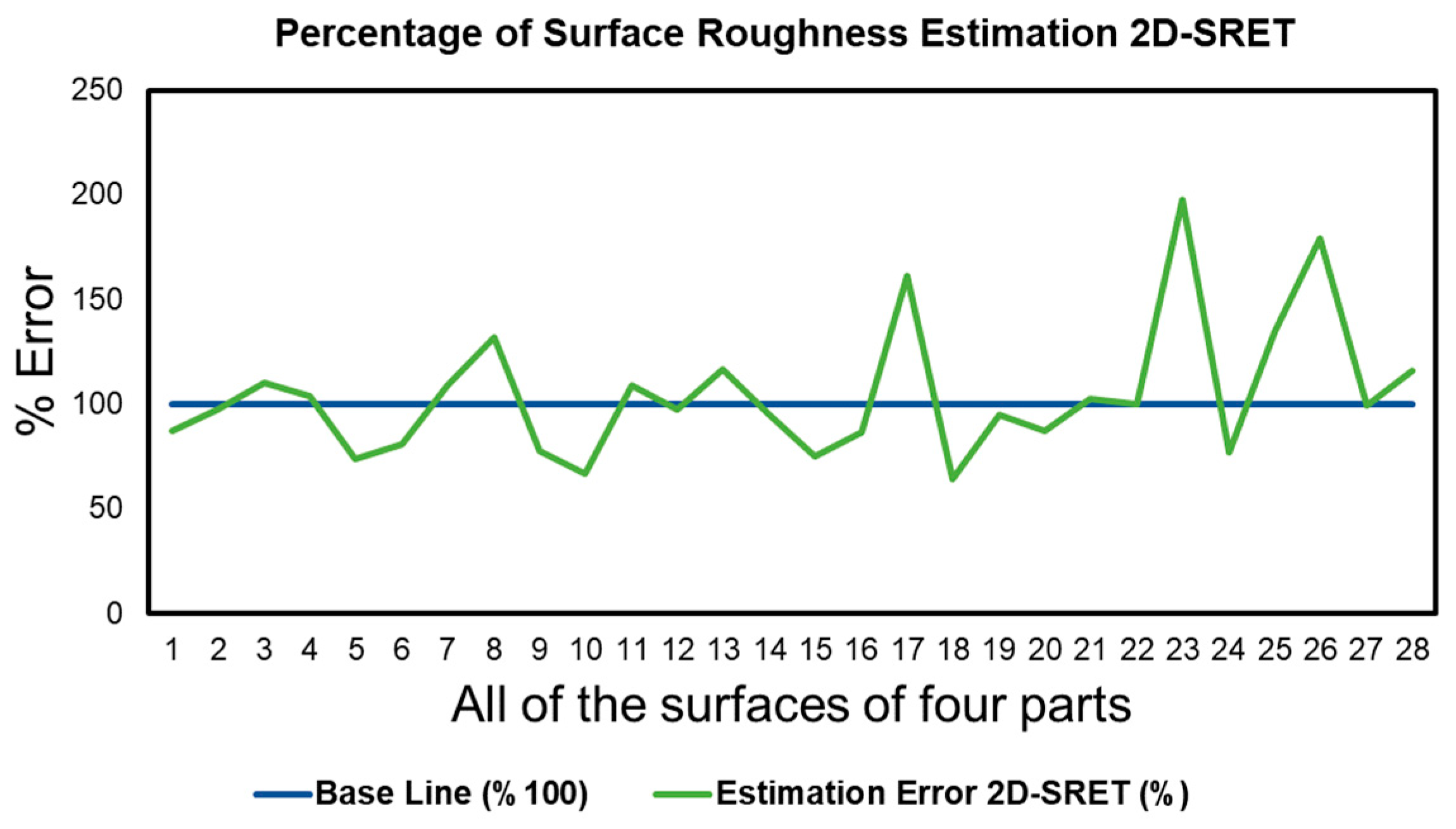
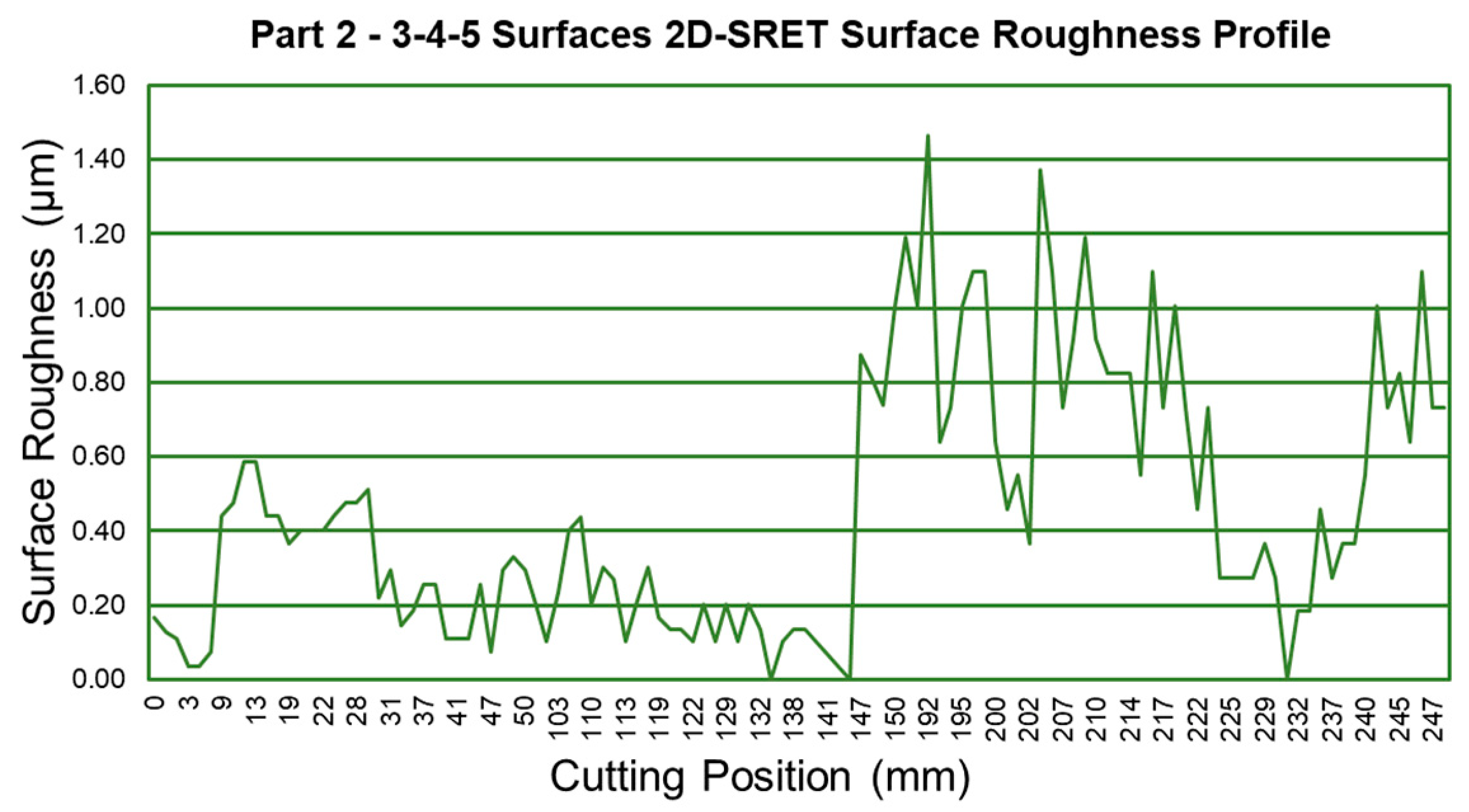
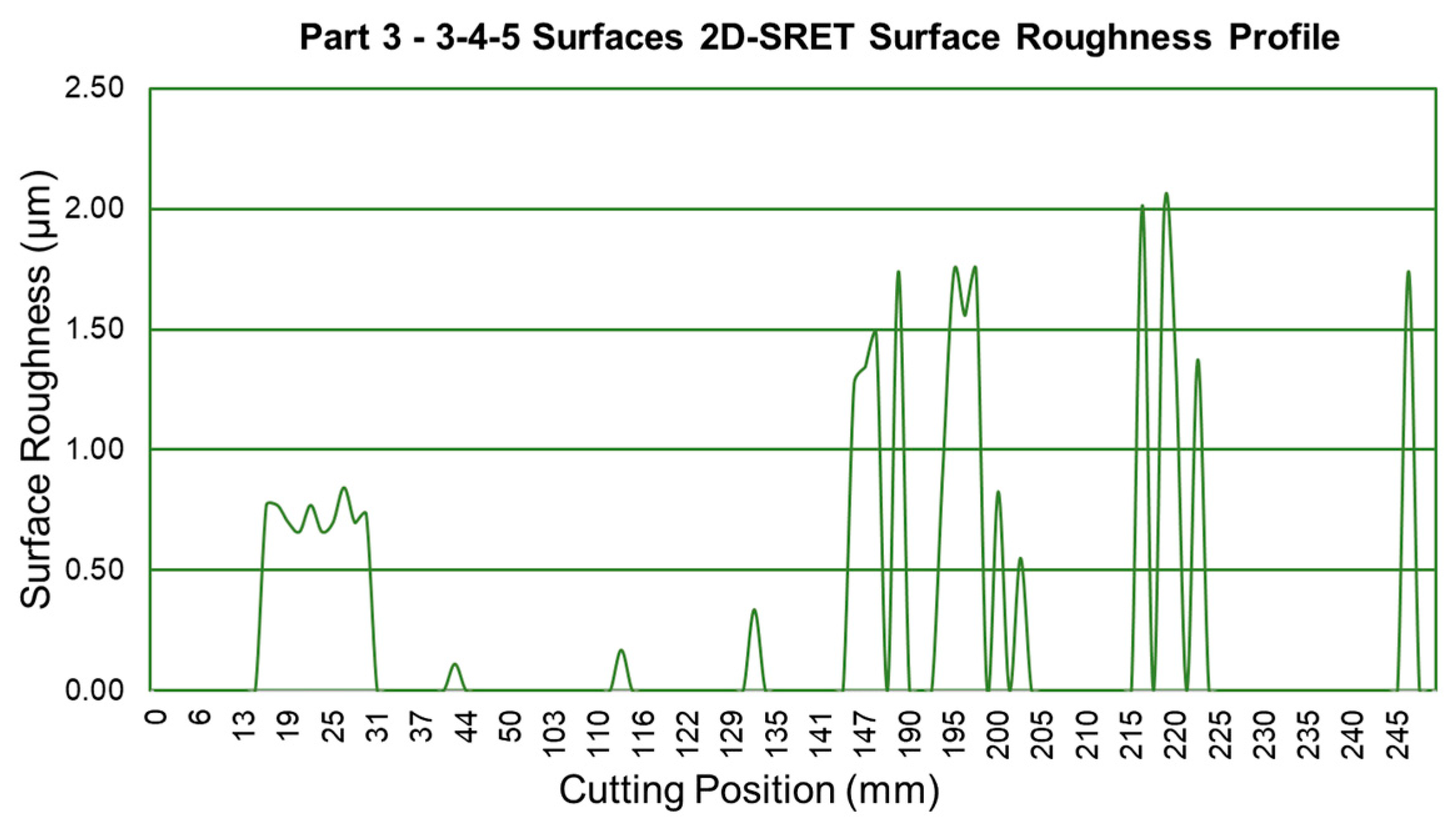
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Algorithm A1. Calculation of force matrix f(dof) | |
| 1 : 2 : 3 : 4 : 5 : 6 : 7 : 8 : 9 : 10 : 11 : 12 : 13 : 14 : 15 : 16 : 17 : 18 : 19 : 20 : 21 : 22 : 23 : 24 : 25 : 26 : 27 : 28 : 29 : 30 : 31 : 32 : 33 : 34 : 35 : 36 : 37 : 38 : 39 : 40 : 41 : 42 : 43 : 44 : 45 : 46 : 47 : 48 : 49 : 50 : 51 : 52 : 53 : 54 : 55 : 56 : 57 : 58 : 59 : 60 : 61 : 62 : 63 : 64 : 65 : 66 : 67 : 68 : 69 : 70 : | Do while (bat.eq.1) step = step + 1 sampling_time = 60 table_feed = 7.5 spindle_speed = 3900*degreetoradian step_y = table_feed / sampling_time step_rotation = spindle_speed/sampling_time if (step.eq. 1) teta(1) = 30*d2rd teta(2) = 90*d2rd teta(3) = 150*d2rd teta(4) = 210*d2rd teta(5) = 270*d2rd teta(6) = 330*d2rd delta_x = 0 delta_y = 0 endif delta_y = delta_y + step_y r = 50 depth_of_cut = 250 − 0.3 do i = 1,6 posx(i) = raga*cos(teta(i)) + 0+deltx posy(i) = raga*sin(teta(i)) − 50 + delty enddo count_1 = 0 count_2 = 0 do j = 1,6 count_2 = count_2 + 1 do jj = 1,nn if (y_p(j) .ge. 0 .and. x(jj,2) .ge. depth_of_cut) if (y_p(j).ge.300) then bat = 2 endif if (x(jj,1) .le. y_p(j) + 2 .and. x(jj,1) .ge. y_p(j) − 2) count_1 = count_1 + 1 mak (count_1) = jj sak(count_1) = count_2 endif endif enddo enddo count_3 = 0 do xz = 1,ne do iu = 1,4 in = 2*(connectivity(xz, iu) − 1) do jg = 1,count_1 if (connectivity(xz,iu).eq.mak(jg)) count_3 = count_3 + 1 dof(count_3) = in + 1 endif enddo enddo enddo zteta = −90*degreetoradian do mm = 1,nara beta = ztet + teta(sak(mm)) do cc = 1,count_1 if (dof(mm) .eq. dof(cc)) f(dof(mm)) = F*sin(beta) + N f(dof(cc)) = F*sin(beta) + N f(dof(mm)) = f(dof(mm))+ f(dof(cc)) else f(dof(mm)) = F*sin(beta) + N endif enddo enddo do gg = 1,6 teta(gg) = teta(gg) + stepsp enddo enddowhile |
References
- Simunovic, G.; Simunovic, K.; Saric, T. Modelling and Simulation of Surface Roughness in Face Milling. Int. J. Simul. Model. 2013, 12, 141–153. [Google Scholar] [CrossRef]
- Ozcelik, B.; Bayramoglu, M. The Statistical Modeling of Surface Roughness in High-Speed Flat End Milling. Int. J. Mach. Tools Manuf. 2006, 46, 1395–1402. [Google Scholar] [CrossRef]
- Hoang, D.T.; Nguyen, N.-T.; Tran, Q.D.; Nguyen, T. Van Cutting Forces and Surface Roughness in Face-Milling of SKD61 Hard Steel. Stroj. Vestn.-J. Mech. Eng. 2019, 65, 375–385. [Google Scholar] [CrossRef]
- Raza, M.H.; Hafeez, F.; Zhong, R.Y.; Imran, A. Investigation of Surface Roughness in Face Milling Processes. Int. J. Adv. Manuf. Technol. 2020, 111, 2589–2599. [Google Scholar] [CrossRef]
- Saini, A.; Chauhan, P.; Pabla, B.; Dhami, S. Multi-Process Parameter Optimization in Face Milling of Ti6Al4V Alloy Using Response Surface Methodology. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2018, 232, 1590–1602. [Google Scholar] [CrossRef]
- Bharathi Raja, S.; Baskar, N. Application of Particle Swarm Optimization Technique for Achieving Desired Milled Surface Roughness in Minimum Machining Time. Expert. Syst. Appl. 2012, 39, 5982–5989. [Google Scholar] [CrossRef]
- Yadav, D.K.; Dixit, N.K.; Agarwal, D.; Khare, S.K. Optimization of Surface Roughness by Design of Experiment Techniques during CNC Milling Machining. Mater. Today Proc. 2022, 52, 1919–1923. [Google Scholar] [CrossRef]
- Yalcin, U.; Karaoglan, A.D.; Korkut, I. Optimization of Cutting Parameters in Face Milling with Neural Networks and Taguchi Based on Cutting Force, Surface Roughness and Temperatures. Int. J. Prod. Res. 2013, 51, 3404–3414. [Google Scholar] [CrossRef]
- Alharthi, N.H.; Bingol, S.; Abbas, A.T.; Ragab, A.E.; El-Danaf, E.A.; Alharbi, H.F. Optimizing Cutting Conditions and Prediction of Surface Roughness in Face Milling of AZ61 Using Regression Analysis and Artificial Neural Network. Adv. Mater. Sci. Eng. 2017, 2017, 7560468. [Google Scholar] [CrossRef]
- Oktem, H.; Erzurumlu, T.; Erzincanli, F. Prediction of Minimum Surface Roughness in End Milling Mold Parts Using Neural Network and Genetic Algorithm. Mater. Des. 2006, 27, 735–744. [Google Scholar] [CrossRef]
- Erzurumlu, T.; Oktem, H. Comparison of Response Surface Model with Neural Network in Determining the Surface Quality of Moulded Parts. Mater. Des. 2007, 28, 459–465. [Google Scholar] [CrossRef]
- Zain, A.M.; Haron, H.; Sharif, S. Prediction of Surface Roughness in the End Milling Machining Using Artificial Neural Network. Expert. Syst. Appl. 2010, 37, 1755–1768. [Google Scholar] [CrossRef]
- Lela, B.; Bajić, D.; Jozić, S. Regression Analysis, Support Vector Machines, and Bayesian Neural Network Approaches to Modeling Surface Roughness in Face Milling. Int. J. Adv. Manuf. Technol. 2009, 42, 1082–1088. [Google Scholar] [CrossRef]
- Razfar, M.R.; Farshbaf Zinati, R.; Haghshenas, M. Optimum Surface Roughness Prediction in Face Milling by Using Neural Network and Harmony Search Algorithm. Int. J. Adv. Manuf. Technol. 2011, 52, 487–495. [Google Scholar] [CrossRef]
- Razfar, M.R.; Asadnia, M.; Haghshenas, M.; Farahnakian, M. Optimum Surface Roughness Prediction in Face Milling X20Cr13 Using Particle Swarm Optimization Algorithm. Proc. Inst. Mech. Eng. B J. Eng. Manuf. 2010, 224, 1645–1653. [Google Scholar] [CrossRef]
- Ghoreishi, R.; Roohi, A.H.; Dehghan Ghadikolaei, A. Analysis of the Influence of Cutting Parameters on Surface Roughness and Cutting Forces in High Speed Face Milling of Al/SiC MMC. Mater. Res. Express 2018, 5, 086521. [Google Scholar] [CrossRef]
- Arizmendi, M.; Jiménez, A. Modelling and Analysis of Surface Topography Generated in Face Milling Operations. Int. J. Mech. Sci. 2019, 163, 105061. [Google Scholar] [CrossRef]
- Parhad, P.; Likhite, A.; Bhatt, J.; Peshwe, D. The Effect of Cutting Speed and Depth of Cut on Surface Roughness During Machining of Austempered Ductile Iron. Trans. Indian Inst. Met. 2015, 68, 99–108. [Google Scholar] [CrossRef]
- Akdemir, A.; Yazman, Ş.; Saglam, H.; Uyaner, M. The Effects of Cutting Speed and Depth of Cut on Machinability Characteristics of Austempered Ductile Iron. J. Manuf. Sci. Eng. 2012, 134, 021013. [Google Scholar] [CrossRef]
- Rao, B.; Shin, Y.C. Analysis on High-Speed Face-Milling of 7075-T6 Aluminum Using Carbide and Diamond Cutters. Int. J. Mach. Tools Manuf. 2001, 41, 1763–1781. [Google Scholar] [CrossRef]
- Rao, B.; Dandekar, C.R.; Shin, Y.C. An Experimental and Numerical Study on the Face Milling of Ti–6Al–4V Alloy: Tool Performance and Surface Integrity. J. Mater. Process Technol. 2011, 211, 294–304. [Google Scholar] [CrossRef]
- Wang, X.; Huang, C.; Zou, B.; Liu, G.; Zhu, H.; Wang, J. Experimental Study of Surface Integrity and Fatigue Life in the Face Milling of Inconel 718. Front. Mech. Eng. 2018, 13, 243–250. [Google Scholar] [CrossRef]
- Geuzaine, C.; Remacle, J.-F. Gmsh: A 3-D Finite Element Mesh Generator with Built-in Pre- and Post-Processing Facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]
- Seco Tools. Available online: https://www.secotools.com/article/p_00005693?language=en (accessed on 4 February 2024).
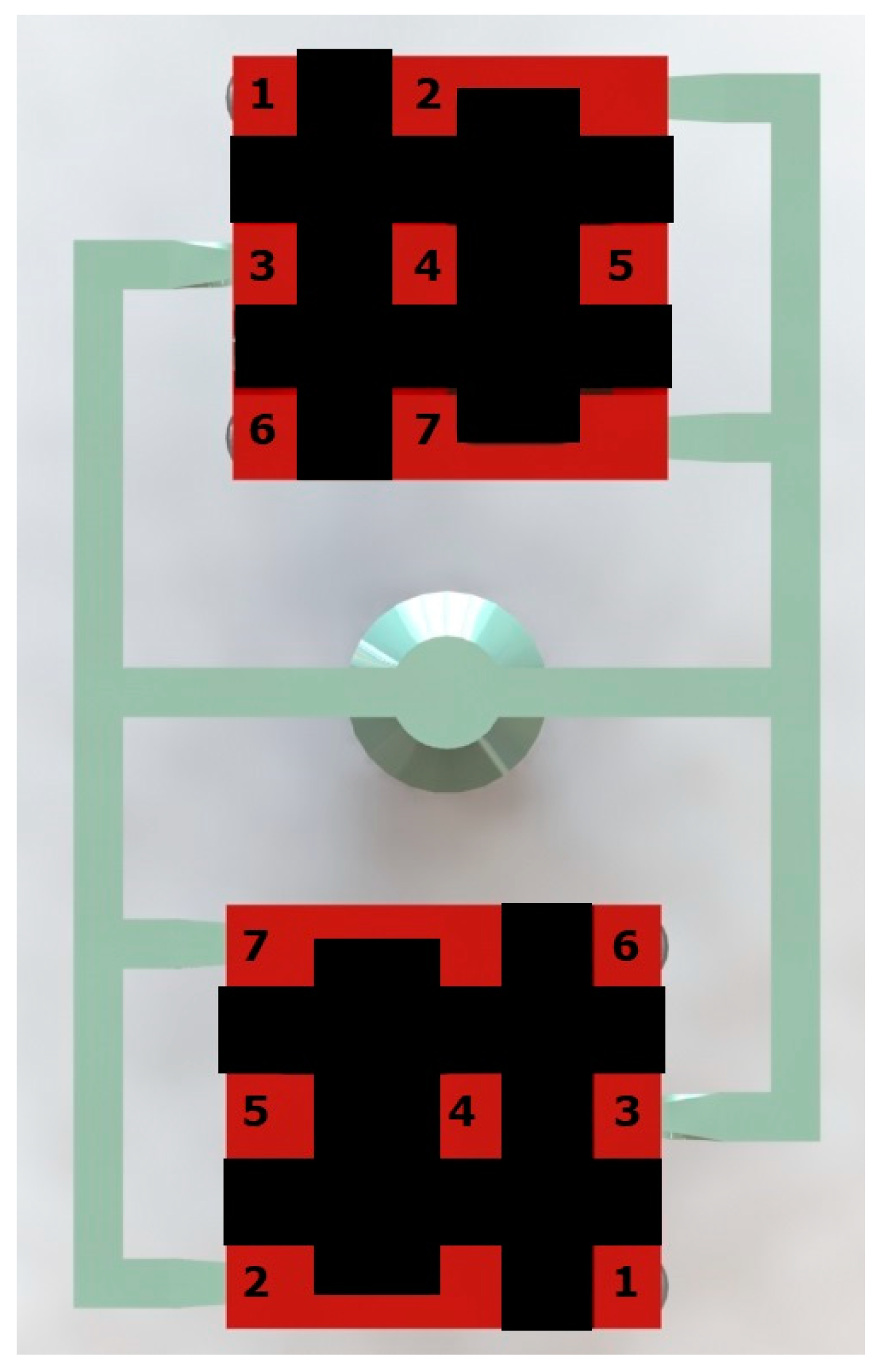




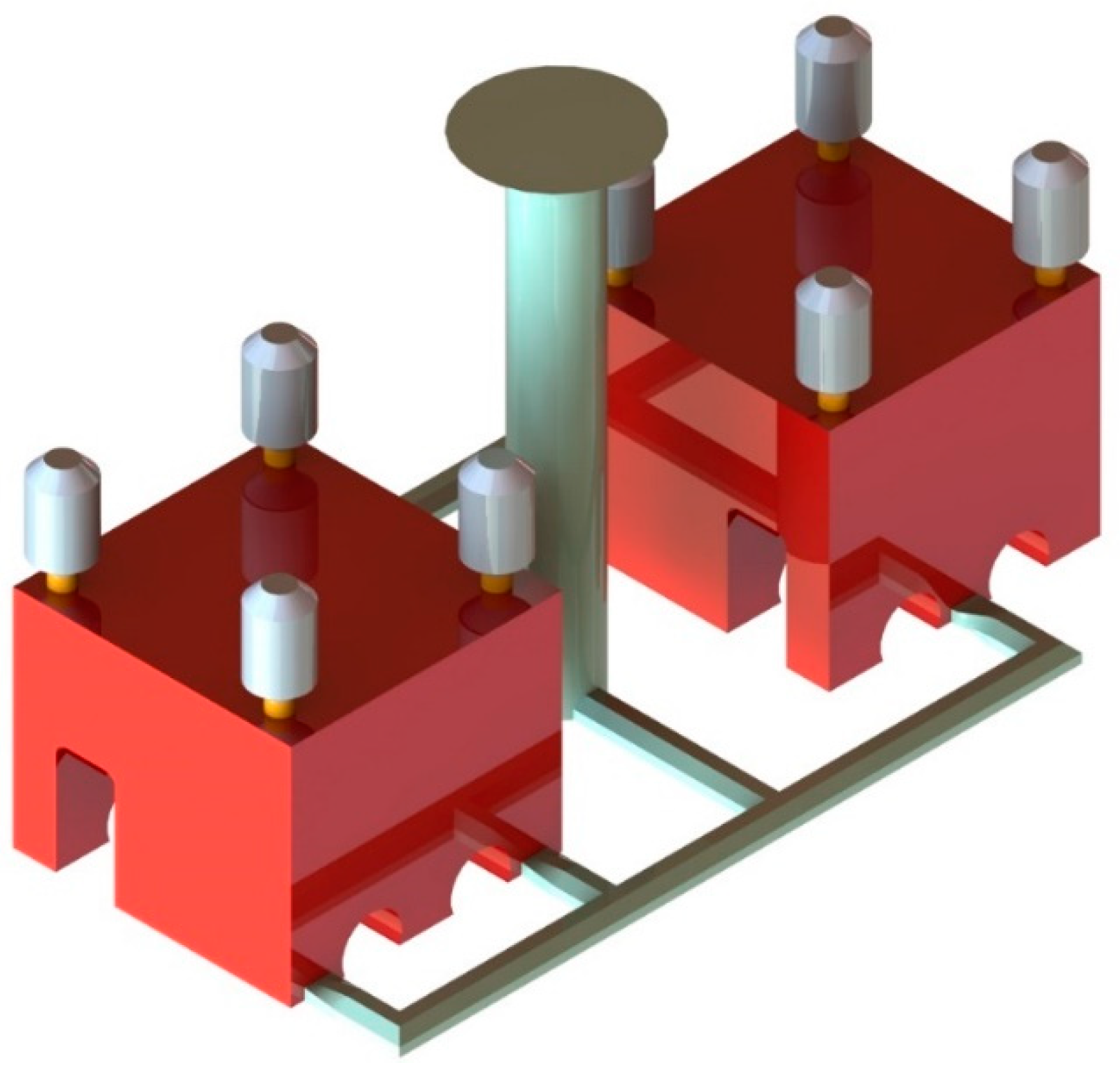
| Element | C | Si | Mn | P | S | Cu | Mg |
|---|---|---|---|---|---|---|---|
| Percentage | 3.47% | 2.24% | 0.31% | 0.012% | 0.01% | 0.59% | 0.061% |
| Melting Pot No. | Treatment Weight (kg) | Fe-Si-Mg Usage | Ladle Inoculation | Late Inoculation | Casting Temperature (°C) |
|---|---|---|---|---|---|
| P1 | 1200 | 1.5% | 0.4% | 0.1% | 1428 |
| Pouring Time (s) | Waiting Time at Production Line (hours) | ||||
| 18.2 | 6 | ||||
| Tool Name | Cutting Diameter (mm) | Number of Inserts |
|---|---|---|
| Seco Tools [24]—R220.43-0100-07W | 100 | 6 |
| Portion No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| Thermal Modulus (cm) | 1.2 | 1.4 | 1.2 | 1.1 | 1.5 | 1.2 | 1.4 |
| Dimensions (mm) | 45 × 45 × 100 | 125 × 35 × 50 | 45 × 30 × 100 | 40 × 25 × 100 | 45 × 60 × 50 | 45 × 45 × 100 | 125 × 35 × 50 |
| Non-Cooled Area Effect | 10% | 30% | 30% | 30% | 30% | 10% | 30% |
| No. | Spindle Speed (rpm) | Feed Rate (mm/min) | Depth of Cut (mm) | Step Over (mm) | Experimental Surf. Rough. [2] (µm) | 2D-SRET Surf. Rough. (µm) |
|---|---|---|---|---|---|---|
| 1 | 8500 | 1320 | 0.7 | 4 | 0.76 | 0.904 |
| 2 | 5500 | 1320 | 0.3 | 4 | 0.86 | 0.789 |
| 3 | 7000 | 2240 | 0.5 | 3 | 1.26 | 1.048 |
| 4 | 5500 | 3400 | 0.7 | 4 | 2.57 | 2.31 |
| 5 | 5500 | 1320 | 0.7 | 2 | 1.09 | 0.987 |
| 8 | 8500 | 3400 | 0.7 | 2 | 0.68 | 0.68 (adaptation) |
| 10 | 8500 | 3400 | 0.3 | 4 | 1.04 | 1.138 |
| 11 | 5500 | 3400 | 0.7 | 2 | 2.74 | 2.61 |
| 22 | 10,000 | 2240 | 0.5 | 3 | 0.91 | 0.997 |
| 26 | 7000 | 2240 | 0.1 | 3 | 0.74 | 0.665 |
| 28 | 4000 | 2240 | 0.5 | 3 | 2.08 | 2.02 |
| Spindle Speed (rpm) | Depth of Cut (mm) | Feed Rate (mm/min) | Experimental Surf. Rough. [9] (µm) | Regression Surf. Rough. [9] (µm) | ANN-Surf. Rough. [9] (µm) | 2D-SRET Surf. Rough. (µm) |
|---|---|---|---|---|---|---|
| 500 | 0.5 | 150 | 0.332 | 0.301 | 0.316 | 0.339 |
| 500 | 1 | 200 | 0.37 | 0.327 | 0.356 | 0.208 |
| 1000 | 0.5 | 100 | 0.184 | 0.193 | 0.158 | 0.153 |
| 1000 | 1 | 150 | 0.207 | 0.224 | 0.208 | 0.177 |
| 1500 | 1 | 100 | 0.181 | 0.164 | 0.162 | 0.155 |
| 1500 | 1.5 | 150 | 0.217 | 0.200 | 0.199 | 0.208 |
| 2000 | 1.5 | 100 | 0.155 | 0.188 | 0.169 | 0.173 |
| 2000 | 2 | 150 | 0.255 | 0.230 | 0.266 | 0.241 |
| No. | Vc (m/min) | Depth of Cut (mm) | Feed Rate (mm/Flute) | Experimental Surf. Rough. [3] (µm) | 2D-SRET Surf. Rough. (µm) |
|---|---|---|---|---|---|
| 1 | 80 | 0.1 | 0.05 | 0.166 | 0.180 |
| 4 | 80 | 0.3 | 0.05 | 0.215 | 0.180 |
| 7 | 80 | 0.5 | 0.05 | 0.185 | 0.182 |
| 11 | 140 | 0.1 | 0.10 | 0.359 | 0.292 |
| 14 | 140 | 0.3 | 0.10 | 0.287 | 0.292 |
| 17 | 140 | 0.5 | 0.10 | 0.372 | 0.350 |
| 19 | 200 | 0.1 | 0.05 | 0.192 | 0.194 |
| 21 | 200 | 0.1 | 0.15 | 0.413 | 0.429 |
| 22 | 200 | 0.3 | 0.05 | 0.200 | 0.196 |
| 24 | 200 | 0.3 | 0.15 | 0.444 | 0.429 |
| 25 | 200 | 0.5 | 0.05 | 0.305 | 0.234 |
| 27 | 200 | 0.5 | 0.15 | 0.492 | 0.492 |
| Surface No. | Spindle Speed (rpm) | Feed Rate (mm/min) | Depth of Cut (mm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|---|---|
| Part 1 Raw Est | 800 | 200 | 0.7 | 0.517 | 0.472 | 0.462 | 0.469 | 0.478 | 0.517 | 0.472 |
| Final Est. | 800 | 200 | 0.7 | 0.62 | 0.661 | 0.554 | 0.516 | 0.717 | 0.620 | 0.661 |
| Experimental | 800 | 200 | 0.7 | 0.713 | 0.677 | 0.504 | 0.496 | 0.970 | 0.765 | 0.607 |
| CMM Flatness | 800 | 200 | 0.7 | 0.004 | 0.000 | 0.002 | 0.001 | 0.004 | 0.003 | 0.003 |
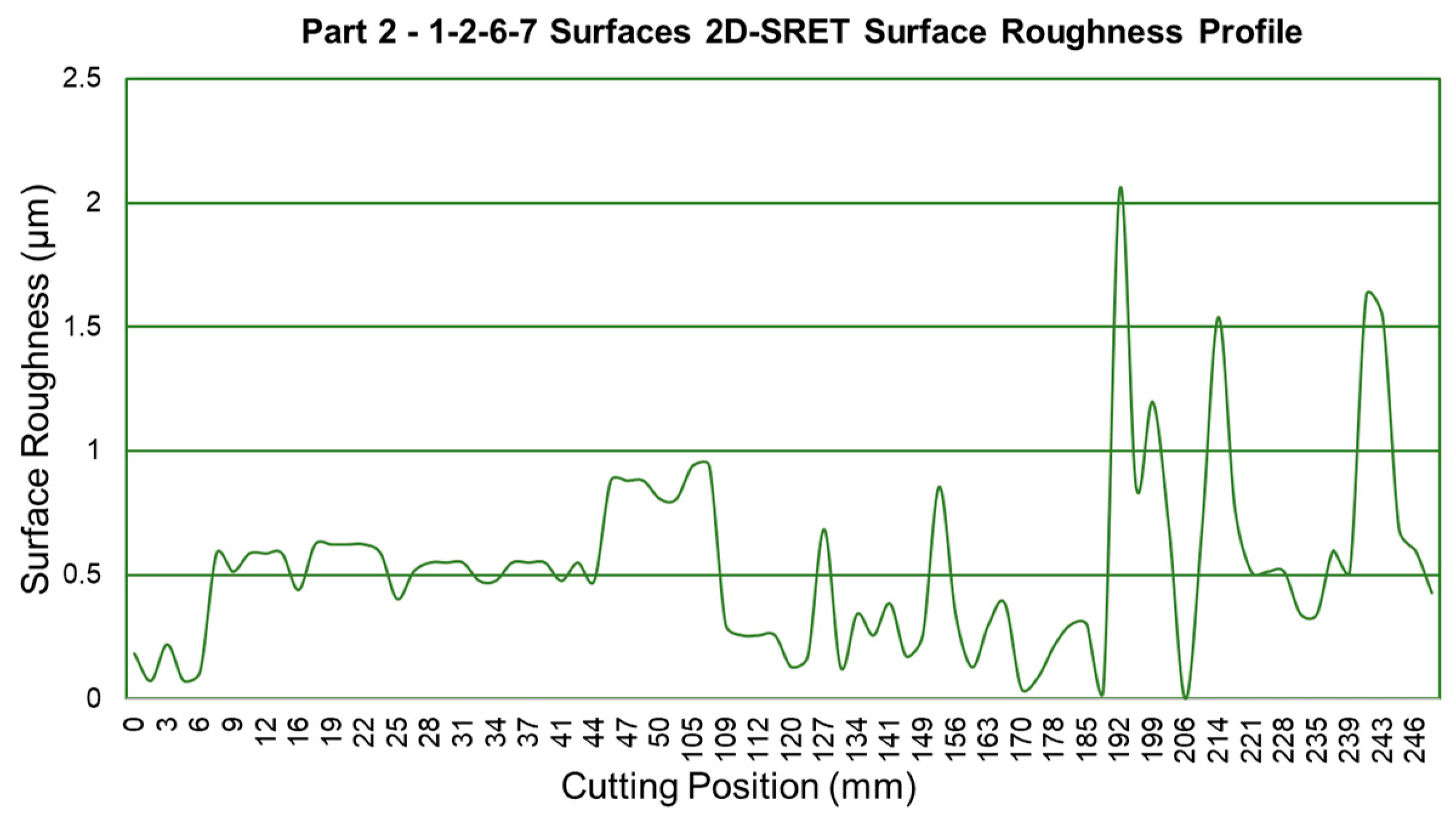
| Part 2 Raw Est. | 750 | 250 | 0.5 | 0.503 | 0.433 | 0.226 | 0.387 | 0.382 | 0.503 | 0.433 |
| Final Est. | 750 | 250 | 0.5 | 0.603 | 0.606 | 0.32 | 0.425 | 0.573 | 0.604 | 0.606 |
| Experimental | 750 | 250 | 0.5 | 0.458 | 0.779 | 0.478 | 0.389 | 0.588 | 0.518 | 0.637 |
| CMM Flatness | 750 | 250 | 0.5 | 0.001 | 0.000 | 0.001 | 0.003 | 0.005 | 0.000 | 0.004 |
| Part 3 Raw Est. | 800 | 150 | 0.6 | 0.626 | 0.685 | 0.964 | 0.656 | 0.758 | 0.626 | 0.685 |
| Final Est. | 800 | 150 | 0.6 | 0.751 | 0.959 | 1.157 | 0.723 | 1.137 | 0.751 | 0.959 |
| Experimental | 800 | 150 | 0.6 | 0.997 | 1.104 | 0.718 | 1.128 | 1.202 | 0.861 | 0.935 |
| CMM Flatness | 800 | 150 | 0.6 | 0.007 | 0.000 | 0.003 | 0.000 | 0.005 | 0.004 | 0.009 |
| Part 4 Raw Est. | 600 | 100 | 0.55 | 0.891 | 1.05 | 0.860 | 0.924 | 1.21 | 0.891 | 1.05 |
| Final Est. | 600 | 100 | 0.55 | 1.069 | 1.47 | 1.032 | 1.016 | 1.815 | 1.069 | 1.47 |
| Experimental | 600 | 100 | 0.55 | 1.069 | 0.743 | 1.336 | 0.757 | 1.013 | 1.079 | 1.266 |
| CMM Flatness | 600 | 100 | 0.55 | 0.004 | 0.000 | 0.004 | 0.000 | 0.002 | 0.003 | 0.007 |
| Thermal Modulus (cm) | 1.2 | 1.4 | 1.2 | 1.1 | 1.5 | 1.2 | 1.4 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teke, I.T.; Ertas, A.H. An Experimental Study on Nodular Iron Machined Surfaces Utilizing a Capable 2D Finite Element Model for Precise Surface Roughness Estimation. Processes 2024, 12, 549. https://doi.org/10.3390/pr12030549
Teke IT, Ertas AH. An Experimental Study on Nodular Iron Machined Surfaces Utilizing a Capable 2D Finite Element Model for Precise Surface Roughness Estimation. Processes. 2024; 12(3):549. https://doi.org/10.3390/pr12030549
Chicago/Turabian StyleTeke, Ibrahim T., and Ahmet H. Ertas. 2024. "An Experimental Study on Nodular Iron Machined Surfaces Utilizing a Capable 2D Finite Element Model for Precise Surface Roughness Estimation" Processes 12, no. 3: 549. https://doi.org/10.3390/pr12030549
APA StyleTeke, I. T., & Ertas, A. H. (2024). An Experimental Study on Nodular Iron Machined Surfaces Utilizing a Capable 2D Finite Element Model for Precise Surface Roughness Estimation. Processes, 12(3), 549. https://doi.org/10.3390/pr12030549







