Soft Sensor Modeling Method Considering Higher-Order Moments of Prediction Residuals
Abstract
1. Introduction
2. Background
2.1. OLS
2.2. CNN
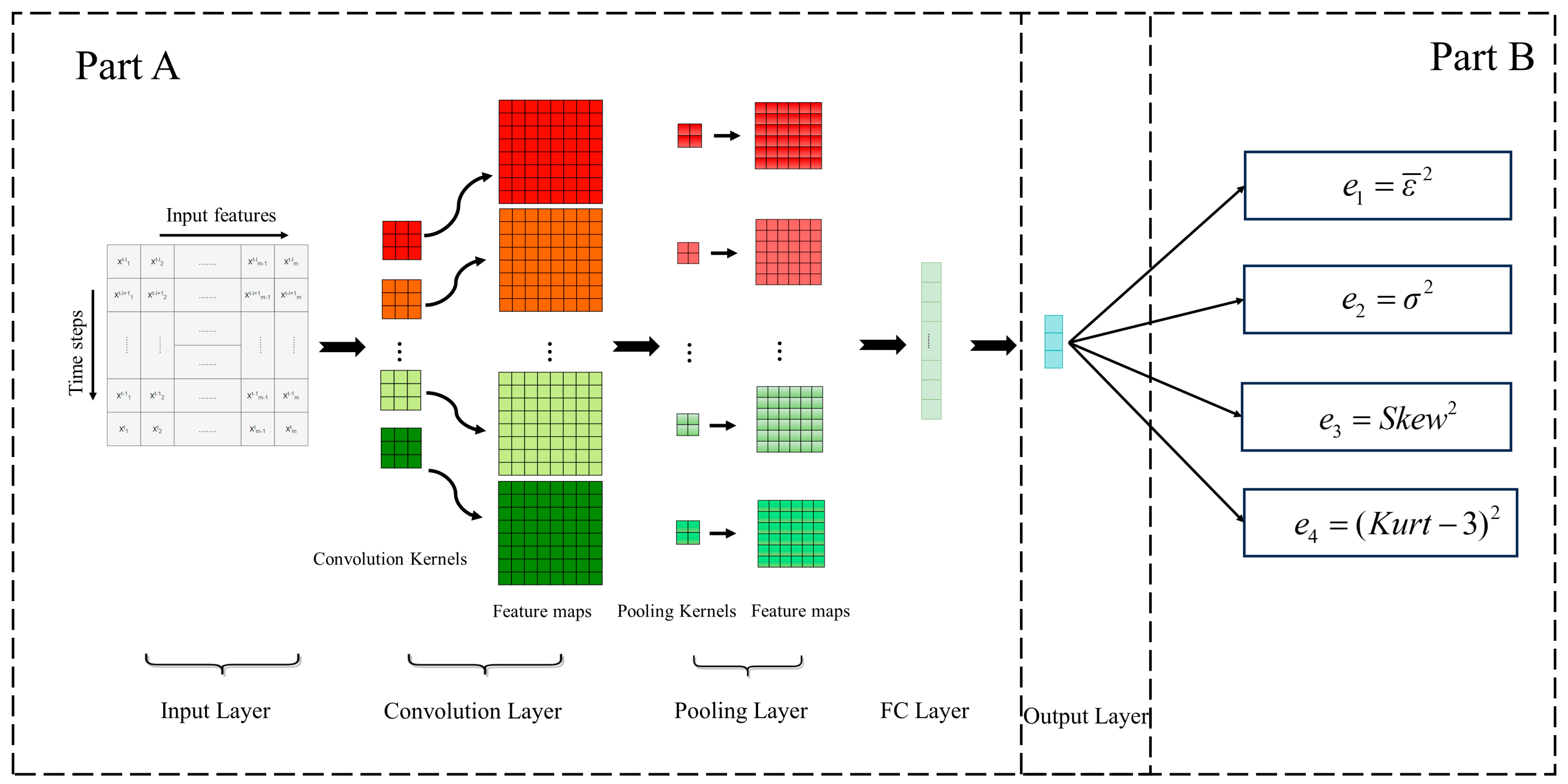
3. Soft Sensor Modeling Method Considering the Higher-Order Moments of Prediction Residuals
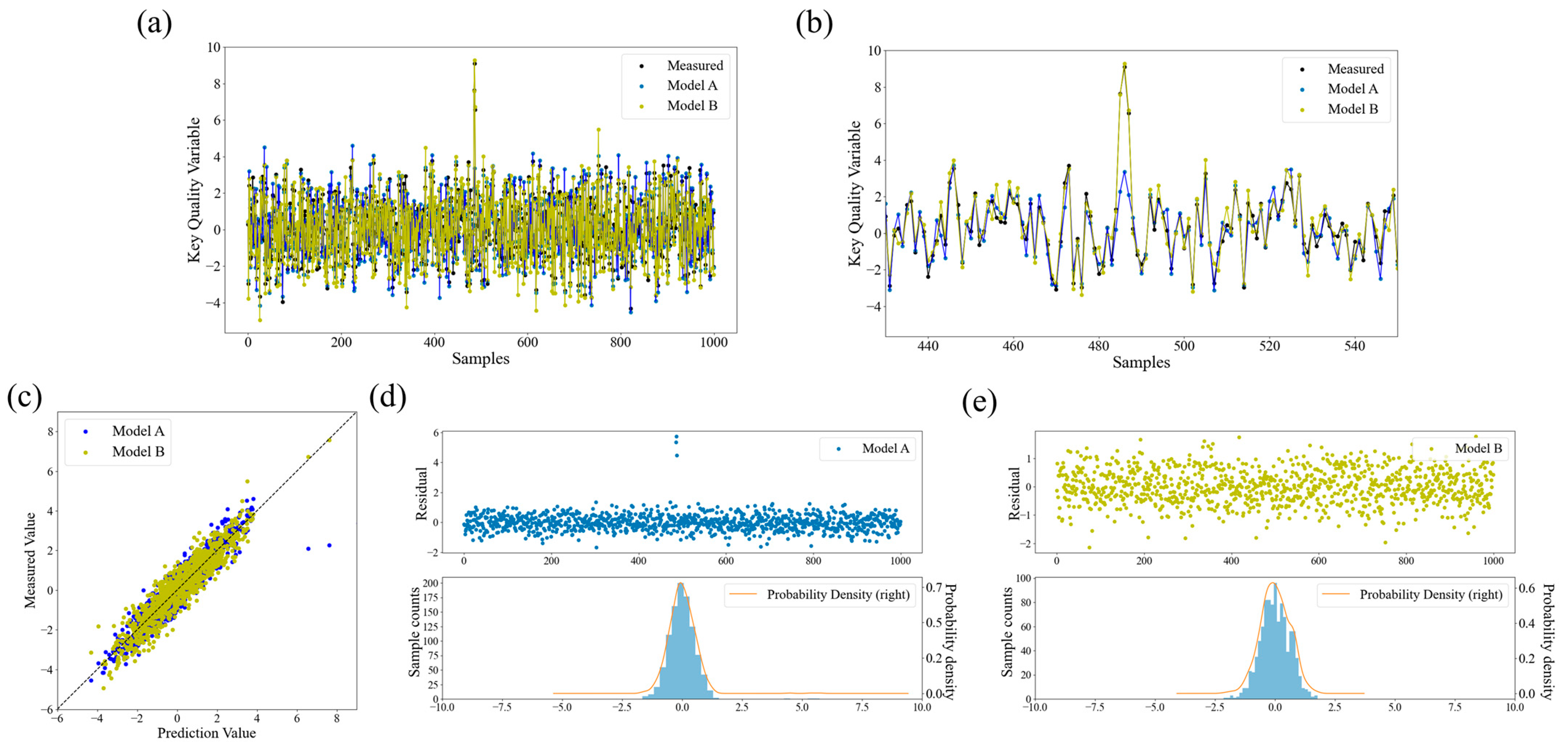
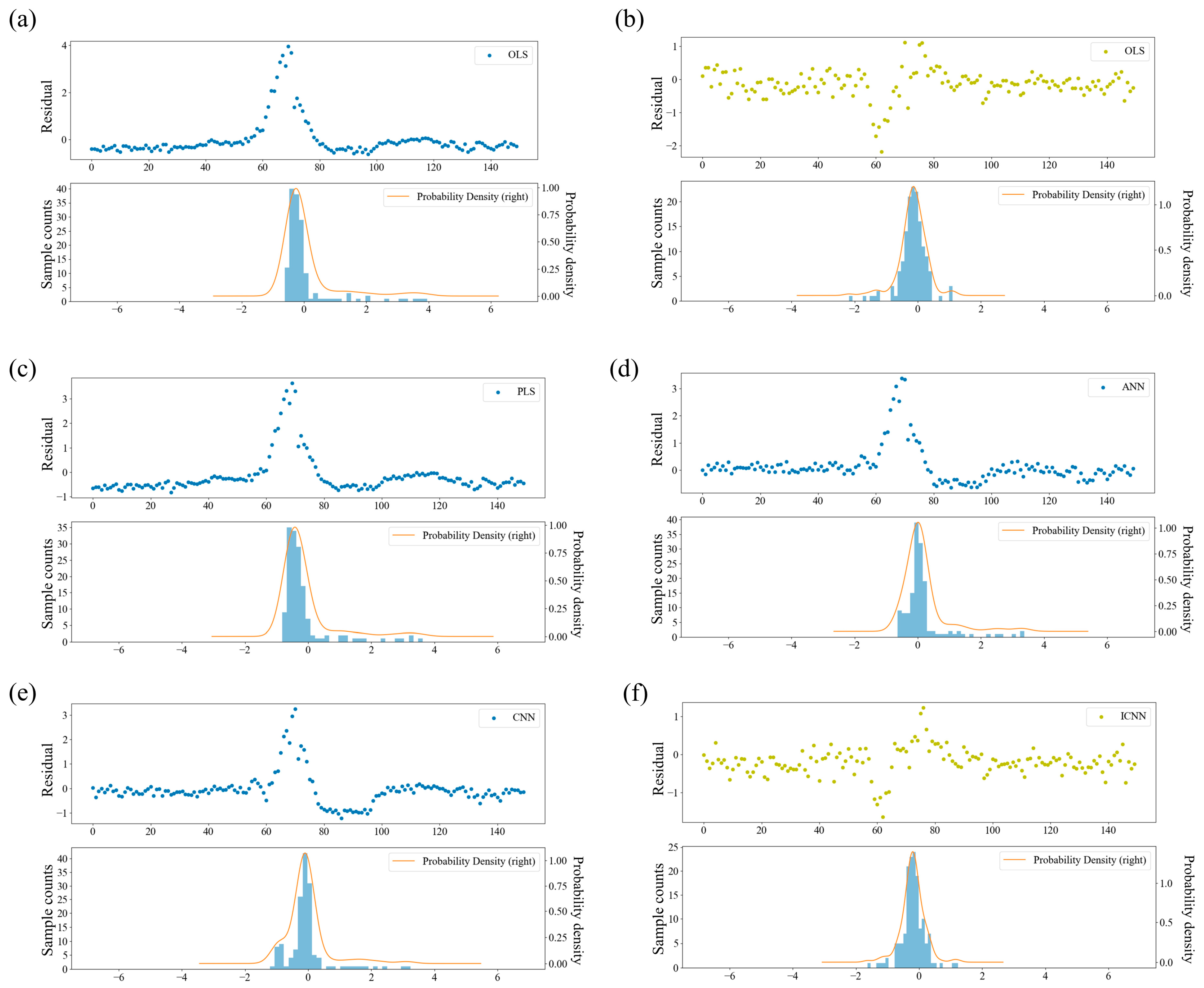
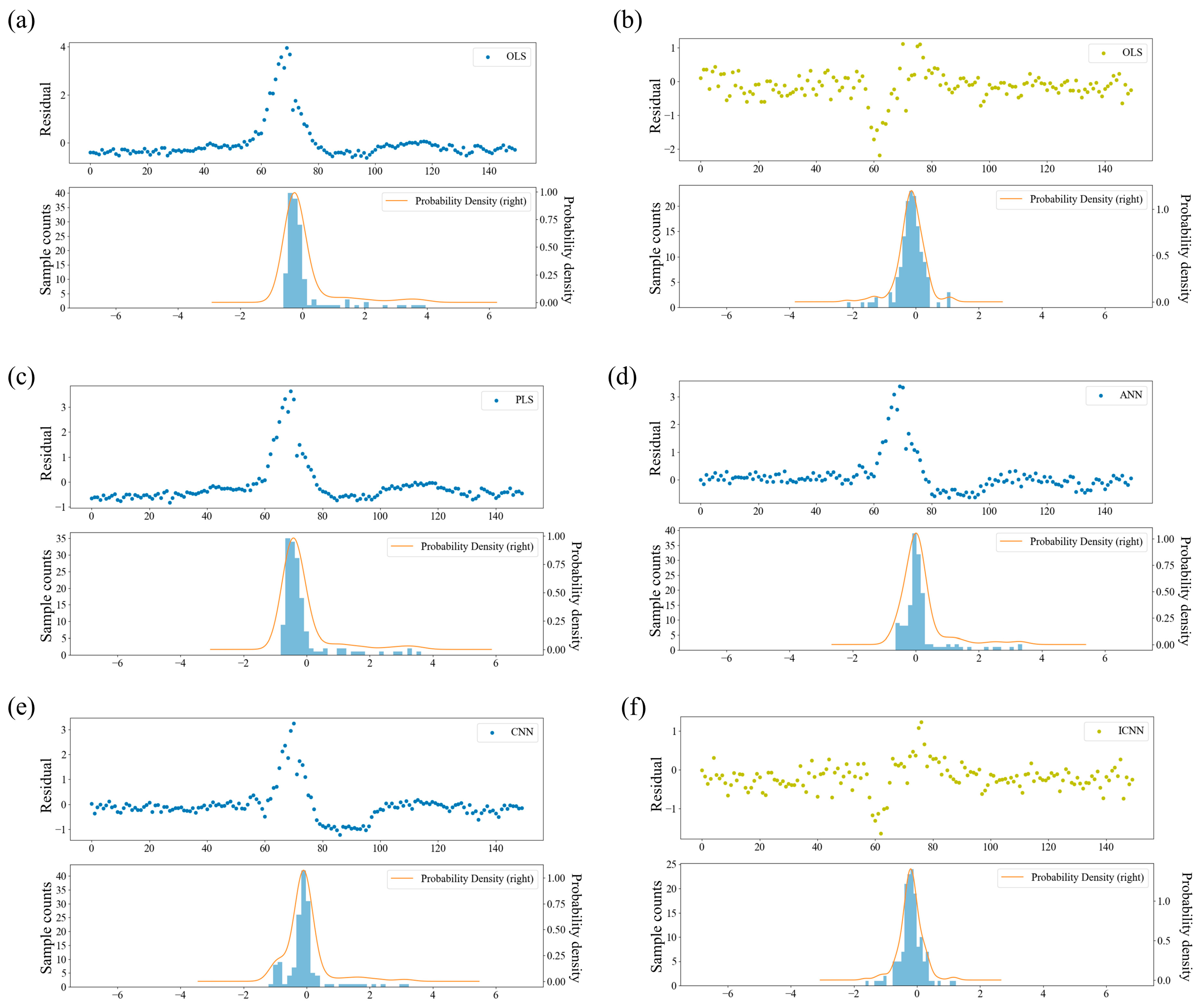
3.1. Residual Analysis
3.2. Improved Ordinary Least Squares (IOLS)
3.3. Improved Convolutional Neural Network (ICNN)
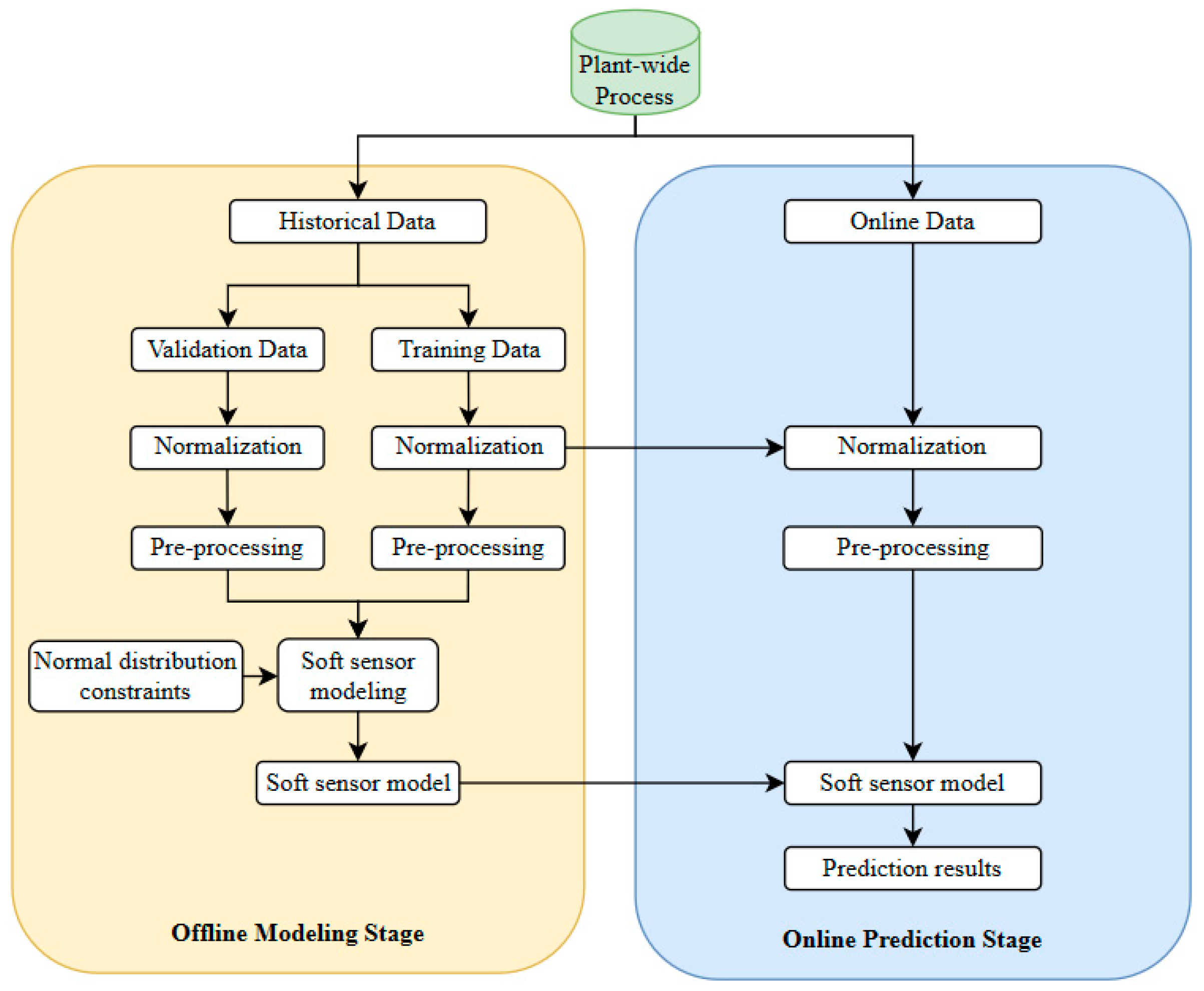
3.4. Framework for Proposed Method
- Offline modeling stage
- Online prediction stage
4. Case Study
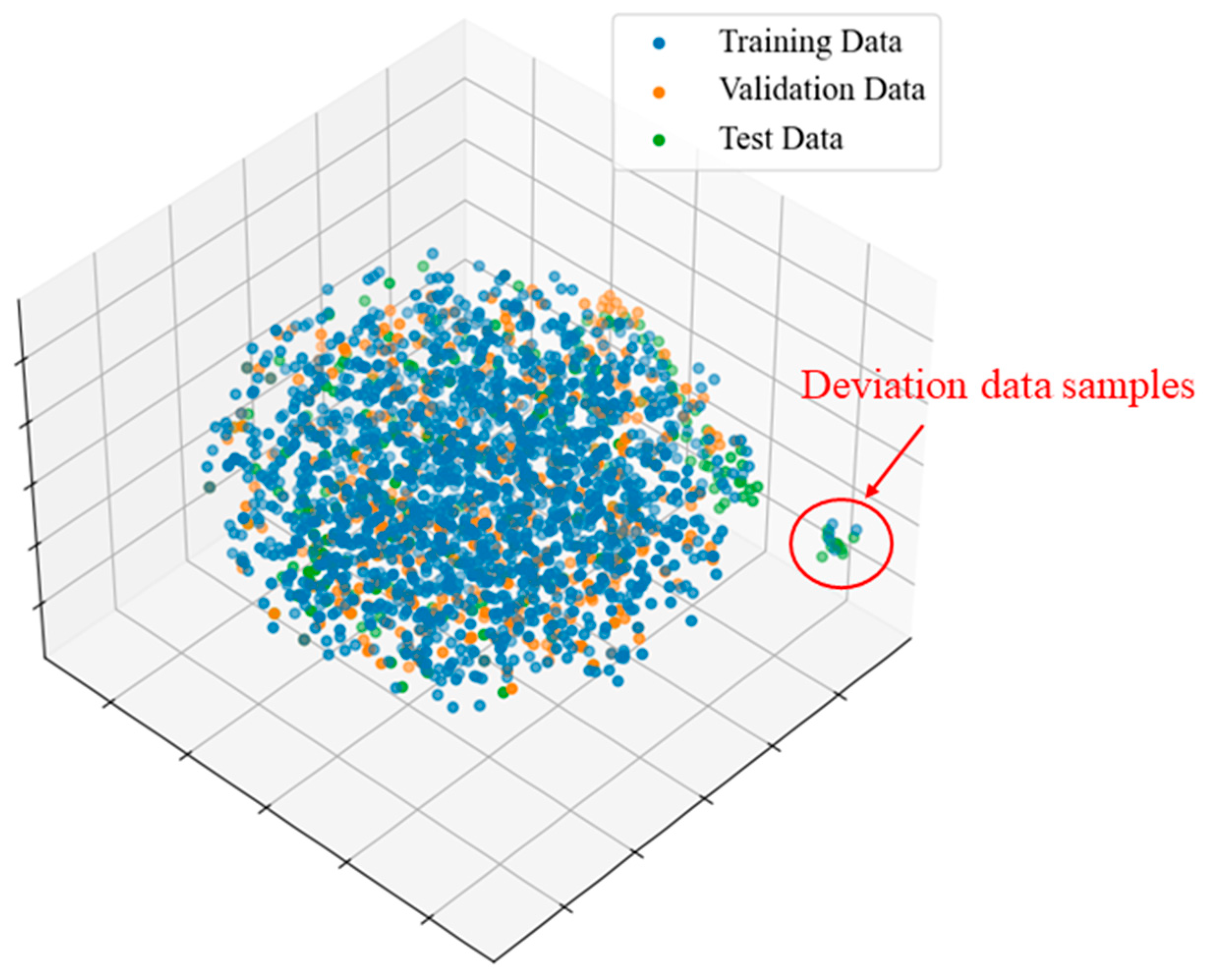
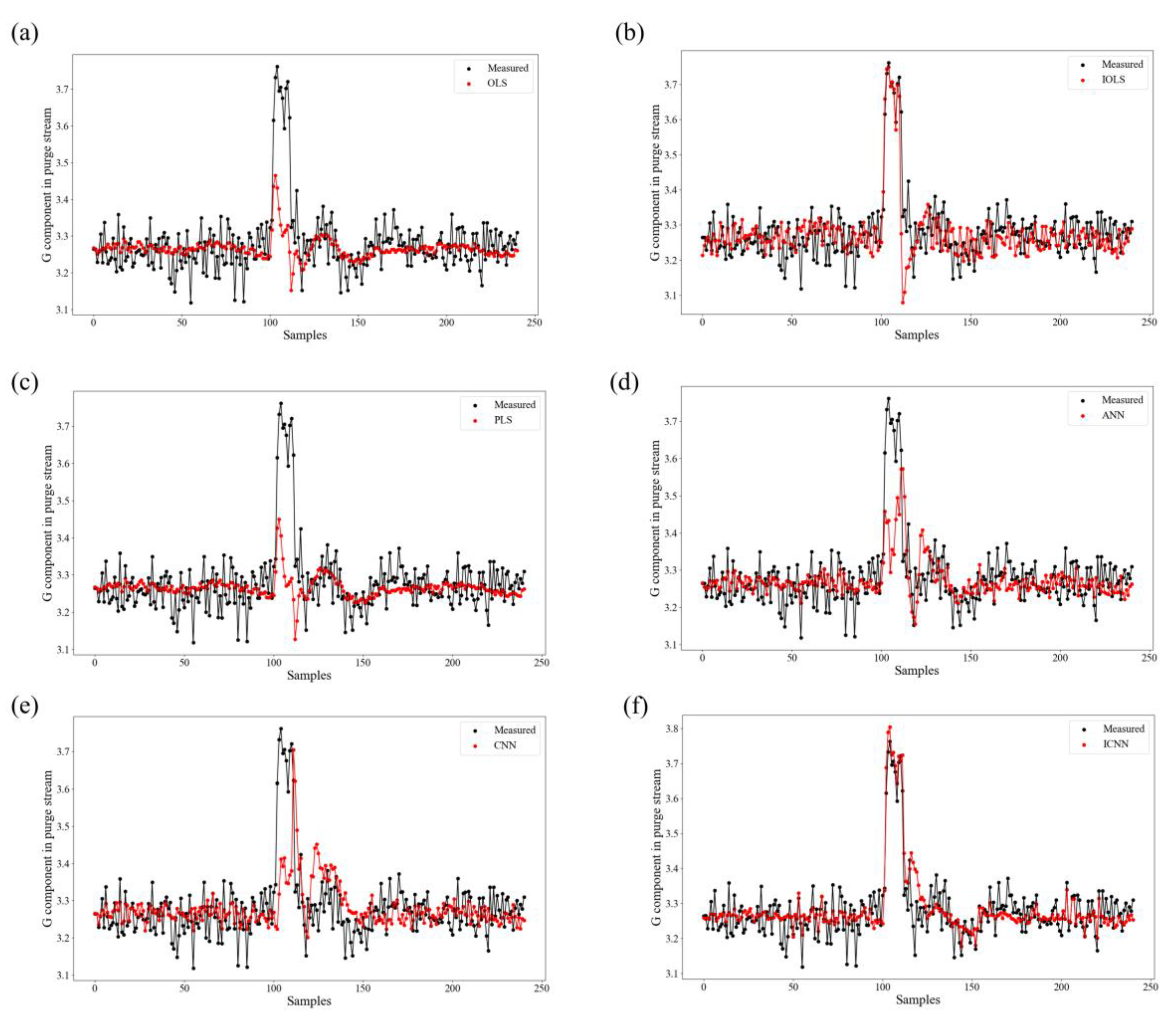
4.1. Tennessee Eastman Process
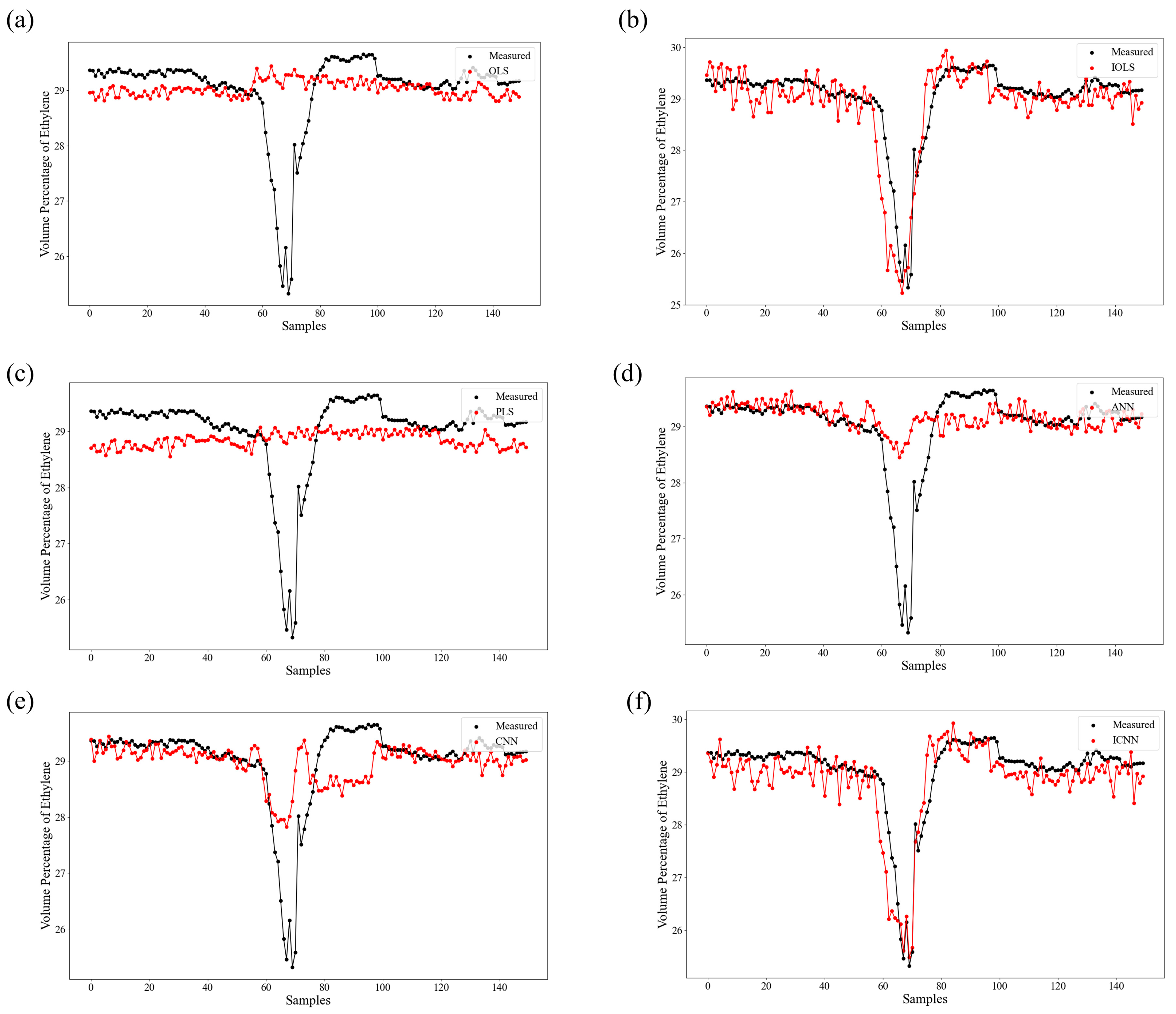
4.2. Industrial Cracking Furnace
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yuan, X.; Huang, B.; Wang, Y.; Yang, C.; Gui, W. Deep learning-based feature representation and its application for soft sensor modeling with variable-wise weighted SAE. IEEE Trans. Ind. Inform. 2018, 14, 3235–3243. [Google Scholar] [CrossRef]
- Kadlec, P.; Grbić, R.; Gabrys, B. Review of adaptation mechanisms for data-driven soft sensors. Comput. Chem. Eng. 2011, 35, 1–24. [Google Scholar] [CrossRef]
- Ma, F.; Wang, J.; Sun, W. A Data-Driven Semi-Supervised Soft-Sensor Method: Application on an Industrial Cracking Furnace. Front. Chem. Eng. 2022, 4, 899941. [Google Scholar] [CrossRef]
- Jiang, Q.; Yan, X.; Yi, H.; Gao, F. Data-driven batch-end quality modeling and monitoring based on optimized sparse partial least squares. IEEE Trans. Ind. Electron. 2019, 67, 4098–4107. [Google Scholar] [CrossRef]
- Jiang, Y.; Yin, S.; Dong, J.; Kaynak, O. A review on soft sensors for monitoring, control, and optimization of industrial processes. IEEE Sens. J. 2020, 21, 12868–12881. [Google Scholar] [CrossRef]
- McAuley, K.B.; MacGregor, J.F. On-line inference of polymer properties in an industrial polyethylene reactor. AIChE J. 1991, 37, 825–835. [Google Scholar] [CrossRef]
- Yuan, X.; Qi, S.; Shardt, Y.A.W.; Wang, Y.; Yang, C.; Gui, W. Soft sensor model for dynamic processes based on multichannel convolutional neural network. Chemom. Intell. Lab. Syst. 2020, 203, 104050. [Google Scholar] [CrossRef]
- Yuan, X.; Li, L.; Shardt, Y.A.W.; Wang, Y.; Yang, C. Deep learning with spatiotemporal attention-based LSTM for industrial soft sensor model development. IEEE Trans. Ind. Electron. 2020, 68, 4404–4414. [Google Scholar] [CrossRef]
- Khosbayar, A.; Valluru, J.; Huang, B. Multi-rate Gaussian Bayesian network soft sensor development with noisy input and missing data. J. Process Control 2021, 105, 48–61. [Google Scholar] [CrossRef]
- Facco, P.; Doplicher, F.; Bezzo, F.; Barolo, M. Moving average PLS soft sensor for online product quality estimation in an industrial batch polymerization process. J. Process Control 2009, 19, 520–529. [Google Scholar] [CrossRef]
- Fujiwara, K.; Kano, M. Efficient input variable selection for soft-senor design based on nearest correlation spectral clustering and group Lasso. ISA Trans. 2015, 58, 367–379. [Google Scholar] [CrossRef] [PubMed]
- Urhan, A.; Alakent, B. Integrating adaptive moving window and just-in-time learning paradigms for soft-sensor design. Neurocomputing 2020, 392, 23–37. [Google Scholar] [CrossRef]
- Kaneko, H.; Funatsu, K. Application of online support vector regression for soft sensors. AIChE J. 2014, 60, 600–612. [Google Scholar] [CrossRef]
- Yu, J. Multiway Gaussian mixture model based adaptive kernel partial least squares regression method for soft sensor estimation and reliable quality prediction of nonlinear multiphase batch processes. Ind. Eng. Chem. Res. 2012, 51, 13227–13237. [Google Scholar] [CrossRef]
- Yuan, X.; Ge, Z.; Song, Z. Locally weighted kernel principal component regression model for soft sensing of nonlinear time-variant processes. Ind. Eng. Chem. Res. 2014, 53, 13736–13749. [Google Scholar] [CrossRef]
- Xie, R.; Jan, N.M.; Hao, K.; Chen, L.; Huang, B. Supervised variational autoencoders for soft sensor modeling with missing data. IEEE Trans. Ind. Inform. 2019, 16, 2820–2828. [Google Scholar] [CrossRef]
- Ji, C.; Ma, F.; Wang, J.; Sun, W. Profitability related industrial-scale batch processes monitoring via deep learning based soft sensor development. Comput. Chem. Eng. 2023, 170, 108125. [Google Scholar] [CrossRef]
- Ma, F.; Ji, C.; Wang, J.; Sun, W. Early identification of process deviation based on convolutional neural network. Chin. J. Chem. Eng. 2023, 56, 104–118. [Google Scholar] [CrossRef]
- Ji, C.; Sun, W. A review on data-driven process monitoring methods: Characterization and mining of industrial data. Processes 2022, 10, 335. [Google Scholar] [CrossRef]
- Ott, R.L.; Longnecker, M.T. An Introduction to Statistical Methods and Data Analysis; Cengage Learning: Belmont, CA, USA, 2015. [Google Scholar]
- Lan, T.; Tong, C.; Yu, H.; Shi, X.; Luo, L. Nonlinear process monitoring based on decentralized generalized regression neural networks. Expert Syst. Appl. 2020, 150, 113273. [Google Scholar] [CrossRef]
- Tong, C.; Lan, T.; Yu, H.; Peng, X. Distributed partial least squares based residual generation for statistical process monitoring. J. Process Control 2019, 75, 77–85. [Google Scholar] [CrossRef]
- Döhler, M.; Mevel, L.; Zhang, Q. Fault detection, isolation and quantification from Gaussian residuals with application to structural damage diagnosis. Annu. Rev. Control 2016, 42, 244–256. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, V.; Sarangi, S.; Singh, O.P. Gearbox fault diagnosis: A higher order moments approach. Measurement 2023, 210, 112489. [Google Scholar] [CrossRef]
- Obuchowski, J.; Zimroz, R.; Wyłomańska, A. Blind equalization using combined skewness–kurtosis criterion for gearbox vibration enhancement. Measurement 2016, 88, 34–44. [Google Scholar] [CrossRef]
- Saufi, S.R.; Ahmad, Z.A.B.; Leong, M.S.; Lim, M.H. Gearbox fault diagnosis using a deep learning model with limited data sample. IEEE Trans. Ind. Inform. 2020, 16, 6263–6271. [Google Scholar] [CrossRef]
- Wen, J.; Li, Y.; Wang, J.; Sun, W. Nonstationary Process Monitoring Based on Cointegration Theory and Multiple Order Moments. Processes 2022, 10, 169. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
- De Myttenaere, A.; Golden, B.; Le Grand, B.; Rossi, F. Mean absolute percentage error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef]
- Hodson, T.O.; Over, T.M.; Foks, S.S. Mean squared error, deconstructed. J. Adv. Model. Earth Syst. 2021, 13, e2021MS002681. [Google Scholar] [CrossRef]
- Willmott, C.J.; Matsuura, K.; Robeson, S.M. Ambiguities inherent in sums-of-squares-based error statistics. Atmos. Environ. 2009, 43, 749–752. [Google Scholar] [CrossRef]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)?–Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef]
- Zhu, Q.-X.; Liu, D.-P.; Xu, Y.; He, Y.-L. Novel space projection interpolation based virtual sample generation for solving the small data problem in developing soft sensor. Chemom. Intell. Lab. Syst. 2021, 217, 104425. [Google Scholar] [CrossRef]
- Bo, C.M.; Li, J.; Sun, C.Y.; Wang, Y.R. The application of neural network soft sensor technology to an advanced control system of distillation operation. In Proceedings of the International Joint Conference on Neural Networks, Portland, OR, USA, 20–24 July 2003; pp. 1054–1058. [Google Scholar]
- Cortese, G.; Holmboe, S.A.; Scheike, T.H. Regression models for the restricted residual mean life for right-censored and left-truncated data. Stat. Med. 2017, 36, 1803–1822. [Google Scholar] [CrossRef] [PubMed]
- Osborne, J. Notes on the use of data transformations. Pract. Assess. Res. Eval. 2002, 8, 1–8. [Google Scholar]
- Ju, X.; Salibián-Barrera, M. Robust boosting for regression problems. Comput. Stat. Data Anal. 2021, 153, 107065. [Google Scholar] [CrossRef]
- Karunasingha, D.S.K. Root mean square error or mean absolute error? Use their ratio as well. Inf. Sci. 2022, 585, 609–629. [Google Scholar] [CrossRef]
- Collis, W.B.; White, P.R.; Hammond, J.K. Higher-order spectra: The bispectrum and trispectrum. Mech. Syst. Signal Process. 1998, 12, 375–394. [Google Scholar] [CrossRef]
- Li, X.; Hu, Y.; Zheng, J.; Li, M.; Ma, W. Central moment discrepancy based domain adaptation for intelligent bearing fault diagnosis. Neurocomputing 2021, 429, 12–24. [Google Scholar] [CrossRef]
- Rezaeianjouybari, B.; Shang, Y. A novel deep multi-source domain adaptation framework for bearing fault diagnosis based on feature-level and task-specific distribution alignment. Measurement 2021, 178, 109359. [Google Scholar] [CrossRef]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. Adv. Neural Inf. Process. Syst. 2017, 60, 84–90. [Google Scholar] [CrossRef]
- Rastegari, M.; Ordonez, V.; Redmon, J.; Farhadi, A. Xnor-net: Imagenet classification using binary convolutional neural networks. arXiv 2016, arXiv:1603.05279. [Google Scholar]
- Yuan, X.; Qi, S.; Wang, Y.; Xia, H. A dynamic CNN for nonlinear dynamic feature learning in soft sensor modeling of industrial process data. Control Eng. Pract. 2020, 104, 104614. [Google Scholar] [CrossRef]
- Zhao, Y.; Ding, B.; Zhang, Y.; Yang, L.; Hao, X. Online cement clinker quality monitoring: A soft sensor model based on multivariate time series analysis and CNN. ISA Trans. 2021, 117, 180–195. [Google Scholar] [CrossRef] [PubMed]
- Zheng, J.; Ma, L.; Wu, Y.; Ye, L.; Shen, F. Nonlinear dynamic soft sensor development with a supervised hybrid CNN-LSTM network for industrial processes. ACS Omega 2022, 7, 16653–16664. [Google Scholar] [CrossRef]
- Ma, F.; Ji, C.; Xu, M.; Wang, J.; Sun, W. Spatial correlation extraction for chemical process fault detection using image enhancement technique aided convolutional autoencoder. Chem. Eng. Sci. 2023, 278, 118900. [Google Scholar] [CrossRef]
- Yan, J.; Tian, X.; Zhou, Q.; Yang, Y. Improvement of Scanlan’s nonlinear model based on residual analysis. KSCE J. Civ. Eng. 2019, 23, 280–286. [Google Scholar] [CrossRef]
- Eglese, R.W. Simulated annealing: A tool for operational research. Eur. J. Oper. Res. 1990, 46, 271–281. [Google Scholar] [CrossRef]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Wang, L.; Koch, D.D.; Hill, W.; Abulafia, A. Pursuing perfection in intraocular lens calculations: III. Criteria for analyzing outcomes. J. Cataract Refract. Surg. 2017, 43, 999–1002. [Google Scholar] [CrossRef]
- Xiong, K.; Wang, S. Robust least mean logarithmic square adaptive filtering algorithms. J. Frankl. Inst. 2019, 356, 654–674. [Google Scholar] [CrossRef]
- Zhang, D. A coefficient of determination for generalized linear models. Am. Stat. 2017, 71, 310–316. [Google Scholar] [CrossRef]
- Downs, J.J.; Vogel, E.F. A plant-wide industrial process control problem. Comput. Chem. Eng. 1993, 17, 245–255. [Google Scholar] [CrossRef]
- Bathelt, A.; Ricker, N.L.; Jelali, M. Revision of the Tennessee Eastman process model. IFAC-Pap. 2015, 48, 309–314. [Google Scholar] [CrossRef]
- Ji, C.; Ma, F.; Wang, J.; Sun, W.; Zhu, X. Statistical method based on dissimilarity of variable correlations for multimode chemical process monitoring with transitions. Process Saf. Environ. Prot. 2022, 162, 649–662. [Google Scholar] [CrossRef]
| Model | Input Dimension | Convolutional Layer | Pooling Layer | Convolutional Layer | FC Layer | Output Layer |
|---|---|---|---|---|---|---|
| CNN | 2D matrix | 3 (3, 3) | Average pooling | 5 (2, 1) | Flatten | 1 |
| ICNN | 2D matrix | 3 (3, 3) | Average pooling | 5 (2, 1) | Flatten | 1 |
| MSE | RMSE | MAE | MSLE | MAPE | R2 | Skew | Kurt | |
|---|---|---|---|---|---|---|---|---|
| OLS | 0.0071 | 0.0845 | 0.0525 | 3.65 × 10−4 | 1.5609 | 0.2452 | −2.2953 | 7.8330 |
| IOLS | 0.0042 | 0.0648 | 0.0472 | 2.29 × 10−4 | 1.4393 | 0.5562 | −0.9265 | 4.2023 |
| PLS | 0.0080 | 0.0895 | 0.0539 | 4.11 × 10−4 | 1.6002 | 0.1521 | −2.5255 | 8.8929 |
| ANN | 0.0060 | 0.0774 | 0.0502 | 3.07 × 10−4 | 1.4979 | 0.3652 | −1.6846 | 7.1492 |
| CNN | 0.0077 | 0.0879 | 0.0564 | 3.97 × 10−4 | 1.6827 | 0.1814 | −1.7075 | 6.9167 |
| ICNN | 0.0023 | 0.0487 | 0.0360 | 1.29 × 10−4 | 1.0985 | 0.7488 | 0.8395 | 2.8176 |
| MSE | RMSE | MAE | MSLE | MAPE | R2 | Skew | Kurt | |
|---|---|---|---|---|---|---|---|---|
| OLS (0‰) | 0.0889 | 0.2983 | 0.1023 | 5.80 × 10−3 | 2.9280 | −8.4157 | −4.3791 | 18.4649 |
| IOLS (0‰) | 0.0763 | 0.2762 | 0.1022 | 4.78 × 10−3 | 2.9435 | −7.0721 | −4.1892 | 17.4595 |
| OLS (2‰) | 0.0092 | 0.0958 | 0.0557 | 4.70 × 10−4 | 1.6487 | 0.0281 | −2.7006 | 9.9766 |
| IOLS (2‰) | 0.0043 | 0.0653 | 0.0484 | 2.29 × 10−4 | 1.4628 | 0.5492 | −0.9236 | 4.9967 |
| OLS (4‰) | 0.0071 | 0.0846 | 0.0525 | 3.65 × 10−4 | 1.5609 | 0.2452 | −2.2953 | 7.8330 |
| IOLS (4‰) | 0.0042 | 0.0648 | 0.0472 | 2.29 × 10−4 | 1.4393 | 0.5562 | −0.9265 | 4.2023 |
| OLS (6‰) | 0.0025 | 0.0497 | 0.0399 | 1.35 × 10−4 | 1.2166 | 0.7385 | 0.1788 | 3.3032 |
| IOLS (6‰) | 0.0024 | 0.0494 | 0.0383 | 1.34 × 10−4 | 1.1708 | 0.7416 | −0.0325 | 3.1601 |
| OLS (8‰) | 0.0024 | 0.0490 | 0.0403 | 1.32 × 10−4 | 1.2286 | 0.7451 | 0.2892 | 3.1451 |
| IOLS (8‰) | 0.0024 | 0.0490 | 0.0375 | 1.32 × 10−4 | 1.1445 | 0.7456 | −0.0765 | 3.6916 |
| OLS (10‰) | 0.0024 | 0.0488 | 0.0391 | 1.31 × 10−4 | 1.1947 | 0.7474 | 0.2648 | 3.3319 |
| IOLS (10‰) | 0.0024 | 0.0489 | 0.0387 | 1.32 × 10−4 | 1.1818 | 0.7468 | 0.1617 | 3.6318 |
| No. | Description | Unit |
|---|---|---|
| x1–x7 | Naphtha mass flow rate | kg/h |
| x8 | Naphtha temperature | °C |
| x9 | Naphtha pressure | Mpag |
| x10–x16 | Diluted steam mass flow rate | kg/h |
| x17 | Diluted steam temperature | °C |
| x18–x23 | Crossover section temperature | °C |
| x24–x29 | Crossover section pressure | Mpag |
| x30, x31 | Temperature in furnace A/B side | °C |
| x32 | Fuel gas flow rate | kg/h |
| x33–x57 | Coil outlet temperature | °C |
| x58–x63 | Outlet pressure | Mpag |
| Model | Input Dimension | Convolutional Layer | Pooling Layer | Convolutional Layer | FC Layer | Output Layer |
|---|---|---|---|---|---|---|
| CNN | 2D matrix | 5 (3, 3) | Average pooling | 8 (2, 1) | Flatten | 1 |
| ICNN | 2D matrix | 5 (3, 3) | Average pooling | 8 (2, 1) | Flatten | 1 |
| MSE | RMSE | MAE | MSLE | MAPE | R2 | Skew | Kurt | |
|---|---|---|---|---|---|---|---|---|
| OLS | 0.6899 | 0.8306 | 0.4671 | 8.30 × 10−4 | 1.6747 | −0.1599 | 3.1527 | 10.0216 |
| IOLS | 0.2086 | 0.4567 | 0.3123 | 2.50 × 10−4 | 1.0896 | 0.6493 | −1.0149 | 4.9531 |
| PLS | 0.6615 | 0.8133 | 0.5602 | 7.93 × 10−4 | 1.9832 | −0.1121 | 3.1218 | 10.0271 |
| ANN | 0.4801 | 0.6929 | 0.3518 | 5.87 × 10−4 | 1.2682 | 0.1928 | 2.9270 | 9.9334 |
| CNN | 0.4342 | 0.6590 | 0.3811 | 5.24 × 10−4 | 1.3529 | 0.2699 | 2.3434 | 8.3853 |
| ICNN | 0.1721 | 0.4150 | 0.3122 | 1.99 × 10−4 | 1.0807 | 0.7105 | −0.0981 | 3.6372 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, F.; Ji, C.; Wang, J.; Sun, W.; Palazoglu, A. Soft Sensor Modeling Method Considering Higher-Order Moments of Prediction Residuals. Processes 2024, 12, 676. https://doi.org/10.3390/pr12040676
Ma F, Ji C, Wang J, Sun W, Palazoglu A. Soft Sensor Modeling Method Considering Higher-Order Moments of Prediction Residuals. Processes. 2024; 12(4):676. https://doi.org/10.3390/pr12040676
Chicago/Turabian StyleMa, Fangyuan, Cheng Ji, Jingde Wang, Wei Sun, and Ahmet Palazoglu. 2024. "Soft Sensor Modeling Method Considering Higher-Order Moments of Prediction Residuals" Processes 12, no. 4: 676. https://doi.org/10.3390/pr12040676
APA StyleMa, F., Ji, C., Wang, J., Sun, W., & Palazoglu, A. (2024). Soft Sensor Modeling Method Considering Higher-Order Moments of Prediction Residuals. Processes, 12(4), 676. https://doi.org/10.3390/pr12040676











