Time-Specific Thresholds for Batch Process Monitoring: A Study Based on Two-Dimensional Conditional Variational Auto-Encoder
Abstract
:1. Introduction
2. Preliminaries
3. Methodology
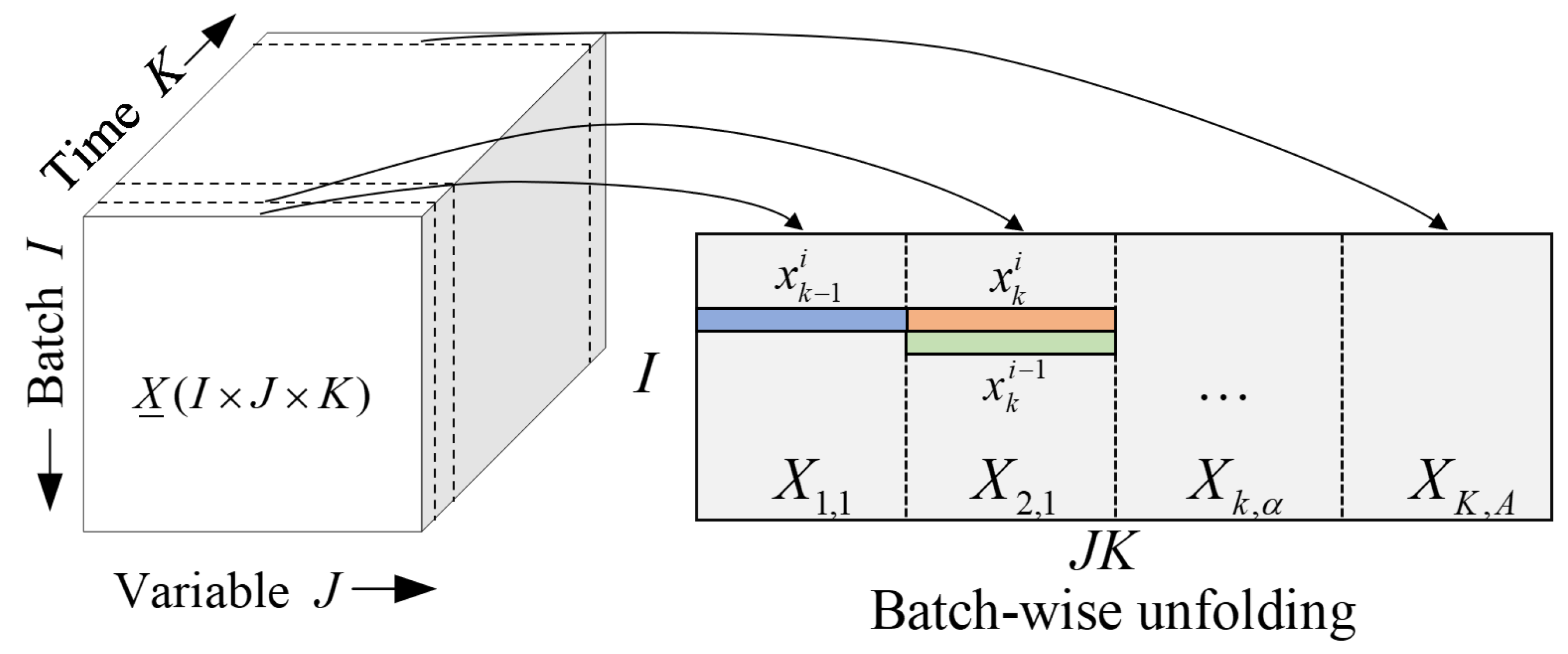
3.1. Batch Data Description
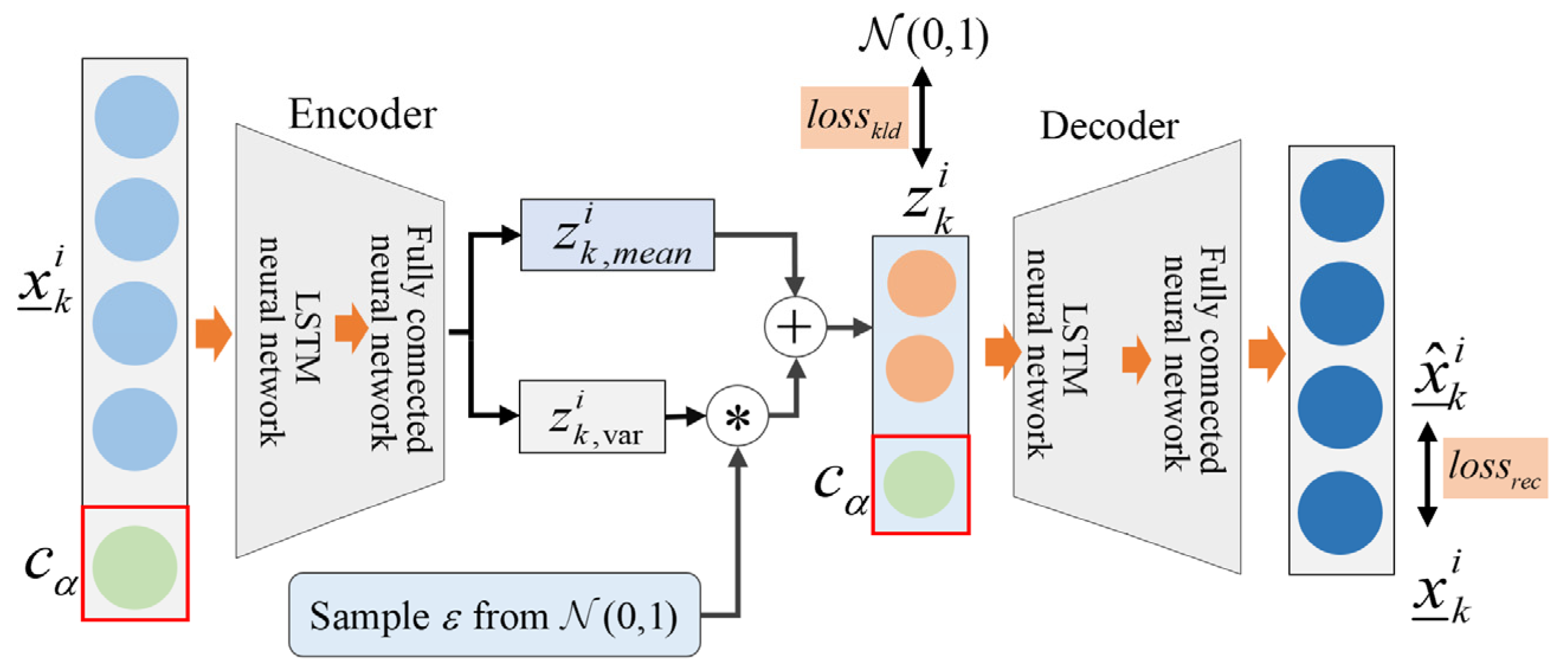
3.2. Structure of CDVAE Model
3.3. Fault Detection and Diagnosis with CDVAE
3.3.1. Fault Detection
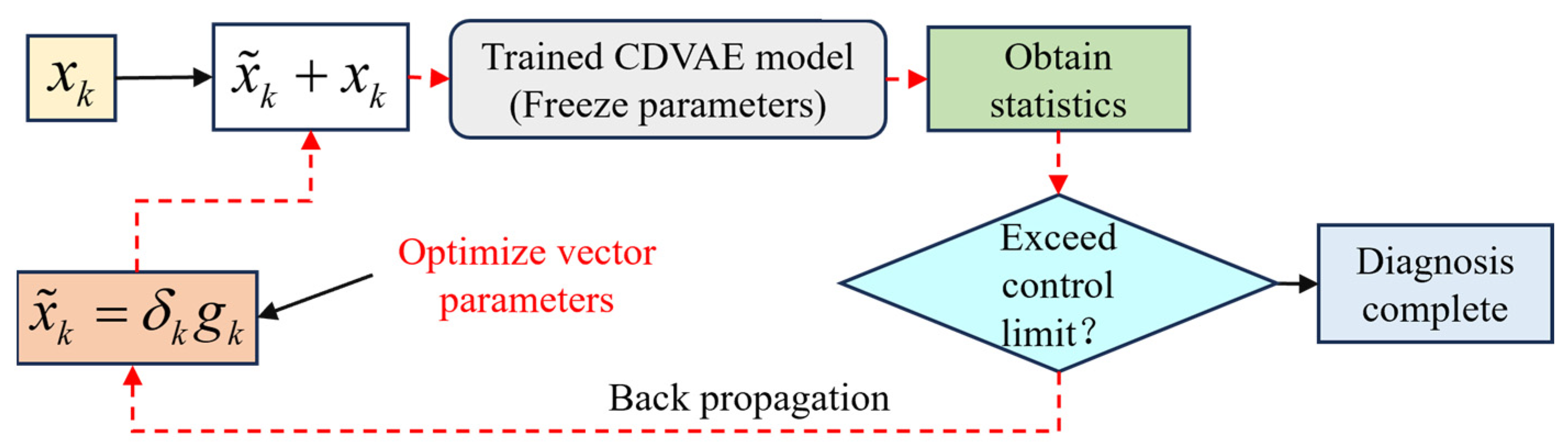
3.3.2. Fault Diagnosis
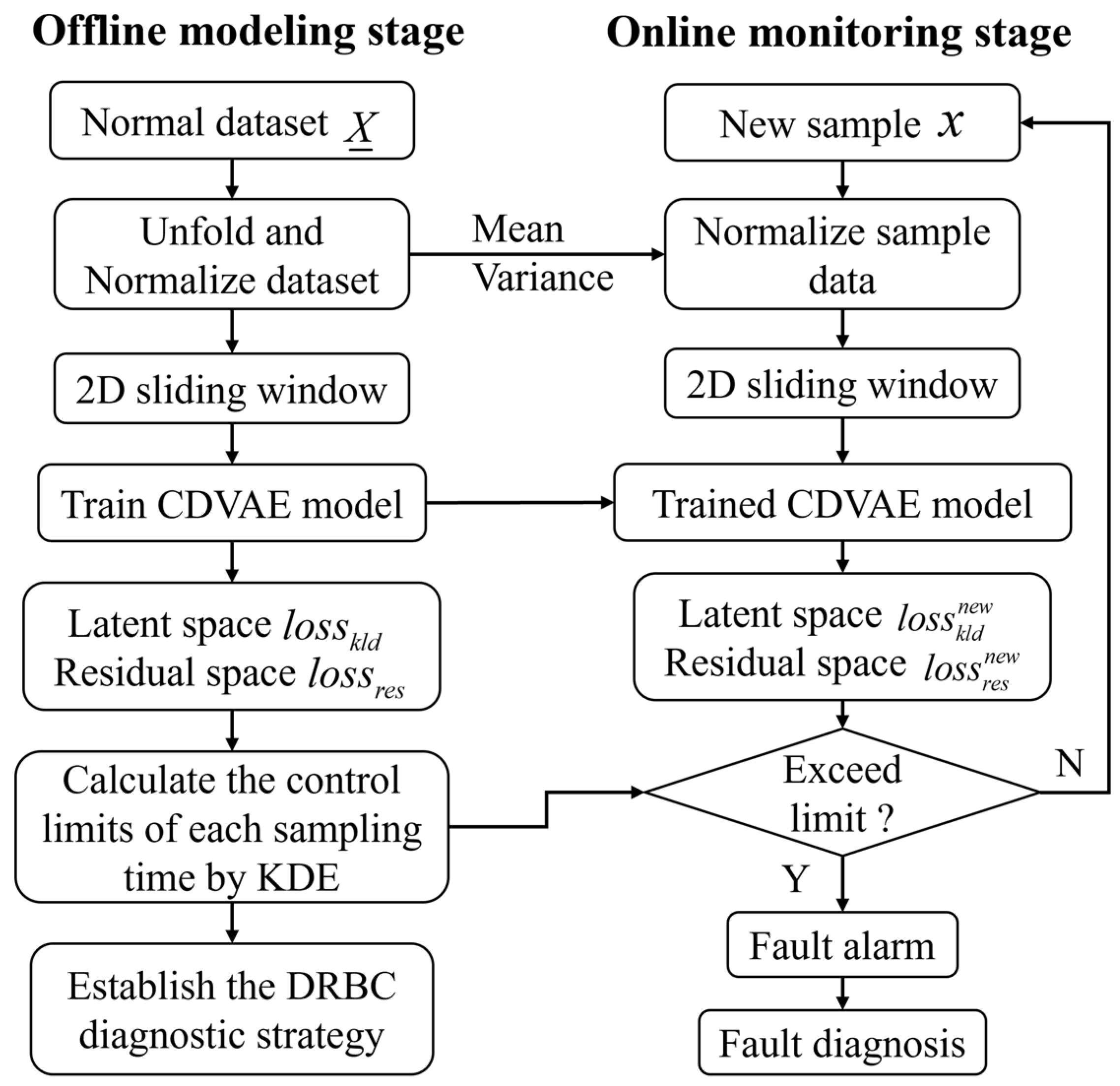
3.4. The Process Monitoring Framework Based on CDVAE
- (a)
- Collect normal historical data;
- (b)
- Batch process data are unfolded and normalized along the batch-wise direction;
- (c)
- Establish a two-dimensional sliding window to obtain an input sequence;
- (d)
- Construct and train the CDVAE model;
- (e)
- Collect statistics corresponding to each sampling moment and use KDE to calculate the control limits of each sampling moment;
- (f)
- Establish the DRBC diagnosis approach based on CDVAE.
- (i)
- Collect real-time production data;
- (ii)
- Standardize sampled data using historical mean and variance;
- (iii)
- Obtain the current sampled input sequence;
- (iv)
- Use the trained CDVAE model to calculate statistics in latent and residual space;
- (v)
- Judge whether the statistics exceed the control limits;
- (vi)
- If the control limit is exceeded, DRBC is used for locating the root cause of the fault.
4. Case Study
4.1. The Penicillin Fermentation Simulation Process
4.1.1. Process Description and Modeling
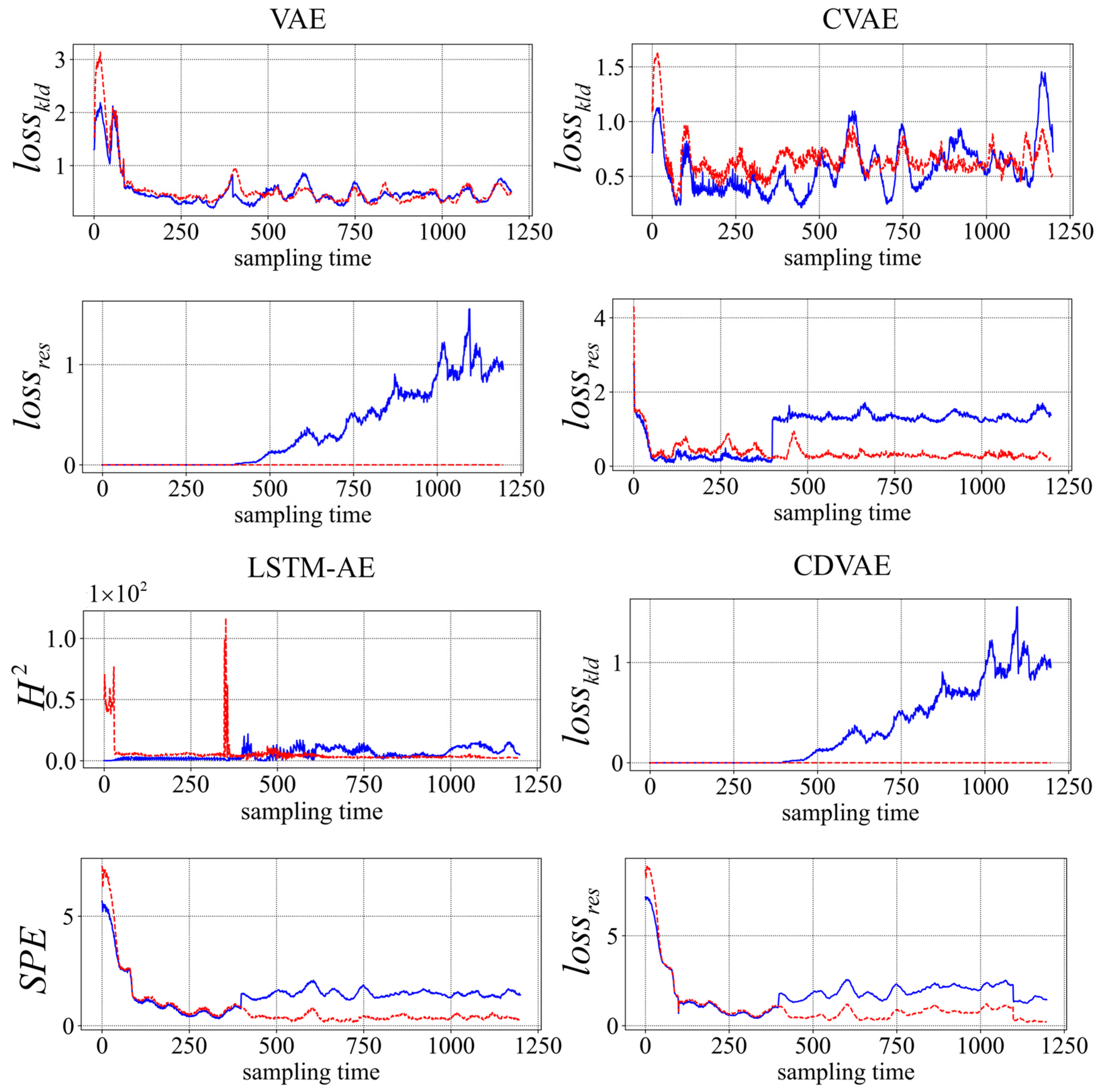
4.1.2. Detection of the Faults
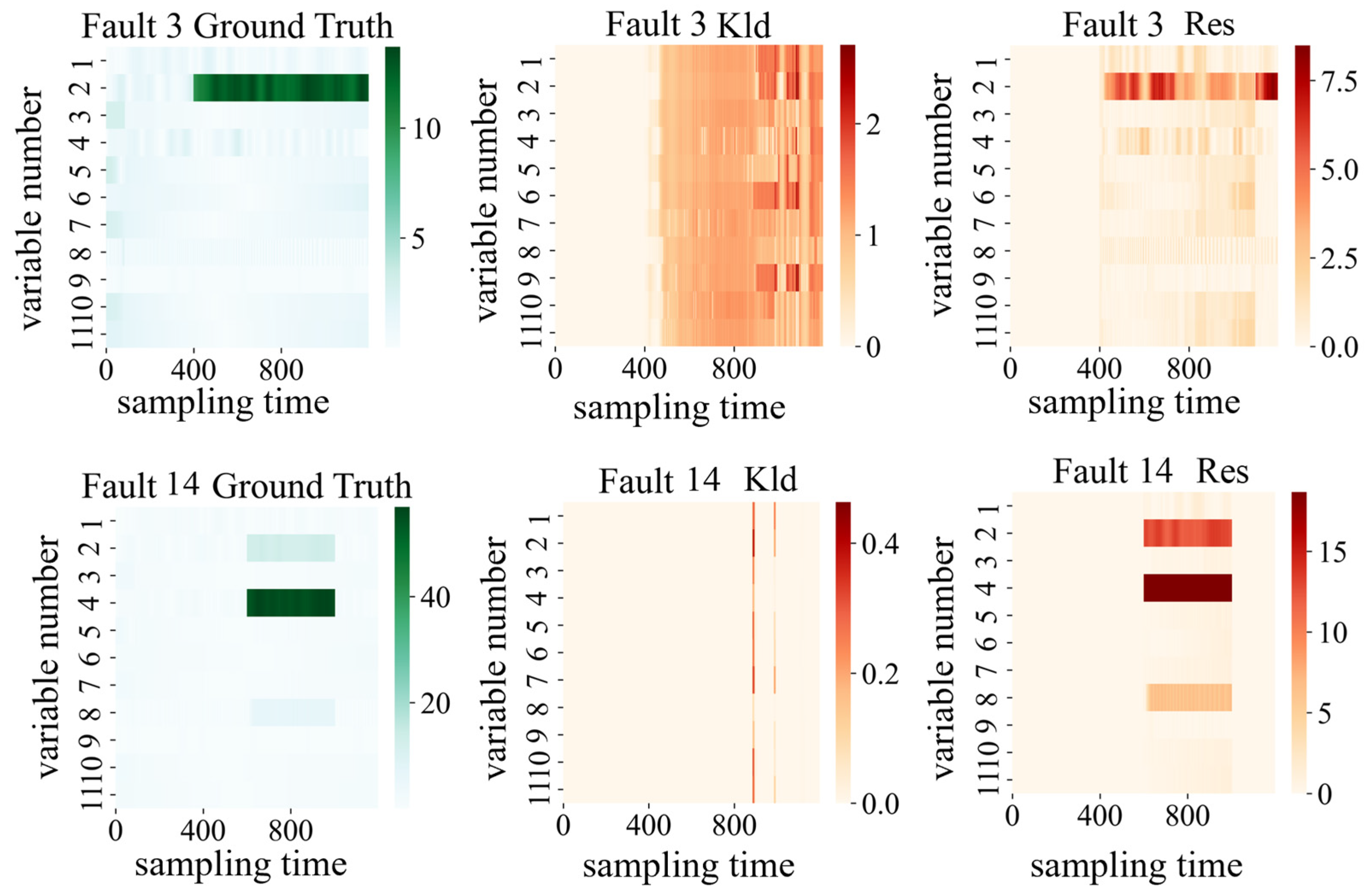
4.1.3. Diagnosis of the Faults
4.2. The Fed-Batch Fermentation Process of L. plantarum
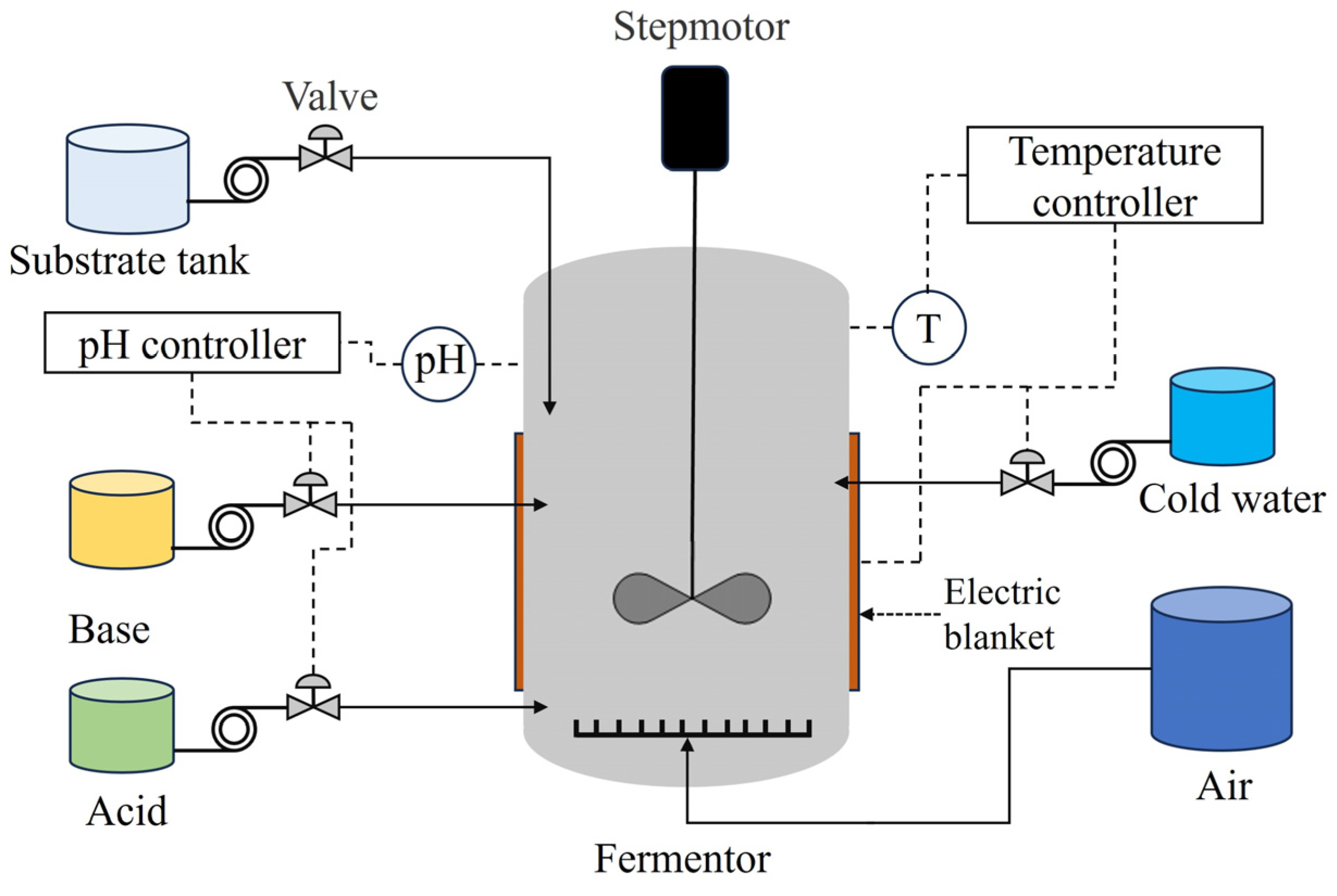
4.2.1. Process Description
4.2.2. Data Collection and Modeling
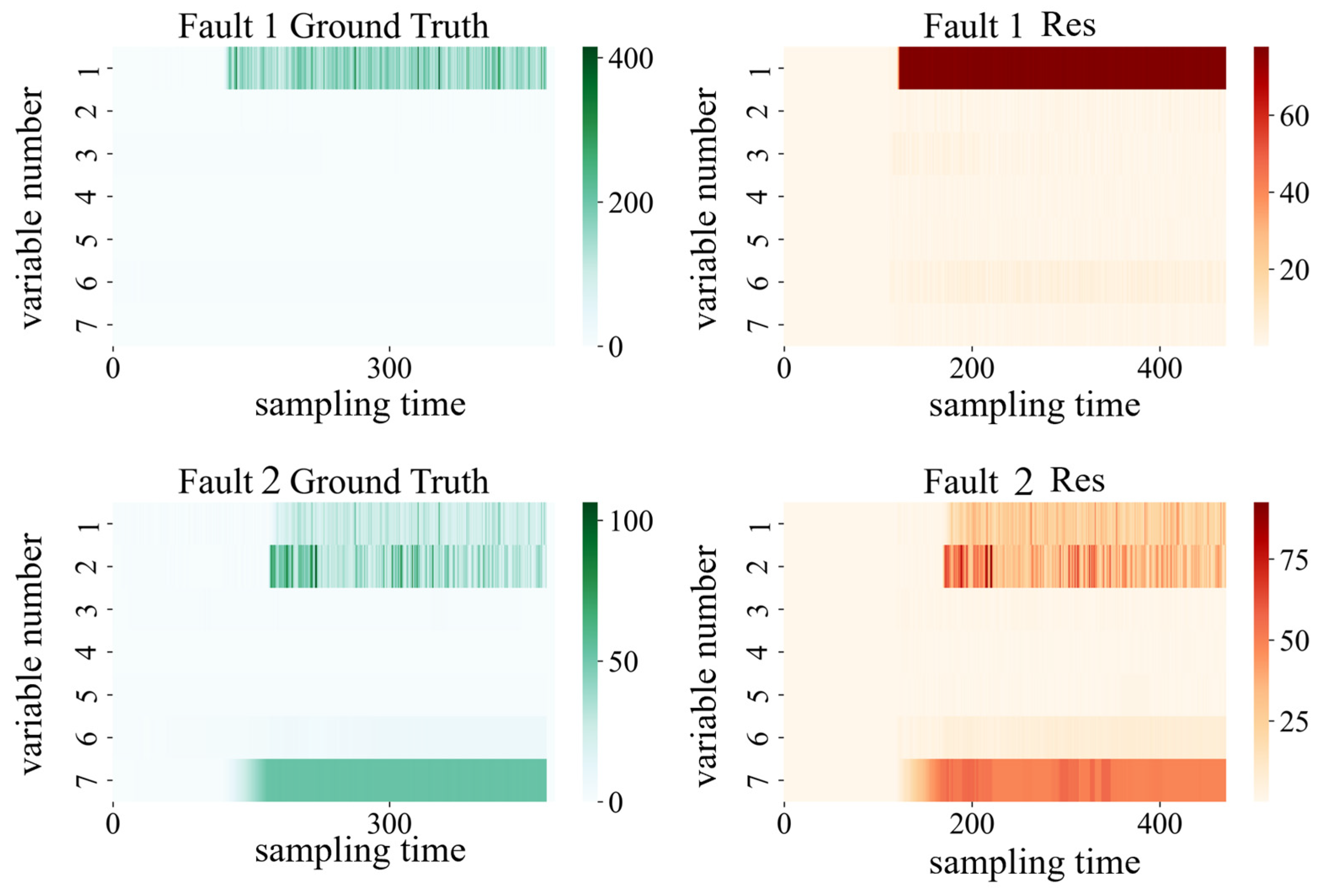
4.2.3. Fault Detection and Diagnosis of Fault 1 and 2
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Statistical process control | SPC |
| Conditional dynamic variational auto-encoder | CDVAE |
| Principle component analysis | PCA |
| Canonical correlation analysis | CCA |
| Partial least square | PLS |
| Variational auto-encoder | VAE |
| Two-dimensional | 2D |
| Kullback–Leibler divergence | KLD |
| Conditional variational auto-encoder | CVAE |
| Long short-term memory | LSTM |
| Kernel density estimation | KDE |
| Deep reconstruction based on contribution | DRBC |
| Fault detection rate | FDR |
| False alarm rate | FAR |
| Long short-term memory auto-encoder Fully connected layer | LSTM-AE FC |
References
- Wang, K.; Rippon, L.; Chen, J.; Song, Z.; Gopaluni, R.B. Data-driven dynamic modeling and online monitoring for multiphase and multimode batch processes with uneven batch durations. Ind. Eng. Chem. Res. 2019, 58, 13628–13641. [Google Scholar] [CrossRef]
- Joshi, T.; Kodamana, H.; Kandath, H.; Kaisare, N. TASAC: A twin-actor reinforcement learning framework with a stochastic policy with an application to batch process control. Ctrl Eng. Pract. 2023, 134, 105462. [Google Scholar] [CrossRef]
- Fransson, M.; Folestad, S. Real-time alignment of batch process data using COW for on-line process monitoring. Chemom. Intell. Lab. Syst. 2006, 84, 56–61. [Google Scholar] [CrossRef]
- Yoo, H.; Kim, B.; Kim, J.W.; Lee, J.H. Reinforcement learning based optimal control of batch processes using Monte-Carlo deep deterministic policy gradient with phase segmentation. Comput. Chem. Eng. 2021, 144, 107133. [Google Scholar] [CrossRef]
- Md Nor, N.; Che Hassan, C.R.; Hussain, M.A. A review of data-driven fault detection and diagnosis methods: Applications in chemical process systems. Rev. Chem. Eng. 2020, 36, 513–553. [Google Scholar] [CrossRef]
- Ren, L.; Meng, Z.; Wang, X.; Zhang, L.; Yang, L.T. A data-driven approach of product quality prediction for complex production systems. IEEE Trans. Ind. Inform. 2020, 17, 6457–6465. [Google Scholar] [CrossRef]
- Qin, S.J. Survey on data-driven industrial process monitoring and diagnosis. Rev. Chem. Eng. 2012, 36, 220–234. [Google Scholar] [CrossRef]
- Chen, J.; Wei-Yann, W. Performance monitoring of MPCA-based control for multivariable batch control processes. J. Taiwan Inst. Chem. Eng. 2010, 41, 465–474. [Google Scholar] [CrossRef]
- Shen, F.; Zheng, J.; Ye, L.; Ma, X. LSTM soft sensor development of batch processes with multivariate trajectory-based ensemble just-in-time learning. IEEE Access 2020, 8, 73855–73864. [Google Scholar] [CrossRef]
- Gu, S.; Chen, J.; Xie, L. Automatic segmentation of batch processes into multi-local state-space models for fault detection. Chem. Eng. Sci. 2023, 267, 118274. [Google Scholar] [CrossRef]
- de Oliveira, B.N.; Valk, M.; Marcondes Filho, D. Fault detection and diagnosis of batch process dynamics using ARMA-based control charts. J. Process Contr. 2022, 111, 46–58. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, Y.; Zhou, D.; Gao, F. Batch process modeling and monitoring with local outlier factor. IEEE Trans. Contr. Syst. Technol. 2018, 27, 1552–1565. [Google Scholar] [CrossRef]
- Chang, P.; Li, R. Process monitoring of batch process based on overcomplete broad learning network. Eng. Appl. Artif. Intell. 2021, 99, 10413. [Google Scholar]
- Jiang, Q.; Gao, F.; Yan, X.; Yi, H. Multiobjective two-dimensional CCA-based monitoring for successive batch processes with industrial injection molding application. IEEE Trans. Ind. Electron. 2018, 66, 3825–3834. [Google Scholar] [CrossRef]
- Liu, Q.; Zhu, Q.; Qin, S.J.; Chai, T. Dynamic concurrent kernel CCA for strip-thickness relevant fault diagnosis of continuous annealing processes. J. Process Control 2018, 67, 12–22. [Google Scholar] [CrossRef]
- Shi, H.; Kim, M.; Liu, H.; Yoo, C. Process modeling based on nonlinear PLS models using a prior knowledge-driven time difference method. J. Taiwan Inst. Chem. Eng. 2016, 69, 93–105. [Google Scholar] [CrossRef]
- Hao, W.; Lu, S.; Lou, Z.; Wang, Y.; Jin, X.; Deprizon, S. A Novel Dynamic Process Monitoring Algorithm: Dynamic Orthonormal Subspace Analysis. Processes 2023, 11, 1935. [Google Scholar] [CrossRef]
- Yu, W.; Zhao, C. Robust monitoring and fault isolation of nonlinear industrial processes using denoising autoencoder and elastic net. IEEE Trans. Control Syst. Technol. 2019, 28, 1083–1091. [Google Scholar] [CrossRef]
- Qin, S.J.; Zheng, Y. Quality-relevant and process-relevant fault monitoring with concurrent projection to latent structures. AIChE J. 2013, 59, 496–504. [Google Scholar] [CrossRef]
- Agarwal, P.; Aghaee, M.; Tamer, M.; Budman, H. A novel unsupervised approach for batch process monitoring using deep learning. Comput. Chem. Eng. 2022, 159, 107694. [Google Scholar] [CrossRef]
- Agarwal, P.; Gonzalez, J.I.; Elkamel, A.; Budman, H. Hierarchical deep LSTM for fault detection and diagnosis for a chemical process. Processes 2022, 10, 2557. [Google Scholar] [CrossRef]
- Lee, S.; Kwak, M.; Tsui, K.L.; Kim, S.B. Process monitoring using variational autoencoder for high-dimensional nonlinear processes. Eng. Appl. Artif. Intell. 2019, 83, 13–27. [Google Scholar] [CrossRef]
- Yan, W.; Guo, P.; Li, Z. Nonlinear and robust statistical process monitoring based on variant autoencoders. Chemometr. Intell. Lab. Syst. 2016, 158, 31–40. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, J.; Ge, Z. Industrial process modeling and fault detection with recurrent Kalman variational autoencoder. In Proceedings of the IEEE 9th Data Driven Control and Learning Systems Conference (DDCLS), Liuzhou, China, 20–22 November 2020. [Google Scholar]
- Zhang, Z.; Jiang, T.; Zhan, C.; Yang, Y. Gaussian feature learning based on variational autoencoder for improving nonlinear process monitoring. J. Process Control 2019, 75, 136–155. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhu, J.; Zhang, S.; Gao, F. Process monitoring using recurrent Kalman variational auto-encoder for general complex dynamic processes. Eng. Appl. Artif. Intell. 2023, 123, 106424. [Google Scholar] [CrossRef]
- Tang, P.; Peng, K.; Dong, J.; Zhang, K.; Jiao, R. A variational autoencoders approach for process monitoring and fault diagnosis. Int. J. Syst. Control Inf. Proc. 2021, 3, 229–245. [Google Scholar] [CrossRef]
- Ren, J.; Ni, D. A batch-wise LSTM-AE decoder network for batch process monitoring. Chem. Eng. Res. Des. 2020, 164, 102–112. [Google Scholar] [CrossRef]
- Qin, S.J.; Li, W. Detection and identification of faulty sensors in dynamic processes. AIChE J. 2001, 47, 1581–1593. [Google Scholar] [CrossRef]
- Zhang, H.; Deng, X.; Zhang, Y.; Hou, C.; Li, C. Dynamic nonlinear batch process fault detection and identification based on two-directional dynamic kernel slow feature analysis. Can. J. Chem. Eng. 2021, 99, 306–333. [Google Scholar] [CrossRef]
- Chang, P.; Ding, C.; Zhao, Q. Fault diagnosis of microbial pharmaceutical fermentation process with non-gaussian and nonlinear coexistence. Chemometr. Intell. Lab. Syst. 2020, 199, 103931. [Google Scholar]
- Jiang, Q.; Yan, S.; Yan, X.; Yi, H.; Gao, F. Data-driven two-dimensional deep correlated representation learning for nonlinear batch process monitoring. IEEE Trans. Ind. Inf. 2020, 16, 2839–2848. [Google Scholar] [CrossRef]
- Wu, S.; Zhang, R. A two-dimensional design of model predictive control for batch processes with two-dimensional (2D) dynamics using extended non-minimal state space structure. J. Process Control 2019, 81, 172–189. [Google Scholar] [CrossRef]
- Yao, H.; Zhao, X.; Li, W.; Hui, Y. Quality-related fault monitoring for multi-phase batch process based on multiway weighted elastic network. Chemometr. Intell. Lab. Syst. 2022, 223, 104528. [Google Scholar] [CrossRef]
- Ye, A.X.; Wang, B.P.; Yang, C.Z. Time sequential phase partition and modeling method for fault detection of batch processes. IEEE Access 2017, 6, 1249–1260. [Google Scholar] [CrossRef]
- Maragathasundari, S.; Eswar, S.K.; Somasundaram, R.S. A study on phases of service and multi-vacation policy in a non-Markovian queuing system. Int. J. Math. Oper. Res. 2022, 21, 444–465. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-encoding variational bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Sohn, K.; Lee, H.; Yan, X. Learning structured output representation using deep conditional generative models. In Proceedings of the Conference and Workshop on NIPS, Montreal, QC, Canada, 7–12 December 2015. [Google Scholar]
- Alcala, C.F.; Qin, S.J. Reconstruction-based contribution for process monitoring. Automatica 2009, 45, 1593–1600. [Google Scholar] [CrossRef]
- Hematillake, D.; Freethy, D.; McGivern, J.; McCready, C.; Agarwal, P.; Budman, H. Design and optimization of a penicillin fed-batch reactor based on a deep learning fault detection and diagnostic model. Ind. Eng. Chem. Res. 2022, 61, 4625–4637. [Google Scholar] [CrossRef]
- Hua, L.; Zhang, C.; Sun, W.; Li, Y.; Xiong, J.; Nazir, M.S. An evolutionary deep learning soft sensor model based on random forest feature selection technique for penicillin fermentation process. ISA Trans. 2023, 136, 139–151. [Google Scholar] [CrossRef]
- Krieger, W.S.; Heras, J.M.; Suarez, C. Lactobacillus plantarum, a new biological tool to control malolactic fermentation: A review and an outlook. Beverages 2020, 6, 2. [Google Scholar] [CrossRef]

| No. | Variables | Unit |
|---|---|---|
| 1 | Aeration rate | L/h |
| 2 | Agitator power | W |
| 3 | Substrate feed rate | L/h |
| 4 | Substrate feed temperature | K |
| 5 | Substrate concentration | g/L |
| 6 | Dissolved oxygen concentration | g/L |
| 7 | Biomass concentration | g/L |
| 8 | Culture volume | L |
| 9 | Carbon dioxide concentration | g/L |
| 10 | pH | / |
| 11 | Fermenter temperature | K |
| Description | Value | |
|---|---|---|
| CDVAE | Encoder network: (, ) → | LSTM (10)→FC (800 + 3)→FC (400)→FC (3) |
| Decoder network: (, ) → | LSTM (3)→FC (400 + 3)→FC (800)→FC (300) | |
| Learning rate | 0.001 | |
| Activate function | “Leaky_Relu” | |
| Training epochs | 500 | |
| Batch size of training samples | 128 |
| No. | Fault Variables | Magnitude | Fault Type | Start Sampling Time | End Sampling Time |
|---|---|---|---|---|---|
| 1 | Agitator power | 2% | Step | 400 | 1200 |
| 2 | Agitator power | 3% | Step | 400 | 1200 |
| 3 | Agitator power | 5% | Step | 400 | 1200 |
| 4 | pH | −2% | Step | 400 | 1200 |
| 5 | pH | −3% | Step | 400 | 1200 |
| 6 | Substrate feed rate | +0.005 L/h | Ramp | 400 | 1200 |
| 7 | Substrate feed rate | −0.01 L/h | Ramp | 400 | 1200 |
| 8 | Aeration rate | −1% | Step | 400 | 1200 |
| 9 | Aeration rate | +2% | Step | 400 | 1200 |
| 10 | Aeration rate | −3% | Step | 400 | 1200 |
| 11 | Aeration rate | +0.02 L/h | Ramp (saturate at 5 L/h) | 400 | 700 |
| 12 | Aeration rate | −0.02 L/h | Ramp (saturate at 5 L/h) | 400 | 700 |
| 13 | Agitator power/pH/ Substrate feed temperature | +5%/+5%/+3% | Step | 600 | 1000 |
| 14 | Agitator power/pH/Substrate feed temperature | +5%/−5%/−3% | Step | 600 | 1000 |
| No. | VAE | CVAE | LSTM-AE | CDVAE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| losskld | lossres | FAR | losskld | lossres | FAR | H2 | SPE | FAR | losskld | lossres | FAR | |
| 1 | 14.0 | 87.3 | 1.5 | 38.5 | 79.2 | 1.1 | 25.6 | 87.8 | 0.42 | 94.3 | 94.7 | 0.12 |
| 2 | 20.3 | 98.5 | 1.7 | 46.5 | 96.3 | 1.2 | 42.3 | 98.3 | 0.35 | 100 | 100 | 0.13 |
| 3 | 41.3 | 100 | 1.6 | 61.4 | 100 | 0.87 | 83.1 | 100 | 0.25 | 100 | 100 | 0.07 |
| 4 | 7.0 | 9.6 | 0.9 | 11.8 | 12.1 | 0.75 | 14.5 | 24.8 | 0.12 | 9.3 | 54.4 | 0.15 |
| 5 | 9.3 | 48.8 | 1.5 | 7.8 | 46.3 | 0.75 | 23.1 | 73.3 | 0.02 | 16.4 | 90.1 | 0.25 |
| 6 | 6.1 | 4.4 | 1.7 | 27.1 | 11.0 | 0.85 | 3.7 | 49.6 | 0.24 | 55.8 | 59.1 | 0.00 |
| 7 | 13.4 | 17.6 | 2.1 | 9.0 | 16.5 | 0.75 | 49.6 | 18.4 | 0.48 | 52.6 | 17.5 | 0.00 |
| 8 | 28.5 | 31.1 | 2.0 | 48.1 | 40.7 | 0.72 | 53.6 | 66.5 | 0.25 | 67.2 | 89.6 | 0.70 |
| 9 | 78.6 | 89.7 | 1.7 | 32.9 | 96.6 | 0.85 | 84.6 | 97.5 | 1.12 | 87.4 | 100 | 0.51 |
| 10 | 93.5 | 97.3 | 2.1 | 72.4 | 100 | 1.35 | 96.4 | 100 | 0.89 | 100 | 100 | 0.30 |
| 11 | 88.7 | 97.67 | 1.8 | 87.3 | 96.3 | 1.23 | 96.3 | 96.6 | 0.25 | 91.7 | 98.7 | 0.00 |
| 12 | 84.1 | 98.34 | 1.7 | 95.7 | 95.7 | 1.24 | 95.0 | 98 | 0.12 | 99.0 | 100 | 0.00 |
| 13 | 95.5 | 100 | 2.3 | 100 | 100 | 1.34 | 95.3 | 100 | 1.12 | 100 | 100 | 0.80 |
| 14 | 100.0 | 100 | 1.8 | 100 | 100 | 1.76 | 95.3 | 100 | 0.85 | 100 | 100 | 0.30 |
| Average | 48.6 | 70.7 | 1.7 | 52.7 | 70.8 | 1.0 | 61.0 | 79.2 | 0.46 | 73.84 | 86.01 | 0.23 |
| No. | Variable | Unit |
|---|---|---|
| 1 | Fermenter temperature | K |
| 2 | pH | / |
| 3 | Dissolved oxygen | / |
| 4 | Agitation rate | r/min |
| 5 | Acid supplements | mL |
| 6 | Base supplements | mL |
| 7 | Feed supplements | mL |
| No. | Fault Variables | Magnitude | Fault Type | Start Sampling Time | End Sampling Time |
|---|---|---|---|---|---|
| 1 | Fermentation temperature | +3 K | Step | 120 | 480 |
| 2 | Fermentation temperature/ pH/Feed supplement | +0.5 K/ +0.3/50 min Delay | Step | 120 | 480 |
| Description | Value | |
|---|---|---|
| CDVAE | Encoder network: (, ) → | LSTM (6)→FC (400 + 3)→FC (200)→FC (3) |
| Decoder network: (, ) → | LSTM (3)→FC (200 + 3)→FC (400)→FC (192) | |
| Learning rate | 0.001 | |
| Activate function | “Leaky_Relu” | |
| Training epochs | 1000 | |
| Batch size of training samples | 128 |
| No. | VAE | CVAE | LSTM-AE | CDVAE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| losskld | lossres | FAR | losskld | lossres | FAR | H2 | SPE | FAR | losskld | lossres | FAR | |
| 1 | 99.1 | 97.2 | 3.8 | 97.5 | 98.8 | 3.0 | 26.3 | 98.3 | 0.6 | 99.7 | 99.7 | 0.0 |
| 2 | 84.1 | 87.5 | 5.1 | 83.6 | 91.6 | 3.5 | 51.1 | 97.5 | 0.5 | 100 | 100 | 0.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Liu, Z.; Lou, X.; Gao, F.; Zhang, Z. Time-Specific Thresholds for Batch Process Monitoring: A Study Based on Two-Dimensional Conditional Variational Auto-Encoder. Processes 2024, 12, 682. https://doi.org/10.3390/pr12040682
Zhu J, Liu Z, Lou X, Gao F, Zhang Z. Time-Specific Thresholds for Batch Process Monitoring: A Study Based on Two-Dimensional Conditional Variational Auto-Encoder. Processes. 2024; 12(4):682. https://doi.org/10.3390/pr12040682
Chicago/Turabian StyleZhu, Jinlin, Zhong Liu, Xuyang Lou, Furong Gao, and Zheng Zhang. 2024. "Time-Specific Thresholds for Batch Process Monitoring: A Study Based on Two-Dimensional Conditional Variational Auto-Encoder" Processes 12, no. 4: 682. https://doi.org/10.3390/pr12040682
APA StyleZhu, J., Liu, Z., Lou, X., Gao, F., & Zhang, Z. (2024). Time-Specific Thresholds for Batch Process Monitoring: A Study Based on Two-Dimensional Conditional Variational Auto-Encoder. Processes, 12(4), 682. https://doi.org/10.3390/pr12040682







