Fully Coupled CFD–DEM Simulation of Oil Well Hole Cleaning: Effect of Mud Hydrodynamics on Cuttings Transport
Abstract
:1. Introduction
2. Model Description
2.1. Fluid Phase Modelling
2.2. Solid Phase Modelling
2.2.1. Solid Phase Motion
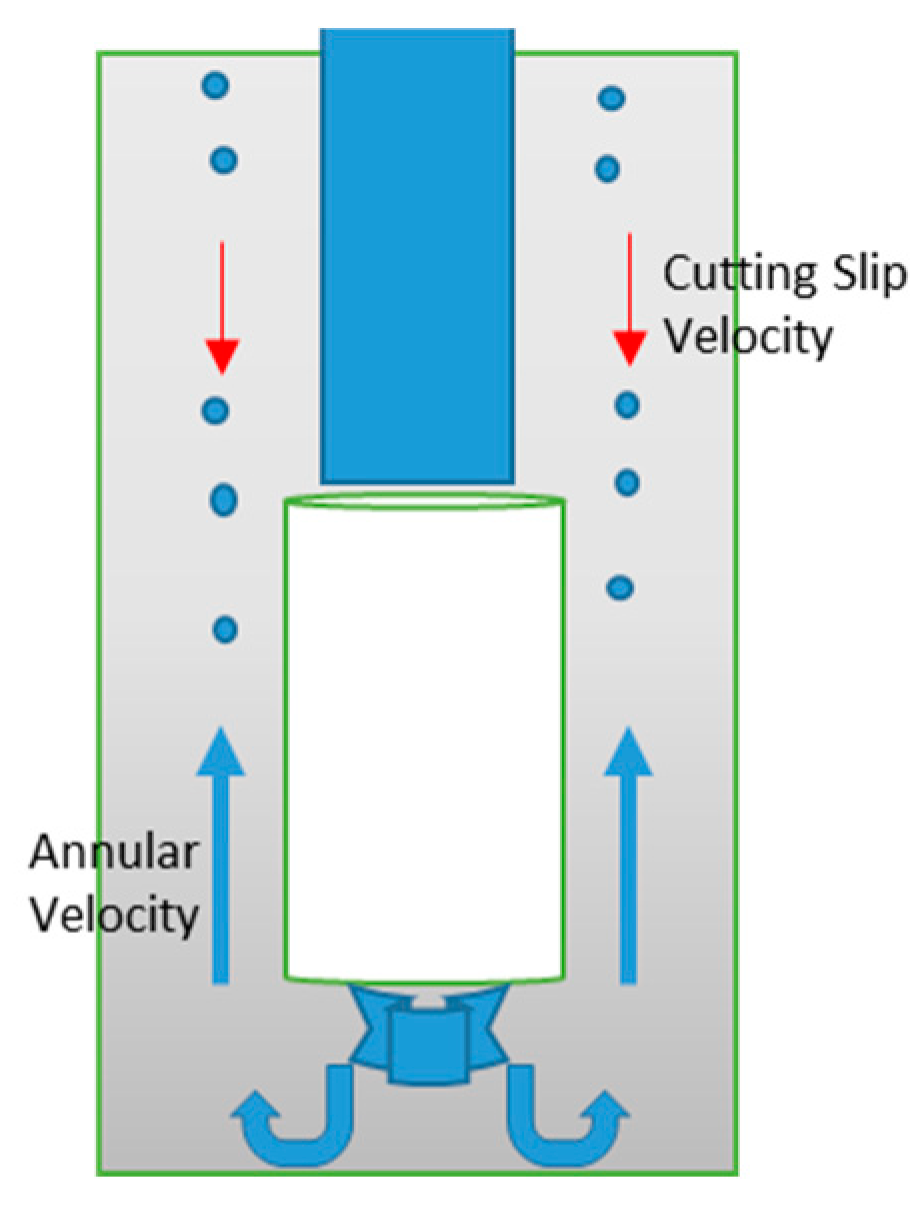
2.2.2. Cuttings Slip Velocity
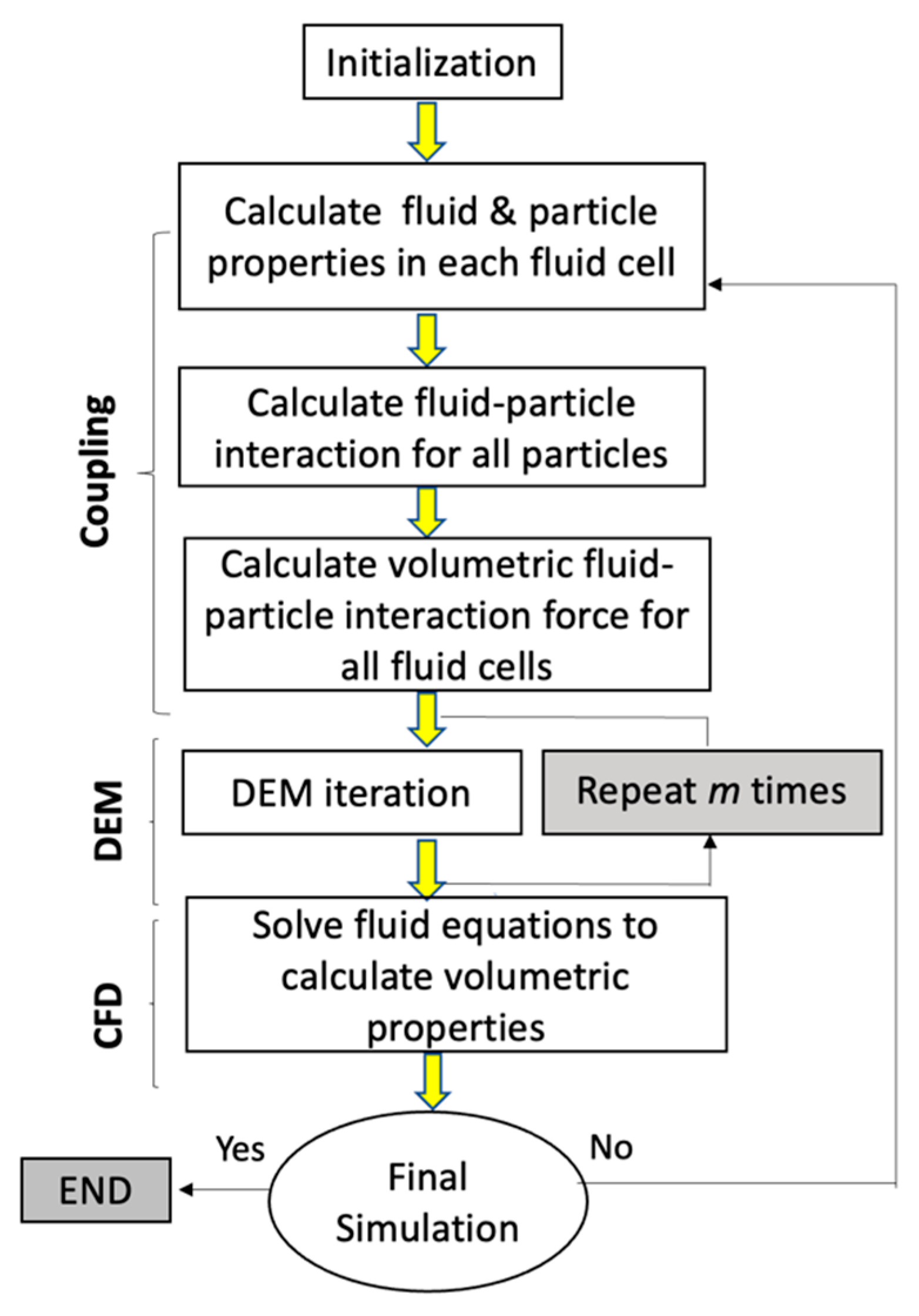
2.3. CFD–DEM Coupling
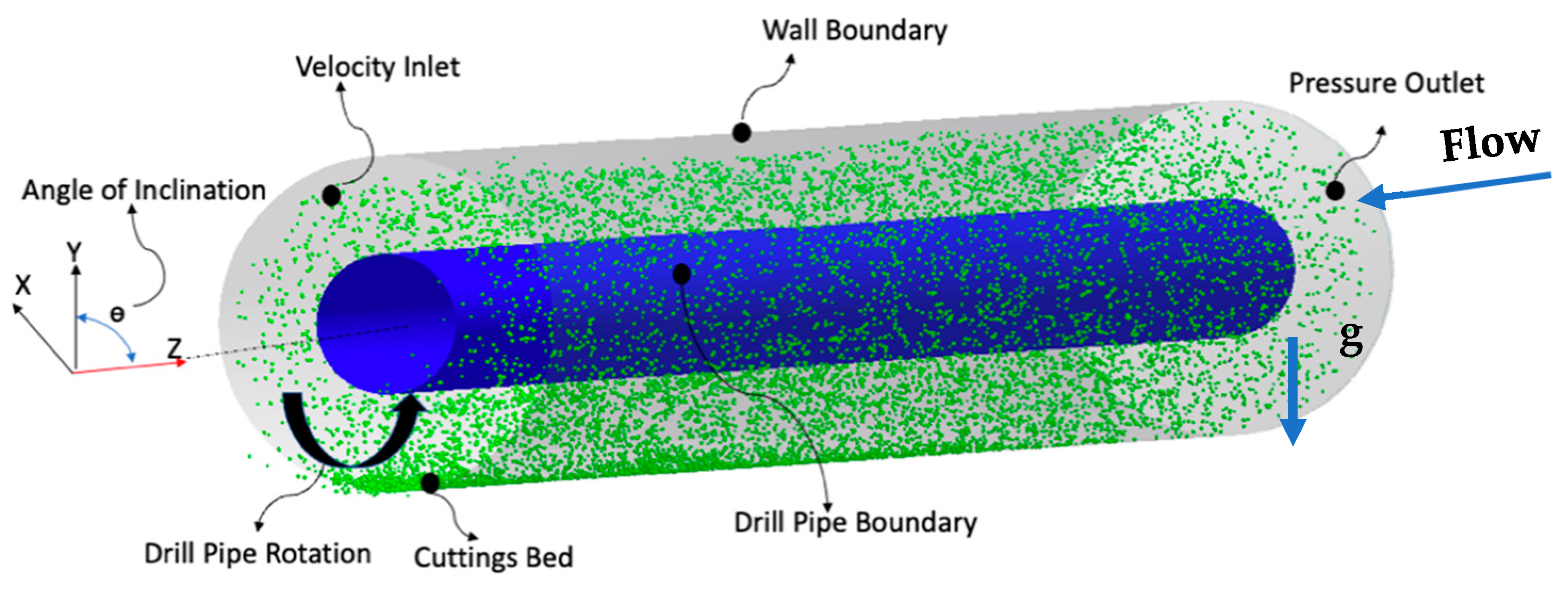
2.4. Model Geometry and Boundary Conditions
2.5. Relative Cuttings Concentration
2.6. Mesh Information
2.7. Mud Properties
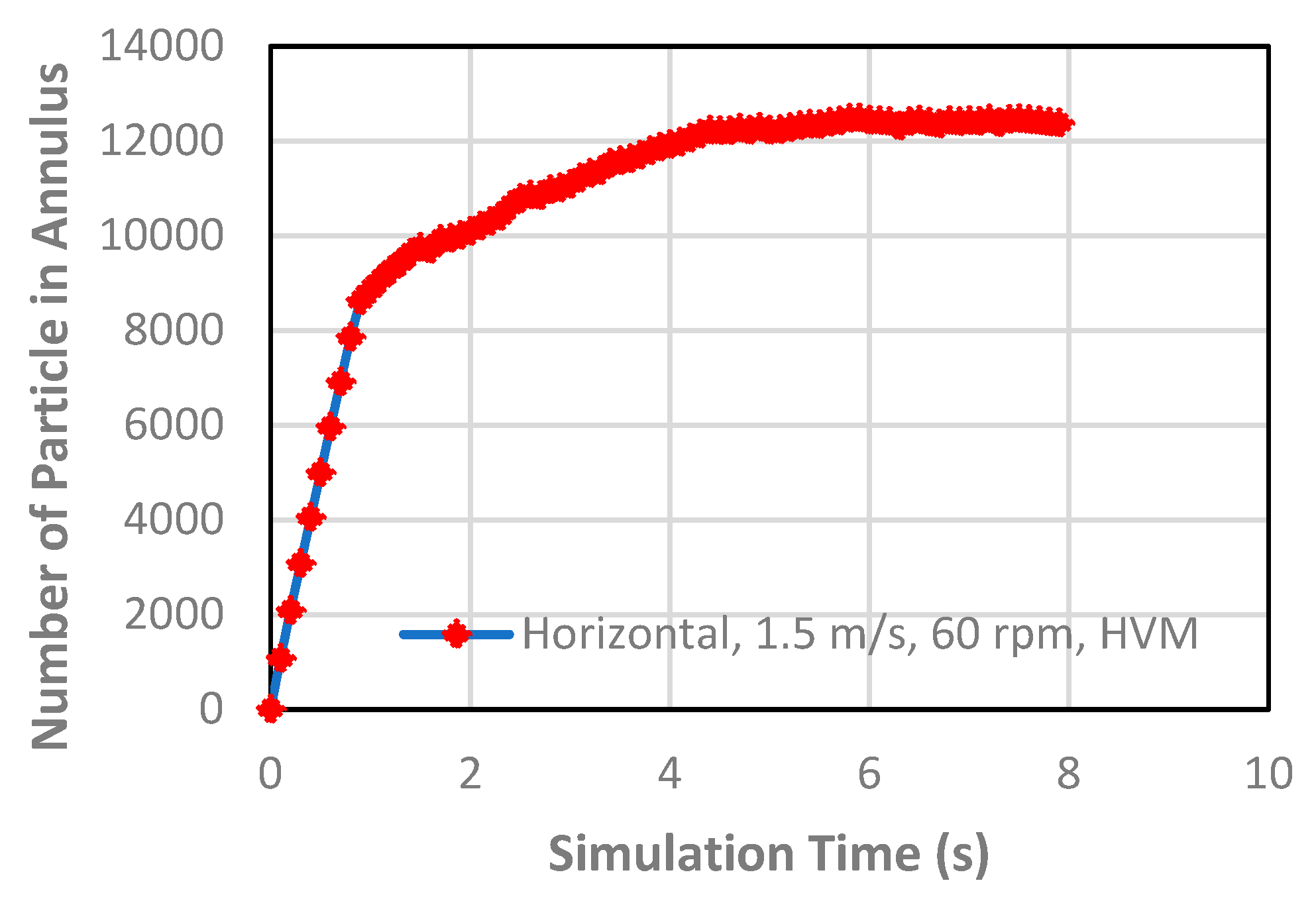
2.8. Steady State Condition
3. Results and Discussion
3.1. Effects of Mud Rheology
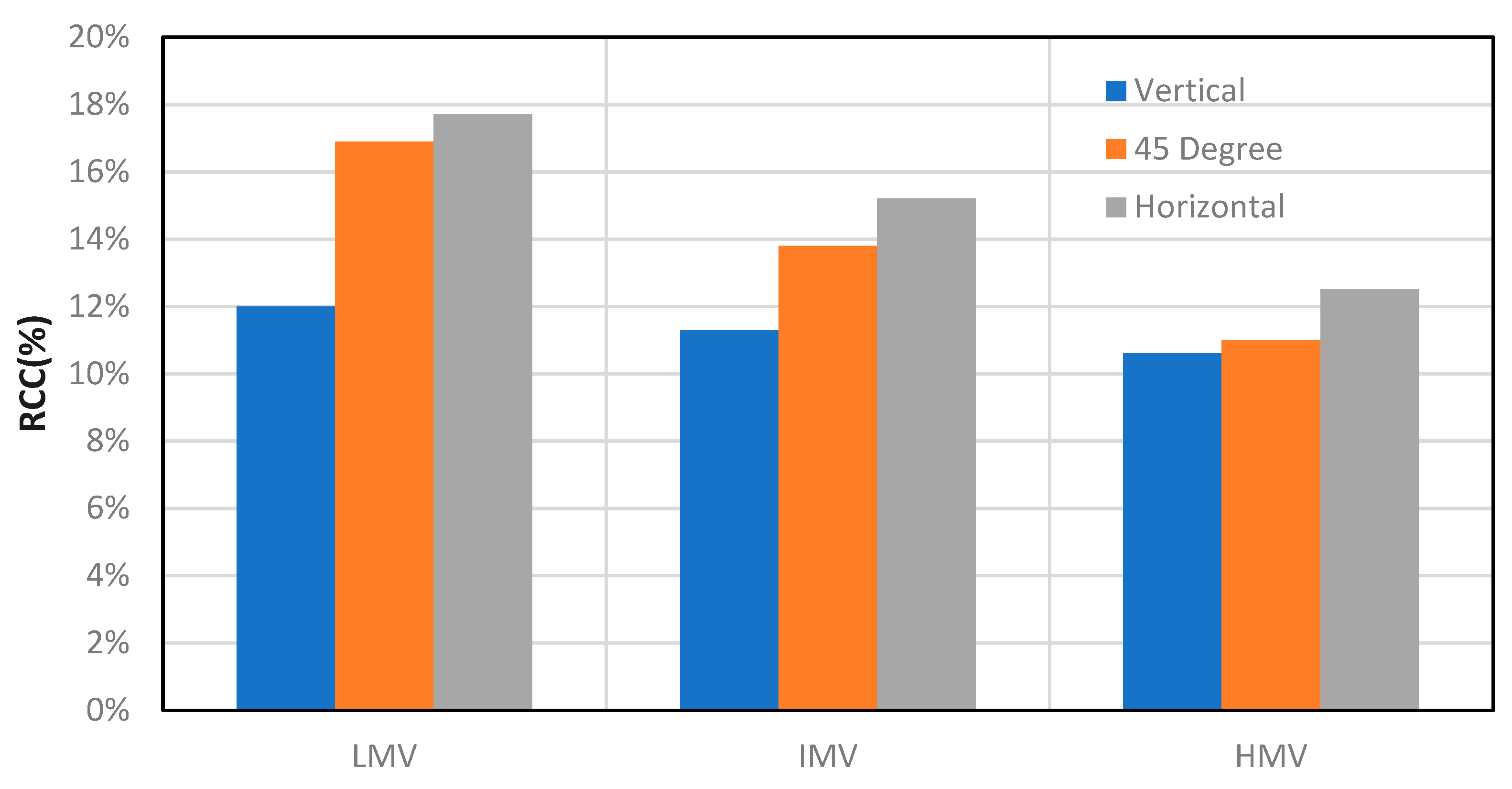
3.2. Effect of Cuttings Size on RCC
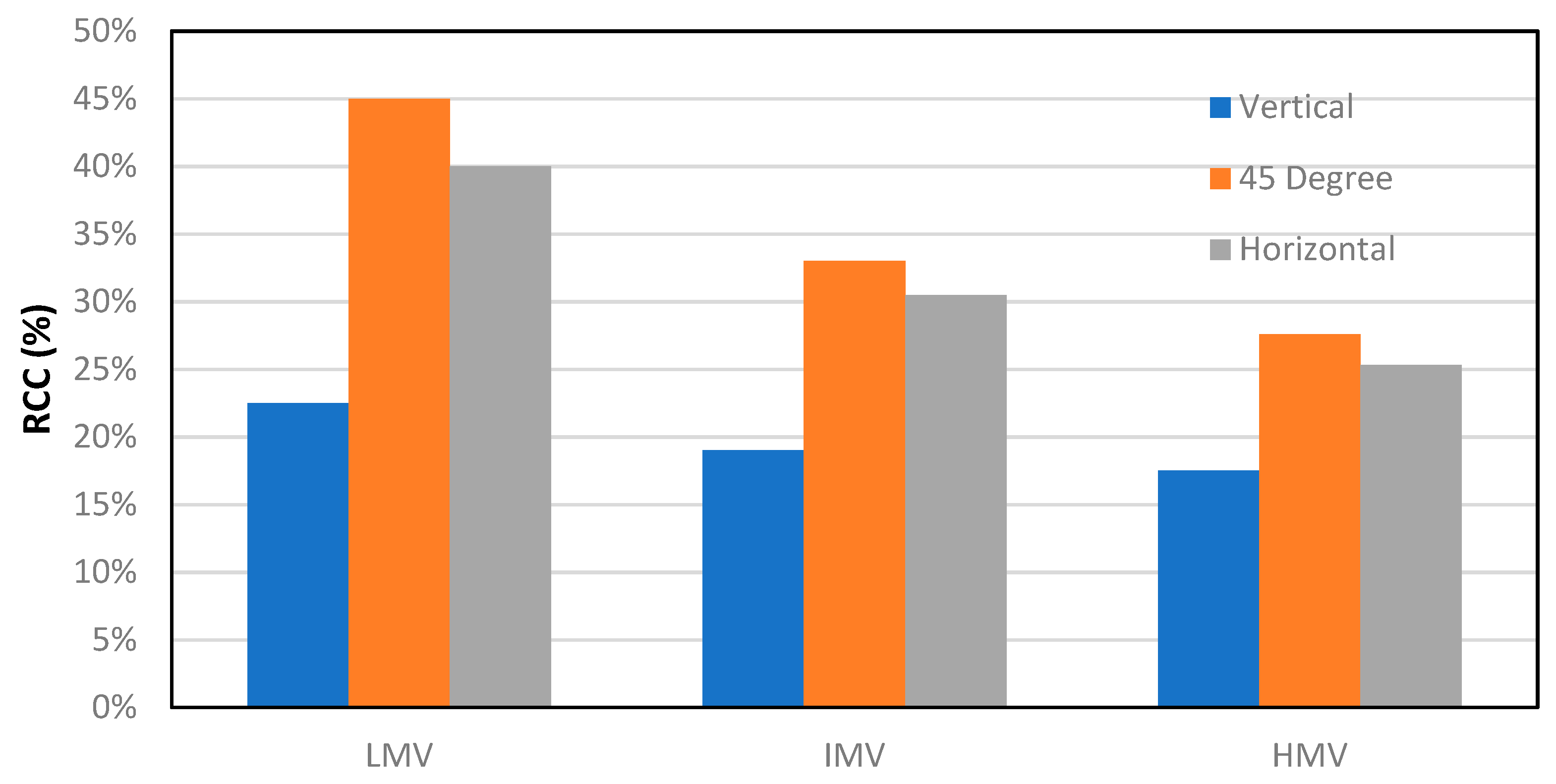
3.3. Effect of Drill Pipe Rotation
3.4. Discussion
4. Conclusions
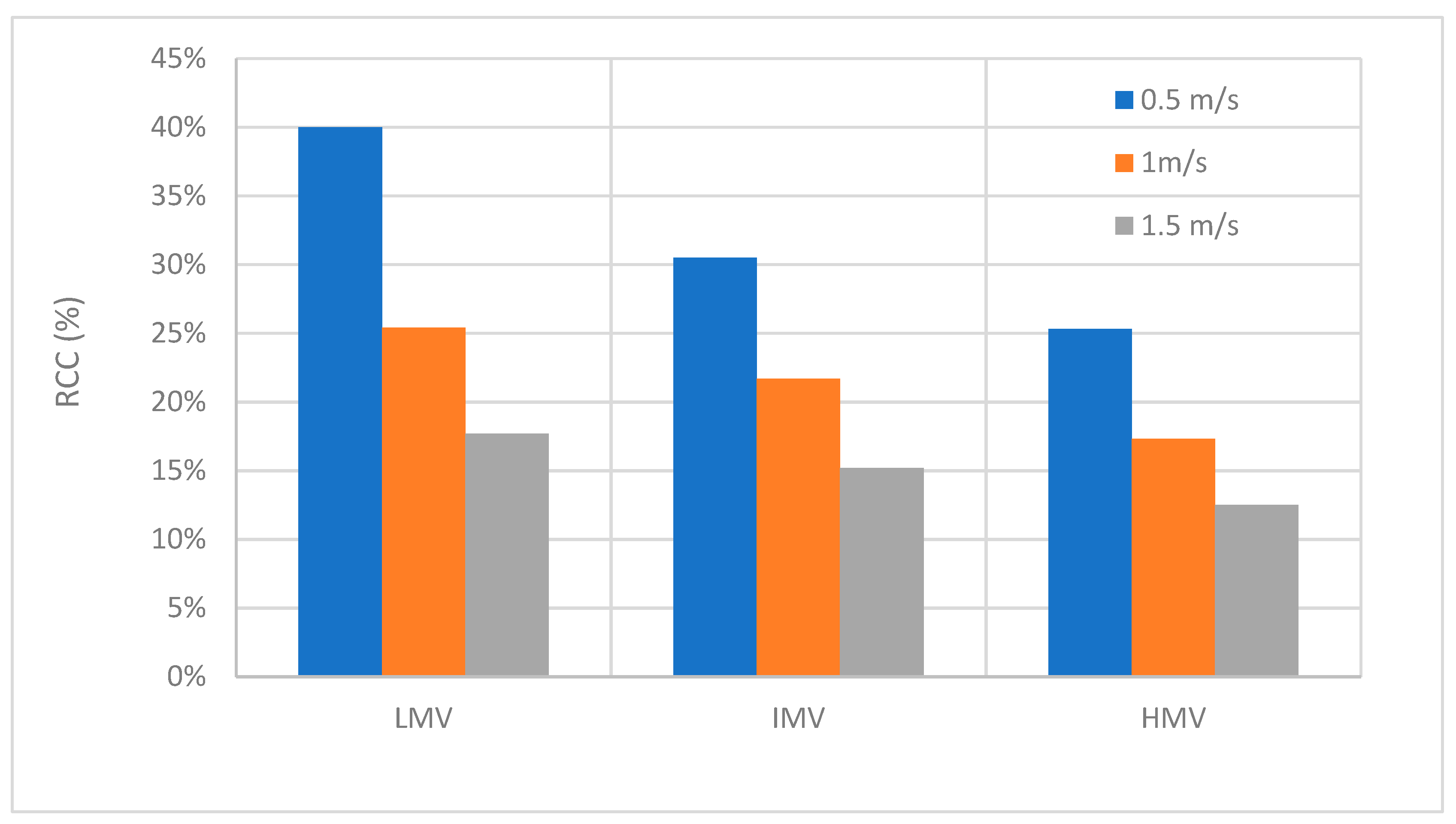
- Mud annular velocity has a dominant effect on RCC. Lower RCC and better cleaning performance can be achieved by increasing mud velocity to its limiting value for all ranges of well inclinations.
- At all well inclination angles, the RCC is lowest at high mud viscosity; however, the effect of mud viscosity is more pronounced at lower annular mud velocities. By increasing the velocity, the impact of mud viscosity on RCC is reduced.
- RCC increases from vertical to horizontal wells at higher mud velocities, but at low mud velocity (0.5 m/s), the 45-degree well has the highest RCC.
- The impact of drill pipe rotation is more pronounced for lower values of annular mud velocity. Increasing drill pipe rotation from zero to 120 rpm improves the cleaning efficiency in deviated annuli at lower velocities, while it has very little effect for the vertical annulus.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zeidler, U.H. An experimental analysis of the transport of drilled particles. Soc. Pet. Eng. J. 1972, 12, 39–48. [Google Scholar] [CrossRef]
- Tomren, P.H.; Lyoho, A.W.; Azar, J.J. Experimental study of cuttings transport in directional wells. SPE Drill. Eng. 1986, 1, 43–56. [Google Scholar] [CrossRef]
- Brown, N.P.; Bern, P.A.; Weaver, A. Cleaning deviated holes: New experimental and theoretical studies. In Proceedings of the SPE/IADC Drilling Conference, New Orleans, LA, USA, 28 February–3 March 1989. [Google Scholar]
- Peden, J.M.; Ford, J.A.; Oyeneyin, M.B. Comprehensive experimental investigation of drilled cuttings transport in inclined wells including the effects of rotation and eccentricity. In Proceedings of the European Petroleum Conference, The Hague, The Netherlands, 21–24 October 1990. [Google Scholar]
- Sifferman, T.R.; Becker, T.E. Hole cleaning in full-scale inclined wellbores. SPE Drill. Eng. 1992, 7, 115–120. [Google Scholar] [CrossRef]
- Bassal, A.A. The Effect of Drillpipe Rotation on Cuttings Transport in Inclined Wellbores. Ph.D. Thesis, University of Tulsa, Tulsa, OK, USA, 1995. [Google Scholar]
- Sanchez, R.A.; Azar, J.J.; Bassal, A.A.; Martins, A.L. The effect of drillpipe rotation on hole cleaning during directional well drilling. In Proceedings of the SPE/IADC Drilling Conference, Amsterdam, The Netherlands, 4–6 March 1997. [Google Scholar]
- Yu, M.; Takach, N.E.; Nakamura, D.R.; Shariff, M.M. An experimental study of hole cleaning under simulated downhole conditions. In Proceedings of the SPE Annual Technical Conference and Exhibition, Anaheim, CA, USA, 11–14 November 2007. [Google Scholar]
- Bilgesu, H.I.; Ali, M.W.; Aminian, K.; Ameri, S. Computational Fluid Dynamics (CFD) as a tool to study cutting transport in wellbores. In Proceedings of the SPE Eastern Regional Meeting, Lexington, KY, USA, 23–26 October 2002. [Google Scholar]
- Bilgesu, H.I.; Mishra, N.; Ameri, S. Understanding the effect of drilling parameters on hole cleaning in horizontal and deviated wellbores using computational fluid dynamics. In Proceedings of the Eastern Regional Meeting, Lexington, KY, USA, 17–19 October 2007. [Google Scholar]
- Wang, Z.-M.; Guo, X.-L.; Li, M.; Hong, Y.-K. Effect of drillpipe rotation on borehole cleaning for extended reach well. J. Hydrodyn. 2009, 21, 366–372. [Google Scholar] [CrossRef]
- Yilmaz, D. Discrete Phase Simulations of Drilled Cuttings Transport Process in Highly Deviated Wells. Master’s Thesis, Louisiana State University, Baton Rouge, LA, USA, 2013. [Google Scholar]
- Rooki, R.; Ardejani, F.D.; Moradzadeh, A.; Norouzi, M. Simulation of cuttings transport with foam in deviated wellbores using computational fluid dynamics. J. Pet. Explor. Prod. Technol. 2014, 4, 263–273. [Google Scholar] [CrossRef]
- Mohammadzadeh, K.; Hashemabadi, S.; Akbari, S. CFD simulation of viscosity modifier effect on cutting transport by oil based drilling fluid in wellbore. J. Nat. Gas Sci. Eng. 2016, 29, 355–364. [Google Scholar] [CrossRef]
- Amanna, B.; Movaghar, M.R.K. Cuttings transport behavior in directional drilling using computational fluid dynamics (CFD). J. Nat. Gas Sci. Eng. 2016, 34, 670–679. [Google Scholar] [CrossRef]
- Tong, T.; Ozbayoglu, E.; Liu, Y. A Transient Solids Transport Model for Solids Removal Evaluation in Coiled-Tubing Drilling. SPE J. 2021, 26, 2498–2515. [Google Scholar] [CrossRef]
- Akhshik, S.; Behzad, M.; Rajabi, M. CFD–DEM approach to investigate the effect of drill pipe rotation on cuttings transport behavior. J. Pet. Sci. Eng. 2015, 127, 229–244. [Google Scholar] [CrossRef]
- Akhshik, S.; Behzad, M.; Rajabi, M. CFD-DEM simulation of the hole cleaning process in a deviated well drilling: The effects of particle shape. Particuology 2016, 25, 72–82. [Google Scholar] [CrossRef]
- Akhshik, S.; Behzad, M.; Rajabi, M. On the particle–particle contact effects on the hole cleaning process via a CFD–DEM model. Part. Sci. Technol. 2016, 34, 736–743. [Google Scholar] [CrossRef]
- Akhshik, S.; Rajabi, M. CFD-DEM modeling of cuttings transport in underbalanced drilling considering aerated mud effects and downhole conditions. J. Pet. Sci. Eng. 2018, 160, 229–246. [Google Scholar] [CrossRef]
- FLUENT Inc. Chapter 10. Modeling Turbulence; FLUENT Inc.: Lebanon, NH, USA, 2001; pp. 1–102. [Google Scholar]
- Saasen, A.; Ytrehus, J.D. Viscosity Models for Drilling Fluids—Herschel-Bulkley Parameters and Their Use. Energies 2020, 13, 5271. [Google Scholar] [CrossRef]
- Sommerfeld, M. Theoretical and experimental modelling of particulate flows. Lect. Ser. 2000, 6, 3–7. [Google Scholar]
- Kuang, S.B.; Yu, A.B.; Zou, Z.S. Computational study of flow regimes in vertical pneumatic conveying. Ind. Eng. Chem. Res. 2009, 48, 6846–6858. [Google Scholar] [CrossRef]
- Rowe, P.N. Drag forces in a hydraulic model of a fluidized bed-part I. Trans. Inst. Chem. Eng. 1961, 39, 43–54. [Google Scholar]
- Zeidler, H.U. An experimental analysis of the transport of drilled particles in an annulus. J. Pet. Technol. 1970, 22, 1055. [Google Scholar]
- Schetz, J.A.; Fuhs, A.E. Fundamentals of Fluid Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 1999. [Google Scholar]
- Sifferman, T.R.; Myers, G.M.; Haden, E.L.; Wahl, H.A. Drill cutting transport in full scale vertical annuli. J. Pet. Technol. 1974, 26, 1295–1302. [Google Scholar] [CrossRef]
- Okrajni, S.; Azar, J.J. The effects of mud rheology on annular hole cleaning in directional wells. SPE Drill. Eng. 1986, 1, 297–308. [Google Scholar] [CrossRef]







| Parameter | Experimental Work of Tomren et al. (1986) [2] | Simulation Data in This Work | Units |
|---|---|---|---|
| Drill string length | 12 | 1.5 | m |
| Angle of inclination | 0, 20, 40, 60, 80 | 0, 45, 90 | deg |
| Wellbore (hole) diameter | 127 | 120 (4.75′′) | mm |
| Drill pipe diameter | 48.26 | 50 | mm |
| Drill pipe rotation (rpm) | 0, 50 | 60, 120 | rpm |
| Eccentricity ratio | 0.5 | 0 | - |
| Fluid behaviour index (n) | 0.65 | 0.65 | - |
| Consistency index (k) | 0.28 | 0.28 | Pa.sn |
| Fluid inlet velocity | 0.58, 0.72, 0.87, 1.1 | 0.5, 1, 1.5 | m/s |
| Fluid density | 1018 | 1018 | Kg/m3 |
| Particle density | 2619 | 2600 | Kg/m3 |
| Particle shear modulus | 10 | MPa | |
| Particle coefficient of restitution | 0.5 | - | |
| Particle coefficient of sliding friction | 0.5 | - | |
| Particle coefficient of rolling friction | 0.05 | - | |
| Cutting diameter (average) | 6.35 | 0.8–1.1 (1), 1.3–1.5 (1.4) | mm |
| Drilling Fluid | Low-Viscosity Mud (LVM) | Intermediate-Viscosity Mud (IVM) | High-Viscosity Mud (HVM) |
|---|---|---|---|
| Apparent Viscosity (Pa·s) | 0.004 | 0.013 | 0.028 |
| Plastic Viscosity (Pa·s) | 0.003 | 0.009 | 0.019 |
| Yield Point (Pa) | 0.5 | 4 | 8 |
| Mud Re | 9000–26,000 | 3000–8000 | 4000–12,000 |
| Particle Re | 1 < 89–143 < 1000 | 1 < 13–18 < 1000 | 1 < 3–6 < 1000 |
| Slip Velocity (m/s) | 0.25–0.4 | 0.12–0.16 | 0.05–0.12 |
| Particle Stokes Number | 1–1.5 | 0.15–0.45 | 0.07–0.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zakeri, A.; Alizadeh Behjani, M.; Hassanpour, A. Fully Coupled CFD–DEM Simulation of Oil Well Hole Cleaning: Effect of Mud Hydrodynamics on Cuttings Transport. Processes 2024, 12, 784. https://doi.org/10.3390/pr12040784
Zakeri A, Alizadeh Behjani M, Hassanpour A. Fully Coupled CFD–DEM Simulation of Oil Well Hole Cleaning: Effect of Mud Hydrodynamics on Cuttings Transport. Processes. 2024; 12(4):784. https://doi.org/10.3390/pr12040784
Chicago/Turabian StyleZakeri, Alireza, Mohammadreza Alizadeh Behjani, and Ali Hassanpour. 2024. "Fully Coupled CFD–DEM Simulation of Oil Well Hole Cleaning: Effect of Mud Hydrodynamics on Cuttings Transport" Processes 12, no. 4: 784. https://doi.org/10.3390/pr12040784
APA StyleZakeri, A., Alizadeh Behjani, M., & Hassanpour, A. (2024). Fully Coupled CFD–DEM Simulation of Oil Well Hole Cleaning: Effect of Mud Hydrodynamics on Cuttings Transport. Processes, 12(4), 784. https://doi.org/10.3390/pr12040784






